Echo-Enabled Harmonic Generation Studies for the FERMI Free-Electron Laser
Abstract
:1. Introduction
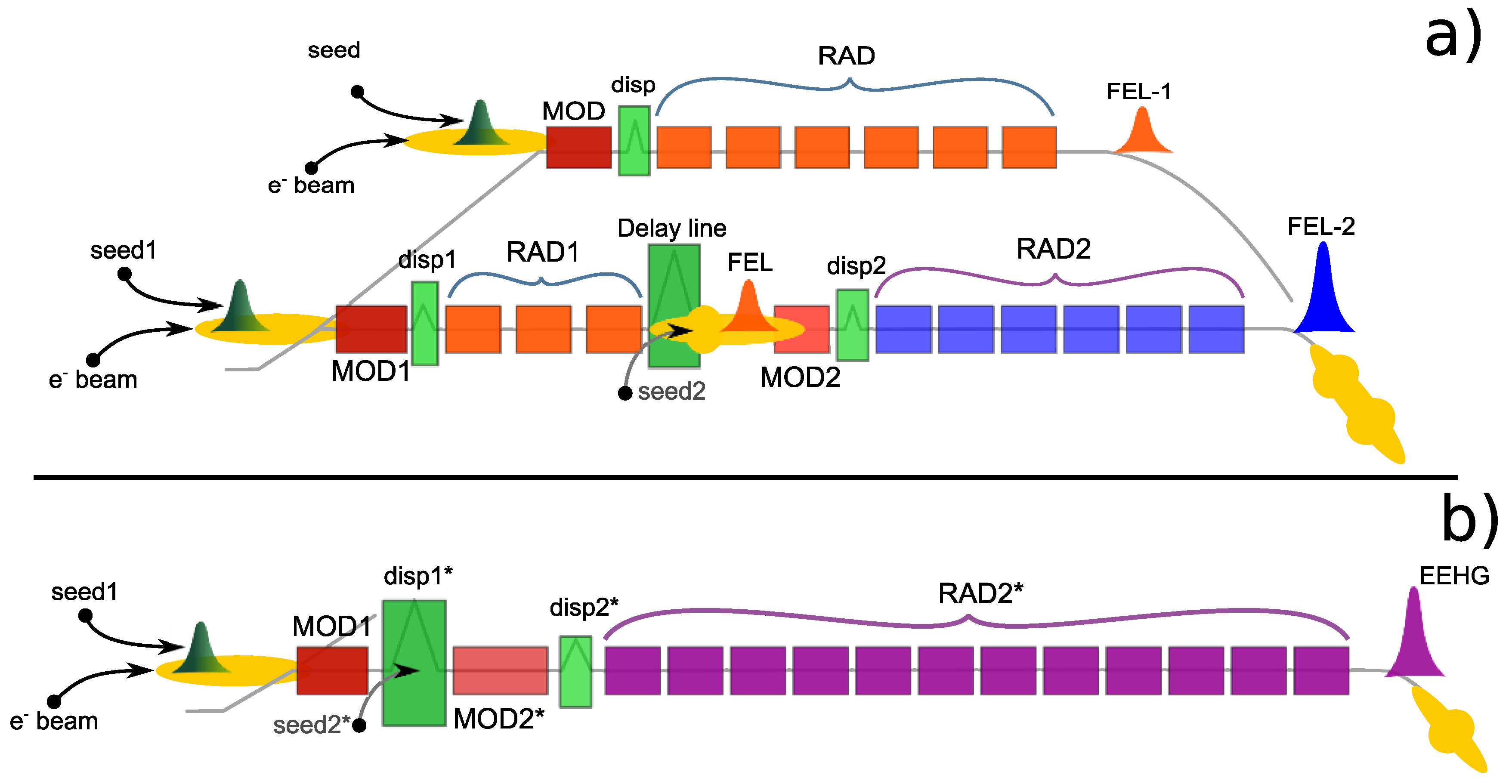
2. Layouts and Methods
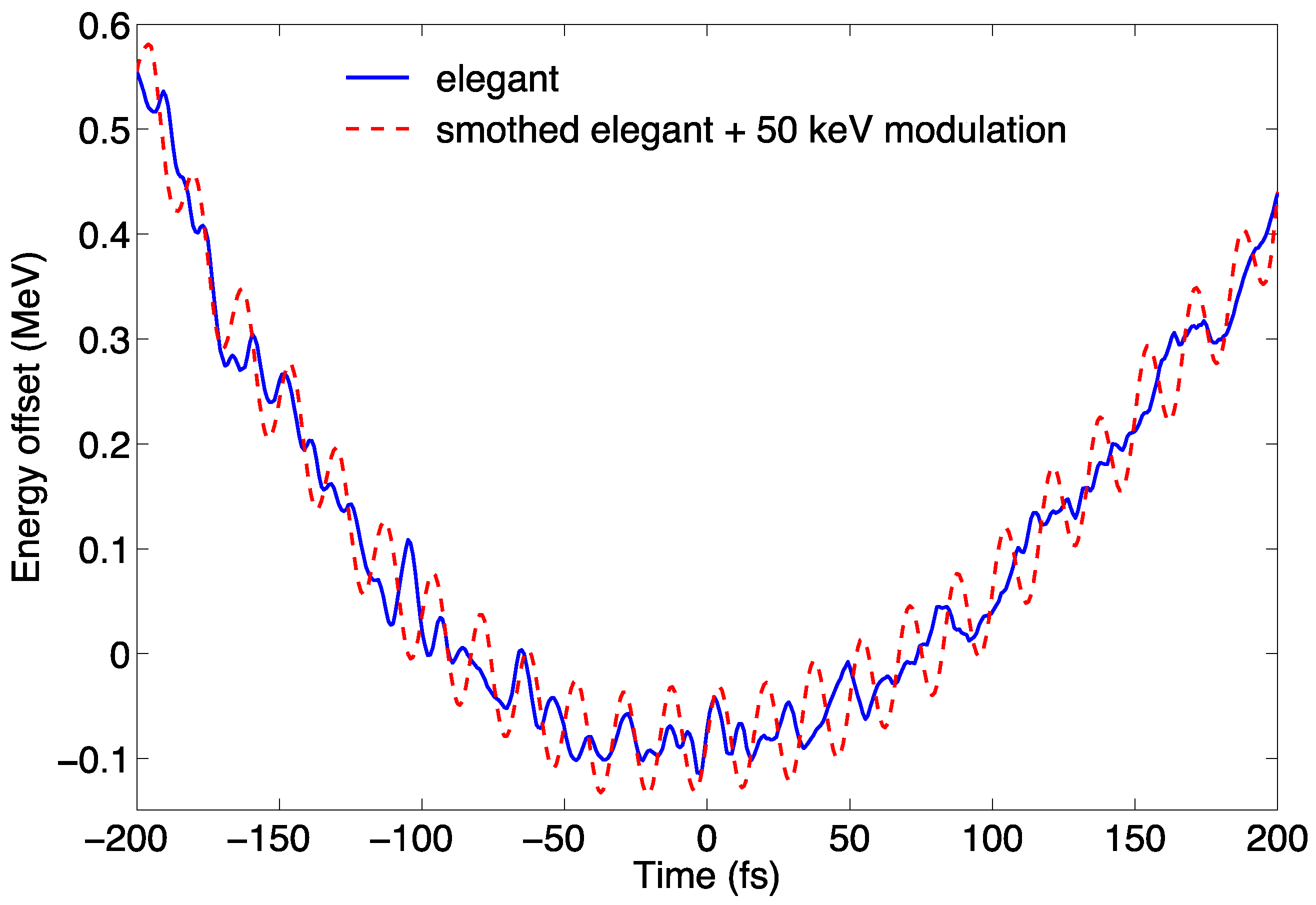
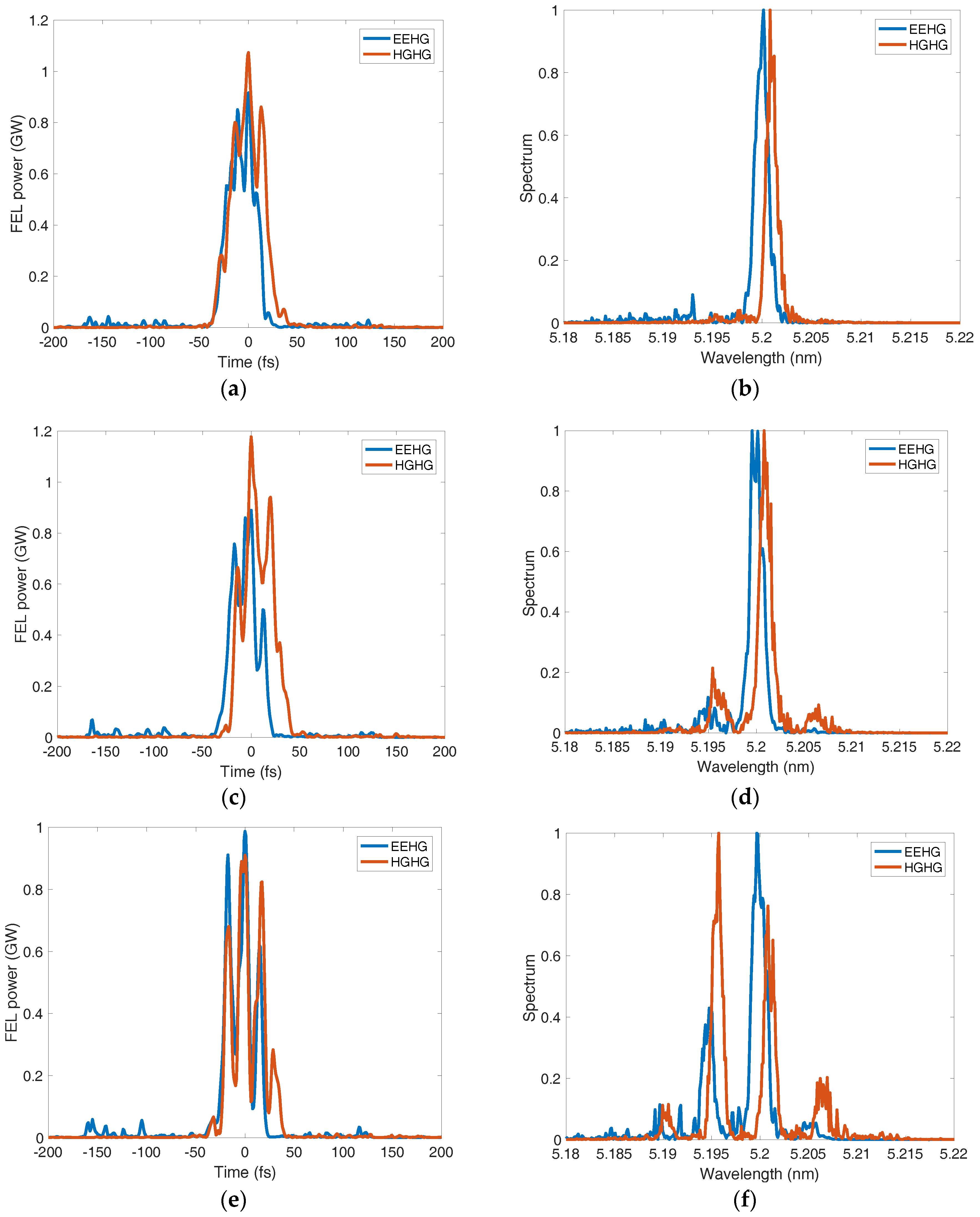
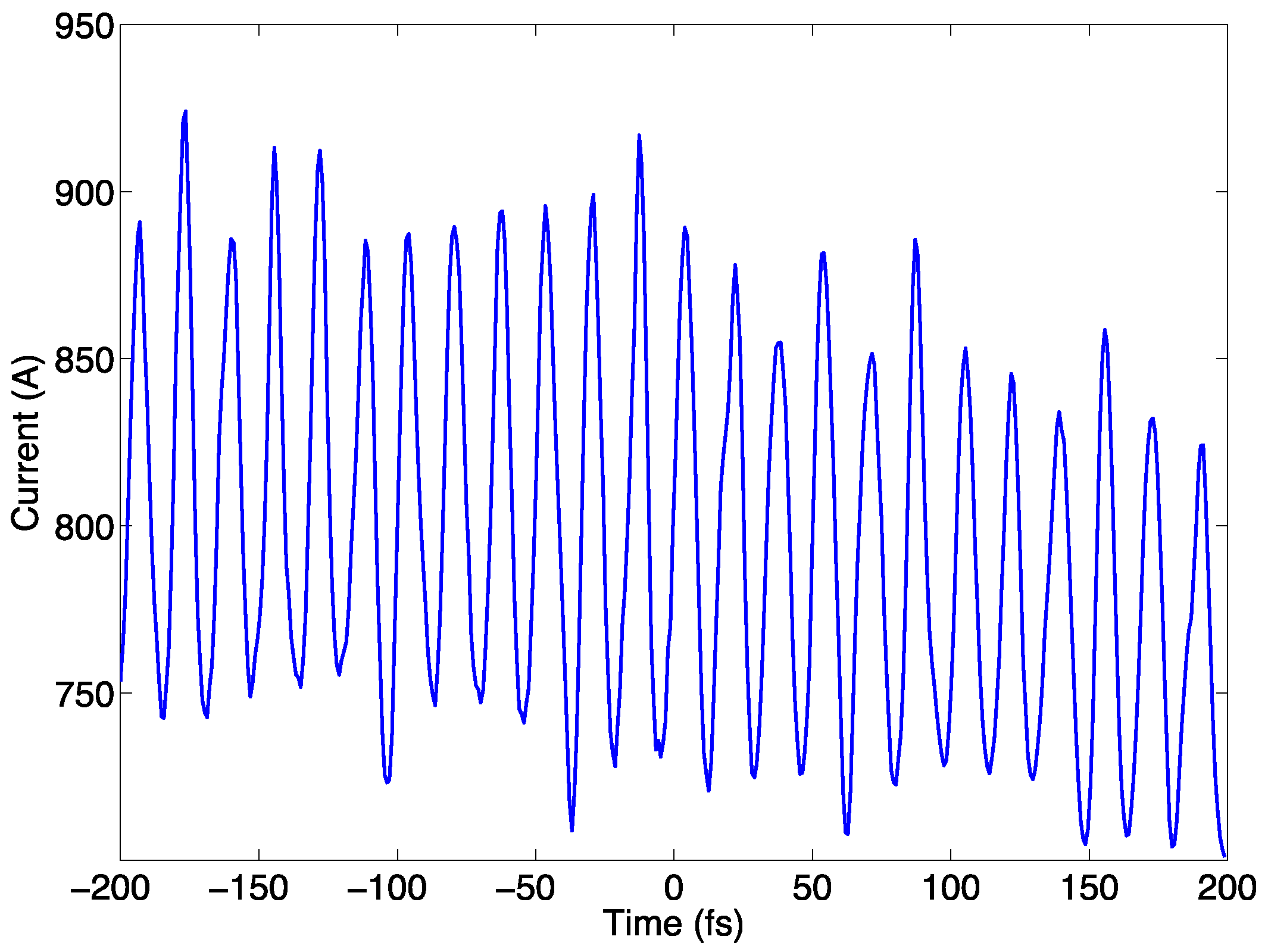
3. Results and Discussion
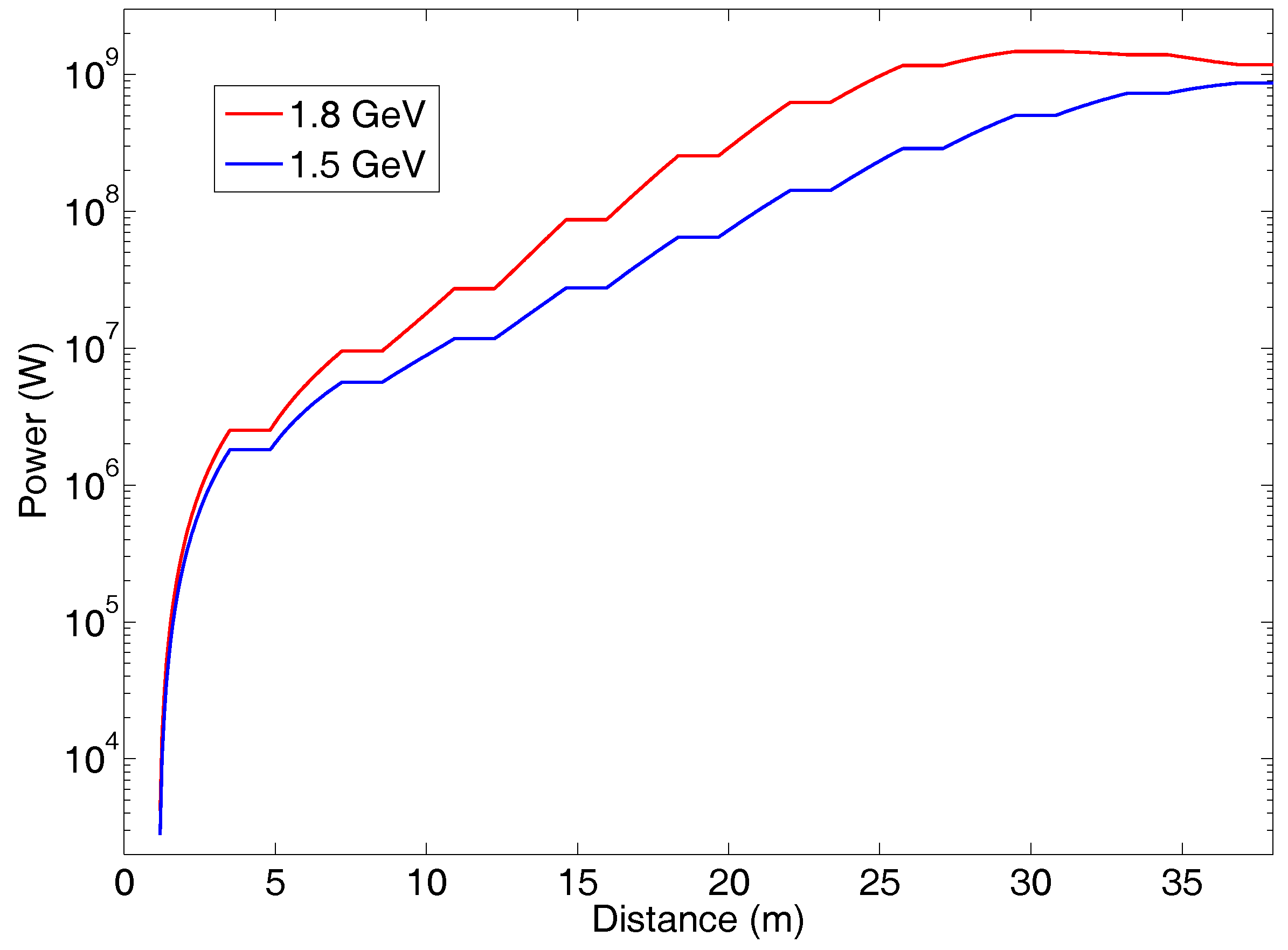
3.1. The 5.2 nm Case
3.2. The 3 nm Case
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chapman, H.N.; Barty, A.; Bogan, M.J.; Boutet, S.; Frank, M.; Hau-Riege, S.P.; Marchesini, S.; Woods, B.W.; Bajt, S.; Benner, W.H.; et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nat. Phys. 2006, 2, 839–843. [Google Scholar] [CrossRef]
- Seibert, M.M.; Ekeberg, T.; Maia, F.R.N.C.; Svenda, M.; Andreasson, J.; Jonsson, O.; Odic, D.; Iwan, B.; Rocker, A.; Westphal, D.; et al. Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 2011, 470, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Berrah, N.; Fang, L.; Murphy, B.; Osipov, T.; Ueda, K.; Kukk, E.; Feifel, R.; van der Meulen, P.; Salen, P.; Schmidt, H.T.; et al. Double-core-hole spectroscopy for chemical analysis with an intense X-ray femtosecond laser. Proc. Natl. Acad. Sci. USA 2011, 108, 16912–16915. [Google Scholar] [CrossRef] [PubMed]
- Ribic, P.R.; Margaritondo, G. Status and prospects of x-ray free-electron lasers (X-FELs): A simple presentation. J. Phys. Appl. Phys. 2012, 45, 213001. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bahr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photon. 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photon. 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photon. 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-angstrom region. Nat. Photon. 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Ferrari, E.; Spezzani, C.; Fortuna, F.; Delaunay, R.; Vidal, F.; Nikolov, I.; Cinquegrana, P.; Diviacco, B.; Gauthier, D.; Penco, G.; et al. Widely tunable two-colour seeded free-electron laser source for resonant-pump resonant-probe magnetic scattering. Nat. Commun. 2016, 7, 10343. [Google Scholar] [CrossRef] [PubMed]
- Bencivenga, F.; Cucini, R.; Capotondi, F.; Battistoni, A.; Mincigrucci, R.; Giangrisostomi, E.; Gessini, A.; Manfredda, M.; Nikolov, I.P.; Pedersoli, E.; et al. Four-wave mixing experiments with extreme ultraviolet transient gratings. Nature 2015, 520, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Prince, K.C.; Allaria, E.; Callegari, C.; Cucini, R.; De Ninno, G.; Di Mitri, S.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Coherent control with a short-wavelength free-electron laser. Nat. Photon. 2016, 10, 176–179. [Google Scholar] [CrossRef]
- Gauthier, D.; Ribič, P.R.; De Ninno, G.; Allaria, E.; Cinquegrana, P.; Danailov, M.B.; Demidovich, A.; Ferrari, E.; Giannessi, L. Generation of Phase-Locked Pulses from a Seeded Free-Electron Laser. Phys. Rev. Lett. 2016, 116, 24801. [Google Scholar] [CrossRef] [PubMed]
- Bonifacio, R.; Pellegrini, C.; Narducci, L.M. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.-J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat. Photon. 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Ratner, D.; Abela, R.; Amann, J.; Behrens, C.; Bohler, D.; Bouchard, G.; Bostedt, C.; Boyes, M.; Chow, K.; Cocco, D.; et al. Experimental Demonstration of a Soft X-Ray Self-Seeded Free-Electron Laser. Phys. Rev. Lett. 2015, 114, 54801. [Google Scholar] [CrossRef] [PubMed]
- Hara, T.; Inubushi, Y.; Katayama, T.; Sato, T.; Tanaka, H.; Tanaka, T.; Togashi, T.; Togawa, K.; Tono, K.; Yabashi, M.; et al. Two-colour hard X-ray free-electron laser with wide tunability. Nat. Commun. 2013, 4, 2919. [Google Scholar] [CrossRef] [PubMed]
- Marinelli, A.; Ratner, D.; Lutman, A.A.; Turner, J.; Welch, J.; Decker, F.-J.; Loos, H.; Behrens, C.; Gilevich, S.; Miahnahri, A.A.; et al. High-intensity double-pulse X-ray free-electron laser. Nat. Commun. 2015, 6, 6369. [Google Scholar] [CrossRef] [PubMed]
- Lutman, A.A.; Maxwell, T.J.; MacArthur, J.P.; Guetg, M.W.; Berrah, N.; Coffee, R.N.; Ding, Y.; Huang, Z.; Marinelli, A.; Moeller, S.; et al. Fresh-slice multicolour X-ray free-electron lasers. Nat. Photon. 2016, 10, 745–750. [Google Scholar] [CrossRef]
- Lambert, G.; Hara, T.; Garzella, D.; Tanikawa, T.; Labat, M.; Carre, B.; Kitamura, H.; Shintake, T.; Bougeard, M.; Inoue, S.; et al. Injection of harmonics generated in gas in a free-electron laser providing intense and coherent extreme-ultraviolet light. Nat. Phys. 2008, 4, 296–300. [Google Scholar] [CrossRef]
- Togashi, T.; Takahashi, E.J.; Midorikawa, K.; Aoyama, M.; Yamakawa, K.; Sato, T.; Iwasaki, A.; Owada, S.; Okino, T.; Yamanouchi, K.; et al. Extreme ultraviolet free electron laser seeded with high-order harmonic of Ti. Opt. Express 2011, 19, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, S.; Azima, A.; Bajt, S.; Bödewadt, J.; Curbis, F.; Dachraoui, H.; Delsim-Hashemi, H.; Drescher, M.; Düsterer, S.; Faatz, B.; et al. Generation of Coherent 19- and 38-nm Radiation at a Free-Electron Laser Directly Seeded at 38 nm. Phys. Rev. Lett. 2013, 111, 114801. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.H. Generation of intense UV radiation by subharmonically seeded single-pass free-electron lasers. Phys. Rev. A 1991, 44, 5178–5193. [Google Scholar] [CrossRef] [PubMed]
- De Ninno, G.; Gauthier, D.; Mahieu, B.; Ribič, P.R.; Allaria, E.; Cinquegrana, P.; Danailov, M.B.; Demidovich, A.; Ferrari, E.; Giannessi, L.; et al. Single-shot spectro-temporal characterization of XUV pulses from a seeded free-electron laser. Nat. Commun. 2015, 6, 8075. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, D.; Ribič, P.R.; De Ninno, G.; Allaria, E.; Cinquegrana, P.; Danailov, M.B.; Demidovich, A.; Ferrari, E.; Giannessi, L.; Mahieu, B.; et al. Spectrotemporal Shaping of Seeded Free-Electron Laser Pulses. Phys. Rev. Lett. 2015, 115, 114801. [Google Scholar] [CrossRef] [PubMed]
- Ribič, P.R.; Gauthier, D.; De Ninno, G. Generation of Coherent Extreme-Ultraviolet Radiation Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2014, 112, 203602. [Google Scholar] [CrossRef]
- De Ninno, G.; Mahieu, B.; Allaria, E.; Giannessi, L.; Spampinati, S. Chirped Seeded Free-Electron Lasers: Self-Standing Light Sources for Two-Color Pump-Probe Experiments. Phys. Rev. Lett. 2013, 110, 64801. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Bencivenga, F.; Borghes, R.; Capotondi, F.; Castronovo, D.; Charalambous, P.; Cinquegrana, P.; Danailov, M.B.; De Ninno, G.; Demidovich, A.; et al. Two-colour pump–probe experiments with a twin-pulse-seed extreme ultraviolet free-electron laser. Nat. Commun. 2013, 4, 2476. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.-H.; Ben-Zvi, I. High-gain harmonic generation of soft X-rays with the “fresh bunch” technique. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 393, 96–99. [Google Scholar] [CrossRef]
- Penn, G. Stable, coherent free-electron laser pulses using echo-enabled harmonic generation. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 110707. [Google Scholar] [CrossRef]
- Stupakov, G. Using the Beam-Echo Effect for Generation of Short-Wavelength Radiation. Phys. Rev. Lett. 2009, 102, 74801. [Google Scholar] [CrossRef] [PubMed]
- Xiang, D.; Stupakov, G. Echo-enabled harmonic generation free electron laser. Phys. Rev. Spec. Top. Accel. Beams 2009, 12, 30702. [Google Scholar] [CrossRef]
- Hemsing, E.; Dunning, M.; Garcia, B.; Hast, C.; Raubenheimer, T.; Stupakov, G.; Xiang, D. Echo-enabled harmonics up to the 75th order from precisely tailored electron beams. Nat. Photon. 2016, 10, 512–515. [Google Scholar] [CrossRef]
- Allaria, E.; Castronovo, D.; Cinquegrana, P.; Craievich, P.; Dal Forno, M.; Danailov, M.B.; D’Auria, G.; Demidovich, A.; De Ninno, G.; Di Mitri, S.; et al. Two-stage seeded soft-X-ray free-electron laser. Nat. Photon. 2013, 7, 913–918. [Google Scholar] [CrossRef]
- Allaria, E.; De Ninno, G.; Xiang, D. Feasibility studies for single stage echo-enabled harmonic in FERMI FEL-2. In Proceedings of FEL2009, Liverpool, UK, 23–28 August 2009.
- Borland, M.; Chae, Y.C.; Emma, P.; Lewellen, J.W.; Bharadwaj, V.; Fawley, W.M.; Krejcik, P.; Limborg, C.; Milton, S.V.; Nuhn, H.-D.; et al. Start-to-end simulation of self-amplified spontaneous emission free electron lasers from the gun through the undulator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 483, 268–272. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Klystron instability of a relativistic electron beam in a bunch compressor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 490, 1–8. [Google Scholar] [CrossRef]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Longitudinal space charge-driven microbunching instability in the TESLA Test Facility linac. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 528, 355–359. [Google Scholar] [CrossRef]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Fawley, W.M. A User Manual for GINGER and Its Post-Processor XPLOTGIN; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2004. [Google Scholar]
- Borland, M. Elegant: A Flexible SDDS-Compliant Code for Accelerator Simulation; Argonne National Lab.: Lemont, IL, USA, 2000. [Google Scholar]
- De Loos, M.J.; van der Geer, S.B. General Particle Tracer: A new 3D code for accelerator and beamline design. In Proceedings of the 5th European Particle Accelerator Conference, Sitges, Spain, 10–14 Junuary 1996; p. 1241.
- Roussel, E.; Ferrari, E.; Allaria, E.; Penco, G.; Di Mitri, S.; Veronese, M.; Danailov, M.; Gauthier, D.; Giannessi, L. Multicolor High-Gain Free-Electron Laser Driven by Seeded Microbunching Instability. Phys. Rev. Lett. 2015, 115, 214801. [Google Scholar] [CrossRef] [PubMed]
- Spampinati, S.; Allaria, E.; Badano, L.; Bassanese, S.; Biedron, S.; Castronovo, D.; Craievich, P.; Danailov, M.B.; Demidovich, A.; De Ninno, G.; et al. Laser heater commissioning at an externally seeded free-electron laser. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 120705. [Google Scholar] [CrossRef]
- Penn, G.; Lawrence Berkeley National Laboratory, Berkeley, CA, USA. Private Communication, 2016.
- Borland, M. Modeling of the microbunching instability. Phys. Rev. Spec. Top. Accel. Beams 2008, 11, 30701. [Google Scholar] [CrossRef]
- Giannessi, L.; Elettra-Sincrotrone Trieste, Trieste, Italy. Private Communication, 2016.
- Ratner, D.; Fry, A.; Stupakov, G.; White, W. Laser phase errors in seeded free electron lasers. Phys. Rev. Spec. Top. Accel. Beams 2012, 15, 30702. [Google Scholar] [CrossRef]
- Zhao, Z.T.; Wang, D.; Chen, J.H.; Chen, Z.H.; Deng, H.X.; Ding, J.G.; Feng, C.; Gu, Q.; Huang, M.M.; Lan, T.H.; et al. First lasing of an echo-enabled harmonic generation free-electron laser. Nat. Photon. 2012, 6, 360–363. [Google Scholar] [CrossRef]
- Hemsing, E.; Dunning, M.; Hast, C.; Raubenheimer, T.O.; Weathersby, S.; Xiang, D. Highly coherent vacuum ultraviolet radiation at the 15th harmonic with echo-enabled harmonic generation technique. Phys. Rev. Spec. Top. Accel. Beams 2014, 17, 70702. [Google Scholar] [CrossRef]
- Huang, Z.; Kim, K.-J. Review of x-ray free-electron laser theory. Phys. Rev. Spec. Top. Accel. Beams 2007, 10, 34801. [Google Scholar] [CrossRef]
- Zhang, Z.; Lindberg, R.; Fawley, W.M.; Huang, Z.; Krzywinski, J.; Lutman, A.; Marcus, G.; Marinelli, A. Microbunching-instability-induced sidebands in a seeded free-electron laser. Phys. Rev. Accel. Beams 2016, 19, 50701. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E. Bunching coefficients in echo-enabled harmonic generation. Phys. Rev. Spec. Top. Accel. Beams 2013, 16, 70702. [Google Scholar] [CrossRef]
| Parameter | Nominal Configuration | Advanced Configuration |
|---|---|---|
| e-beam peak current I (A) | 700 | 1000 |
| e-beam energy E (GeV) | 1.4 | 1.8 |
| slice energy spread σE (keV) | 150 | 250 |
| emittance ε (mm mrad) | 1 | 1 |
| e-beam size (μm) | 70 | 70 |
| 1st R56 (mm) | 2.1 | 8 |
| 2nd R56 (μm) | 74 | 85 |
| 1st seed peak power (MW) | 10.7 | 10.7 |
| 1st energy modulation (keV) | 450 | 450 |
| 2nd seed peak power (MW) | 135 | 151 |
| 2nd energy modulation (keV) | 824 | 868 |
| Parameter | Current | Modified |
|---|---|---|
| 2nd modulator period (mm) | 55 | 110 |
| 2nd modulator length (m) | 2.42 | 1.54 |
| delay line R56 (mm) | 1 | 2.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rebernik Ribič, P.; Roussel, E.; Penn, G.; De Ninno, G.; Giannessi, L.; Penco, G.; Allaria, E. Echo-Enabled Harmonic Generation Studies for the FERMI Free-Electron Laser. Photonics 2017, 4, 19. https://doi.org/10.3390/photonics4010019
Rebernik Ribič P, Roussel E, Penn G, De Ninno G, Giannessi L, Penco G, Allaria E. Echo-Enabled Harmonic Generation Studies for the FERMI Free-Electron Laser. Photonics. 2017; 4(1):19. https://doi.org/10.3390/photonics4010019
Chicago/Turabian StyleRebernik Ribič, Primož, Eléonore Roussel, Gregory Penn, Giovanni De Ninno, Luca Giannessi, Giuseppe Penco, and Enrico Allaria. 2017. "Echo-Enabled Harmonic Generation Studies for the FERMI Free-Electron Laser" Photonics 4, no. 1: 19. https://doi.org/10.3390/photonics4010019
APA StyleRebernik Ribič, P., Roussel, E., Penn, G., De Ninno, G., Giannessi, L., Penco, G., & Allaria, E. (2017). Echo-Enabled Harmonic Generation Studies for the FERMI Free-Electron Laser. Photonics, 4(1), 19. https://doi.org/10.3390/photonics4010019






