1. Introduction
Quantum cascade lasers (QCLs) are high-power light-emitting sources in the midinfrared (mid-IR) and THz parts of the electromagnetic spectrum. They are electrically driven, unipolar semiconductor devices that achieve population inversion based on quantum confinement and tunneling [
1]. The use of different III-V semiconductors and their alloys enables great flexibility in the design of the QCL active region. Widespread commercial applications of QCLs, especially in portable sensing, require mid-IR QCL operation that is at room-temperature (RT), continuous-wave (CW), with watt-level power and high wall-plug efficiency (WPE, the fraction of power converted to light) [
2,
3,
4] and the structures have to be reliable long-term under these high-power CW operating conditions. In recent years, great advances have been made in mid-IR QCLs [
3,
5,
6] using the InGaAs/InAlAs material system on the InP substrate, especially within the first atmospheric window (3–5
m). Room-temperature, continuous-wave lasing has been demonstrated throughout this wavelength range: 5.1 W power with 21% WPE at
m [
7], 2.5 W with 12.5% WPE [
8] and 3 W with 12.7% WPE at
m [
9], and watt-level powers with a WPE of 6% at
m [
10]. At shorter wavelengths, RT CW operation has also been achieved, but with lower powers: 400 mW at 3.4–3.55
m [
11] and mW power at 3–3.2
m [
12].
While good operating powers and WPEs have been achieved in devices close to
m wavelengths, long-term reliable RT CW operation at high powers (in excess of a few hundred mW) remains a challenge due to high thermal stress [
13,
14] that is worst in short-wavelength devices that have high strain and high thermal impedance mismatch between layers [
10,
11,
15,
16]. In addition to improved device longevity, what is needed is better CW temperature performance, with weaker temperature dependencies of the threshold current density
, with
being the characteristic temperature, and of the differential quantum efficiency
, also known as the slope efficiency, with a characteristic temperature
[
14]. Recently, deep-well structures with tapered-barrier active regions have demonstrated significant improvements in the
and
values with respect to those in the conventional
m device [
8], underscoring that suppression of leakage paths plays a key role in temperature performance [
4,
14,
17]. However, the microscopic mechanisms and leakage pathways that contribute to these empirical performance parameters remain unclear.
Detailed transport simulation can offer insights into the microscopic physics of QCL operation [
18]. Electron transport in GaAs-based quantum cascade lasers in both mid-IR and THz regimes has been successfully simulated via semiclassical (rate equations [
19,
20,
21] and Monte Carlo [
22,
23,
24,
25]) and quantum techniques (density matrix [
26,
27,
28,
29,
30], nonequilibrium Green’s functions (NEGF) [
31], and lately Wigner functions [
32]). InP-based mid-IR QCLs have been addressed via semiclassical [
33] and quantum transport approaches (8.5-
m [
34] and 4.6-
m [
35,
36] devices). Short-wavelength structures [
8] have very thin wells and barriers, so coherent transport in them has pronounced coherent features, which cannot be addressed semiclassically. While NEGF simulations [
35,
36] accurately and comprehensively capture quantum transport in these devices, they are computationally demanding. Density-matrix approaches offer a good compromise: they have considerably lower computational overhead than NEGF but are still capable of describing coherent-transport features. Unfortunately, density-matrix techniques commonly employ phenomenological dephasing times [
27,
30,
34,
37].
In this paper, we provide a quantum-transport simulation of the 4.6-
m InP-based QCL by Bai
et al. [
8]. The simulation stems from a recently developed density-matrix theoretical formalism based on a completely positive Markovian master equation [
32], which rigorously captures quantum transport between quasibound states, with full account of tunneling as well as scattering processes. The technique accurately treats decoherence and dephasing, thus removing the need for phenomenological dephasing times. We show that the simulated current density-field curves, population inversion, and emitted wavelength all show very good agreement with experiment, provided that one accounts for the barrier-height variation with barrier thickness (thin barriers do not have full height) and incorporates the interplay between strain and mass disparity among layers via a slowly spatially varying effective mass. We also calculate the
value and the subband electronic temperatures, and demonstrate the importance of coherent tunneling transport for describing the injection process.
3. Results
The device we consider is the
-μm (270-meV) QCL proposed in [
8], with additional information given in [
39]. The authors used a buried ridge design to obtain
W of emitted power and a wall-plug efficiency of
at room temperature in continuous-wave operation. The QCL core is based on a heterostructure design with potential wells made from In
Ga
As and potential barriers made from In
Al
As.
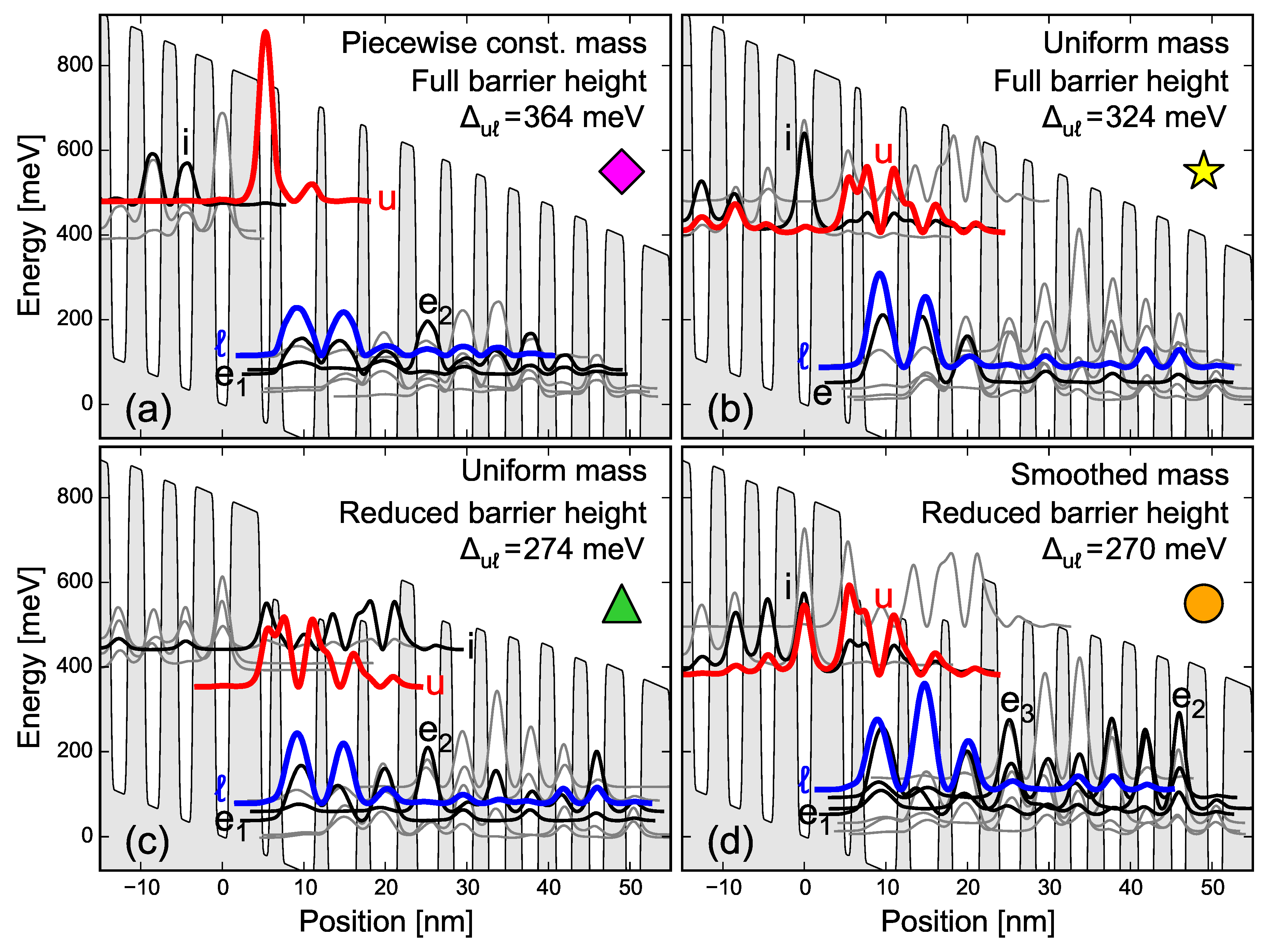
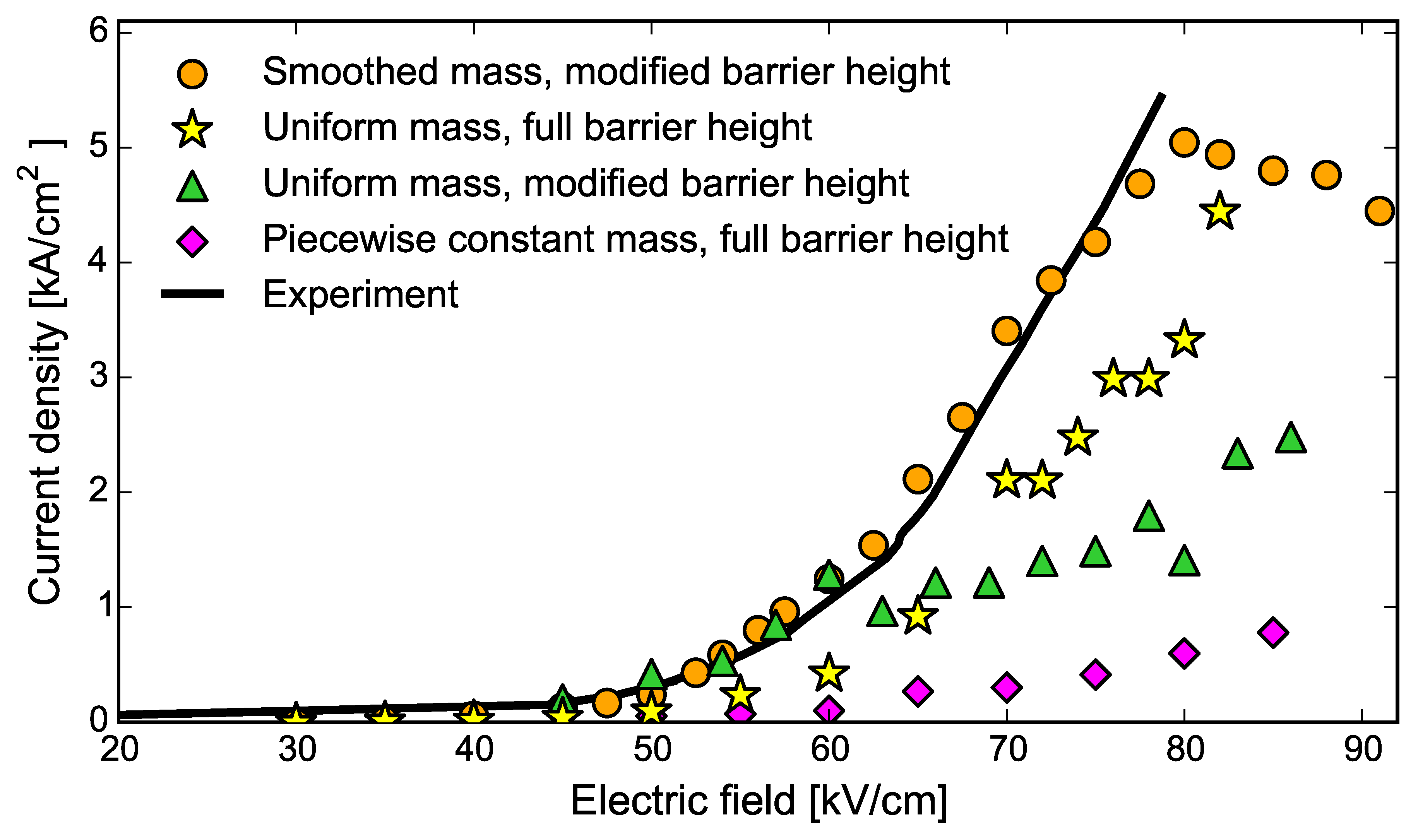
Figure 1 shows the sensitivity of the band structure to the effective mass and to the barrier height in the active region, where several thin barriers are found. The corresponding current density
versus field (
) curves are presented in
Figure 2 and illustrate how the effective mass and barrier height choice would manifest in these experimentally accessible characteristics. We now analyze this data in detail.
Figure 1a shows the calculated band structure at the design electric field (82 kV/cm) using a piecewise-constant effective mass (the effective mass changes abruptly at well/barrier interfaces). The well and barrier materials have effective masses of
and
of the electron rest mass, respectively (barrier effective mass is obtained by linear interpolation between AlAs and InAs). The conduction band discontinuity between the two materials has been estimated to be approximately 800 meV [
39]. The most striking feature in
Figure 1a is that we obtain an energy difference
meV between the upper (u) and lower (
ℓ) lasing level, which is
higher than the experimentally observed value of 270 meV. There is very little overlap between the injector states and the upper lasing level, resulting in inefficient injection. These shortcomings are reflected in the
curve in
Figure 2 (purple diamonds), where the room-temperature current density is about 10 times lower than in experiment and we do not observe population inversion in transport simulations. It is clear that modeling the effective mass as piecewise-constant does not give satisfactory results. However, this approach has been used successfully to describe GaAs/AlGaAs-based devices [
32] as well as devices based on lattice-matched InGaAs/InAlAs [
34]. A possible explanation is that in the cases of GaAs/Al
Ga
As and lattice-matched InGaAs/InAlAs, the difference in effective masses is smaller. For example, the ratio of the effective masses in Al
Ga
As and GaAs is about
, while the ratio is about
for lattice-matched InGaAs/InAlAs. On the other hand, the ratio of the effective masses of In
Al
As and In
Ga
As is about
. Another aspect is that the considered structure is highly strained, which affects effective mass.
Figure 1b shows the band structure calculated assuming a uniform effective mass, given by the weighted average of the well and barrier effective masses; the weight of well (barrier) mass is the total thickness of wells (barriers) in a stage divided by the stage length. We can see that the band structure is much more favorable to lasing, with an injector state that efficiently injects into the upper lasing level. The corresponding
curve in
Figure 2 (yellow stars) has a fairly good agreement with experiments, and we observe a population inversion in transport simulations. However, the calculated energy seperation between the upper and lower lasing levels at the design field of 82 kV/cm is 324 meV, about
higher than in experiments.
The energy of the upper lasing level is very sensitive to the height of the potential barriers in the active region (the three barriers to the right of the injector barrier) because the upper lasing level has a high amplitude in the classically forbidden region inside the barriers. These barriers are only several monolayers thick (
–
nm), and it is plausible that they do not reach the bulk value of the conduction band discontinuity (800 meV).
Figure 1c shows the calculated band structure assuming a uniform effective mass and a barrier height
V that depends on the barrier thickness
W as
where
meV is the full barrier height and
nm, which is between three and four monolayers. This specific value of
was chosen because it gives an energy difference
meV at the design electric field, which is within
of the experimentally observed value of 270 meV. However, using this approach, the injector state cannot inject efficiently into the upper lasing level, the calculated current density shown in
Figure 2 (green triangles) is three times lower than in experiment, and we do not observe a population inversion between the upper and lower lasing levels in transport simulations.
Figure 1d shows the calculated band structure with the thickness-dependent barrier height (Equation (
3), as in
Figure 1c), but with a middle ground between uniform and piecewise-constant mass: we assume a position-dependent effective mass, given by
where
is a piecewise-constant effective mass and
σ is a smoothing length. The smoothing length affects the relative energy difference between the injector state and the upper lasing level. A smoothing length of
σ = 8 nm results in the best alignment between these two states at the predicted design electric field [
8]. Smoothing qualitatively captures the effects of strain and barrier thinness on the effective mass. With a smoothed mass, an electron is heavier in the injector, where the InAlAs barriers (with higher bulk mass) dominate, and lighter in the active region, with more InGaAs wells (regions with lower bulk mass). By smoothing the mass, the states localized in the injector (where electrons are now heavier, and energies roughly follow
) are lowered and brought into alignment with the upper lasing level, without the energy difference
being considerably affected. From the band structure in
Figure 1d, we can see that the lasing energy is within 1 meV of the experimentally observed value and the overlap between the upper lasing level and the injection level is favorable for efficient injection. The simulated room-temperature
curve in
Figure 2 (orange circles) shows excellent agreement with experiment.
The approximations of a smoothed, position-dependent effective mass and barrier-height reduction in very thin layers are intuitively plausible: they capture the fact that properties that characterize bulk materials, such as the effective masses and band offsets, cannot be guaranteed to hold within layers that are only 3–4 monolayers thick. Further experimental studies are needed to benchmark the degree of energy barrier lowering in thin layers.
We note that an energy-dependent effective mass has been been employed previously to calculate the band structure and transport in QCLs [
33,
36,
40,
41], but this is not a viable option within our approach. An energy-dependent effective mass makes the Schrödinger Equation (
2) effectively a nonlinear eigenvalue problem [
40,
41], so the eigenstates associated with different energies are no longer guaranteed to be orthogonal. However, orthogonality of the eigenstates is an absolutely critical property in the derivation of the master equation for the density matrix, specifically in the derivation of the dissipative term [
32,
38,
42]. With a nonorthonormal eigenbasis of the Hamiltonian without scattering, the positivity of the density matrix upon evolution according to a master equation would no longer be guaranteed, which can lead to unphysical behavior. This further justifies the approximation of a smoothed, position-dependent effective mass within the presented approach.
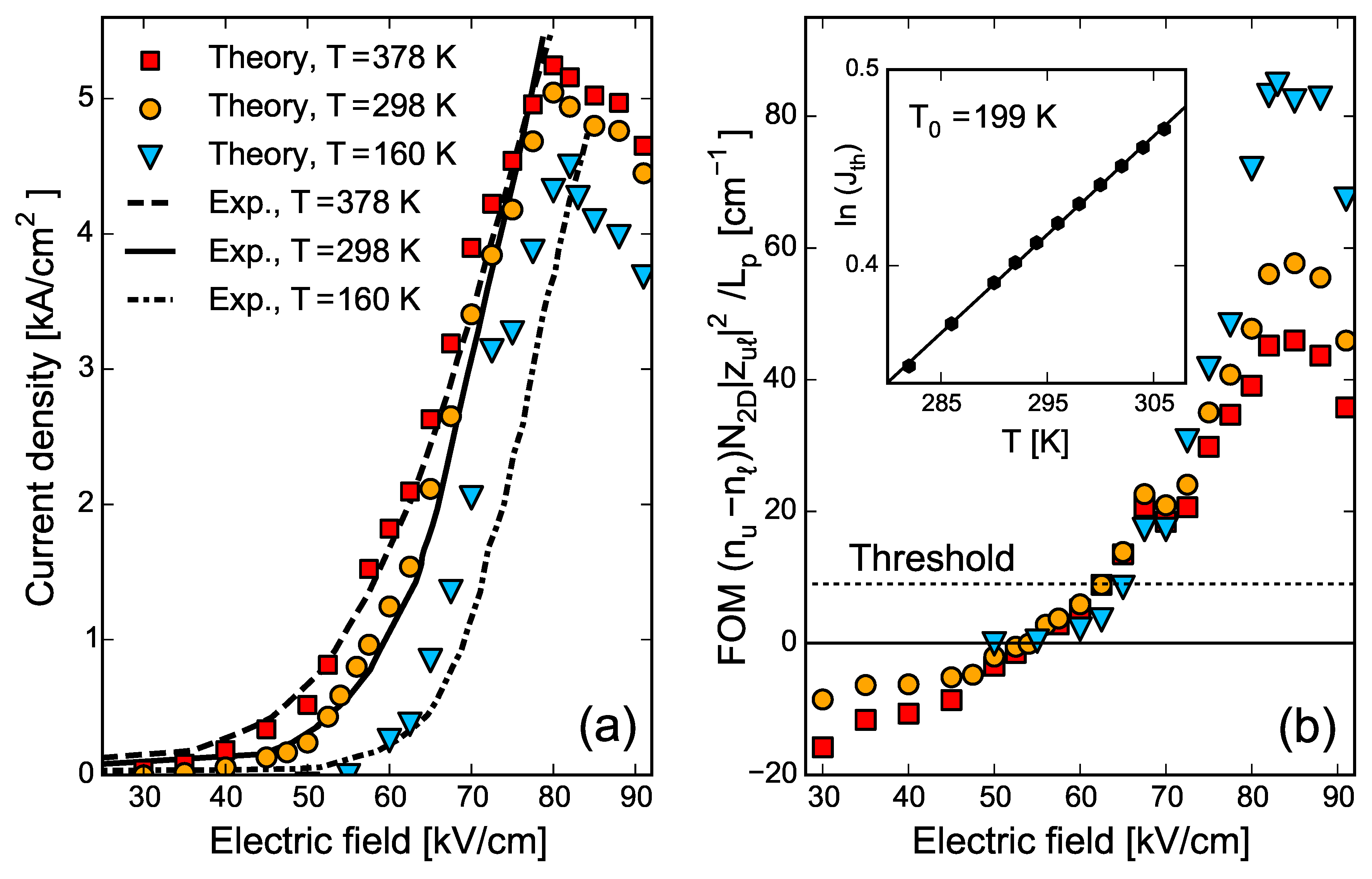
Figure 3a shows a comparison between the calculated current density and experiment at different temperatures. All calculations henceforth have a smoothed effective mass and modified barriers heights, as in
Figure 1, and assume a temperature equal to the experimental heat-sink temperature (in reality, some lattice heating takes place). We obtain very good agreement with measured current density at 298 K and 378 K; however, the calculation somewhat overestimates the current density at 160 K. The difference between theory and experiment at low temperatures can be explained by the increased relative importance of interface roughness, alloy, and impurity scattering (not included in our model) at low temperatures.
Figure 3b shows the figure of merit (FOM), given by Equation (
1d),
versus field at different temperatures. For temperatures of 298 k and 378 K, the largest FOM is reached for the field strength of 85 kV/cm, which is in the negative differential resistance (NDR) region and beyond the maximum experimental field strength. However, at a temperature of 160 K, the onset of NDR is shifted to higher fields (83 kV/cm) and experimental results are provided up to
kV/cm, reaching the field strength of maximum predicted gain. This result could be a factor in the much greater device performance at 160 K, where emitted power of
W was measured, compared with
W at room temperature [
8].
The considered device was reported to have a threshold current density
kA/cm
at room temperature (298 K) [
8]. A comparison between
Figure 3a,b shows that this value of current density corresponds to a field of
kV/cm and a
cm
, which is close to the onset of population inversion (54 kV/cm). Note that the FOM is not modal gain; it is proportional to modal gain, with a proportionality constant that is weakly temperature dependent. We therefore define
cm
as a criterion for the onset of lasing. Then, we calculate the threshold current density
as the current corresponding to the field that yields
, which enables us to compute
for temperatures around 298 K. The calculated temperature variation follows
, as depicted in the inset to
Figure 3b, which shows
vs. T near room temperature. The slope of the best linear fit yields
K; the experiment gives 143 K. The discrepancy between between experiment and theory can be attributed to the omission of alloy, interface, and impurity scattering, and to lack of nonequilibrium phonons [
25]. We note that a prior study [
43] of the structure in [
8], which employed rate equations, the effect of elastic scattering on lifetimes and electroluminescence linewidth, and upper-level electronic temperatures based on Vitiello
et al.’s [
44] measurement of the electron-lattice coupling constant on 4.8-
m-emitting conventional QCL, gave a
value of 167 K.
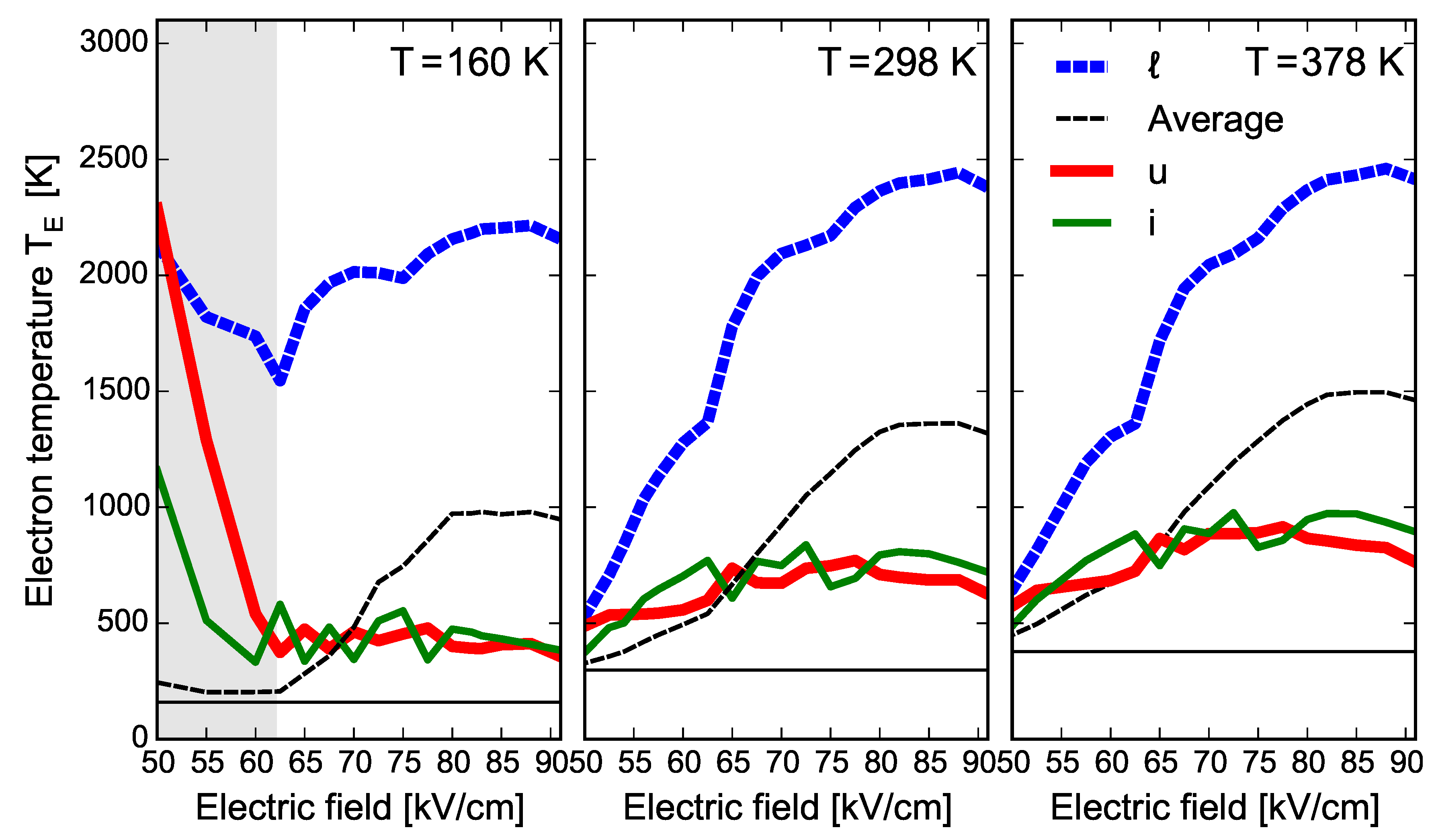
Figure 4 shows the subband electron temperatures (measuring the average in-plane kinetic energy of electrons in a subband, Equation (
1e)) in the injector, upper lasing, and lower lasing levels, as a function of electric field for lattice temperatures of 160 K (left), 298 K (middle), and 378 K (right). Also shown is the weighted average electron temperature for a stage, with subband occupations acting as weights. Significant electron heating takes place: the weighted average electron temperature around the design field (
kV/cm) is between 1000 and 1500 K. The injector and upper lasing levels are cooler than average, with electron temperatures between 400 K and 1000 K around the design field. These high electron temperatures in the upper lasing state will increase carrier leakage and impact the
value [
43]. The lower lasing level is considerably hotter than average, with electron temperatures in the range 2200 to 2400 K; the extractor states (not shown) have comparable temperatures to the lower lasing level. The high electron temperature in the lower lasing level is intuitively plausible: this level is populated by electrons that scattered from the upper to the lower lasing level and thus possess approximately 240 meV of excess kinetic energy (240 meV corresponds to a temperature of
K) [
45].
The low-field trends at 160 K differ from higher lattice temperatures because the upper and injector states have practically no occupation, so their electronic temperature calculated as the subband ensemble average of kinetic energy is not meaningful; this is implied by the boxed gray region in the left panel. The (meaningless) high temperature comes from the very few electrons that scatter into the two states and scatter out quickly, before they have enough time to thermalize. At low lattice temperature and field, practically all the electrons ( 95%) are in the lowest energy state in the injector (not shown in
Figure 4). This state is “cold” and, because of its high occupation, it determines the average electron temperature for all subbands, which is why the average electron temperature is lower than those of u,
ℓ, and i. However, at higher lattice temperatures, electrons can access u and i from from the injector ground state via polar optical phonon absorption; the population of these subbands becomes appreciable and the electron temperature becomes a more meaningful measure of the average electron energy in these subbands.
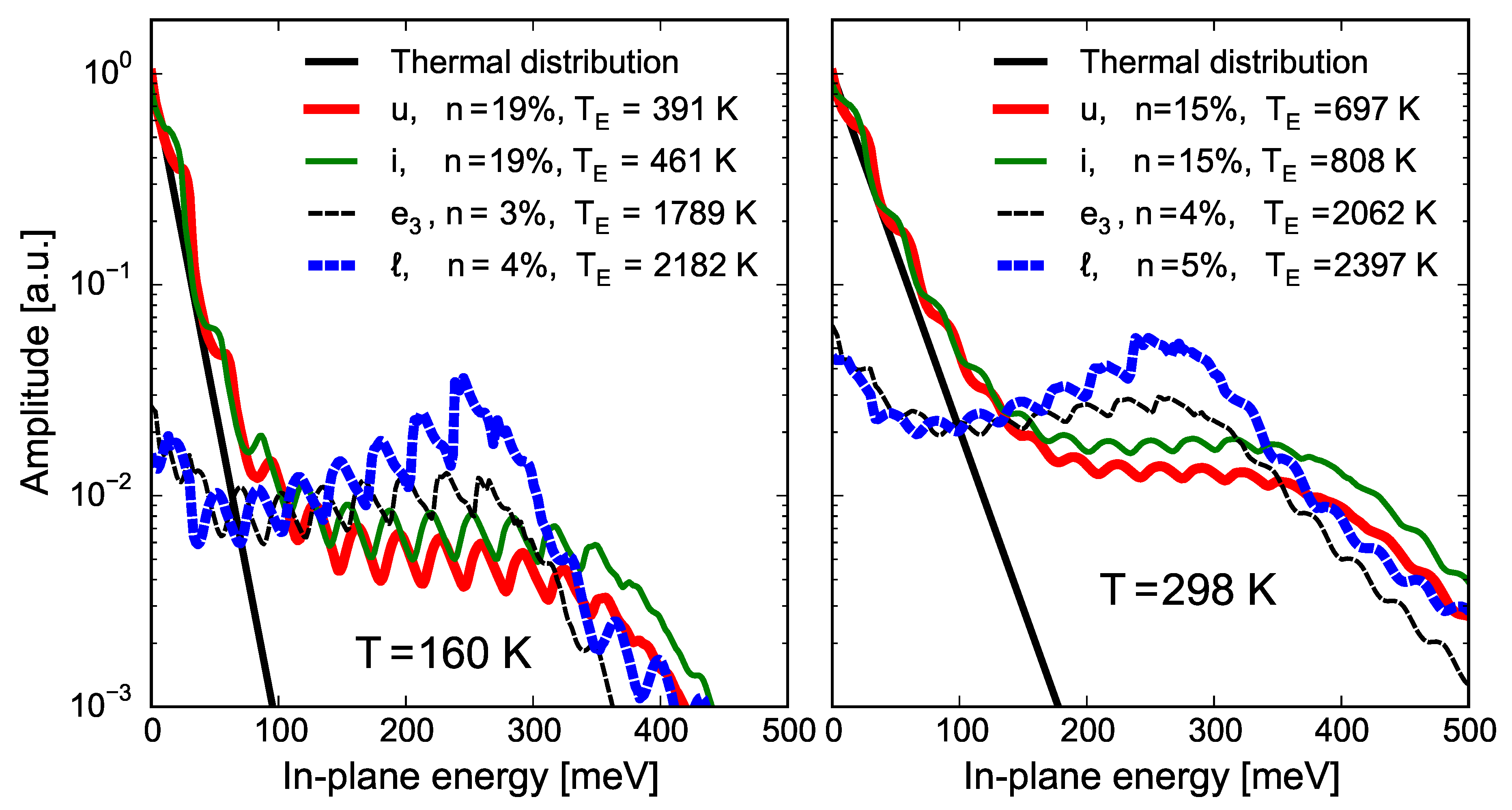
Figure 5 shows the in-plane energy distribution for different subbands at a field strength of 82 kV/cm, for lattice temperatures of 160 K (left panel) and 298 K (right panel). Nonthermal electron distributions have been obtained previously using both semiclassical and quantum transport approaches for various QCL structures in the mid-IR [
25,
33,
46,
47]. The in-plane distributions for the injector and upper lasing levels have similar shapes: at low energies (0–100 meV), both distributions are well described by a heated Maxwellian (
i.e., they are linear in these semilog plots). However, at higher energies, both distributions have a broad tail, which is reflected in the high electron temperatures of the injector and upper lasing levels (391 to 461 K, respectively, and for the lattice temperature of 160 K, and 697 to 808 K, respectively, at the lattice temperature of 298 K). Neither the lower lasing level nor the
extractor distributions resemble a Maxwellian. Both states have nearly flat distributions, reaching up to the photon energy of 270 meV and yielding very high electron temperatures (up to 2397 K for the lower lasing level for a lattice temperature of 298 K). All in-plane distributions exhibit oscillations with a period equal to the optical phonon energy of 32 meV (also observed in NEGF simulations [
36]). The oscillations are more prominent at low temperatures; electron–electron scattering, which we did not account for but which is generally important at low temperatures, would help randomize in-plane energy and smoothen out these oscillations.
While distributions over in-plane energy are clearly nonthermal, we note that the effective electronic temperature, being a single parameter, enables us to compare characteristic subband energies between different subbands across different electric fields and heat-sink temperatures. Subband electronic temperatures are very useful in building intuition about quantities related to characteristic electronic kinetic energy (e.g., the backfilling current, the shunt-type leakage currents within the active region, the rate of escape into the continuum), which are widely used in simplified phenomenological models and greatly help with QCL design.
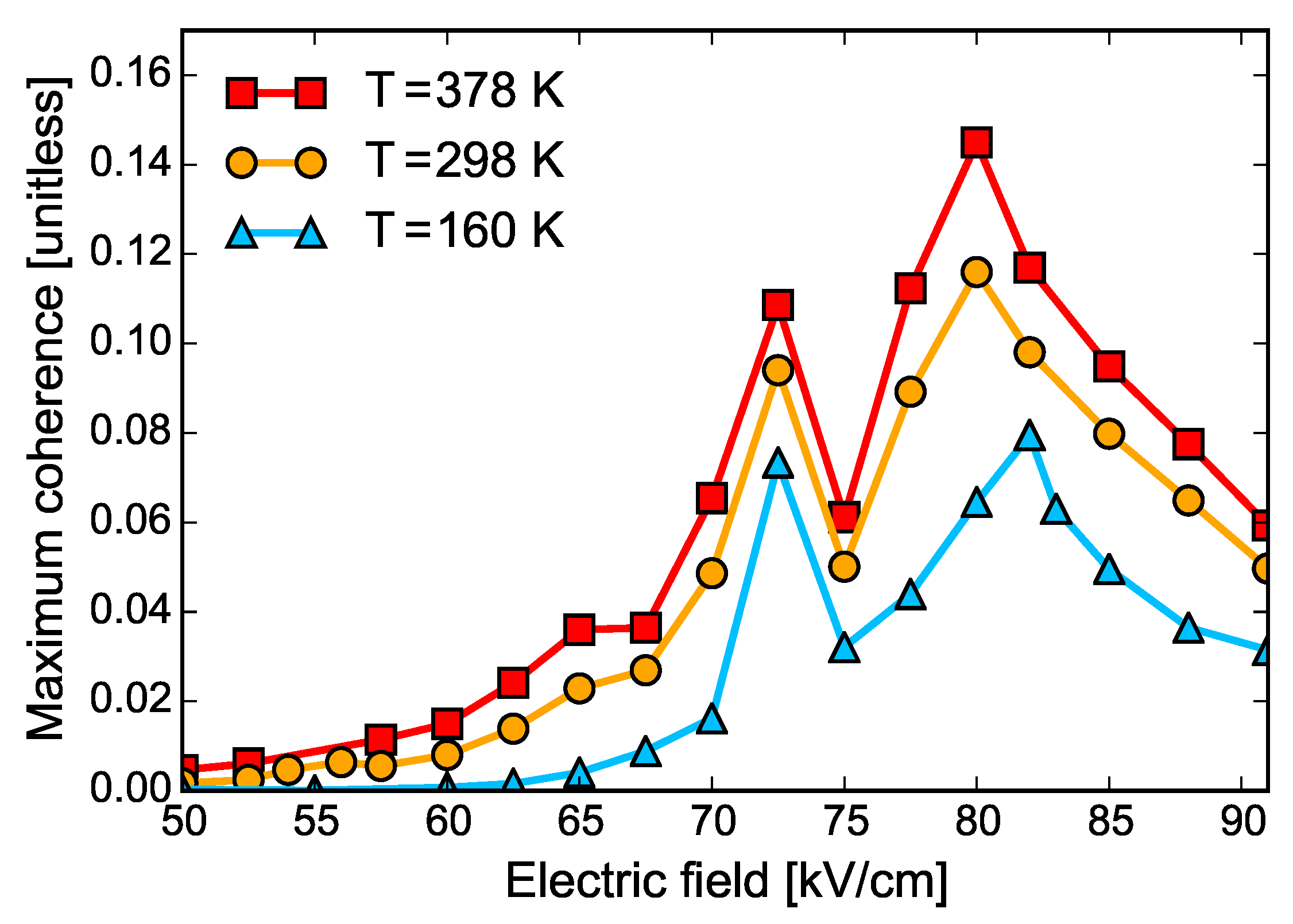
Figure 6 shows the magnitude of the ratio of the largest coherence
with
to the largest diagonal density-matrix element
. This quantity gives us an idea of the importance of including coherences in the model. We see that coherences can be up to
of the largest diagonal matrix element and that coherences are highest around the design lasing field of 82 kV/cm. The peak around 80–82 kV/cm is due to the coherence between the upper lasing level and the injector state. The coherence peak around 72 kV/cm is due to two states localized in the injector region. Large coherences arise when two states have considerable spatial overlap and a small energy difference, which is clearly the case for the upper lasing state and the injector state at 82 kV/cm (see
Figure 1d). We note that this alignment is known to be very problematic in semiclassical simulations, leading to numerical spikes in current. This level crossing is recognized as very important in density-matrix simulations, but usually treated phenomenologically [
27,
30,
34,
37]. Here, our approach is based on a rigorous density-matrix framework, where treatment of coherences is accurate and on an equal footing with the occupations. We conclude that, in order to accurately model injection in QCLs, it is critical to include the coherence between the injector state into the upper lasing level.
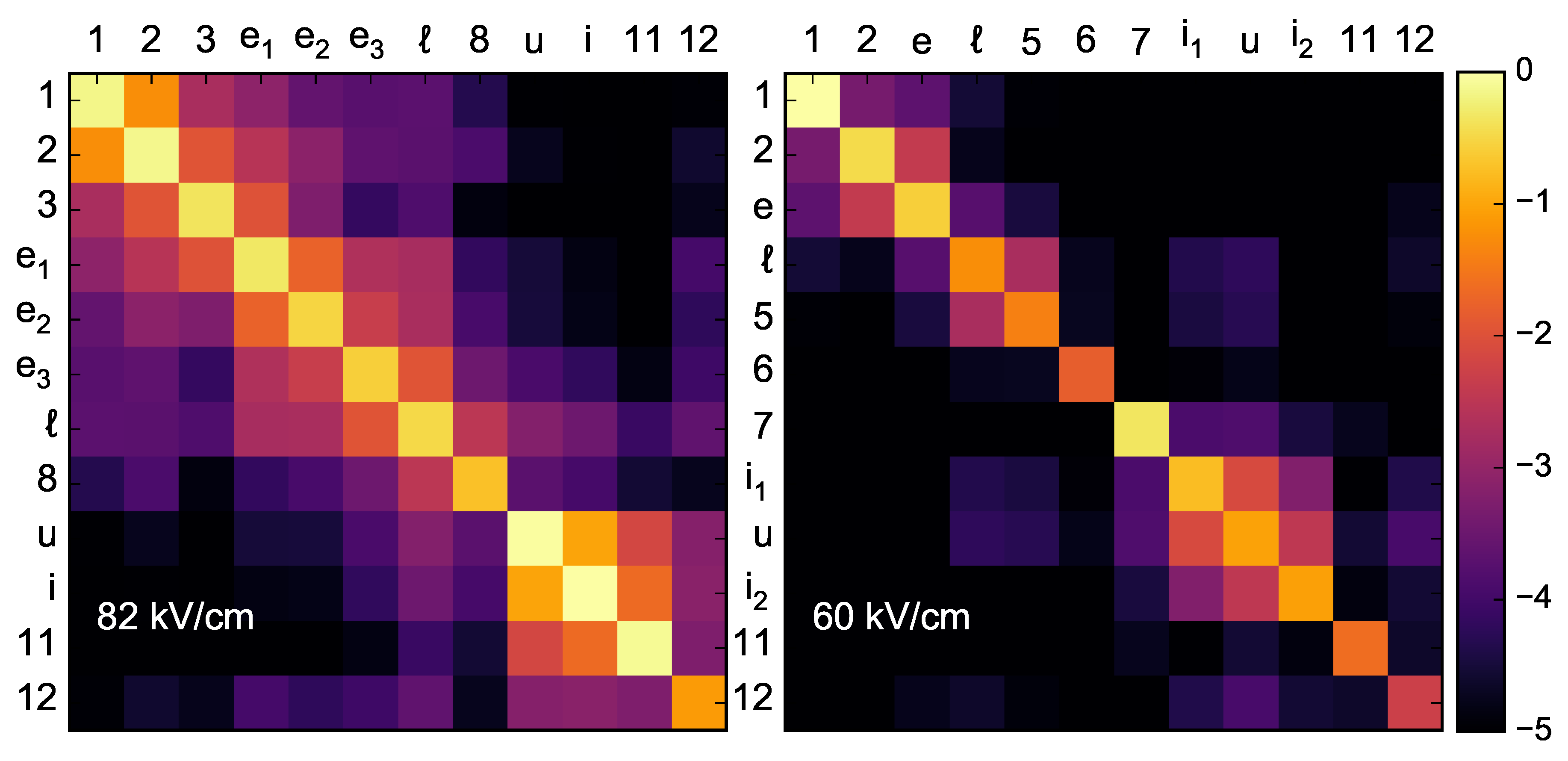
Figure 7 shows a plot of log
around lasing for a lattice temperature of 298 K and a field strength of 82 kV/cm (left panel). Important states are given labels, while other states’ thin gray curves in
Figure 1d are given numbers in order of increasing energy. Normalization is chosen such that the greatest diagonal value is one. Around the design lasing field, the greatest coherence is between the injector and upper lasing level (
) and is about
of the largest diagonal element. The second largest coherence is
(
) and all other coherences are smaller than
of the largest diagonal element. The greatest coherence involving the lower lasing level is
, which means the lower lasing level couples most strongly to the
extractor state, which, in turn, means that
is the most effective extractor state. The right panel of
Figure 7 shows the density matrix for a field strength of 60 kV/cm, which is slightly below threshold (
kV/cm). It is apparent that the coherences are considerably smaller at lower fields. The corresponding band structure is not shown, but the most important states are labeled. The greatest coherences are again between the upper lasing level and the injector states (there are two efficient injector states,
and
, at this field). The greatest coherences are
, between the upper lasing level and the
injector state (
). The coherence between the lower lasing level and the extractor state has a magnitude of
, indicating very inefficient extraction from the lower lasing level. It is noteworthy that coherences are very small overall at this near-threshold field, which indicates that a semiclassical transport description would be fairly accurate. In contrast, a semiclassical simulation is unlikely to be accurate for the description of transport at the design lasing field. This finding amends the conventional wisdom that transport in mid-IR QCL is largely incoherent and sheds light on the great importance of coherences, particularly in describing the injection process.