Effective Linewidth of Semiconductor Lasers for Coherent Optical Data Links
Abstract
:1. Introduction
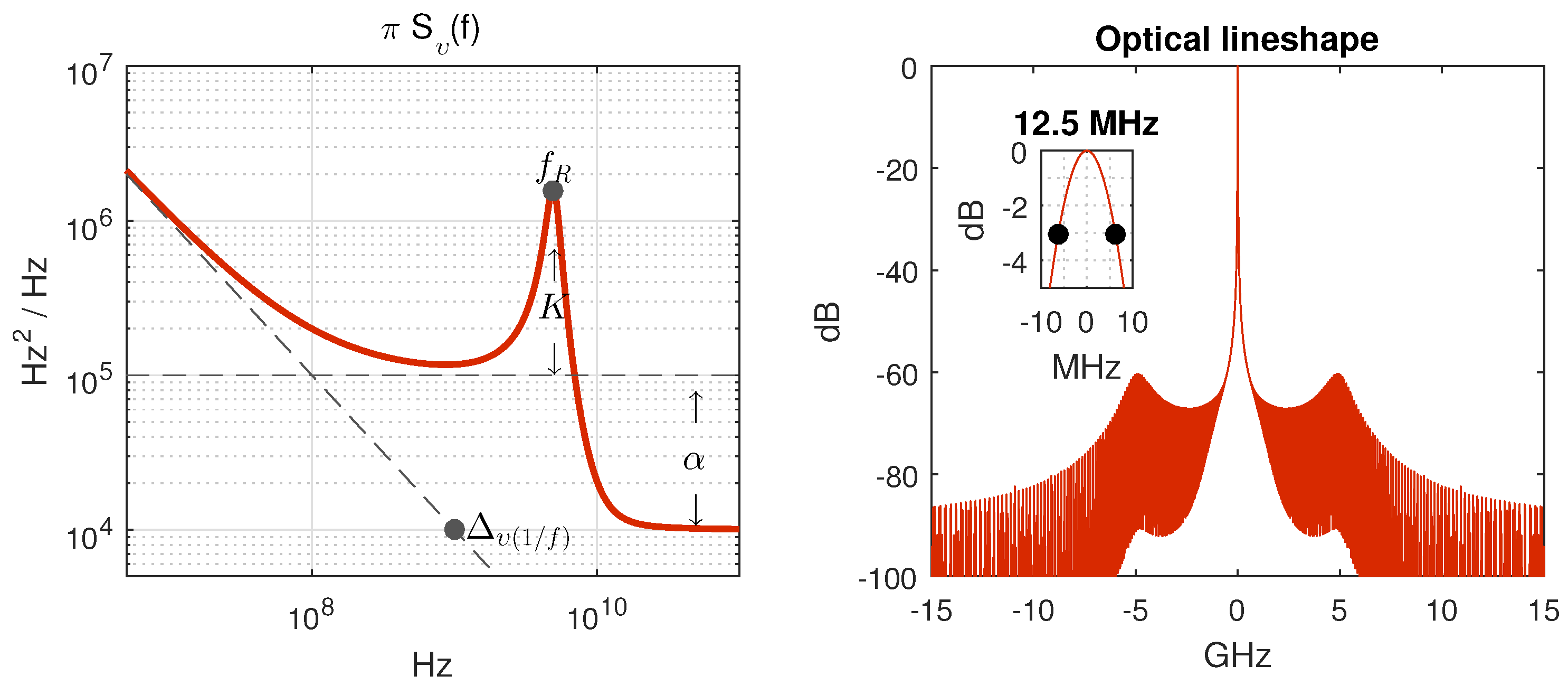
2. Semiconductor Laser Frequency Noise Model
- describes the level of noise at 1 GHz.
- describes the level of the intrinsic frequency noise at low frequencies.
- is the resonance frequency.
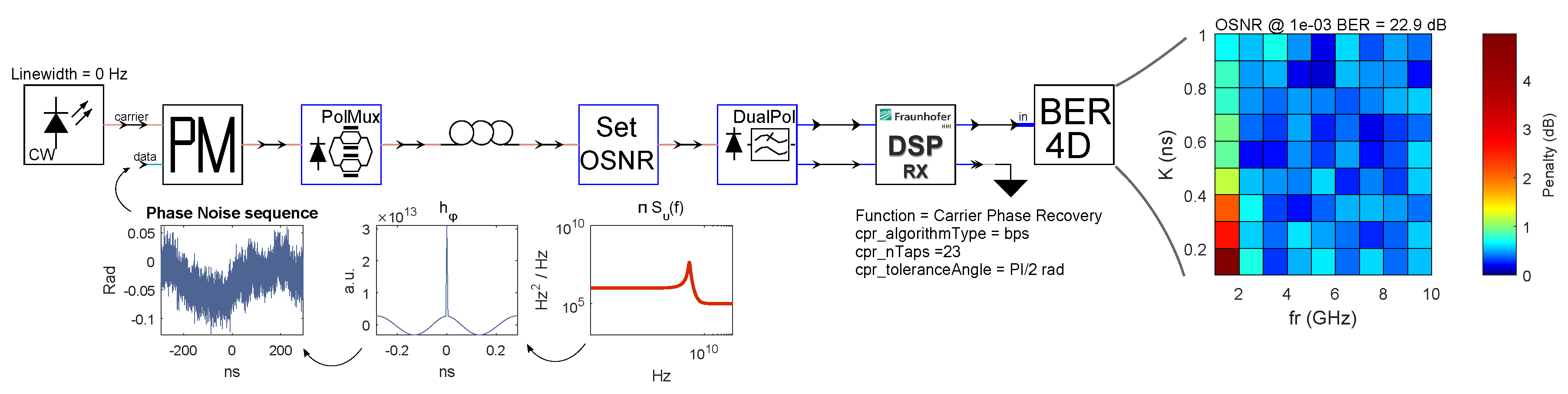
- K-factor describes how the damping rate increases with relaxation frequency. The K-factor of semiconductor lasers is approximately bias independent and in the range of 0.1–1 ns.
- α parameter determines the magnitude of the carrier induced noise.
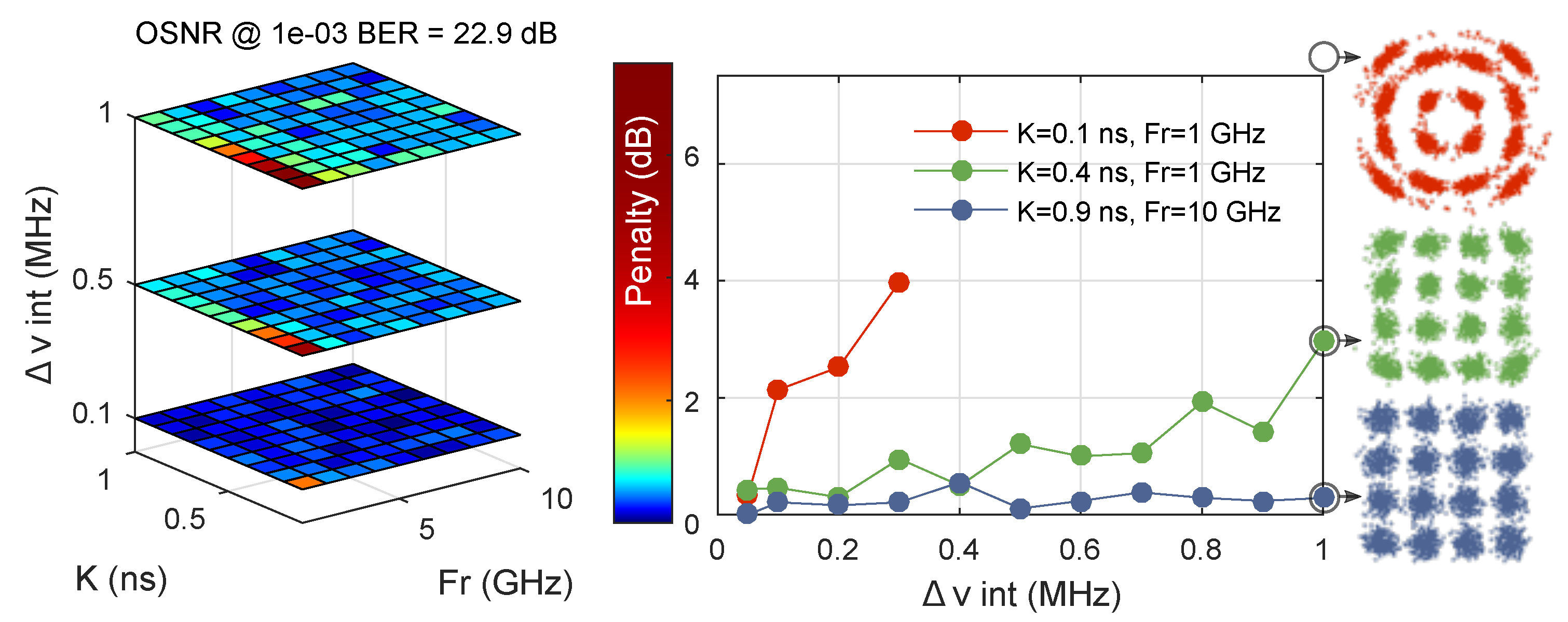
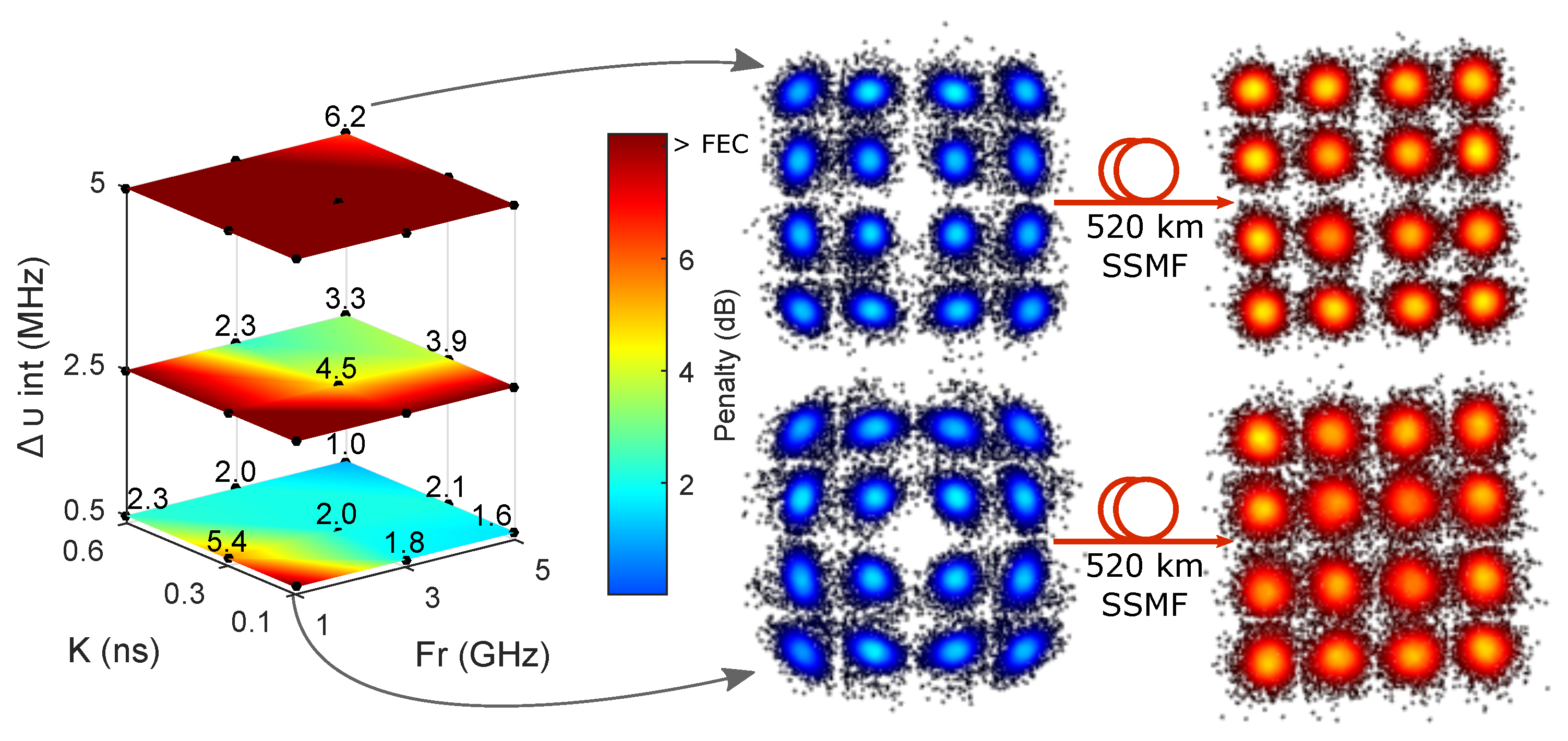
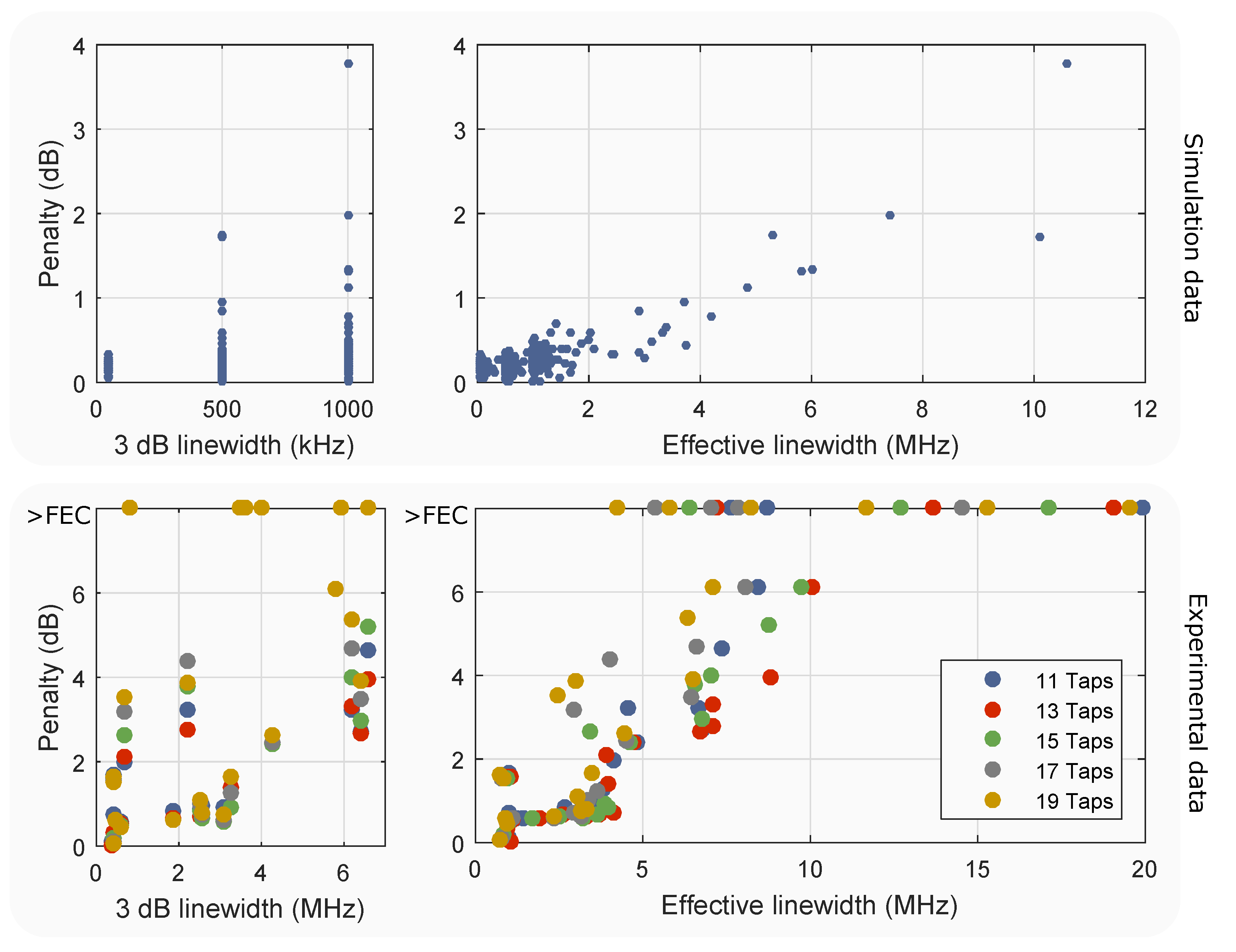
3. Impact on System Performance: Simulations
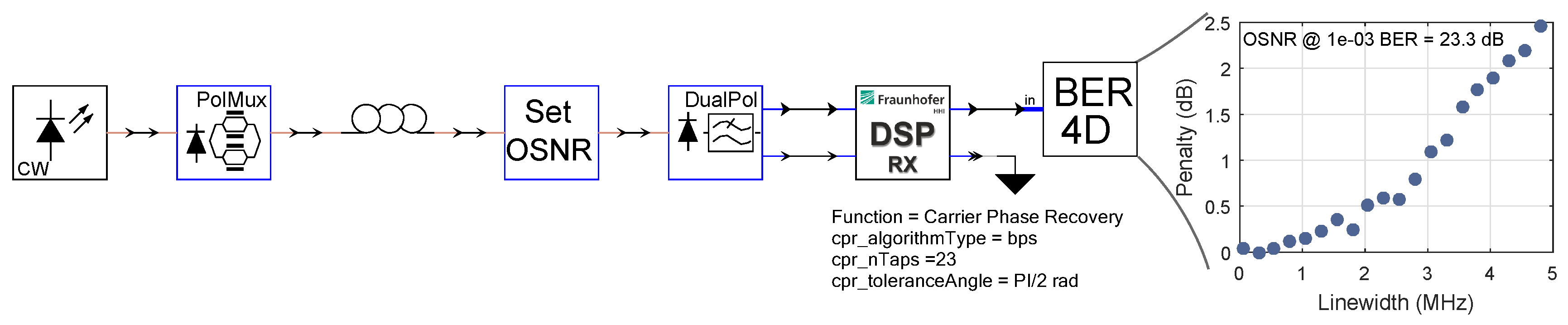
4. Impact On System Performance: Experiment
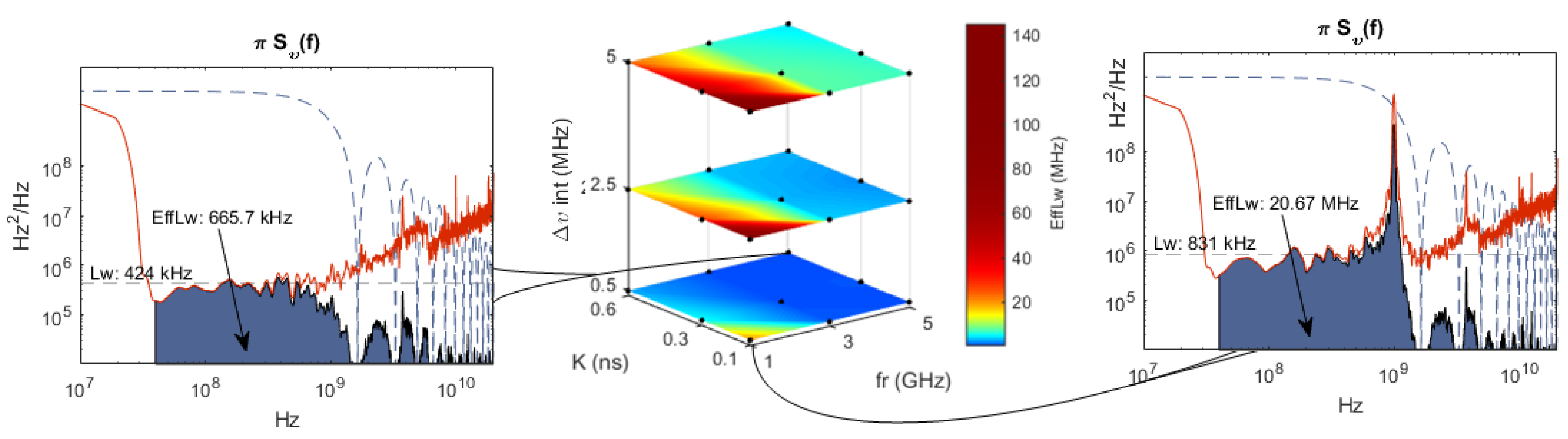
5. Effective Linewidth
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gallion, P.; Debarge, G. Quantum phase noise and field correlation in single frequency semiconductor laser systems. IEEE J. Quantum Electron. 1984, 20, 343–349. [Google Scholar] [CrossRef]
- Navarro, J.R.; Kakkar, A.; Pang, X.; Ozolins, O.; Schatz, R.; Olmedo, M.I.; Jacobsen, G.; Popov, S. Carrier phase recovery algorithms for coherent optical circular mQAM systems. J. Lightwave Technol. 2016, 34, 2717–2773. [Google Scholar] [CrossRef]
- Zibar, D.; Carvalho, L.; Piels, M.; Doberstein, A.; Diniz, J.; Nebendahl, B.; Franciscangelis, C.; Estaran, J.; Haisch, H.; Gonzalez, N.G.; et al. Bayesian filtering for phase noise characterization and carrier synchronization of up to 192 Gb/s PDM 64-QAM. In Proceedings of the 2014 European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3.
- Sun, H. Clock and carrier recovery for coherent receivers. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3.
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef] [PubMed]
- Chraplyvy, A.; Liou, K.; Tkach, R.; Eisenstein, G.; Jhee, Y.; Koch, T.; Anthony, P.; Chakrabarti, U. Simple narrow-linewidth 1.5 μm InGaAsP DFB external-cavity laser. Electron. Lett. 1986, 22, 88–90. [Google Scholar] [CrossRef]
- Kikuchi, K.; Okoshi, T. Measurement of FM noise, AM noise , and field spectra of 1.3 μm InGaAsP FB lasers and determination of the linewidth enhancement factor. IEEE J. Quantum Electron. 1985, 21, 1814–1818. [Google Scholar] [CrossRef]
- Shi, K.; Smyth, F.; Anandarajah, P.M.; Reid, D.; Yu, Y.; Barry, L.P. Linewidth of SG-DBR laser and its effect on DPSK transmission. Opt. Commun. 2010, 283, 5040–5045. [Google Scholar] [CrossRef]
- Bartholf, F.; Chang, P. Cost effective metro photonics enabled by coherent optics. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015; Optical Society of America: Washington, DC, USA, 2015. [Google Scholar]
- Ciena. WaveLogic Photonics Coherent Select; Technical Report; Ciena Corporation: Hanover, MD, USA, 2015. [Google Scholar]
- Schmitt, A. 100G+ Coherent Optical Equipment Ports; Technical Report; IHS Infonetics: Douglas County, CO, USA, 2015. [Google Scholar]
- Olmedo, M.I.; Pang, X.; Udalcovs, A.; Schatz, R.; Zibar, D.; Jacobsen, G.; Popov, S.; Monroy, I.T. Impact of carrier induced frequency noise from the transmitter laser on 28 and 56 Gbaud DP-QPSK metro links. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 11–14 November 2014.
- Olmedo, M.I.; Pang, X.; Piels, M.; Schatz, R.; Jacobsen, G.; Popov, S.; Monroy, I.T.; Zibar, D. Carrier recovery techniques for semiconductor laser frequency noise for 28 Gbd DP-16QAM. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015.
- Olmedo, M.I.; Pang, X.; Schatz, R.; Zibar, D.; Jacobsen, G.; Popov, S.; Monroy, I.T. Digital signal processing approaches for phase noise tolerant coherent transmission systems. Opt. Metro Netw. Short Haul Syst. 2015. [Google Scholar] [CrossRef]
- Piels, M.; Olmedo, M.I.; Xue, W.; Pang, X.; Schaffer, C.; Schatz, R.; Jacobsen, G.; Monroy, I.T.; Mork, J.; Popov, S.; et al. Laser rate equation-based filtering for carrier recovery in characterization and communication. J. Lightwave Technol. 2015, 33, 3271–3279. [Google Scholar] [CrossRef]
- Huynh, T.N.; Nguyen, L.; Barry, L.P. Phase noise characterization of SGDBR lasers using phase modulation detection method with delayed self-heterodyne measurements. J. Lightwave Technol. 2013, 31, 1300–1308. [Google Scholar] [CrossRef]
- Kikuchi, K. Impact of 1/f-type FM noise on coherent optical communications. Electron. Lett. 1987, 23, 885–887. [Google Scholar] [CrossRef]
- Kikuchi, K. Effect of 1/f-type FM noise on semiconductor-laser linewidth residual in high-power limit. IEEE J. Quantum Electron. 1989, 25, 684–688. [Google Scholar] [CrossRef]
- Mercer, L. 1/f frequency noise effects on self-heterodyne linewidth measurements. J. Lightwave Technol. 1991, 9, 485–493. [Google Scholar] [CrossRef]
- Matsuda, K.; Bessho, H.; Hasegawa, K.; Yoshida, T.; Ishida, K. A study of laser white and brownian FM noise in coherent QPSK signals. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014.
- Pfau, T.; Hoffmann, S.; Noe, R. Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations. J. Lightwave Technol. 2009, 27, 989–999. [Google Scholar] [CrossRef]
- Borkowski, R.; Zibar, D.; Tafur Monroy, I. Anatomy of a digital coherent receiver. IEICE Trans. Commun. 2014, 97, 1528–1536. [Google Scholar] [CrossRef]
- Kakkar, A.; Navarro, J.R.; Schatz, R.; Louchet, H.; Pang, X.; Ozolins, O.; Jacobsen, G.; Popov, S. Comprehensive study of equalization-enhanced phase noise in coherent optical systems. J. Lightwave Technol. 2015, 33, 4834–4841. [Google Scholar] [CrossRef]
- Kakkar, A.; Ozolins, O.; Navarro, J.R.; Pang, X.; Olmedo, M.I.; Schatz, R.; Louchet, H.; Jacobsen, G.; Popov, S. Design of coherent optical systems impaired by EEPN. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–22 March 2016.
- Kikuchi, K. Characterization of semiconductor-laser phase noise and estimation of bit-error rate performance with low-speed offline digital coherent receivers. Opt. Express 2012, 20, 5291–5302. [Google Scholar] [CrossRef] [PubMed]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglesias Olmedo, M.; Pang, X.; Schatz, R.; Ozolins, O.; Louchet, H.; Zibar, D.; Jacobsen, G.; Tafur Monroy, I.; Popov, S. Effective Linewidth of Semiconductor Lasers for Coherent Optical Data Links. Photonics 2016, 3, 39. https://doi.org/10.3390/photonics3020039
Iglesias Olmedo M, Pang X, Schatz R, Ozolins O, Louchet H, Zibar D, Jacobsen G, Tafur Monroy I, Popov S. Effective Linewidth of Semiconductor Lasers for Coherent Optical Data Links. Photonics. 2016; 3(2):39. https://doi.org/10.3390/photonics3020039
Chicago/Turabian StyleIglesias Olmedo, Miguel, Xiaodan Pang, Richard Schatz, Oskars Ozolins, Hadrien Louchet, Darko Zibar, Gunnar Jacobsen, Idelfonso Tafur Monroy, and Sergei Popov. 2016. "Effective Linewidth of Semiconductor Lasers for Coherent Optical Data Links" Photonics 3, no. 2: 39. https://doi.org/10.3390/photonics3020039
APA StyleIglesias Olmedo, M., Pang, X., Schatz, R., Ozolins, O., Louchet, H., Zibar, D., Jacobsen, G., Tafur Monroy, I., & Popov, S. (2016). Effective Linewidth of Semiconductor Lasers for Coherent Optical Data Links. Photonics, 3(2), 39. https://doi.org/10.3390/photonics3020039








