Two-Stage n-PSK Partitioning Carrier Phase Recovery Scheme for Circular mQAM Coherent Optical Systems

Abstract

A novel two-stage n-PSK partitioning carrier phase recovery (CPR) scheme for circular multilevel quadrature amplitude modulation (C-mQAM) constellations is presented. The first stage of the algorithm provides an initial rough estimation of the received constellation, which is utilized in the second stage for CPR. The performance of the proposed algorithm is studied through extensive simulations at the forward error correction bit error rate targets of 3.8 × 10⁻³ and 1 × 10⁻² and is compared with different CPR algorithms. A significant improvement in the combined linewidth symbol duration product (ΔνT_s) tolerance is achieved compared to the single-stage n-PSK partitioning scheme. Superior performance in the ΔνT_s tolerance compared to the blind phase search algorithm is also reported. The relative improvements with respect to other CPR schemes are also validated experimentally for a 28-Gbaud C-16QAM back-to-back transmission system. The computational complexity of the proposed CPR scheme is studied, and reduction factors of 24.5 | 30.1 and 59.1 | 63.3 are achieved for C-16QAM and C-64QAM, respectively, compared to single-stage BPS in the form of multipliers | adders.

1. Introduction

High-order modulation formats together with coherent detection and digital signal processing (DSP) have attracted significant attention to increase spectral efficiency in coherent optical transmission systems [1]. Carrier phase recovery (CPR) algorithms play a key role in these systems for the estimation and compensation of the phase noise induced by free running lasers. High-order modulation formats impose stringent requirements on the performance of these algorithms, as the distance between constellation points reduces with the increase in modulation order. The blind phase search (BPS) algorithm [2] and the N-th power approach [3] have typically been proposed for CPR in square multilevel quadrature amplitude modulations (Sq-mQAM) [4,5,6]. Although the BPS algorithm achieves a high phase noise tolerance, it requires a large computational complexity especially for high-order modulations where the required number of test phases increases. On the other hand, the N-th power concept requires less hardware complexity but comes at the expense of a poorer phase noise tolerance, as the relative number of suitable constellation points for phase estimation decreases with the modulation order. Different two-stage CPR schemes, which include both approaches, have been proposed to achieve similar phase noise tolerance as single-stage BPS while relaxing its computational complexity [7,8,9,10,11,12].

Due to its particular shape, circular multilevel quadrature amplitude modulation (C-mQAM) constellations provide a higher phase noise tolerance compared to Sq-QAM constellations. The n-PSK partitioning CPR scheme for C-mQAM constellations proposed in [13,14] achieves a relatively high linewidth tolerance with a low computational complexity. However, the algorithm requires a priori amplitude discrimination for symbol classification, which undermines its performance at low optical signal-to-noise ratios (OSNRs). In this paper, we propose a novel two-stage n-PSK partitioning CPR algorithm for C-mQAM constellations to alleviate this problem. The first stage of the algorithm provides an initial constellation estimation utilizing the n-PSK partitioning algorithm based on ring selection. The second stage utilizes this estimated constellation to classify the received symbols employing optimal symbol decision boundaries and applies the rest of the n-PSK partitioning process. The combined linewidth symbol duration product (ΔνT_s) tolerance of the proposed algorithm is studied through extensive simulations and is compared with different CPR algorithms to evaluate its relative performance improvement. The performance of the proposed algorithm is also experimentally evaluated in a 28-Gbaud back-to-back C-16QAM transmission system and compared with that of the other CPR schemes. The computational complexity of the proposed algorithm is finally studied in detail and a modification in the algorithm to reduce its computational complexity is also proposed.

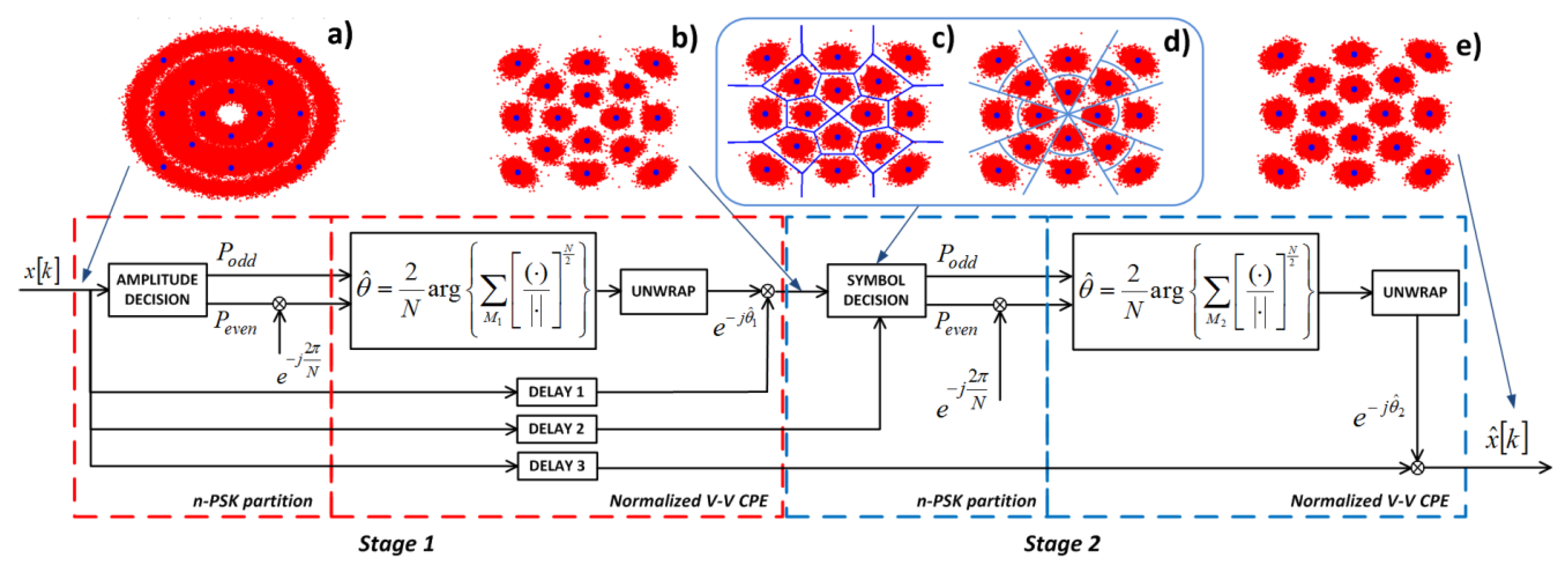
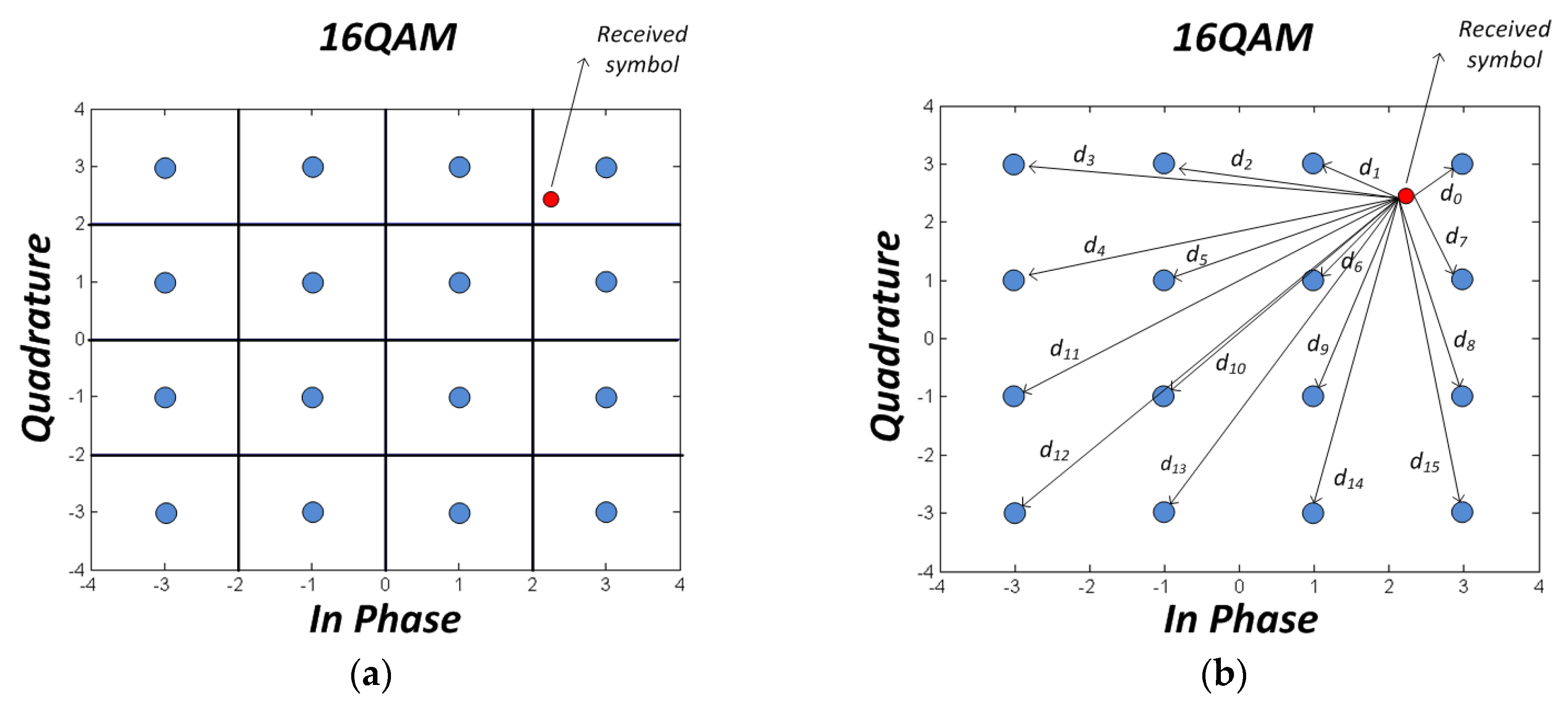
2. Two-Stage n-PSK Partitioning Scheme for C-mQAM

The C-mQAM constellations studied in this paper have been proposed in [15] and are illustrated in Figure 1 for C-16QAM and C-64QAM. Figure 1 also shows the bit mapping, differential sector decoding, and amplitude odd/even symbol classes, which were proposed in [14] and are employed in this paper. The proposed CPR scheme is divided in two stages, and its block diagram is depicted in Figure 2. The first stage corresponds to the n-PSK partitioning CPR algorithm [14]. The second stage is composed of the same functional blocks as the first stage. However, symbol classification in the second stage is performed using optimal decision boundaries on the output data of the first stage. Optimal decision boundaries are defined in this section and for the rest of the paper as optimal in the presence of only additive white Gaussian noise (AWGN) in order to relax the overall complexity of the algorithm. However, we notice that large ΔνT_s-values will result in residual phase noise requiring a different, higher complex approach for optimal symbol classification.

The amplitude of the received symbols in Figure 2 (inset a) is firstly calculated in the first stage to classify the symbols into an odd or even class. Then, a $e^{-j\frac{2\pi }{N}}$ phase rotation is performed for the symbols belonging to even classes, where N represents the total number of different phases of the C-mQAM constellation points. After this process, it is notable that the modulation components of the symbols belonging to odd and even amplitudes are aligned. The N/2-th power operation is then performed in the Viterbi and Viterbi (V&V) module over a block of M₁ symbols, which is considered for averaging the AWGN. This results in a phase noise estimator ${\widehat{\theta }}_1$ for the symbol in the middle of the block after the unwrap operation. The phase noise estimator is used to compensate for the phase noise of the input symbols, and the corrected symbols in Figure 2 (inset b) are fed into the second stage of the CPR scheme. The input symbols in the second stage therefore correspond to an estimation of the received constellation. This constellation estimation is then used for a better classification of the input symbols of the first stage in Figure 2 (inset a) into odd or even classes. It is noticeable that the ring selection process is now avoided as symbols are classified using optimal decision boundaries in Figure 2 (inset c) in the symbol decision module, which increases the accuracy of the classification process. Sub-optimal decision boundaries in Figure 2 (inset d) can also be considered for a computational complexity reduction of the symbol decision process, as explained in Section 5. The rest of the modules in the second stage are performed as explained for the first stage. However, a different block size M₂ can be considered for the second stage. Finally, a phase noise estimator ${\widehat{\theta }}_2$ is used to compensate for the phase noise of the input symbols, and the final corrected symbols are shown in Figure 2 (inset e). It is notable that symmetrical rotations of the constellation due to cycle slips occurring in the first stage of the algorithm do not affect the odd/even classification in the symbol decision module of the second stage and consequently have no impact on the overall performance of the CPR scheme.

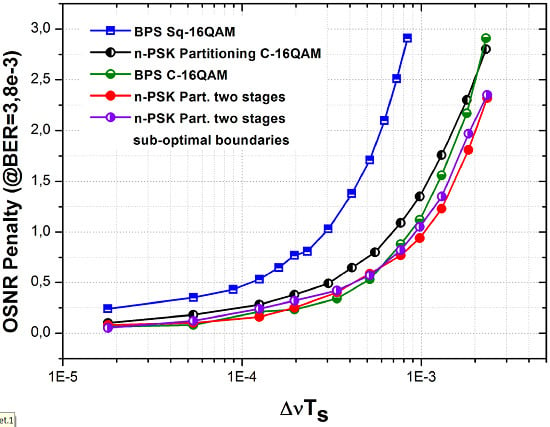
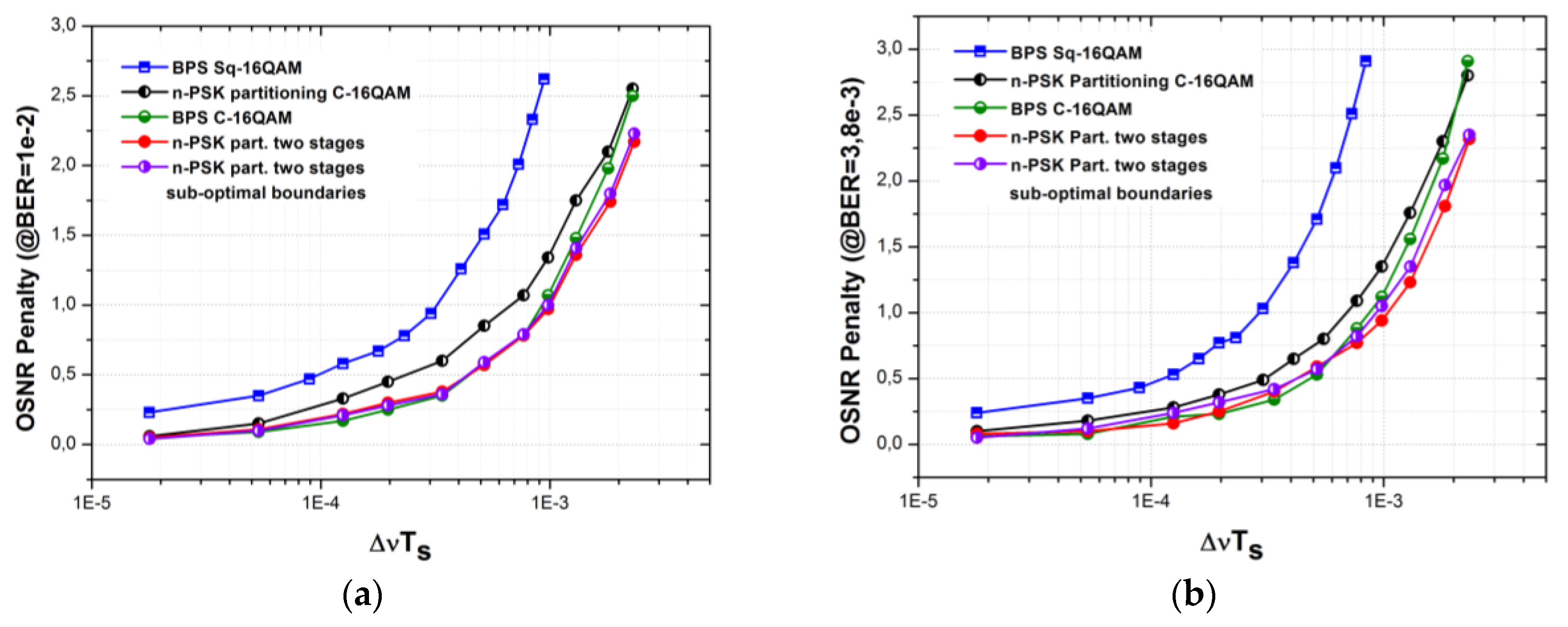
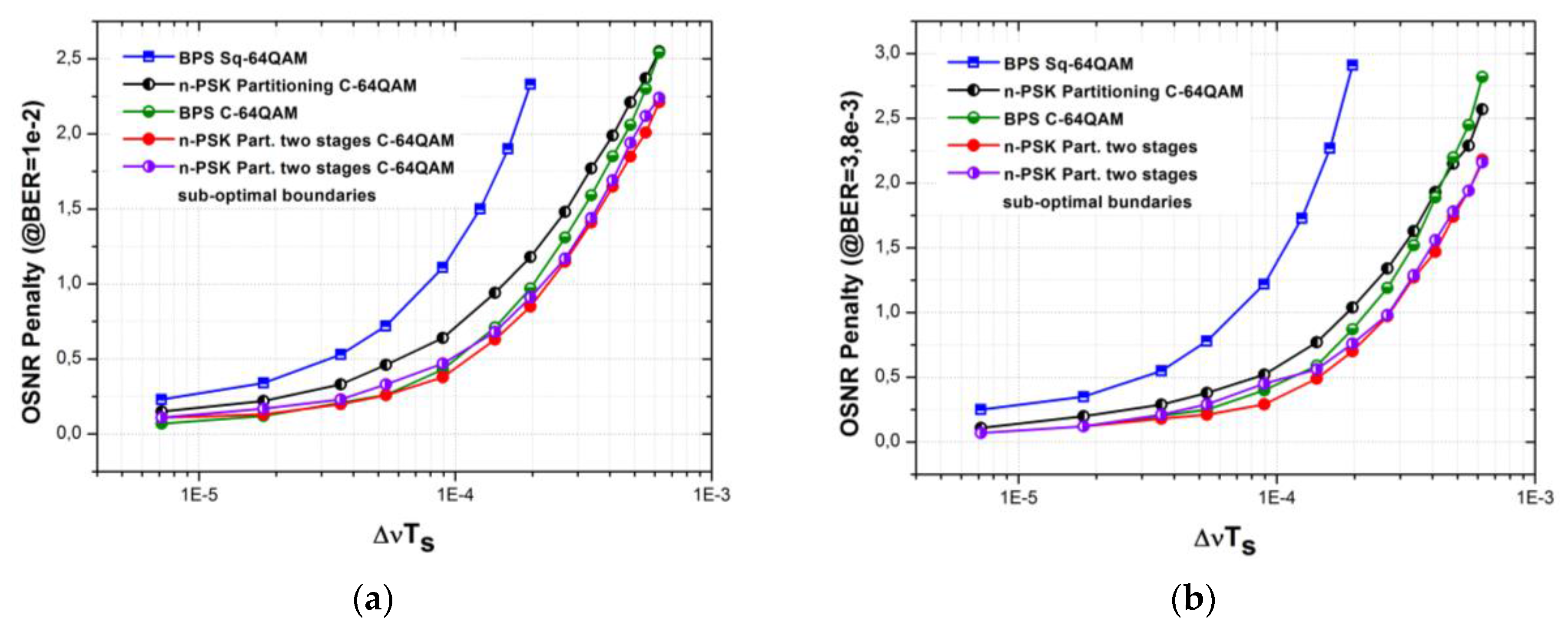
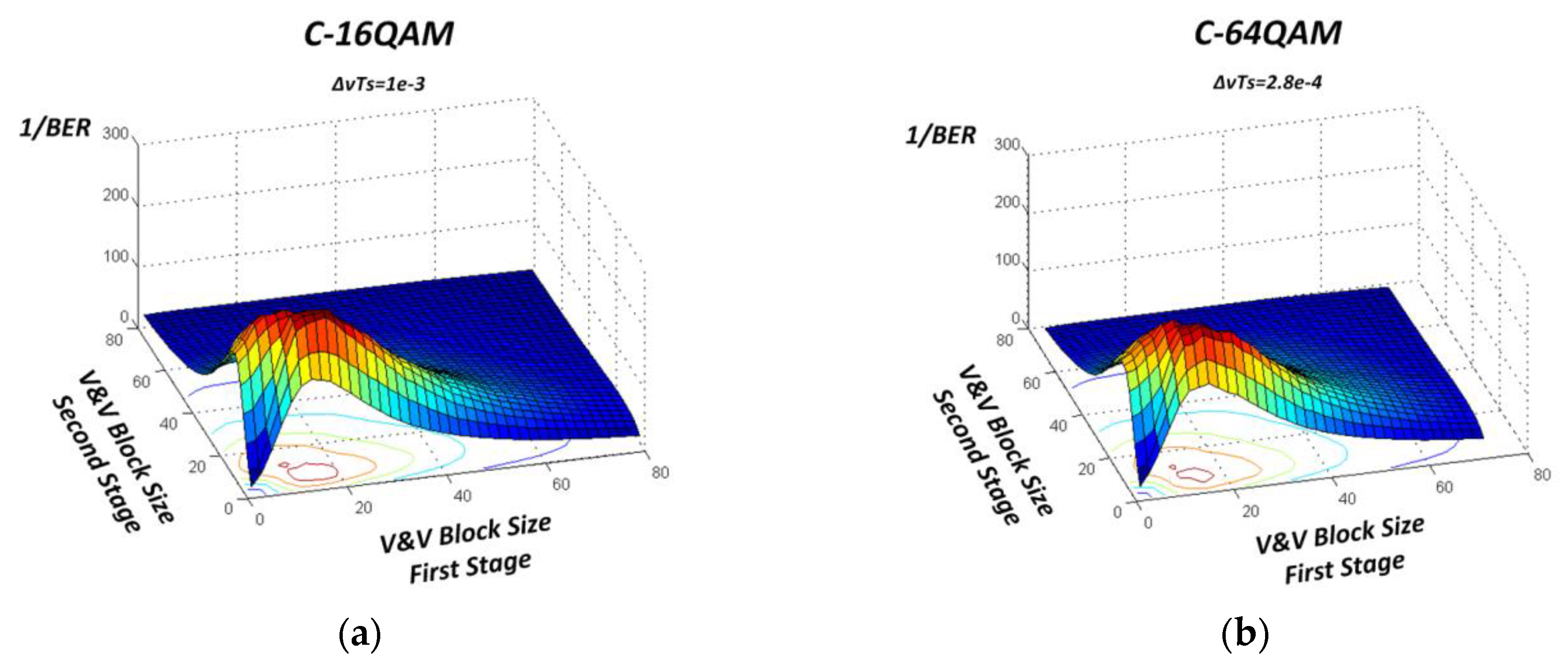
3. Simulation Setup and Results

Extensive simulations were carried out in VPItransmissionMaker^TM (VPIphotonics GmbH, Berlin, Germany) [16] to evaluate the performance of the proposed CPR scheme. The simulation setup corresponds to the transmission of a pseudorandom bit sequence (PRBS) with a sequence length of 2¹⁵ − 1 bits mapped onto 2¹⁷ symbols in a 28-Gbaud back-to-back transmission system. The outgoing signal after the transmitter is loaded with AWGN emulating erbium-doped fiber amplifier noise. Then, the signal is directly fed in the receiver and passed to a DSP-based demodulator where different CPR algorithms are applied for their relative performance evaluation. In order to mitigate the effect of cycle slips, the symbols are then differentially decoded [14], and the number of bit errors is counted for the bit error rate (BER) evaluation.

The performance of the proposed algorithm is compared to the single-stage n-PSK partitioning algorithm, BPS algorithm in Sq-mQAM constellations (BPS_Sq-mQAM), and BPS in C-mQAM constellations (BPS_C-mQAM). The bit mapping employed for Sq-QAM constellations can be seen in [2], while the bit mapping for C-mQAM constellations is illustrated in Figure 1. The performance of all the algorithms is evaluated at BER target limits of 1 × 10⁻² and 3.8 × 10⁻³ assuming the use of forward error correction (FEC). The number of test phases β in BPS_Sq-16QAM is set to 32 while β = 64 for BPS_Sq-64QAM. β is set to 32 for both BPS_C-16QAM and BPS_C-64QAM due to a π/4 rotational symmetry of C-64QAM constellations. The block length of all the algorithms has been optimized to show the best performance for each of the points in the figures.

Figure 3 shows the OSNR sensitivity penalties versus the ΔνT_s for C-16QAM and Sq-16QAM employing different CPR schemes at BER targets of 1 × 10⁻² (Figure 3a) and 3.8 × 10⁻³ (Figure 3b). The proposed two-stage n-PSK partitioning improves the performance of the single-stage n-PSK partitioning and achieves a performance superior to the BPS_C-16QAM algorithm. The probability of wrongly classifying symbols during the ring selection process in the single-stage n-PSK algorithm increases for low OSNR values. This process is avoided in the proposed two-stage n-PSK partitioning, as symbol classification is performed using optimal decision boundaries resulting in an improved performance of the algorithm. The use of sub-optimal boundaries in Figure 2 (inset d) results in a similar performance and is proposed here to reduce the computational complexity of the algorithm as explained in Section 5.

Figure 4 shows the OSNR sensitivity penalties versus the ΔνT_s for C-64QAM and Sq-64QAM employing different CPR schemes at BER targets of 1 × 10⁻² (Figure 4a) and 3.8 × 10⁻³ (Figure 4b). As in the previous case, the proposed two-stage n-PSK partitioning CPR scheme outperforms the n-PSK partitioning algorithm and provides higher performance than the BPS_C-64QAM.

The influence of the block size for each of the stages that comprise the proposed scheme on the BER performance is illustrated in Figure 5 for C-16QAM and C-64QAM. The results are obtained for a ΔνT_s corresponding to 1 dB OSNR sensitivity penalty. It is observed that, in this case, a larger block size in the first stage, compared to the block size of the second stage, provides the optimum performance of the algorithm. This is attributable to the wrongly classified symbols during the ring selection process in the first stage that require a larger block size for its averaging.

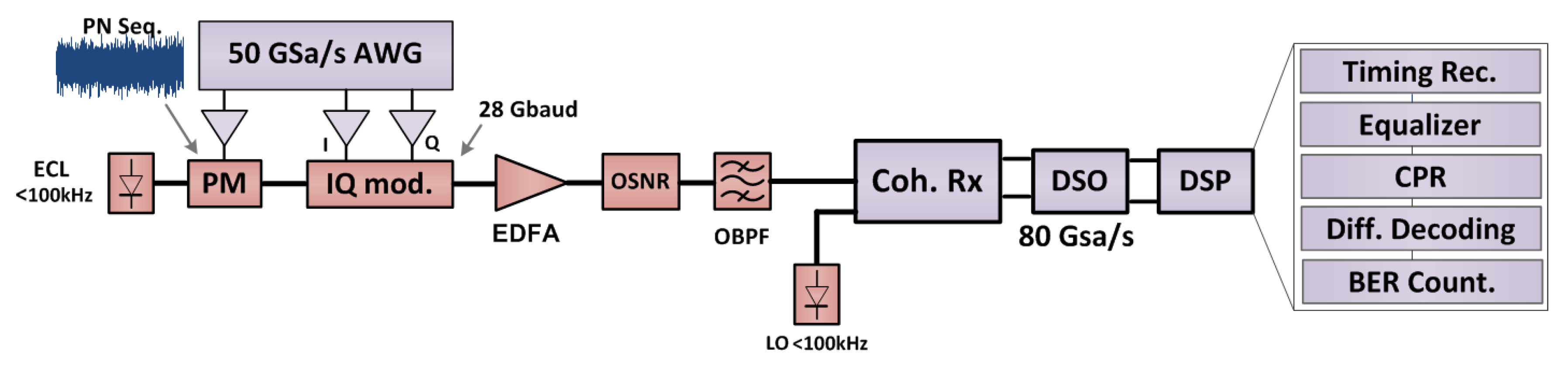
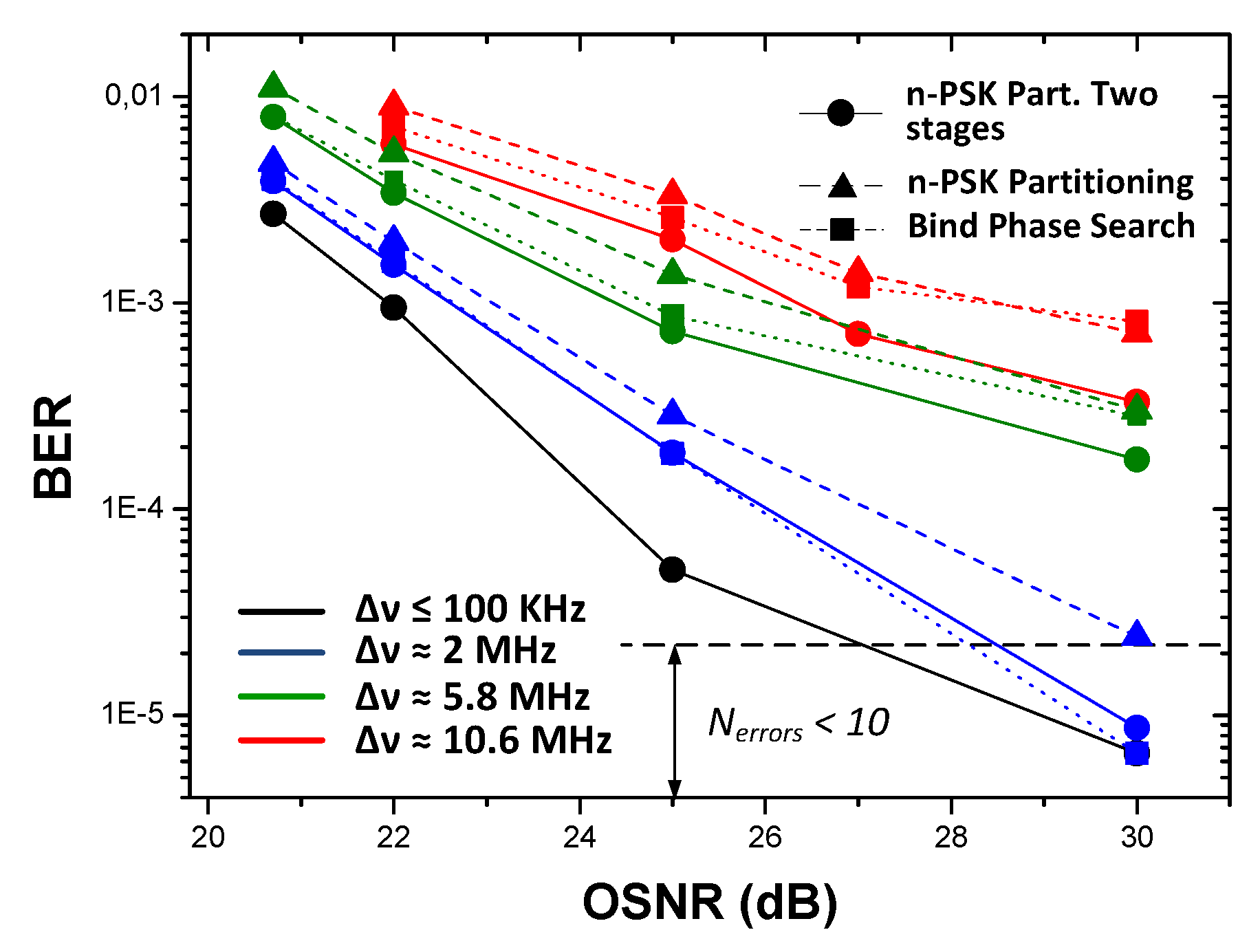
4. Experimental Setup and Results

Figure 6 illustrates the experimental setup for the performance evaluation of the proposed CPR scheme. The transmitter is composed of an arbitrary waveform generator and an optical IQ modulator. A pseudorandom bit sequence consisting of 2¹⁵ − 1 bits is generated and mapped onto symbols belonging to a C-16QAM constellation according to the bit mapping shown in Figure 1. The I and Q output electrical signals are firstly linearly amplified and fed in the optical IQ modulators that have a 3-dB bandwidth of 25 GHz. The incoming electrical signal is modulated onto the transmitter laser having a ~100-kHz intrinsic linewidth. A phase modulator is used to manipulate the frequency noise power spectral density of the transmitting laser. The arbitrary waveform generator is used to generate phase noise sequences corresponding to different white frequency noise levels which are linearly amplified and fed in the optical phase modulator in order to emulate the phase noise of a semiconductor laser [17,18]. In order to avoid patterning effects and discontinuities in the phase noise sequence while it is being repeated in the AWG, the phase noise sequence needs to be large enough to ensure randomness and can be mirrored so as to match the initial and final points of the generated sequence [18]. The outgoing 28-Gbaud C-16QAM signal is amplified using an EDFA and loaded with noise in the OSNR module. The OSNR module consists of an optical attenuator and an automatic gain control EDFA with constant output power. The signal is then directly fed into the coherent receiver and passed to the DSP module where the data was demodulated offline with different CPR algorithms in order to evaluate their performance. The Gardner algorithm was employed to achieve clock recovery, while the constant modulus algorithm followed by the multi-modulus algorithm were used for equalization [19,20]. Differential decoding was employed in all cases to mitigate the effect of cycle slips [14]. The BER versus OSNR performance of the proposed algorithm is compared with the BPS_C-16QAM and the single-stage n-PSK partitioning algorithms, as shown in Figure 7. The block length of each of the algorithms studied was optimized in each of the points of the curves to show the best performance. The number of test phases, β, was set to 32 in BPS_C-16QAM. The proposed two-stage n-PSK partitioning CPR scheme provides a higher performance compared to the other algorithms, and this performance gain increases with the laser linewidth. The OSNR penalty depends on the reference OSNR level to achieve a specified BER target, and it scales nonlinearly for different OSNR reference levels. Therefore, considering the extra OSNR implementation penalty in the experimental setup, the penalties observed in the experimental curves can be seen to be higher compared to those obtained in simulations where the OSNR reference was of 18.6 dB and 17.5 dB for BER targets of 3.8 × 10⁻³ and 1 × 10⁻², respectively.

5. Computational Complexity

In this section, the proposed algorithm is compared with the rest of the algorithms studied in this paper in terms of computational complexity. Six real multiplications and two summations are assumed to perform the 4-th power operation in the V&V module [8]. Nine real multiplications and three summations are assumed in the case of the 8-th power operation [14]. Two approaches are considered for the implementation of the symbol decision circuit (DC) module in the BPS algorithm, which is illustrated in Figure 8. In order to map a received symbol to one of the symbols in the constellation, the distance between the received symbol and all the constellation points can be performed. The received symbol is mapped to the constellation point where the calculated distance is the minimum (Figure 8b). For the rest of the paper, we consider this approach as hard decision and denote it with DC = 1. For the case of Sq-mQAM constellations, the decision circuit can be implemented employing only comparators in the I and Q components of the received symbol as the decision boundaries lay on a square grid (Figure 8a) and is considered in this paper as soft decision with notation DC = 0. However, this approach comes at the expense of a worse process performance, as it is not resilient enough to shape distortions of the received constellation. These two approaches are considered as the best- and worst-case scenarios (in terms of computational complexity), and any other implementation of the DC module will result in a computational complexity within the range of these two cases. The hard decision approach is considered in this paper for C-mQAM constellations, as their optimal decision boundaries have a pentagonal shape in the complex plane. The hardware implementation of the hard decision approach would require two real multipliers and three real adders for each of the distance calculations, while only comparators are required in the soft decision approach. The use of sub-optimal boundaries in Figure 2 (inset d) relaxes the complexity of the DC (in terms of multiplications/additions) for C-mQAM constellations, as the decision is made based on the angle and amplitude of the symbol requiring three real multipliers and one real adder for each symbol decision.

Figure 9 illustrates the flow chart of the proposed algorithm for the evaluation of its computational complexity. The red dashed line indicates the reusability of the calculations between modules. The calculations of the V&V module in the first stage are reused in the second stage, and a sign change performed on the bit representing the sign of the floating point number is performed for symbols belonging to even classes. The implementation proposed in Figure 9 forces the maximum block length of the second stage to be equal or smaller than the first stage (M₂ ≤ M₁). The computational complexity derivation of the first stage was detailed in [14], and its calculation for the second stage in terms of real-valued multiplications and summations is as follows:

• Each of the decision symbol circuit modules requires DC^mult, DC^sum, and DC^comp multiplications, summations, and comparisons, respectively.
• The summation of the I and Q components of M₂ symbols requires 2M₂ − 2 adders.
• The division inside the argument function requires one multiplication. A small look-up table can be used for the argument calculation. Unwrap operation requires a comparator and one summation. Multiplications and divisions of the power of two can be performed through bitwise shifting operations.
• In order to retrieve the I and Q components a small size look up table is required. Two comparators and an adder are needed to keep the calculated value in the range of [0,2π).
• 4M₂ multiplications and 2M₂ summations are required for phase correction of the input symbols.

The computational complexity calculations of the proposed algorithm and the BPS algorithm are illustrated in

Table 1. Computational complexity of various CPR algorithms.

	Real Multipliers	Real Adders	Comparators
BPSSq-mQAM	$6M\beta +M(\beta +1)\cdot D{C}_{Sq}^{mult}+4M$	$6M\beta +M(\beta +1)\cdot D{C}_{Sq}^{sum}-\beta +2M+2$	$\beta +M(\beta +1)\cdot D{C}_{Sq}^{comp}+2$
BPSC-mQAM	$6M\beta +M(\beta +1)\cdot D{C}_{Circ}^{mult}+4M$	$6M\beta +M(\beta +1)\cdot D{C}_{Circ}^{sum}-\beta +2M+2$	$\beta +M(\beta +1)\cdot D{C}_{Circ}^{comp}+2$
n-PSK2Stages C-16QAM	$10M_1+8M_2+2M_2\cdot D{C}_{Circ}^{mult}+2$	$5M_1+6M_2+2M_2\cdot D{C}_{Circ}^{sum}$	$3M_1+6+2M_2\cdot D{C}_{Circ}^{comp}$
n-PSK2Stages C-64QAM	$13M_1+8M_2+2M_2\cdot D{C}_{Circ}^{mult}+2$	$6M_1+6M_2+2M_2\cdot D{C}_{Circ}^{sum}$	$7M_1+6+2M_2\cdot D{C}_{Circ}^{comp}$
n-PSK2Stages C-16QAM sub-optimal	$10M_1+M_2(8+(D{C}_{Sub}^{mult}+\cdot D{C}_{Circ}^{mult}))+2$	$5M_1+6M_2+M_2\cdot (D{C}_{Sub}^{sum}+\cdot D{C}_{Circ}^{sum})$	$3M_1+6+M_2\cdot (D{C}_{Sub}^{comp}+\cdot D{C}_{Circ}^{comp})$
n-PSK2Stages C-64QAM sub-optimal	$13M_1+M_2(8+(D{C}_{Sub}^{mult}+\cdot D{C}_{Circ}^{mult}))+2$	$6M_1+6M_2+M_2\cdot (D{C}_{Sub}^{sum}+\cdot D{C}_{Circ}^{sum})$	$7M_1+6+M_2\cdot (D{C}_{Sub}^{comp}+\cdot D{C}_{Circ}^{comp})$

Note: DC: Decision Circuit complexity; M: Filter length; M₁, M₂: Filter lengths of the first and second stage, respectively; β: Number of test phases; Sq: Square constellations; Circ: Circular constellations; mult: multiplications; sum: summations comp: comparators.

. Block-based concept, unwrapping function and the final symbol decision module are assumed in all the calculations, as explained for the proposed two-stage n-PSK partitioning case.

Table 2. Computational complexity reduction factors relative to two-stage n-PSK partitioning algorithm employing sub-optimal decision boundaries in the symbol decision circuit module.

Algorithm	Reduction Factors [DC = 1, M1 = M2 = 19] (Multipliers | Adders)	Specifications
BPS Sq-16QAM	3.8 | 3.3 24.5 | 30.1	M = 19, β = 32, DC = 0 M = 19, β = 32, DC = 1
BPS Sq-64QAM	2.6 | 1.9 59.1 | 63.3	M = 19, β = 64, DC = 0 M = 19, β = 64, DC = 1
BPS C-16QAM	24.5 | 30.1	M = 19, β = 32, DC = 1
BPS C-64QAM	29.1 | 32.2	M = 19, β = 32, DC = 1

Note: DC = 1 implies hard decision (worst-case complexity). DC = 0 implies soft decision.

shows the computational complexity reduction factors of the proposed algorithm, utilizing sub-optimal decision boundaries (see Figure 2; inset d) relative to the BPS algorithm. In the case of C-16QAM compared to Sq-16QAM, the computational complexity reduction factor is in the range of 3.8–24.5 in the required number of real multipliers, and this factor is between 3.3 and 30.1 for the number of real adders depending on the implementation of the DC module. In the case of C-64QAM compared to Sq-64QAM, the computational complexity reduction factor is in the range of 2.6–59.1 in the number of real multipliers, and in the range of 1.9–63.3 for the number of real adders depending on the implementation of the DC module. Computational complexity reduction factors of 24.5 | 30.1 and 29.1 | 32.2 for the proposed two-stage n-PSK partitioning are achieved compared to BPS applied to C-16QAM and C-64QAM constellations, respectively. The computational complexity reduction factors are summarized, for the case of optimal boundaries, in

Table 3. Computational complexity reduction factors relative to two-stage n-PSK partitioning algorithm employing optimal decision boundaries in the symbol decision circuit module.

Algorithm	Reduction Factors [DC = 1, M1 = M2 = 19] (Multipliers | Adders)	Specifications
BPS Sq-16QAM	2.4 | 1.8 15.2 | 16.6	M = 19, β = 32, DC = 0 M = 19, β = 32, DC = 1
BPS Sq-64QAM	1.4 | 0.9 31.8 | 32.5	M = 19, β = 64, DC = 0 M = 19, β = 64, DC = 1
BPS C-16QAM	15.2 | 16.6	M = 19, β = 32, DC = 1
BPS C-64QAM	16.1 | 16.5	M = 19, β = 32, DC = 1

Note: DC = 1 implies hard decision (worst-case complexity). DC = 0 implies soft decision.

.

6. Conclusions

A novel two-stage CPR scheme for C-mQAM constellations based on the n-PSK partitioning algorithm is presented. The low-performance ring selection process in the single-stage n-PSK algorithm is alleviated by using optimal decision boundaries in the second stage of the algorithm. Simulation results on the performance of the proposed CPR algorithm show a noticeable improvement in phase noise tolerance compared to the single-stage n-PSK partitioning algorithm. The phase noise tolerance of the proposed algorithm is also compared with the BPS_C-mQAM algorithm showing a superior performance. Furthermore, the computational complexity of the algorithm is studied in detail and compared to the BPS algorithm in C-mQAM and Sq-QAM constellations in order to assess the computational complexity reduction factors. Utilization of sub-optimal boundaries in the DC module is also proposed to further reduce the computational complexity of the algorithm while achieving similar ΔνT_s tolerance. Computational complexity reduction factors of at least 3.8 | 3.3 in the form of multipliers | adders relative to BPS_Sq-16QAM are reported which can reach values of 24.5 | 30.1 for the best-case implementation of the DC module. Compared to the BPS_C-16QAM, computational complexity reduction group factors of 24.5 | 30.1 are achieved.