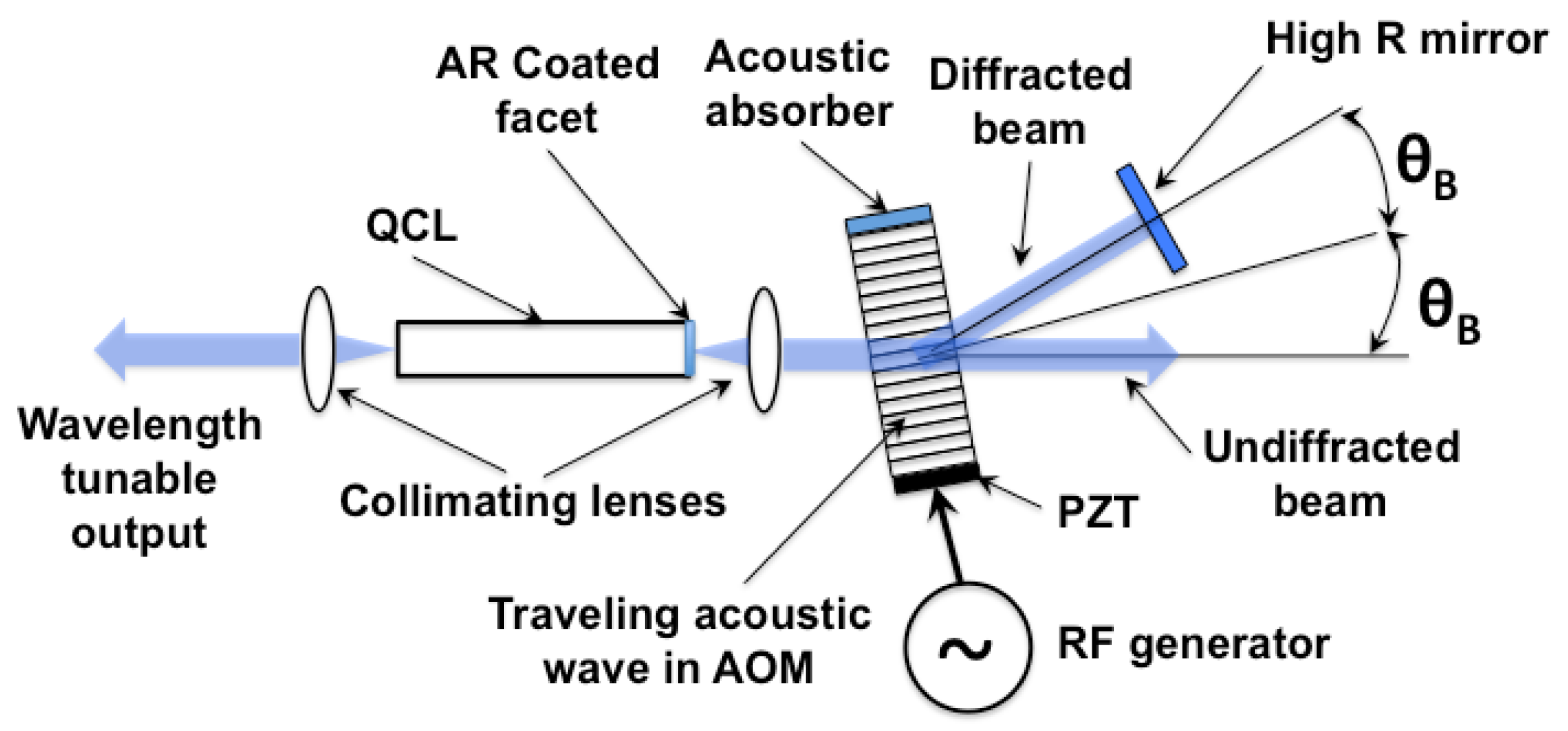
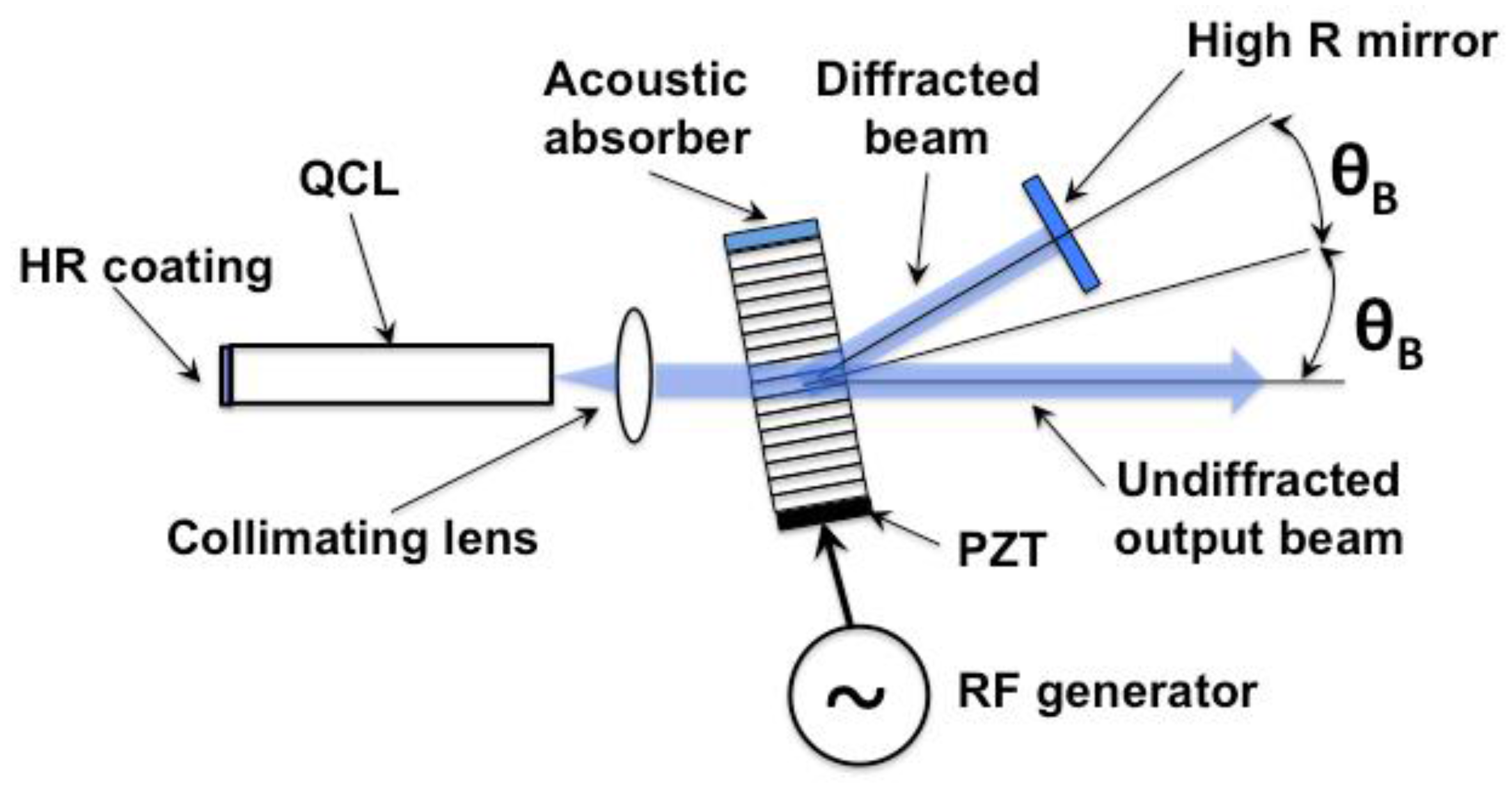
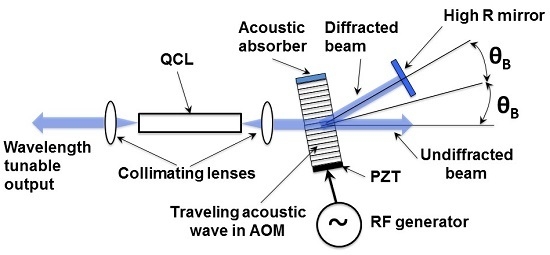
3.1. Response Time
The response time of the change in the optical wavelength with a change in the AOM frequency is the main advantage of the new configuration. The response time has two components: (1) propagation time of the acoustic wave from the piezoelectric transducer to the edge of the optical beam going through the AOM (this propagation distance is designated here as L); and (2) the propagation time for the acoustic wave across the optical beam (diameter of the beam is designated as Db). The first “delay” is the latency time and does not represent the response time of the change of the optical wavelength when AOM frequency is changed. The latency time can be shortened, almost arbitrarily, by reducing the distance between the acoustic transducer and the position of the optical beam. The actual response time, therefore, is determined by the acoustic wave transit time across the optical beam. For the present case, the time it takes an acoustic wave to propagate from the piezoelectric transducer across the germanium material to the edge of the optical beam is t1 and time for the acoustic wave to cross the optical beam is t2. The time t2 is the actual response time of the AOM for changing the optical wavelength. As mentioned above, t1 can be shortened to almost zero. However, there are limitations on how short t2 can be. If t2 is made too short by making the optical beam diameter small, the optical wave will interact with a fewer number of acoustic waves and therefore the linewidth of the output will increase. The linewidth of the optical output can be reduced by making the optical beam diameter larger, but that occurs at the expense of the response time. The optimal linewidth/response time balance is application driven.
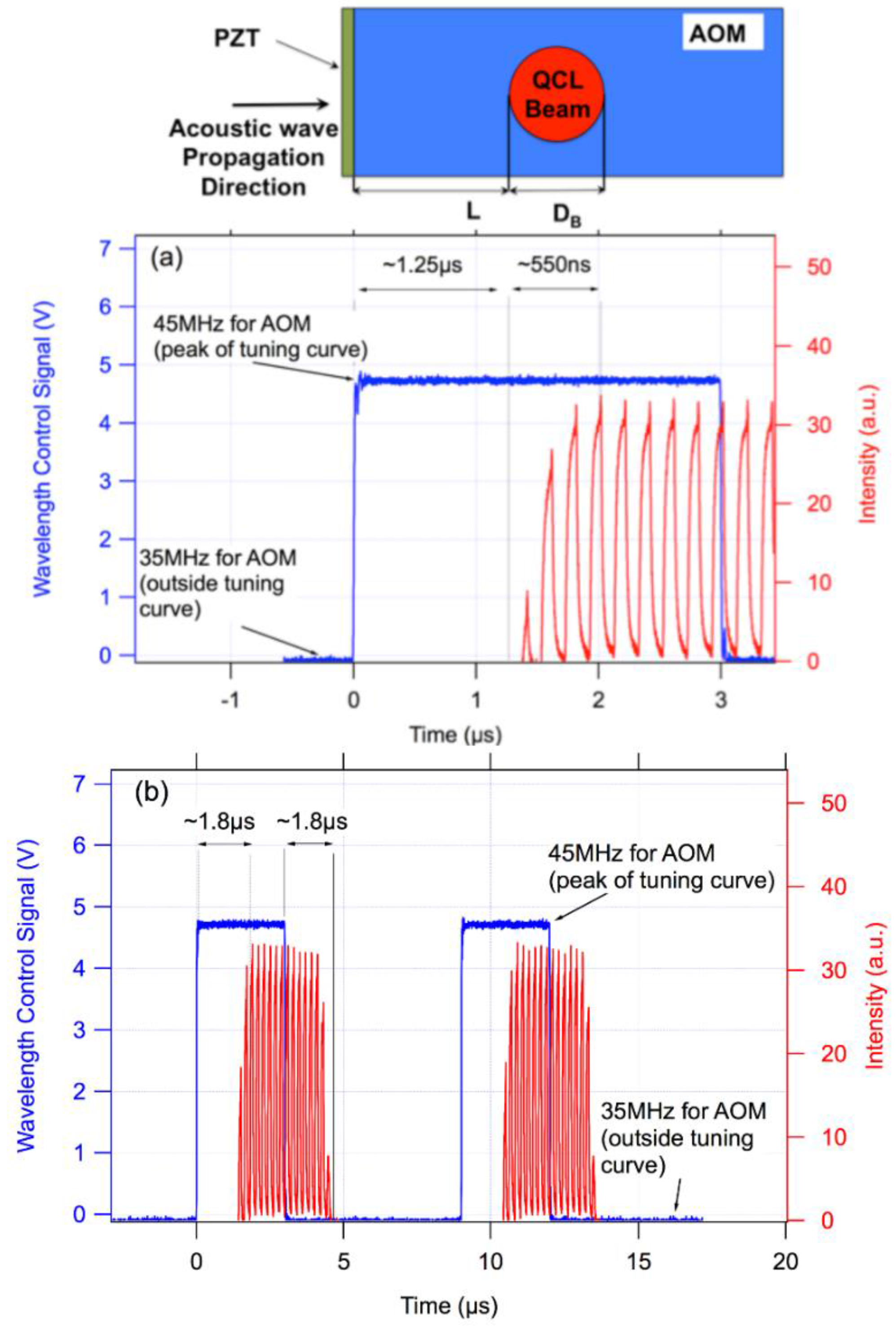
Figure 2 shows measured response time of the system as AOM frequency switches from 35 MHz (outside of the tuning curve) to 45 MHz (center of the tuning curve). The blue curve in
Figure 2 shows the AOM frequency control signal and the red curve shows the optical signal from the laser measured with a room temperature mercury-cadmium-telluride (MCT) detector, which consists of pulses of duration 100 ns and repetition period of 200 ns. AOM frequency is initially equal to 35 MHz, outside of the tuning curve of the laser. The optical signal level from the laser is at zero level since the Bragg condition is not satisfied anywhere in the laser gain spectrum. AOM frequency is abruptly changed to 45 MHz at time
t = 0. AOM frequency of 45 MHz corresponds to the peak of the gain curve. It takes approximately
t1 =
L/
vs = 1.25 μs for the acoustic signal with the new frequency to reach the area where the optical beam is incident on the crystal (
vs is sound velocity). When the sound signal with the new frequency reaches that area, the optical signal starts growing. It reaches its maximum value at
t2 = 550 ns +
t1, in a good agreement with the calculated travelling time across the beam area
t2 =
DB/
vs = 3.4 mm/(5.5 mm/μs) ~ 600 ns (
Figure 2a). The AOM frequency switches back to 35 MHz at
t = 3 μs. The process is repeated: It takes about
t1 +
t2 =1.8 μs for the laser to completely shut down (
Figure 2b).
As mentioned above, the latency time t1 is proportional to L and can be almost arbitrarily minimized by designing the AOM so that the piezoelectric transducer generating the sound wave is positioned closer to the beam area. Time t2, which is the actual wavelength switching time, on the other hand, is determined by the AOM material and beam size. It is, however, already well below 1 μs. Thus, if we change the AOM frequency between two values, say f1 and f2, the laser wavelength will switch between two corresponding values in a time less than 1 μs, the latency time notwithstanding.
3.2. Continuous Wave Operation
Two variations of the AOM approach are possible. The first one is when the acoustic wave reflects from the side opposite to the sound wave transducer, which creates a standing sound wave in the crystal. The standing acoustic waves occur at discrete acoustic frequencies defined by crystal dimensions and sound wave speed. Therefore, corresponding laser wavelengths are also discrete. A more interesting approach, explored in References [
7,
8], is when a sound wave absorber is positioned opposite end of the AOM crystal from the transducer. This is the travelling sound wave case. Since the standing wave resonance does not need to be satisfied, continuous wavelength tuning is available for this configuration.
A corollary property of the travelling wave approach is a frequency-shifted feedback. As the laser beam propagates through the crystal, it experiences the Doppler shift equal to the sound wave frequency. The frequency shift is doubled when the beam reflected by the high reflectivity back mirror propagates through the crystal again before coupling back into the laser waveguide. The frequency shift prevents constructive interference and formation of axial optical modes in the laser (corresponding to the round trip time for the overall laser cavity) when zero-reflectivity anti-reflection coating is used on the laser facet facing the AOM. As a consequence, emission spectrum for the AOM controlled lasers in the travelling wave configuration is expected to be different from that for traditional Fabry-Perot and external cavity devices.
Emission spectrum of lasers, including AOM-controlled QCLs, is seeded by spontaneous emission events in the gain medium. Therefore, phase consideration between these random events is not important. Each of the spontaneous emission events results into the formation of a broad spectral line as the beam propagates back and forth in the cavity. The resultant (integrated) spectrum is defined by the gain/loss spectrum, the AOM frequency response, and the frequency shift.
It was shown in Reference [
11] that the integrated emission spectrum for an AOM-controlled laser, seeded by a broad spontaneous emission, has a nearly Gaussian shape with an estimated spectral full width at half maximum
given by
where
is the roundtrip frequency shift and
is the spectral width of the AOM frequency response. The expression in Equation (2) was derived assuming that material gain/loss spectral width was much larger than
. As a consequence, Equation (2) is independent of gain spectrum width. In addition, it was also assumed in Equation (2) that
was much larger than both
and free spectral range of the external cavity setup. These assumptions are generally applicable to AOM-controlled QCLs. For the external cavity setup described in the present work,
= 2 × 45 MHz = 90 MHz and
cm
−1. Both parameters are calculated assuming that the beam propagated twice through the modulator during the roundtrip. For these values of
and
, calculated value for
is approximately 1.3 cm
−1.
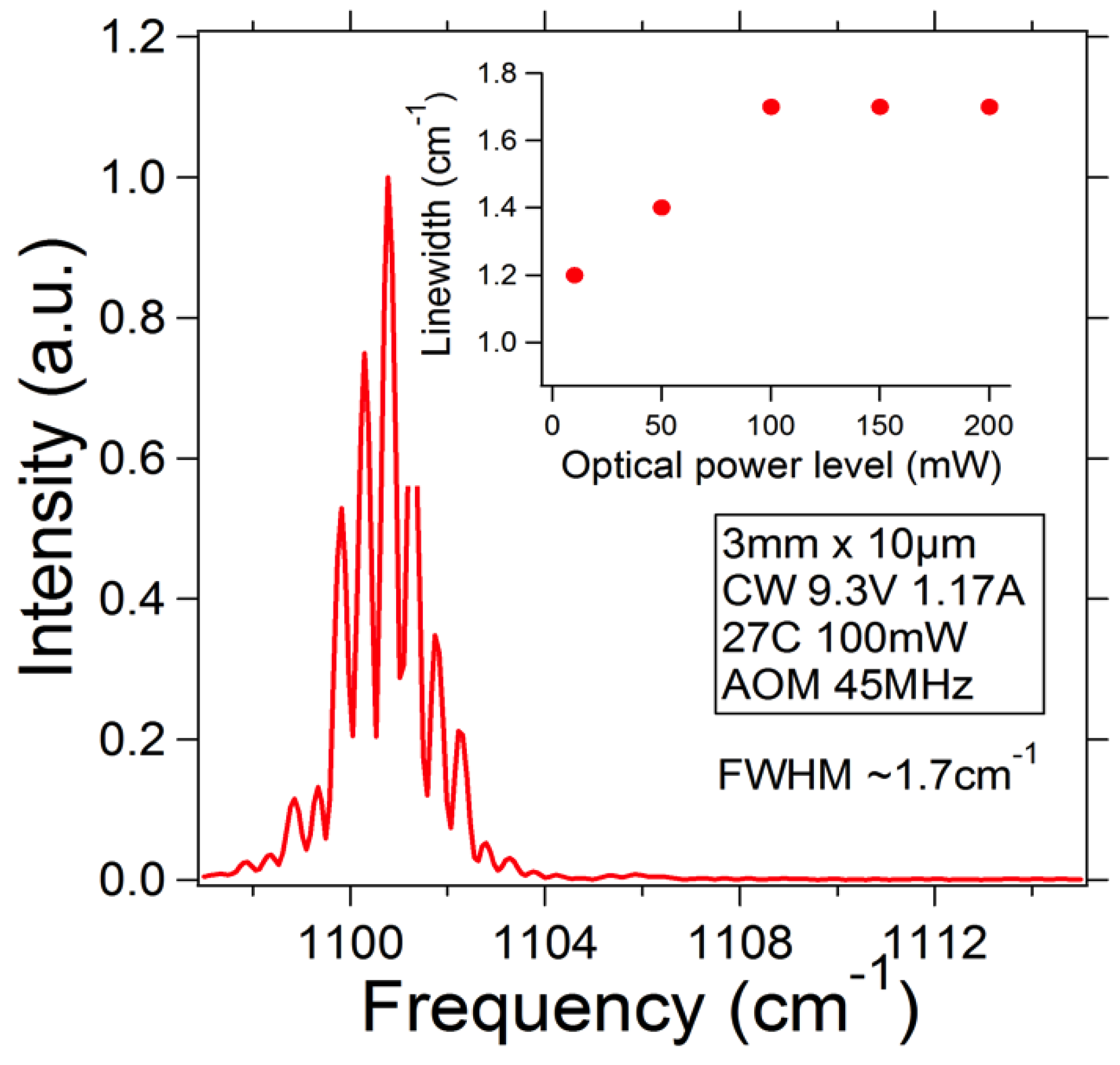
Figure 3 shows that measured continuous-wave (CW) linewidth for a 3 mm × 10 μm AOM-controlled QCL epi-down mounted on an AlN submount at a high power level (output power ~100 mW; driving conditions 1.17 A, 9.3 V, 300 K; AOM frequency 45 MHz) was approximately equal to 1.7 cm
−1, in a good agreement with the model results. The spectra were measured using a Bruker FTIR spectrometer with approximately 30 s scanning time. The inset for
Figure 3 also shows that linewidth narrowed to ~1 cm
−1 in the vicinity of laser threshold as the spectral region where laser gain equals mirror losses becomes comparable to or less than the spectral width of the AOM response. Linewidth did not change appreciably with power level when the laser operated significantly above threshold. The emission spectrum is slightly asymmetric, as predicted in Reference [
12], and modulated at free spectral range of the laser chip due to a residual reflectivity of the anti-reflection coated facet. For a zero reflectivity coating, a broad single emission line is expected.
The relatively large linewidth could be a limitation for the usefulness of AOM-controlled EC QCLs with a frequency shifted feedback for some applications. This linewidth is, however, sufficiently narrow for numerous other applications, including improvised explosive device (IED) detection and combustion/explosion diagnostics, where absorption features are typically in the range of tens of wavenumbers. If necessary, the linewidth can be significantly reduced employing the standing wave configuration, without sacrificing the response time.
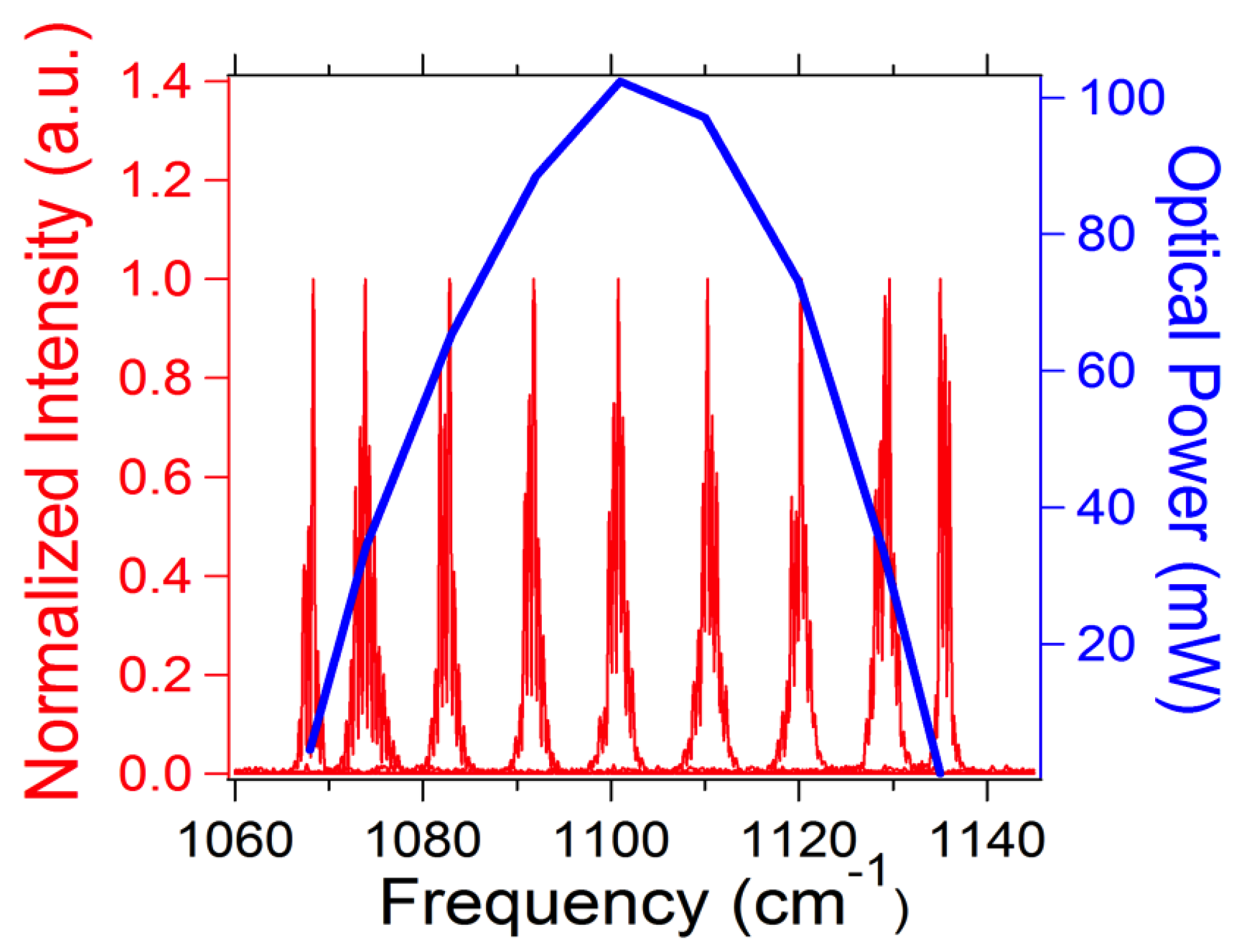
The CW tuning curve for the laser at a 100-mW power level is shown in
Figure 4. The data were collected under the same conditions as the data in
Figure 3. The laser tuning range under these driving parameters covered a spectral range from 1070 cm
−1 to 1135 cm
−1 when AOM frequency was changed from 43.5 MHz to 46.5 MHz.
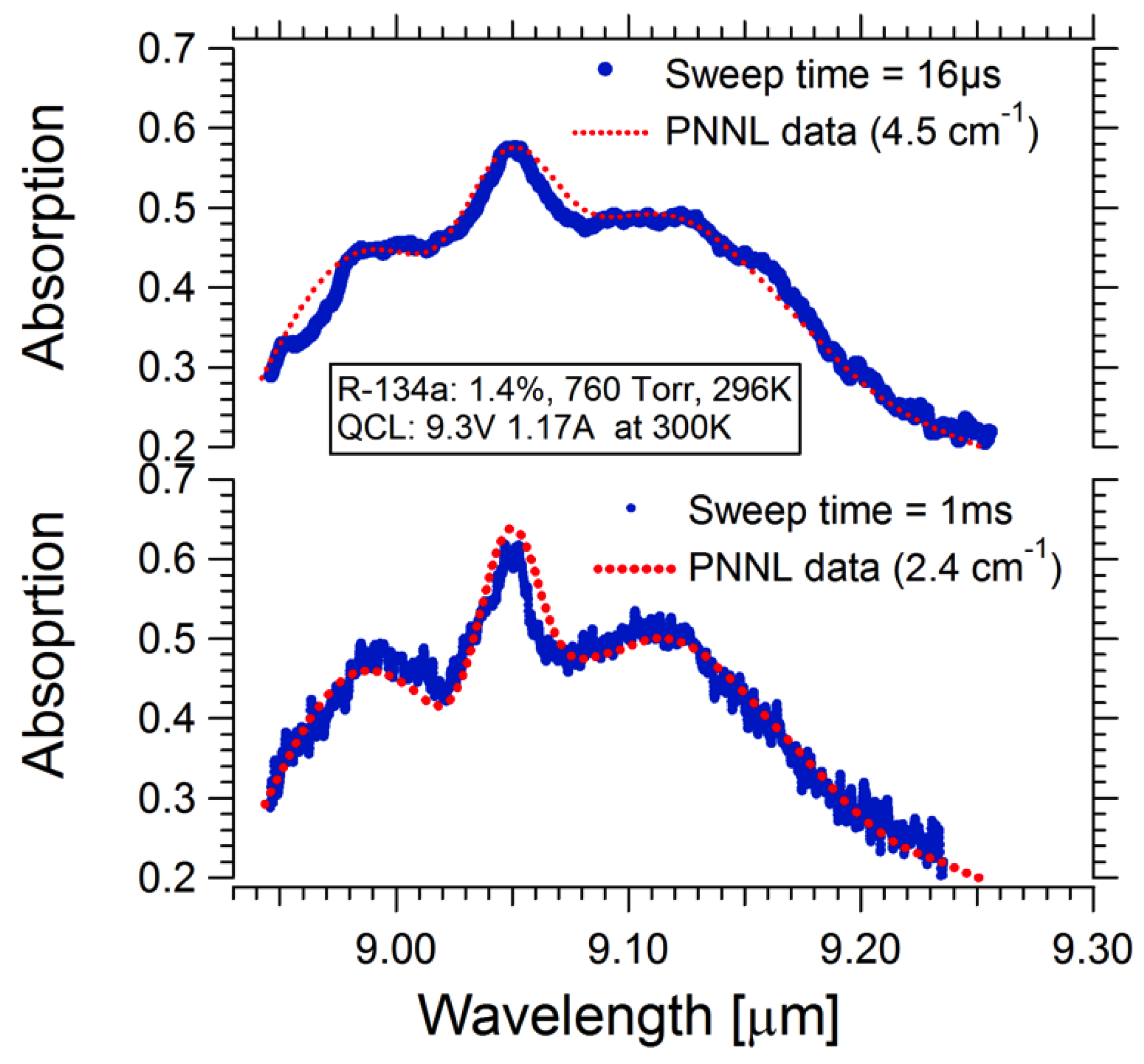
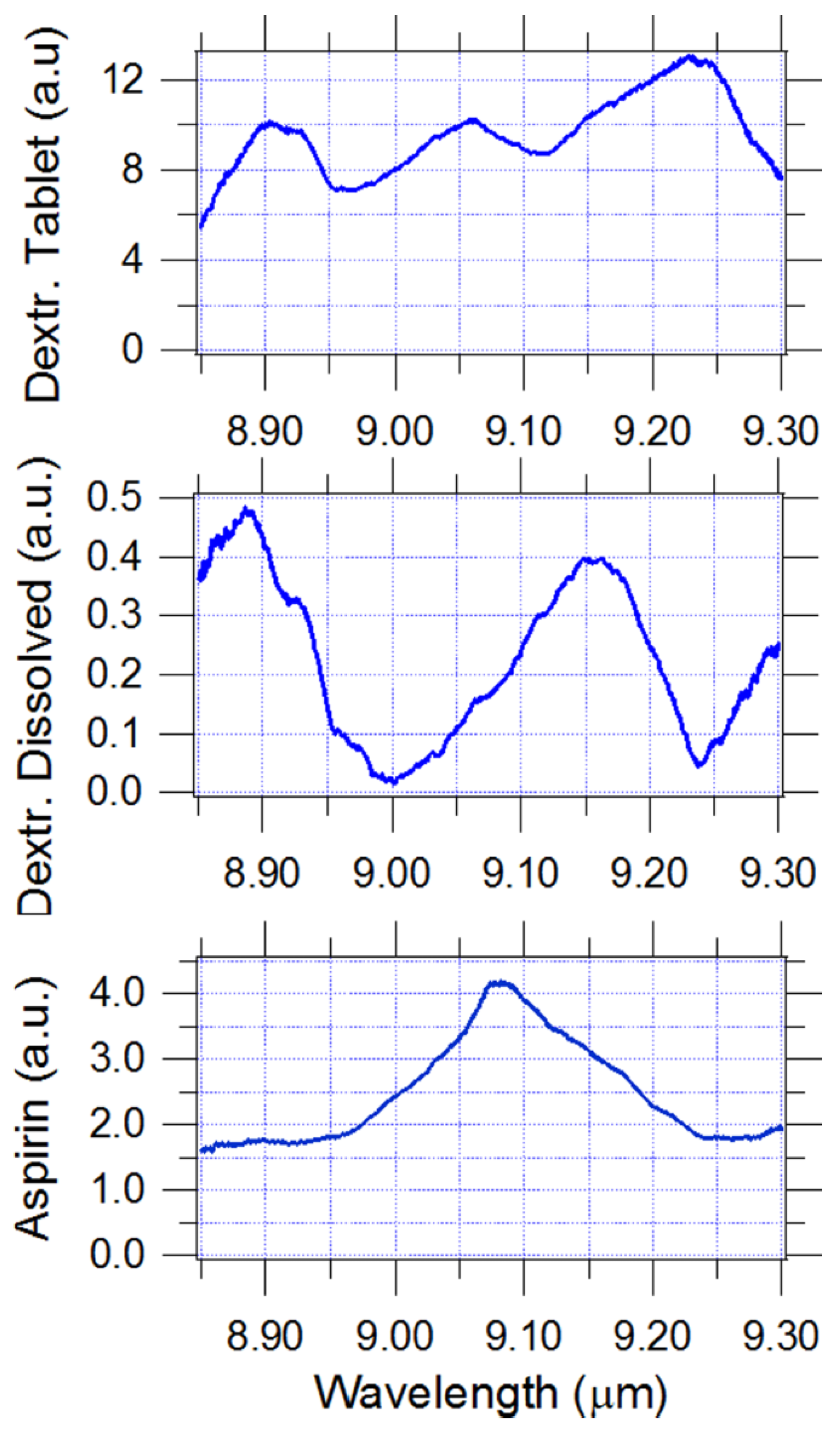
Figure 5 compares transmission spectra for refrigerant R134a (CAS no. 811-97-2) collected with a slow (1 ms) and fast (16 μs) sweep time. It is evident from the figure that the measured spectrum gets smoother as sweep time reduces. The effect can be explained noting that the effective linewidth is expected to increase for short sweep times. The increase in the linewidth required to match the simulated and experimental results is due to the chirp in the sound wave frequency across the area on the crystal illuminated by the beam. The chirp is caused by the continuous frequency sweep from one edge of the tuning curve to the other one within a short period of time. This leads to a spatial variation in the phase grating period created by the sound wave. The frequency spread is approximately a product of scanning rate and time required for sound wave to cross the illuminated area. In terms of the parameters controlled in the experiment, the additional line broadening
can be estimated as:
where
is the tuning range for the laser (~70 cm
−1),
Tsweep is the time taken to sweep emission frequency across the entire tuning range, and
ttr is the sound wave transit time across the beam.
Comparison between the experimental and simulation data (
Figure 5) shows that Equation (3) well describes the additional line broadening with reduction in sweep time: the additional line broadening for 16 μs sweep time compared to the 1-ms case is estimated to be 2.5 cm
−1, in a good agreement with 2.1 cm
−1 deduced from
Figure 5. Therefore, the effective line broadening effect can be taken into account using Equation (3) when ultra-short scanning rates are used.
3.3. Quasi-Continuous Wave Operation
Due to a significant active region temperature rise (up to 100 K), the tuning range of CW EC QCLs is limited. It can be significantly extended by operating the QCL in a quasi-cw (QCW), as opposed to CW, mode of operation with a MHz-scale repetition rate and a duty cycle in the range of 20%–60%. The QCW operation allows the laser active region to cool down during the “off-cycles”, which in turn leads to a reduced average active region temperature and a higher laser performance [
13]. The change of the QCL operation from the CW regime to the QCW regime is expected to lead to a change in linewidth due to the wavelength (thermal) chirp during electrical power cycling. Wavelength tuning and linewidth for the QCW operation are separately discussed below.
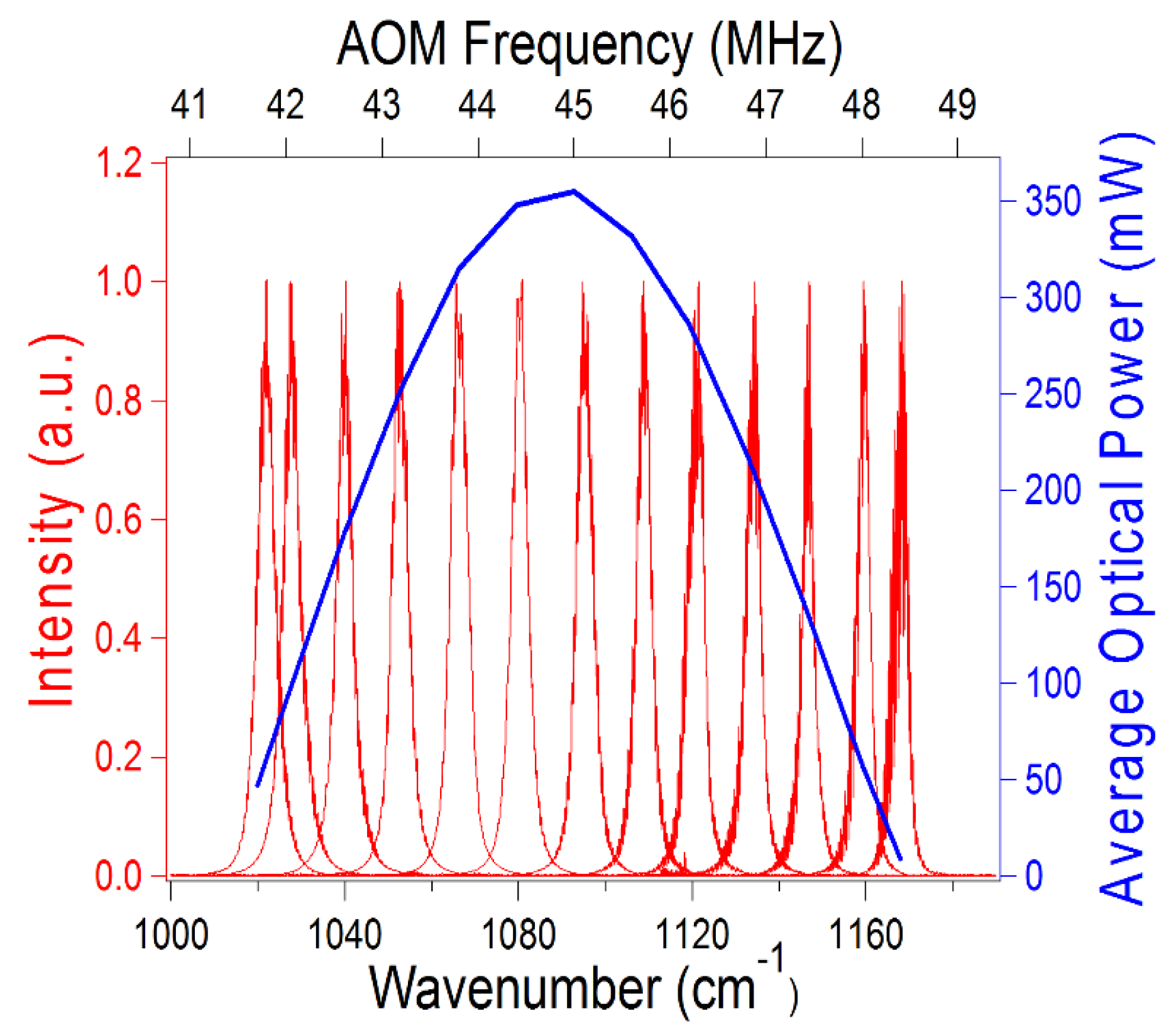
Figure 6 shows a measured tuning curve for the same laser in QCW mode (350 ns pulses and 50% duty cycle) as AOM frequency was changed from 41.7 MHz to 48.5 MHz (approximately 1/3 of the available frequency range). AOM input power was fixed at 35 W, which corresponded to approximately 90% diffraction efficiency and estimated 70% effective coupling efficiency of the external cavity. The emission wavelength for the EC laser tuned from 1020 cm
−1 (9.8 μm) to 1170 cm
−1 (8.5 μm), twice that of CW operation for the same laser. These results clearly demonstrate that a much wider tuning range can be achieved in QCW mode without sacrificing average optical power.
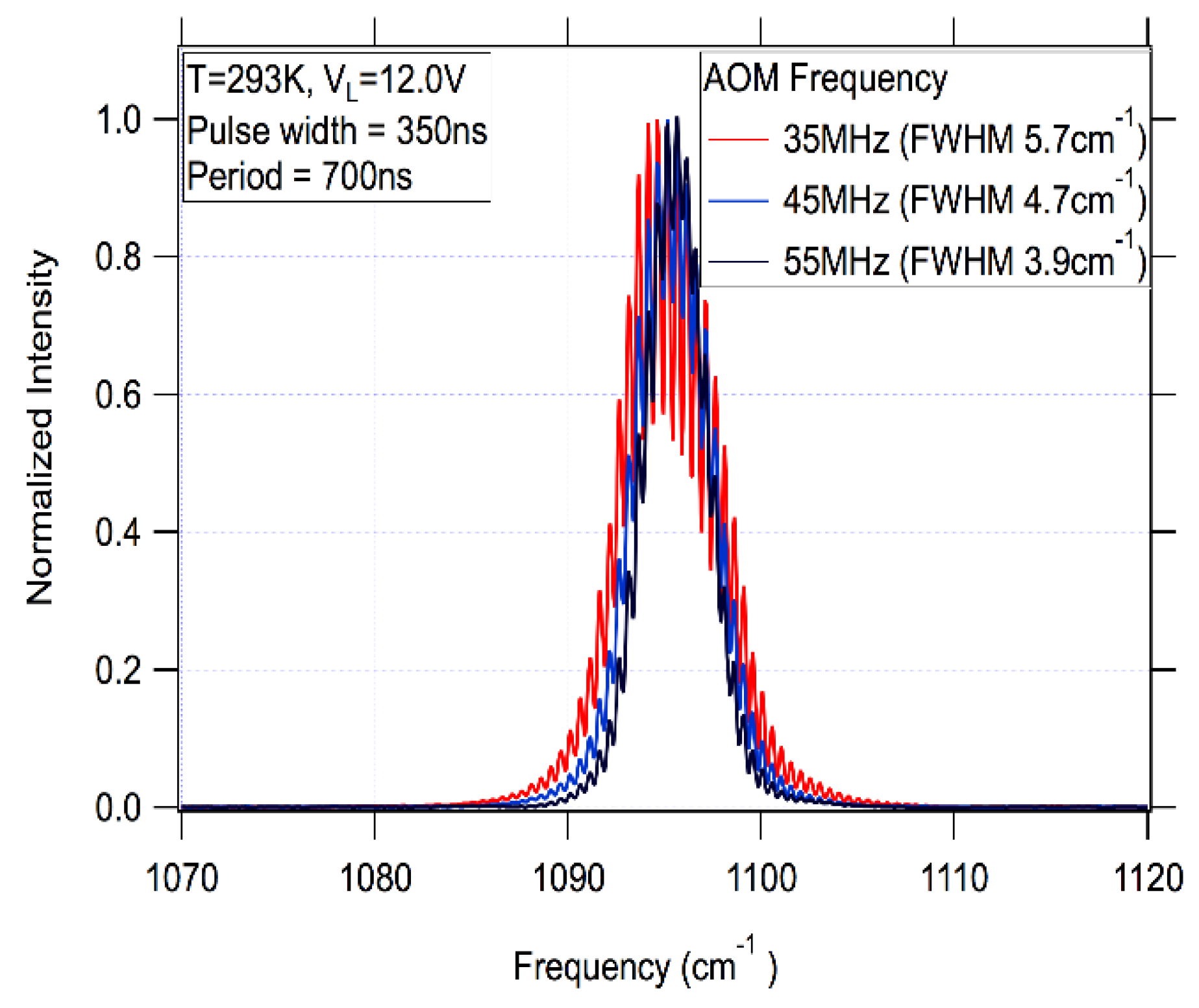
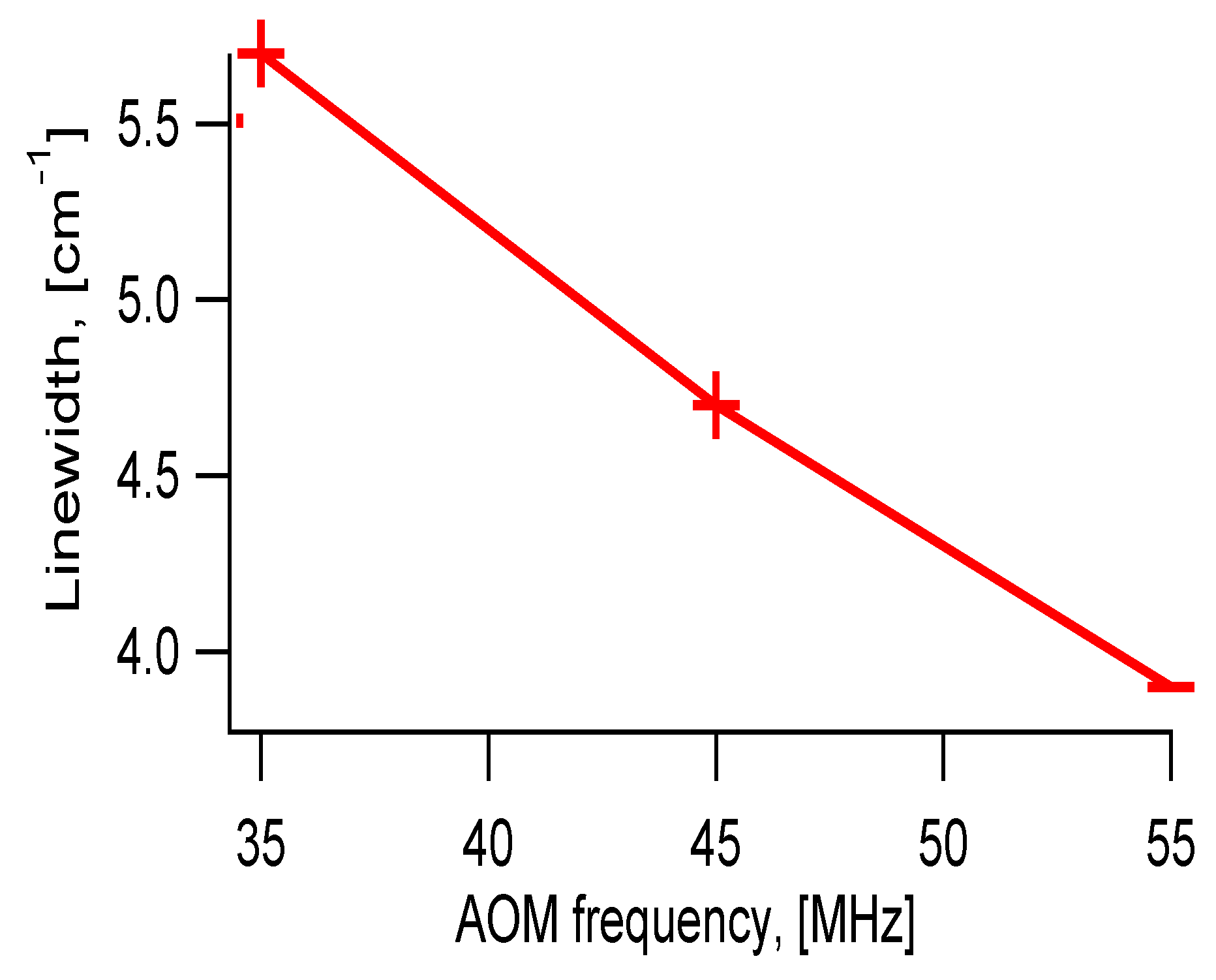
Measured QCL emission spectrum linewidth for AOM central frequency of 45 MHz was 4.7 cm
−1. The increase in linewidth compared to that for CW mode of operation is attributed to the thermal wavelength chirp. The linewidth can be changed by aligning the system so that it operates at a different AOM central frequency (different Bragg condition). Employment of a higher AOM frequency will result into a larger number of illuminated acoustic grating periods and, therefore, to a proportionately narrower linewidth. To demonstrate this effect we measured linewidth for different AOM central frequencies. The increase in the central AOM frequency from 35 MHz to 55 MHz led to a linear reduction in emission linewidth from 5.7 cm
−1 to 3.9 cm
−1, as shown in
Figure 7 and
Figure 8. During these measurements, the position of the high reflectivity mirror was adjusted to keep the lasing wavelength unchanged.
3.5. Future Directions for AOM Tuned QCLs
For the configuration shown in
Figure 1, a substantial fraction of the optical power is lost with the undiffracted beam (diffraction efficiency ~80%). The undiffracted beam can be used as the output beam, as shown in
Figure 11. A very interesting aspect of the new configuration is that AOM RF power can be used to balance the laser feedback and output power. For example, AOM RF power can be (dynamically) tuned to reach the optimal efficiency for each emission wavelength under the tuning curve. This is analogous to controlling front facet reflectivity for the traditional Fabry-Perot chips. However, instead of being fixed by coating layers thicknesses, in this case, the effective reflectivity can be easily electronically adjusted on a microsecond scale.
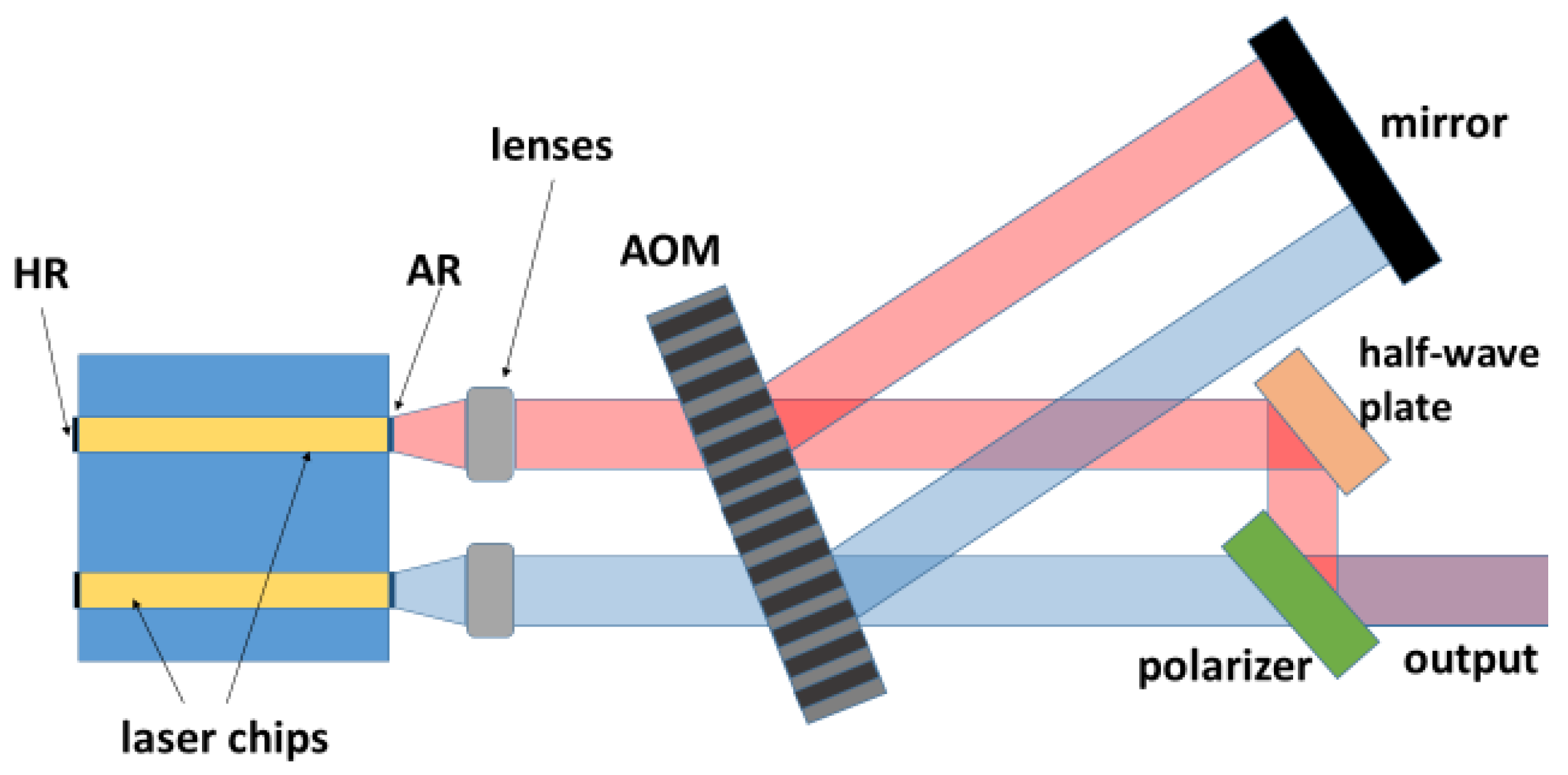
In contrast to the mechanical grating configuration, a single AOM can control several lasers emitting at different wavelengths at the same time. As shown in
Figure 12, two or more emitters with complementary spectral coverages can be combined in a single system without increasing system size and weight. Each of these emitters can be designed to have a broad gain and, therefore, broad tuning range capability [
14,
15]. Their output optical beams can be combined in a single beam using either the polarization beam combining approach or the dichroic beam combining approach. The multiple-emitter configuration is projected to result into a tunable laser source with an ultra-broad coverage (4–12 μm) and ultra-rapid wavelength tuning.
Additionally, unlike mechanical grating tuned QCLs, the AOM-tuned QCLs can be made to operate at more than one wavelength at a time by driving the AOM crystal with a combination of frequencies. Each one of the RF drive frequency sets up an independent grating period, which forces the QCL to operate at different wavelengths simultaneously. As a consequence, several absorption features can be tracked at the same time. Again, the wavelengths can be changed, independently, on a microsecond time scale.
The AOM that was used in References [
7,
8] required water-cooling. However, our experimental results showed that input RF power of only 20–25 W was sufficient for efficient module operation. That level of power dissipated in the crystal can be removed using thermo-electrical cooling (TEC)/air-cooling, a much more compact and power efficient approach. The air-cooled AOM-controlled QCL can be packaged in a “shoebox-size” platform designed for handheld applications.