Lateral Modes in Quantum Cascade Lasers
Abstract
:1. Introduction
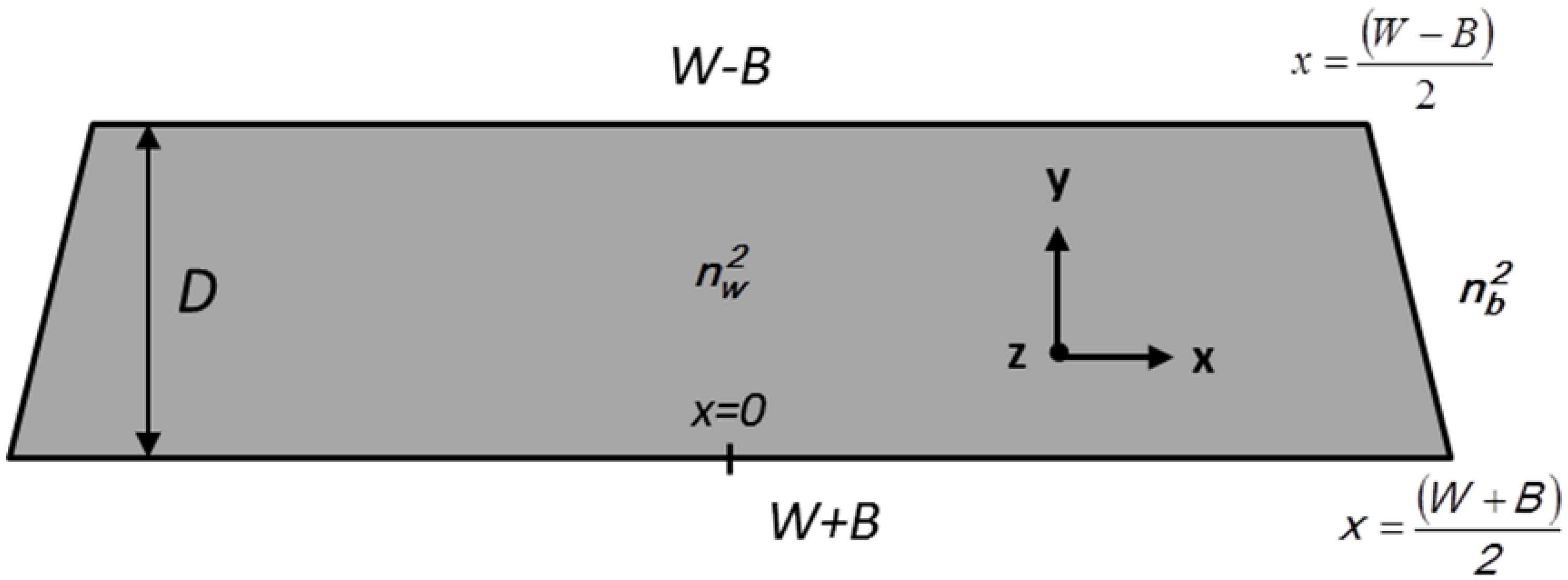
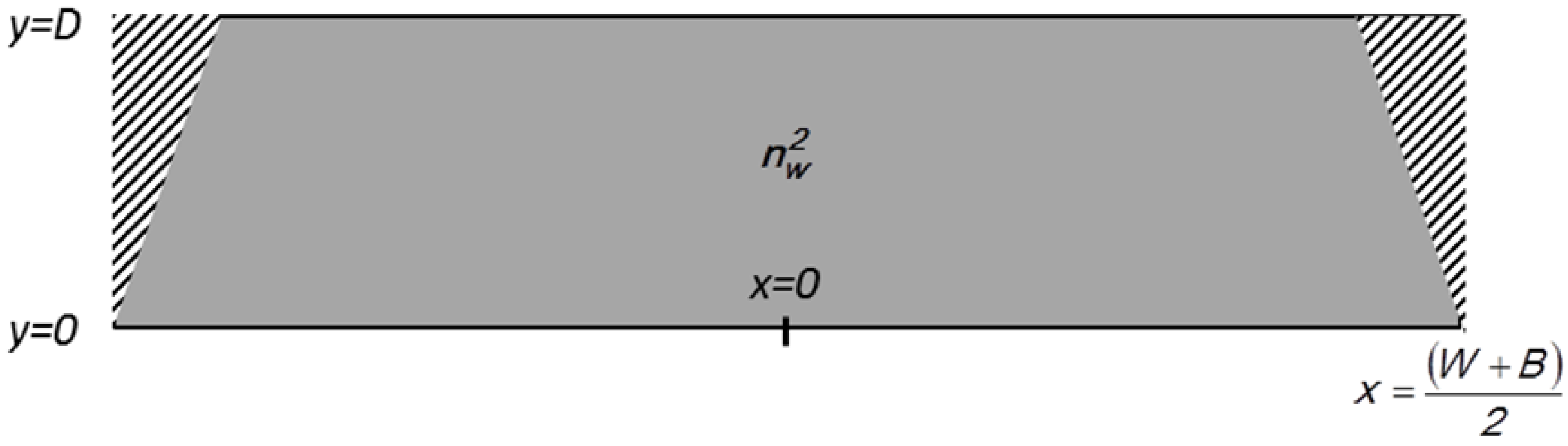
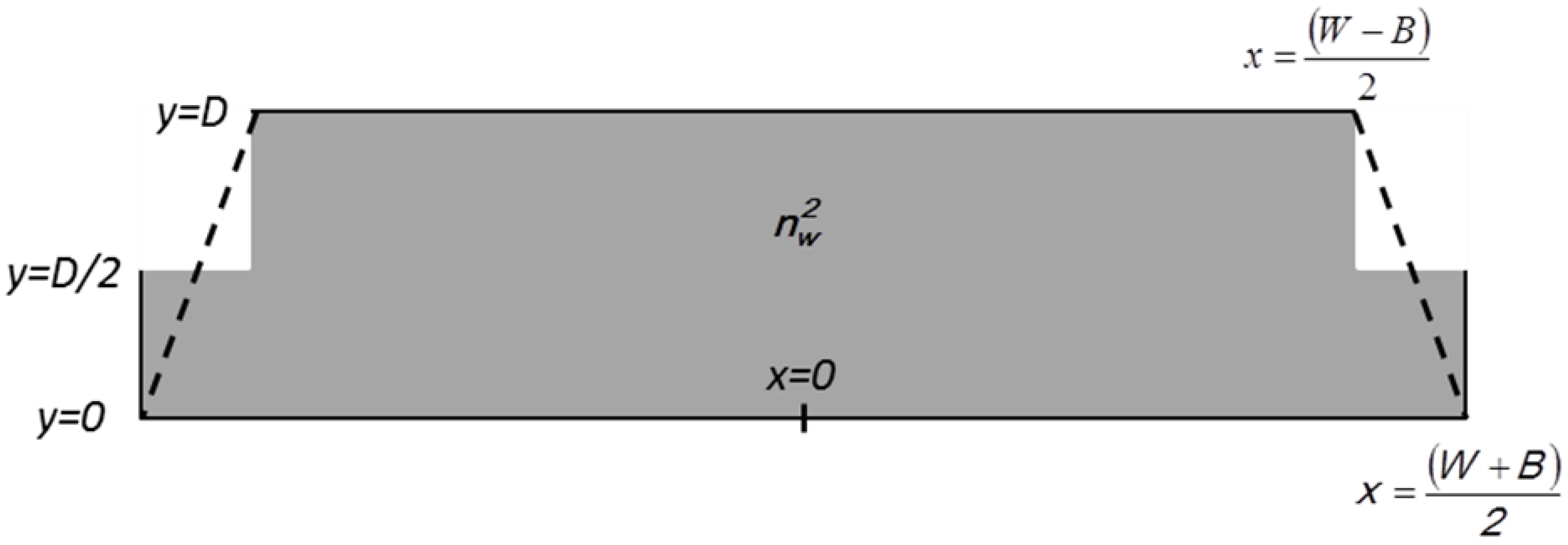
2. Perturbation Approach to the Trapezoidal Waveguide Modes
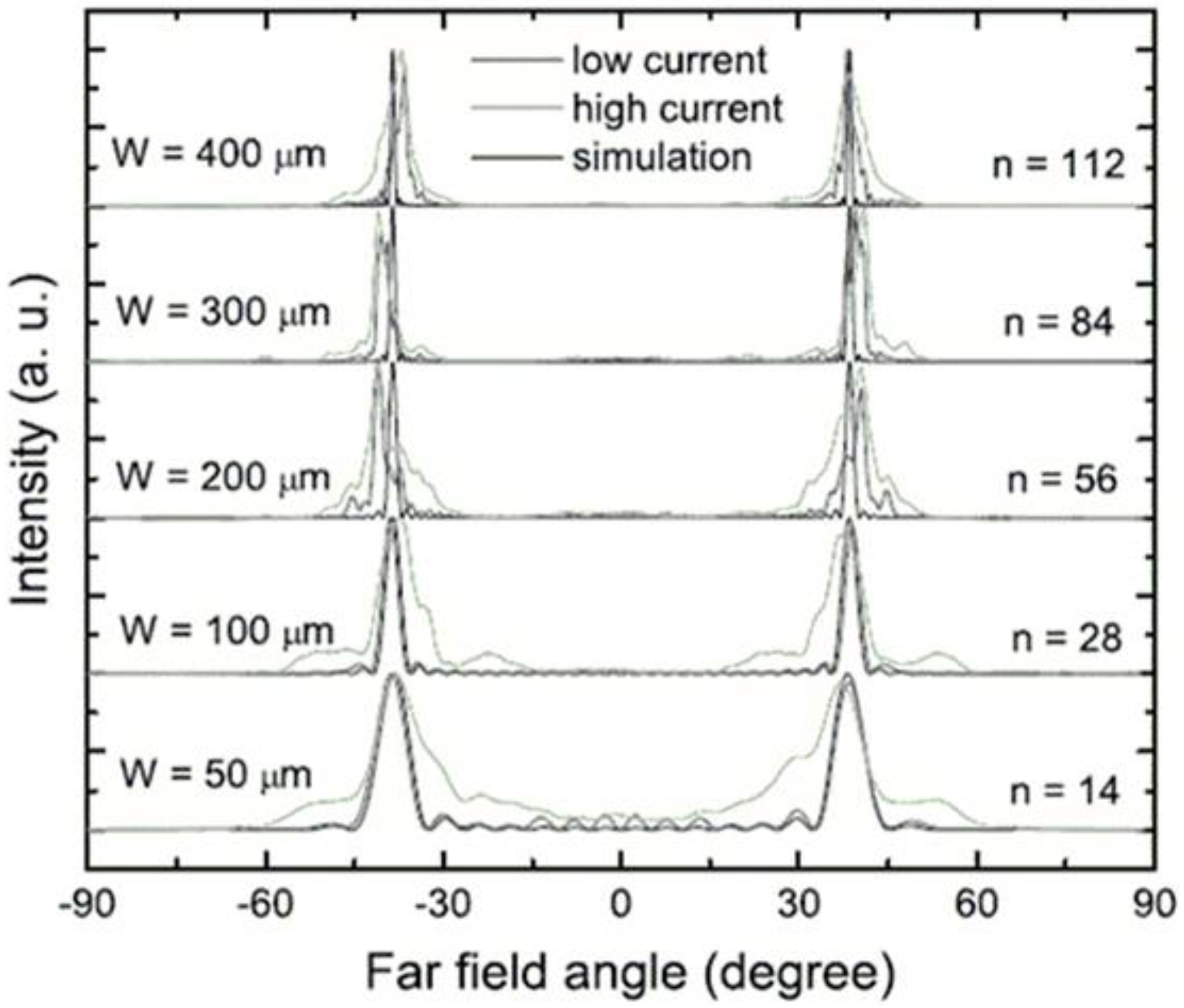
3. Examples of QCL Cavity Mode Calculations
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Razeghi, M.; Bandyopadhyay, N.; Bai, Y.; Lu, Q.; Slivken, S. Recent Advances in Mid Infrared (3–5 μm) Quantum Cascade Lasers. Opt. Mat. Exp. 2013, 3, 1873–1884. [Google Scholar] [CrossRef]
- Bai, Y.; Slivken, S.; Darvish, S.R.; Haddadi, A.; Gokden, B.; Razeghi, M. High Power Broad Area Quantum Cascade Lasers. Appl. Phys. Lett. 2009, 95, 221104. [Google Scholar] [CrossRef]
- Yu, N.; Diehl, L.; Cubukcu, E.; Pflügl, C.; Bour, D.; Corzine, S.; Zhu, J.; Höfler, G.; Crozier, K.B.; Capasso, F. Near-field Imaging of Quantum Cascade Laser Transverse Modes. Opt. Express 2007, 15, 13227–13235. [Google Scholar] [CrossRef] [PubMed]
- Toor, F.; Sivco, D.L.; Liu, H.E.; Gmachl, C.F. Effect of Waveguide Sidewall Roughness on the Threshold Current Density and Slope Efficiency of Quantum Cascade Lasers. Appl. Phys. Lett. 2008, 93, 031104. [Google Scholar] [CrossRef]
- Marcuse, D. Theory of Dielectric Optical Waveguides; Academic Press: New York, NY, USA, 1991. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dente, G.C.; Tilton, M. Lateral Modes in Quantum Cascade Lasers. Photonics 2016, 3, 11. https://doi.org/10.3390/photonics3010011
Dente GC, Tilton M. Lateral Modes in Quantum Cascade Lasers. Photonics. 2016; 3(1):11. https://doi.org/10.3390/photonics3010011
Chicago/Turabian StyleDente, Gregory C., and Michael Tilton. 2016. "Lateral Modes in Quantum Cascade Lasers" Photonics 3, no. 1: 11. https://doi.org/10.3390/photonics3010011
APA StyleDente, G. C., & Tilton, M. (2016). Lateral Modes in Quantum Cascade Lasers. Photonics, 3(1), 11. https://doi.org/10.3390/photonics3010011




