Abstract
We present an extensive study of equalization enhanced phase noise (EEPN) in coherent optical system for all practical electronic dispersion compensation configurations. It is shown that there are only eight practicable all-electronic impairment mitigation configurations. The non-linear and time variant analysis reveals that the existence and the cause of EEPN depend on the digital signal processing (DSP) schemes. There are three schemes that in principle do not cause EEPN. Analysis further reveals the statistical equivalence of the remaining five system configurations resulting in EEPN. In three of them, EEPN is due to phase noise of the transmitting laser, while in the remaining two, EEPN is caused by the local oscillator. We provide a simple look-up table for the system designer to make an informative decision regarding practicable configuration choice and design.
1. Introduction
Coherent detection in optical communication was extensively studied in the 80’s and 90’s because of its ability to achieve high receiver sensitivity. But the invention of erbium-doped fiber amplifiers along with its own complexity and other practical deficiencies made coherent optical communication less attractive [1,2,3,4,5]. The advancements in high speed digital signal processing (DSP) have revived the interest in coherent communications. Together, they have the potential to increase the spectral efficiency, compensate for linear transmission impairments and also achieve carrier synchronization [6,7,8,9]. However, it is observed that the received constellation in uncompensated coherent optical links, even after DSP, remains influenced by enhanced noise commonly known as equalization enhanced phase noise (EEPN) [10,11,12,13,14,15,16]. Various studies have been performed with both simulations and system experiments to evaluate these impairments for different modulations on receiver carrier recovery and adaptive equalizers [17,18,19]. This noise enhancement is shown to be in both phase and amplitude dimensions and will also cause time jitter [20,21,22], which is not observed in systems with ideal dispersion compensation in the optical domain. We recently revisited this phenomenon and show in [23] with a frequency domain analysis that the EEPN-induced transmission penalty is mainly due to low frequency noise of the local oscillator (LO). Hence, elimination of the frequency noise below a certain cutoff frequency significantly reduces the transmission penalty even in extreme cases. The results were experimentally validated in [24]. Based on the findings in [23,24,25], a realistic implementation of the mitigation technique was proposed in [26].
In our recent paper [27], we presented a rigorous nonlinear and time variant analysis (non-LTI) of the most common system configuration with post-reception electronic dispersion compensation (EDC) followed by carrier phase recovery (CPR). Statistical properties were derived and closed form expressions of the necessary LO linewidth and/or mitigation bandwidth essential for the system design were given. Based on the finding of this paper, the physical origin of EEPN can be understood by considering three different coherent reception scenarios as shown in Figure 1 above. It is important to note the transmitting laser and the LO laser have an asymmetric relationship with respect to dispersive transmission fiber. The transmitting laser output after the in-phase and quadrature phase (IQ) modulator is multiplied with the dispersive fiber transfer function, while the LO convolves with the same transfer function in the photodetectors (in frequency domain). Thus, it is critical to consider the evolution of the signal from source to destination in order to understand EEPN. In the first scenario of homodyne reception, the time domain electrical signal is modulated on an ideal transmitting laser centered at f0 using an IQ modulator. This signal is temporally broadened during the transmission over a dispersive fiber. The broadened optical pulse is coherently received using an ideal LO with central frequency f0 matched to the transmitting laser. The original transmitted pulse is then ideally recovered by the static EDC. Now, if the same broadened optical pulse is received using heterodyne detection with an ideal LO with a central frequency, f1 shifts from the transmitting laser frequency. The received pulse after coherent reception in this scenario has a broadening equal to the pulse received with homodyne detection, but the pulse is delayed by a factor proportional to the accumulated dispersion and relative frequency difference f1. The EDC is able to compensate for the dispersion-induced broadening but not the delay induced by the heterodyne detection. However, this delay is not critical in this ideal heterodyne case since the entire symbol sequence suffers the same constant delay, which can be easily compensated. In the last scenario, reception using an LO with a non-zero Lorentzian linewidth is considered. As illustrated by the figure, the coherent reception with this LO will result in reception of a complex superposition of several broadened versions of the pulse, each with an individual delay (and amplitude) proportional to the frequency shift (and amplitude) of the corresponding side band component of the LO laser. Similar to the heterodyne case, the static EDC is able to compensate for the broadening but not the delay of different received versions of the pulse. Thus, the phenomenon of EEPN is reminiscent of multipath interference in radio.
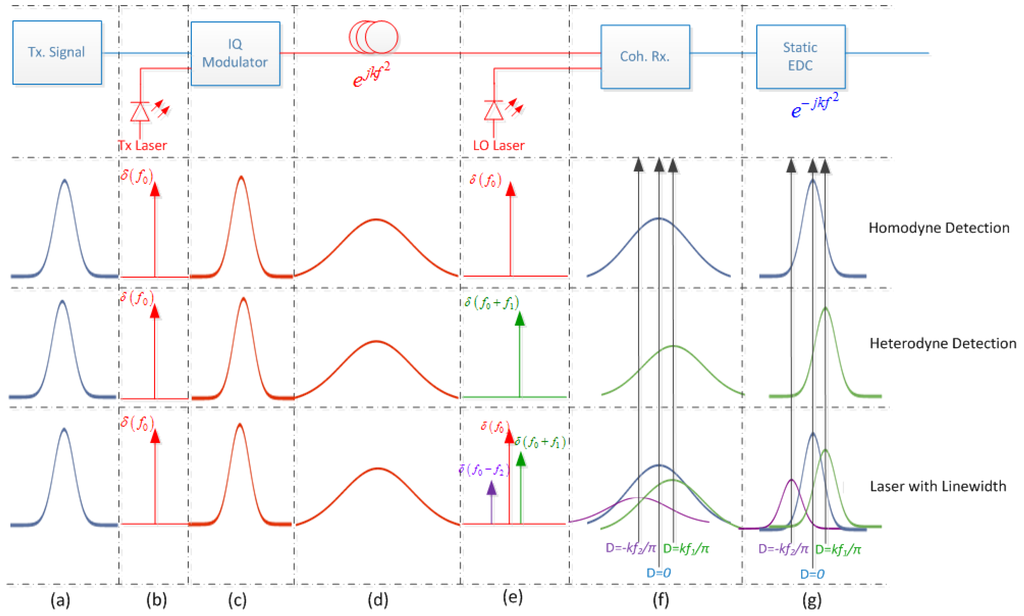
Figure 1.
Physical explanation of EEPN in the most common coherent optical system configuration with electronic dispersion compensation. (a) Time domain electrical pulse to be modulated on the Tx laser, (b) Ideal transmitting laser (c) Optical pulse at the output of optical IQ modulator (d) Optical pulse after transmitting through dispersive fiber (e) Local Oscillator laser for three different scenarios (f) Received time domain signal after coherent detection (g) Received signal after static dispersion equalizer. Note: D depicts the delay relative to the pulse with homodyne detection with ideal LO as could be seen from Equation (4); considering only pulse envelop for visual understanding.
The analysis of origin of EEPN in this specific all-electronic mitigation configuration highlights the important property of asymmetry between the transmitting and receiving laser in such coherent links. Thus, the order in which the all-electronic mitigation is performed is critical for the origin and impact of EEPN in any such link. It is important to note that there are more than one DSP schemes practicable in coherent optical systems with EDC (e.g., [12, 13]) apart from the one covered in [27]. The origin and impact of EEPN in such schemes remain unknown. Therefore, an extensive analysis of EEPN in all practicable DSP schemes is crucial for the system designers to make an informative choice.
In this paper, we present a non-LTI analysis of EEPN for all practicable DSP schemes in coherent optical systems with EDC. The analysis reveals that the existence and origin of EEPN depends on the DSP scheme for electronic impairment mitigation. We show that there are only eight DSP schemes that are practicable. Some of these schemes do not result in EEPN, whereas the remaining schemes result in EEPN, and in spite of having different sources, are statistically equivalent. The results that are useful for a system designer to make an informed decision are summarized in the form of a simple look-up table.
This paper is organized as follows. In Section 2, we discuss practically realizable system configurations with EDC. In Section 3, we derive time and frequency domain responses for all these configurations. These responses are then utilized to obtain statistical properties of the received signal for all the configurations. In Section 4, the results that are useful for a system designer to make an informed choice are discussed and summarized. The conclusions are finally drawn in Section 5.
2. Practicable Schemes Employing All-Electronic Impairment Mitigation
In this section, we discuss possible implementations of a coherent optical system utilizing all-electronic impairment mitigation. For the analysis, without loss of generality, we utilize the base band equivalent representation of the system configurations. A generalized system configuration for coherent optical systems employing all-electronic impairment mitigation is shown in Figure 2. In coherent digital communications, the information is encoded in phase and/or amplitude to achieve high spectral efficiency, depending on modulation format, for each polarization. In the following analysis, without loss of generality, we consider a power normalized representation of the components, so that the net system gain remains unity, independent of the transmitted constellation. In general, the incoming bits are mapped on symmetrically distributed symbols cn in the complex plane. This results in a symbol train at the rate Rb/m, where m is the number of bits encoded per symbol and Rb is the incoming bit rate. The symbol train with symbol period Ts = m/Rb is convolved with a pulse shaping filter represented by the Fourier transform pair to generate a band limited continuous signal with Fourier transform pair r(t). Then, the band-limited signal is pre-processed in some system configurations to a priori compensate for the impairments such as channel chromatic dispersion (CD) and/or laser phase noise. The resultant pre-processed signal is modulated on the transmitting laser to generate the output signal. The stochastic base band equivalent representation of the transmitting laser Tx before modulation can be written as . The transmitter output passes through the all-pass dispersive fiber with the response . The accumulated dispersion factor , where β2 is the group velocity dispersion parameter (GVD), l is the fiber length, D is the dispersion coefficient, c is the speed of light and f0 is the central optical frequency. Finally, the signal is coherently detected with an LO having a stochastic base band equivalent response of .
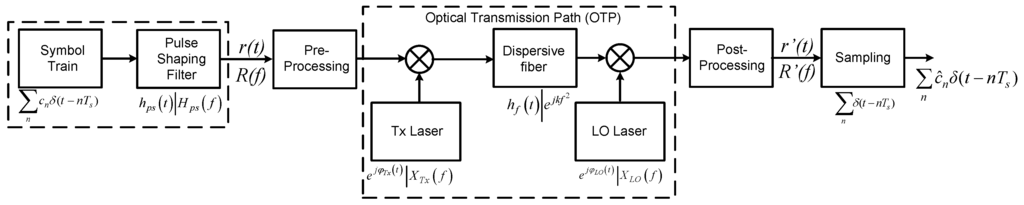
Figure 2.
Generalized system model of a coherent optical system with electronic dispersion compensation. The Fourier transform pairs of the signal and the response of components are indicated.
The Optical Transmission Path (OTP) consists of the following operations: modulation on Tx laser, transmission over the fiber link and coherent detection with LO laser. The detected signal is then processed to mitigate the residual impairments, which are not pre-mitigated on the transmitter side. The received signal after post-processing is given by the Fourier transform pair . The post-processing might also involve filtering with an optimally matched filter in the presence of additive white Gaussian noise (AWGN) to improve signal quality. However, as shown in [11,27], the linear filtering has a negligible impact on EEPN because its spectrum is almost identical to the signal spectrum. Hence, in these analyses, without compromising stringency, we neglect the matched filtering operation. The validity of this consideration for all system configurations shall be proved later. Furthermore, as the sampling is a memoryless operation, sampling and then performing CPR is equivalent to performing CPR followed by sampling operation. Thus, a generalized system configuration can be modeled as shown in Figure 2. In the following analysis, the mitigation transfer functions are modeled as the inverse of the impairment sources assuming ideal compensation. The Fourier transform pair of the mitigation operations for EDC and CPR are given by and where “Laser” represents transmitting laser Tx, local oscillator LO, or combined recovery for both Tx and LO given by Tx + LO.
As discussed earlier, due to the possibility of both pre-and post-processing, more than one system configuration is feasible. Therefore, it is imperative to ascertain the practically implementable configuration out of a large number of possibilities that could be conceptualized by permuting the order and position (pre and/or post) of the three mitigation operations that are equalization of the fiber CD, CPR for Tx and CPR for LO. The first option resulting from the permutations is to perform all the impairment mitigation in the pre-processing block. This implies transmitting a pre-distorted signal so that after interacting with the physical source of impairments, the original signal is restored. This configuration is not practically feasible as it would require a priori knowledge of the phase noise information of the LO laser well ahead in time. It would also require an additional spectral channel to transmit this information to the transmitter side with hardware overhead without offering any reasonable advantage. Thus, in the analysis, we discard all permutations requiring CPR of the LO laser to be performed on the transmitter side.
The second obvious permutation option is to perform processing of all impairments after coherent detection. The first choice in this category is to perform equalization followed by combined CPR for both Tx and LO lasers as given by the Scheme 1 (see Table 1). This is the most common configuration and can be implemented with blind feed-forward mitigation based on the estimation from the received signal only [7]. The analysis of this configuration for EEPN impact was provided in [27]. The second feasible scheme in all-post processing category is given by Scheme 2 (see Table 1). In this configuration the combined carrier phase recovery is performed before dispersion EDC. This configuration can be realized in practice by utilizing the radio frequency (RF) pilot tone as proposed in [13,14]. The RF pilot tone contains the combined phase information from both the transmitter and receiver and provides reasonable performance in the back-to-back case. The next possible scheme is given by Scheme 3 (see Table 1), where the CPR of the LO is performed before the equalizer and the CPR of the Tx after the equalizer. In [25,26], it is realized by extracting phase noise information from the LO laser using low bandwidth digital coherence enhancement. Later, the compensation is performed before the equalizer in the post-processing block. A permutation of Scheme 3 could be to perform CPR for the Tx before the equalizer and CPR for LO after the equalizer. This configuration requires estimation of the transmitter phase noise independent of the LO phase noise, which is not possible after reception. Alternatively, it could be implemented by extracting the phase noise information on the transmitter side and then transmitting it together with data to the receiver side. This process is practically unbeneficial for same reason as discussed for performing CPR of LO on the transmitter side.

Table 1.
All practicable schemes for electronic impairment mitigation in coherent optical systems.
The other category of configurations is to distribute impairment mitigation operations between pre-and post-processing blocks. The first subset of this category is to perform only the CPR for Tx on the transmitter side and equalization along with CPR for LO on the receiver side. The CPR for Tx in the pre-processing block requires information of the Tx phase noise a priori to data modulation. This can be realized by using low speed digital coherence enhancement proposed in [25,26]. The post-processing can have two variants depicted by Schemes 4 and 5. The post-processing in Scheme 4 can be realized in the similar manner as Scheme 1. Meanwhile, in Scheme 5, it can be realized in the similar manner as Scheme 3. The second subset of this category is to perform the pre-equalization and post CPR for Tx and LO combined (see Scheme 6). This configuration has been discussed and evaluated in [12]. It is feasible when the system has a priori information about the route of the optical signal in the network. In the last subset of these configurations, the equalization and the CPR for Tx are performed in the pre-processing block. Meanwhile, the CPR for LO is performed in the post-processing block. This subset (see Schemes 7 and 8) can be practically realized using the digital coherence enhancement proposed in [25] and [26]. Schemes such as distributing the amount of EDC between the pre- and post-processing blocks are discarded as they do not provide any additional advantage as shown later. Thus, the study of all possible permutations results in only eight pragmatic configurations summarized in Table 1.
3. Analysis of EEPN in Practicable System Configurations
In this section, we perform mathematical analysis of all pragmatic configurations (see Table 1). The analysis provides time and frequency domain responses of the signal influenced by EEPN. Please note that the extended explanation on the derivations of the time domain responses from the frequency domain along with the statistical properties and parameters can be found in [27].
3.1. Analysis of Scheme 1
Scheme 1 corresponds to the specific realization of Figure 2 in which equalization is performed in the post-processing block followed by combined CPR for Tx and LO as given in Table 1. The frequency domain response of the received signal is then given by
where and the combined CPR . Performing the operation in Equation (1) in the order of their physical occurrence, due to a non-associative relationship between multiplication and convolution, we obtain
The frequency domain analysis reveals that the linear accumulated channel dispersion, i.e., , is compensated by the linear channel equalizer . However, the intermixing of side bands of the dispersed signal and the LO output in the intensity sensitive photodetectors are not compensated for in the linear equalizer, which results in an enhancement of noise.
Taking the inverse Fourier transform (IFT) of Equation (2) gives the time domain response as
We can observe from Equation (3), that each side band component of the LO demodulates a delayed version of the transmitted signal r(t). The delay is proportional to its frequency component relative to the central frequency (zero in the base band equivalent case). Thus, EEPN is caused by the interference of these multiple delayed versions of the original signal r(t) with itself. For digital modulations, then Equation (3) can be written as
In Equation (4), n = 0 gives the original transmitted symbol along with intra symbol interference, while n ≠ 0 corresponds to inter symbol interference.
Performing the statistical analysis by following the steps given in [27] indicates that the received signal impaired by EEPN is zero mean with variance
3.2. Analysis of Scheme 2
Scheme 2 corresponds to the specific realization of Figure 2 with only post-processing in the order given in Table 1. The frequency domain response of the received signal is given by
where and the combined CPR . Performing the operations in Equation (6) we obtain
In this case, the linear accumulated channel dispersion i.e., , is also compensated by the linear channel equalizer and the frequency noise of the LO is compensated by the corresponding CPR. The role of the LO laser in this case is substituted by that of the Tx CPR. In an ideal case, it is the complex conjugate of the Tx laser phase noise.
Taking the IFT of Equation (7) gives the time domain response as
We can observe from Equation (8), that each side band component of the Tx CPR effectively demodulates a delayed version of the transmitted signal r(t). The delay is proportional to its frequency component relative to the central frequency (zero in the base band equivalent case). For digital modulation, Equation (8) can be written as
In Equation (9), n = 0 gives the original transmitted symbol along with intra symbol interference, while n ≠ 0 corresponds to inter symbol interference. The statistical analysis shows that Scheme 2 has identical statistical properties as Scheme 1, except for the fact that in Scheme 2, the role of the LO laser is replaced by the transmitting laser CPR, resulting in the variance
3.3. Analysis of Scheme 3
Scheme 3 corresponds to the specific realization of Figure 2 in which the CPR for LO in the post-processing is performed before equalization and the CPR for the Tx laser after it, as given in Table 1. The frequency domain response of the received signal is given by
where . The operations in Equation (11) are performed in the order of their physical occurrence. We observe that all mitigation functions ideally compensate the corresponding impairments. Thus, the received signal in an ideal case is equal to the transmitted signal r(t), resulting in zero EEPN. Since this scheme does not have EEPN ideally, the mean and variance due to EEPN are both zero.
3.4. Analysis of Scheme 4
Scheme 4 corresponds to the specific realization of Figure 2 with Tx CPR performed in the pre-processing block and LO CPR and equalization in the post-processing block in the order given in Table 1. The frequency domain response of the received signal is given by
In Equation (12), the phase noise from the transmitter is compensated by the pre-processing CPR for the transmitting laser. Performing the operations in Equation (12), we obtain
Taking the IFT of Equation (13) gives the time domain response, which is equal to the received signal in Scheme 1 for an ideal transmitting laser, as can be seen from Equation (4)
We can observe from Equation (14), each side band component of the LO demodulates a delayed version of the transmitted signal r(t). The delay is proportional to its frequency component relative to the central frequency (zero in the base band equivalent case), similar to Scheme 1. For digital modulation, Equation (14) can be written as
In Equation (15), n = 0 gives the original transmitted symbol along with intra symbol interference, while n ≠ 0 corresponds to inter symbol interference. The source of EEPN in this scheme is LO laser similar to Scheme 1. Thus, performing the statistical analysis of the received signal yields the variance and mean equal to that obtained in Scheme 1.
3.5. Analysis of Scheme 5
Scheme 5 corresponds to the specific realization of Figure 2 consisting of pre-processing for Tx laser and post-processing for LO laser along with EDC in the order given in Table 1. The frequency domain response of the received signal is
In Equation (16), similar to Scheme 3, all mitigation functions ideally compensate the corresponding, resulting in no EEPN in an ideal compensation scenario.
3.6. Analysis of Scheme 6
Scheme 6 corresponds to the specific realization of Figure 2 with pre-EDC and post carrier phase recovery. The frequency domain response of the received signal is
where the combined CPR . In this case, the CPR of the LO compensates for the LO phase noise, and the system is influenced mainly by the transmitter phase noise. Performing the operation in Equation (17) in the order of their physical occurrence we obtain
In this scheme, the equalizer behaves as the source of CD, which is compensated by fiber dispersion with conjugate response. Thus, the EEPN is generated at the modulator with Tx laser as the source.
Taking the IFT of Equation (18) gives the time domain response as
We can observe from Equation (19) that each side band component of the Tx generates a delayed version of the transmitted signal r(t). The delay is proportional to its frequency component relative to the central frequency (zero in the base band equivalent case). For digital modulation, Equation (19) can be written as
In Equation (20), n = 0 gives the original transmitted symbol along with intra symbol interference, while n ≠ 0 corresponds to inter symbol interference. Performing the DSP as per Scheme 6 results in the received signal variance given by
It can be seen that for this Scheme, the variance of the received signal is equivalent to that obtained in Schemes 1, 2 and 4. The only difference is that in this Scheme, the contributing sources of EEPN are Tx laser and pre-EDC block, resulting in a change of sign of the accumulated dispersion in the variance.
3.7. Analysis of Scheme 7
Scheme 7 corresponds to the specific realization of Figure 2 consisting of pre-processing for both EDC and Tx laser in the given order followed by post-processing for LO as given in Table 1. The frequency domain response of the received signal is given by
Performing the operations in Equation (22), we see that similar to Schemes 3 and 5, this scheme ideally does not result in EEPN.
3.8. Analysis of Scheme 8
Scheme 8 corresponds to the specific realization of Figure 2 consisting of pre-processing for both Tx laser and EDC in the given order followed by post-processing for LO as given in Table 1. The frequency domain response of the received signal is given by
where . In this case, as in Scheme 6, the CPR of the LO compensates for the LO phase noise, and the system is influenced mainly by the transmitter phase noise. Performing the operation in Equation (23) in the order of their physical occurrence we obtain
The equalizer behaves as the source of CD, which is compensated by fiber dispersion with conjugate response. Taking the IFT of Equation (24) gives the time domain response as
We can observe from Equation (25) that each side band component of the Tx laser generates a delayed version of the transmitted signal r(t). The delay is proportional to its frequency component relative to the central frequency (zero in the base band equivalent case). For digital modulation Equation (25) can be written as
In Equation (26), n = 0 gives the original transmitted symbol along with intra symbol interference, while n ≠ 0 corresponds to inter symbol interference.
In this case, similar to Scheme 6, the contributing sources are Tx laser and the pre-EDC module on the transmitter side. The LO laser phase noise is ideally compensated with a corresponding CPR. Thus, performing the statistical analysis of the received signal yields the variance and mean equal to those obtained in Scheme 6.
It is interesting to note that in all the cases resulting in EEPN, it could be observed from the frequency domain response that the noise spectrum is a slightly broadened version of the signal spectrum R(f). The broadening is governed by the linewidth of the laser, which is normally negligible compared to the signal baud rate. This results in an EEPN spectrum almost identical to the signal spectrum. Thus, the matched filtering has negligible influence on the EEPN noise as shown in [11,27].
4. System Design Aspects
It is essential for the system designer to be able to estimate the impact of EEPN for different system configurations in order to make an informed choice. The system designer can either opt for a system configuration with tolerable penalty or a configuration that allows for mitigation of EEPN. In case of the system configurations resulting in EEPN, it is important to know the required linewidth to limit the penalty below a certain limit. While in the configuration that facilitates EEPN mitigation (see Schemes 3, 5 and 7), it is essential to know the EEPN mitigation bandwidth so as to limit the penalty below a certain limit in a practical implementation.
The statistical properties and parameters of the received stochastic signal for all eight practicable schemes are obtained from the responses derived in Section 3. Table 2 summarizes all the useful information related to EEPN that one needs to know for a given configuration, in order to make an informed choice. The first column in the table provides the identification code of a given scheme. The second column gives the source of EEPN in a given configuration, if any. The variance of the received signal influenced by EEPN is given in column three. Finally, the last column states the required parameter in order to design the system with given digital impairment processing configuration. In Schemes 1, 2, 4, 6 and 8, it is essential for the system designer to know the tolerable linewidth to limit the EEPN penalty below a certain limit p dB. The analytical expression of tolerable linewidth, for systems utilizing Lorentzian linewidth laser and Nyquist pulse shaping, in terms of system specification is given by [27],
where OSNRref_inband is the reference in band OSNR. Similarly, the mitigation bandwidth in Schemes 3, 5 and 7 utilizing a Lorentzian linewidth laser to limit penalty below p dB, for a general modulation format is given by [27].

Table 2.
Look-up table useful for system design for all practicable schemes of coherent optical systems with EDC.
Figure 3a depicts the tolerable linewidth for 1 dB OSNR penalty versus the Baudrate-Distance product for higher order constellations. It can be observed that the tolerable linewidth falls sharply with increase in the modulation order and/or Baudrate-Distance Product, thus, imposing strict requirements on the laser source responsible for EEPN in a given configuration. Figure 3b shows the OSNR penalty versus ideally required mitigation bandwidth for different modulation order in links utilizing Scheme 3, 5 or 7 for laser linewidth equal to 4 MHz. It can be seen that the achievable OSNR penalty due to residual EEPN improves exponentially with an increase in the mitigation bandwidth.
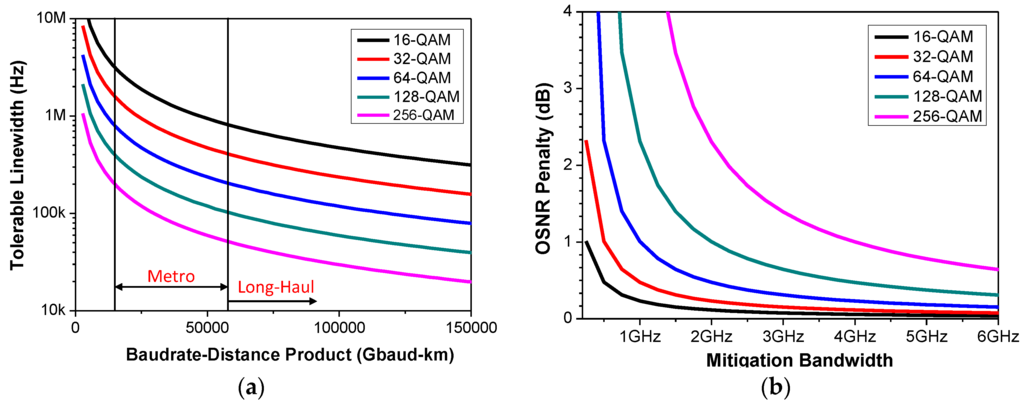
Figure 3.
Ideal Analytical Curves for Tolerable Linewidth and Mitigation Bandwidth. (a) Tolerable Linewidth for 1 dB OSNR penalty versus Baudrate-Distance Product for different higher order constellations in different regimes such as metro and long-haul (b) OSNR penalty versus Mitigation Bandwidth for different higher order modulation and intrinsic laser linewidth of 4 MHz.
In all the cases, EEPN is due to intermixing of the side band of the dispersed signal with that of the laser phase noise in the multiplication operation. The analysis shows that EEPN generation depends on the relative order of CPRTx, EDC and CPRLO and OTP. LO laser is the source of EEPN only in Schemes with EDC in the post-processing block and when the carrier recovery of LO is performed after EDC (see Schemes 1 and 4). In other schemes resulting in EEPN (see Schemes 2, 6 and 8), EEPN is due to interaction of the dispersed signal with the Tx laser phase noise or its conjugate. Schemes 3, 5 and 7 do not result in EEPN as ideal impairment compensation avoids interaction of the dispersed signal with laser phase noise. Finally, as shown in the previous section, all of the five configurations resulting in EEPN are statistically equivalent. Thus, the distributing amount of the impairment mitigation, such as EDC between pre- and post-processing blocks, does not provide any additional advantage due to this statistical equivalence.
5. Conclusions
We present analysis of all practicable DSP schemes. Existence of only eight practicable digital pre- and/or post-processing configurations for coherent optical systems is shown. There are three configurations that do not result in EEPN in spite of all-electronic impairment mitigation. In three out of the five remaining configurations, the phase noise in the transmitting laser is the source of EEPN. Meanwhile, in the remaining two configurations, the local oscillator laser is the source of EEPN. These five configurations irrespective of the source have equal EEPN penalty irrespective of the order of processing for identical transmitter and local oscillator laser characteristics. The analysis provides a simple look-up table useful for system designers to make an informed decision regarding system configuration and design.
Acknowledgments
This work was supported by EU projects ICONE, gr. #608099 and GRIFFON, gr. #324391.
Author Contributions
A.K., S.P. and G.J. proposed the concept, A.K., R.S., and H.L. initiated the study, A.K., J.R.N. and R.S. carried out the analytics. A.K., J.R.N., R.S., X.P. and O.O. designed and conducted the calculations. R.S., G.J., and S.P. guided the studies. A.K., J.R.N., R.S., X.P., O.O., H.L., G.J., and S.P. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AWGN | Additive White Gaussian Noise |
| CD | Chromatic Dispersion |
| CPR | Carrier Phase Recovery |
| DSP | Digital Signal Processing |
| EDC | Electronic Dispersion Compensation |
| EEPN | Equalization Enhanced Phase Noise |
| GVD | Group Velocity Dispersion |
| IQ | In-phase and quadrature phase |
| IFT | Inverse Fourier Transform |
| LO | Local Oscillator |
| N/A | Not Applicable |
| Non-LTI | Non-linear Time Variant |
| OTP | Optical Transmission Path |
| QAM | Quadrature Amplitude Modulation |
| Tx | Transmitter |
References
- Garrett, I.; Jacobsen, M. Theory for Optical Heterodyne Narrow-Deviation FSK Receivers with Delay Demodulation. J. Lightwave Technol. 1988, 6, 1415–1423. [Google Scholar] [CrossRef]
- Jacobsen, G. Performance of DPSK and CPFSK Systems with Significant Post-Detection Filtering. J. Lightwave Technol. 1993, 11, 1622–1631. [Google Scholar] [CrossRef]
- Chan, B.; Conradi, J. On the non-Gaussina noise in erbium doped fiber amplifiers. J. Lightwave Technol. 1997, 15, 680–687. [Google Scholar] [CrossRef]
- Jacobsen, G.; Bertilsson, K.; Xiaopin, Z. WDM Transmission System Performance: Influence of Non-Gaussian Detected ASE Noise and Periodic DEMUX Characteristic. J. Lightwave Technol. 1998, 16, 1804–1812. [Google Scholar] [CrossRef]
- Elrefaie, A.F.; Wagner, R.E.; Atlas, D.A.; Daut, G.D. Chromatic dispersion limitation in coherent lightwave transmission systems. J. Lightwave Technol. 1988, 6, 704–709. [Google Scholar] [CrossRef]
- Ip, E.; Lau, A.P.T.; Barros, D.J.F.; Kahn, J.M. Coherent detection in optical fiber systems. Opt. Express 2008, 18, 753–791. [Google Scholar] [CrossRef]
- Savory, S.J. Digital Coherent Optical Receivers: Algorithms and Subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Garrett, I.; Jacobsen, G. Phase noise in weakly coherent systems. IEE Proc. J. Optoelectron. 1989, 136, 159–165. [Google Scholar] [CrossRef]
- Ip, E.; Kahn, J.M. Carrier Synchronization for 3- and 4-bit-per-Symbol Optical Transmission. J. Lightwave Technol. 2005, 23, 4110–4124. [Google Scholar] [CrossRef]
- Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for coherent-detection systems using electronic digital signal processing. Opt. Express 2008, 16, 15718–15727. [Google Scholar] [CrossRef] [PubMed]
- Lau, A.P.T.; Shen, T.S.R.; Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for 100 Gb/s transmission and beyond with coherent detection. Opt. Express 2010, 18, 17239–17251. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, G.; Lidón, M.S.; Xu, T.; Popov, S.; Friberg, A.T.; Zhang, Y. Influence of pre- and post compensation of chromatic dispersion on equalization enhanced phase noise in coherent multilevel systems. J. Opt. Commun. 2012, 32, 257–261. [Google Scholar] [CrossRef]
- Jacobsen, G.; Xu, T.; Popov, S.; Sergeyev, S. Study of EEPN mitigation using modified RF pilot and Viterbi-Viterbi based phase noise compensation. Opt. Express 2013, 21, 12351–12362. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, G.; Xu, T.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. EEPN and CD study for coherent optical nPSK and nQAM systems with RF pilot based phase noise compensation. Opt. Express 2012, 20, 8862–8870. [Google Scholar] [CrossRef] [PubMed]
- Xie, C. Local oscillator phase noise induced penalties in optical coherent detection systems using electronic chromatic dispersion compensation. In Proceedings of the Conference on Optical Fiber Communication—Incudes Post Deadline Papers, 2009 (OFC 2009), San Diego, CA, USA, 22–26 March 2009.
- Fatadin, I.; Savory, S.J. Impact of phase to amplitude noise conversion in coherent optical systems with digital dispersion compensation. Opt. Express 2010, 18, 16273–16278. [Google Scholar] [CrossRef] [PubMed]
- Oda, S.; Ohshima, C.; Tanaka, T.; Tanimura, T.; Nakashima, H.; Koizumi, N.; Hoshida, T.; Zhang, H.; Tao, Z.; Rasmussen, J.C. Interplay between local oscillator phase noise and electrical chromatic dispersion compensation in digital coherent transmission system. In Proceedings of the 2010 36th European Conference and Exhibition on Optical Communication (ECOC), Torino, Italy, 19–23 September 2010.
- Zhuge, Q.; Chen, C.; Plant, D.V. Dispersion-enhanced phase noise effects on reduced-guard-interval CO-OFDM transmission. Opt. Express 2011, 19, 4472–4484. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhuge, Q.; Xu, X.; El-Sahn, Z.A.; Mousa-Pasandi, M.E.; Morsy-Osman, M.; Chagnon, M.; Qiu, M.; Plant, D.V. Experimental investigation of the equalization-enhanced phase noise in long haul 56 Gbaud DP-QPSK systems. Opt. Express 2012, 20, 13841–13846. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.P.; Lau, A.P.T.; Shieh, W. Equalization-enhanced phase noise induced timing jitter. Opt. Lett. 2011, 36, 585–587. [Google Scholar] [CrossRef] [PubMed]
- Farhoudi, R.; Ghazisaeidi, A.; Rusch, L.A. Performance of carrier phase recovery for electronically dispersion compensated coherent systems. Opt. Express 2012, 20, 26568–26582. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Kschischang, F.R. Coded-Aided Phase Tracking for Coherent Fiber Channels. J. Lightwave Technol. 2014, 32, 1041–1047. [Google Scholar] [CrossRef]
- Kakkar, A.; Schatz, R.; Pang, X.; Rodrigo Navarro, J.; Louchet, H.; Ozolins, O.; Jacobsen, G.; Popov, S. Impact of local oscillator frequency noise on coherent optical systems with electronic dispersion compensation. Opt. Express 2015, 23, 11221–11226. [Google Scholar] [CrossRef] [PubMed]
- Kakkar, A.; Pang, X.; Ozolins, O.; Schatz, R.; Rodrigo Navarro, J.; Louchet, H.; Jacobsen, G.; Popov, S. A Path to Use Large Linewidth LO in 28 Gbd 16-QAM Metro Links. In Proceedings of the European Conference and Exhibition on Optical Communications (ECOC), Valencia, Spain, 29 September 2015.
- Colavolpe, G.; Foggi, T.; Forestieri, E.; Secondini, M. Phase Noise Sensitivity and Compensation Techniques in Long-Haul Coherent Optical Links. In Proceedings of the 2010 IEEE Global Telecommunications Conference (GLOBECOM 2010) (GLOBECOM), Miami, FL, USA, 6–10 December 2010.
- Kakkar, A.; Rodrigo Navarro, J.; Schatz, R.; Pang, X.; Louchet, H.; Ozolins, O.; Jacobsen, G.; Popov, S. Mitigation of EEPN in Coherent Optical Systems with Low Speed Digital Coherence Enhancement. Photonics Technol. Lett. 2015, 27, 1942–1945. [Google Scholar] [CrossRef]
- Kakkar, A.; Rodrigo Navarro, J.; Louchet, H.; Schatz, R.; Pang, X.; Ozolins, O.; Jacobsen, G.; Popov, S. Comprehensive Study of Equalization Enhanced Phase Noise in Coherent Optical Systems. J. Lightwave Technol. 2015, 33, 4834–4841. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).