Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators
Abstract
:1. Introduction
2. Double-Slot Hybrid Plasmonic Ring
2.1. Schematic and Simulation Method
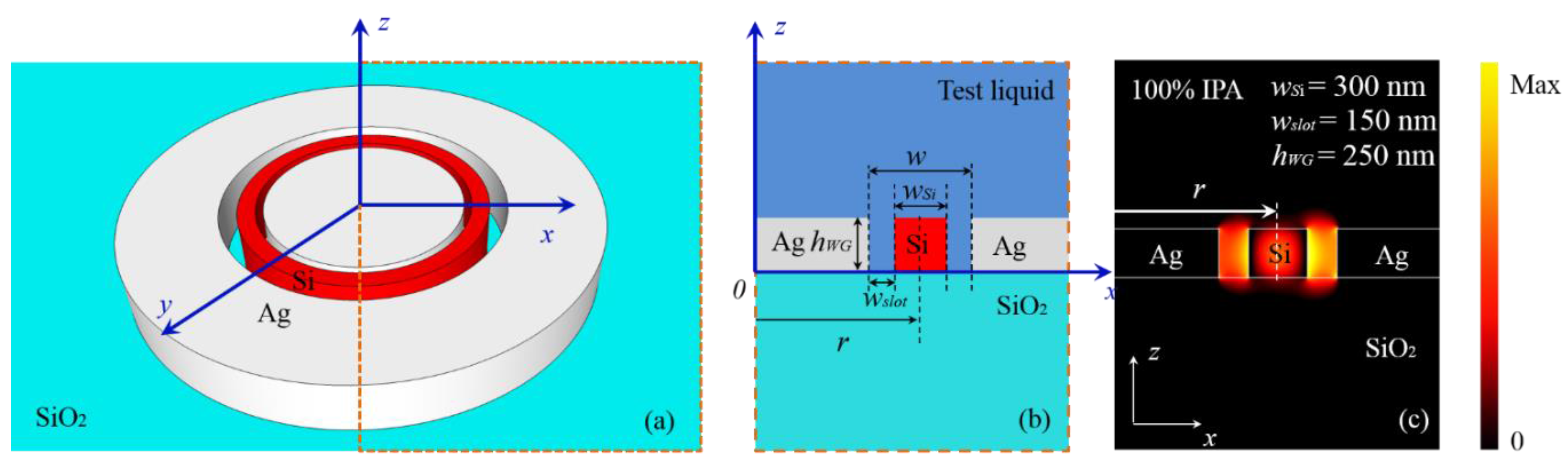
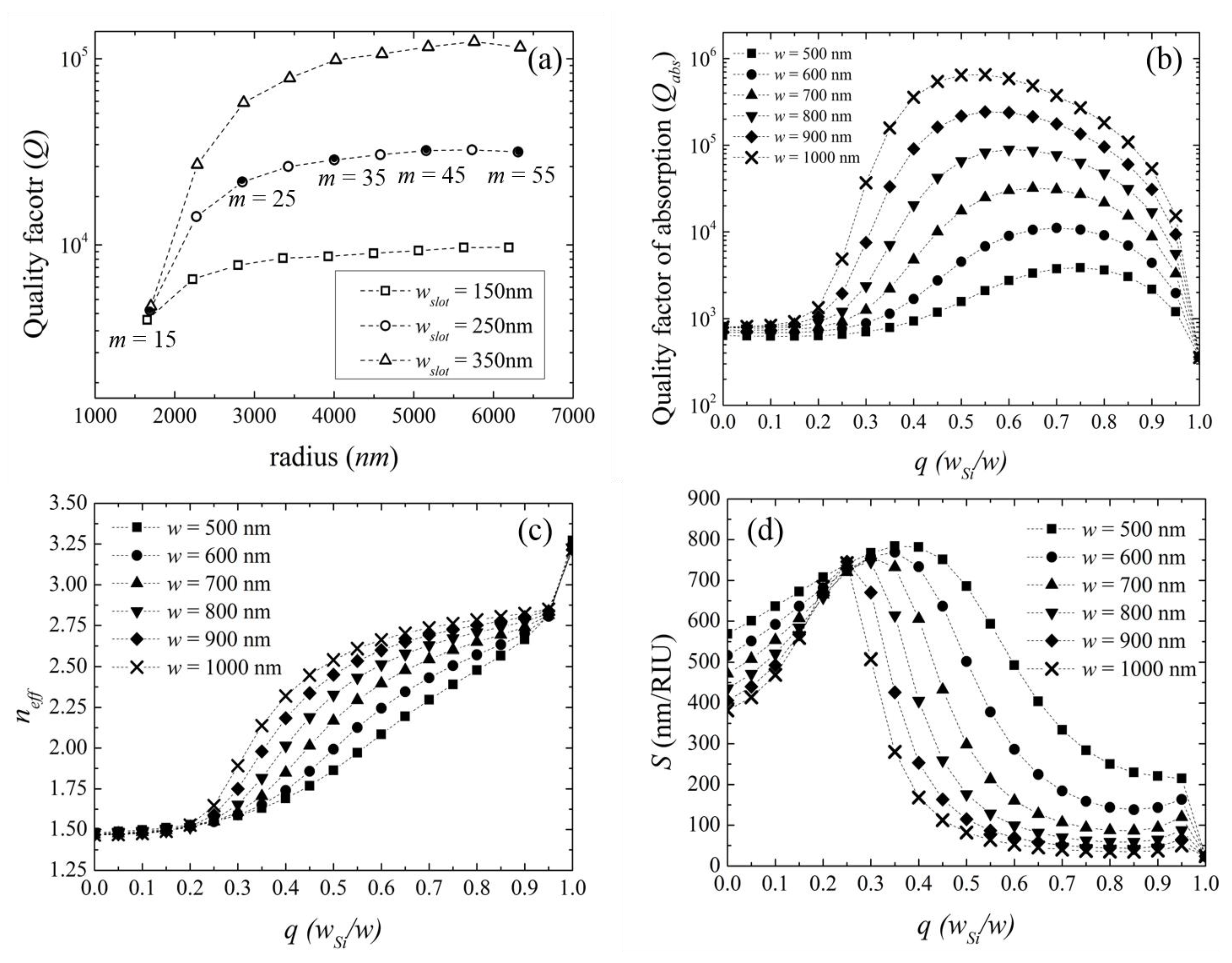
2.2. Model Investigation
3. Experimental Realization
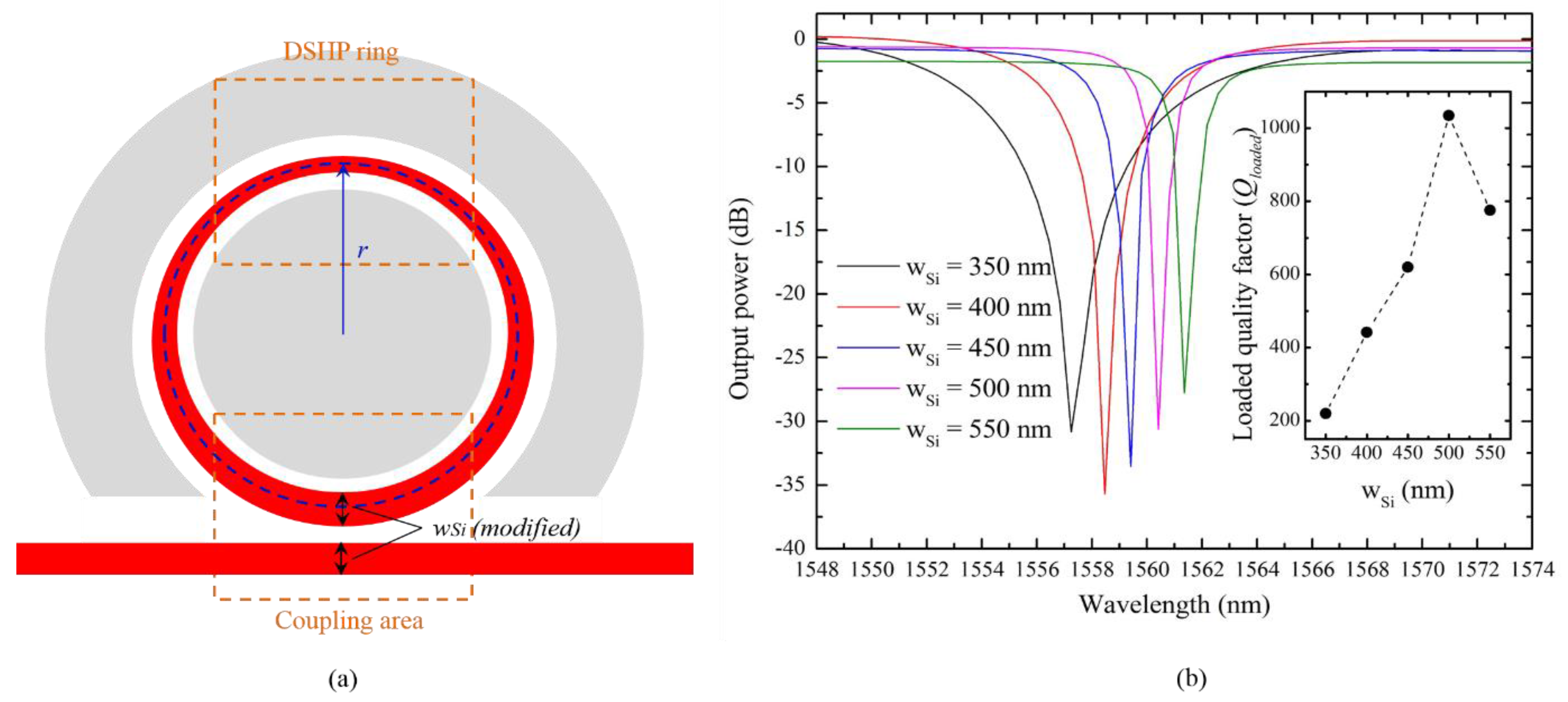
3.1. Si Side-Coupled DSHP Ring Resonator Design
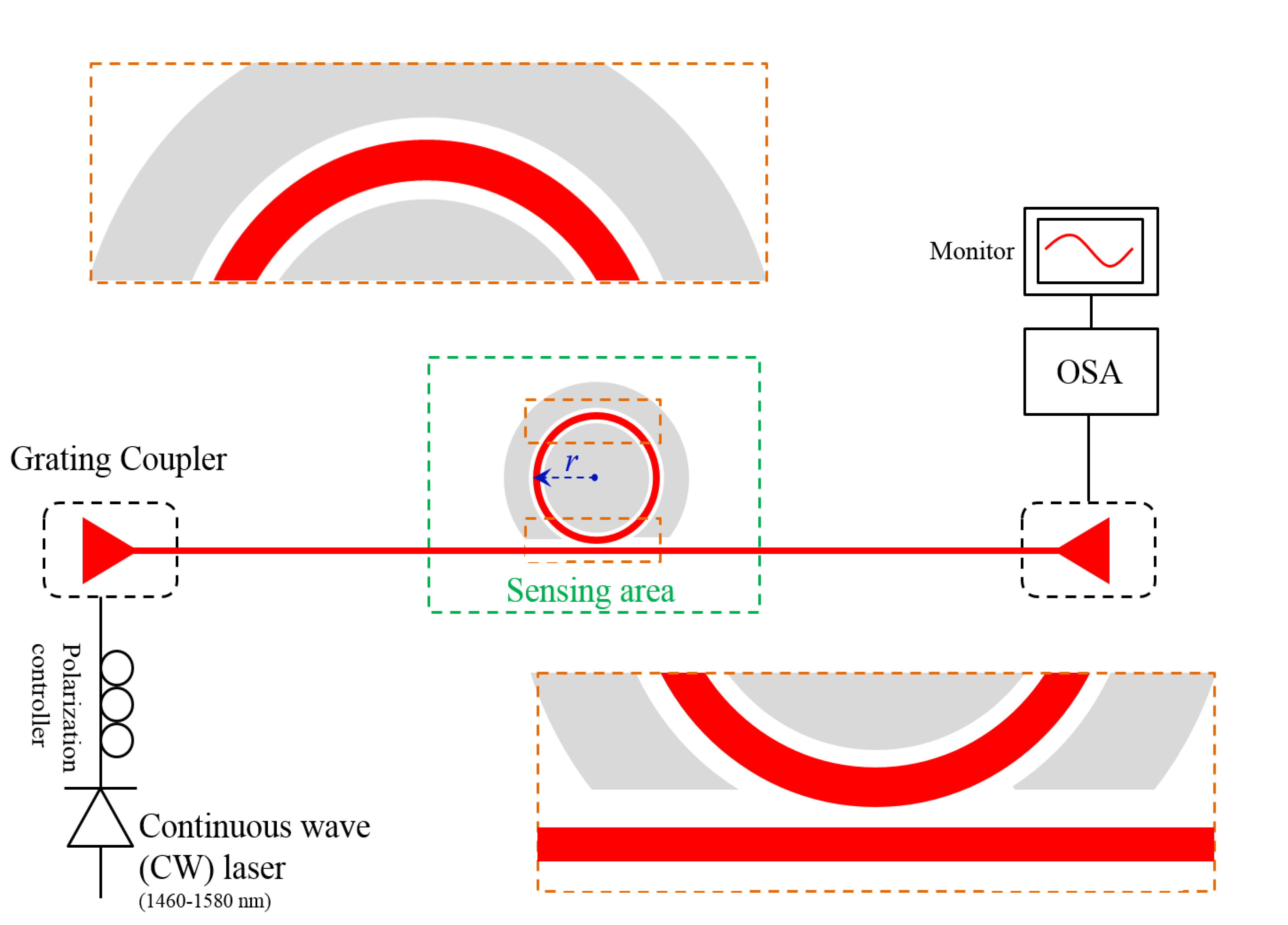
3.2. Fabrication and Measurement Setup
3.3. Characterization Results

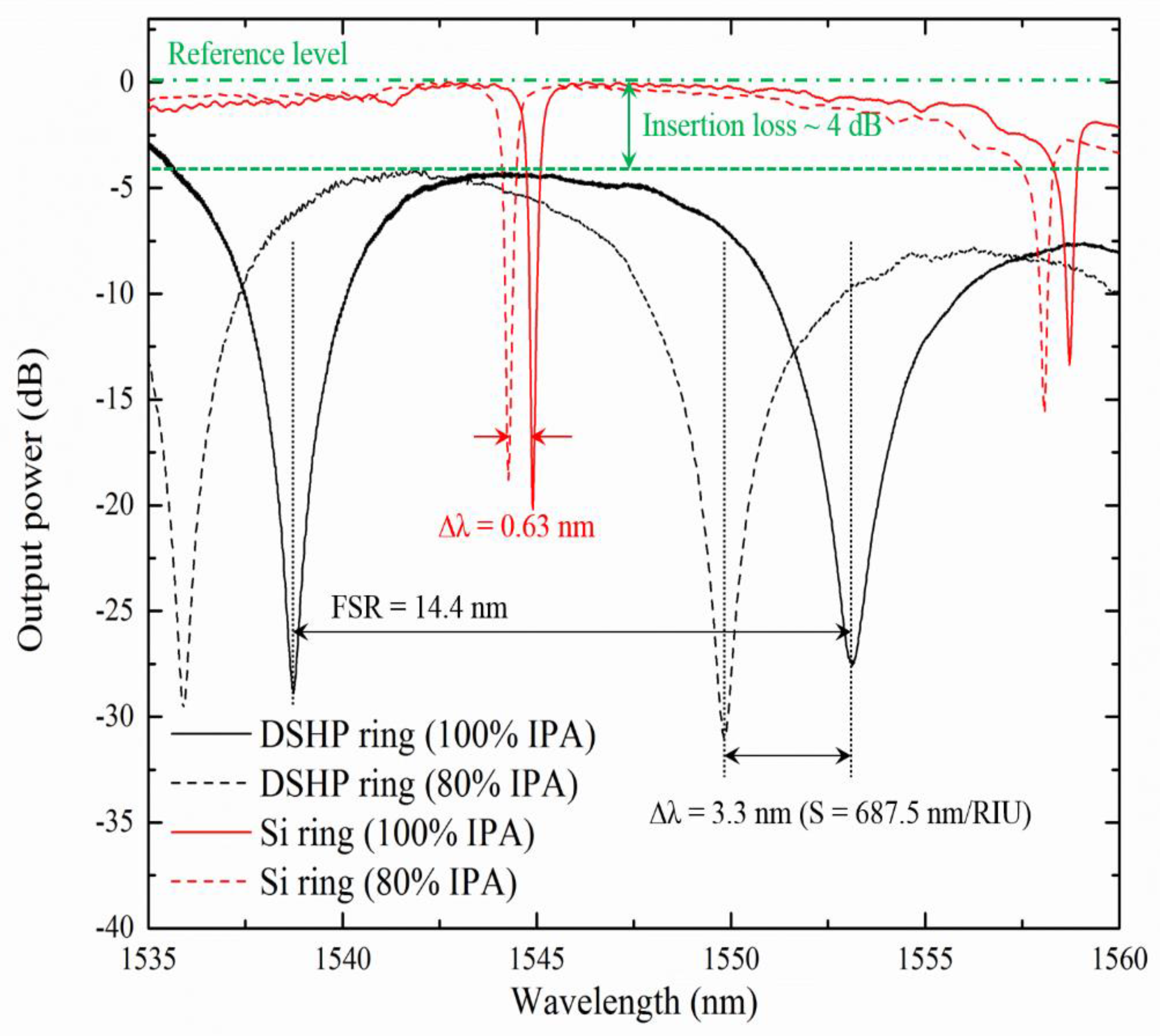
4. Loaded Q Factor Modification
5. Discussion
| Waveguide structure | Width × Height | Radius | Q Factor | S (nm/RIU) | DL (RIU) | Reference |
|---|---|---|---|---|---|---|
| Si waveguide | 500 nm × 220 nm | ≈ 5 μm | 20,000 | 70 | 3.75 × 10−6 | [2] |
| Si slot waveguide | 640 nm × 220 nm | > 5 μm | 500 | 298 | 4.2 × 10−5 | [16] |
| SiN slot waveguide | 1150 nm × 250 | 70 μm | 1,800 | 212.13 | 2.3 × 10−5 | [15] |
| DSHP waveguide | 950 nm × 250 nm | 6 μm | 300 (1034) * | 687.5 | 2.57 × 10−5 (5.37 × 10−6) * | This paper |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Soref, R.A. Silicon-based optoelectronics. Proc. IEEE 1993, 81, 1687–1706. [Google Scholar] [CrossRef]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- Densmore, A.; Xu, D.-X.; Waldron, P.; Janz, S.; Cheben, P.; Lapointe, J.; Delâge, A.; Lamontagne, B.; Schmid, J.; Post, E. A silicon-on-insulator photonic wire based evanescent field sensor. IEEE Photon. Technol. Lett. 2006, 18, 2520–2522. [Google Scholar] [CrossRef]
- Dong, P.; Liao, S.; Feng, D.; Liang, H.; Zheng, D.; Shafiiha, R.; Kung, C.-C.; Qian, W.; Li, G.; Zheng, X. Low Vpp, ultralow-energy, compact, high-speed silicon electro-optic modulator. Opt. Express 2009, 17, 22484–22490. [Google Scholar] [CrossRef] [PubMed]
- Wangüemert-Pérez, G.J.; Cheben, P.; Ortega-Moñux, A.; Alonso-Ramos, C.; Pérez-Galacho, D.; Halir, R.; Molina-Fernández, I.; Xu, D.-X.; Schmid, J.H. Evanescent field waveguide sensing with subwavelength grating structures in silicon-on-insulator. Opt. Lett. 2014, 39, 4442–4445. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Li, M.; He, J.-J. Highly-sensitive silicon-on-insulator sensor based on two cascaded micro-ring resonators with vernier effect. Opt. Commun. 2011, 284, 156–159. [Google Scholar] [CrossRef]
- Li, G.; Zheng, X.; Yao, J.; Thacker, H.; Shubin, I.; Luo, Y.; Raj, K.; Cunningham, J.E.; Krishnamoorthy, A.V. 25 Gb/s 1V-driving CMOS ring modulator with integrated thermal tuning. Opt. Express 2011, 19, 20435–20443. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Fan, X. Characterization of sensing capability of optofluidic ring resonator biosensors. Appl. Phys. Lett. 2010, 97. [Google Scholar] [CrossRef]
- Liu, A.; Jones, R.; Liao, L.; Samara-Rubio, D.; Rubin, D.; Cohen, O.; Nicolaescu, R.; Paniccia, M. A high-speed silicon optical modulator based on a metal–oxide–semiconductor capacitor. Nature 2004, 427, 615–618. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Dai, D. Highly sensitive si nanowire-based optical sensor using a Mach–Zehnder interferometer coupled microring. Opt. Lett. 2010, 35, 4229–4231. [Google Scholar] [PubMed]
- Xu, Q.; Manipatruni, S.; Schmidt, B.; Shakya, J.; Lipson, M. 12.5 gbit/s carrier-injection-based silicon micro-ring silicon modulators. Opt. Express 2007, 15, 430–436. [Google Scholar] [CrossRef] [PubMed]
- Alloatti, L.; Korn, D.; Palmer, R.; Hillerkuss, D.; Li, J.; Barklund, A.; Dinu, R.; Wieland, J.; Fournier, M.; Fedeli, J. 42.7 gbit/s electro-optic modulator in silicon technology. Opt. Express 2011, 19, 11841–11851. [Google Scholar] [CrossRef] [PubMed]
- Yamada, H.; Chu, T.; Ishida, S.; Arakawa, Y. Si photonic wire waveguide devices. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1371–1379. [Google Scholar] [CrossRef]
- Schmidt, H.; Yin, D.; Barber, J.P.; Hawkins, A.R. Hollow-core waveguides and 2-d waveguide arrays for integrated optics of gases and liquids. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 519–527. [Google Scholar] [CrossRef]
- Barrios, C.A.; Gylfason, K.B.; Sánchez, B.; Griol, A.; Sohlström, H.; Holgado, M.; Casquel, R. Slot-waveguide biochemical sensor. Opt. Lett. 2007, 32, 3080–3082. [Google Scholar] [CrossRef] [PubMed]
- Claes, T.; Molera, J.G.; de Vos, K.; Schacht, E.; Baets, R.; Bienstman, P. Label-free biosensing with a slot-waveguide-based ring resonator in silicon on insulator. IEEE Photon. J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- Liu, Q.; Tu, X.; Kim, K.W.; Kee, J.S.; Shin, Y.; Han, K.; Yoon, Y.-J.; Lo, G.-Q.; Park, M.K. Highly sensitive Mach–Zehnder interferometer biosensor based on silicon nitride slot waveguide. Sens. Actuators B Chem. 2013, 188, 681–688. [Google Scholar] [CrossRef]
- Prieto, F.; Sepulveda, B.; Calle, A.; Llobera, A.; Domínguez, C.; Abad, A.; Montoya, A.; Lechuga, L.M. An integrated optical interferometric nanodevice based on silicon technology for biosensor applications. Nanotechnology 2003, 14, 907–912. [Google Scholar] [CrossRef]
- Wang, X.; Grist, S.; Flueckiger, J.; Jaeger, N.A.; Chrostowski, L. Silicon photonic slot waveguide Bragg gratings and resonators. Opt. Express 2013, 21, 19029–19039. [Google Scholar] [CrossRef] [PubMed]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.; Li, J.; Palmer, R.; Korn, D.; Muehlbrandt, S.; van Thourhout, D. High-speed plasmonic phase modulators. Nat. Photon. 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Dai, D.; He, S. Low-loss hybrid plasmonic waveguide with double low-index nano-slots. Opt. Express 2010, 18, 17958–17966. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Dai, D.; Thylén, L.; Wosinski, L. High-sensitivity liquid refractive-index sensor based on a Mach-Zehnder interferometer with a double-slot hybrid plasmonic waveguide. Opt. Express 2015, 23, 25688–25699. [Google Scholar] [CrossRef] [PubMed]
- Oxborrow, M. Traceable 2-D finite-element simulation of the whispering-gallery modes of axisymmetric electromagnetic resonators. IEEE Trans. Microw. Theory Tech. 2007, 55, 1209–1218. [Google Scholar] [CrossRef]
- Wei, T.; Han, Y.; Li, Y.; Tsai, H.-L.; Xiao, H. Temperature-insensitive miniaturized fiber inline Fabry-Perot interferometer for highly sensitive refractive index measurement. Opt. Express 2008, 16, 5764–5769. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F.; Huffman, D.R. Absorption and scattering of light by small particles; John Wiley & Sons: Weinheim, Germany, 2008. [Google Scholar]
- Sun, X.; Wosinski, L.; Thylen, L. Nanoscale surface plasmon polariton disk resonators, a theoretical analysis. IEEE J. Sel. Top. Quantum Electron. 2016, 22. [Google Scholar] [CrossRef]
- Lou, F.; Dai, D.; Thylen, L.; Wosinski, L. Design and analysis of ultra-compact EO polymer modulators based on hybrid plasmonic microring resonators. Opt. Express 2013, 21, 20041–20051. [Google Scholar] [CrossRef] [PubMed]
- Saleh, B.E.; Teich, M.C. Resonator Optics in Fundamentals of Photonics; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Tang, Y.; Wang, Z.; Wosinski, L.; Westergren, U.; He, S. Highly efficient nonuniform grating coupler for silicon-on-insulator nanophotonic circuits. Opt. Lett. 2010, 35, 1290–1292. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Sherry, L.J.; Jin, R.; Mirkin, C.A.; Schatz, G.C.; van Duyne, R.P. Localized surface plasmon resonance spectroscopy of single silver triangular nanoprisms. Nano Lett. 2006, 6, 2060–2065. [Google Scholar] [CrossRef] [PubMed]
- Dalton, L.; Robinson, B.; Jen, A.; Ried, P.; Eichinger, B.; Sullivan, P.; Akelaitis, A.; Bale, D.; Haller, M.; Luo, J. Electro-optic coefficients of 500 pm/v and beyond for organic materials. Proc. SPIE 2005, 5935. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Dai, D.; Thylén, L.; Wosinski, L. Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators. Photonics 2015, 2, 1116-1130. https://doi.org/10.3390/photonics2041116
Sun X, Dai D, Thylén L, Wosinski L. Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators. Photonics. 2015; 2(4):1116-1130. https://doi.org/10.3390/photonics2041116
Chicago/Turabian StyleSun, Xu, Daoxin Dai, Lars Thylén, and Lech Wosinski. 2015. "Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators" Photonics 2, no. 4: 1116-1130. https://doi.org/10.3390/photonics2041116
APA StyleSun, X., Dai, D., Thylén, L., & Wosinski, L. (2015). Double-Slot Hybrid Plasmonic Ring Resonator Used for Optical Sensors and Modulators. Photonics, 2(4), 1116-1130. https://doi.org/10.3390/photonics2041116







