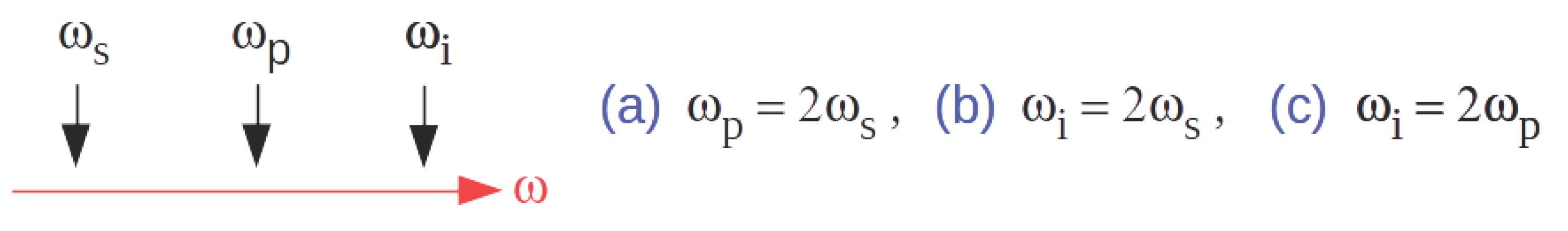1. Introduction
The nonlinear phenomenon of Four-Wave Mixing (FWM) in optical fibers [
1,
2] has been studied extensively over the past few decades owing to its wide range of applications in parametric amplifiers and frequency conversion [
3,
4], supercontinuum generation [
5,
6], squeezed-state generation [
7], quantum-state-preserving frequency conversion [
8], entangled photon pair generation [
9], and heralded single photon generation [
10]. The first observation of FWM in glass optical fibers was reported by Stolen et al. in 1974 [
11].
For efficient nonlinear interactions and especially for the observation of FWM, proper phase-matching of the nonlinearly interacting beams is required [
12]. Phase-matching can be achieved by various methods, such as the near zero-dispersion wavelength matching [
13,
14], birefringence matching [
15,
16,
17], divided-pump process [
3,
18], and intermodal phase-matching [
19,
20,
21]. In this work, we focus on intermodal phase-matching using a degenerate FWM scheme [
19], where both pump photons are at the same wavelength and propagate in the same fiber mode. The primary advantage of the degenerate FWM scheme with intermodal phase-matching is that the phase-matching can be achieved with idler, pump, and signal frequencies having large spectral separations [
4,
19].
In a conventional degenerate-pump fiber optical parametric amplifier, if pump and signal co-propagate in the fiber, they can exchange energy and also generate the idler. Signal and idler can grow together if the pump power is sufficiently larger than that of the signal and idler. In principle, it is possible to generate both the idler and signal in an optical fiber using only the pump beam [
4], where the signal and idler are seeded from the quantum vacuum noise. Alternatively, it is possible to send strong signal and idler beams into an optical fiber and generate pump photons from the quantum vacuum [
22]. We would like to highlight the convention used in this manuscript for labeling the interacting beams as the idler, pump, and signal, which is based on their frequencies
,
, and
, respectively. The terms idler, pump, and signal only signify the decreasing order in frequency of the three waves interacting in the degenerate FWM process (
) and have nothing to do with which frequencies are actually injected into the fiber at the input. For example, in Ref. [
22], based on our convention, signal and idler lasers are injected into the fiber while pump photons are generated spontaneously along the fiber.
The main purpose of this article is to show that it is possible to couple a laser beam and its frequency-doubled daughter into a multimode optical fiber through degenerate FWM process and generate a new wavelength in this process. The frequency-doubled daughter can be generated in an external crystal with a large
nonlinearity [
23]. For example, the 1064 nm laser beam generated from an Nd:YAG (neodymium-doped yttrium aluminum garnet) laser can be frequency doubled by a nonlinear crystal to 532 nm: if both the 1064 nm and 532 nm beams are injected into a multimode optical fiber, it is possible for them to interact via FWM and generate a new wavelength. Here, it will be argued that this possibility is within the design parameter range of conventional multimode optical fibers. Moreover, our analysis shows that this possibility necessitates a lower-bound for the core-cladding index contrast of the multimode optical fiber.
This paper focuses on the phase-matching conditions among multiple spatial modes, and because these conditions do not depend on the polarization state of the participating waves, it is assumed that all waves are linearly polarized along the axis and that they maintain their state of polarization while propagating in the MMF. However, the polarization state of the waves can affect the strength of the FWM process, which can be easily incorporated into an analysis that concerns the rate of the processes.
2. Energy Conservation and Phase Matching
For degenerate FWM with intermodal phase-matching, the idler, pump, and signal fields can each belong to a different spatial mode of the optical fiber. A necessary condition for the observation of FWM is the conservation of energy, where the sum of the energy of the annihilated photons must be equal to the sum of the energy of the generated photons. This condition is expressed as
where Ω is the frequency shift for the degenerate FWM process.
For the FWM process, the input source and its frequency-doubled daughter can either be in the form of: (a) the pump-signal (
,
) pair, where
, or (b) the idler-signal (
,
) pair, where
. These possibilities are shown in
Figure 1 and will be referred to as
scenario (a) and
scenario (b), respectively.
The above mentioned scenarios can be combined with the photon energy conservation in Equation (
1) to obtain
There may seem to be a third scenario, which is marked as
scenario (c) with
in
Figure 1; however, using Equation (
1), it can be seen that this scenario results in
, which is unphysical. Therefore, the only two possibilities are
scenario (a) and
scenario (b) that will be discussed in the rest of this manuscript.
Intermodal phase-matching relies on the difference between the dispersion properties of different modes in a multimode optical fiber, where unlike a single-mode fiber, phase-matching can be achieved without any assistance from the nonlinear phase shift. Using the intermodal phase-matching and a single-mode pump configuration, it is possible to obtain larger spectral shifts between the idler, pump, and signal compared with other phase-matching techniques [
18,
24]. This is particularity important for
scenario (a) and
scenario (b) because the frequency shift Ω should be quite large in either case, as can be seen in Equation (
2). The statement for the intermodal phase-matching in the absence of nonlinear phase shift can be expressed as
where
signifies the propagation constant of the signal and so on. The
argument in
emphasizes (somewhat redundantly here) that the propagation constant is evaluated at
, and the superscript labels the spatial mode in which the signal is propagating. The same convention applies to the idler and pump.
The phase-matching expression of Equation (
3) can be written as only a function of
and Ω. It is convenient (and accurate for most applications) to expand Equation (
3) to the second order in Ω around
to obtain [
4,
19]
where all
are evaluated at
. As before, the superscript labels the spatial mode in which the idler, pump, and signal propagate. The subscript identifies the order of the Taylor expansion in Ω.
and
in Equation (
4) are equal to the inverse of the group velocities of the signal mode and idler mode, respectively, and both are evaluated at the pump frequency
. If the signal and idler propagate in the same spatial mode, e.g., as is the case with a single-mode optical fiber, then
and the term linear in Ω vanishes in Equation (
4). Even if the signal and idler propagate in different spatial modes, the difference between the group velocities of these spatial modes is often very small [
4] (especially because
and
are both evaluated at
) and the linear term in Ω has only a minor effect on determining the solution for Ω in the quadratic Equation
4. Fibers can also be engineered to have modes with equal group velocities at certain wavelengths; e.g., common commercial graded index multimode fibers are designed such that all their modes have equal group velocities at 850 nm wavelength [
25,
26].
We can write Equation (
4) as
where
The solution to the quadratic Equation (
5) can be expressed as
where we have assumed that
[
4]. Also, without loss of generality, Ω in Equation (
7) is taken to be the absolute value of the solution of Equation (
5) so that it can represent the frequency shift of the idler relative to the pump. In this manuscript, our intention is to present a basic feasibility analysis for
scenario (a) and
scenario (b) and derive order of magnitude limits on the fiber specifications; therefore, it is permissible to drop the nearly negligible
term and use the approximate expression
in the rest of this manuscript.
We have made certain assumption in our derivations; e.g., we have only kept terms up to the second order in Ω around
in Equation (
4), or we have assumed that the group velocities of the modes are nearly equal. These assumptions are reasonably valid for conventional weakly guiding optical fibers; however, one needs to be cautious when extending such analyses to strongly guided fibers for which the dispersive waveguiding effects are prominent (see e.g., Ref. [
27]). In such cases, a fully numerical study is warranted to explore the parametric interactions suggested here.
Figure 1.
Idler, pump, and signal interact via the degenerate FWM mechanism inside an optical fiber. (a) In scenario (a), the input source and its frequency-doubled daughter constitute the pump-signal (, ) pair, where ; (b) In scenario (b), the input source and its frequency-doubled daughter constitute the the idler-signal (, ) pair, where ; and (c) scenario (c) with idler-pump (, ) pair and results in , so it is unphysical.
Figure 1.
Idler, pump, and signal interact via the degenerate FWM mechanism inside an optical fiber. (a) In scenario (a), the input source and its frequency-doubled daughter constitute the pump-signal (, ) pair, where ; (b) In scenario (b), the input source and its frequency-doubled daughter constitute the the idler-signal (, ) pair, where ; and (c) scenario (c) with idler-pump (, ) pair and results in , so it is unphysical.
3. Lower-Bound on the Core-Cladding Refractive Index Step
Equation (
8) can be used to drive a constraint on the core-cladding refractive index step of the multimode fiber within which
scenario (a) or
scenario (b) can be observed. The effective refractive index of each guided mode in an optical fiber is between the core refractive index (
) and cladding refractive index (
). If we apply this to the idler, pump, and signal spatial modes at the pump frequency
, we get
Equation (
9) combined with the definition of
from Equation (
6) results in
where Equation (
8) has also been used in the last step.
In Equation (
10), for most practical purposes,
of Equation (
6) can be accurately described by only the chromatic dispersion, and the waveguiding contribution to its value can be ignored in the phase-matching process, as has also been verified numerically in similar situations [
4,
19]. Therefore, we can assume that
where
and
. The expression for
in Equation (
11) can be used in Equation (
10) to obtain
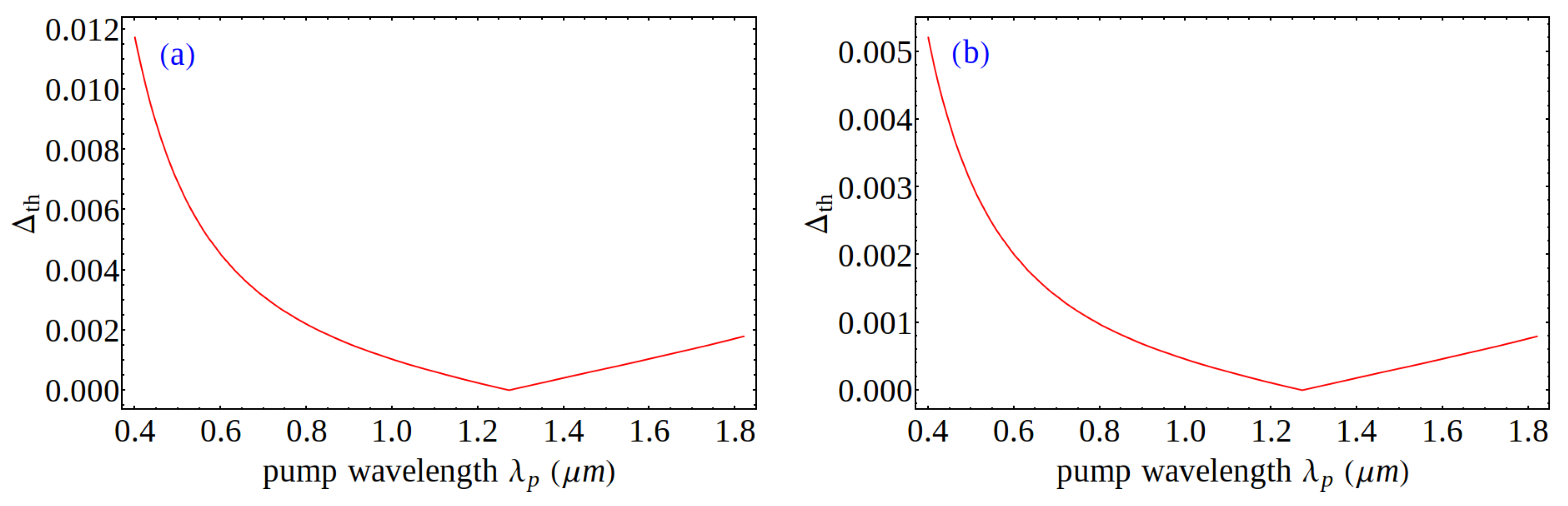
The inequality expression of 12 presents an approximate lower bound for the relative step index Δ to achieve intermodal phase matching, where
can be evaluated using the Sellmeier equation for fused silica. The statement for the lower bound of the relative step index Δ is general and applies to any intermodal phase matching process, subject to the approximations used so far; in order to use it for
scenario (a) and
scenario (b) of
Figure 1, we must use the appropriate values of Ω from Equation (
2). In
Figure 2, the lower-bound for the relative step index is plotted for
scenario (a) and
scenario (b) of
Figure 1, as a function of the pump wavelength
. We emphasize again the term pump is merely used to label the beam with the middle frequency in the idler, pump, and signal triplet as shown in
Figure 1. The required threshold refractive index step is well within the practical ranges used to fabricate commercial multimode optical fibers. Therefore, we conclude that the observation of the FWM parametric process using a laser beam and its frequency-doubled daughter is feasible in a multimode optical fiber.
Figure 2.
The lower-bound for the relative step index is plotted as a function of the pump wavelength for scenarios depicted in
Figure 1 and Equation (
2): (
a) for
scenario (a) with
; and (
b) for
scenario (b) with
.
Figure 2.
The lower-bound for the relative step index is plotted as a function of the pump wavelength for scenarios depicted in
Figure 1 and Equation (
2): (
a) for
scenario (a) with
; and (
b) for
scenario (b) with
.
4. Intermodal Phase-Matching for a Graded-Index Multimode Optical Fiber
Other interesting observations can also be reported for
scenario (a) and
scenario (b). For example, for a graded-index multimode optical fiber, the refractive index profile is given by
where
R is the core radius,
is the maximum refractive index in the center of the core, Δ is the relative index difference between the core and cladding, and
characterizes a near parabolic-index profile in the core (
), and
in the cladding (
) [
25,
26,
28]. The propagation constant of an optical mode labeled by an integer mode group
g is given by
Given the definition of
in Equation (
6) and the formula for the propagation constants of the modes in Equation (
14) (evaluated at the pump frequency
), we can write
where
G is an integer that is determined by the mode group numbers of the idler (
), pump (
), and signal (
) modes and is given by
. The reason that
G is integer-valued is that
and
cannot differ by one; otherwise, they would have different angular momenta and the conservation of angular momentum would prevent the FWM interaction [
4,
19,
29]. Using Equation (
8), we can rewrite Equation (
15) as
where
can be approximated by Equation (
11). Equation (
16) states that the degenerate intermodal FWM scenario is possible only if
X is equal to an integer, where the value of the integer
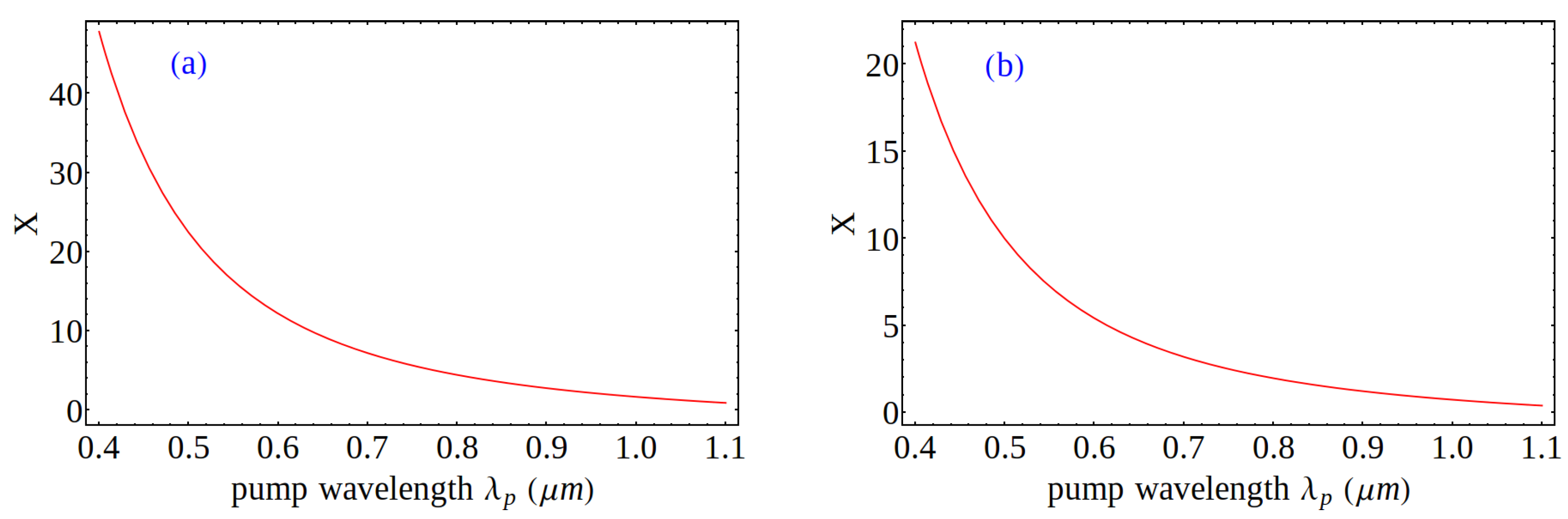
G determines the range of possibilities for the mode group numbers in which the idler, pump, and signal can propagate to interact via FWM. In
Figure 3,
is plotted for
scenario (a) or
scenario (b) of
Figure 1 as a function of the pump wavelength
.
Figure 3.
X from Equation (
16) is plotted as a function of the pump wavelength for scenarios depicted in
Figure 1 and Equation (
2) for a graded-index multimode optical fiber: (
a) for
scenario (a) with
; and (
b) for
scenario (b) with
. The degenerate intermodal FWM scenario is possible only if
X is equal to an integer.
Figure 3.
X from Equation (
16) is plotted as a function of the pump wavelength for scenarios depicted in
Figure 1 and Equation (
2) for a graded-index multimode optical fiber: (
a) for
scenario (a) with
; and (
b) for
scenario (b) with
. The degenerate intermodal FWM scenario is possible only if
X is equal to an integer.
5. Discussion
Both
scenario (a) and
scenario (b) of
Figure 1 are possible in a multimode optical fiber. However, there is a fundamental difference between these two scenarios.
scenario (a) is a stimulated FWM process, because two pump photons and one signal photon are available from classical laser sources at each FWM interaction and the idler is generated through the classical parametric conversion. On the other hand,
scenario (b) is a spontaneous FWM process, because one idler photon and one signal photon are available from the classical laser sources, while another pump photon must be supplied by the quantum vacuum noise to trigger the FWM process. Therefore,
scenario (a) is inherently much more efficient than
scenario (b). In practice,
scenario (a) can be viewed as a two-step process to achieve third harmonic generation [
30,
31]: the original laser at
is partially frequency-doubled to
by an external crystal with a large
nonlinearity; then the original laser and its frequency-doubled daughter are mixed together in the multimode optical fiber and under appropriate phase-matching condition, they can generate the idler whose frequency is three times larger than
, i.e. the original laser frequency.
A suggested experiment for
scenario (a) is to start with a laser operating at
=1550 nm, frequency-double the laser to
=775 nm, and then mix the 1550 nm and 775 nm light sources in a conventional graded-index multimode optical fiber to generate
=516.7 nm. To observe
scenario (a), the expected value of
X at
=775 nm is around
. Recall that
; therefore, if the 775 nm beam is efficiently coupled to the lowest order Gaussian-like mode of the graded-index multimode fiber with
, we will need to have
. The value of
is also determined by the mode into which the 1550 nm laser is coupled; e.g., if
, then
which is a well-guided mode in a conventional graded-index multimode optical fiber [
25,
28]. Because efficient FWM requires
G to be an integer, it is advisable to use a tunable laser as the seed, because
X varies from
to
if
changes from 1500 nm to 1600 nm; therefore, crossing an integer value of
X is guaranteed.
The merits of this work are two-fold: First, it is possible to use this technique to generate new wavelengths with a single laser and its frequency doubled daughter; however, this would require precise tuning of the fiber characteristics or the laser wavelength. Second, this analysis provides a platform to interpret nonlinear fiber experiments. When a high power laser from a frequency-doubled source is coupled into an optical fiber, it is possible for the source to be contaminated with the pre-frequency-doubled laser beam. In certain situations, this can give rise to clear peaks in the output spectrum that are the result of the nonlinear beating between the source and the contaminant. Our analysis points out to this possibility when experimental measurements are analyzed and interpreted.
The discussions in this manuscript have focused on the degenerate FWM process. It is possible to extend the analysis to the case of the non-degenerate FWM, where the two pump photons belong to different modes or have different frequencies. If the two pump photons belong to different modes but are at the same frequency, a generalization of scenario (a) with a classical parametric FWM process is feasible, as long as the pump photons are coupled to the right modes. However, if the two pump photons have different frequencies, only one of them can be supplied from the frequency-doubled daughter laser of scenario (a); therefore, the FWM process will be inefficient because it will need to be assisted by the quantum vacuum noise.