Dynamics of a Low-Dimensional Model for Short Pulse Mode Locking

Abstract

Emerging ultra-fast mode-locked lasers are now capable of generating pulses in the few to sub-femtosecond regime. Using recent theoretical innovations around the short pulse equation, we characterize the mode locking dynamics using a low-dimensional representation of the pulse parameters. The theory is formulated using a variational approach, since linearization of the exact solution is not tractable. The dominant dynamics can be characterized in a geometrical way using phase-plane analysis. Of note is our ability to determine the underlying bifurcations that occur due to changes in the fiber laser cavity parameters, including the onset of the multi-pulsing instability. The theory can aid in design principles for generating robust and highly-stable mode-locked pulses.

1. Introduction

Technological advances have revolutionized the state-of-the-art in ultrafast science, so that the production of few-cycle optical pulses in the 5–8 femtosecond regime have become routine with Ti:sapphire laser cavities. Innovations that have allowed such performance gains center on precision engineering for dispersion compensation (using, for instance, chirped mirrors) and saturable absorption (saturable quantum wells on the mirrors) to ensure self-starting [1,2,3,4,5,6]. These cavity engineering advances have also allowed modern day researchers to push ultra-fast science into the sub-femtosecond regime or attosecond regime [7,8], where the field of attosecond physics is allowing for transformative science [9,10,11]. Not only can we potentially establish a new absolute standard of time [12,13], we can now measure atomic and molecular physics at the fastest time-scales, including molecular vibrations, chemical reactions, single electron transition events [7] and light-matter interactions. Theoretical models in this ultra-fast regime currently lag the rapid pace of experimental development. To this end, we explore the underlying dynamics of the recently-proposed short pulse equation, specifically as it applies to mode locking. Indeed, we characterize the stability (and instabilities) of the mode-locked solutions, showing them to have attractor-like dynamics that depend on the various parameters tuned via the precision engineering mentioned previously.

To understand the current theoretical limitations of mode-locked laser models, one only has to consider their underlying assumptions. Specifically, many of the leading theories in mode-locked lasers are based on a center-frequency expansion of the electromagnetic field [14,15,16]. Thus, by assumption, the asymptotic reduction given by this theory assumes at leading order a delta-function-like spectrum, which is in complete contradiction to the octave-spanning spectrum generated for ultra-fast pulses. This contradiction between theory and experiment in the femtosecond to sub-femtosecond regime has motivated a new set of theoretical considerations based on the so-called short pulse equation [17,18,19,20,21,22], which unlike the center-frequency expansion, assumes at leading order that the pulse approaches a delta-function in time, not in frequency. The short pulse expansion is clearly the correct asymptotic regime for describing optical pulses in tens of femtoseconds or less. Like the master mode locking equation, an analogous version can be derived to describe mode locking in the few-cycle regime [21,22]. This provides a beginning theoretical treatment for a more precise and quantitative understanding of the pulse formation, dynamics and interactions at the this timescale.

A highly-attractive feature of standard mode locking theory is the existence of a body of literature on perturbation theory for mode-locked pulse solutions. Rooted in soliton perturbation theory [23,24], the theory has been the primary tool for making critical theoretical predictions concerning physical phenomena, such as the Gordon–Haus timing jitter [25], soliton self-frequency shifting [26], mode locking operation [14,27], the effect of dispersive radiation [28], soliton collisions [29] and four-wave mixing interactions of solitons [30]. Without the underpinnings of soliton perturbation theory, it in unclear if much theoretical progress or insight could have been gained in the master mode locking theory, thus leaving the system to simulation studies alone. This theoretical framework was recently extended to the short pulse equation [31]. We build upon this theoretical construct to perform a comprehensive evaluation of the stability and dynamics of pulses in the short pulse equation, deriving visualizations of mode locking performance and mechanisms of instability to be avoided in ultra-fast systems. Such readily-accessible diagnostics provide valuable insights for the engineering of modern-day ultra-fast systems.

2. Governing Equations and Reduced Models

In the subsections that follow, the theoretical underpinnings of the short pulse theory are outlined and a reduced order model developed from perturbation theory. The reduced model is what allows us to construct detailed stability analyses of the mode locking dynamics.

2.1. Short Pulse Equation

Short pulse mode locking theory is rooted in Maxwell's equations. Several recent papers have detailed the ultra-short pulse limit in order to model the propagation few-cycle optical pulses [17,18,19,20]. In contrast to the standard envelope-carrier wave approximation, these theories assume a broad-band pulse, avoiding the center-frequency approximation. A rescaling [32,33] allows pulse evolution in a Kerr medium to be given by the so-called short pulse equation (SPE),

$$u_{xt}-u-\frac{1}{6}{\left(u^3\right)}_{xx}=0$$

(1)

where $u,x$ and t are rescalings of the electric field, propagation distance and time, respectively. The subscripts denote partial derivatives. (see [17] and [32]). When modeling laser pulses, the SPE equation is perturbed with dissipative terms accounting for attenuation, bandwidth-limited gain and intensity discrimination (saturable absorption) in order to characterize mode locking [14,15]. Much like the Haus master mode locking approach [16], efforts have been made to develop a general qualitative theory for ultra-short mode locking, thus a short pulse master mode locking (SPMML) equation [21,22] has been developed where additional gain and dissipative terms capture the mode locking physics.

Like its center-frequency counterpart nonlinear Schrödinger equation (NLS), the SPE is Hamiltonian and integrable [19,32] and has special soliton-like solutions. Integrability is a hallmark feature of soliton systems, and the SPE's Hamiltonian nature allows the perturbation method that we employ here [31]. The SPE admits exact solutions, which are derived from breather solutions to the integrable sine-Gordon [33]. These approximately look like a left-moving envelope modulated by a right-moving sinusoid. Unfortunately, a stability analysis of this solution is currently intractable, since it is not possible to separate the solution in time and space.

For broad pulses, solutions to the SPE asymptotically approach the standard wave packet of a hyperbolic secant modulated with a sinusoid. In this limit, the SPE and NLS solitons are comparable, with the exception that the fast carrier is explicit in the SPE solution. As the pulse contains fewer cycles of the carrier oscillations, the NLS approximation breaks down. It is this limit that is of greatest interest, since this models the approach to attosecond physics. In this limit, the SPE becomes numerically stiff as the solution approaches the few-cycle regime.

2.2. Alternative Formulations of Short Pulse Dynamics

The SPE formulation is one of several models developed in the literature to help characterize pulse propagation in the few-cycle regime. One of the first derivations along these lines was provided by Brabec and Kraus [34]. Indeed, they used a novel approach to derive a general three-dimensional wave equation to first order in the propagation coordinate that is applicable to the single-cycle regime of nonlinear optics. Their evolution equation, which covers a broad range of phenomena in nonlinear optics, provides an accurate description of the evolution of the wave packet envelope down to pulse durations as short as one carrier oscillation cycle. Porras [35] generalized the method so as to treat diffraction and self-focusing in a better way, but which also neglected the nonlinearity. The culmination of these early methods ultimately led to the optical pulse propagation equation (UPPE) of Kolesik and Moloney [36,37]. Their UPPE, which is also derived directly from Maxwell's equations, provides a seamless transition between various nonlinear envelope equations in the literature and the full vector Maxwell's equations. They specifically demonstrate the UPPE equation in the context of supercontinuum generation in air and compare their results to the scalar model of Brabec and Krausz. The fully-vectorial aspects of the model are a major advantage of the model and were illustrated in the context of extreme focusing of a femtosecond pulse. Thus, unlike SPE, the UPPE is capable of a full three-dimensional description of the electromagnetic field. However, unlike the SPE, limiting analytic results are not known, thus making it more difficult to provide insights available with the SPE and SPE perturbation theory [31].

In addition to the variety of slowly-varying envelope approaches, directly modeling the interaction of the ultra-short light with matter is also possible. Perhaps the earliest theory proposed to do so was advocated by Leblond and Sanchez in 2003 [38]. In their model, they derive governing equations for optical pulse propagation in a medium described by a two-level Hamiltonian, without the use of the slowly-varying envelope approximation. In their analysis, they assume that the resonance frequency of the two-level atoms is either well above or well below the inverse of the characteristic duration of the pulse. In doing so, they reduce the propagation problem to a modified Korteweg–de Vries or a sine-Gordon equation. Moreover, they are able to derive analytical solutions of these equations, which are rather close in shape and spectrum to pulses in the two-cycle regime produced experimentally, which shows that soliton-type propagation of the latter can be envisaged. This approach was generalized by Rozanov et al. [39] to the study of the propagation of few-cycle pulses in a two-component medium consisting of nonlinear amplifying and absorbing two-level centers embedded into a linear and conductive host material. Their analysis first considered a linear theory of propagation of short pulses in a purely-conductive material and demonstrated the diffusive behavior for the evolution of the low-frequency components of the magnetic field in the case of relatively strong conductivity. Then, numerical simulations were carried out in the frame of the full nonlinear theory involving a Maxwell–Drude–Bloch model to reveal the stable creation and propagation of few-cycle dissipative solitons under excitation by incident femtosecond optical pulses of relatively high energies. They demonstrated that the broadband losses that were introduced by the medium conductivity represented the main stabilization mechanism for the dissipative few-cycle solitons.

2.3. Short Pulse Master Mode Locking Equation

With the inclusion of linear loss, bandwidth-limited gain and saturable absorption, the SPE is modified to [21,22]:

$$u_{xt}-u-\frac{1}{6}{\left(u^3\right)}_{xx}={\left(g\left(t\right)({\tau }_2{u}_{xx}+{\tau }_4{u}_{xxxx})-\gamma u+\beta u^3\right)}_x$$

(2)

where $g\left(t\right)$ is the time-varying coefficient of the bandwidth-limited, saturating gain [14,15]:

$$g\left(t\right)=\frac{2g_0}{1+{\parallel u\parallel }^2/E_0}$$

(3)

The parameter $g_0$ is the gain pumping strength; $E_0$ is the cavity saturation energy; and ${\parallel u\parallel }^2={\int }_{-\infty }^{\infty }{\left|u\right|}^{2}dt$. Note that since the left-hand side effectively describes the time evolution of $u_x$, the dissipative terms on the right-hand side also must be differentiated with respect to $x.$ The parameters ${\tau }_2,{\tau }_4$ describe the width of the gain windows, which can be modeled by:

$$P\left(\omega \right)={\tau }_2{\omega }^2-{\tau }_4{\omega }^4$$

(4)

in the frequency domain. Thus, ${\tau }_2,{\tau }_4$ govern both the separation of the windows, hence the carrier frequency, as well as the width of the gain windows, which ultimately determines pulse width. We will see that the parameter ${\tau }_4$ can be used as a bifurcation parameter. This model produces the mode locking dynamics expected in practice [21,22]. As such, we consider this as the underlying governing equation for ultra-short mode locking behavior.

2.4. Reduced Model

Given the underlying Hamiltonian structure of the SPE, a variational method can be easily implemented within the short pulse theory, as outlined in [31]. The goal of the Lagrangian approach is to constrain the mode-locked pulse evolution to a physically-realizable manifestation of the evolution dynamics. In standard soliton perturbation theory, one chooses the general soliton solution [40]. In the case of the SPE, the natural choice of ansatz is the limit of the exact solution. Thus, we assume an ansatz for the potential function for $u(x,t)$ of the form:

$$\varphi (t,x)=\eta \left(t\right)\mathrm{sech}\left(k\right(t\left)\right(x-b\left(t\right)\left)\right)sin\left(\right(x-\theta \left(t\right))$$

(5)

so that $\varphi (t,x)=u_x(t,x).$ Note that we choose to hold ω fixed at one. Differentiating this potential function with respect to x gives a wave packet that asymptotically approaches both the familiar NLS soliton solution, as well as the exact solution SPE. This ansatz does not account for the phase chirp, whose effect is small in practice. However, it does give an explicit description of the pulse's phase, which is absent in any envelope equation, such as the NLS. In fact, for moderately-broad pulses, the exact solution approximately satisfies this form with the pulse amplitude approximately four-times the pulse inverse-width, $\eta \left(t\right)\approx 4k$ and the pulse speed approximately equal to one.

The variational reduction using Equation (5) renders a manageable $4\times 4$ system of differential equations for study. To begin, the non-local gain dynamics reduces to:

$$g\left(t\right)\approx \frac{2g_0}{1+{\eta }^2/k}$$

(6)

This is used with the variational framework in order to produce a reduced system of differential equations. To leading order, all parameter evolutions depend only on the amplitude and inverse width functions. Specifically, the amplitude and width dynamics decouple from the remaining parameters, thus reducing the dynamics further to a two-dimensional system for η and k, which is amenable to phase-plane analysis. When $k\ne 0$, the governing reduced-model evolution can be written conveniently as [31]:

$$\begin{array}{ccc}\hfill \frac{d\eta }{dt}& =& f(\eta ,k)=-\gamma \eta +\frac{f_G\left(k\right)}{D(k,\eta )}\eta +0.4\beta {\eta }^3\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \frac{dk}{dt}& =& h(\eta ,k)=\frac{h_G\left(k\right)}{D(k,\eta )}-0.2\beta k{\eta }^2\hfill \end{array}$$

(8)

for the amplitude-width interaction. The remaining two variables modeling time-shifts and phase changes are slaved to the amplitude and width through the differential equations:

$$\begin{array}{ccc}\hfill \frac{db}{dt}& =& -0.06{\left(\frac{\eta }{k}\right)}^2\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \frac{d\theta }{dt}& =& 1-0.06{\eta }^2\hfill \end{array}$$

(10)

Note that the following definitions apply:

$$\begin{array}{ccc}\hfill f_G& =& 4g_0((1.075{\tau }_2-1.51{\tau }_4)+(0.25{\tau }_2-4.56{\tau }_4)k^2)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill h_G& =& 4g_0((1.15{\tau }_2-2.02{\tau }_4)k-(0.50{\tau }_2+5.125{\tau }_4)k^3)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill D(k,\eta )& =& 1+{\eta }^2/k\hfill \end{array}$$

(13)

When $k=0$, the above equations are rewritten in an equivalent form that is well defined. The reduced model allows for a phase-plane analysis of the dynamics and stability of the pulse solutions of the SPE mode locking. This geometrical description is valuable in providing a qualitative description of the attractor dynamics generated from the additional mode locking terms and further providing insight into potential instabilities.

In what follows, an in-depth analysis of the phase-plane dynamics will be considered. However, beforehand, it is important to compare the reduced two-dimensional ODE system (8) to the full governing SPE mode locking equations. Recall that the variational method here is strictly valid only for PDEs that are nearly Hamiltonian. Thus, we first compare a dissipative system with small mode locking perturbations: $g_0=0.015,\gamma =0.0035,\beta =0.001.$ We see that for appropriate initial conditions, the reduced model agrees reasonably well with the PDE model, as shown by Figure 1a. When larger dissipation parameters are used, $g_0=0.25,\gamma =0.25,\beta =0.05$, the resulting pulse is shorter. More significantly, for these parameter values, mode locking in the PDE system is more robust, as shown by the rapid convergence and uniformity of mode-locked solutions in Figure 1b. However, since the perturbation terms are large, the agreement between ODE and PDE is expected to be only qualitative. The next section will investigate the stability of fixed points in the ODE system, in order to make predictions about mode-locked pulse solutions for the PDE.

3. Phase-Plane Analysis and Stability of Mode Locking

The Lagrangian reduction technique advocated here provides a valuable, geometrical interpretation of mode locking stability. Although not quantitatively accurate, it reflects the underlying stability and instability mechanisms in a qualitative, easily-interpretable manner. Moreover, the two-dimensional nature of the reduction allows for simple phase-plane visualizations of dynamics and bifurcations. In what follows, we will first consider the phase-plane analysis and stability of physically-realizable mode locking solutions. The results will then be applied in the next section to understanding the bifurcations in the laser cavity.

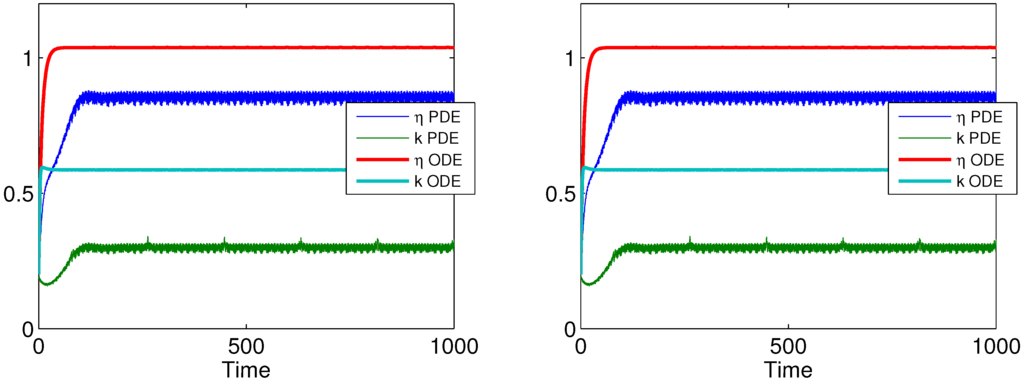
Figure 1. When all mode locking terms are included, stable pulses are possible. Here, parameter values are chosen to be perturbatively small, $g_0=0.015,\gamma =0.0035,\beta =0.001.$ ODE shows reasonable agreement with the full PDE, but does not reflect the oscillations inherent in the PDE model at this low dissipation. When the magnitude of dissipative perturbation is increased, the ODE agrees only qualitatively with PDE. Parameter values are $g_0=0.25,\gamma =0.25,\beta =0.05.$ However, the stability of such solutions is greatly enhanced, as evidenced by the robust mode locking in the PDE model, as well as the large negative eigenvalues associated with the ODE.

Figure 1. When all mode locking terms are included, stable pulses are possible. Here, parameter values are chosen to be perturbatively small, $g_0=0.015,\gamma =0.0035,\beta =0.001.$ ODE shows reasonable agreement with the full PDE, but does not reflect the oscillations inherent in the PDE model at this low dissipation. When the magnitude of dissipative perturbation is increased, the ODE agrees only qualitatively with PDE. Parameter values are $g_0=0.25,\gamma =0.25,\beta =0.05.$ However, the stability of such solutions is greatly enhanced, as evidenced by the robust mode locking in the PDE model, as well as the large negative eigenvalues associated with the ODE.

3.1. Nullclines and Fixed Points

The fixed points and nullclines of the phase plane dynamics of (8) are critical for determining the qualitative dynamics of the SPE mode locking. We will see that there is always a fixed point at the origin and one fixed point on each axis. The fixed point on the k-axis occurs when $h_G=0$, at $(k_0,0)$, where $k_0=\sqrt{(1.15{\tau }_2-2.02{\tau }_4)/(0.5{\tau }_2+5.125{\tau }_4)}$. The fixed point on the η-axis occurs at $(0,\sqrt{\gamma /(0.40\beta })$, which is at the intersection of the upper branch of the η nullcline. Furthermore, depending on system parameters, there will be one non-trivial fixed point with $k>0,\eta >0$, at the intersection of the nullclines. These points are of most interest, as they correspond to pulse solutions with finite amplitude and width. In particular, the transition of a fixed point from the lower branch of the nullcline to the upper branch has significant implications for mode locking.

When $\eta \ne 0,k\ne 0$, the nullclines for η and k are found by setting the $f(\eta ,k)$ and $g(\eta ,k)$ in Equation (8) to zero. Note that for all non-trivial solutions, the phase and position evolve according to Equation (10), so that the solutions of interest are fixed points only in the two-dimensional subspace and not the full four-dimensional system. Multiplying by the denominator of the gain term in Equation (3), which depends on η and k, gives rise to two equations that are quadratic in ${\eta }^2$ and whose coefficients are functions of $k.$ The η and k nullclines are the set of all $(k,\eta )$ pairs, such that:

$$\begin{array}{c}\hfill 0.4\beta {\eta }^4/k+\left(0.4\beta -\gamma /k\right){\eta }^2+(f_G-\gamma )=0\end{array}$$

(14)

$$\begin{array}{c}\hfill h_G-0.2\beta {\eta }^4-0.2\beta k{\eta }^2=0\end{array}$$

(15)

respectively.

Using the quadratic formula, the nullclines can be written such that η is a function of k, provided care is taken that ${\eta }^2$ is real and non-negative for each. Fixed points exist at any intersection of these two curves. We will see that for sufficiently small values of ${\tau }_4$, both branches of the η nullcline will be important.

Holding parameters $g0=0.25,\gamma =0.15,\beta =0.05$ fixed, we vary bandwidth parameters τ to see how pulse parameters change. We will hold ${\tau }_2=1.$ As ${\tau }_4$ increases, the width of the gain window decreases, leading to fewer modes being amplified and, hence, lower amplitude pulses. The location of the fixed point as a function of ${\tau }_4$ is computed numerically. Figure 2 shows this trend. As ${\tau }_4$ is decreased, the fixed point moves up and to the right, leading to taller and narrower pulses. We first investigate solutions as ${\tau }_4$ becomes large. As ${\tau }_4$ is increased, the fixed point moves toward the origin, corresponding to smaller and broader pulses.

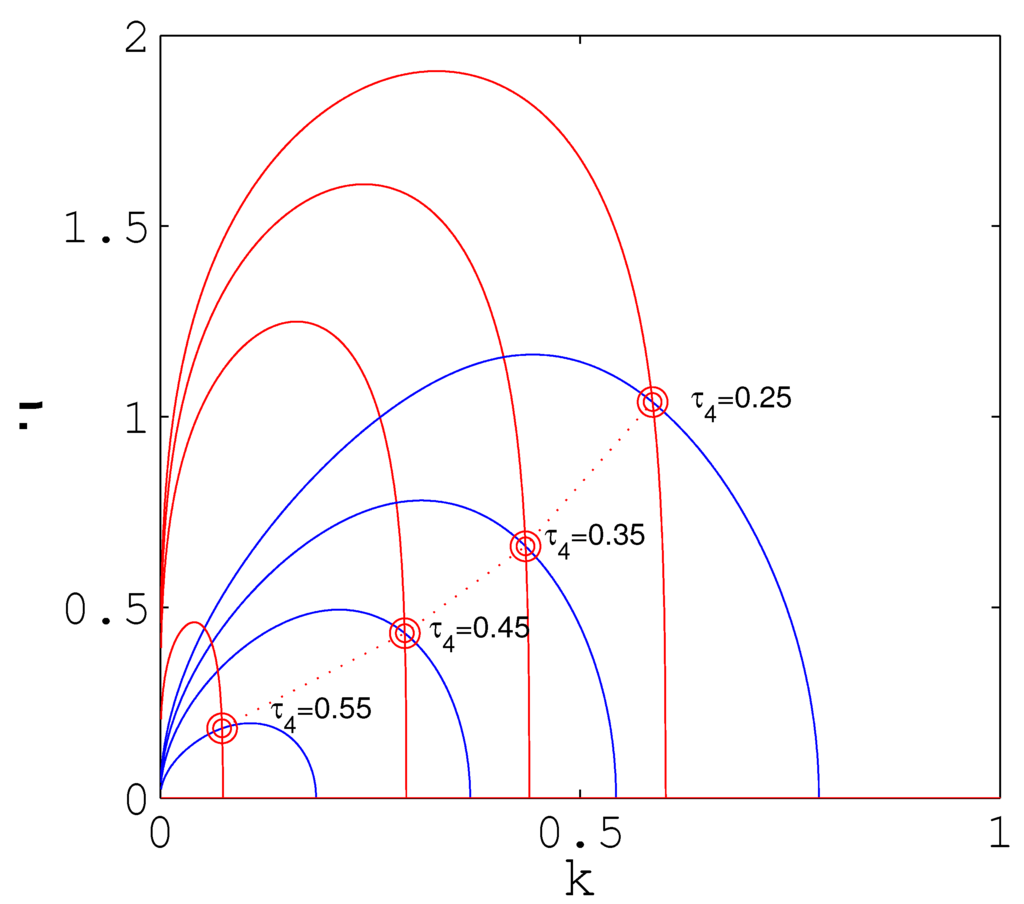
Figure 2. As the bandwidth parameter ${\tau }_4$ decreases, fixed points move up and to the right. Values of (from the left) ${\tau }_4=0.55,0.45,0.35,0.25.$ For ${\tau }_4>0.57$, the k nullcline ceases to exist.

Figure 2. As the bandwidth parameter ${\tau }_4$ decreases, fixed points move up and to the right. Values of (from the left) ${\tau }_4=0.55,0.45,0.35,0.25.$ For ${\tau }_4>0.57$, the k nullcline ceases to exist.

We find the intersection of the nullclines to determine the position of the fixed points and plot them in Figure 3. This increase in amplitude takes a dramatic shift for values of ${\tau }_4<0.20$, suggesting some kind of bifurcation. In the following subsection, we will characterize the stability of all of the fixed points, and in the next section, we will investigate the bifurcation structure to determine how this jump in pulse amplitude occurs.

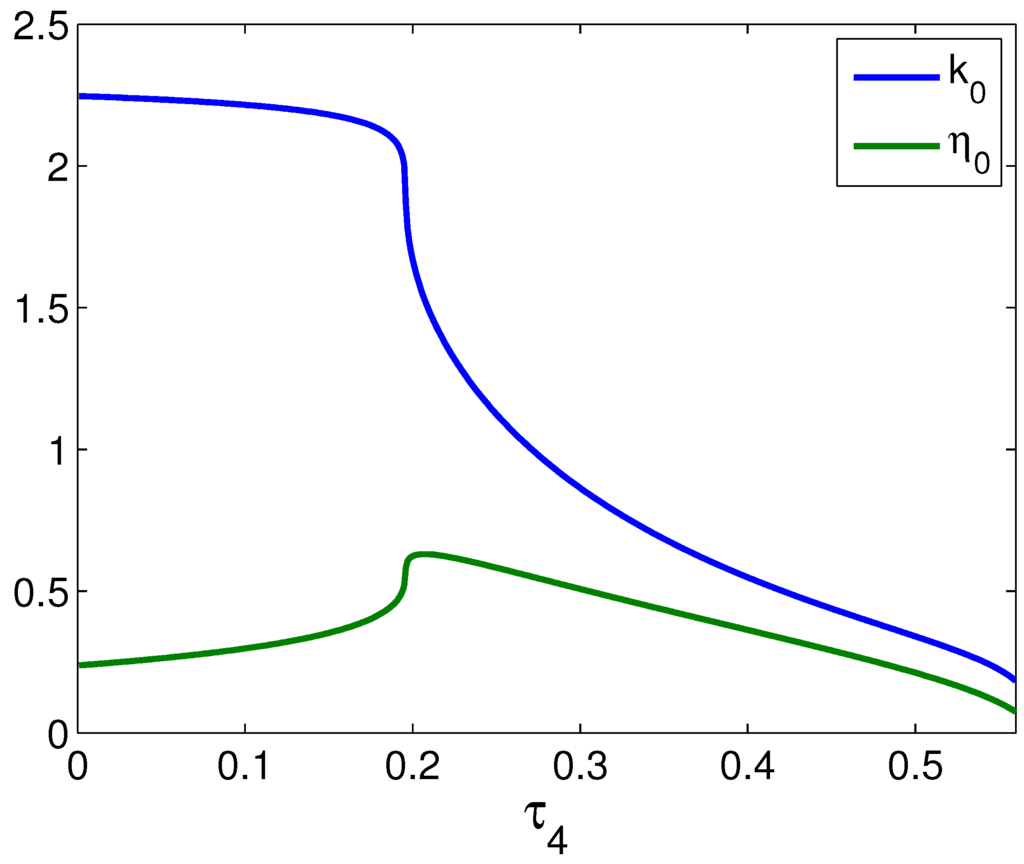
Figure 3. Pulses become taller and more narrow for large ${\tau }_4$ as ${\tau }_4$ decreases. At around ${\tau }_4=0.196$, fixed points jump to the upper branch, and pulses immediately become much taller and broader (smaller k). The stability of the fixed point changes at almost that point, as well.

Figure 3. Pulses become taller and more narrow for large ${\tau }_4$ as ${\tau }_4$ decreases. At around ${\tau }_4=0.196$, fixed points jump to the upper branch, and pulses immediately become much taller and broader (smaller k). The stability of the fixed point changes at almost that point, as well.

Figure Figure 4 shows nullclines and phase plane portraits for two parameter sets, one with very small dissipative perturbation and one with a larger perturbation. In the first case, the system is nearly Hamiltonian, with system parameters $g0=0.015,\gamma =0.0035,\beta =0.001$. The second figure is the phase portrait associated with much larger dissipation terms. $g_0=0.25,\gamma =0.25,\beta =0.05.$ The resulting pulse is shorter ($k=0.60$ instead of $0.20$), which is ultimately the desired result. Furthermore, we will show in the next subsection that large perturbations also lead to increased pulse stabilization, which is critical in practice for mode locking operation.

3.2. Stability

Once the stationary solutions to the two-dimensional system for (8) are established, the stability of each can be determined. The Jacobian matrix for (8), whose eigenvalues determine the stability of a given solution, is given by:

$$J=\left[\begin{array}{cc}{f}_{\gamma }+\left(\frac{f_G}{D}-\frac{f_G}{D^2}\frac{\partial D}{\partial \eta }\right)+3f_{\beta }{\eta }^2& \left(\frac{1}{D}\frac{\partial f_G}{\partial k}-\frac{1}{D^2}\frac{\partial D}{\partial k}\right)\eta +\frac{\partial 0.4\beta }{\partial k}{\eta }^3\\ -\frac{h_G}{D^2}\frac{\partial D}{\partial \eta }+2-0.2\beta k\eta & \left(\frac{1}{D}\frac{\partial h_G}{\partial k}-\frac{h_G}{D^2}\frac{\partial D}{\partial k}\right)+\frac{\partial -0.2\beta k}{\partial k}{\eta }^2\end{array}\right]$$

(16)

where $\eta ,k,D$ are all evaluated at a given fixed point.

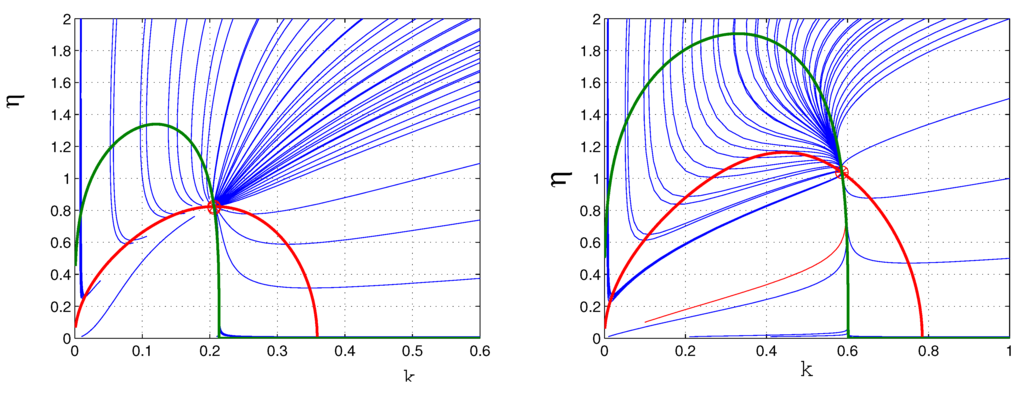
Figure 4. Phase portrait for the two-dimensional ODE shows convergence to fixed point at about $\eta =0.82,k=0.206$ using small parameter perturbation (left) and $\eta =1.05,k=0.58$ using large parameter perturbation (right). The red curve is the η nullcline, and the green curve is the k nullcline. Blue lines are trajectories, all of which are attracted to the fixed point. The larger dissipative terms in the second panel give rise to a shorter pulse (larger k).

Figure 4. Phase portrait for the two-dimensional ODE shows convergence to fixed point at about $\eta =0.82,k=0.206$ using small parameter perturbation (left) and $\eta =1.05,k=0.58$ using large parameter perturbation (right). The red curve is the η nullcline, and the green curve is the k nullcline. Blue lines are trajectories, all of which are attracted to the fixed point. The larger dissipative terms in the second panel give rise to a shorter pulse (larger k).

Figure 4 shows the phase planes for two sets of parameter sets, one with very small dissipative perturbation and one with a larger perturbation. In each case, fixed points occur at the origin and at one point in the positive $(\eta ,k)$ quadrant. The eigenvalues of the Jacobian matrix Equation (16) evaluated at the fixed point $(k,\eta )=(0.206,0.82)$ are both negative, so it is an attractor. However, they are also small in absolute value (${\lambda }_{1,2}=-0.0044,-0.0035)$, indicating that convergence to the fixed point is slow. One should not expect convergence to a pulsed solution in the PDE unless initial conditions are carefully chosen. This is illustrated by the oscillations in the PDE results shown in Figure 1a. Note that the amplitude of these oscillations is largely independent of initial conditions. It seems that they do not correspond to any neglected imaginary part in the eigenvalues. The second panel of Figure 4 is the phase portrait associated with much larger perturbation. The parameters $g_0=0.25,\gamma =0.15,\beta =0.05$ are about two orders of magnitude greater. The resulting pulse is shorter ($k=0.60$ instead of $0.20$). More significantly, the mode locking is more robust, with eigenvalues of J given by ${\lambda }_{1,2}=-0.413,-0.113$, also about two orders of magnitude larger than the weak dissipation case. This drives the solutions quickly to the attracting fixed point or mode-locked SPE solution. For these parameter values, mode locking in the PDE system will correspondingly be much more robust, as illustrated in Figure 1b, where PDE solutions converge quickly and remain fixed. Recall that since the perturbations are large, the ODE and PDE are not expected to agree quantitatively.

Finally, there is always a fixed point to the system at the origin, which corresponds to a zero amplitude sine wave of infinite extent. If the origin is an attractor, then mode locking is not viable, at least for initial conditions near the origin. If it is unstable, then mode locking may be feasible, even from low levels of noise. Thus, we must consider its stability as well, since this helps determine the ability of an SPE cavity to self-start from noise. When $\eta =0,k=0$, it is clear that the off-diagonal terms of the Jacobian matrix are both zero, so the eigenvalues are simply the diagonal entries, given by:

$$\begin{array}{ccc}\hfill {\lambda }_1& =& \gamma +4g_0(1.075{\tau }_2-1.51{\tau }_4)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\lambda }_2& =& 4g_0(1.15{\tau }_2-2.02{\tau }_4)\hfill \end{array}$$

(18)

If ${\lambda }_1<0$, this is because the loss (γ) is too large in comparison to the gain, leading to an exponential decay mode along the η-axis. This is in complete accordance with the lossy example from [31]. On the other hand, if ${\lambda }_2<0$, this is because ${\tau }_4$ is too large in comparison to ${\tau }_2$, leading to a decay mode along the k-axis, which is a spreading of the pulse. Recall that ${\tau }_2$ and ${\tau }_4$ govern the spectral gain width of the optical amplifier. If the gain windows are too narrow, only a few modes can be amplified, leading to an extended sinusoid, rather than a localized pulse. For all parameter values, this happens when ${\tau }_4/{\tau }_2\ge 1.15/2.04\approx 0.569.$

4. Bifurcations in the SPE Mode Locking Model

The construction of fixed points and null clines allows us now to consider the bifurcation structure of the governing evolution (8), which determines parameter regimes for which mode locking is possible and also predicts when a pulsed laser suffers from harmonic pulse-splitting. Since the larger perturbations give rise to more robust mode locking behavior, we will consider only this regime in this subsection, but a similar result holds for all sets of parameters. We hold fixed parameters $g0=0.25,\gamma =0.15,\beta =0.05$; we will use the bandwidth parameters τ to study these bifurcations. We will hold ${\tau }_2=1$ fixed and vary ${\tau }_4$.

As ${\tau }_4$ increases, the width of the gain window decreases, leading to fewer modes being amplified and, hence, lower amplitude pulses. The location of the fixed point as a function of ${\tau }_4$ is computed numerically. Figure 2 and Figure 3 show this trend. As ${\tau }_4$ is decreased, the fixed point moves up and to the right in the phase plane, leading to taller and narrower pulses. We first investigate solutions as ${\tau }_4$ becomes large. As ${\tau }_4$ is increased, the fixed point moves toward the origin, corresponding to smaller and broader pulses. For sufficiently large ${\tau }_4$, the k nullcline ceases to be real. Thus, for all $(k,\eta )$ values in the plane, k is decreasing. This happens when ${\lambda }_2=0$, which we saw in the last section happens when ${\tau }_4>0.569.$ In this instance, the origin is a saddle point, attracting along the k-axis and repelling along the η-axis until trajectories meet the η nullcline. Such solutions correspond to an extended sine wave of finite amplitude. This can happen when the gain is sufficiently large to overcome cavity losses and amplify only a few modes (continuous wave operation), but the mode locking term is insufficient to lock them into a single localized pulse. This region of parameter space is small. For ${\tau }_4>0.6125$, ${\lambda }_1$ becomes negative, and the origin becomes a stable node. At this point, not only does the mode locking mechanism fail, but the gain is insufficient to overcome loss. From the ODE perspective, this is also the value for which the η nullcline ceases to exist.

Of greater interest is the behavior of fixed points in the first quadrant, which correspond to pulses of finite width and amplitude. For all values of ${\tau }_4>0.20$, the location of the only non-trivial fixed point is at the intersection of the k nullcline with the lower branch of the η nullcline, as shown in the top two panels of Figure 5. Qualitatively, these fixed points all have the same stability. As ${\tau }_4$ decreases, the two branches of the η nullcline approach one another and meet when ${\tau }_4=0.196.$ For ${\tau }_4<0.196$, both the upper and lower branches of η nullcline have gaps for some small interval of k, as shown in the lower two panels. That is, within that k interval, η is always increasing. When this split occurs, the fixed point is to the left of this split and initially remains on the lower branch. As ${\tau }_4$ decreases further, this gap widens, and eventually, the fixed point moves onto the upper branch of the η nullcline, as shown in the lower right panel.

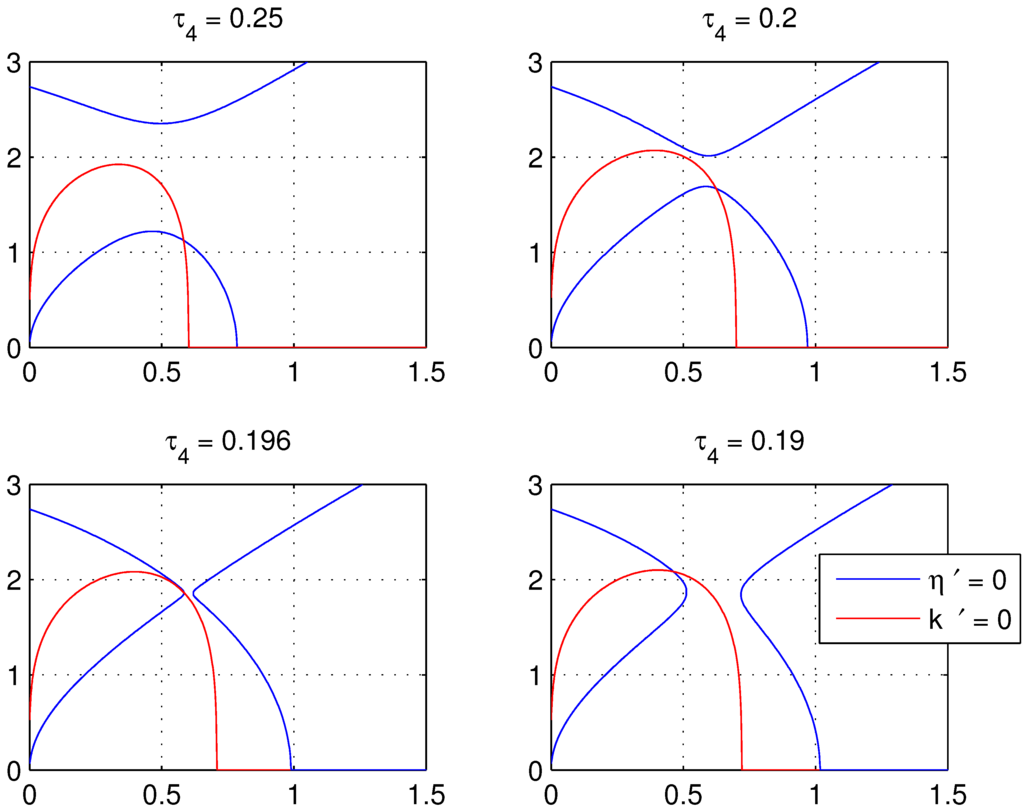
Figure 5. As ${\tau }_4$ decreases, fixed point moves up. When ${\tau }_4=0.1962$, there exists a region of k for which ${\eta }^{\prime }>0$. At about ${\tau }_4<0.162$, the fixed point exists only on the upper branch of the η nullcline.

Figure 5. As ${\tau }_4$ decreases, fixed point moves up. When ${\tau }_4=0.1962$, there exists a region of k for which ${\eta }^{\prime }>0$. At about ${\tau }_4<0.162$, the fixed point exists only on the upper branch of the η nullcline.

By evaluating Equation (16), we can readily determine the stability of each fixed point. The real and imaginary parts of the eigenvalues are shown in Figure 6. We see that for ${\tau }_4>0.1962$, the eigenvalues are real and negative, indicating that the fixed point is a stable node, corresponding to the phase planes in the upper panels of Figure 5. In this parameter regime, mode locking is feasible. Even as the fixed point moves to the left of the gap, as in the bottom left panel of Figure 5, its stability initially remains unchanged. For a narrow region of parameter space, for $0.194<{\tau }_4<0.196$, the eigenvalues of Equation (16) become complex conjugate, with a negative real part. Thus, the fixed point becomes a stable spiral and still attracts nearby trajectories. When ${\tau }_4<0.194$, the system undergoes a supercritical Hopf bifurcation, and the fixed point becomes an unstable spiral.

In this bifurcation, a limit cycle is created around the unstable spiral as indicated by Figure 7. This limit cycle increases with decreasing ${\tau }_4.$ In the top panels, ${\tau }_4=0.192$, and trajectories are repelled from the fixed point and the unstable spiral in what appears to be a stable limit cycle. The top right panel indicates that these high amplitude oscillations persist indefinitely. As ${\tau }_4$ decreases further, a third bifurcation occurs, in which the limit cycle expands and collides with the stable manifold of the saddle on the k-axis and is destroyed. However, for values of ${\tau }_4$ near this bifurcation, solutions also enter a quasi-periodic orbit for a finite time, but eventually are repelled and attracted along the stable manifold of the saddle point on the η-axis, as shown in the lower panels of Figure 7.

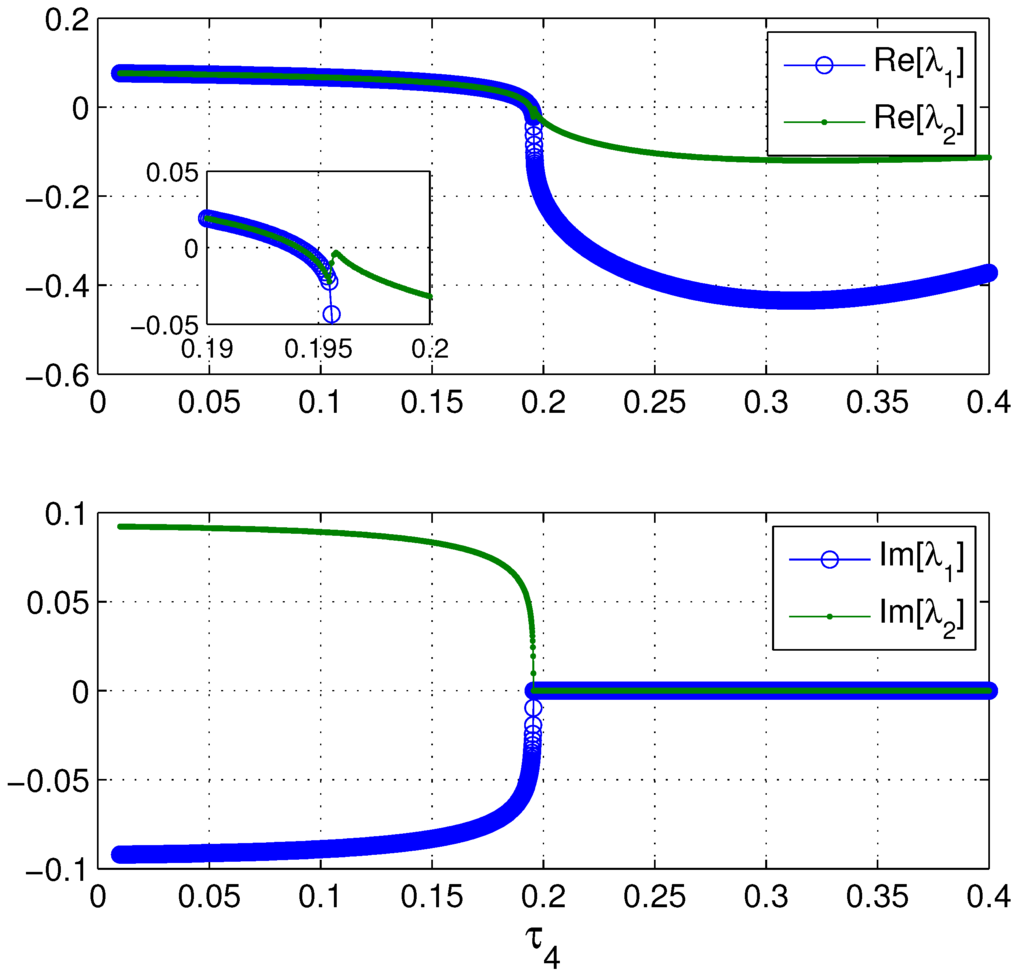
Figure 6. The fixed point is a stable attractor on the lower branch of the η nullcline until about ${\tau }_4=0.1962$, when the fixed point jumps to the upper branch of the nullcline. At ${\tau }_4=0.1960$, the fixed point becomes a stable spiral. At about ${\tau }_4=0.1940$, the system undergoes a Hopf bifurcation, and solutions tend to a stable limit cycle, which vanishes for ${\tau }_4<0.192$.

Figure 6. The fixed point is a stable attractor on the lower branch of the η nullcline until about ${\tau }_4=0.1962$, when the fixed point jumps to the upper branch of the nullcline. At ${\tau }_4=0.1960$, the fixed point becomes a stable spiral. At about ${\tau }_4=0.1940$, the system undergoes a Hopf bifurcation, and solutions tend to a stable limit cycle, which vanishes for ${\tau }_4<0.192$.

For those parameter values when ${\tau }_4$ is sufficiently small, the ODE model predicts that solutions spiral away and eventually grow exponentially tall along the η-axis. For long times, the PDE does not exhibit this behavior. Rather, solutions receive sufficient gain that their amplitude grows, and they undergo an instability, leading to pulse splitting, the onset of which exhibits amplitude oscillations, characteristic of the unstable spiral. Since the ansatz for this paper does not permit multi-pulse solutions, we cannot expect the comparison to hold in this region. However, the ODE model does accurately predict the instability of pulsed solutions for sufficiently small ${\tau }_4$ and accurately predicts that this instability is oscillatory, as is typically the case with pulse pulsing. Figure 8 shows two solutions to the PDE, one for ${\tau }_4=0.150$ and another at ${\tau }_4=0.14.$ As ${\tau }_4$ is reduced, the single-pulse solution becomes unstable and splits into two. Note that the bottom right panel shows that the amplitude remains about constant for long times, until around $t=800$, after which the amplitude goes through oscillations before stabilizing to the two-pulse solution. This is in complete accordance with the prediction of the ODE model, as predicted by the Hopf bifurcation and illustrated in Figure 7.

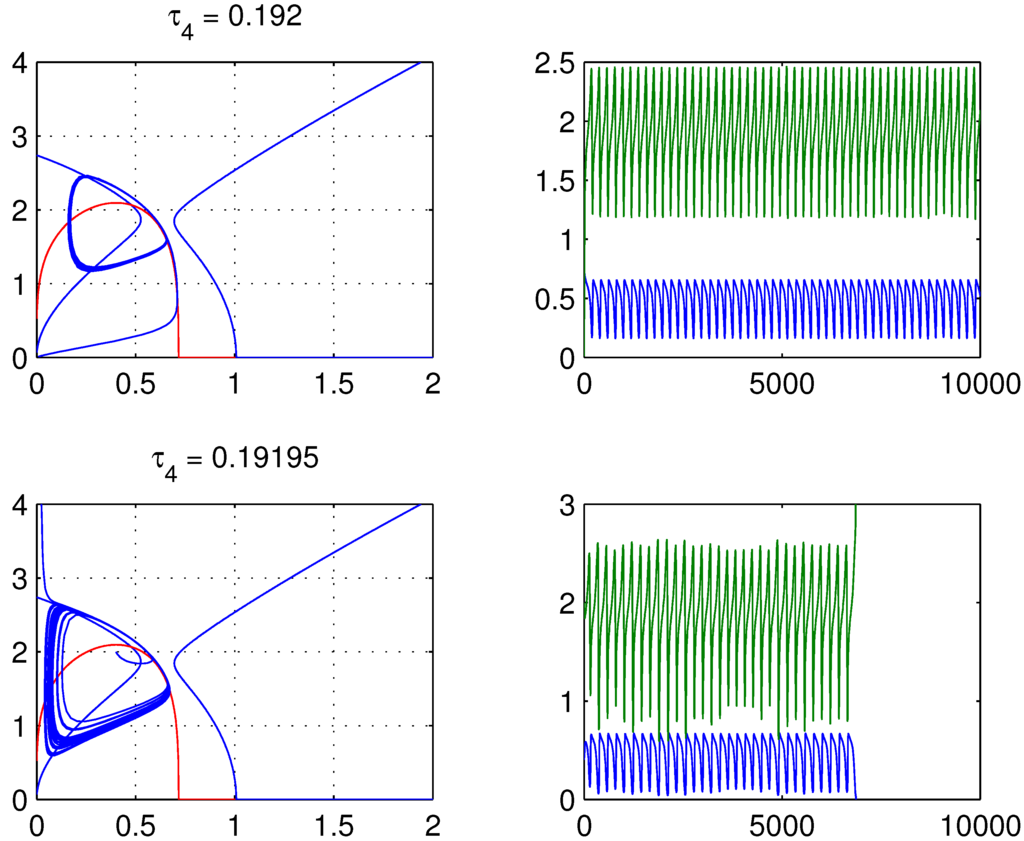
Figure 7. For ${\tau }_4<0.194$, the only fixed point is an unstable spiral. However, for a short band of ${\tau }_4$, there appears to be a limit cycle. For ${\tau }_4<0.19195$, this limit cycle exhibits its instability only after a long period of time. This corresponds to the breathing characteristic of a pulse undergoing harmonic pulse splitting. For smaller values of ${\tau }_4$, the transition to instability is nearly instantaneous.

Figure 7. For ${\tau }_4<0.194$, the only fixed point is an unstable spiral. However, for a short band of ${\tau }_4$, there appears to be a limit cycle. For ${\tau }_4<0.19195$, this limit cycle exhibits its instability only after a long period of time. This corresponds to the breathing characteristic of a pulse undergoing harmonic pulse splitting. For smaller values of ${\tau }_4$, the transition to instability is nearly instantaneous.

Although the ansatz selected does not admit it, the PDE admits another solution with two lower amplitude pulses with the same $L^2$ norm as the unstable one. Thus, the solution ansatz can be modified to include two different pulses that are well separated in space. Each of the two pulses has the same parameters as a solution with lower effective $g_0$:

$$g_{0eff}=g_0\frac{1+{\eta }_0^2/k}{1+2{\eta }_0^2/k}$$

(19)

For example, the ODE for ${\tau }_4=0.170,g_0=0.25$ has an unstable spiral at $(0.389,2.155)$. However, one can predict a two-pulse solution, each of which will have the same amplitude and width as a single-pulse solution to the $g_0=0.1307$ case. For ${\tau }_4=0.170$ and $g0=0.1307$, the ODE model has a stable node at (0.753, 0.871), corresponding to stable pulses, which are lower in amplitude. Figure 8 shows two solutions to the PDE, one for ${\tau }_4=0.15$ and another at ${\tau }_4=0.14$. Thus, the stability results advocated here can be extended to handle multi-pulse mode locking and the instability driving the multi-pulsing instability. Indeed, the multi-pulsing instability is the most important instability observed in practice, as it significantly limits the power per pulse [43,44,45].

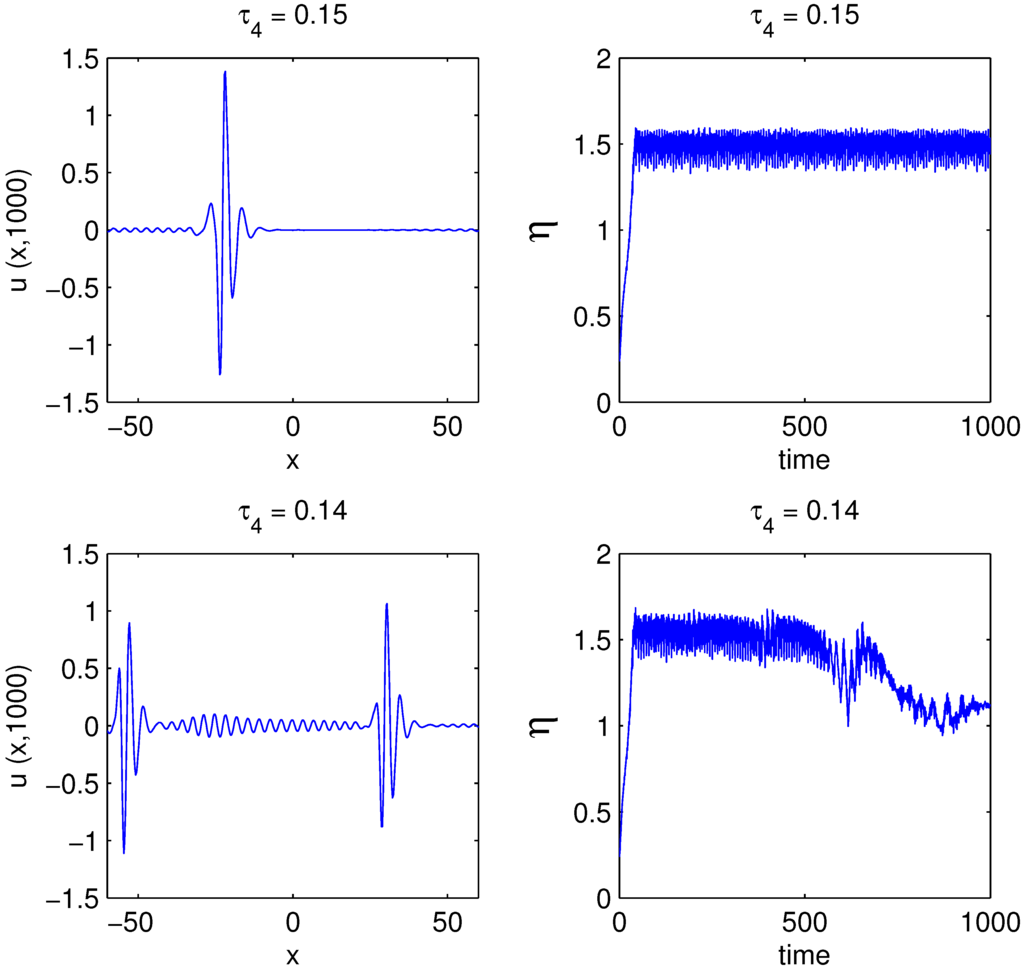
Figure 8. As the bandwidth parameter ${\tau }_4$ decreases, amplitudes increase until becoming unstable, as predicted by the ODE model. In fact, solutions to the PDE undergo harmonic pulse splitting, as evidenced here.

Figure 8. As the bandwidth parameter ${\tau }_4$ decreases, amplitudes increase until becoming unstable, as predicted by the ODE model. In fact, solutions to the PDE undergo harmonic pulse splitting, as evidenced here.

5. Conclusion

With the emerging frontier of attosecond physics, there is renewed demand for theoretical models rooted in Maxwell's equations that are capable of providing an underlying theoretical description of short pulse dynamics [17,18,19,20] and short pulse mode locking theory [21,22]. Especially important are methods that capture the underlying stability, bifurcations and operating regimes of ultra-fast devices, like mode-locked lasers. In this manuscript, a reduced-order theoretical model has been developed for understanding short pulse propagation. The theory is based on a variational approach versus direct linearization due to the implicit nature of the short pulse solution. Much like the success of previous variational reductions [40,41], the short pulse variational framework provides an easy-to-use theoretical description of the pulse evolution, thus providing a valuable modeling tool for understanding the state-of-the-art sub-femtosecond pulses currently being generated in research laboratories. Indeed, the fundamental nature of the pulse instabilities can be discovered from geometrical methods (phase-plane analysis) of dynamical systems.

Given the limited theoretical work to date on short pulse theory, it makes sense to develop methods capable of pushing forward our understanding of this important propagation regime. Although it is very difficult to model the evolution of electromagnetic energy in a quantitatively accurate manner without detailed knowledge of the full gain spectrum, the proposed qualitative assessments are critical for characterizing pulse instabilities in the sub-femtosecond regime. This greatly extends the limited outlook and validity of envelop-based approaches (such as NLS with additional terms) in the sub-femtosecond regime, giving an alternative to modeling the dynamics under extreme conditions. With the advent of octave-spanning lasers, the exploration of the fundamental nature of atomic and molecular physics at the fastest time scales, including molecular vibrations, chemical reactions and light-matter interactions, is finally a realistic possibility [7]. Additionally, as a result, developing a new theory for this regime, such as the SPE mode locking theory, will become of increasing importance.