Four-Wave Optical Parametric Amplification in a Raman-Active Gas
Abstract
:1. Introduction
2. Theoretical Background
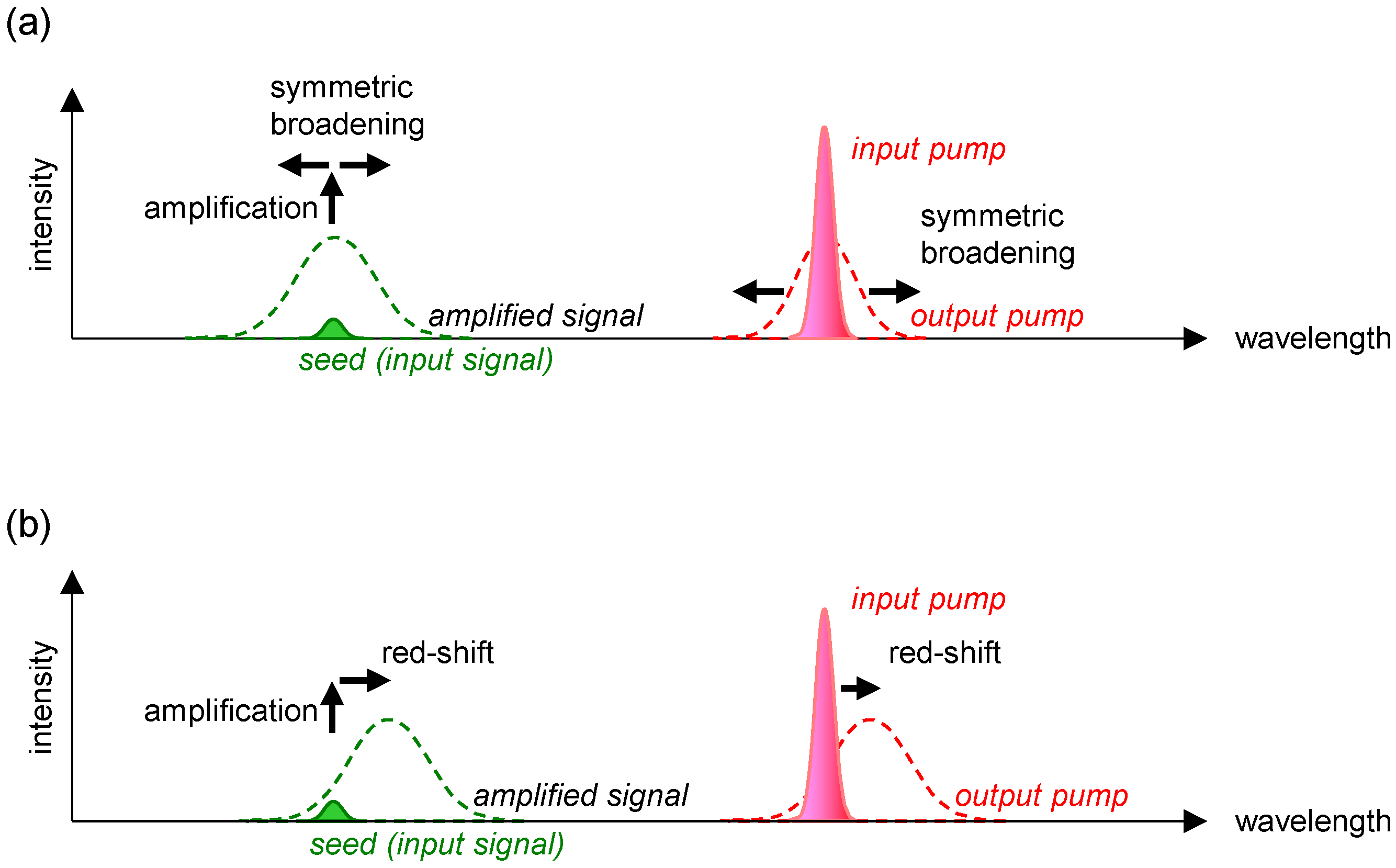
3. Experimental Investigation

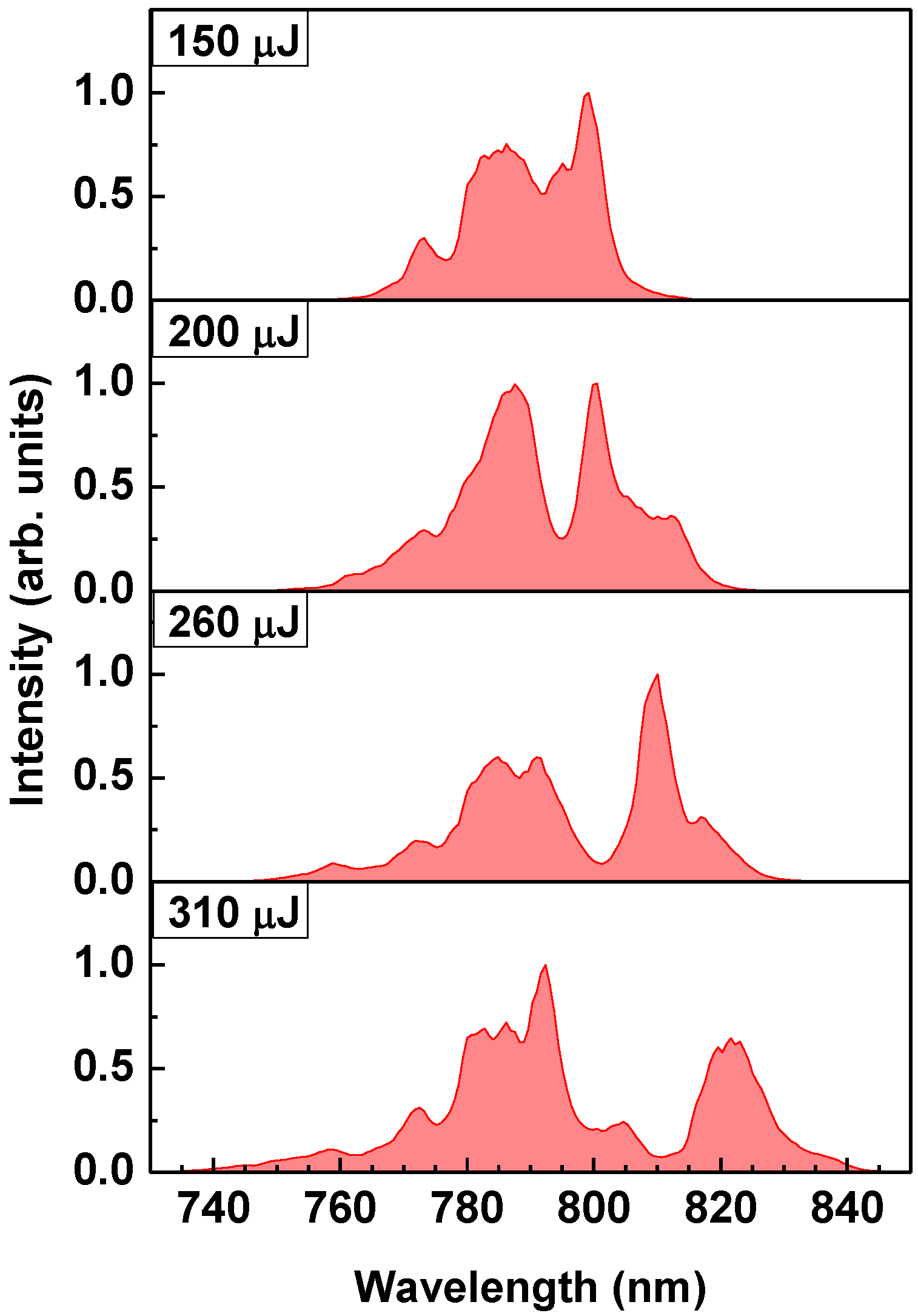
4. Results and Discussion
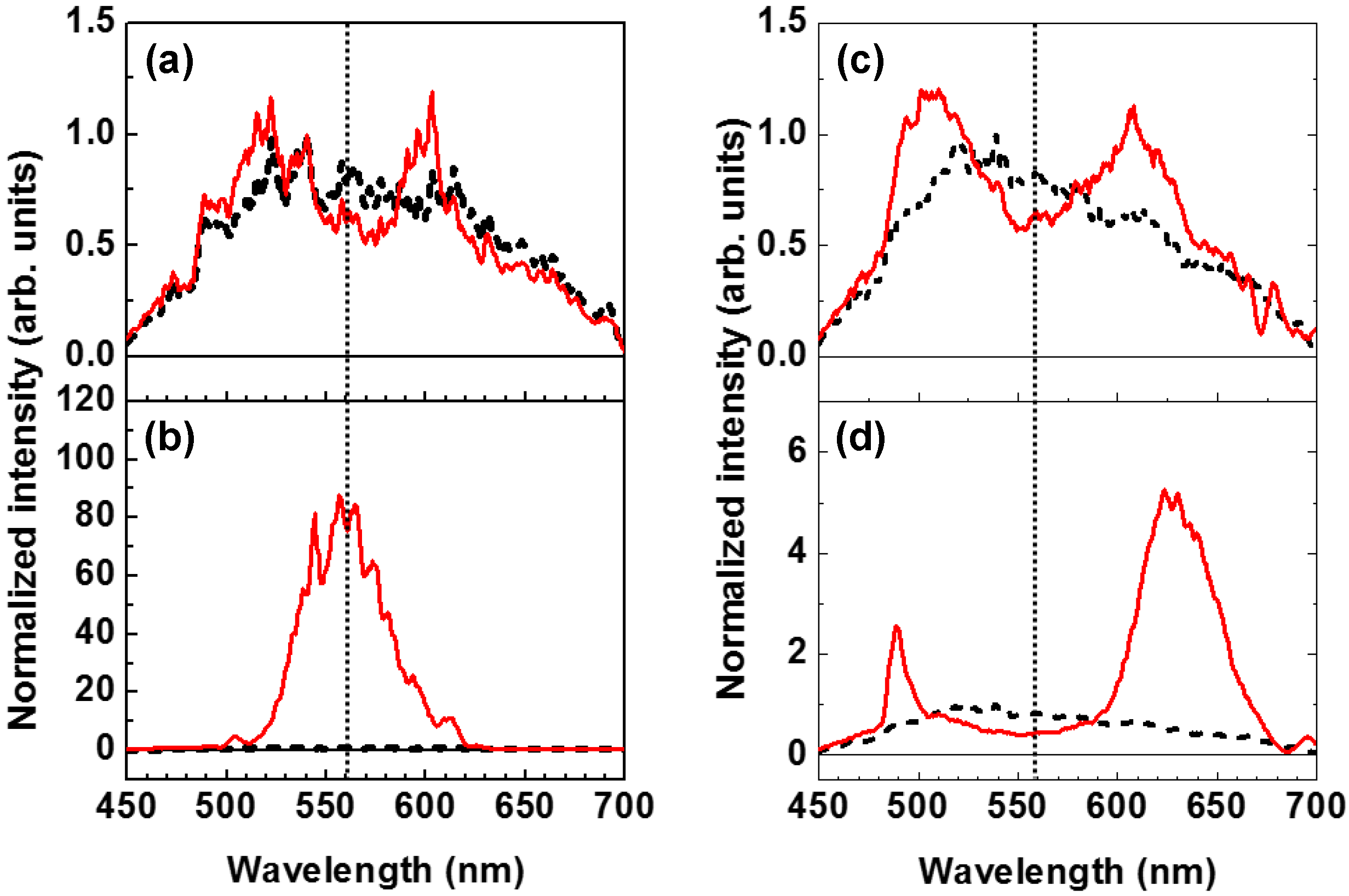
4.1. Spectral Redshift during Signal Amplification
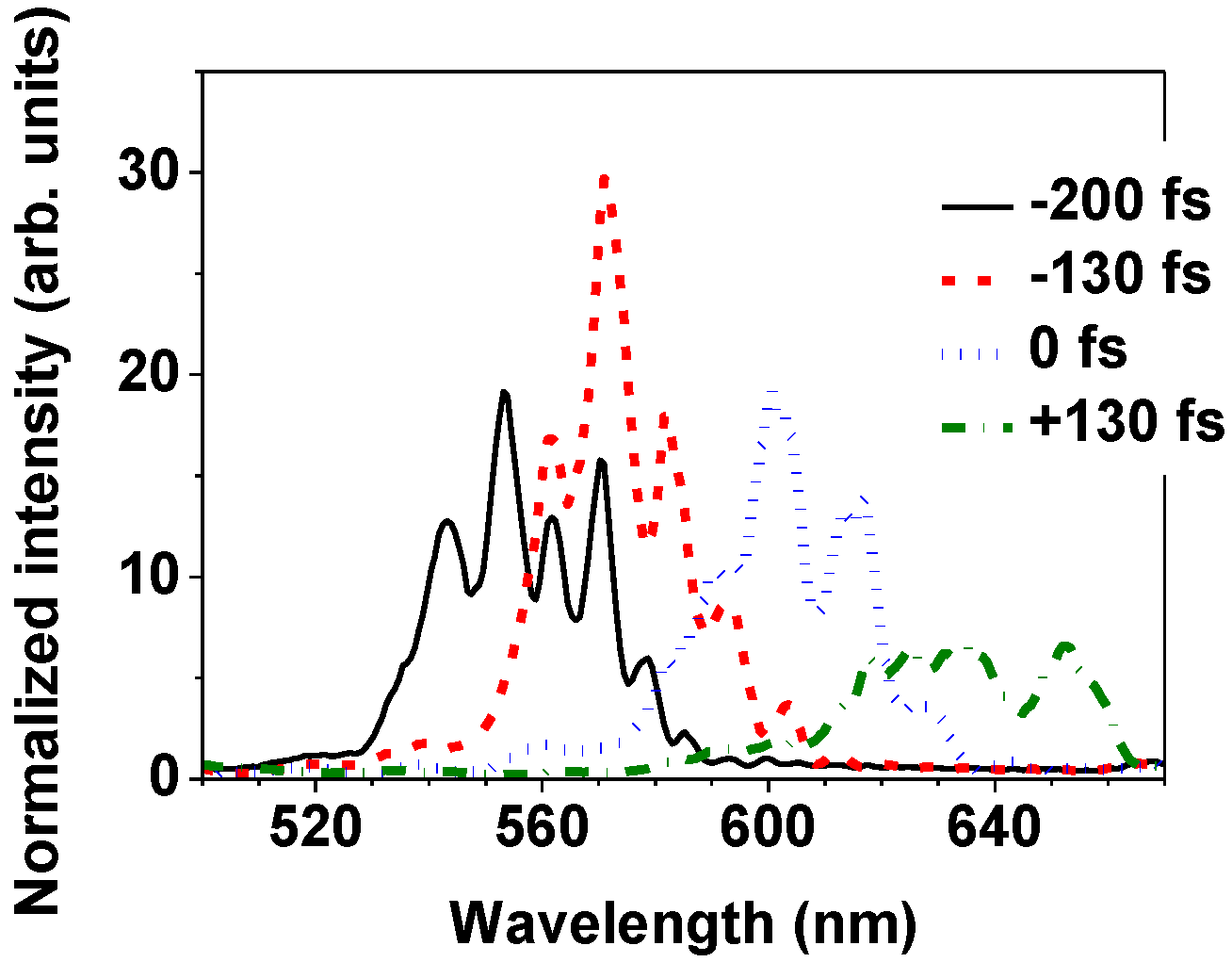
4.2. Excitation of Rotational Wavepackets by the Pump Pulse and the Signal Modulation
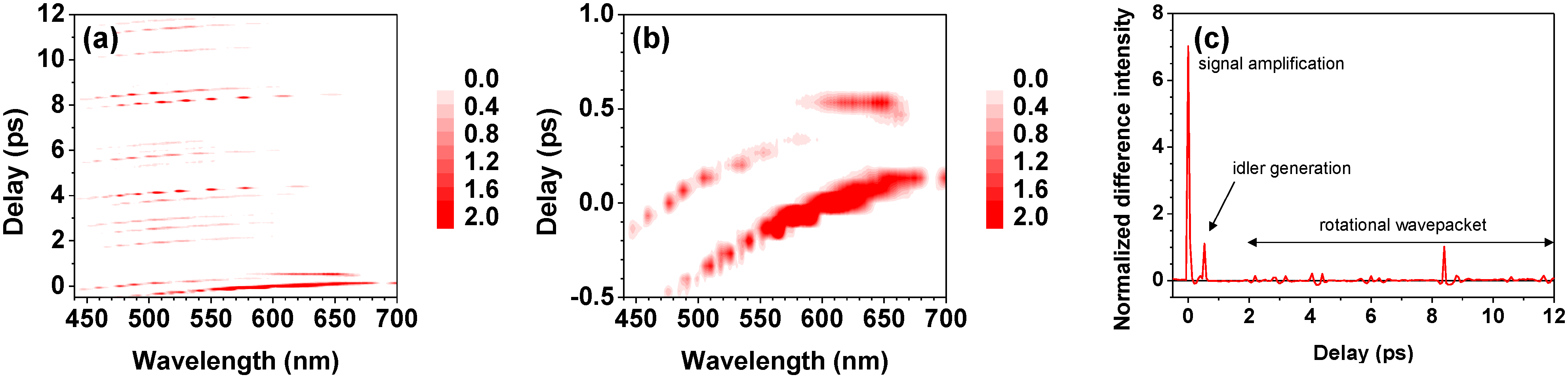
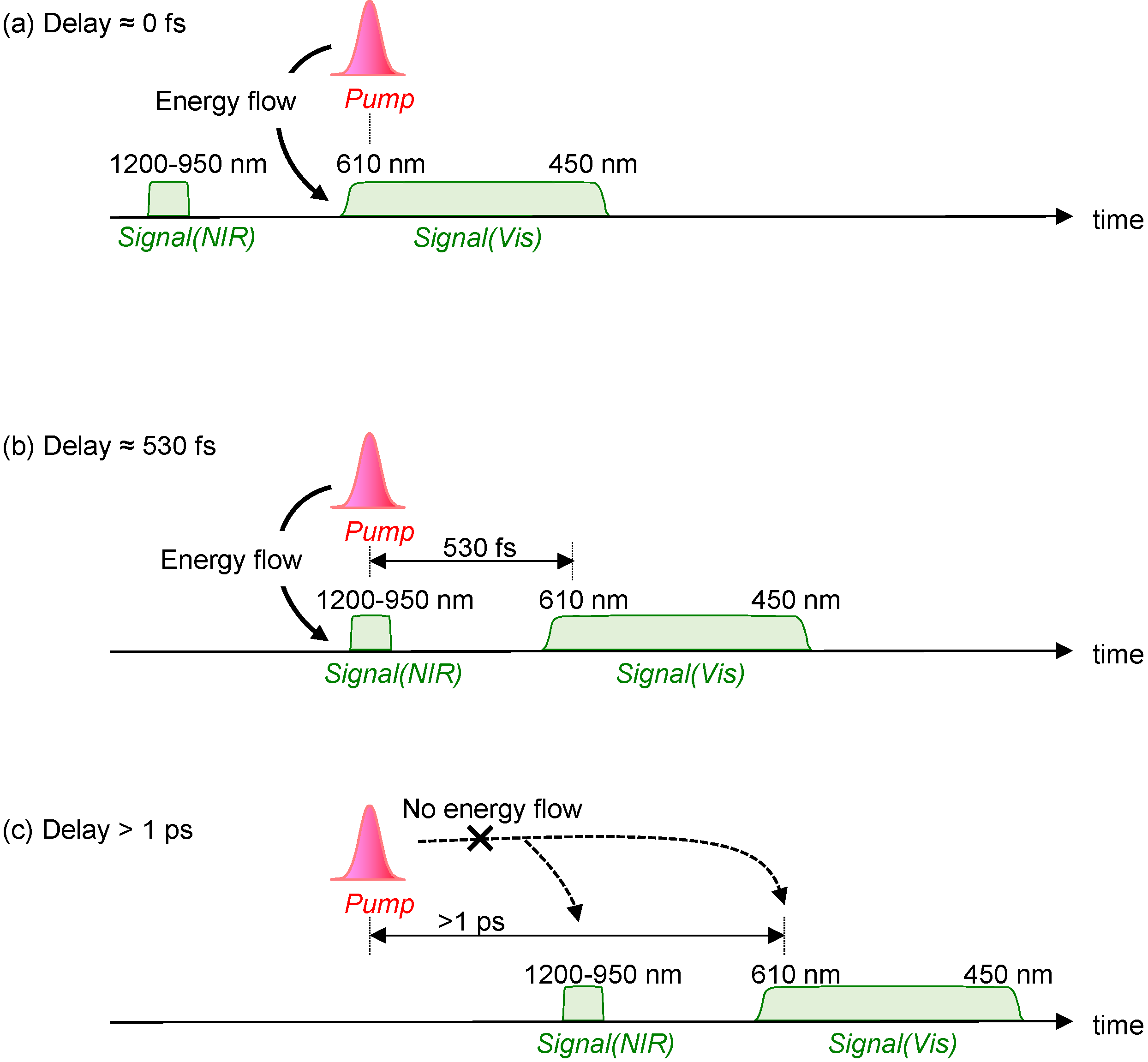
5. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Shirakawa, A.; Sakane, I.; Kobayashi, T. Pulse-front-matched optical parametric amplification for sub-10-fs pulse generation tunable in the visible and near infrared. Opt. Lett. 1998, 23, 1292–1294. [Google Scholar] [CrossRef] [PubMed]
- Baltuska, A.; Fuji, T.; Kobayashi, T. Visible pulse compression to 4 fs by optical parametric amplification and programmable dispersion control. Opt. Lett. 2002, 27, 306–308. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, D.; Homann, C.; Tautz, R.; Scharrer, M.; Russell, P.S.J.; Krausz, F.; Veisz, L.; Riedle, E. Approaching the full octave: Noncollinear optical parametric chirped pulse amplification with two-color pumping. Opt. Express 2010, 18, 18752–18762. [Google Scholar] [CrossRef] [PubMed]
- Harth, A.; Schultze, M.; Lang, T.; Binhammer, T.; Rausch, S.; Morgner, U. Two-color pumped OPCPA system emitting spectra spanning 1.5 octaves from VIS to NIR. Opt. Express 2012, 20, 3076–3081. [Google Scholar] [CrossRef] [PubMed]
- Witte, S.; Zinkstok, R.T.; Hogervorst, W.; Eikema, K.S.E. Generation of few-cycle terawatt light pulses using optical parametric chirped pulse amplification. Opt. Express 2005, 13, 4903–4908. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, D.; Veisz, L.; Tautz, R.; Tavella, F.; Schmid, K.; Pervak, V.; Krausz, F. Generation of sub-three-cycle, 16 TW light pulses by using noncollinear optical parametric chirped-pulse amplification. Opt. Lett. 2009, 34, 2459–2461. [Google Scholar] [CrossRef] [PubMed]
- Schmid, K.; Veisz, L.; Tavella, F.; Benavides, S.; Tautz, R.; Herrmann, D.; Buck, A.; Hidding, B.; Marcinkevicius, A.; Schramm, U.; et al. Few-cycle laser-driven electron acceleration. Phys. Rev. Lett. 2009, 102, 124801. [Google Scholar] [CrossRef] [PubMed]
- Dubietis, A.; Tamosauskas, G.; Polesana, P.; Valiulis, G.; Valtna, H.; Faccio, D.; Di Trapani, P.; Piskarskas, A. Highly efficient four-wave parametric amplification in transparent bulk Kerr medium. Opt. Express 2007, 15, 11126–11132. [Google Scholar] [CrossRef] [PubMed]
- Valtna, H.; Tamosauskas, G.; Dubietis, A.; Piskarskas, A. High-energy broadband four-wave optical parametric amplification in bulk fused silica. Opt. Lett. 2008, 33, 971–973. [Google Scholar] [CrossRef] [PubMed]
- Faccio, D.; Grün, A.; Bates, P.K.; Chalus, O.; Biegert, J. Optical amplification in the near-infrared in gas-filled hollow-core fibers. Opt. Lett. 2009, 34, 2918–2920. [Google Scholar] [CrossRef] [PubMed]
- Kida, Y.; Imasaka, T. Optical parametric amplification of a supercontinuum in a gas. Appl. Phys. B 2013, 116, 673–680. [Google Scholar] [CrossRef]
- Yan, Y.-X.; Gamble, E.B.; Nelson, K.A. Impulsive stimulated scattering: General importance in femtosecond laser pulse interactions with matter, and spectroscopic applications. J. Chem. Phys. 1985, 83, 5391–5399. [Google Scholar] [CrossRef]
- Korn, G.; Dühr, O.; Nazarkin, A. Observation of Raman Self-Conversion of fs-Pulse Frequency due to Impulsive Excitation of Molecular Vibrations. Phys. Rev. Lett. 1998, 81, 1215–1218. [Google Scholar] [CrossRef]
- Wittmann, M.; Nazarkin, A.; Korn, G. New regime of fs-pulse stimulated Raman scattering. Appl. Phys. B 2000, 70, 261–267. [Google Scholar] [CrossRef]
- Bartels, R.A.; Weinacht, T.C.; Wagner, N.; Baertschy, M.; Greene, C.H.; Murnane, M.M.; Kapteyn, H.C. Phase Modulation of Ultrashort Light Pulses using Molecular Rotational Wave Packets. Phys. Rev. Lett. 2001, 88, 013901. [Google Scholar] [CrossRef]
- Noack, F.; Steinkellner, O.; Tzankov, P.; Ritze, H.-H.; Herrmann, J.; Kida, Y. Generation of sub-30 fs ultraviolet pulses by Raman induced phase modulation in nitrogen. Opt. Express 2005, 13, 2467–2474. [Google Scholar] [CrossRef] [PubMed]
- Darginavičius, J.; Tamošauskas, G.; Valiulis, G.; Dubietis, A. Broadband four-wave optical parametric amplification in bulk isotropic media in the ultraviolet. Opt. Commun. 2009, 282, 2995–2999. [Google Scholar] [CrossRef]
- Ripoche, J.-F.; Grillon, G.; Prade, B.; Franco, M.; Nibbering, E.; Lange, R.; Mysyrowicz, A. Determination of the time dependence of N2 in air. Opt. Commun. 1997, 135, 310–314. [Google Scholar] [CrossRef]
- Nibbering, E.; Grillon, G.; Franco, M.A.; Prade, B.S.; Mysyrowicz, A. Determination of the inertial contribution to the nonlinear refractive index of air, N2, and O2 by use of unfocused high-intensity femtosecond laser pulses. J. Opt. Soc. Am. B 1997, 14, 650–660. [Google Scholar] [CrossRef]
- Diels, J.-C.; Rudolph, W. Ultrashort Laser Pulse Phenomena, 2nd ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Durfee, C.G.; Misoguti, L.; Backus, S.; Kapteyn, H.C.; Murnane, M.M. Phase matching in cascaded third-order processes. J. Opt. Soc. Am. B 2002, 19, 822–831. [Google Scholar] [CrossRef]
- Peck, E.R.; Reeder, K. Dispersion of Air. J. Opt. Soc. Am. 1972, 62, 958–962. [Google Scholar] [CrossRef]
- Marcatili, E.A.J.; Schmeltzer, R.A.R. Hollow Metallic and Dielectric Waveguides for Long Distance Optical Transmission and Lasers. Bell Syst. Tech. J. 1964, 43, 1783–1809. [Google Scholar] [CrossRef]
- Calegari, F.; Vozzi, C.; Gasilov, S.; Benedetti, E.; Sansone, G.; Nisoli, M.; De Silvestri, S.; Stagira, S. Rotational Raman Effects in the Wake of Optical Filamentation. Phys. Rev. Lett. 2008, 100, 123006. [Google Scholar] [CrossRef] [PubMed]
- Calegari, F.; Vozzi, C.; Stagira, S. Optical propagation in molecular gases undergoing filamentation-assisted field-free alignment. Phys. Rev. A 2009, 79, 023827. [Google Scholar] [CrossRef]
- Krylov, V.; Rebane, A.; Erni, D.; Ollikainen, O.; Wild, U.; Bespalov, V.; Staselko, D. Stimulated Raman amplification of femtosecond pulses in hydrogen gas. Opt. Lett. 1996, 21, 2005–2007. [Google Scholar] [CrossRef] [PubMed]
- Vodchits, A.I.; Shvedko, A.G.; Orlovich, V.A.; Kozich, V.P.; Werncke, W. Stimulated Raman amplification of ultrashort seed pulses in compressed methane. J. Opt. Soc. Am. B 2005, 22, 453–458. [Google Scholar] [CrossRef]
- Abdolvand, A.; Nazarkin, A.; Chugreev, A.V.; Kaminski, C.F.; Russell, P.S.J. Solitary Pulse Generation by Backward Raman Scattering in H2-Filled Photonic Crystal Fibers. Phys. Rev. Lett. 2009, 103, 183902. [Google Scholar] [CrossRef] [PubMed]
- Trabold, B.M.; Abdolvand, A.; Euser, T.G.; Walser, A.M.; Russell, P.S.J. Amplification of higher-order modes by stimulated Raman scattering in H2-filled hollow-core photonic crystal fiber. Opt. Lett. 2013, 38, 600–602. [Google Scholar] [CrossRef] [PubMed]
- Imasaka, T.; Kawasaki, S.; Ishibashi, N. Generation of more than 40 laser emission lines from the ultraviolet to the visible regions by two-color stimulated raman effect. Appl. Phys. B 1989, 49, 389–392. [Google Scholar] [CrossRef]
- Yavuz, D.; Walker, D.; Shverdin, M.; Yin, G.; Harris, S.E. Quasiperiodic Raman Technique for Ultrashort Pulse Generation. Phys. Rev. Lett. 2003, 91, 233602. [Google Scholar] [CrossRef] [PubMed]
- Sali, E.; Mendham, K.J.; Tisch, J.W.G.; Halfmann, T.; Marangos, J.P. High-order stimulated Raman scattering in a highly transient regime driven by a pair of ultrashort pulses. Opt. Lett. 2004, 29, 495–497. [Google Scholar] [CrossRef] [PubMed]
- Sensarn, S.; Goda, S.N.; Yin, G.Y.; Harris, S.E. Molecular modulation in a hollow fiber. Opt. Lett. 2006, 31, 2836–2838. [Google Scholar] [CrossRef] [PubMed]
- Bauerschmidt, S.T.; Novoa, D.; Abdolvand, A.; Russell, P.S.J. Broadband-tunable LP01 mode frequency shifting by Raman coherence waves in a H2-filled hollow-core photonic crystal fiber. Optica 2015, 2, 536–539. [Google Scholar] [CrossRef]
- Motoyoshi, K.; Kida, Y.; Imasaka, T. High-Energy, Multicolor Femtosecond Pulses from the Deep Ultraviolet to the Near Infrared Generated in a Hydrogen-Filled Gas Cell and Hollow Fiber. Appl. Sci. 2014, 4, 318–330. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kida, Y.; Imasaka, T. Four-Wave Optical Parametric Amplification in a Raman-Active Gas. Photonics 2015, 2, 933-945. https://doi.org/10.3390/photonics2030933
Kida Y, Imasaka T. Four-Wave Optical Parametric Amplification in a Raman-Active Gas. Photonics. 2015; 2(3):933-945. https://doi.org/10.3390/photonics2030933
Chicago/Turabian StyleKida, Yuichiro, and Totaro Imasaka. 2015. "Four-Wave Optical Parametric Amplification in a Raman-Active Gas" Photonics 2, no. 3: 933-945. https://doi.org/10.3390/photonics2030933
APA StyleKida, Y., & Imasaka, T. (2015). Four-Wave Optical Parametric Amplification in a Raman-Active Gas. Photonics, 2(3), 933-945. https://doi.org/10.3390/photonics2030933





