Dynamics of a Dispersion-Managed Passively Mode-Locked Er-Doped Fiber Laser Using Single Wall Carbon Nanotubes
Abstract
:1. Introduction
2. Methods
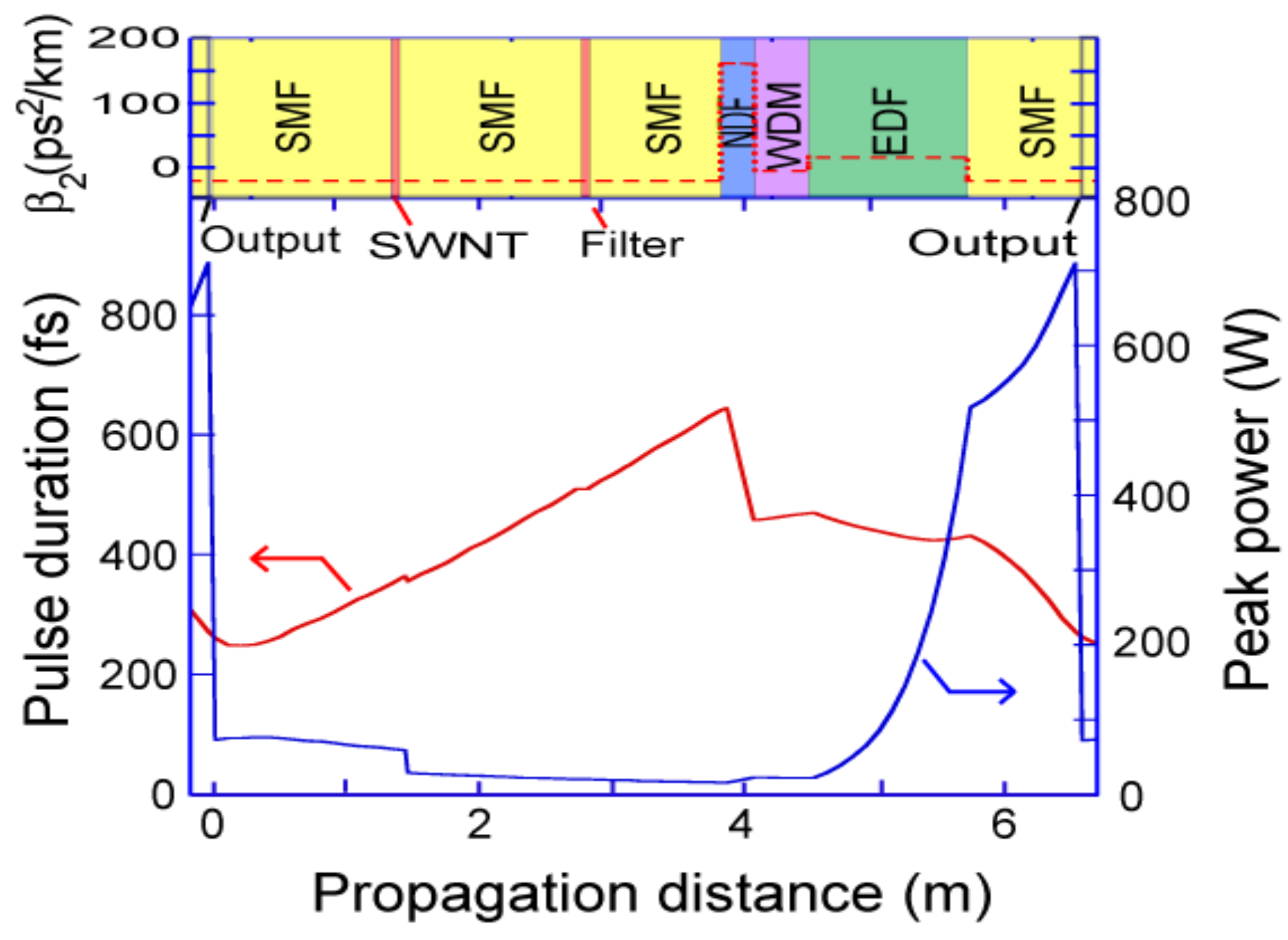
2.1. Setup of Ultrashort Pulse Fiber Laser with SWNT Film
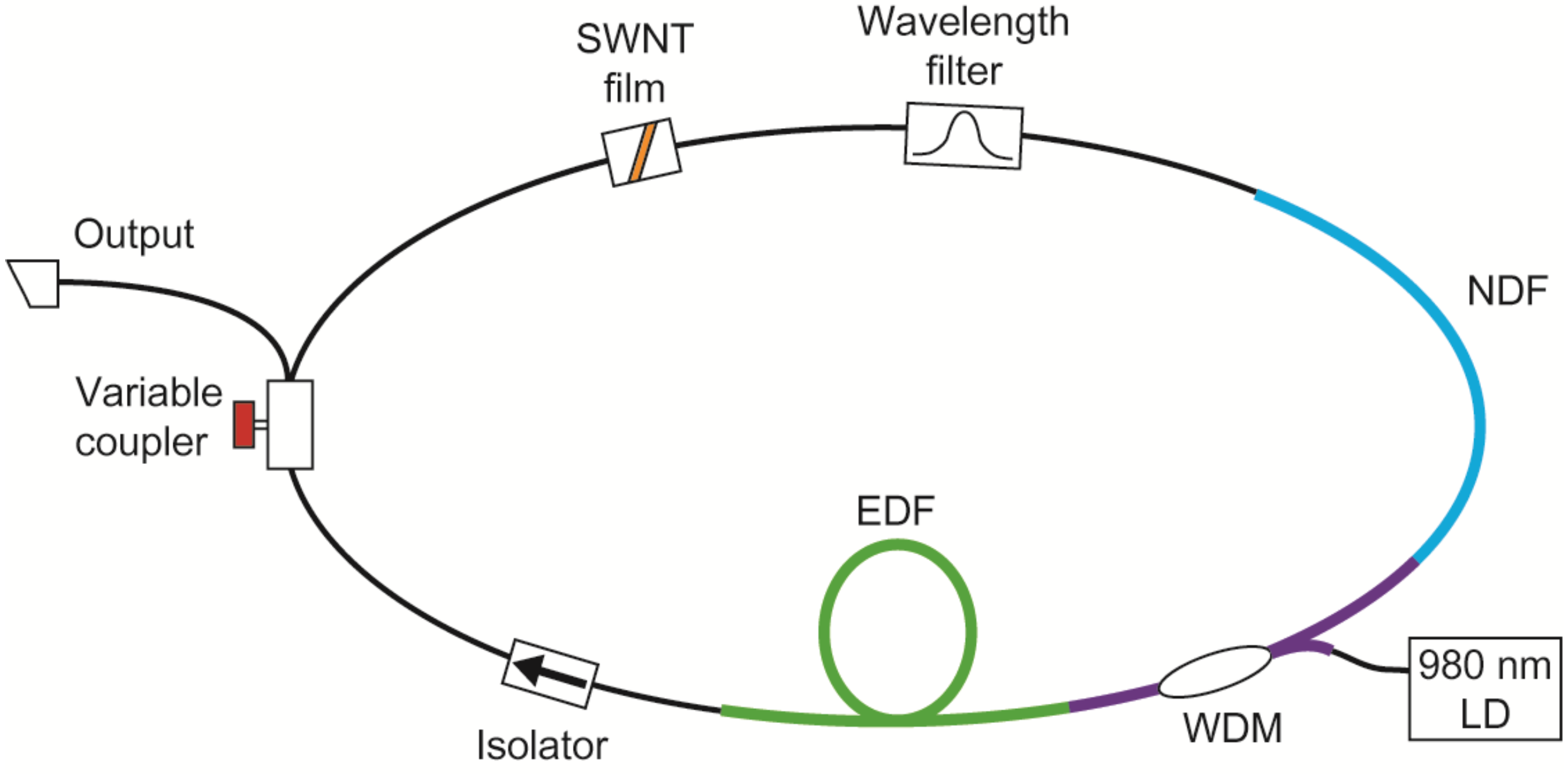
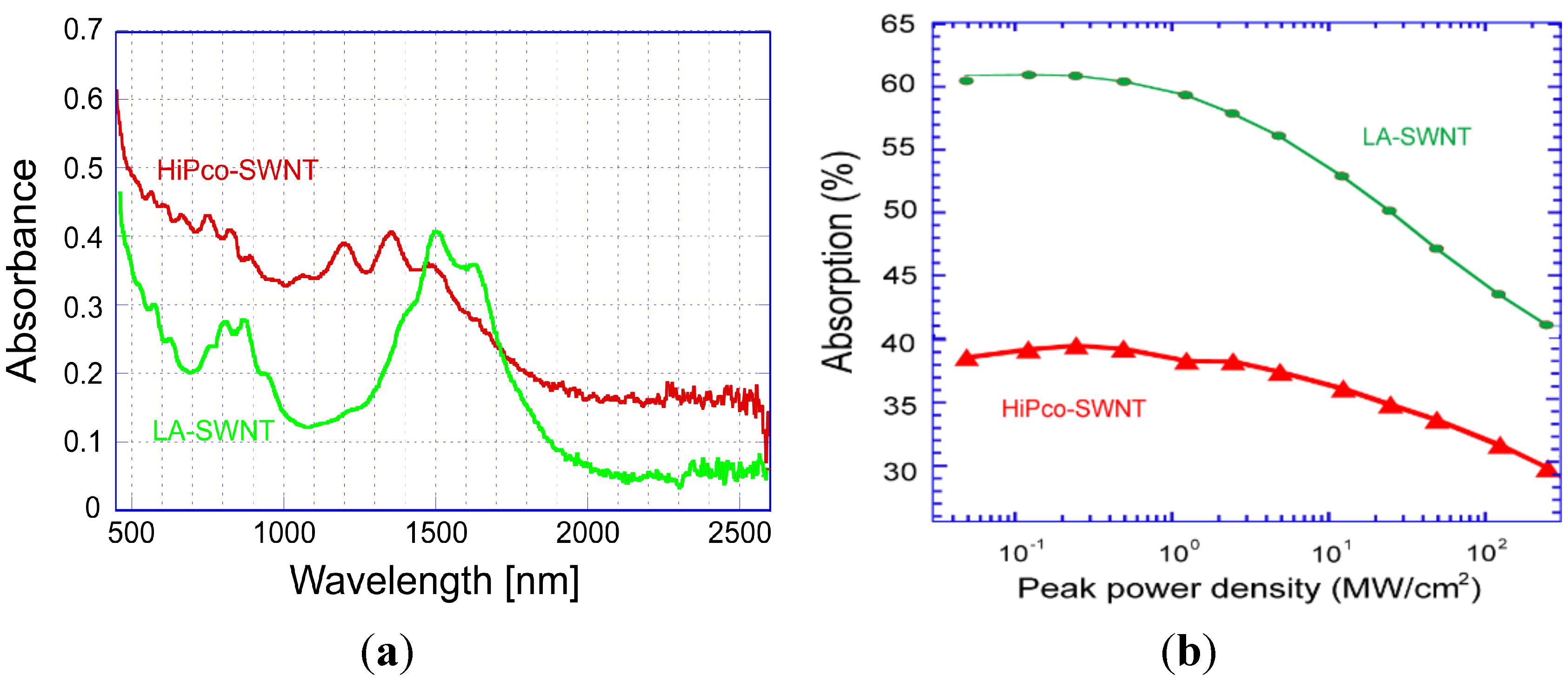
2.2. Numerical Model
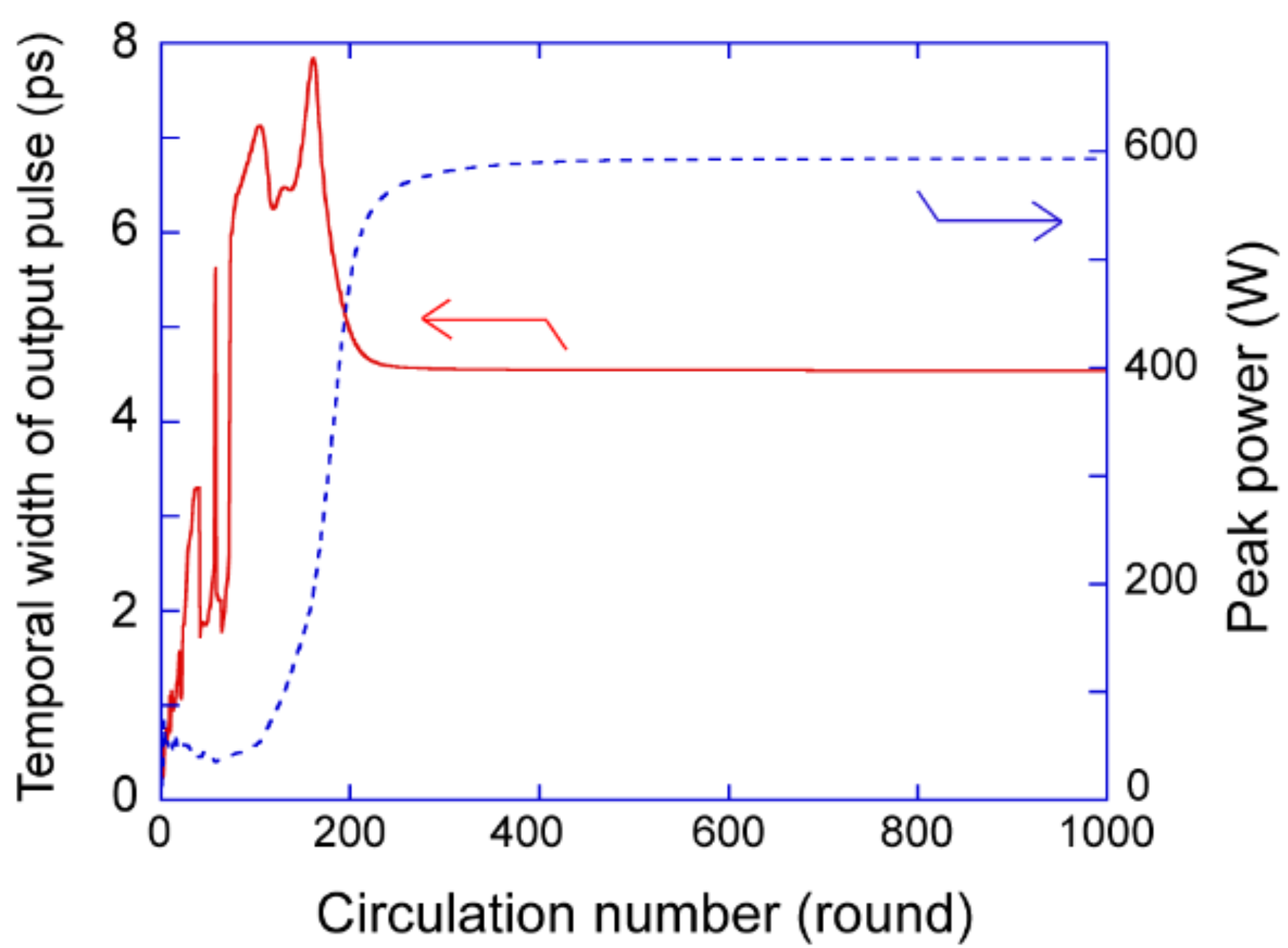
3. Results and Discussions
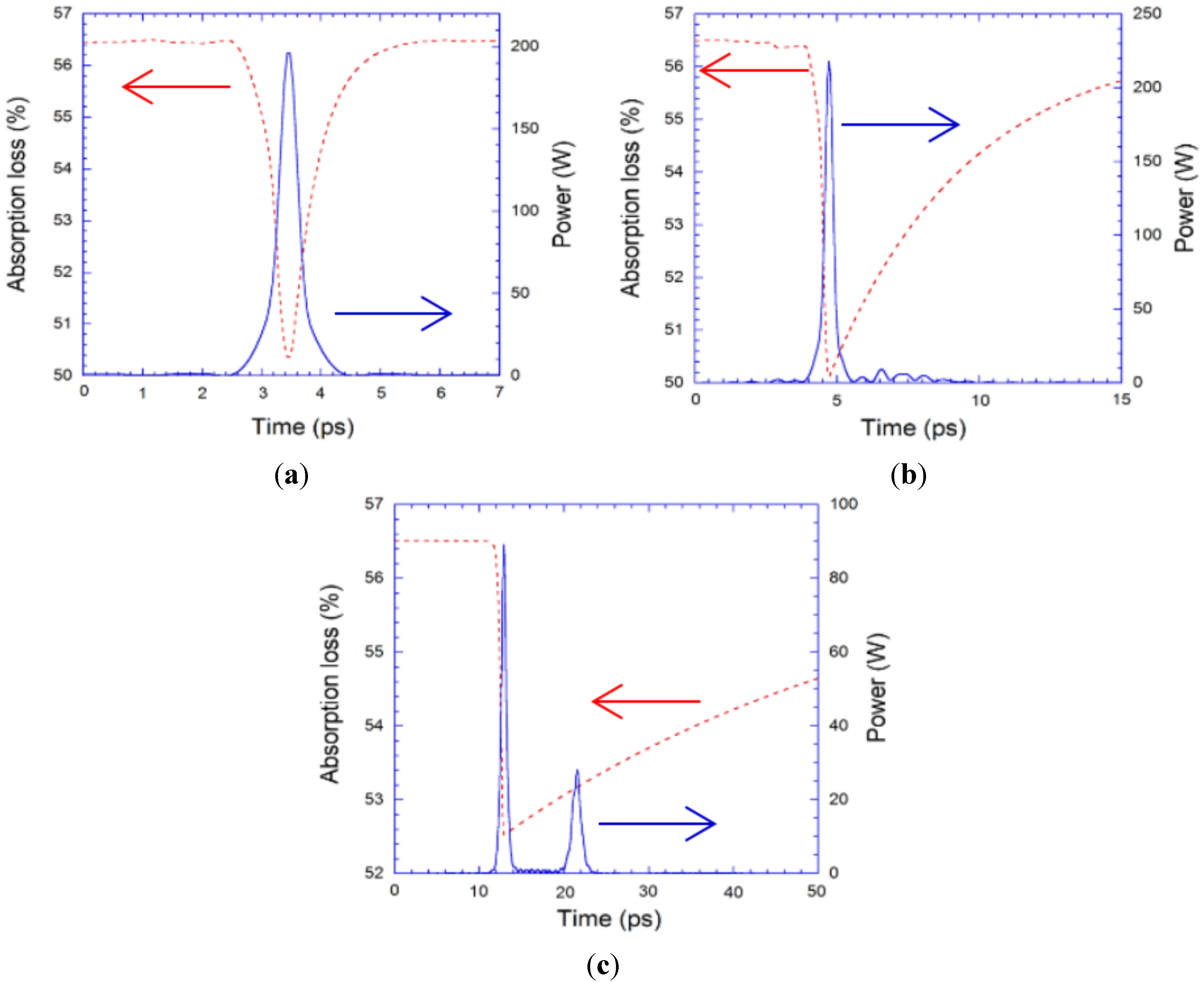
3.1. Soliton Mode-Locking Regime (DT < 0)
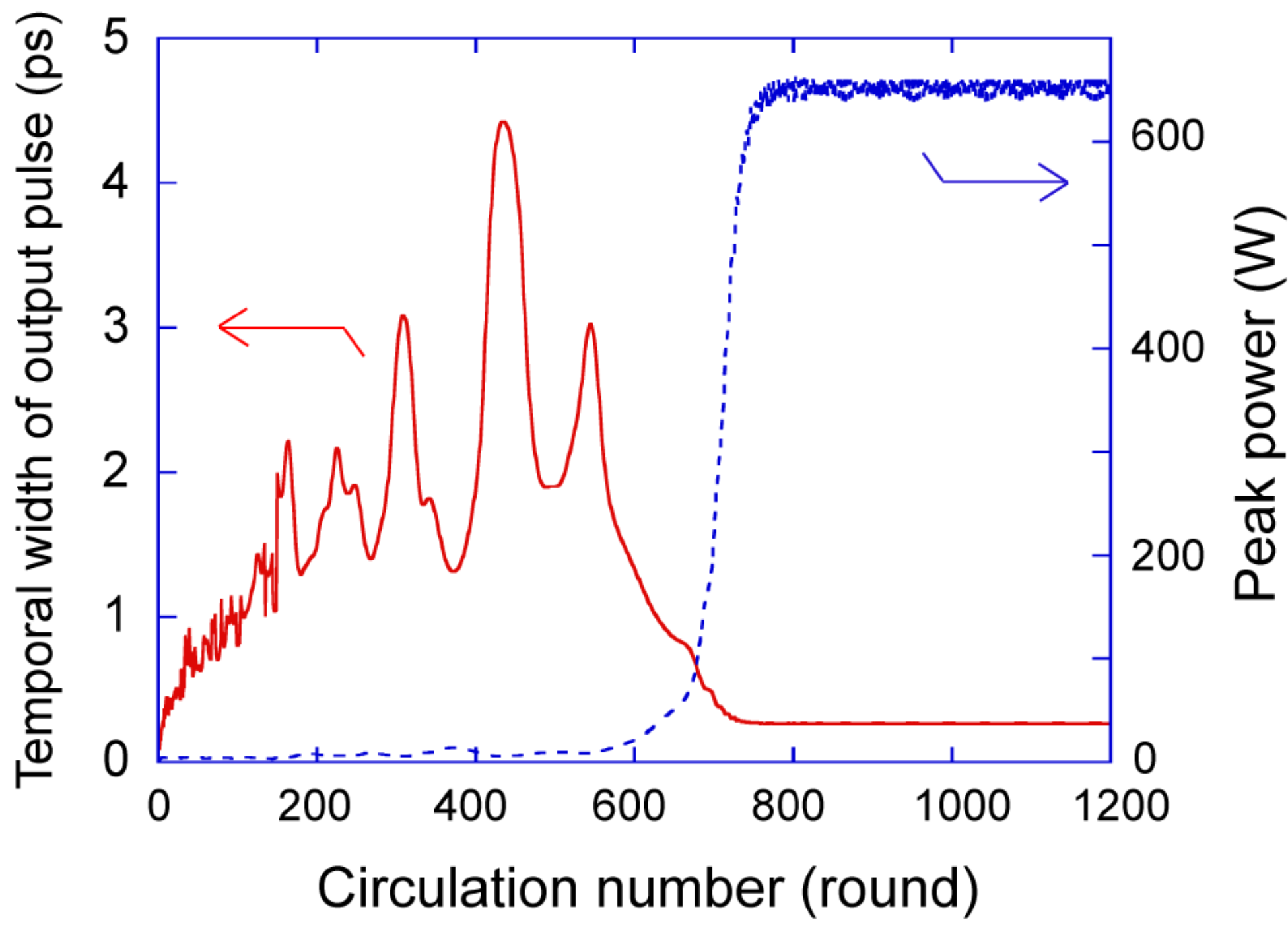
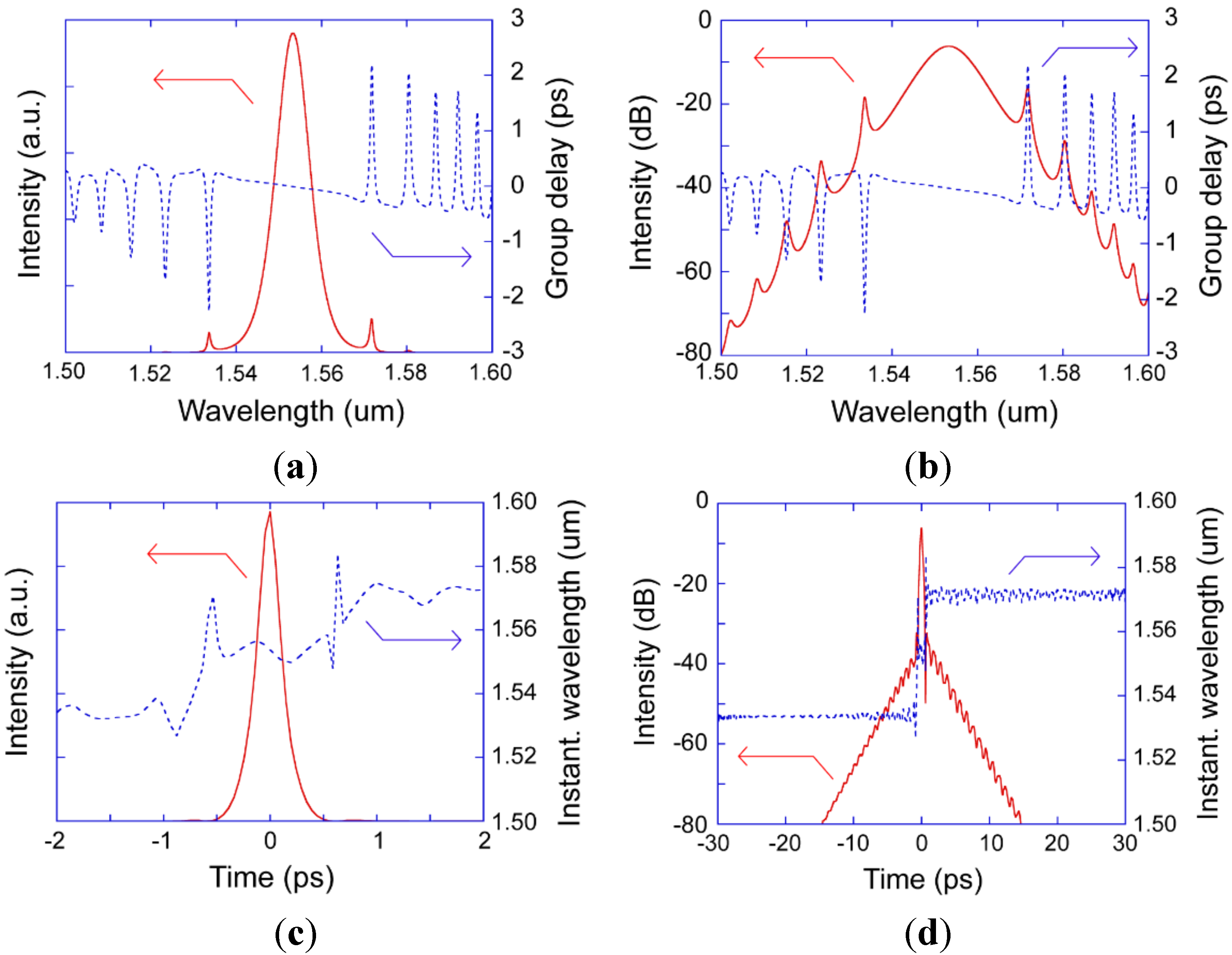
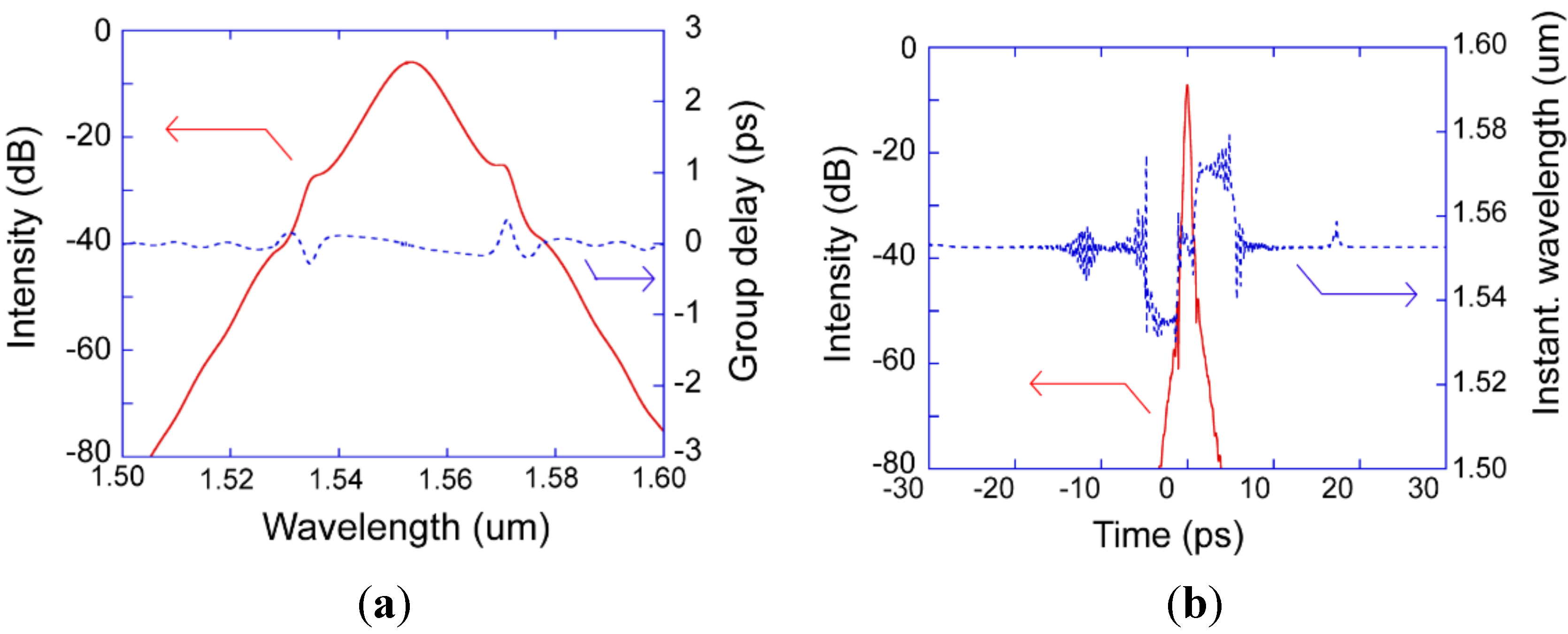
3.2. Dissipative-Soliton Mode-Locking Regime (DT > 0)
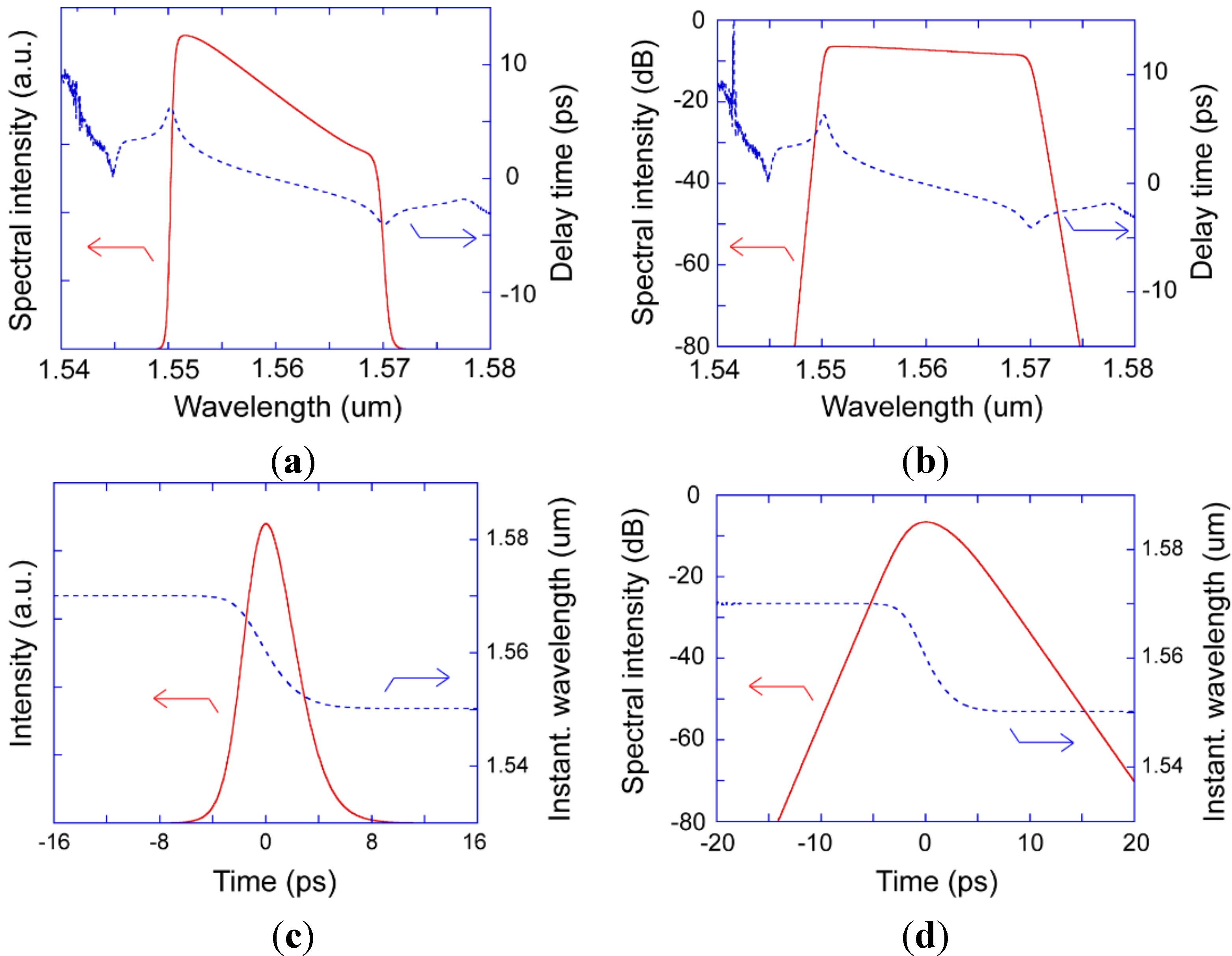
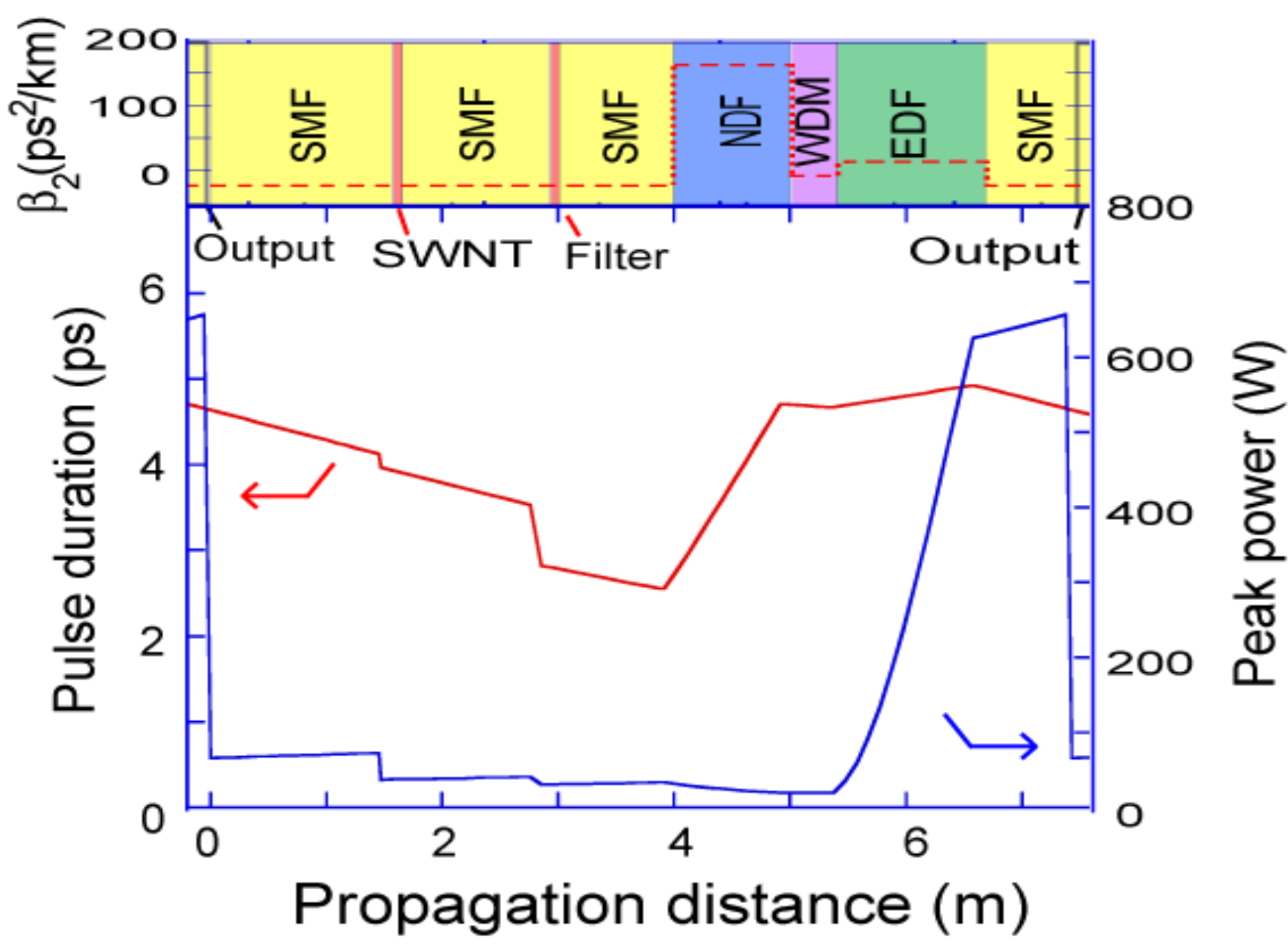
3.3. Stretched-Pulse Mode-Locking Regime (DT ~ 0)
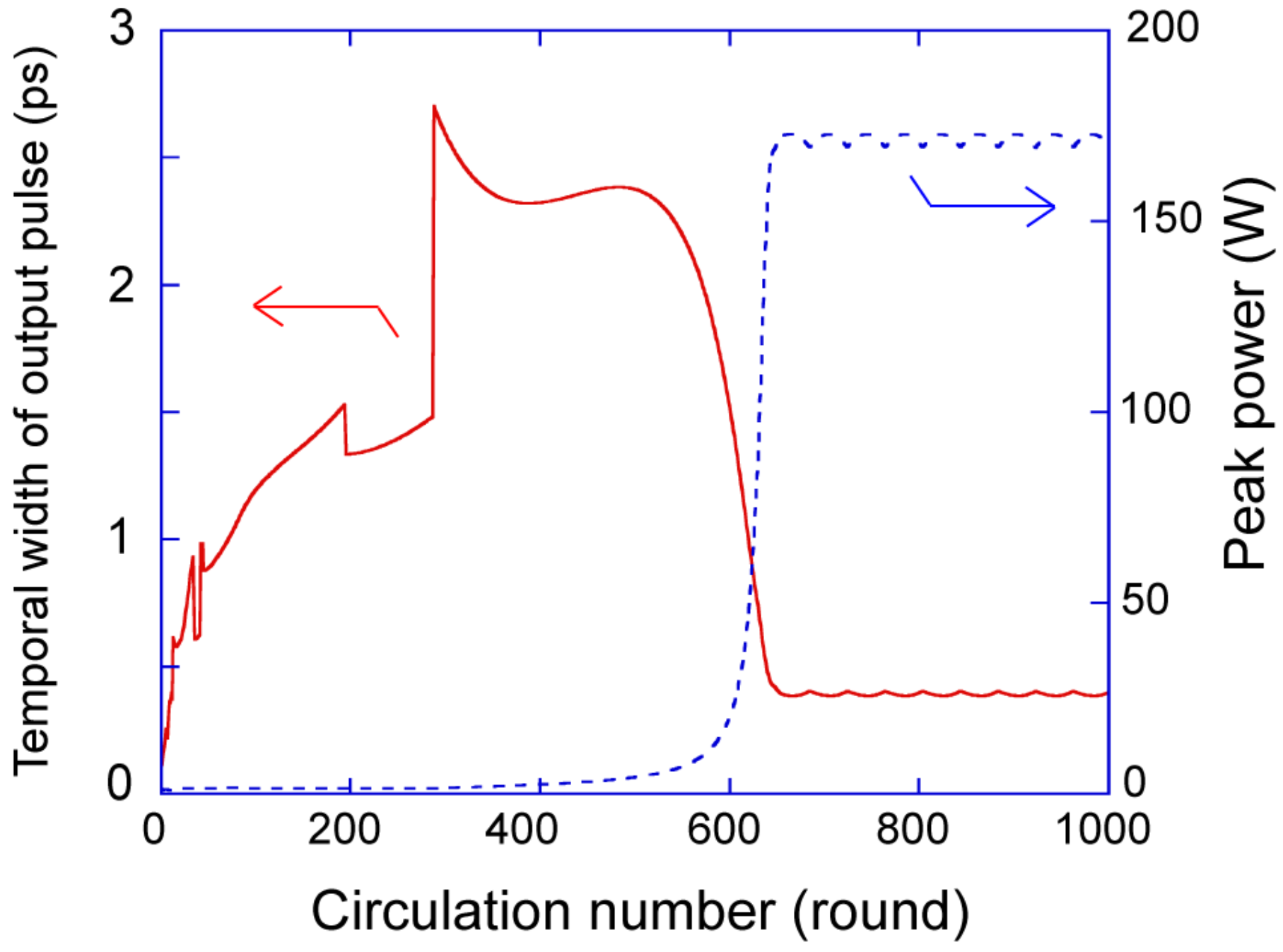
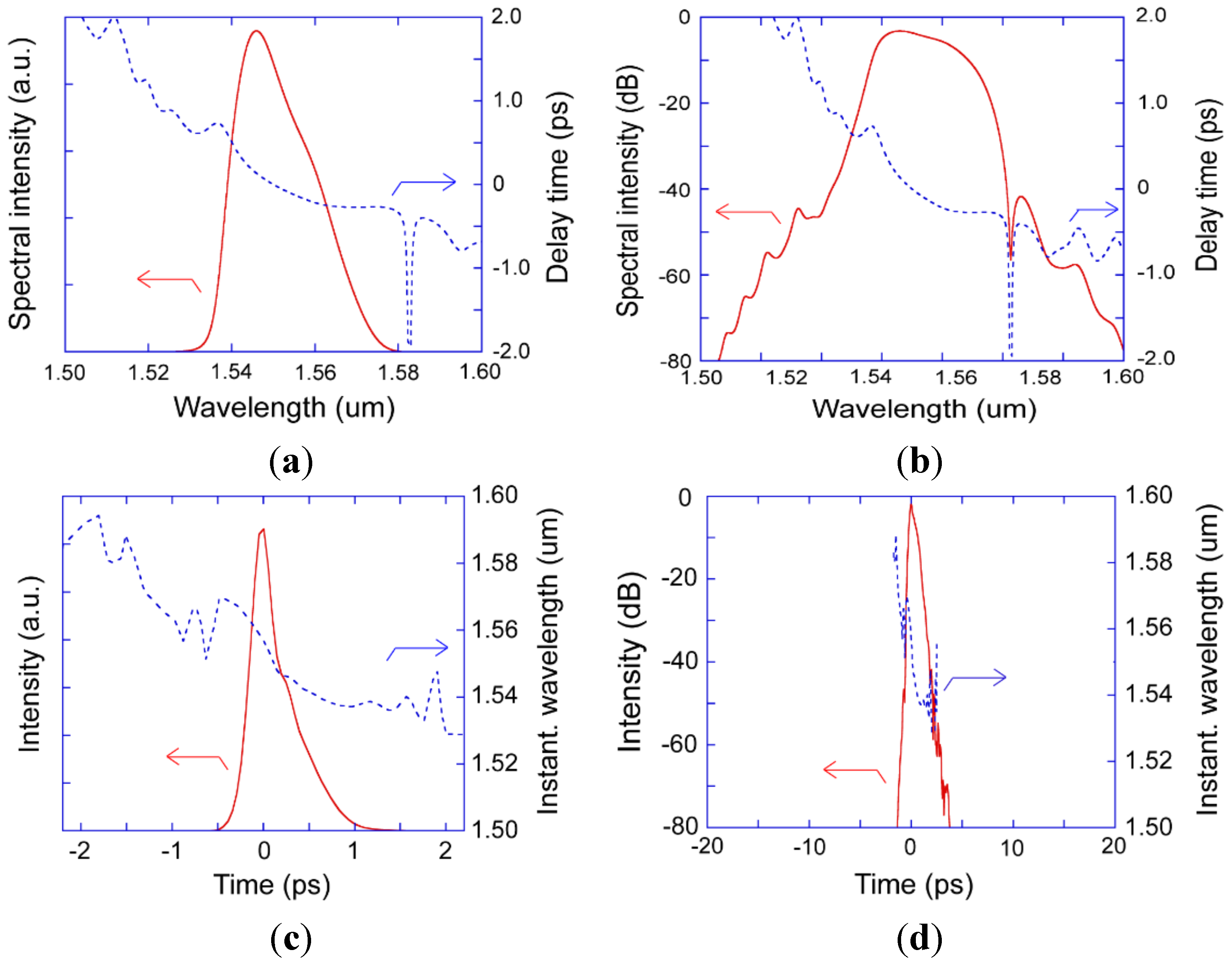
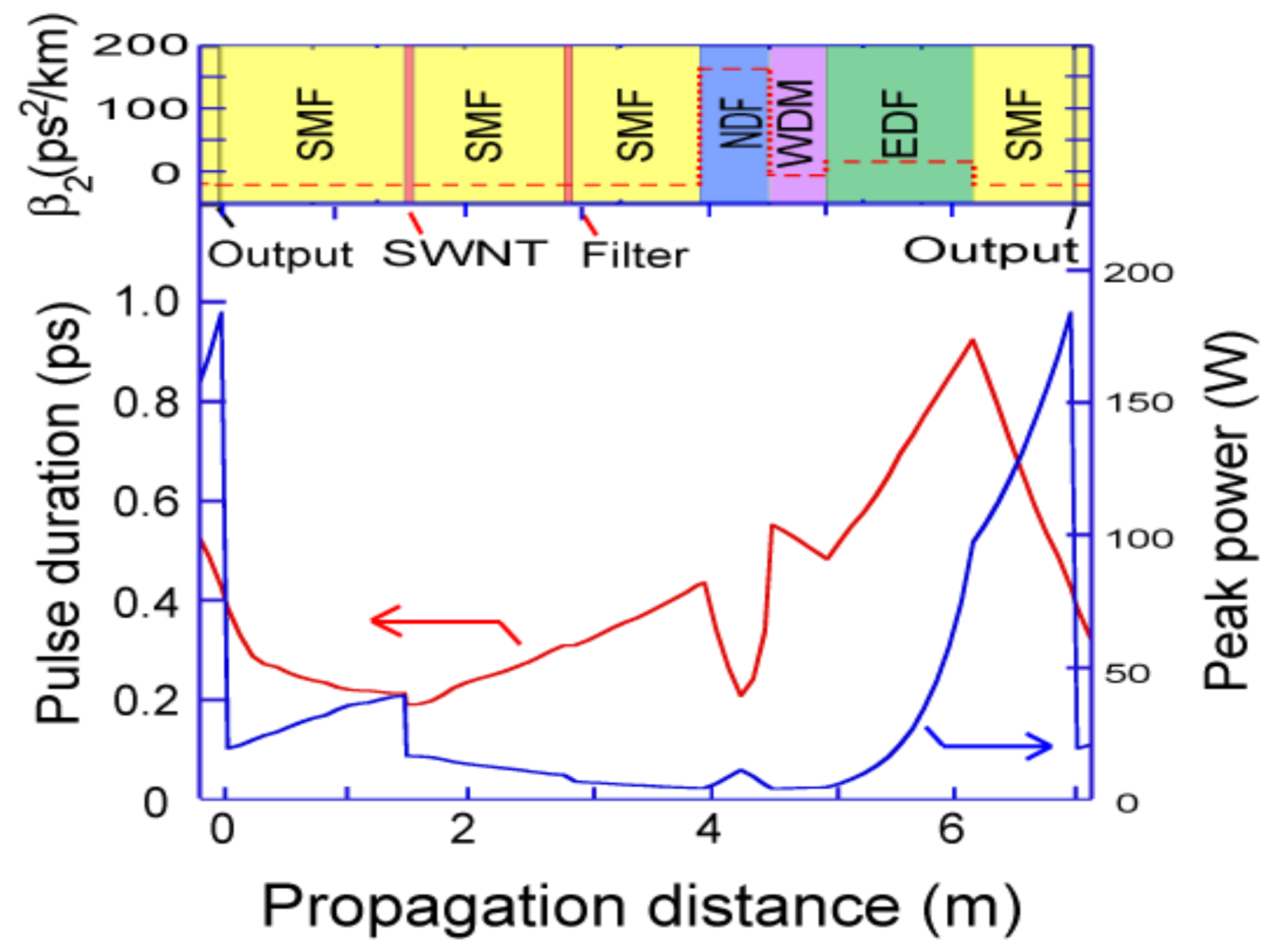
3.4. Dependence on Net Dispersion, DT

3.5. Effect of Response Time and Modulation Depth of SWNT Film
4. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Set, S.Y.; Yamaguchi, H.; Tanaka, Y.; Jablonski, M.; Sakakibara, Y.; Rozhin, A.; Tokumoto, M.; Kataura, H.; Achiba, Y.; Kikuchi, K. Mode-locked fiber lasers based on a saturable absorber incorporating carbon nanotubes. In Proceedings of the Optical Fiber Communication Conference, Atlanta, GA, USA, 23–28 March 2003.
- Yamashita, S.; Inoue, Y.; Maruyama, S.; Murakami, Y.; Yaguchi, H.; Jablonski, M.; Set, S.Y. Saturable absorbers incorporating carbon nanotubes directly synthesized onto substrates and fibers and their application to mode-locked fiber lasers. Opt. Lett. 2004, 29, 1581–1583. [Google Scholar] [CrossRef] [PubMed]
- Sakakibara, Y.; Kintaka, K.; Rozhin, A.G.; Itatani, T.; Soe, W.M.; Itatani, H.; Tokumoto, M.; Kataura, H. Optically uniform carbon nanotube-polyimide nanocomposite: Application to 165 fs mode-locked fiber laser and waveguide. In Proceedings of the 31st European Conference on Optical Communication, Glasgow, UK, 25–29 September 2005; Volume 1, p. 38.
- Rozhin, A.G.; Sakakibara, Y.; Namiki, S.; Tokumoto, M.; Kataura, H.; Achiba, Y. Sub-200-fs pulsed erbium-doped fiber laser using a carbon nanotube-polyvinylalcohol mode locker. Appl. Phys. Lett. 2006, 88, 051118. [Google Scholar] [CrossRef]
- Nakazawa, M.; Nakahara, S.; Hirooka, T.; Yoshida, M.; Kaino, T.; Komatsu, K. Polymer saturable absorber materials in the 1.5 μm band using poly-methyl-methacrylate and polystyrene with single-wall carbon nanotubes and their application to a femtosecond laser. Opt. Lett. 2006, 31, 915–917. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.W.; Yamashita, S.; Goh, C.S.; Set, S.Y. Carbon nanotube mode lockers with enhanced nonlinearity via evanescent field interaction in D-shaped fibers. Opt. Lett. 2007, 32, 148–150. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, J.W.; Windeler, R.S.; DiGiovanni, D.J. Optically driven deposition of single-wall carbon-nanotube saturable absorbers on optical fiber end-faces. Opt. Express 2007, 15, 9176–9183. [Google Scholar] [CrossRef] [PubMed]
- Kieu, K.; Mansuripur, M. Femtosecond laser pulse generation with a fiber taper embedded in carbon nanotube/polymer composite. Opt. Lett. 2007, 32, 2242–2244. [Google Scholar] [CrossRef] [PubMed]
- Hasan, T.; Sun, Z.; Wang, F.; Bonaccorso, F.; Tan, P.H.; Rozhin, A.G.; Ferrari, A.C. Nanotube-polymer composites for ultrafast photonics. Adv. Mater. 2009, 21, 3874–3899. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Ferrari, A.C. Ultrafast lasers mode-locked by nanotubes and grapheme. Phys. E 2012, 44, 1082–1091. [Google Scholar] [CrossRef]
- Martinez, A.; Sun, Z. Nanotube and graphene saturable absorbers for fiber lasers. Nat. Photon. 2013, 7, 842–845. [Google Scholar] [CrossRef]
- Song, Y.W.; Yamashita, S.; Maruyama, S. Single-walled carbon nanotubes for high-energy optical pulse formation. Appl. Phys. Lett. 2008, 92, 021115. [Google Scholar] [CrossRef]
- Im, J.H.; Choi, S.Y.; Rotermund, F.; Yeom, D. All-fiber Er-doped dissipative soliton laser based on evanescent field interaction with carbon nanotube saturable absorber. Opt. Express 2010, 18, 22141–22146. [Google Scholar] [CrossRef] [PubMed]
- Nishizawa, N.; Seno, Y.; Sumimura, K.; Sakakibara, Y.; Itoga, E.; Kataura, H.; Itoh, K. All-polarization maintaining Er-doped ultrashort-pulse fiber laser using carbon nanotube saturable absorber. Opt. Express 2008, 16, 9429–9435. [Google Scholar] [CrossRef] [PubMed]
- Senoo, Y.; Nishizawa, N.; Sakakibara, Y.; Sumimura, K.; Itoga, E.; Kataura, H.; Itoh, K. Polarization-maintaining, high-energy, wavelength-tunable, Er-doped ultrashort pulse fiber laser using carbon-nanotube polyimide film. Opt. Express 2009, 17, 20233–20240. [Google Scholar] [CrossRef] [PubMed]
- Nishizawa, N.; Nozaki, Y.; Itoga, E.; Kataura, H.; Sakakibara, Y. Dispersion-managed, high-power, Er-doped ultrashort-pulse fiber laser using carbon-nanotube polyimide film. Opt. Express 2011, 19, 21874–21879. [Google Scholar] [CrossRef] [PubMed]
- Nozaki, Y.; Nishizawa, N.; Itoga, E.; Kataura, H.; Sakakibara, Y. Power scaling of dispersion-managed Er-doped ultrashort pulse fiber laser with single wall carton nanotubes. Opt. Lett. 2012, 37, 5079–5081. [Google Scholar] [CrossRef] [PubMed]
- Wise, F.W.; Chong, A.; Renninger, W.H. High-energy femtosecond fiber lasers based on pulse propagation at normal dispersion. Laser Photon. Rev. 2008, 2, 58–73. [Google Scholar] [CrossRef]
- Baumgartl, M.; Ortac, B.; Schreiber, T.; Limpert, J.; Tunnermann, A. Ultrashort pulse formation and evolution in mode-locked fiber lasers. Appl. Phys. B 2011, 104, 523–536. [Google Scholar] [CrossRef]
- Renninger, W.H.; Chong, A.; Wise, F.W. Pulse shaping and evolution in normal-dispersion mode-locked fiber lasers. IEEE J. Select. Top. Quantum Electron. 1999, 5, 1385–1391. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Z.; Xu, P.; Du, G.; Wang, F.; Ruan, S.; Sun, Z.; Hasan, T. Pulse dynamics in carbon nanotube mode-locked fiber lasers near zero cavity dispersion. Opt. Express 2015, 23, 19947–19958. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.H.; Kieu, K.; Peyghambarian, N.; Jones, R.J. Low noise erbium fiber fs frequency comb based on a tapered-fiber carbon nanotube design. Opt. Express 2011, 19, 5313–5318. [Google Scholar] [CrossRef] [PubMed]
- Kawagoe, H.; Ishida, S.; Aramaki, M.; Sakakibara, Y.; Omoda, E.; Kataura, H.; Nishizawa, N. Development of a high power supercontinuum source in the 1.7 um wavelength region for highly penetrative ultrahigh-resolution optical coherence tomography. Biomed. Opt. Express 2014, 5, 932–943. [Google Scholar] [CrossRef] [PubMed]
- Freudiger, C.W.; Yang, W.; Holtom, G.R.; Peyghambarian, N.; Xie, X.S.; Kieu, K.Q. Stimulated Raman scattering microscopy with a robust fiber laser source. Nat. Photon. 2014, 8, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Newbury, N.R.; Washburn, B.R. Theory of the frequency comb output from a femtosecond fiber laser. IEEE J. Quant. Electron. 2005, 41, 1388–1402. [Google Scholar] [CrossRef]
- Nakajima, Y.; Inaba, H.; Hosaka, K.; Monishima, K.; Onae, A.; Yasuda, M.; Kohno, T.; Kawato, S.; Kobayashi, T.; Katsuyama, T.; et al. A multi-branch, fiber-based frequency comb with millihertz-level relative linewidths using an intra-cavity electro-optic modulator. Opt. Express 2010, 18, 1667–1676. [Google Scholar] [CrossRef] [PubMed]
- Glandorf, L.N.; Johnson, T.A.; Kobayashi, Y.; Diddams, S.A. Impact of dispersion on amplitude and frequency noise in a Yb-fiber laser comb. Opt. Lett. 2011, 36, 1578–1580. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics, 2nd ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Schreiber, T.; Ortac, B.; Limpert, J.; Tunnermann, A. On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations. Opt. Express 2007, 15, 8252–8262. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Buckley, J.; Renninger, W.; Wise, F. All-normal-dispersion femtosecond fiber laser. Opt. Express 2006, 14, 10095–10100. [Google Scholar] [CrossRef] [PubMed]
- Cabasse, A.; Ortac, B.; Martel, G.; Hideur, A.; Limpert, J. Dissipative solitons in a passively mode-locked Er-doped fiber with strong normal dispersion. Opt. Express 2008, 16, 19322–19329. [Google Scholar] [CrossRef] [PubMed]
- Bale, B.G.; Boscolo, S.; Turitsyn, S.K. Dissipative dispersion-managed solitons in mode-locked lasers. Opt. Lett. 2009, 34, 3286–3288. [Google Scholar] [CrossRef] [PubMed]
- Kieu, K.; Wise, F.W. Self-similar and stretched-pulse operation of Erbium-doped fiber lasers with carbon nanotubes saturable absorber. In Proceedings of the Conference on Laser Electro-Optics, Baltimore, MD, USA, 2–4 June 2009.
- Tamura, K.; Ippen, E.P.; Haus, H.A.; Nelson, L.E. 77-fs pulse generation from a stretched-pulse mode-locked all-fiber ring laser. Opt. Lett. 1993, 18, 1080–1082. [Google Scholar] [CrossRef] [PubMed]
- Kartner, F.X.; der Au, J.A.; Keller, U. Mode-locking with slow and fast saturable absorbers—What’s the difference? IEEE J. Select. Top. Quantum Electron. 1998, 4, 159–168. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishizawa, N.; Jin, L.; Kataura, H.; Sakakibara, Y. Dynamics of a Dispersion-Managed Passively Mode-Locked Er-Doped Fiber Laser Using Single Wall Carbon Nanotubes. Photonics 2015, 2, 808-824. https://doi.org/10.3390/photonics2030808
Nishizawa N, Jin L, Kataura H, Sakakibara Y. Dynamics of a Dispersion-Managed Passively Mode-Locked Er-Doped Fiber Laser Using Single Wall Carbon Nanotubes. Photonics. 2015; 2(3):808-824. https://doi.org/10.3390/photonics2030808
Chicago/Turabian StyleNishizawa, Norihiko, Lei Jin, Hiromichi Kataura, and Youichi Sakakibara. 2015. "Dynamics of a Dispersion-Managed Passively Mode-Locked Er-Doped Fiber Laser Using Single Wall Carbon Nanotubes" Photonics 2, no. 3: 808-824. https://doi.org/10.3390/photonics2030808
APA StyleNishizawa, N., Jin, L., Kataura, H., & Sakakibara, Y. (2015). Dynamics of a Dispersion-Managed Passively Mode-Locked Er-Doped Fiber Laser Using Single Wall Carbon Nanotubes. Photonics, 2(3), 808-824. https://doi.org/10.3390/photonics2030808



