Gain and Threshold Current in Type II In(As)Sb Mid-Infrared Quantum Dot Lasers
Abstract
:1. Introduction
2. Experimental Section
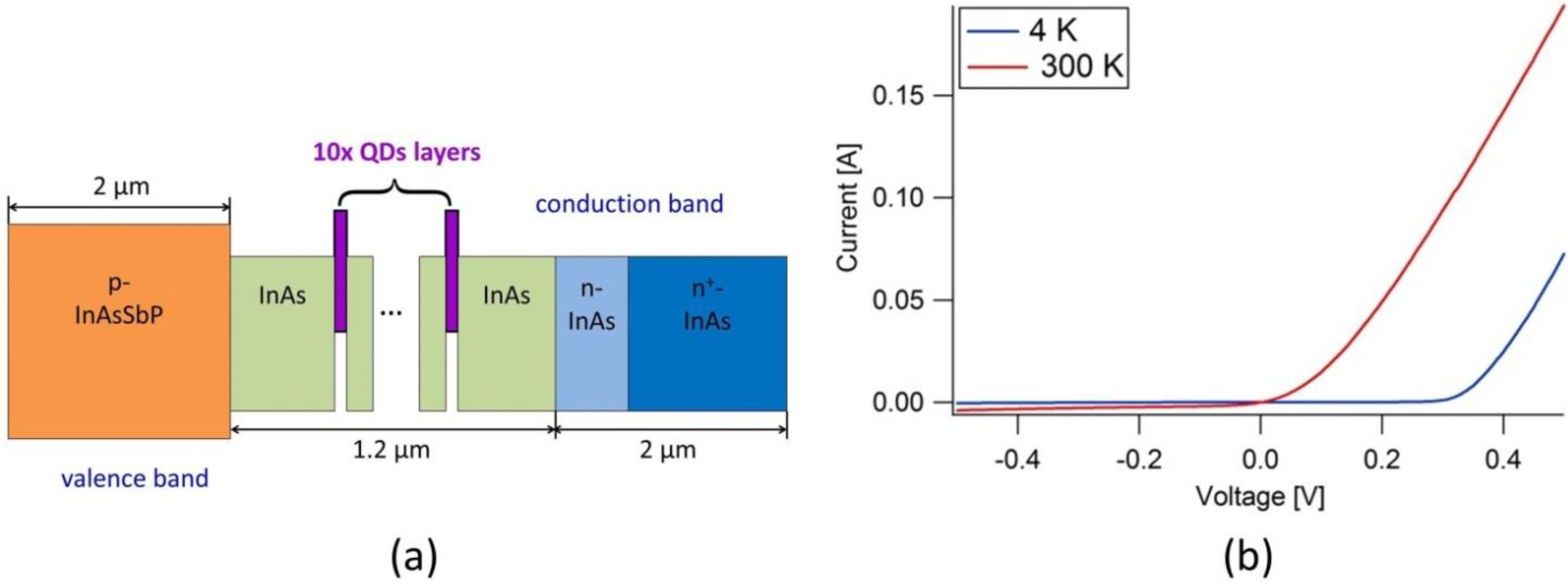
3. Results and Discussion
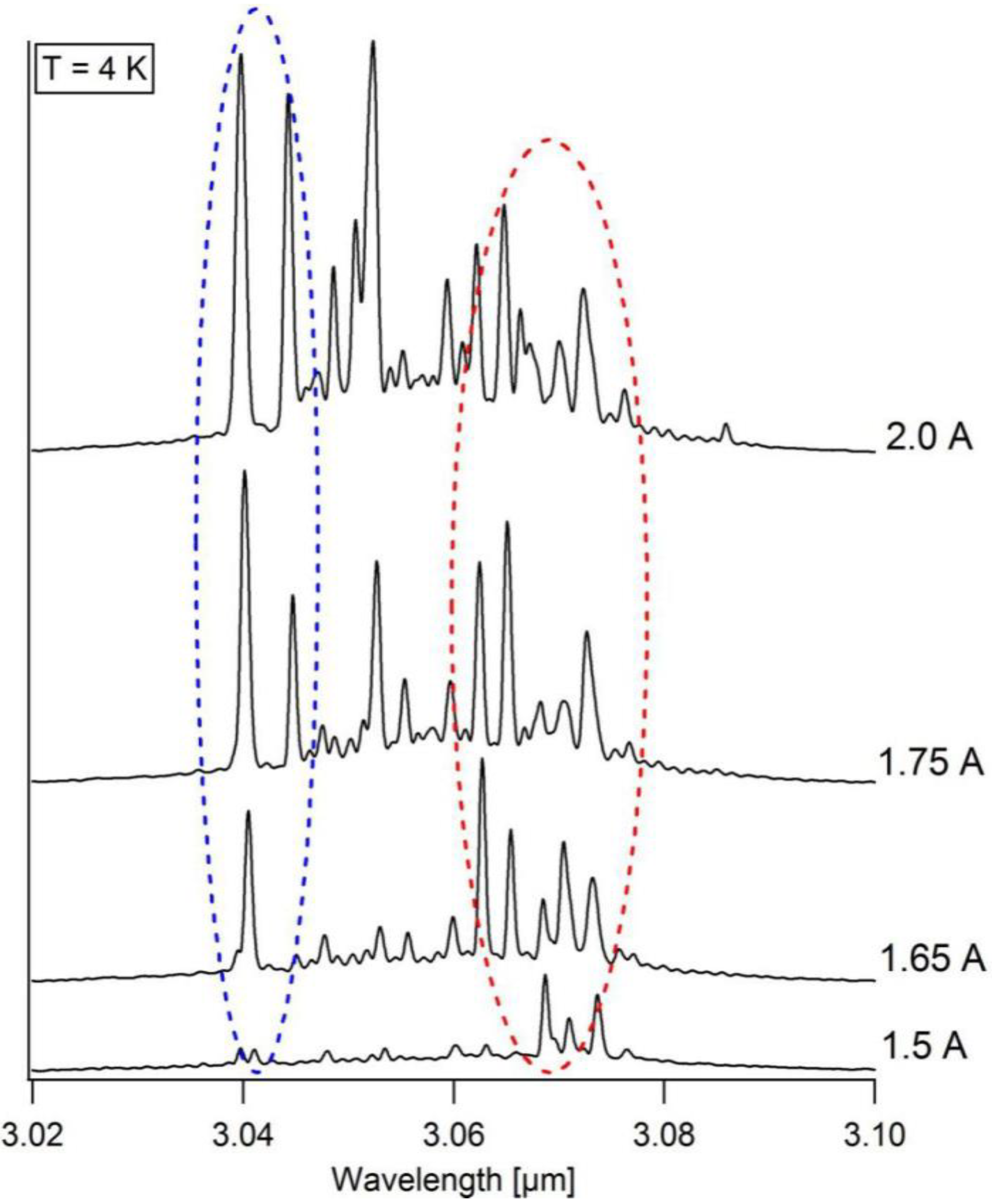
3.1. Gain from InSb QDs
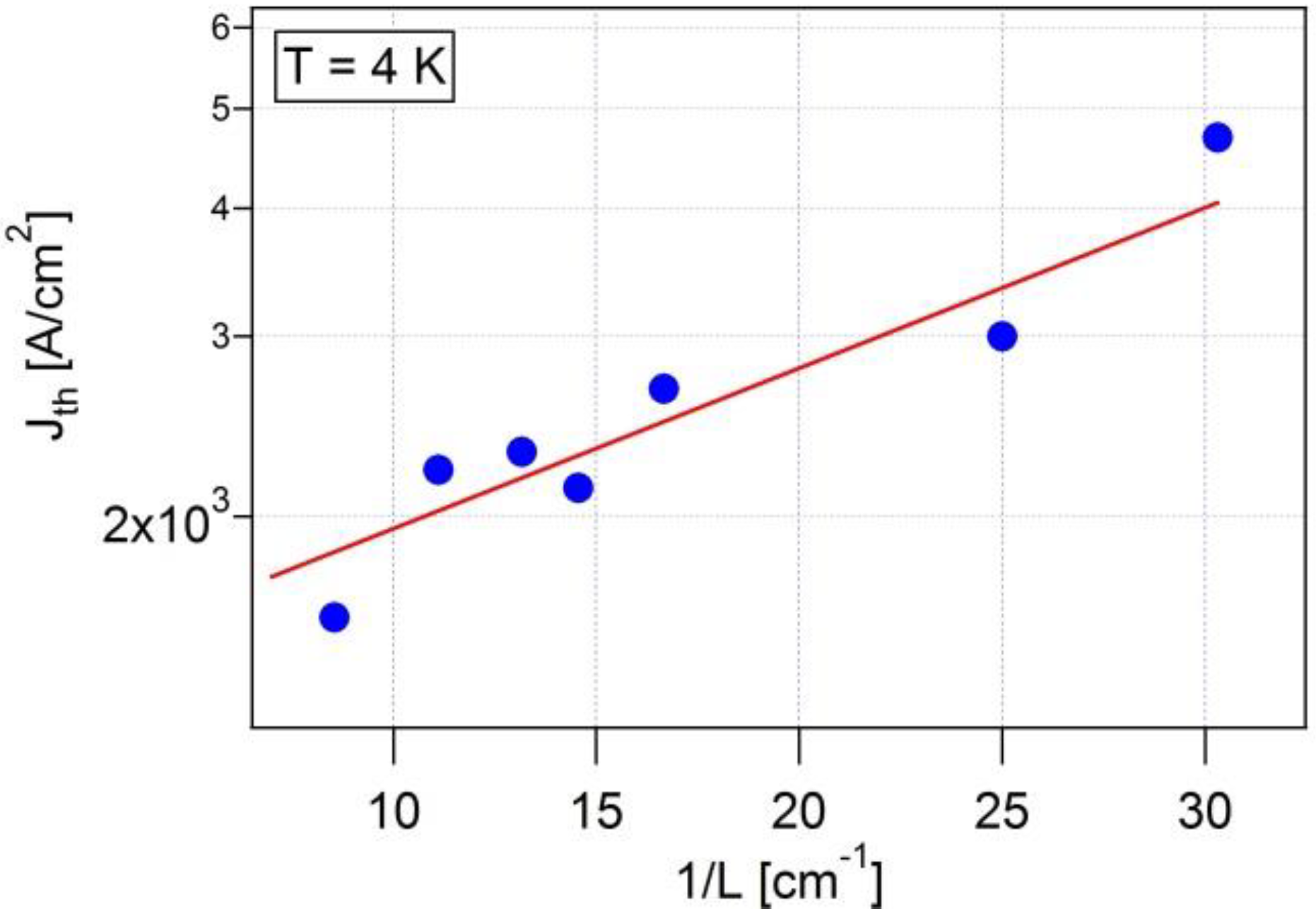
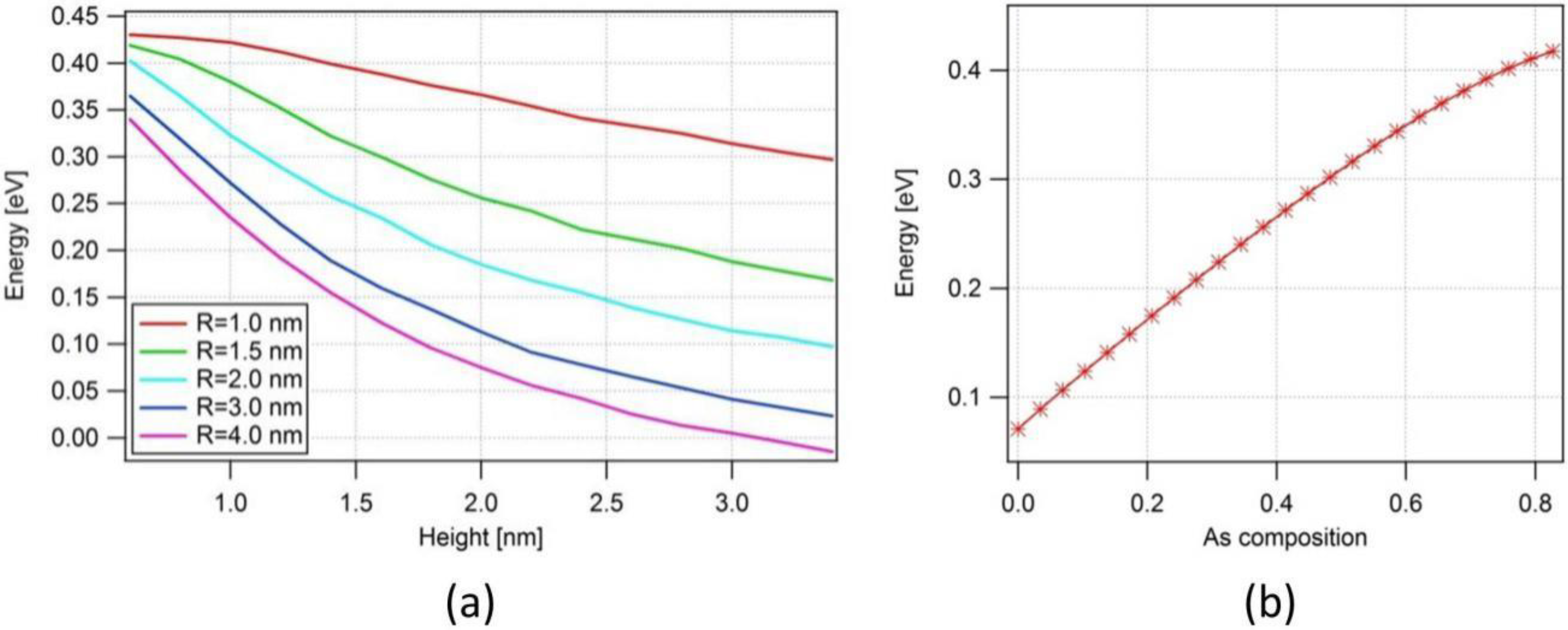
3.2. Spontaneous Emission
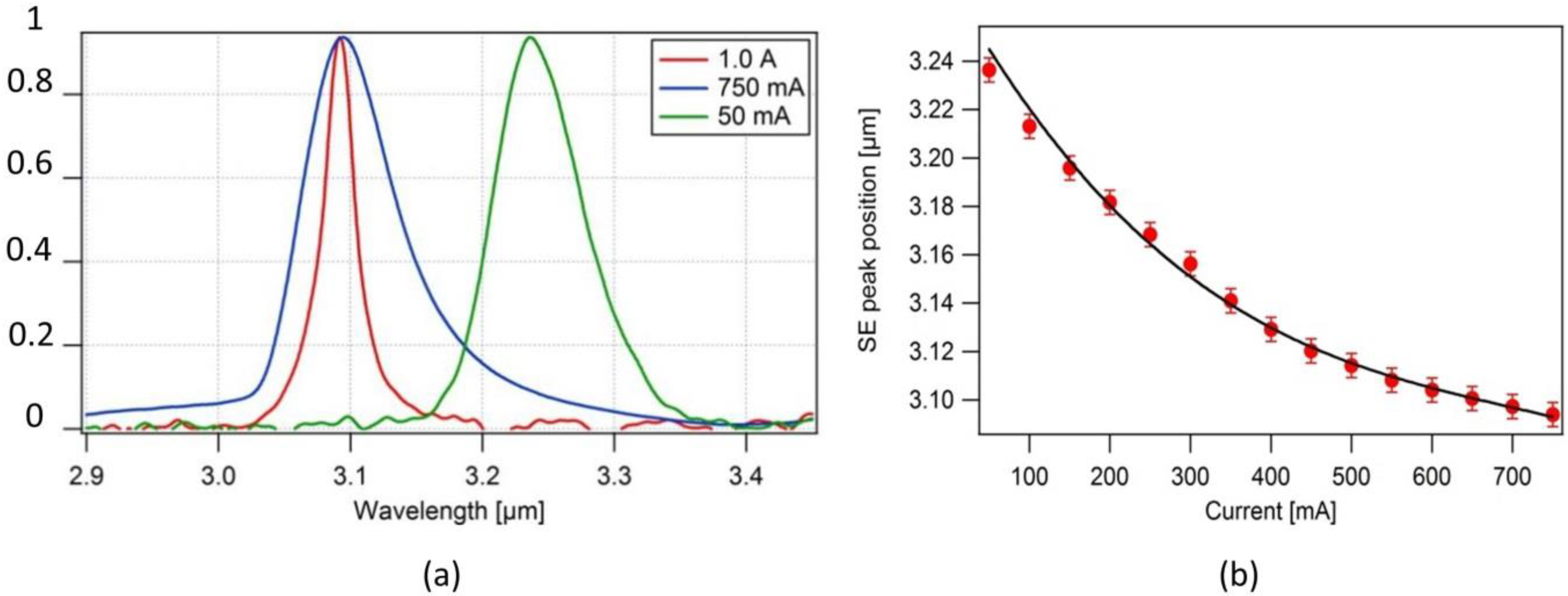
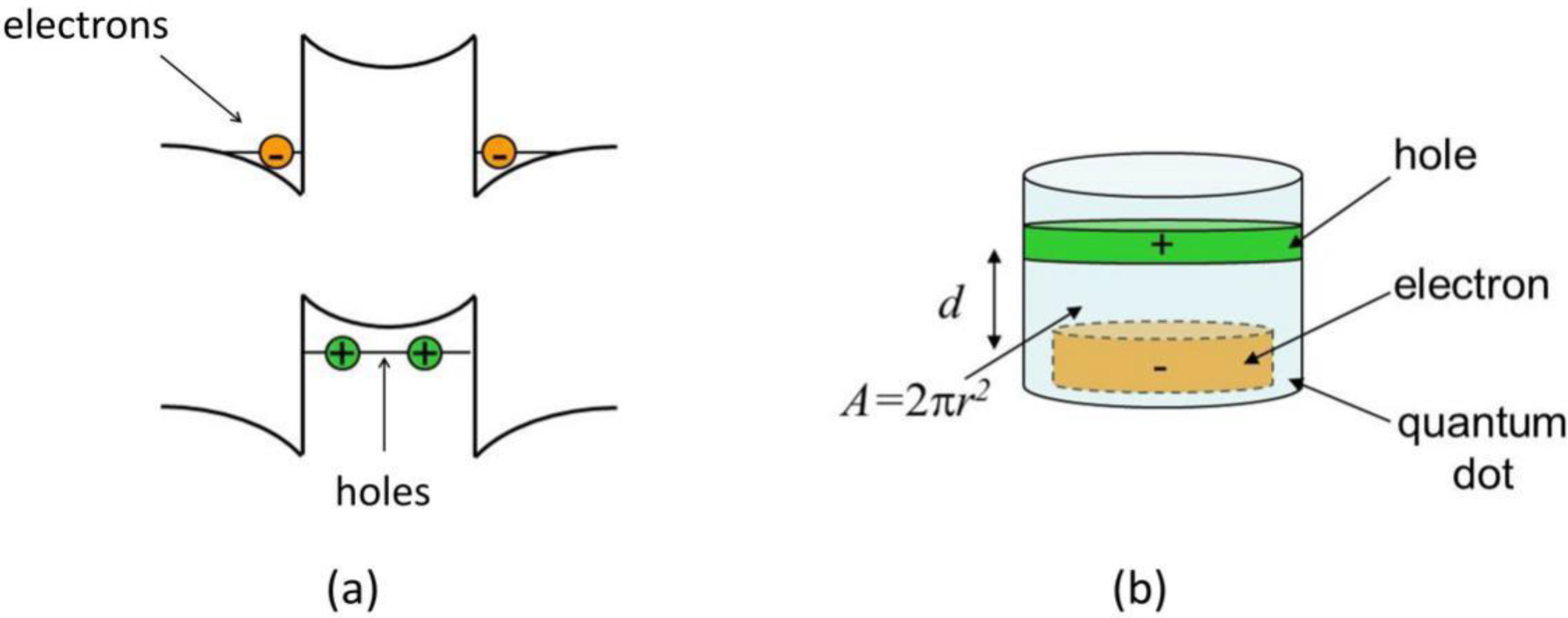
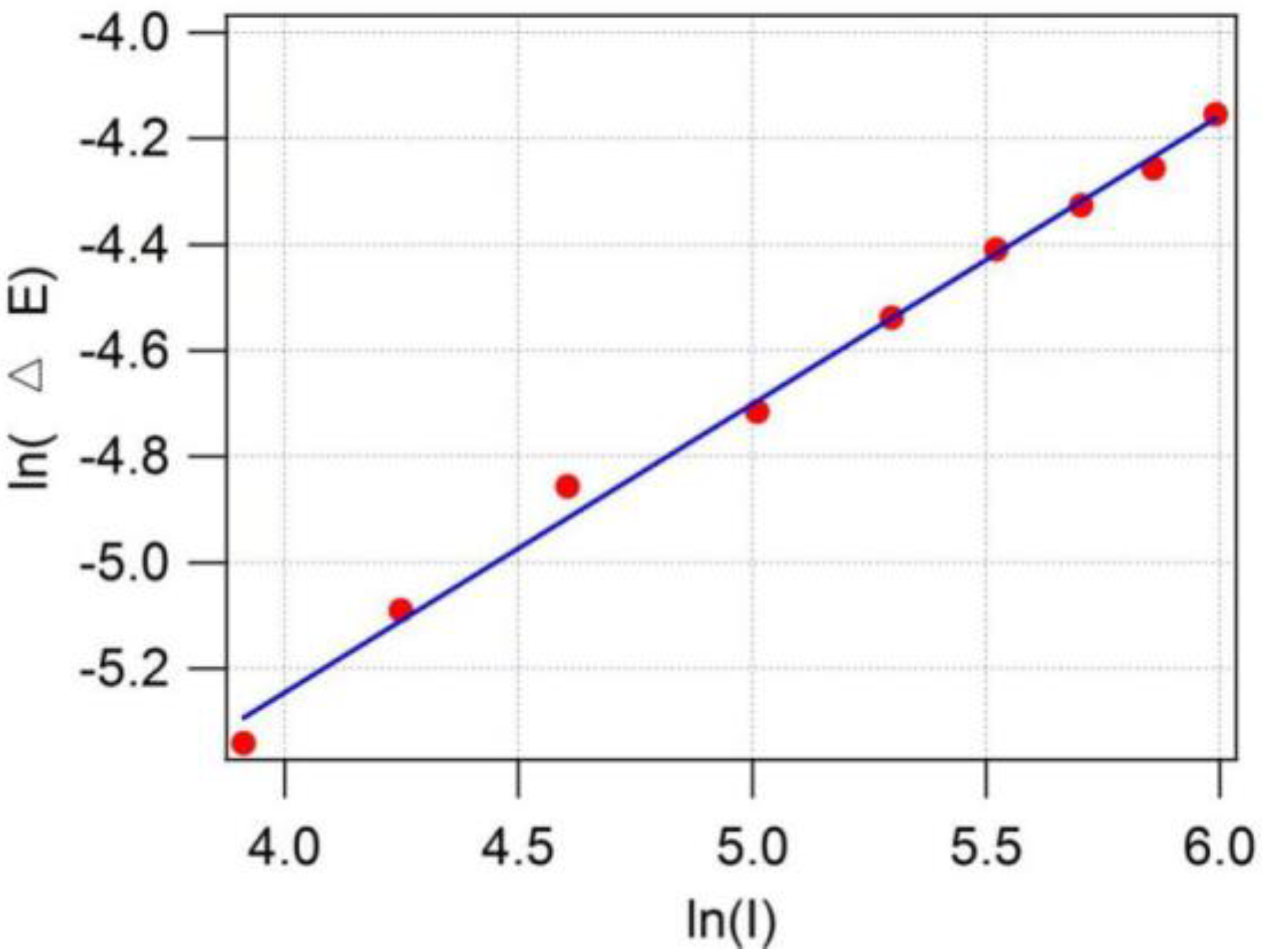
3.3. Non-Radiative current
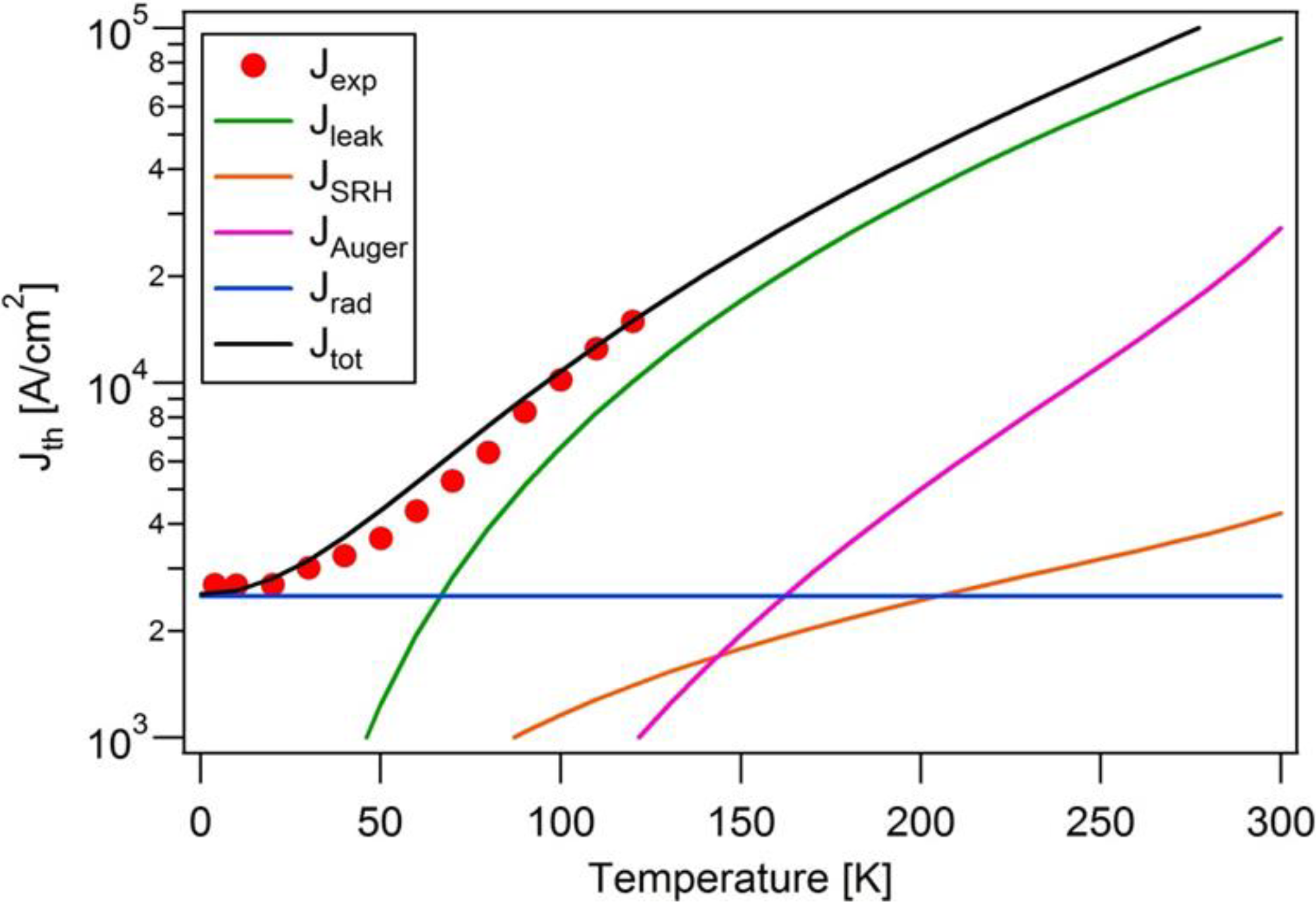
4. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Krier, A.; Yin, M.; Smirnov, V.; Batty, P.; Carrington, P.J.; Solovev, V.; Sherstnev, V. The development of room temperature LEDs and lasers for the mid-infrared spectral range. Phys. Status Solidi(a) 2008, 205, 129–143. [Google Scholar] [CrossRef]
- Yin, Z.; Tang, X. A review of energy bandgap engineering in III–V semiconductor alloys for mid-infrared laser applications. Solid. State. Electron. 2007, 51, 6–15. [Google Scholar] [CrossRef]
- Range, W.; Hosoda, T.; Kipshidze, G.; Tsvid, G.; Shterengas, L.; Belenky, G. Type-I GaSb-based laser diodes operating in 3.1- to 3.3-um wavelength range. IEEE Photon. Technol. Lett. 2010, 22, 718–720. [Google Scholar] [CrossRef]
- Yao, Y.; Hoffman, A.J.; Gmachl, C.F. Mid-infrared quantum cascade lasers. Nat. Photonics 2012, 6, 432–439. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Bewley, W.W.; Canedy, C.L.; Kim, C.S.; Kim, M.; Lindle, J.R.; Merritt, C.D.; Abell, J.; Meyer, J.R. Mid-IR type-II interband cascade lasers. IEEE J. Sel. Top. Quant. Electron. 2011, 17, 1435–1444. [Google Scholar] [CrossRef]
- Coleman, J.J.; Young, J.D.; Garg, A. Semiconductor quantum dot lasers: a tutorial. Semicond. Sci. Technol. 2011, 29, 499–510. [Google Scholar]
- Solov’ev, V.A.; Carrington, P.; Zhuang, Q.; Lai, K.T.; Haywood, S.K.; Ivanov, S.V.; Krier, A. InSb/InAs nanostructures grown by molecular beam epitaxy using Sb2 and As2 fluxes. In Proceedings of the 13th International Conference on Narrow Gap Semiconductors 2007, Guildford, UK, 8–12 July 2007; pp. 129–131.
- Carrington, P.J.; Solov’ev, V.A.; Zhuang, Q.; Krier, A.; Ivanov, S.V. Room temperature midinfrared electroluminescence from InSb/InAs quantum dot light emitting diodes. Appl. Phys. Lett. 2008, 93, 091101. [Google Scholar] [CrossRef]
- Carrington, P.J.; Solov’ev, V.A.; Zhuang, Q.; Ivanov, S.V.; Krier, A. InSb quantum dot LEDs grown by molecular beam epitaxy for mid-infrared applications. Microelectron. J. 2009, 40, 469–472. [Google Scholar] [CrossRef]
- Solov’ev, V.A.; Sedova, I.V.; Lyublinskaya, O.G.; Semenov, A.N.; Mel’tser, B.Y.; Sorokin, S.V.; Terent, Y.V.; Ivanov, S.V. Midinfrared injection-pumped laser based on a III–V/II–VI hybrid heterostructure with submonolayer InSb insets. Tech. Phys. Lett. 2005, 31, 235–237. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yujobo, K.; Kaizu, T. Stranski-Krastanov growth of InAs quantum dots with narrow size distribution. Jpn. J. Appl. Phys. 2000, 39, 1245–1248. [Google Scholar] [CrossRef]
- Wilk, A.; El Gazouli, M.; El Skouri, M.; Christol, P.; Grech, P. Type-II InAsSb/InAs strained quantum-well laser diodes emitting at 3.5 µm. Appl. Phys. Lett. 2000, 77, 2298. [Google Scholar] [CrossRef]
- Kirstaedter, N.; Schmidt, O.G.; Ledentsov, N.N.; Bimberg, D.; Ustinov, V.M.; Egorov, A.Y.; Zhukov, A.E.; Maximov, M.V.; Kop’ev, P.S.; Alferov, Z.I. Gain and differential gain of single layer InAs/GaAs quantum dot injection lasers. Appl. Phys. Lett. 1996, 69, 1226. [Google Scholar] [CrossRef]
- Lelarge, F.; Rousseau, B.; Dagens, B.; Poingt, F.; Pommereau, F.; Accard, A. Room temperature continuous-wave operation of buried ridge stripe lasers using InAs-InP (100) quantum dots as active core. IEEE Photon. Technol. Lett. 2005, 17, 1369–1371. [Google Scholar] [CrossRef]
- Lu, Q.; Zhuang, Q.; Marshall, A.; Kesaria, M.; Beanland, R.; Krier, A. InSb quantum dots for the mid-infrared spectral range grown on GaAs substrates using metamorphic InAs buffer layers. Semicond. Sci. Technol. 2014, 29, 075011. [Google Scholar] [CrossRef]
- Yeap, G.H.; Rybchenko, S.I.; Itskevich, I.E.; Haywood, S.K. Type-II InAsxSb1−x/InAs quantum dots for midinfrared applications: Effect of morphology and composition on electronic and optical properties. Phys. Rev. B 2009, 79, 075305. [Google Scholar] [CrossRef]
- Lu, Q.; Zhuang, Q.; Hayton, J.; Yin, M.; Krier, A. Gain and tuning characteristics of mid-infrared InSb quantum dot diode lasers. Appl. Phys. Lett. 2014, 105, 031115. [Google Scholar] [CrossRef]
- Joullié, A.; Christol, P. GaSb-based mid-infrared 2–5 μm laser diodes. CR Phys. 2003, 4, 621–637. [Google Scholar] [CrossRef]
- Janssens, K.L.; Partoens, B.; Peeters, F.M. Magnetoexcitons in planar type-II quantum dots in perpendicular magnetic field. Phys. Rev. B 2001, 64, 155324. [Google Scholar] [CrossRef]
- Lyublinskaya, O.G.; Solov’ev, V.A.; Semenov, A.N.; Meltser, B.Y.; Terent’ev, Y.V.; Prokopova, L.A.; Toropov, A.A.; Sitnikova, A.A.; Rykhova, O.V.; Ivanov, S.V.; et al. Temperature-dependent photoluminescence from type-II InSb/InAs quantum dots. J. Appl. Phys. 2006, 99, 093517. [Google Scholar] [CrossRef]
- Ledentsov, N.N.; Bohrer, J.; Beer, M.; Heinrichsdorff, F.; Grundmann, M.; Bimberg, D. Radiative states in type-II GaSb/GaAs quantum wells. Phys. Rev. B 1995, 52, 58–66. [Google Scholar] [CrossRef]
- Sun, C.; Wang, G.; Bowers, J.E.; Brar, B.; Blank, H. Optical investigations of the dynamic behavior of GaSb/GaAs quantum dots. Appl. Phys. Lett. 1996, 68, 1543–1545. [Google Scholar] [CrossRef]
- Gradkowski, K.; Pavarelli, N.; Ochalski, T.J.; Williams, D.P.; Tatebayashi, J.; Huyet, G.; O’Reilly, E.P.; Huffaker, D.L. Complex emission dynamics of type-II GaSb/GaAs quantum dots. Appl. Phys. Lett. 2009, 95, 061102. [Google Scholar] [CrossRef]
- Tatebayashi, J.; Khoshakhlagh, A.; Huang, S.H.; Balakrishnan, G.; Dawson, L.R.; Huffaker, D.L.; Bussian, D.A.; Htoon, H.; Klimov, V. Lasing characteristics of GaSb/GaAs self-assembled quantum dots embedded in an InGaAs quantum well. Appl. Phys. Lett. 2007, 90, 261115. [Google Scholar] [CrossRef]
- Choulis, S.A.; Andreev, A.; Merrick, M.; Adams, A.R.; Murdin, B.N.; Krier, A.; Sherstnev, V.V. High-pressure measurements of mid-infrared electroluminescence from InAs light-emitting diodes at 3.3 μm. Appl. Phys. Lett. 2003, 82, 1149. [Google Scholar] [CrossRef] [Green Version]
- Mani, H. Realization and study of a double hetero-structure InAsSb/InAsSbP laser emitting beyond 3 micrometer. Ph.D. thesis, Université des sciences et techniques de Montpellier 2, Montpellier, France, 1989. [Google Scholar]
- Fathpour, S.; Mi, Z.; Bhattacharya, P.; Kovsh, A.R.; Mikhrin, S.S.; Krestnikov, I.L.; Kozhukhov, A.V.; Ledentsov, N.N. The role of Auger recombination in the temperature-dependent output characteristics (T0 = ∞) of p-doped 1.3 μm quantum dot lasers. Appl. Phys. Lett. 2004, 85, 5164–5166. [Google Scholar] [CrossRef]
- Meyer, J.R.; Felix, C.L.; Bewley, W.W.; Vurgaftman, I.; Aifer, E.H.; Olafsen, L.J.; Lindle, J.R.; Hoffman, C.A.; Yang, M.-J.; Bennett, B.R.; et al. Auger coefficients in type-II InAs/Ga1-xInxSb quantum wells. Appl. Phys. Lett. 1998, 73, 2857–2859. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Zhuang, Q.; Krier, A. Gain and Threshold Current in Type II In(As)Sb Mid-Infrared Quantum Dot Lasers. Photonics 2015, 2, 414-425. https://doi.org/10.3390/photonics2020414
Lu Q, Zhuang Q, Krier A. Gain and Threshold Current in Type II In(As)Sb Mid-Infrared Quantum Dot Lasers. Photonics. 2015; 2(2):414-425. https://doi.org/10.3390/photonics2020414
Chicago/Turabian StyleLu, Qi, Qiandong Zhuang, and Anthony Krier. 2015. "Gain and Threshold Current in Type II In(As)Sb Mid-Infrared Quantum Dot Lasers" Photonics 2, no. 2: 414-425. https://doi.org/10.3390/photonics2020414
APA StyleLu, Q., Zhuang, Q., & Krier, A. (2015). Gain and Threshold Current in Type II In(As)Sb Mid-Infrared Quantum Dot Lasers. Photonics, 2(2), 414-425. https://doi.org/10.3390/photonics2020414




