Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers

Abstract

We present analytic treatment of the three different dynamic regimes found in quantum-dot laser turn-on and modulation dynamics. A dynamic coupling, and thus density-dependent scattering lifetimes between dots and reservoir, are identified to be crucial for a realistic modeling. We derive a minimal model for the quantum-dot laser dynamics that can be seeded with experimentally accessible parameters, and give explicit analytic equations that are able to predict relaxation-oscillation frequency and damping rate.

1. Introduction

Semiconductor lasers, including quantum-dot (QD) lasers, are generally class-B lasers, following the classification due to Arecchi [1]. As such, they exhibit dynamical behavior that is characterized predominantly by the two-dimensional phase-space given by the optical power (or field amplitude) and the gain, defined by the inversion of the optically resonant transitions [2]. Within this effectively two-dimensional phase-plane the laser can exhibit damped oscillatory motion about the fixed point, known as relaxation oscillations (ROs). For the case of a quasi-equilibrium between the carriers, e.g., within the sub-bands in quantum-well (QW) lasers, these oscillations can be modeled using simple two-variable rate-equation systems [3,4] for the total charge carrier number N and photon number S. However, for QD lasers the situation is more complex as there are different carrier types with separate dynamics [5,6,7]. Depending on the scattering timescales between these carrier types different limiting cases have been discussed [8,9]. As introduced in [10,11], three different dynamical regimes can be defined, which will be analytically described within this paper.

The relaxation oscillations of a laser define the laser response to small perturbations from its lasing fixed point. Therefore, the RO damping and frequency already can give an indication about the stability properties of lasers, as well as its small-signal modulation capabilities. For example, when the laser operation is perturbed by optical feedback, e.g., due to reflections, the critical feedback strength needed to destabilize the cw operation of the laser is directly proportional to the RO damping ${\Gamma }_{\mathrm{RO}}$ [12,13,14]. In applications where a constant output power is required, strong damping of the relaxation oscillations is therefore favorable. The RO frequency is also important for modulation applications, as a modulation of the laser with a frequency near ${\omega }_{\mathrm{RO}}$ can resonantly excite relaxation oscillations and lead to unwanted nonuniform laser responses [15,16,17,18].

The aim of this paper is to identify the mechanisms responsible for the qualitative differences in the dynamics between QD lasers and conventional class-B lasers. To this end, starting from a more complex microscopic description [19], we will derive a minimal QD laser model that can describe the three qualitatively different dynamic regimes characteristic for QD lasers. Although being of minimal complexity, the accuracy of our model goes beyond existing rate-equation models [17,18,20]. Compared to existing minimal models [8,9], we allow for a feeding of the model with experimentally accessible parameters by separating the effects of varying carrier distribution and varying carrier lifetime. An asymptotic analysis of the resulting rate-equations will be performed, similar to [9,21], to give explicit equations for the RO parameters in the different dynamic regimes.

2. Minimal Quantum-Dot Laser Model

In the following, we will derive the minimal rate-equation model used to qualitatively describe the QD laser dynamics. The charge-carrier scattering between the reservoir and QD states due to Auger-scattering can be expressed as [22]

$$\begin{array}{cc}\hfill \frac{\partial }{\partial t}\rho {|}_{sc}& =S^{\mathrm{in}}(1-\rho )-S^{\mathrm{out}}\rho =S^{\mathrm{eff}}({\rho }^{\mathrm{eq}}-\rho )\hfill \end{array}$$

(1)

after defining an effective scattering rate $S^{\mathrm{eff}}=S^{\mathrm{in}}+S^{\mathrm{out}}$ and the quasi-equilibrium QD occupation probability ${\rho }^{\mathrm{eq}}=S^{\mathrm{in}}/(S^{\mathrm{in}}+S^{\mathrm{out}})$. This scattering term is used to describe the dynamic equations of the QD laser governed by the reservoir charge-carrier density w, the QD charge-carrier occupation probability ρ, and the photon density S (in units of the quantum-dot density $N^{\mathrm{QD}}$):

$$\begin{array}{cc}\hfill \dot{w}& =J-\frac{w}{T_1}-2N^{\mathrm{QD}}{S}^{\mathrm{eff}}({\rho }^{\mathrm{eq}}-\rho )\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill \dot{\rho }& =S^{\mathrm{eff}}({\rho }^{\mathrm{eq}}-\rho )-\frac{\rho }{T_{\mathrm{sp}}}-g(2\rho -1)S\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill \dot{S}& =2g(2\rho -1)S-2\kappa S\hfill \end{array}$$

(2c)

Here, J is the pump current density per QW layer, $T_1$ is the QW charge-carrier lifetime. The QD lifetime is given by $T_{\mathrm{sp}}$, g is the gain coefficient, and $2\kappa$ is the photon loss rate. The in and out-scattering rates in Equation (1) depend on the quasi-Fermi level ${\mu }^{\mathrm{eq}}$ within the charge-carrier reservoir and are related by the detailed-balance relationship

$$\begin{array}{cc}\hfill S^{\mathrm{out}}& =S^{\mathrm{in}}exp\left(\frac{{\epsilon }_{\mathrm{QD}}-{\mu }^{\mathrm{eq}}}{k_{B}T}\right)\hfill \end{array}$$

(3)

with the QD single-particle energy ${\epsilon }_{\mathrm{QD}}$, Boltzmann’s constant $k_B$, and the quasi-equilibrium temperature T. Both the in-scattering rate $S^{in}$ as well as the detailed balance relation depend nonlinearly on the charge-carrier density in the reservoir [22]. Furthermore, we introduce the normalized reservoir density $N=w/\left(2N^{\mathrm{QD}}\right)$ (along with a rescaled pump current J). In order to reduce the complexity of the charge-carrier scattering we linearize the quasi-equilibrium occupation ${\rho }^{\mathrm{eq}}$ around the corresponding threshold value ${\rho }^{\mathrm{th}}$ and the value $N^0$ defined as $N^0=N^{\mathrm{th}}-\frac{{\rho }^{\mathrm{th}}}{Rd{T}_{sp}}$, where $N^{\mathrm{th}}$ is the normalized reservoir carrier density at threshold. We can thus write

$$\begin{array}{c}\hfill {\rho }^{\mathrm{eq}}\approx {\rho }^{\mathrm{th}}+d(N-N^0)\end{array}$$

(4)

The threshold QD occupation can be easily calculated from Equation (2c):

$$\begin{array}{cc}\hfill {\rho }^{\mathrm{th}}& =\frac{g+\kappa }{2g}\hfill \end{array}$$

(5)

The coefficient $d\approx \frac{\partial }{\partial N}{\rho }^{\mathrm{eq}}{|}_{N^0}$ describes the change of the quasi-equilibrium QD occupation with respect to the normalized reservoir density close to the threshold. A large d thus means a strong change of the QD occupation with variations in the reservoir carrier density which is reach with a large energy separation, while a small d is realized for QD levels energetically close to the reservoir carriers. The detailed-balance relation thus enters the minimal QD laser model in a linearized fashion. An important feature of QD lasers is the imperfect clamping of charge-carriers above threshold [5,23]. The deviation of the charge-carrier densities from their threshold values, however, should be sufficiently small for the linear approximation in Equation (4) to be sufficiently accurate. The effective charge-carrier scattering rate, $S^{\mathrm{eff}}$, is in the following treated as a constant parameter, $R=S^{\mathrm{eff}}{\left(N\right)|}_{N^0}$, in order to investigate the different dynamic regimes of the QD laser. Thus, the density dependence of $S^{\mathrm{eff}}$ is neglected and only enters via d into the dynamics. We then treat R as a free parameter to investigate the different dynamic regimes. The resulting QD laser equations thus read:

$$\begin{array}{cc}\hfill \dot{N}& =J-\frac{N}{T_1}-R\left({\rho }^{\mathrm{th}}+d(N-N^0)-\rho \right)\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill \dot{\rho }& =R\left({\rho }^{\mathrm{th}}+d(N-N^0)-\rho \right)-\frac{\rho }{T_{\mathrm{sp}}}-g(2\rho -1)S\hfill \end{array}$$

(6b)

$$\begin{array}{cc}\hfill \dot{S}& =2g(2\rho -1)S-2\kappa S\hfill \end{array}$$

(6c)

3. Numerical Results

We proceed by performing a linear stability analysis of the above QD laser equations. The Lyapunov exponents λ are given by the eigenvalues of the Jacobian and can be calculated by solving the characteristic equation,

$$0=-\lambda \left[\left(\frac{1}{T_1}+dR+\lambda \right)\left(\frac{1}{T_{\mathrm{sp}}}+R-2gS+\lambda \right)-d{R}^2\right]-4g\kappa S\left(\frac{1}{T_1}+dR+\lambda \right)$$

(7)

The solution of this equation is shown in Figure 1, in terms of the RO frequency ${\omega }_{\mathrm{RO}}$ and damping rate ${\Gamma }_{\mathrm{RO}}$, defined by $\lambda =-{\Gamma }_{\mathrm{RO}}\pm i{\omega }_{\mathrm{RO}}$. Here, we distinguish between two different QD structures: a weakly confined QD (shallow dot) and a QD with stronger confinement (deep dot), which differ in the QD-QW coupling coefficient d. Furthermore, we evaluate the eigenvalues at a photon number corresponding to the value at twice the threshold pump current at a scattering rate R extracted from microscopic calculations [24,25], which yields $S=0.068$ ($S=0.009$) for the shallow (deep) QD structure.

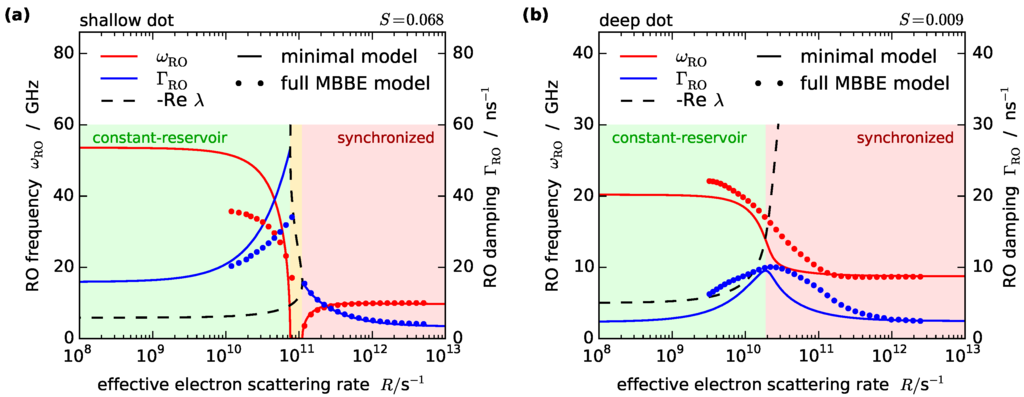
Figure 1. Relaxation oscillation (RO) frequency ${\omega }_{\mathrm{RO}}=\left|\mathrm{Im}\lambda \right|$ (solid red) and damping rate ${\Gamma }_{\mathrm{RO}}=-\mathrm{Re}\lambda$ (solid blue) determined from Equation (7) for the (a) shallow and (b) deep quantum-dot (QD) laser as a function of the effective electron scattering rate R, for constant photon number S. The dashed black line denotes purely real eigenvalues which are not related to ROs. The circles denote the RO parameters extracted numerically from the full microscopically based balance equation (MBBE) model [19]. The green, yellow, and red shaded areas denote the constant-reservoir, overdamped, and synchronized regimes, respectively. $T_{\mathrm{sp}}=2$ns, $g=230$ns${}^{-1}$, $\kappa =50$ns${}^{-1}$. (a) $T_1=0.17$ns, $S=0.068$, $d=0.035$; (b) $T_1=0.2$ns, $S=0.009$, $d=0.25$.

Figure 1. Relaxation oscillation (RO) frequency ${\omega }_{\mathrm{RO}}=\left|\mathrm{Im}\lambda \right|$ (solid red) and damping rate ${\Gamma }_{\mathrm{RO}}=-\mathrm{Re}\lambda$ (solid blue) determined from Equation (7) for the (a) shallow and (b) deep quantum-dot (QD) laser as a function of the effective electron scattering rate R, for constant photon number S. The dashed black line denotes purely real eigenvalues which are not related to ROs. The circles denote the RO parameters extracted numerically from the full microscopically based balance equation (MBBE) model [19]. The green, yellow, and red shaded areas denote the constant-reservoir, overdamped, and synchronized regimes, respectively. $T_{\mathrm{sp}}=2$ns, $g=230$ns${}^{-1}$, $\kappa =50$ns${}^{-1}$. (a) $T_1=0.17$ns, $S=0.068$, $d=0.035$; (b) $T_1=0.2$ns, $S=0.009$, $d=0.25$.

In terms of the scattering-rate dependence of the eigenvalues, the two QD structures reveal qualitative different behaviors, as shown in Figure 1. The shallow dot shows pronounced ROs (${\omega }_{\mathrm{RO}}>{\Gamma }_{\mathrm{RO}}$) for slow scattering (constant-reservoir regime), which become increasingly dampened until they disappear in the overdamped regime around $R\approx {10}^{11}$s ${}^{-1}$. For even higher scattering (synchronized regime), pronounced slower ROs reappear. The deep-dot structure, on the other hand, reveals a smooth transition between the fast oscillations in the constant-reservoir regime to the slower oscillations in the synchronized regime, with a less pronounced peak in the damping in between.

Additionally, we have plotted the results from our microscopically based balance equation (MBBE) model [19] in Figure 1, which takes into account the first two inhomogeneously broadened localized QD states and distinguishes between electron and hole dynamics, as well as models the dynamic temperature change of the charge carriers. We have extracted the values of g, $T_{\mathrm{sp}}$, $T_1$, and S at twice the threshold current from the MBBE model. The value of d was obtained by fitting the RO parameters resulting from Equation (7) to the ones calculated from the MBBE model. Note that the photon number S stays constant in Figure 1, corresponding to an adjustment of the pump current with R. The RO parameters in the MBBE model were acquired from fits to the intensity time-series after a small perturbation. The scattering-rate dependence was investigated by multiplying our microscopically calculated scattering rates with a constant factor and evaluating the electron scattering rate in the steady-state. In general, a very good quantitative agreement of the minimal QD laser model and the full MBBE model can be seen for fast scattering, and a good qualitative agreement for smaller R, with the overdamped regime for the shallow dot and a local maximum of the damping in the deep-dot case. The differences between the two approaches mainly stem from the additional scattering processes including the QD excited state in the MBBE, which influence the effective scattering rate, as we have checked by excluding this effect in the numerics (not shown here). In the minimal model, only the scattering between the QD ground state and the QW is taken into account. Furthermore, the separate dynamics of electrons and holes and the spectral-hole burning in the inhomogeneously broadened QD ensemble lead to quantitative differences especially for slow scattering.

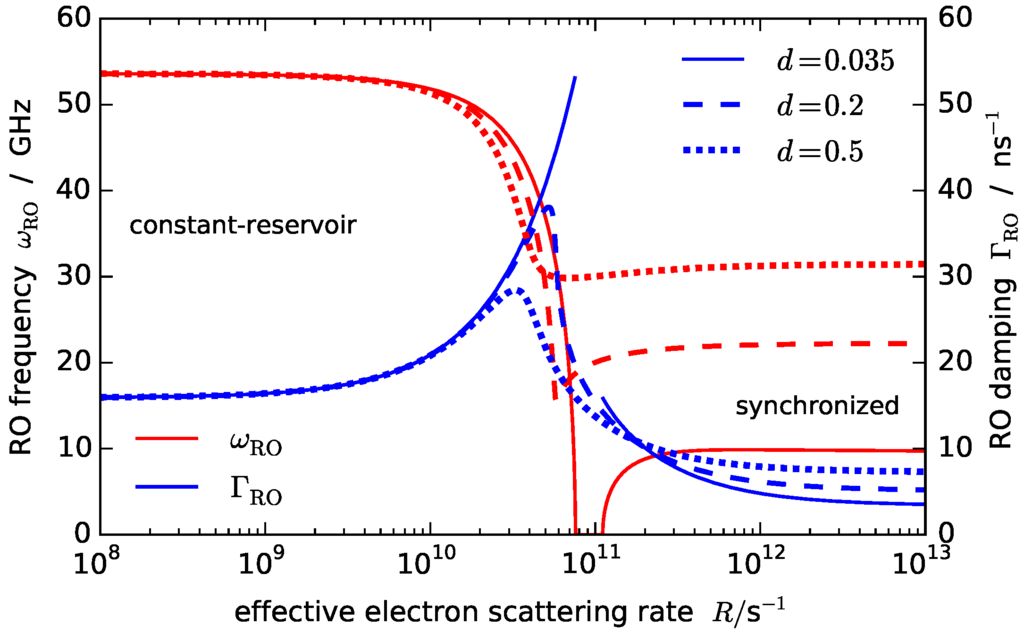
Figure 2. RO frequency ${\omega }_{\mathrm{RO}}$ (red) and damping rate ${\Gamma }_{\mathrm{RO}}$ (blue) determined from Equation (7) for different QD-quantum-well (QW) carrier distribution coefficients: $d=0.035$ (solid line) describing small energy separation, $d=0.2$ (dashed line), and $d=0.5$ (dotted line) corresponding to a large energetic distance. Other parameters as in Figure 1a.

Figure 2. RO frequency ${\omega }_{\mathrm{RO}}$ (red) and damping rate ${\Gamma }_{\mathrm{RO}}$ (blue) determined from Equation (7) for different QD-quantum-well (QW) carrier distribution coefficients: $d=0.035$ (solid line) describing small energy separation, $d=0.2$ (dashed line), and $d=0.5$ (dotted line) corresponding to a large energetic distance. Other parameters as in Figure 1a.

Equation (7) allows us to investigate the underlying cause of the qualitative differences between the scattering-rate dependencies of the two QD structures. The most prominent difference between the two cases is the value of the detailed-balance coefficient d. Its effect is shown in Figure 2, where for the shallow dot we have varied the value of d and evaluated the RO parameters in dependence of R (again keeping the photon number S constant). For increasing d, we observe a transition between the well-separated three dynamic regimes to the smooth transition between the constant-reservoir and synchronized regime, along with a substantial increase of the RO frequency in the synchronized regime. This behavior shows that the detailed balance of the in and out-scattering rates plays a crucial role in determining the dynamics for moderate to high scattering rates. This is an important result as most models usually neglect this dependence and use constant in and out-scattering rates [26,27,28]. Those models cannot describe the third regime of quantum-dot laser dynamics. Assuming a linear increase of the scattering rates and neglecting the detailed balance, as done in [8,9], leads to similar limits, however mixing the effects of scattering rate R (Coulomb interaction) and carrier distribution coupling d (energy band structure) in one parameter. Note that increasing R and simultaneously decreasing d corresponds to the limit of increasing B in [9]. Our microscopic calculations of the scattering rates show that most QD lasers will operate within the synchronized regime where the effect of the coupling between QD and reservoir occupation becomes important. A correct description of the detailed balance via a dependence of the quasi-equilibrium QD occupation ${\rho }^{\mathrm{eq}}$ on the reservoir density is therefore required to accurately predict the QD laser behavior.

4. Analytic Approximation

Given its cubic nature, the solutions of the characteristic Equation (7) can in principle be explicitly determined. However, this would result in lengthy and complicated expressions with little practical value, as the dependencies on different parameters would be hidden in the multitude of terms. The idea to circumvent these issues is to expand the characteristic equation in terms of one or more small parameters, and solve the reduced problem [3,21]. Depending on the choice of expansion, the resulting eigenvalues describe the original system well around the chosen expansion point or parameter. In the following, we derive analytic expressions for the RO parameters in the constant-reservoir and synchronized regimes.

4.1. Slow Scattering – Constant-Reservoir Regime

At first, we will try to derive a simpler expression for the eigenvalues in the constant-reservoir regime. Here, the QD charge-carrier dynamics dominate, while the reservoir provides a nearly constant charge carrier influx into the active quantum-dot states. As such, the QD and QW should only be weakly coupled. This leads us to a choice of expansion: The direct coupling between the QD and reservoir carriers is determined by the coefficient d. We will therefore expand Equation (7) in terms of d. We assume that the eigenvalues can be written in the form

$$\begin{array}{cc}\hfill \lambda & ={\lambda }_0+d{\lambda }_1+O\left(d^2\right)\hfill \end{array}$$

(8)

We proceed by inserting this into Equation (7). Since our assumption was that d should be small, we can at first neglect all resulting terms of order d or higher, as the remaining terms should dominate the dynamics. The resulting zeroth-order characteristic equation is given by

$$\begin{array}{cc}\hfill 0& =4g\kappa S{T}_{\mathrm{sp}}\hfill \\ & +\left(1+R{T}_{\mathrm{sp}}+2gS{T}_{\mathrm{sp}}+4g\kappa S{T}_1{T}_{\mathrm{sp}}\right){\lambda }_0\hfill \\ & +\left(T_1+T_{\mathrm{sp}}+R{T}_1{T}_{\mathrm{sp}}+2gS{T}_1{T}_{\mathrm{sp}}\right){{\lambda }_0}^2\hfill \\ & +T_1{T}_{\mathrm{sp}}{{\lambda }_0}^3\hfill \end{array}$$

(9)

which has two complex solutions,

$$\begin{array}{cc}\hfill {\lambda }_0& =-{\Gamma }_{\mathrm{RO}}^{\mathrm{cr}},0\pm i_{\mathrm{RO}}^{\mathrm{cr}},0\hfill \end{array}$$

(10)

with the zeroth-order relaxation oscillation damping and frequency in the constant-reservoir regime (superscript cr):

$$\begin{array}{cc}\hfill {\Gamma }_{\mathrm{RO}}^{\mathrm{cr}},0& =\frac{1}{2}\left(\frac{1}{T_{\mathrm{sp}}}+R+2gS\right)\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{RO}}^{\mathrm{cr}},0& =\sqrt{4g\kappa S-{({\Gamma }_{\mathrm{RO}}^{\mathrm{cr}},0)}^2}\hfill \end{array}$$

(11b)

This result is identical to the expressions for the RO parameters obtained from simple two-variable laser rate-equation systems [3], apart from an additional $\frac{R}{2}$ in the relaxation oscillation damping rate. This can be understood by a decrease of the effective carrier lifetime in the quantum-dot states due to the scattering process: The carriers will be driven towards their equilibrium distribution with the effective rate $({T_{\mathrm{sp}}}^{-1}+R)$. Note that a similar expression was found in [21] by starting with the full QD laser rate-equations and similar electron and hole lifetimes. The zeroth-order analytic approximation describes the eigenvalues in the limit of slow scattering very well, as depicted in Figure 3. The term ${\left({\Gamma }_{\mathrm{RO}}^{\mathrm{cr}},0\right)}^2$ in the RO frequency is commonly neglected in the limit of weakly damped ROs. The strong increase in ${\Gamma }_{\mathrm{RO}}$ with R, however, makes this term important, and is the reason for the appearance of the overdamped regime ($\mathrm{Re}{\omega }_{\mathrm{RO}}=0$). In the deep-dot case the analytic approximation slightly overestimates the RO frequency at the high-scattering border of the constant-reservoir regime. Here, the assumption $d\to 0$ fails, and higher order corrections in d must be taken into account for better reproduction. The first-order correction to Equation (11) is given in the appendix.

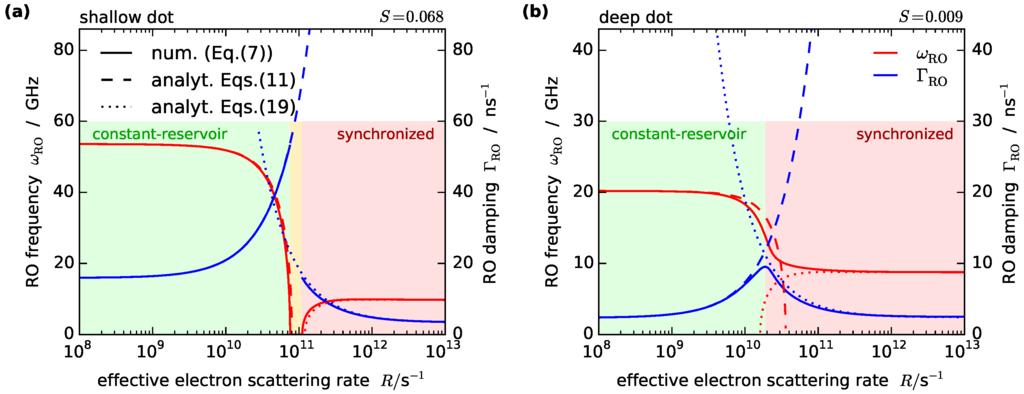
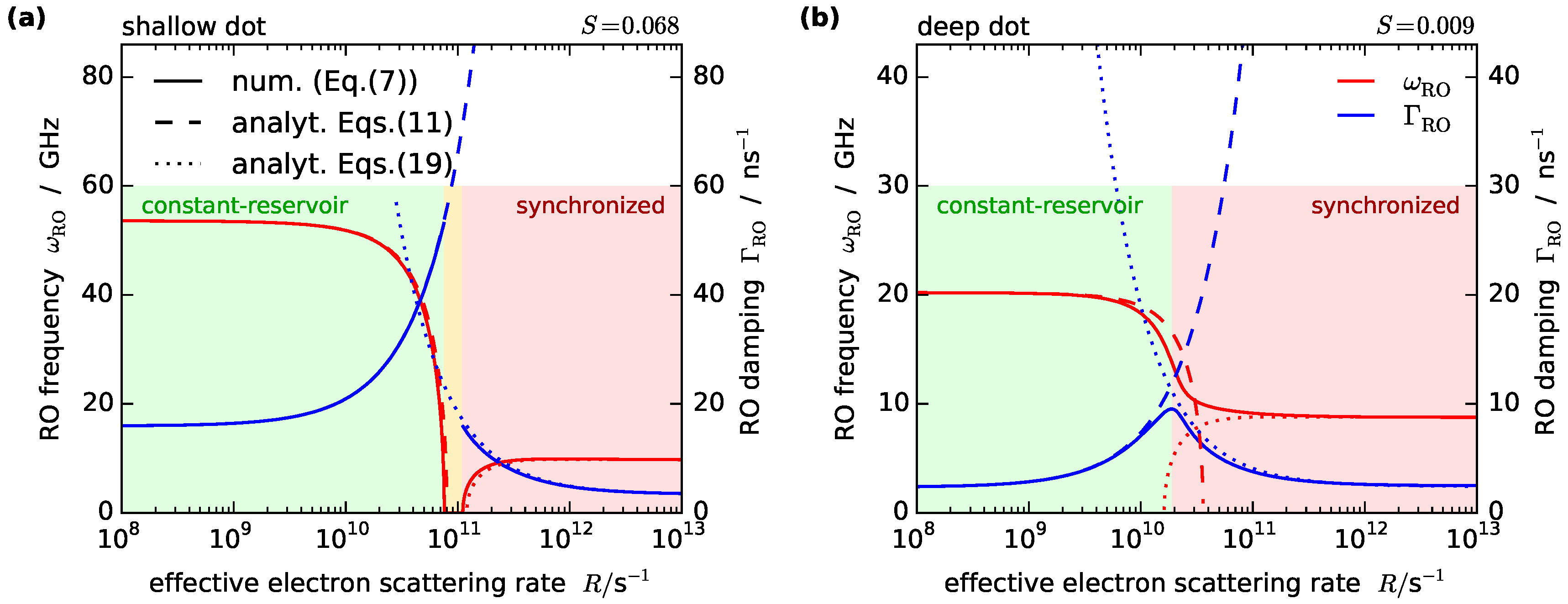
Figure 3. Comparison between the exact eigenvalue solutions of Equation (7) (solid lines) and the analytic approximations of Equation (11) (dashed), and Equation (19) (dotted) for the (a) shallow and (b) deep QD laser in dependence of the effective electron scattering rate R (keeping S constant), cf. Figure 1.

Figure 3. Comparison between the exact eigenvalue solutions of Equation (7) (solid lines) and the analytic approximations of Equation (11) (dashed), and Equation (19) (dotted) for the (a) shallow and (b) deep QD laser in dependence of the effective electron scattering rate R (keeping S constant), cf. Figure 1.

4.2. Fast Scattering – Synchronized Regime

Next, we will look at the synchronized regime (superscript s) for fast charge carrier scattering and derive analytic equations for predicting the relaxation oscillation frequency and damping. So far this limit was analytically treated in [9] but without separating the effects of carrier lifetime and carrier distribution coupling. In the limit of $R\to \infty$ only terms of highest order in R will define the dynamics of the QD laser, whereas the remaining terms can be neglected. Most importantly, the cubic term in λ will not contribute to the dynamics. We thus rewrite the characteristic Equation (7) in the high-R limit as

$$\begin{array}{cc}\hfill 0& ={\left({\omega }_{\mathrm{res}}^s\right)}^2+2{\Gamma }_{\mathrm{RO}}^s\lambda +{\lambda }^2\hfill \end{array}$$

(12)

which immediately yields the eigenvalues

$$\begin{array}{c}\hfill \lambda =-{\Gamma }_{\mathrm{RO}}^s\pm i{\omega }_{\mathrm{RO}}^s\end{array}$$

(13)

with

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{RO}}^s& =\sqrt{{\left({\omega }_{\mathrm{res}}^s\right)}^2-{\left({\Gamma }_{\mathrm{RO}}^s\right)}^2}\hfill \end{array}$$

(14)

By rewriting Equation (7) in powers of λ and comparing with Equation (12) we identify the damping and resonance frequency:

$$\begin{array}{cc}\hfill {\Gamma }_{\mathrm{RO}}^s& =\frac{2dgS+\frac{1}{T_1}+\frac{d}{T_{\mathrm{sp}}}+\frac{1}{R}\left(4g\kappa S+\frac{1}{T_1}2gS+\frac{1}{T_1{T}_{\mathrm{sp}}}\right)}{2\left(1+d+\frac{1}{R}(2gS+\frac{1}{T_1}+\frac{1}{T_{\mathrm{sp}}})\right)}\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{res}}^s& ={\left[\frac{4g\kappa S\left(d+\frac{1}{R{T}_1}\right)}{1+d+\frac{1}{R}\left(2gS+\frac{1}{T_1}+\frac{1}{T_{\mathrm{sp}}}\right)}\right]}^{\frac{1}{2}}\hfill \end{array}$$

(15b)

We proceed by expanding the above expressions in terms of the inverse scattering rate $r:=\frac{1}{R}$ around $r=0$, corresponding to the limit $R\to \infty$. The zeroth-order term is evaluated to

$$\begin{array}{cc}\hfill {\Gamma }_{\mathrm{RO}}^{s,0}& =\frac{2dgS+\frac{1}{T_1}+\frac{d}{T_{\mathrm{sp}}}}{2(1+d)}\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{res}}^{s,0}& =\sqrt{\frac{4dg\kappa S}{1+d}}\hfill \end{array}$$

(16b)

The first-order correction is given by

$$\begin{array}{cc}\hfill {\Gamma }_{\mathrm{RO}}^{s,1}& =\frac{1}{R}\left(\frac{2g\kappa S}{1+d}-\frac{\frac{1}{{T_1}^2}+d{\left(\frac{1}{T_{\mathrm{sp}}}+2gS\right)}^2}{2{(1+d)}^2}\right)\hfill \end{array}$$

(17a)

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{res}}^{s,1}& =\frac{1}{R}\sqrt{\frac{dg\kappa S}{1+d}}\left(\frac{\frac{1}{T_1}-d\left(\frac{1}{T_{\mathrm{sp}}}+2gS\right)}{d(1+d)}\right)\hfill \end{array}$$

(17b)

We now further note the following estimations

$$\begin{array}{cccccc}\hfill gS& \gg \frac{1}{T_{\mathrm{sp}}}\hfill & \hfill g\kappa S& \gg \frac{1}{{T_1}^2}\hfill & \hfill g\kappa S& \gg d{g}^2{S}^2\hfill \end{array}$$

(18)

which hold for moderate output power. We can thus approximate the RO parameters in the synchronized regime in first-order expansion in $\frac{1}{R}$ as

$$\begin{array}{cc}\hfill {\Gamma }_{\mathrm{RO}}^s& \approx \frac{2dgS+\frac{1}{T_1}}{2(1+d)}+\frac{2g\kappa S}{R(1+d)}\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill {\omega }_{\mathrm{res}}^s& \approx \sqrt{\frac{4dg\kappa S}{1+d}}\left(1+\frac{\frac{1}{T_1}-2dgS}{2Rd(1+d)}\right)\hfill \end{array}$$

(19b)

with the RO frequency given by Equation (14).

The comparison between the numerically evaluated eigenvalues of the characteristic Equation (7) and the approximation is shown in Figure 3. The agreement between the two approaches is very good as can be seen by inspecting the dashed line (analytic approximations for the constant carrier regime described by Equation (11), and the dotted line (analytic approximation of Equation (19) describing the constant reservoir regime). Only in the deep-dot case the analytic expression for the RO frequency deviates from the numeric result, as the regime boundary is approached. Also, Equation (19) confirms that, without the detailed-balance coupling coefficient d, the synchronized regime for high scattering rates could not be described (with constant scattering rates R), as for $d=0$, the RO frequency would be zero. The reservoir carrier lifetime $T_1$ now enters the RO damping, emphasizing the direct contribution of the reservoir carriers to the relaxation oscillations, while in the constant-reservoir regime only the QD carriers are involved. Furthermore, the increase of the RO frequency with increasing d, which we observed in Figure 2, is also predicted by the above equations. This suggests that, when a high resonance frequency is required, e.g., for high-speed modulation purposes, a close coupling between the reservoir and QD occupations is advantageous.

5. Conclusions

In this paper, we have derived a minimal, three-variable, QD laser rate-equation model that separately treats the influence of scattering rates and quasi-equilibrium carrier distribution by taking into account the detailed balance between the in and out-scattering rates of the carrier reservoir and the QD states. We have shown that this model can qualitatively describe the three distinct dynamic regimes of QD lasers appearing when the effective charge-carrier scattering rate is varied. Contrary to rate-equation models, where the in and out-scattering rates are constant, our model correctly predicts the appearance of the synchronized dynamic regime for high scattering rates, with pronounced relaxation oscillations. Our microscopic calculations suggest that most QD lasers will operate within this synchronized regime, emphasizing the importance of a correct modeling approach.

Depending on the QD-QW coupling coefficient d, the transition between the constant-reservoir regime for slow scattering and the synchronized regime is either smooth (high d), or via an overdamped regime (low d), corresponding to different QD structures. We have derived approximate analytic expressions for the RO frequency and damping in the different dynamic regimes as a function of experimentally accessible parameters, which give further insight into the QD laser dynamics.