Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers
Abstract
:1. Introduction
2. Minimal Quantum-Dot Laser Model
3. Numerical Results
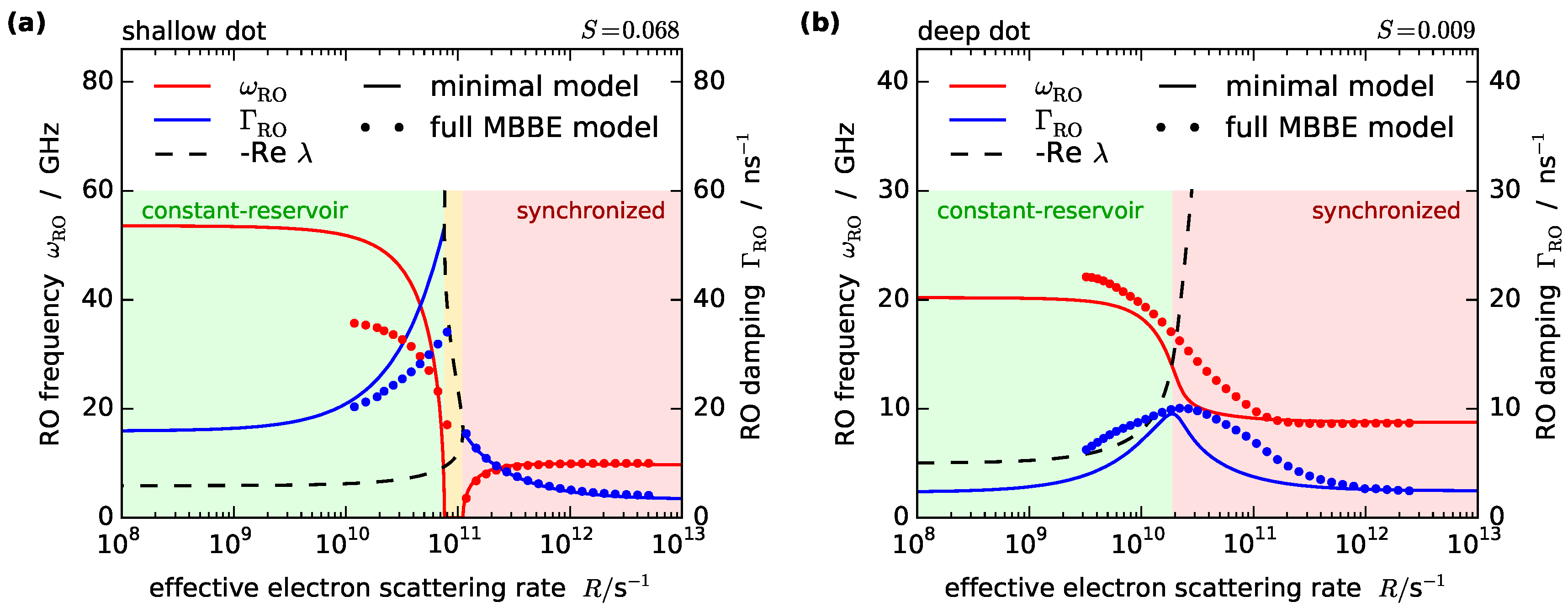
4. Analytic Approximation
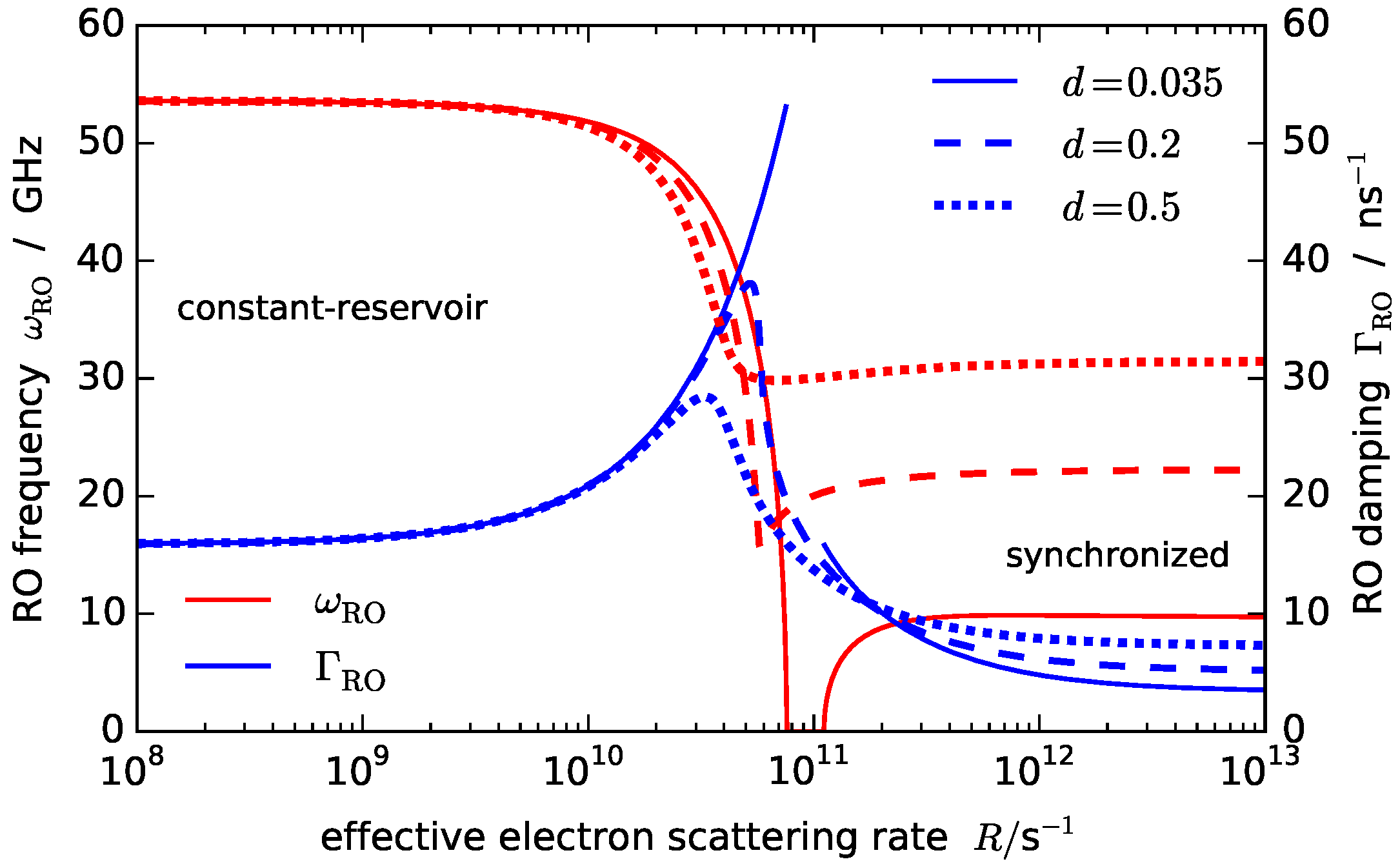
4.1. Slow Scattering – Constant-Reservoir Regime
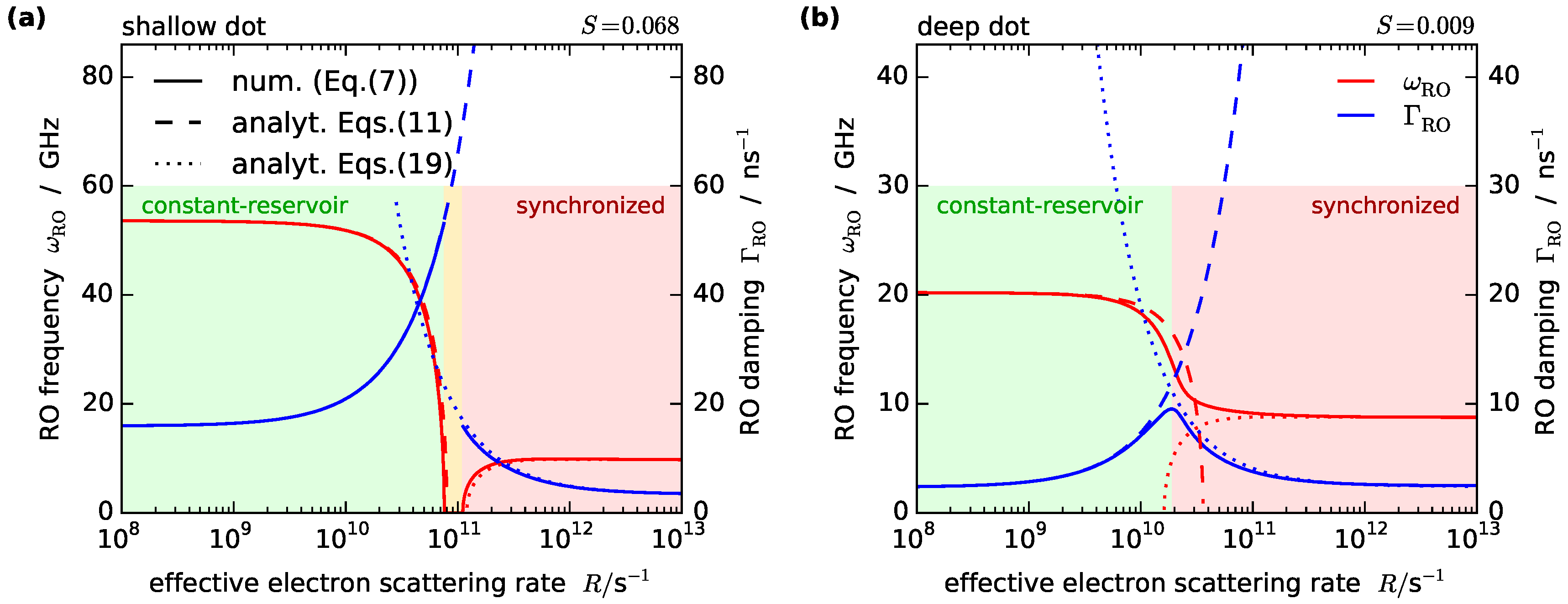
4.2. Fast Scattering – Synchronized Regime
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Analytic first-order corrections in the synchronized regime
References
- Arecchi, F.T.; Lippi, G.L.; Puccioni, G.P.; Tredicce, J.R. Deterministic Chaos in Laser with Injected Signal. Opt. Commun. 1984, 51, 308–315. [Google Scholar] [CrossRef]
- Chow, W.W.; Koch, S.W. Semiconductor-Laser Fundamentals; Springer: Berlin, Germany, 1999. [Google Scholar]
- Erneux, T.; Glorieux, P. Laser Dynamics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Coldren, L.A.; Corzine, S.W.; Mashanovitch, M. Diode Lasers and Photonic Integrated Circuits, 2nd ed.; Wiley Sons: New York, NY, USA, 2012. [Google Scholar]
- Lüdge, K.; Schöll, E. Quantum-dot lasers—Desynchronized nonlinear dynamics of electrons and holes. IEEE J. Quant. Electron. 2009, 45, 1396–1403. [Google Scholar] [CrossRef]
- Gioannini, M.; Rossetti, M. Time-Domain Traveling Wave Model of Quantum Dot DFB Lasers. IEEE J. Sel. Top. Quant. Electron. 2011, 17, 1318–1326. [Google Scholar] [CrossRef]
- Lingnau, B.; Lüdge, K.; Chow, W.W.; Schöll, E. Failure of the α-factor in describing dynamical instabilities and chaos in quantum-dot lasers. Phys. Rev. E 2012, 86. 065201(R). [Google Scholar] [CrossRef]
- O’Brien, D.; Hegarty, S.P.; Huyet, G.; Uskov, A.V. Sensitivity of quantum-dot semiconductor lasers to optical feedback. Opt. Lett. 2004, 29, 1072–1074. [Google Scholar] [CrossRef] [PubMed]
- Erneux, T.; Viktorov, E.A.; Mandel, P. Time scales and relaxation dynamics in quantum-dot lasers. Phys. Rev. A 2007, 76, 023819. [Google Scholar] [CrossRef]
- Lingnau, B.; Lüdge, K.; Chow, W.W.; Schöll, E. Influencing modulation properties of quantum-dot semiconductor lasers by electron lifetime engineering. Appl. Phys. Lett. 2012, 101, 131107. [Google Scholar] [CrossRef]
- Lüdge, K.; Lingnau, B.; Otto, C.; Schöll, E. Understanding electrical and optical modulation properties of semiconductor quantum-dot lasers in terms of their turn-on dynamics. Nonlinear Phenom. Complex Syst. 2012, 15, 350–359. [Google Scholar]
- Mørk, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback-Theory and experiment. IEEE J. Quant. Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Levine, A.M.; van Tartwijk, G.H.M.; Lenstra, D.; Erneux, T. Diode lasers with optical feedback: Stability of the maximum gain mode. Phys. Rev. A 1995, 52, R3436. [Google Scholar] [CrossRef] [PubMed]
- Otto, C.; Lüdge, K.; Schöll, E. Modeling quantum dot lasers with optical feedback: sensitivity of bifurcation scenarios. Phys. Stat. Sol. 2010, 247, 829–845. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Optoelectronic Devices; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Coleman, J.J. The development of the semiconductor laser diode after the first demonstration in 1962. Semicond. Sci. Technol. 2012, 27, 090207. [Google Scholar] [CrossRef]
- Wang, C.; Grillot, F.; Even, J. Impacts of Wetting Layer and Excited State on the Modulation Response of Quantum-Dot Lasers. IEEE J. Quant. Electron. 2012, 48, 1144–1150. [Google Scholar] [CrossRef] [Green Version]
- Grillot, F.; Wang, C.; Naderi, N.; Even, J. Modulation Properties of Self-Injected Quantum Dot Semiconductor Diode Lasers. IEEE J. Quant. Electron. 2013, 19, 1900812. [Google Scholar] [CrossRef]
- Lingnau, B.; Chow, W.W.; Schöll, E.; Lüdge, K. Feedback and injection locking instabilities in quantum-dot lasers: A microscopically based bifurcation analysis. New J. Phys. 2013, 15, 093031. [Google Scholar] [CrossRef]
- Markus, A.; Chen, J.X.; Gauthier-Lafaye, O.; Provost, J.G.; Paranthoen, C.; Fiore, A. Impact of Intraband Relaxation on the Performance of a Quantum-Dot Laser. IEEE J. Sel. Top. Quant. Electron. 2003, 9, 1308. [Google Scholar] [CrossRef]
- Lüdge, K.; Schöll, E.; Viktorov, E.A.; Erneux, T. Analytic approach to modulation properties of quantum dot lasers. J. Appl. Phys. 2011, 109, 103112. [Google Scholar] [CrossRef]
- Lüdge, K. Nonlinear Laser Dynamics—From Quantum Dots to Cryptography; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Röhm, A.; Lingnau, B.; Lüdge, K. Understanding Ground-State Quenching in Quantum-Dot Lasers. IEEE J. Quant. Electron. 2015, 51, 2000211. [Google Scholar] [CrossRef]
- Nielsen, T.R.; Gartner, P.; Jahnke, F. Many-body theory of carrier capture and relaxation in semiconductor quantum-dot lasers. Phys. Rev. B 2004, 69, 235314. [Google Scholar] [CrossRef]
- Majer, N.; Lüdge, K.; Schöll, E. Cascading enables ultrafast gain recovery dynamics of quantum dot semiconductor optical amplifiers. Phys. Rev. B 2010, 82, 235301. [Google Scholar] [CrossRef]
- Gioannini, M. Ground-state quenching in two-state lasing quantum dot lasers. J. Appl. Phys. 2012, 111, 043108. [Google Scholar] [CrossRef]
- Wang, C.; Lingnau, B.; Lüdge, K.; Even, J.; Grillot, F. Enhanced Dynamic Performance of Quantum Dot Semiconductor Lasers Operating on the Excited State. IEEE J. Quant. Electron. 2014, 50, 723–731. [Google Scholar] [CrossRef]
- Wu, Y.; Asryan, L.V. Direct and indirect capture of carriers into the lasing ground state and the light-current characteristic of quantum dot lasers. J. Appl. Phys. 2014, 115, 103105. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lingnau, B.; Lüdge, K. Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers. Photonics 2015, 2, 402-413. https://doi.org/10.3390/photonics2020402
Lingnau B, Lüdge K. Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers. Photonics. 2015; 2(2):402-413. https://doi.org/10.3390/photonics2020402
Chicago/Turabian StyleLingnau, Benjamin, and Kathy Lüdge. 2015. "Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers" Photonics 2, no. 2: 402-413. https://doi.org/10.3390/photonics2020402
APA StyleLingnau, B., & Lüdge, K. (2015). Analytic Characterization of the Dynamic Regimes of Quantum-Dot Lasers. Photonics, 2(2), 402-413. https://doi.org/10.3390/photonics2020402



