Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films
Abstract
:1. Introduction
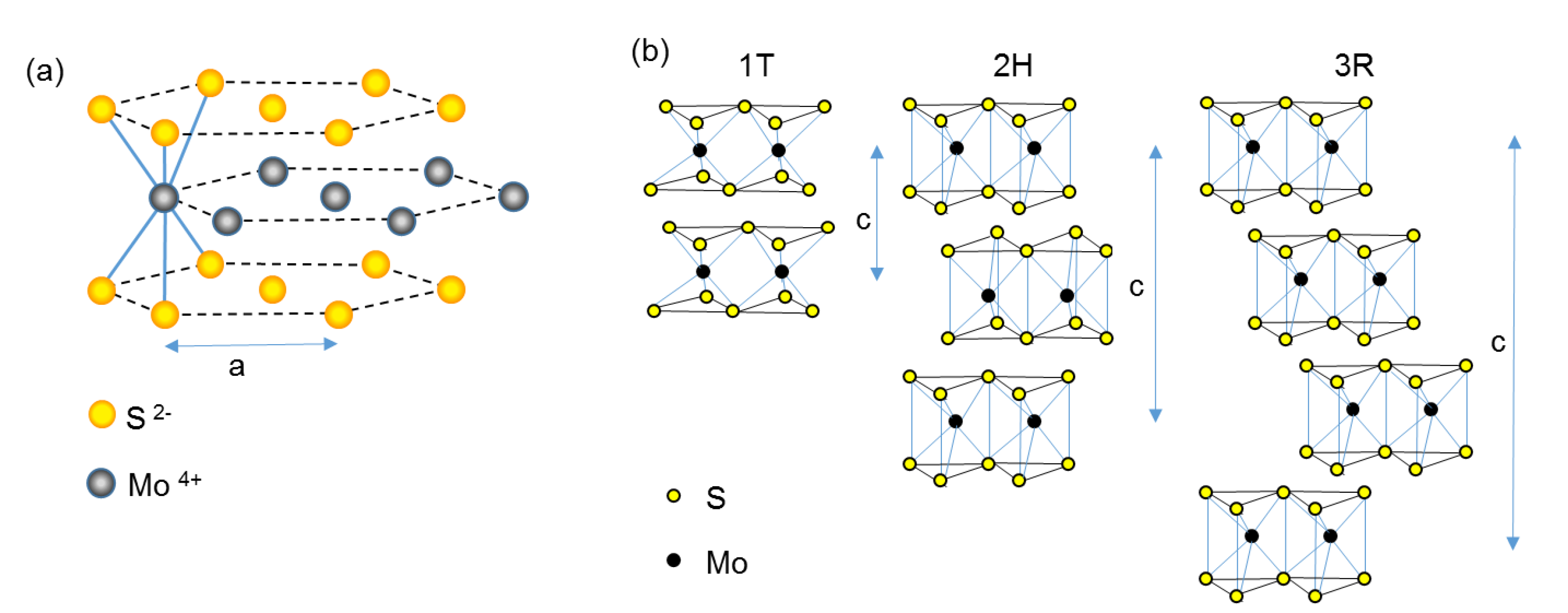
2. Crystal Structure
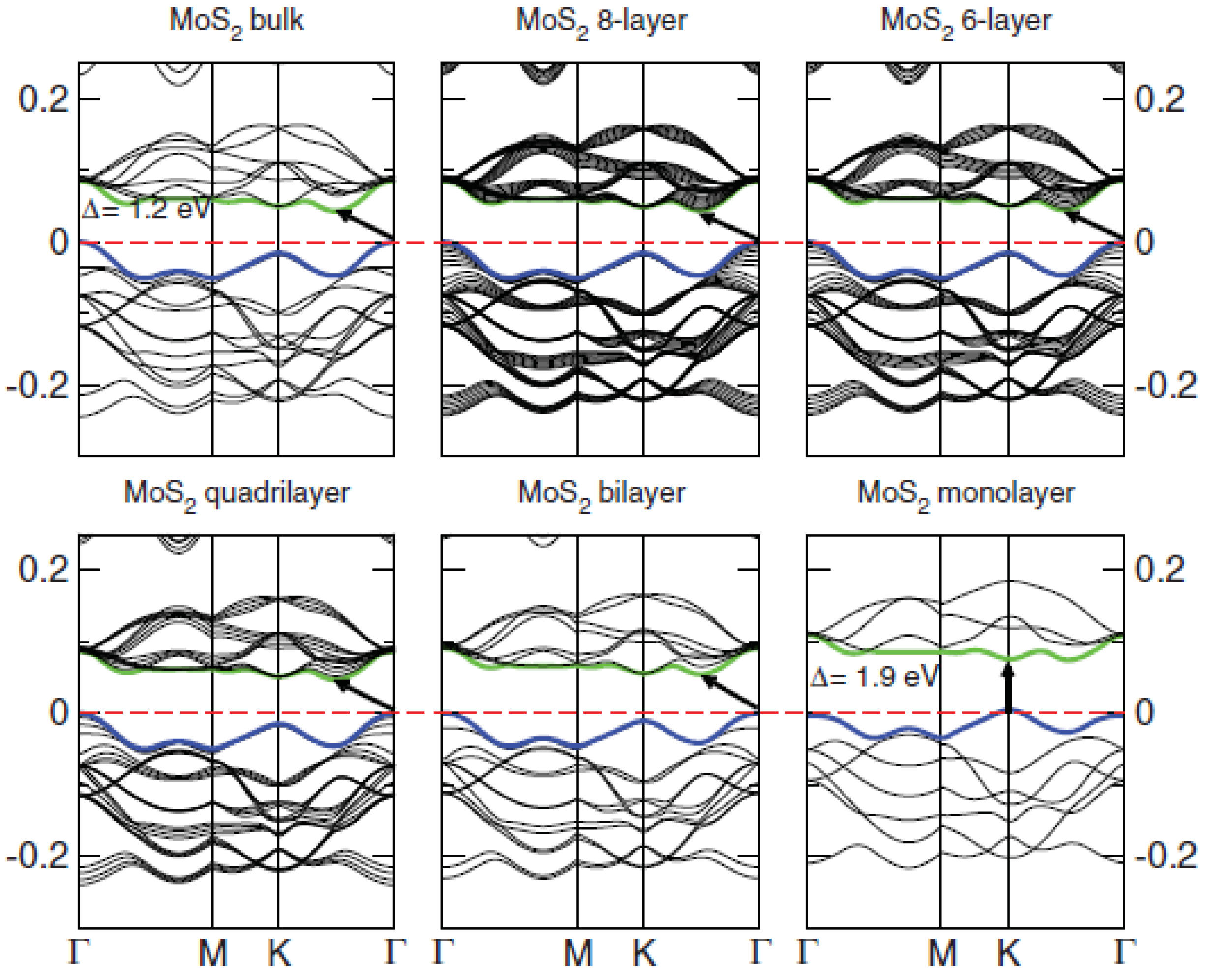
3. Electronic Band Structure: Optical and Optoelectronic Properties
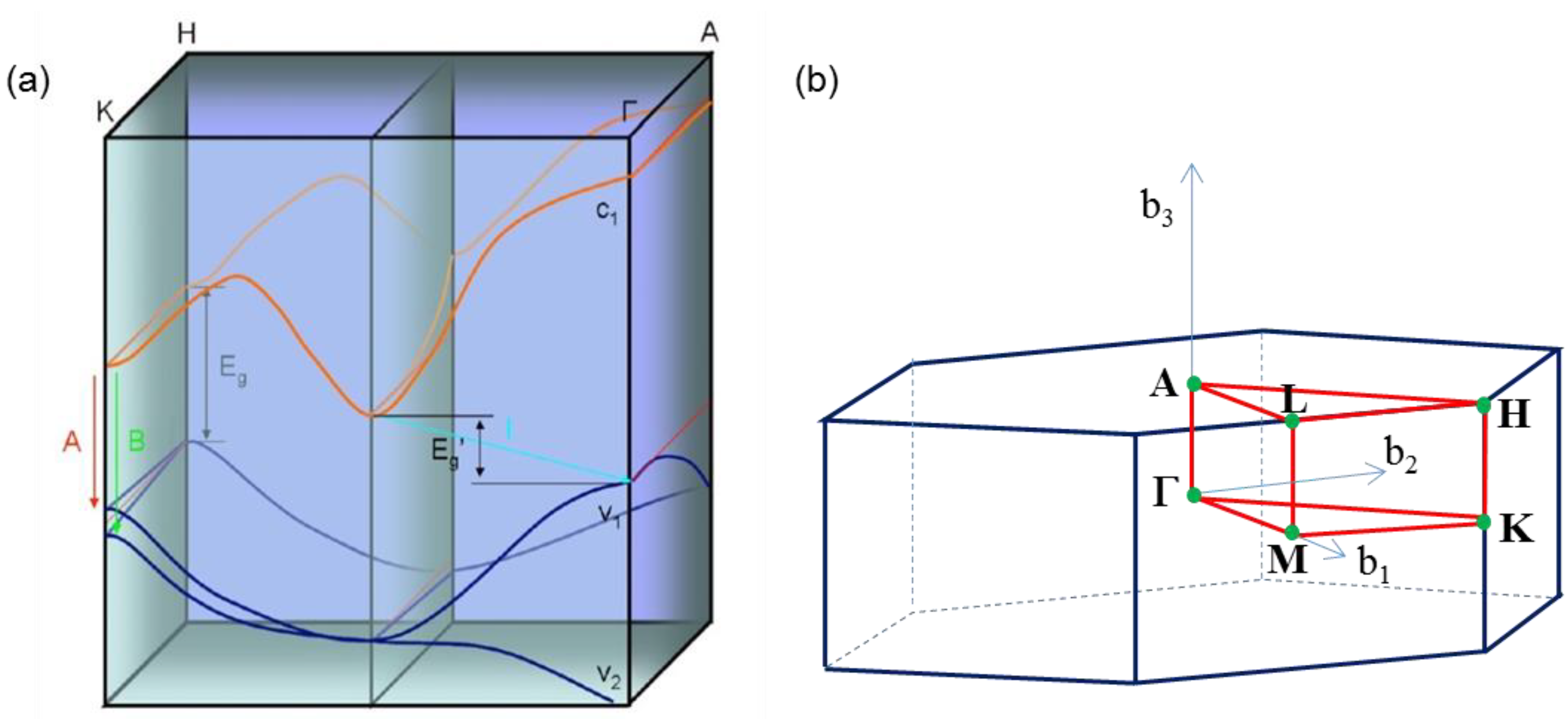
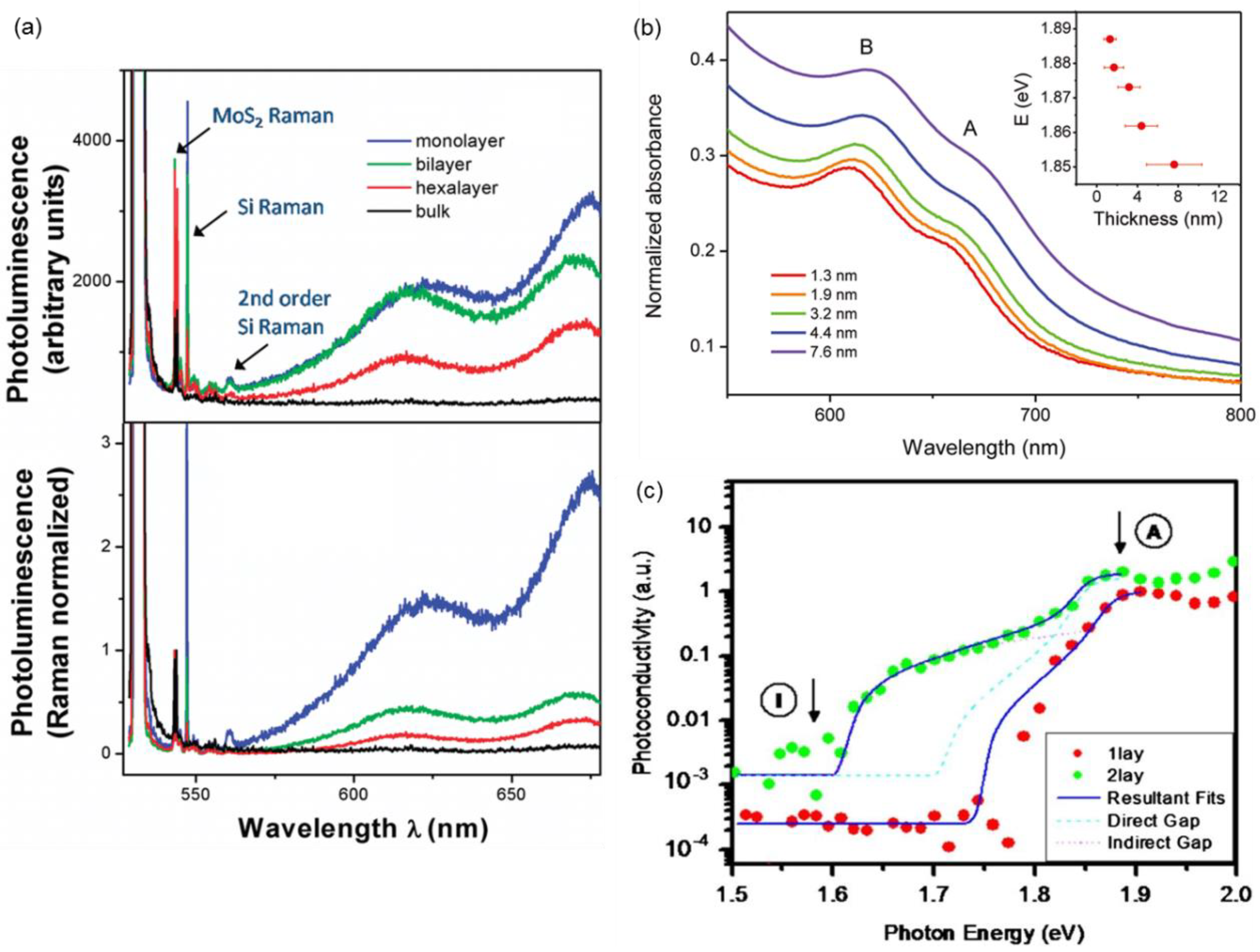
| 1.929 ± 0.005 | 2.136 ±.008 |
| 1.845 ± 0.008 | 2.053 ± 0.01 |
| 1.88 | 2.06 |
| 1.9255 | 2.137 |
| 1.92 | 2.124 |
| 1.9449 | 2.1376 |
| 1.90 | 2.10 |
| 1.91 | 2.11 |
| 1.82 | 1.95 |
| 1.78 | 1.96 |
| 1.88 | 2.03 |
| 1.85 | 1.98 |
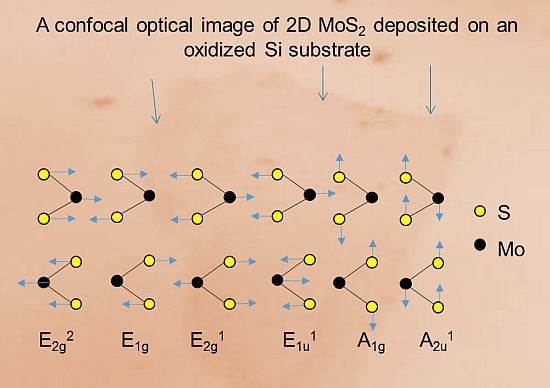
4. Lattice Dynamic: Raman Scattering and IR Absorption
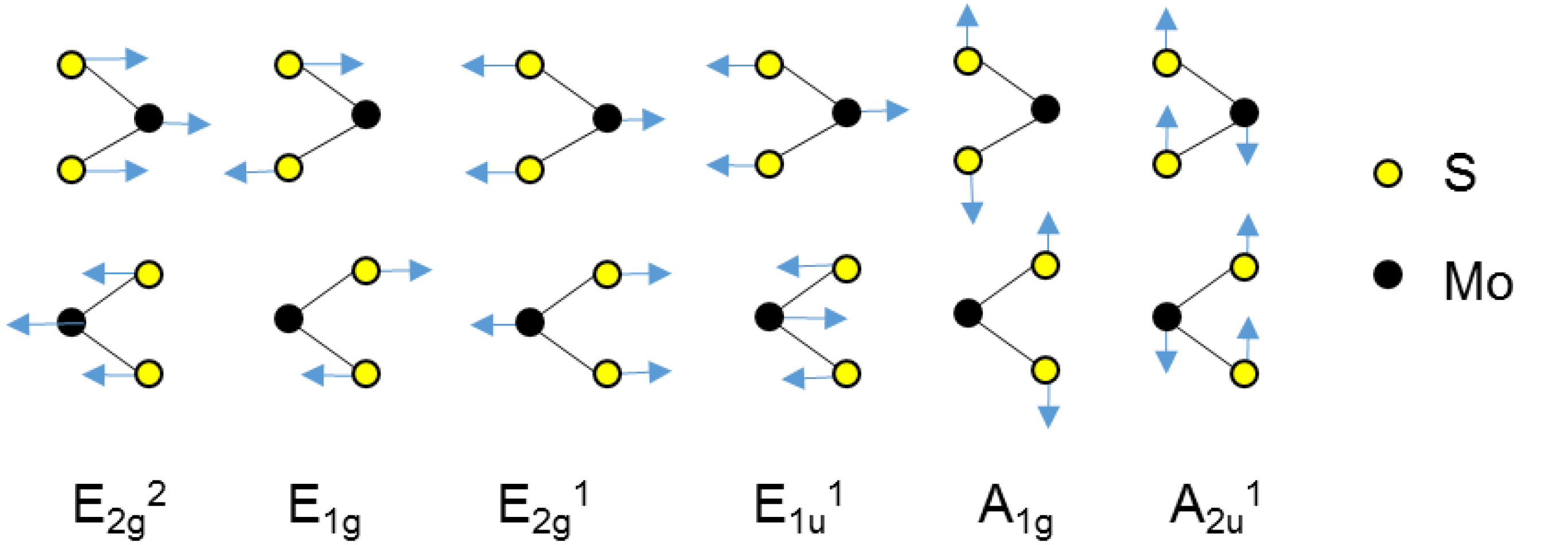
| C3v(S) | D3h(Mo) | D6h(MoS2(Γ)) | Transformation Properties | Activity | Vibration Direction | Atoms Involved | Frequency(cm−1) |
|---|---|---|---|---|---|---|---|
| A1 | A1’ | A1g | (αxx + αyy,αzz) | Raman | Out | S | 409 |
| A2’ | B1u | - | Inactive | Out | S | 403 | |
| A2 | A1’’ | B2g1 | - | Inactive | Out | Mo + S | 475 |
| B2g2 | - | Inactive | Out | Mo + S | 56 | ||
| A2’’ | A2u1 | Tz | IR(E) | Out | Mo + S | 470 | |
| A2u2 | Tz | Acoustic | Out | Mo + S | - | ||
| E | E’ | E2g1 | (αxx - αyy,αzz) | Raman | In | Mo + S | 383 |
| E1u1 | (Tx,Ty) | IR(E) | In | Mo + S | 384 | ||
| E2g2 | (αxx - αyy,αzz) | Raman | In | Mo + S | 34 | ||
| E1u2 | (Tx,Ty) | Acoustic | In | Mo + S | - | ||
| E’’ | E1g | (αyz,αzx) | Raman | In | S | 286 | |
| E2u | - | Inactive | In | S | 297 |
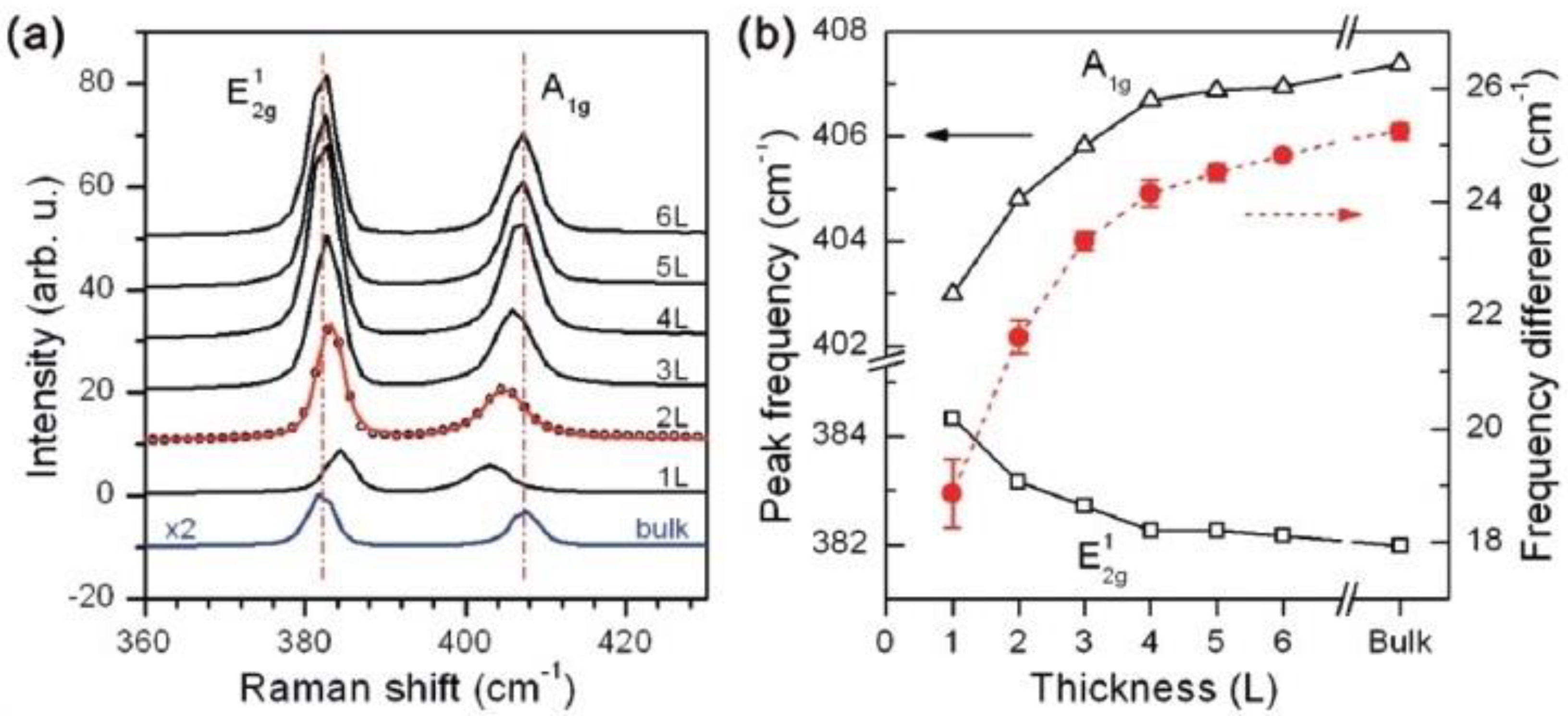
| Laser (nm) | E2g1 Mode Frequency (cm−1) | A1g Mode Frequency (cm−1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 L | 2 L | 3 L | 4 L | bulk | 1 L | 2 L | 3 L | 4 L | bulk | ||
| 325 | 384.2 | 382.8 | 382.8 | 382.7 | 382.5 | 404.9 | 405.5 | 406.3 | 407 | 407.8 | |
| 488 | 384.7 | 383.3 | 383.2 | 382.9 | 383 | 402.8 | 405.5 | 406.5 | 407.4 | 408 | |
| 514.5# | 384.3 | 383.2 | 382.7 | 382.3 | 382 | 403 | 404.8 | 405.8 | 406.7 | 407.8 | |
| 514.5* | 386.1 | 383.1 | - | 383.7 | 383.3 | 404.7 | 406.8 | - | 408 | 408.6 | |
| 532 | 384.7 | 382.5 | 382.4 | 382.4 | 383 | 402.7 | 404.9 | 405.7 | 406.7 | 407.8 | |
| 632.8 | 385 | 383.8 | 383.3 | 382.9 | 381.5 | 403.8 | 404.8 | 405 | 406 | 406.6 | |
| 632.8* | 386.4 | 383.1 | - | 383.3 | 382.8 | 405 | 406.2 | - | 407.3 | 408.3 | |
5. Resonant Raman Scattering
| Phonon Frequency (cm−1) | ||||
|---|---|---|---|---|
| Γ[80,85,86] | M[97] | M[84] | K[84] | |
| 409 | 397 | 412 | 408 | |
| E2g1 | 383 | 373 | 370 | 345 |
| E1g | 287 | 294 | 330 | 336 |
| 309 | ||||
| E2g2 | 34 | - | 233(LA) | 241(LA) |
| 160(ZA) | 192(ZA) | |||
| LA | - | 234 | 235 | 241 |

- Difference process:
- Combination process: ,
6. Conclusions
Acknowledgements
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva1, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. PNAS 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Elias, D.C.; Gorbachev, R.V.; Mayorov, A.S.; Morozov, S.V.; Zhukov, A.A.; Blake, P.; Ponomarenko, L.A.; Grigorieva, I.V.; Novoselov, K.S.; Guinea, F.; et al. Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 2011, 7, 701–704. [Google Scholar]
- Chen, H.; Müller, M.B.; Gilmore, K.J.; Wallace, G.G.; Li, D. Mechanically Strong, Electrically Conductive, and Biocompatible Graphene Paper. Adv. Mater. 2008, 20, 3557–3561. [Google Scholar]
- Lin, M.W.; Ling, C.; Zhang, Y.; Yoon, H.J.; Cheng, M.M.-C.; Agapito, L.A.; Kioussis, N.; Widjaja, N.; Zhou, Z. Room-temperature high on/off ratio in suspended graphene nanoribbon field-effect transistors. Nanotechnology 2011, 22, 265201. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Ci, L.J.; Lu, H.; Sorokin, P.B.; Jin, C.; Ni, J.; Kvashnin, A.G.; Kvashnin, D.G.; Lou, J.; Yakobson, B.I.; Ajayan, P.M. Large Scale Growth and Characterization of Atomic Hexagonal Boron Nitride Layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.K.; Hsu, A.; Jia, X.; Kim, S.M.; Shi, Y.; Hofmann, M.; Nezich, D.; Rodriguez-Nieva, J.F.; Dresselhaus, M.; et al. Synthesis of Monolayer Hexagonal Boron Nitride on Cu Foil Using Chemical Vapor Deposition. Nano Lett. 2012, 12, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Qin, S.Y.; Savaikar, M.A.; Wang, J.; Hao, B.; Zhang, D.; Banyai, D.; Jaszczak, J.A.; Clark, K.W.; et al. Room-Temperature Tunneling Behavior of Boron Nitride Nanotubes Functionalized with Gold Quantum Dots. Adv. Mater. 2013, 25, 4544–4548. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Xie, M.; Kayastha, V.; Wang, J.; Yap, Y.K. Patterned Growth of Boron Nitride Nanotubes by Catalytic Chemical Vapor Deposition. Chem. Mater. 2010, 22, 1782–1787. [Google Scholar] [CrossRef]
- Wang, J.S.; Lee, C.H.; Yap, Y.K. Recent advancements in boron nitride nanotubes. Nanoscale 2010, 2, 2028–2034. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.S.; Kayastha, V.K.; Yap, Y.K.; Fan, Z.; Lu, J.G.; Pan, Z.; Ivanov, I.N.; Puretzky, A.A.; Geohegan, D.B. Low temperature growth of boron nitride nanotubes on substrates. Nano Lett. 2005, 5, 2528–2532. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.A.; Yoffe, A.D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Yoffe, A.D. Layer compounds. Annu. Rev. Mater. Sci. 1973, 3, 147–170. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotech. 2011, 6, 147–150. [Google Scholar] [CrossRef]
- Yoon, Y.; Ganapathi, K.; Salahuddin, S. How good can monolayer MoS2 transistors be? Nano Lett. 2011, 11, 3768–3773. [Google Scholar] [CrossRef] [PubMed]
- Frindt, R.F.; Yoffe, A.D. Physical Properties of Layer Structures: Optical Properties and Photoconductivity of Thin Crystals of Molybdenum Disulphide. Proceedings A 1963, 27369–27383. [Google Scholar]
- Dickinson, R.G.; Pauling, L. The crystal structure of molybdenite. J. Am. Chem. Soc. 1923, 45, 1466–1471. [Google Scholar]
- Jellinek, P.; Brauer, G.; Müller, H. Molybdenum and Niobium Sulphides. Nature 1960, 185, 185376–185377. [Google Scholar] [CrossRef]
- Jiménez Sandoval, S.; Yang, D.; Frindt, R.F.; Irwin, J.C. Raman study and lattice dynamics of single molecular layers of MoS2. Phys. Rev. B 1991, 44, 3955–3962. [Google Scholar] [CrossRef]
- Wypych, F.; Schollhorn, R. 1T-Mos2, a New Metallic Modification of Molybdenum-Disulfide. J. Chem. Soc. -Chem. Commun. 1992, 19, 1386–1388. [Google Scholar] [CrossRef]
- Enyashin, A.N.; Yadgarov, L.; Houben, L.; Popov, I.; Weidenbach, M.; Tenne, R.; Bar-Sadan, M.; Seifert, G. New Route for Stabilization of 1T-WS2 and MoS2 Phases. J. Phys. Chem. C 2011, 115, 24586–24591. [Google Scholar] [CrossRef]
- Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from chemically exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef] [PubMed]
- Mattheiss, L.F. Band Structures of Transition-Metal-Dichalcogenide Layer Compounds. Phys. Rev. B 1973, 8, 3719–3740. [Google Scholar] [CrossRef]
- Shepherd, F.R.; Williams, P.M. Photoemission studies of the band structures of transition metal dichalcogenides. I. Groups IVA and IVB. J. Phys. C: Solid State Phys. 1974, 4416, 74416–74426. [Google Scholar]
- Shepherd, F.R.; Williams, P.M. Photoemission studies of the band structures of transition metal dichalcogenides. II. Groups VA and VIA. J. Phys. C: Solid State Phys. 1974, 4427, 74427–74439. [Google Scholar]
- Bromley, R.A.; Murray, R.B.; Yoffe, A.D. The band structures of some transition metal dichalcogenides. III. Group VIA trigonal prism materials. J. Phys. C: Solid State Phys. 1972. [Google Scholar] [CrossRef]
- Bromley, R.A. A Semi-Emprical Tight-Banding Calculation of the Band Structure of MoS2. Phys. Lett. 1970, 33, 33242–33243. [Google Scholar] [CrossRef]
- Mattheiss, L.F. Energy Bands for 2H-NbSe2 and 2H-MoS2. Phys. Rev. Lett. 1973, 30, 784–787. [Google Scholar] [CrossRef]
- Edmondson, D.R. Electronic band structure of the layer-type crystal 2H-MoS2. Solid State Commun. 1972, 10, 101085–101088. [Google Scholar] [CrossRef]
- Coehoorn, R.; Haas, C.; de Groot, R.A. Electronic structure of MoSe2, MoS2, and WSe2. II. The nature of the optical band gaps. Phys. Rev. B 1987, 35, 6203–6206. [Google Scholar]
- Reshak, A.H.; Auluck, S. Band structure and optical response of 2H-MoX2 compounds (X = S, Se, and Te). Phys. Rev. B 2005. [Google Scholar] [CrossRef]
- Li, T.S.; Galli, G.L. Electronic properties of MoS2 nanoparticles. J. Phys. Chem. C 2007, 111, 16192–16196. [Google Scholar] [CrossRef]
- Lebègue, S.; Eriksson, O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 2009, 79, 115409. [Google Scholar] [CrossRef]
- Kuc, A.; Zibouche, N.; Heine, T. Influence of quantum confinement on the electronic structure of the transition metal sulfide TS2. Phys. Rev. B 2011, 83, 245213. [Google Scholar]
- Ding, Y.; Wang, Y.; Ni, J.; Shi, L.; Shi, S.; Tang, W. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M = Mo, Nb, W, Ta; X = S, Se, Te) monolayers. Phys. B: Condens. Matt. 2011, 406, 2254–2260. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413. [Google Scholar] [CrossRef]
- Kadantsev, E.S.; Hawrylak, P. Electronic structure of a single MoS2 monolayer. Solid State Commun. 2012, 152, 909–913. [Google Scholar] [CrossRef]
- Yun, W.S.; Han, S.W.; Hong, S.C.; Kim, I.G.; Lee, J.D. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M = Mo, W; X = S, Se, Te). Phys. Rev. B 2012. [Google Scholar] [CrossRef]
- Kam, K.K.; Parklnclon, B.A. Detailed Photocurrent Spectroscopy of the Semiconducting Grouping VI Transition Metal Dichalcogenides. J. Phys. Chem. 1982, 86, 86463–86467. [Google Scholar] [CrossRef]
- Coehoorn, R.; Haas, C.; Dijkstra, J.; Flipse, C.J.; de Groot, R.A.; Wold, A. Electronic structure of MoSe2, MoS2, and WSe2. I. Band-structure calculations and photoelectron spectroscopy. Phys. Rev. B 1987, 35, 6195–6202. [Google Scholar]
- Kobayashi, K.; Yamauchi, J. Electronic structure and scanning-tunneling-microscopy image of molybdenum dichalcogenide surfaces. Phys. Rev. B Condens. Matt. 1995, 51, 17085–17095. [Google Scholar] [CrossRef]
- Frey, G.L.; Elani, S.; Homyonfer, M.; Feldman, Y.; Tenne, R. Optical-absorption spectra of inorganic fullerenelike MS2 (M = Mo, W). Phys. Rev. B 1998. [Google Scholar] [CrossRef]
- Böker, T.; Severin, R.; Müller, A.; Janowitz, C.; Manzke, R.; Voß, D.; Krüger, P.; Mazur, A.; Pollmann, J. Band structure of MoS2, MoSe2, and α-MoTe2: Angle-resolved photoelectron spectroscopy and ab initio calculations. Phys. Rev. B 2001. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; James, H.; Jie, S.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010. [Google Scholar] [CrossRef]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging photoluminescence in monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Yeh, P.-C.; Zaki, N.; Zhang, D.; Sadowski, J.T.; Al-Mahboob, A.; van der Zande, A.M.; Chenet, D.A.; Dadap, J.I.; Herman, I.P. Direct Measurement of the Thickness-Dependent Electronic Band Structure of MoS2 Using Angle-Resolved Photoemmision Spectroscopy. Phys. Rev. Lett. 2013, 111, 106801. [Google Scholar]
- Sundaram, R.S.; Engel, M.; Lombardo, A.; Krupke, R.; Ferrari, A.C.; Avouris, Ph.; Steiner, M. Electroluminescence in single layer MoS2. Nano Lett. 2013, 13, 1416–1421. [Google Scholar]
- Eknapakul, T.; King, P.D.; Lombardo, A.; Krupke, R.; Ferrari, A.C.; Avouris, P.; Steiner, M. Electronic structure of a quasi-freestanding MoS2 monolayer. Nano Lett. 2014, 14, 1312–1316. [Google Scholar] [CrossRef] [PubMed]
- Sandormirskii, V.B. Dependence of the forbiffen-band width of semiconducting films on their thickness and temperature. SOVIET PHYS. JETP 1963, 16, 1630–1631. [Google Scholar]
- Sandomirskii, V.B. Quantum Size Effect in a Semimetal Film. SOVIET PHYS. JETP 1967, 25, 101–106. [Google Scholar]
- Consadori, F.; Frindt, R.F. Crystal Size Effects on the Exciton Absorption Spectrum of WSe2. Phys. Rev. B 1970, 2, 4893–4896. [Google Scholar] [CrossRef]
- Evans, B.L.; Young, P.A. Exciton spectra in thin crystals the diamagnetic effect. Proc. Phy. Soc. 1967, 91, 91475–91482. [Google Scholar]
- Yoffe, A.D. Low-dimensional systems: Quantum size effects and electronic properties of semiconductor microcrystallites (zero-dimensional systems) and some quasi-two-dimensional systems. Adv. Phys. 1993, 42, 173–262. [Google Scholar] [CrossRef]
- Williams, P.M.; Shepherd, F.R. He II photoemission studies of transition metal dichalcogenides. J. Phys. C: Solid State Phys. 1973. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Yin, Z.; Li, H.; Li, H.; Jiang, L.; Shi, Y.; Sun, Y.; Lu, G.; Zhang, Q.; Chen, X.; Zhang, H. Single-layer MoS2 phototransistor. ACS Nano 2012, 6, 674–680. [Google Scholar]
- Beal, A.R.; Knights, J.C.; Liang, W.Y. Transmission spectra of some transition metal dichalcogenides. II. Group VIA: Trigonal prismatic coordination. J. Phys. C: Solid State Phys. 1972, 5, 53540–53551. [Google Scholar]
- Kasowski, R.V. Band Structure of MoS2 and NbS2. Phys. Rev. Lett. 1973, 30, 1175–1178. [Google Scholar] [CrossRef]
- Bullett, D.W. Electronic Band-Structure and Bonding in Transition-Metal Layered Dichalcogenides by Atomic Orbital Methods. J. Phys. C-Solid State Phys. 1978, 11, 4501–4514. [Google Scholar] [CrossRef]
- Tanaka, M.; Fukutani, H.; Kuwabara, G. Excitons in VI B Transition Metal Dichalcogenides. J. Phys. Soc. Japan 1978, 45, 1899–1904. [Google Scholar]
- Khan, M.R.; Goldsmith, G.J. Optical, Electro-Optical and Transport-Properties of MoS2. II Nuovo Cimento D 1983, 2, 665–686. [Google Scholar] [CrossRef]
- Wood, K.; Pendry, J.B. Layer Method for Band-Structure of Layer Compounds. Phys. Rev. Lett. 1973, 31, 1400–1403. [Google Scholar] [CrossRef]
- Hind, S.P.; Lee, P.M. KKR calculations of the energy bands in NbSe2, MoS2 and alpha MoTe2. J. Phys. C: Solid State Phys. 1980, 13, 13349–13357. [Google Scholar] [CrossRef]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 2012, 86, 115409. [Google Scholar] [CrossRef]
- Huisman, R.; De Jonge, R.; Haas, C.; Jellinek, F. Trigonal-Prismatic Coordination in Solid Compounds of Transition Metals. J. Phys. C: Solid State Phys. 1971, 356, 56–66. [Google Scholar]
- Jiang, H. Electronic Band Structures of Molybdenum and Tungsten Dichalcogenides by the GW Approach. J. Phys. Chem. C 2012, 116, 7664–7671. [Google Scholar] [CrossRef]
- Cheiwchanchamnangij, T.; Lambrecht, W.R.L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 2012, 85, 205302. [Google Scholar] [CrossRef]
- Komsa, H.-P.; Krasheninnikov, A.V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 2012, 86, 241201. [Google Scholar] [CrossRef]
- Shi, H.; Pan, H.; Zhang, Y.-W.; Yakobson, B.I. Quasiparticle band structures and optical properties of strained monolayer MoS2 and WS2. Phys. Rev. B 2013, 87, 155304. [Google Scholar]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Optical Spectrum of MoS2: Many-Body Effects and Diversity of Exciton States. Phys. Rev. Lett. 2013, 111, 216805. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Cao, T.; O’Brien, K.; Zhu, H.; Yin, X.; Wang, Y.; Louie, S.G.; Zhang, X. Probing excitonic dark states in single-layer tungsten disulphide. Nature 2014, 513, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.H.; Wu, C.S.; Huang, Y.S.; Liao, P.C.; Tiong, K.K. Temperature dependence of energies and broadening parameters of the band-edge excitons of Mo1-xWxS2 single crystals. J. Phys.-Condens. Matt. 1998, 10, 9317–9328. [Google Scholar] [CrossRef]
- Acrivos, J.V.; Liang, W.Y.; Wilson, J.; Yoffe, A. Optical studies of metal-semiconductor transmutations produced by intercalation. J. Phys. C: Solid State Phys. 1971, 4, L18–L20. [Google Scholar] [CrossRef]
- Beal, A.R.; Hughes, H.P. Kramers-Kronig Analysis of the Reflectivity Spectra of 2h-MoS2, 2h-MoSe2 and 2h-MoTe2. J. Phys. C-Solid State Phys. 1979, 12, 881–890. [Google Scholar] [CrossRef]
- Fortin, E.; Raga, F. Excitons in Molybdenum-Disulfide. Phys. Rev. B 1975, 11, 905–912. [Google Scholar] [CrossRef]
- Sekine, T.; Uchinokura, K.; Nakashizu, T.; Matsuura, E.; Yoshizaki, R. Dispersive Raman Mode of Layered Compound 2H MoS2 under the resonant condition. J. Phys. Soc. Japan 1984, 53, 811–818. [Google Scholar]
- Frey, G.L.; Tenne, R.; Matthews, M.J.; Dresselhaus, M.S.; Dresselhaus, G. Raman and resonance Raman investigation of MoS2 nanoparticles. Phys. Rev. B 1999, 60, 2883–2892. [Google Scholar] [CrossRef]
- Verble, J.L.; Wieting, T.J. Lattice Mode Degeneracy in MoS2 and Other Layer Compounds. Phys. Rev. Lett. 1970, 25, 362–365. [Google Scholar] [CrossRef]
- Wieting, T.J.; Verble, J.L. Infrared and Raman Studies of Long-Wavelength Optical Phonons in Hexagonal MoS2. Phys. Rev. B 1971, 3, 4286–4292. [Google Scholar] [CrossRef]
- Lee, C.; Yan, H.; Brus, L.E.; Heinz, T.F.; Hone, J.; Ryu, S. Anomalous lattice vibrations of single- and few-layer MoS2. ACS Nano 2010, 4, 2695–2700. [Google Scholar] [CrossRef] [PubMed]
- Agnihotri, O.P.; Sehgal, H.K.; Garg, A.K. Laser Excited Raman Spectra of Gr. VI Semiconducting Compounds.pdf. Solid state Commun. 1973, 12, 12135–12138. [Google Scholar]
- Tsachi, L.; Spanier, J.E. A Comprehensive Spectral Analysis of Multiphonon Resonant Raman Scattering in 2H-MoS2. arXiv 2014. [Google Scholar]
- Chen, J.M.; Wang, C.S. Second order Raman spectrum of MoS2. Solid State Commun. 1974, 14, 14857–14860. [Google Scholar] [CrossRef]
- Stacy, A.M.; Hodul, D.T. Raman spectra of IVB and VIB transition metal disulfides using laser energies near the absorption. J. Phys. Chem. Solids 1985, 46, 405–409. [Google Scholar] [CrossRef]
- Scherer, J.R.; Bailey, G.F.; Kint, S. Simple Optical Geometry for Obtaining Raman Back Scattering. Analy. Chem. 1971, 43, 1917–1918. [Google Scholar] [CrossRef]
- Shriver, D.F.; Dunn, J.B.R. The Backscattering Geometry for Raman Spectroscopy of Colored Materials. Appl. Spectrosc. 1974, 28, 319–323. [Google Scholar] [CrossRef]
- Verble, J.L.; Wietling, T.J. Rigid-layer lattice vibrations and van der waals bonding in hexagonal MoS2. Solid State Commun. 1972, 11, 11941–11944. [Google Scholar] [CrossRef]
- Bromley, R.A. The lattice vibrations of the MoS2 structure. Philosoph. Mag. 1971, 23, 1417–1427. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Yap, C.C.R.; Tay, B.K.; Edwin, T.H.T.; Olivier, A.; Baillargeat, D. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Function. Mater. 2012, 22, 1385–1390. [Google Scholar] [CrossRef]
- Bertrand, P. Surface-phonon dispersion of MoS2. Phys. Rev. B 1991, 44, 5745–5749. [Google Scholar] [CrossRef]
- Chakraborty, B.; Matte, H.S.S.R.; Sood, A.K.; Rao, C.N.R. Layer-dependent resonant Raman scattering of a few layer MoS2. J. Raman Spectrosc. 2013, 44, 92–96. [Google Scholar] [CrossRef]
- Mrstik, B.; Kaplan, R.; Reinecke, T.L.; Van Hove, M.; Tong, S.Y. Surface-structure determination of the layered compounds MoS2 and NbSe2 by low-energy electron diffraction. Phys. Rev. B 1977, 15, 897–900. [Google Scholar] [CrossRef]
- Wieting, T.J.; Verble, J.L. Interlayer Bonding and the Lattice Vibrations of β-GaSe. Phys. Rev. B 1972, 5, 1473–1479. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1996, 55, 10355. [Google Scholar] [CrossRef]
- Wakabayashi, N.; Smith, H.G.; Nicklow, R.M. Lattice dynamics of hexagonal MoS2 studied by neutron scattering. Phys. Rev. B 1975, 12, 659–663. [Google Scholar] [CrossRef]
- Livneh, T.; Sterer, E. Resonant Raman scattering at exciton states tuned by pressure and temperature in 2H-MoS2. Phys. Rev. B 2010, 81, 195209. [Google Scholar] [CrossRef]
- Fan, J.-H.; Gao, P.; Zhang, A.M.; Zhu, B.-R.; Zeng, H.-L.; Cui, X.-D.; He, R.; Zhang, Q.-M. Resonance Raman scattering in bulk 2H-MX2 (M = Mo, W; X = S, Se) and monolayer MoS2. J. Appl. Phys. 2014, 115, 053527. [Google Scholar] [CrossRef]
- Gołasa, K.; Grzeszczyk, M.; Leszczyński, P.; Faugeras, C.; Nicolet, A.A.L.; Wysmołek, A.; Potemski, M.; Babiński, A. Multiphonon resonant Raman scattering in MoS2. Appl. Phys. Lett. 2014, 104, 092106. [Google Scholar] [CrossRef]
- Golasa, K.; Grzeszczyk, M.; Korona, K.P.; Bożek, R.; Binder, J.; Szczytko, J.; Wysmołek, A.; Babiński, A. Optical Properties of Molybdenum Disulfide (MoS2). ACTA PHYS. POLONICA A 2013, 124, 849–851. [Google Scholar]
- McDevitf, N.T.; Zabinski, J.S.; Donley, M.S.; Bultman, J.E. Disorder-Induced Low-Frequency Raman Band Observed in Deposited MoS2 Films. Appl. Spectrosc. 1994, 48, 733–736. [Google Scholar] [CrossRef]
- Windom, B.C.; Sawyer, W.G.; Hahn, D.W. A Raman Spectroscopic Study of MoS2 and MoO3: Applications to Tribological Systems. Tribol. Lett. 2011, 42, 301–310. [Google Scholar] [CrossRef]
- Gołasa, K.; Grzeszczyk, M.; Bożek, R.; Leszczyński, P.; Wysmołek, A.; Potemski, M.; Babiński, A. Resonant Raman scattering in MoS2—From bulk to monolayer. Solid State Commun. 2014, 197, 19753–19756. [Google Scholar] [CrossRef]
- Ghosh, P.N.; Maiti, C.R. Interlayer Force and Davydov Splitting in 2H-MoS2. Phys. Rev. B 1983, 28, 2237–2239. [Google Scholar] [CrossRef]
- Najmaei, S.; Liu, Z.; Ajayan, P.M.; Lou, J. Thermal effects on the characteristic Raman spectrum of molybdenum disulfide (MoS2) of varying thicknesses. Appl. Phys. Lett. 2012, 100, 013106. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Winslow, D.; Zhang, D.; Pandey, R.; Yap, Y.K. Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films. Photonics 2015, 2, 288-307. https://doi.org/10.3390/photonics2010288
Ye M, Winslow D, Zhang D, Pandey R, Yap YK. Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films. Photonics. 2015; 2(1):288-307. https://doi.org/10.3390/photonics2010288
Chicago/Turabian StyleYe, Mingxiao, Dustin Winslow, Dongyan Zhang, Ravindra Pandey, and Yoke Khin Yap. 2015. "Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films" Photonics 2, no. 1: 288-307. https://doi.org/10.3390/photonics2010288
APA StyleYe, M., Winslow, D., Zhang, D., Pandey, R., & Yap, Y. K. (2015). Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films. Photonics, 2(1), 288-307. https://doi.org/10.3390/photonics2010288