Optimization of Unrepeatered Optical Communication Systems and the Applications in Cabled Ocean Observatories
Abstract
1. Introduction
2. Principle and Key Components
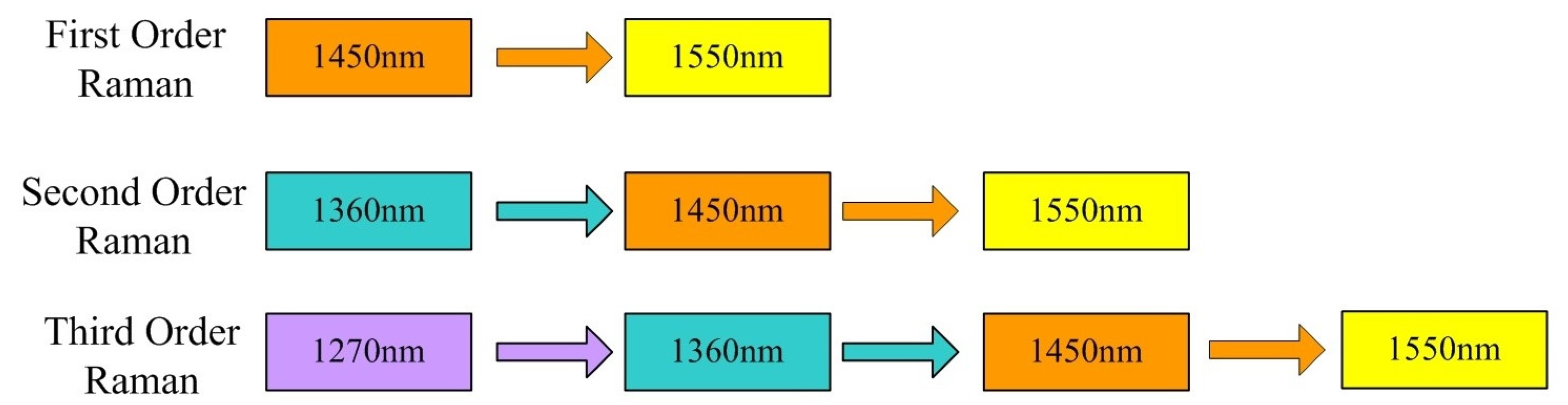
2.1. High-Order Raman Amplification
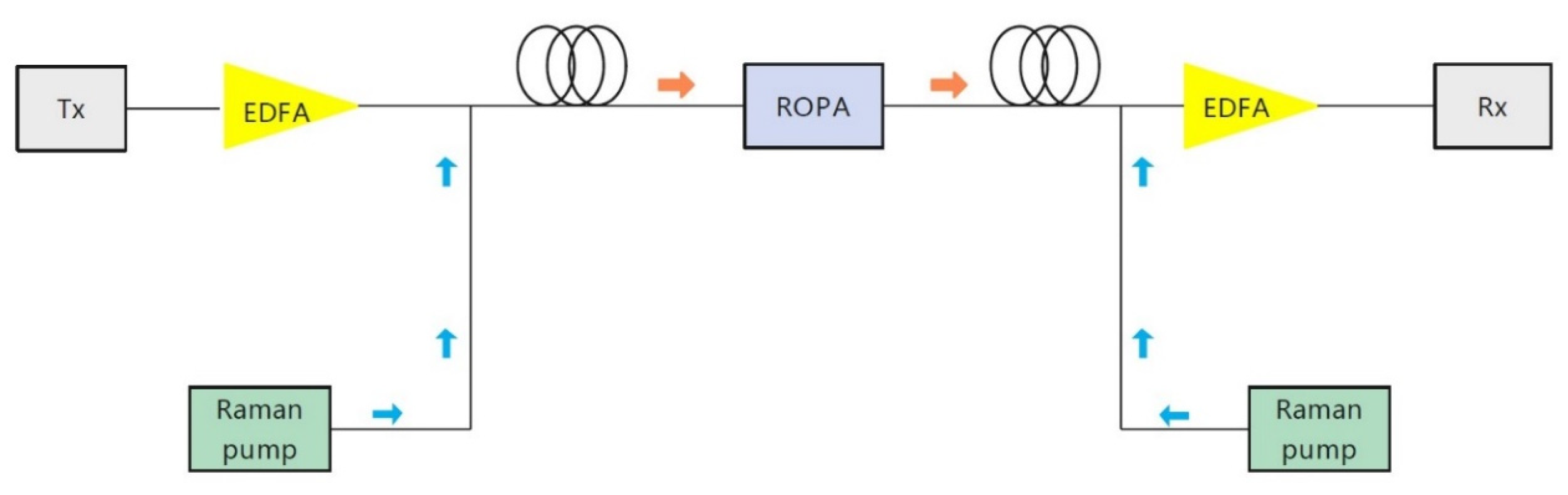
2.2. Remote Optical Pumping Amplifier
3. System Optimization
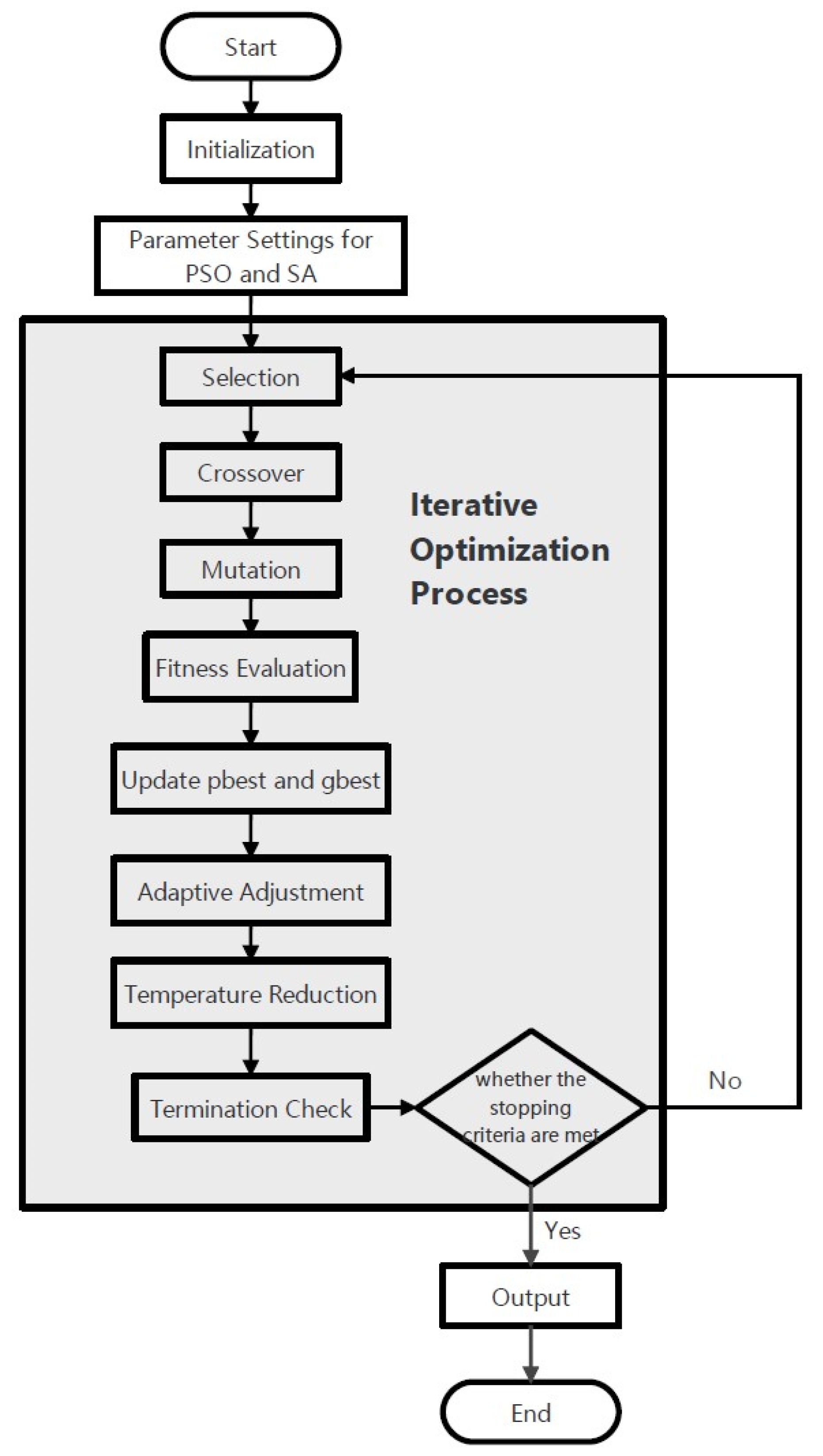
3.1. Optimization Methodology
- (1)
- Initialization
- a.
- Signal Gain
- b.
- Noise
- c.
- Pump Noise
- d.
- Attenuation of Signal Light in the EDF
- e.
- Position of the ROPA
- (2)
- Parameter Settings
- (3)
- GA-Selection
- Fitness Value Computation
- b.
- Cumulative Probability Calculation
- c.
- Parent Selection
- (4)
- GA-Crossover
- Parent Selection
- b.
- Crossover Point Selection
- c.
- Gene Exchange
- (5)
- GA-Mutation
- Mutation Individual Selection
- b.
- Mutation Gene Determination
- c.
- Gaussian Mutation
- (6)
- PSO—Fitness Evaluation
- a.
- Initialization
- b.
- Fitness Computation
- (7)
- PSO—Updating Personal and Global Best Positions
- a.
- Updating Personal Best Position
- b.
- Updating Global Best Position
- (8)
- PSO—Updating Velocity and Position
- (9)
- SA—Temperature Reduction
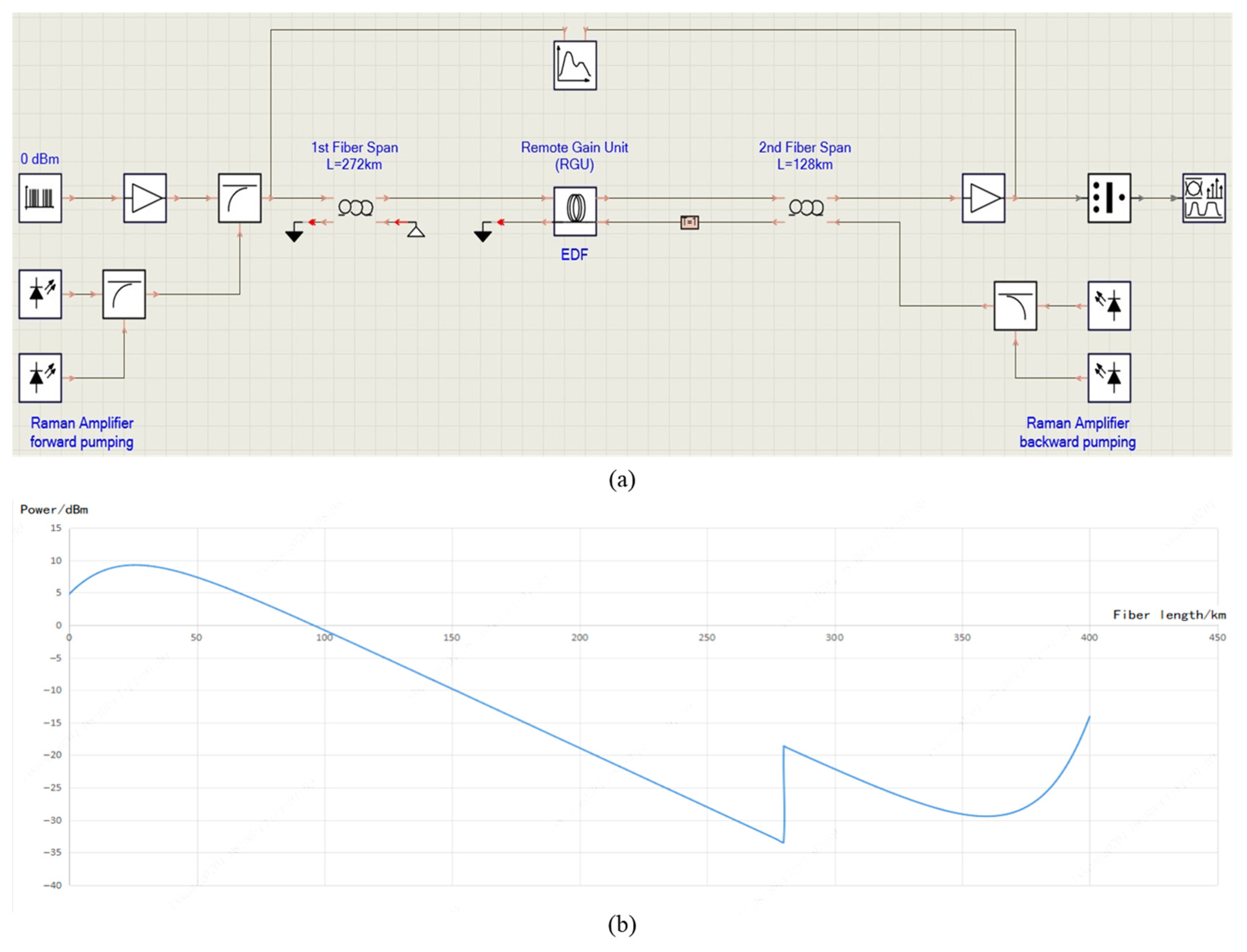
3.2. Computational Results
3.3. Simulation Results
4. Experimental Verification
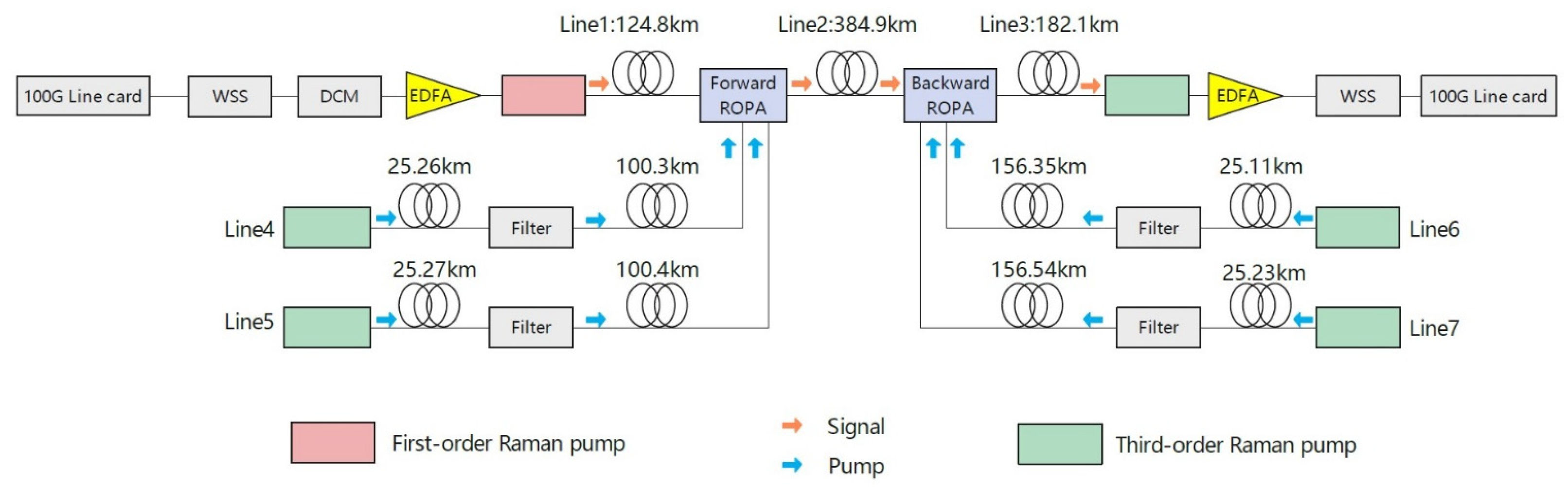
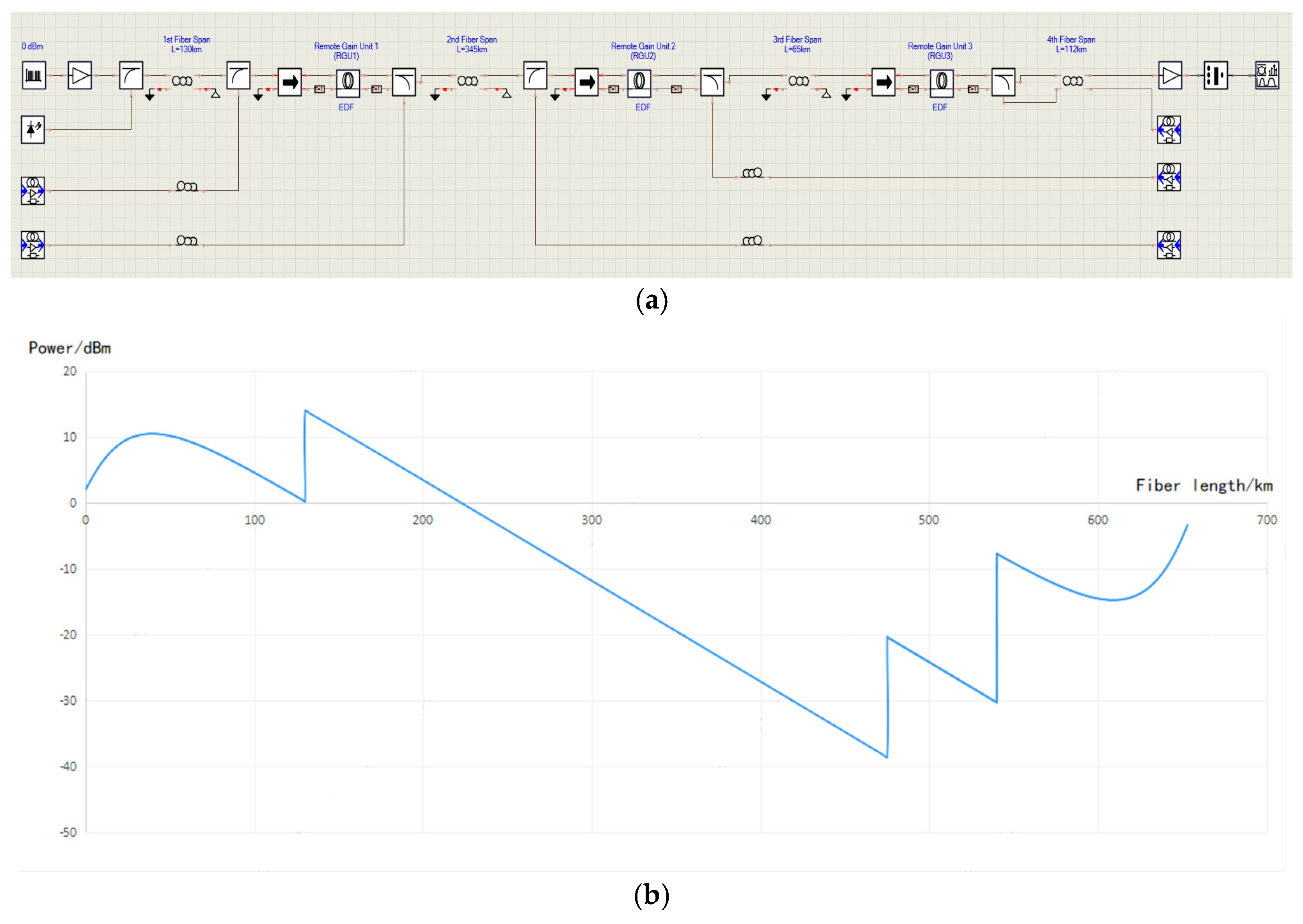
4.1. Experimental Configuration
- (1)
- Optical Fiber
- (2)
- Light Source and Optical Amplifier Module
- (3)
- Transmission Equipment
4.2. Experimental Design
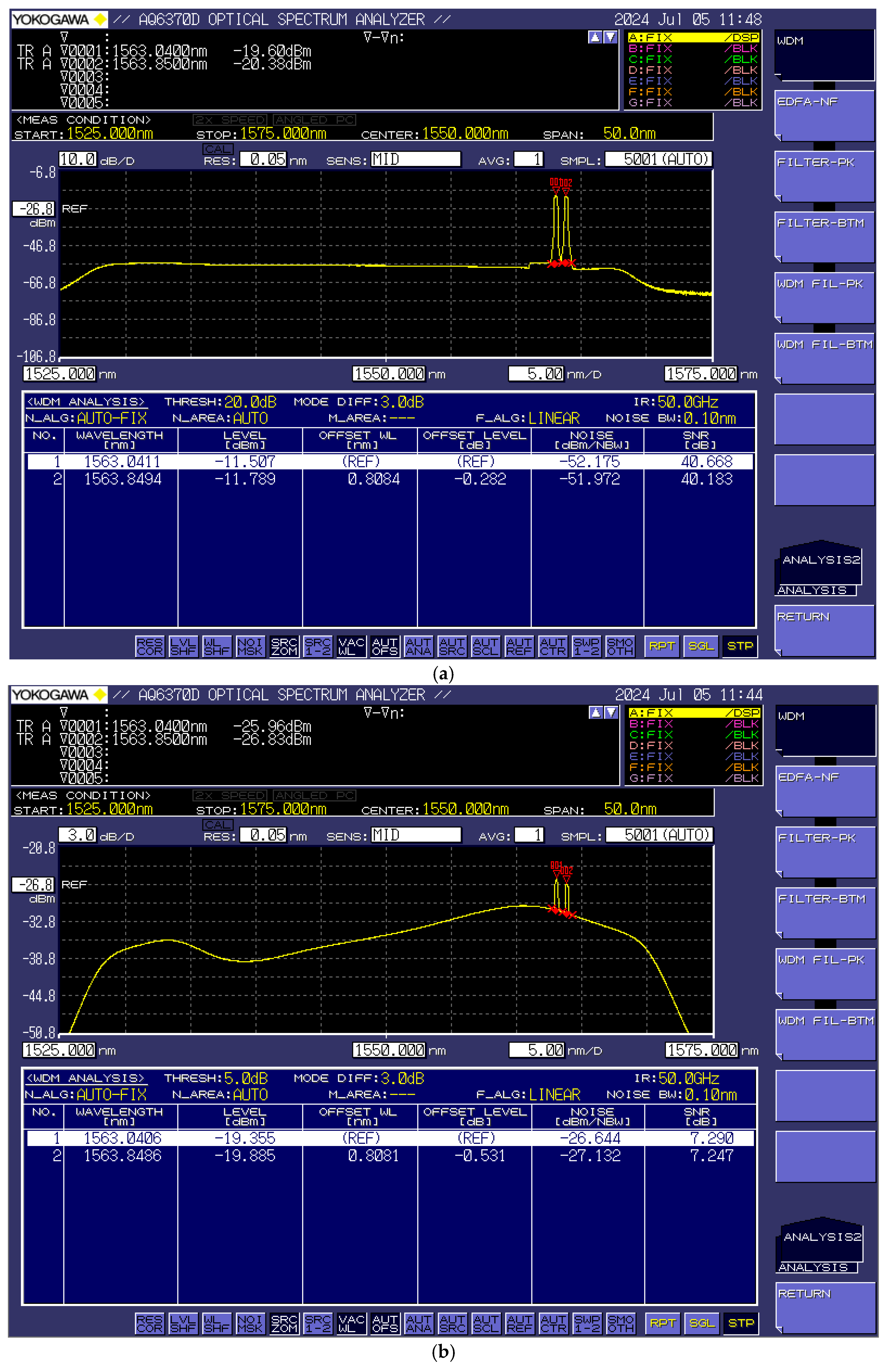
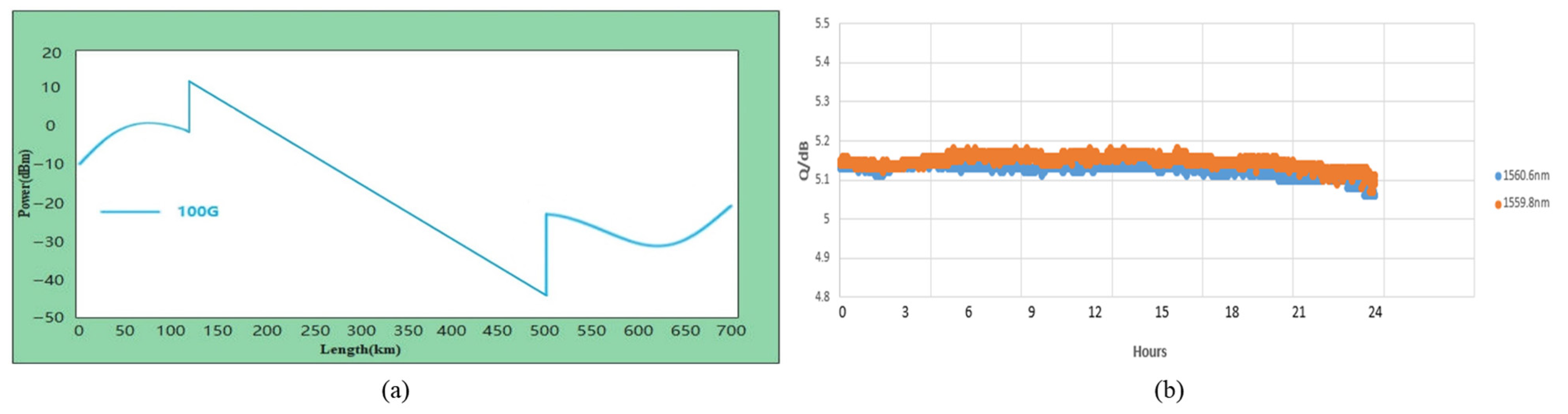
4.3. Experimental Results and Analysis
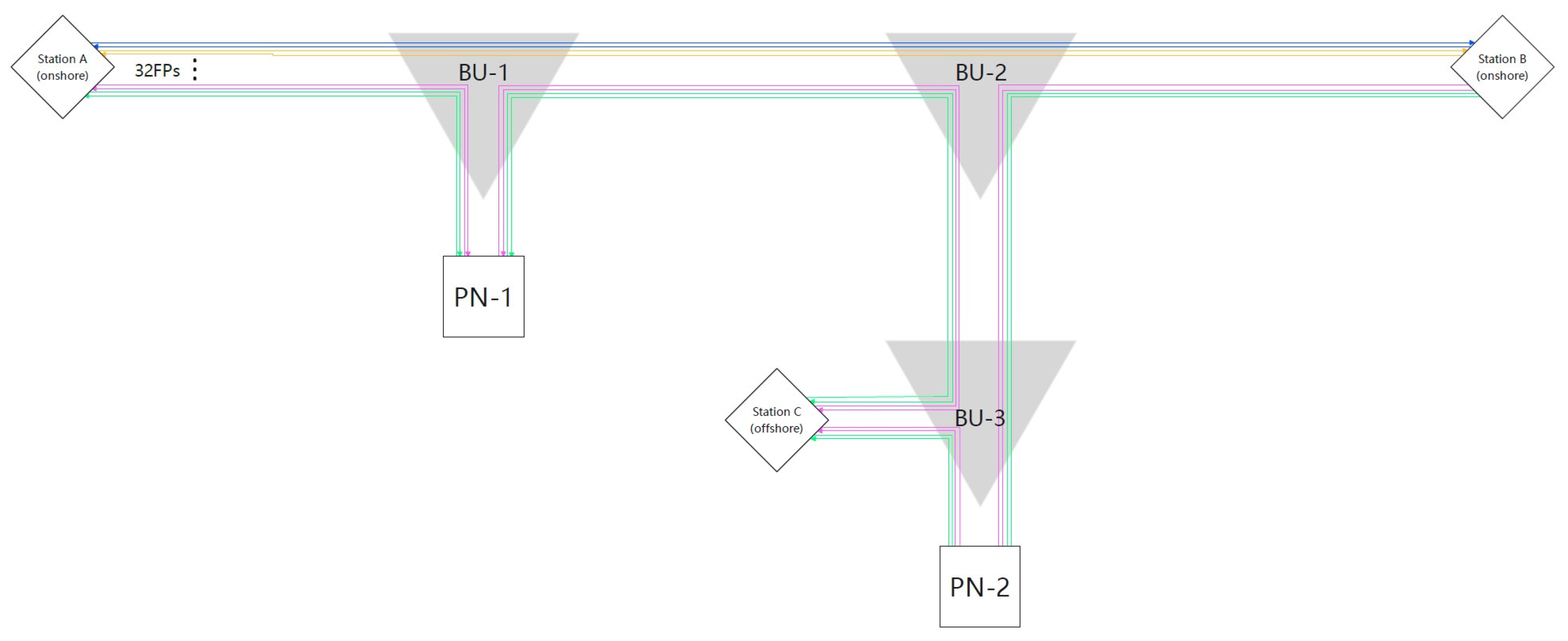
5. Applications in Cabled Ocean Observatories
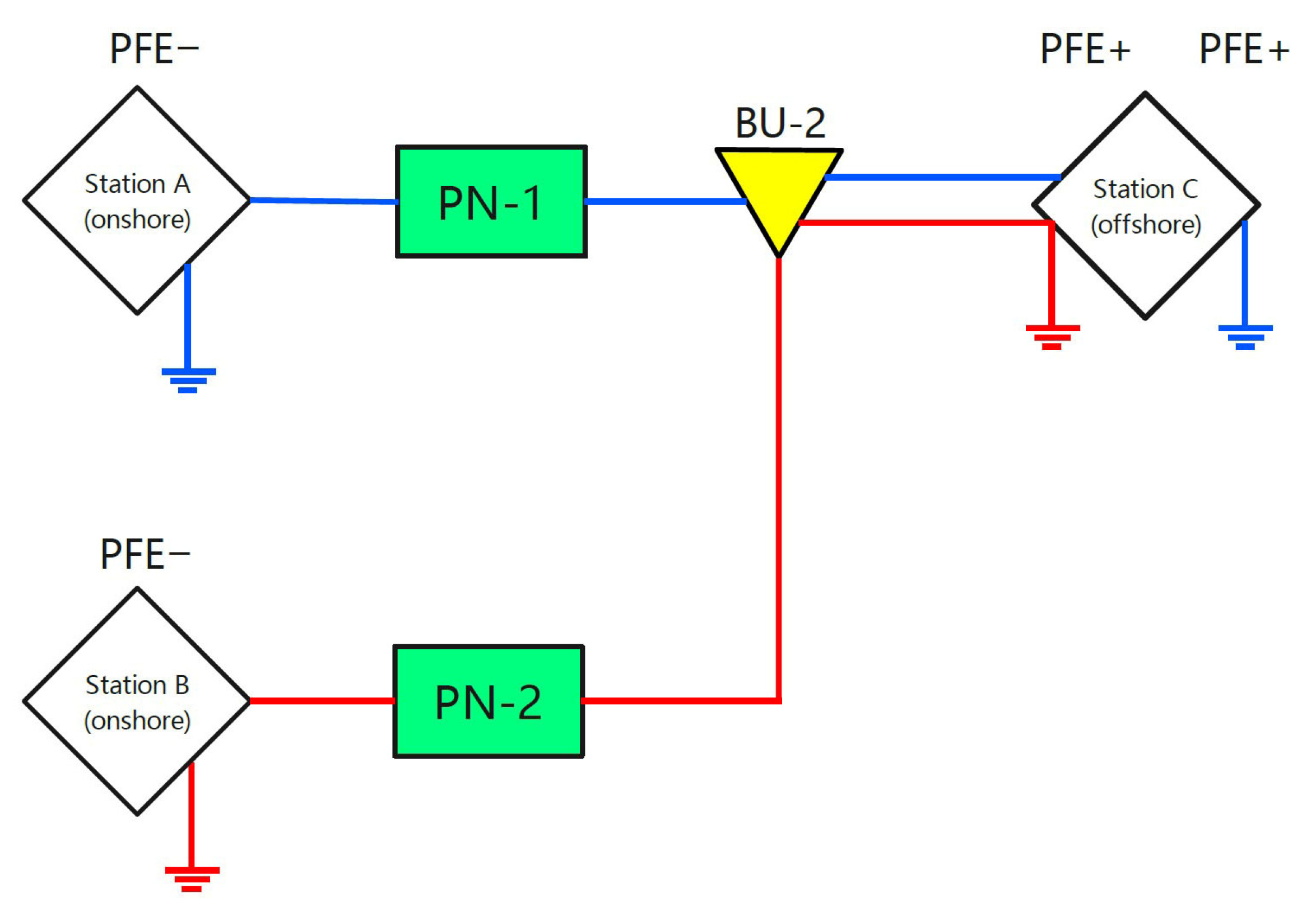
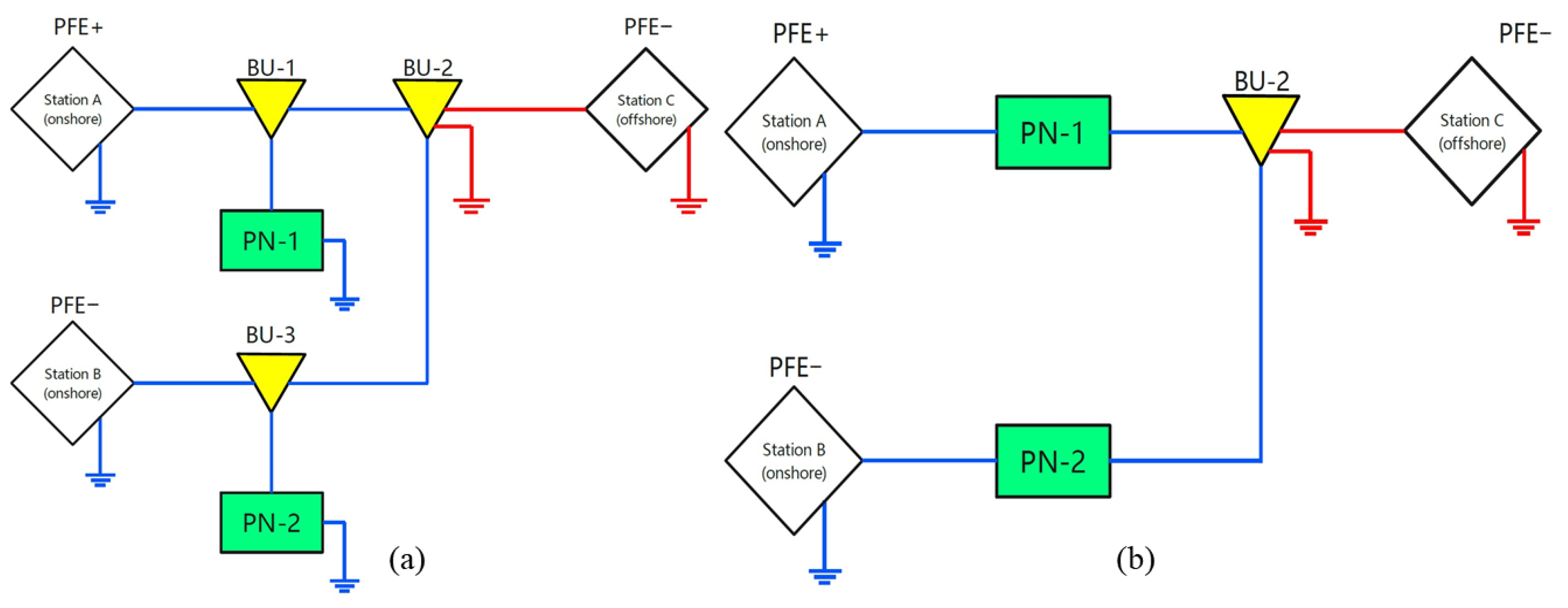
5.1. Case Study: Repeatered vs. Unrepeatered Schemes
- (1)
- Repeatered Scheme
- (2)
- Unrepeatered Scheme
- (1)
- Adjust the Cable Type
- (2)
- Adjust the Routing Scheme
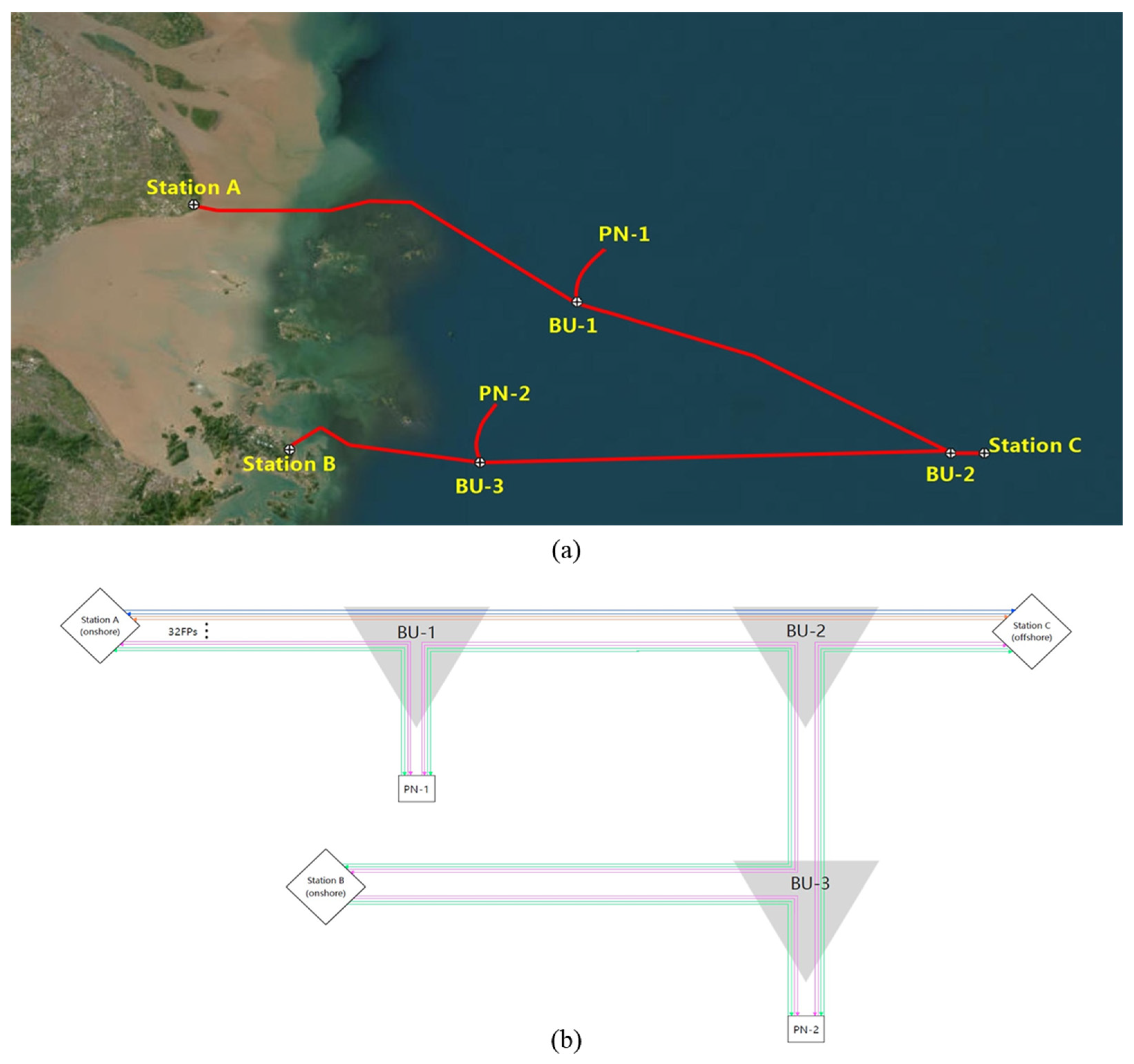
5.2. Stimulation for Unrepeatered Scheme
5.3. Comprehensive Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- First Iteration
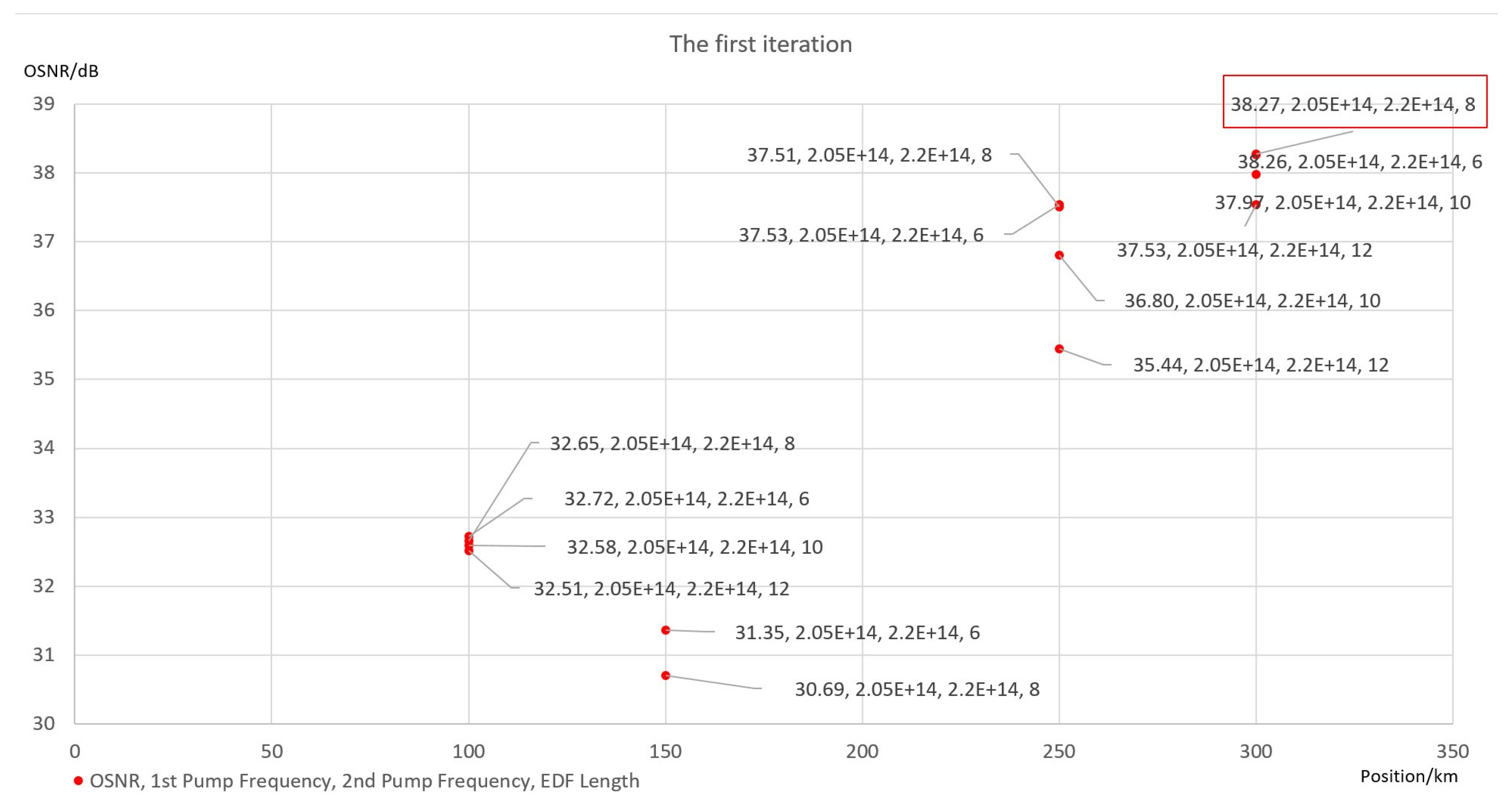
- (2)
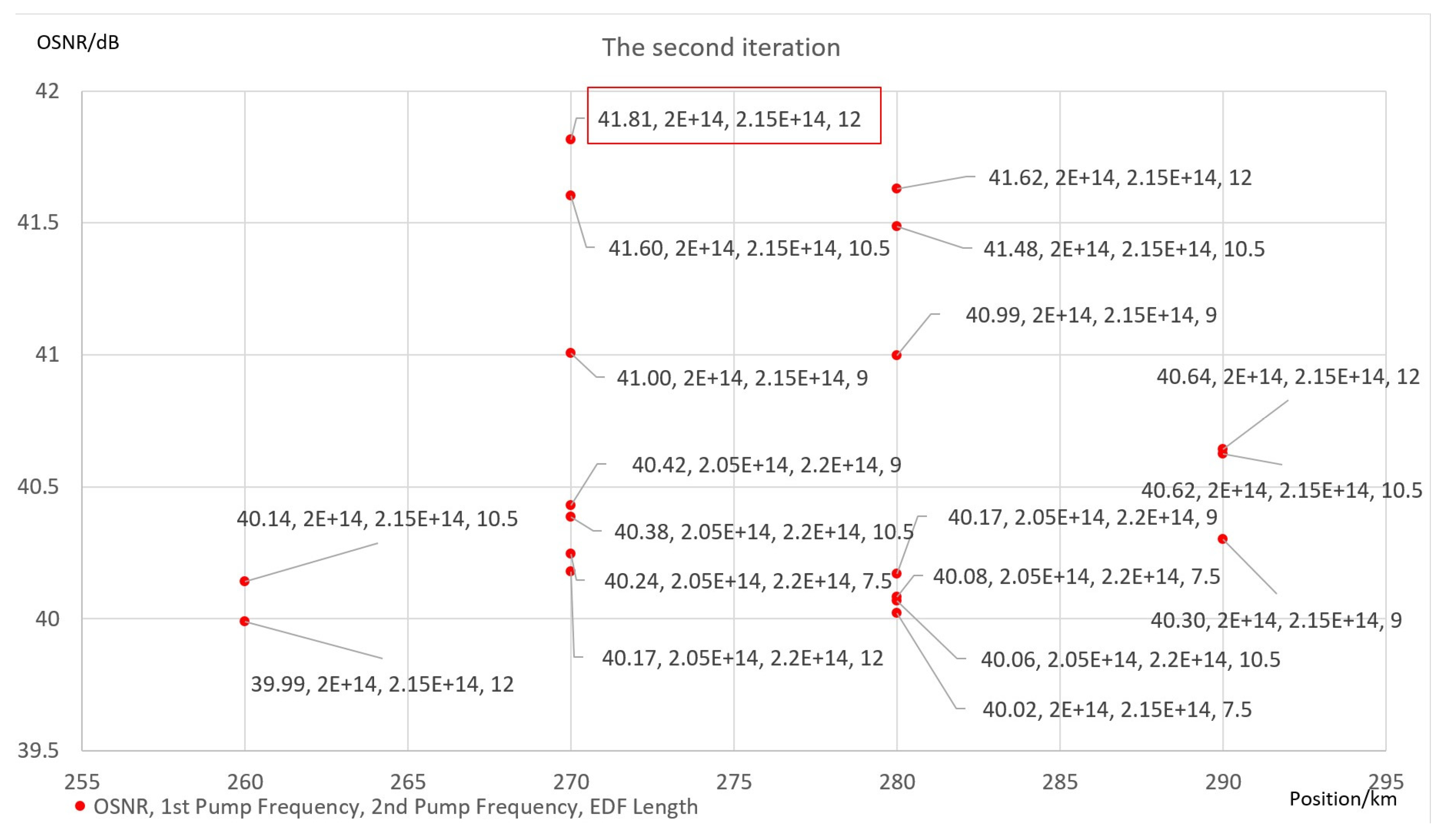
- Second Iteration
- (3)
- Third Iteration

- (4)
- Fourth Iteration

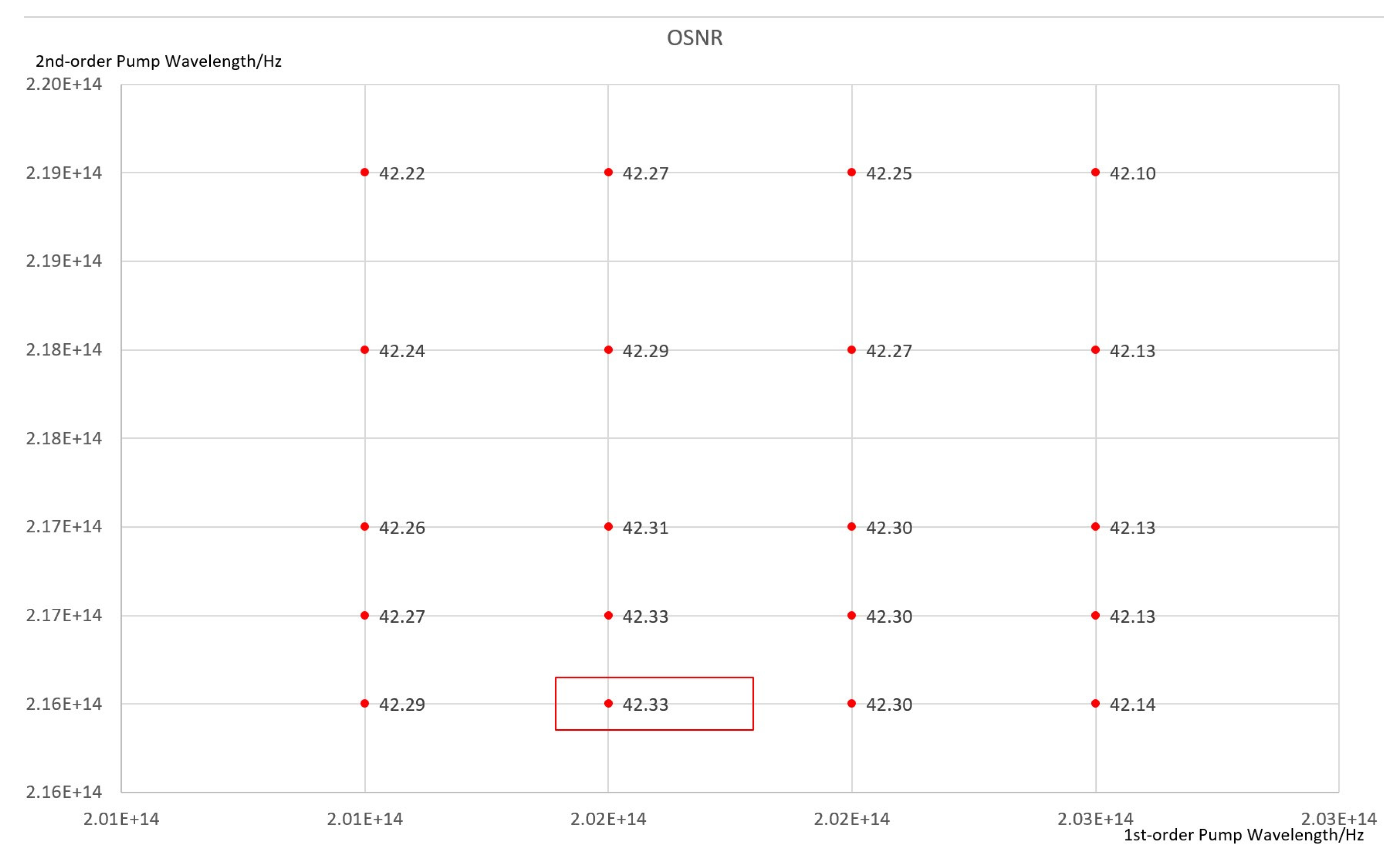
- (5)
- Pump Frequency Matching
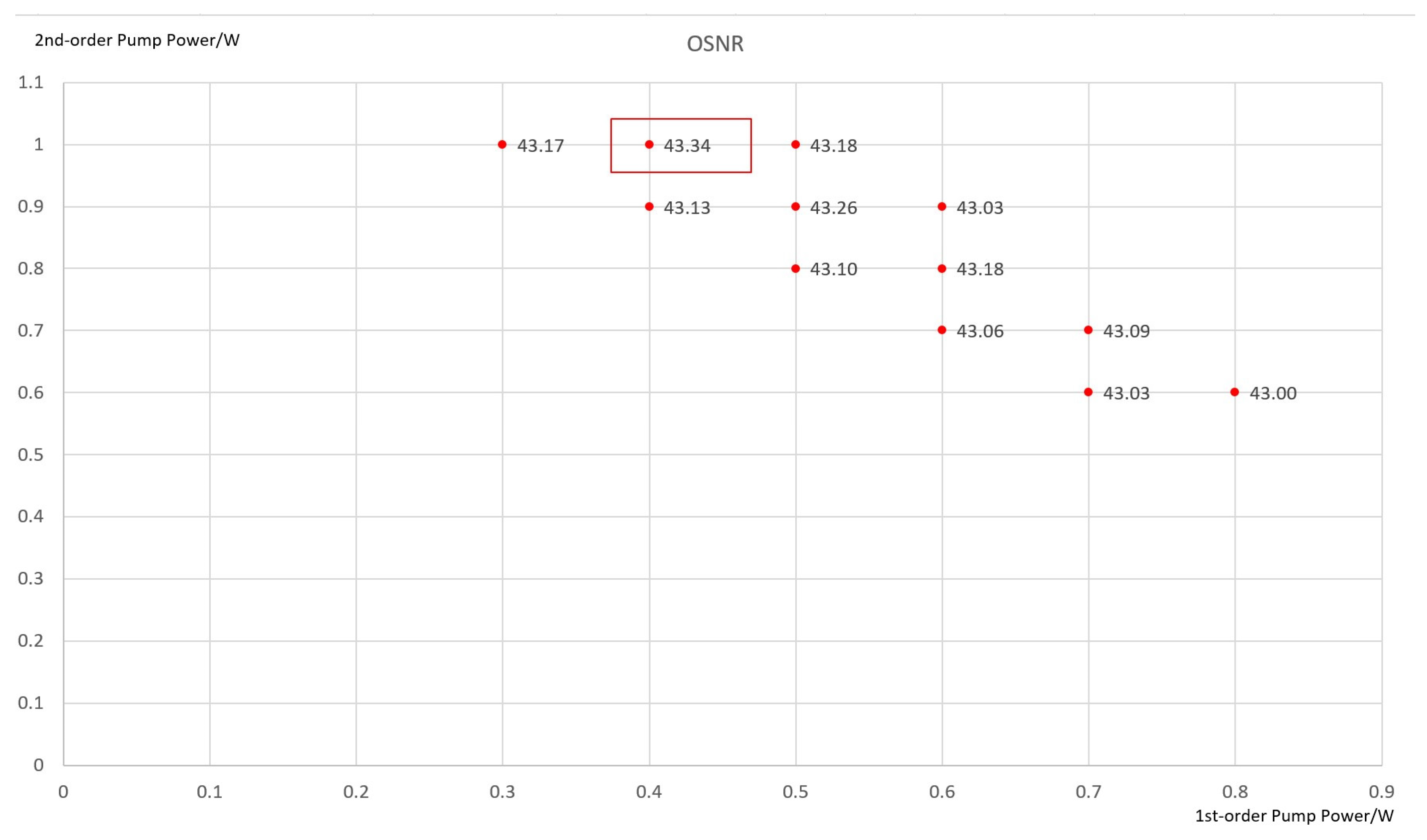
- (6)
- Pump Power Matching
References
- Barnes, C.R.; Best, M.M.R.; Johnson, F.R.; Pautet, L.; Pirenne, B. Challenges, benefits, and opportunities in installing and operating cabled ocean observatories: Perspectives from NEPTUNE Canada. IEEE J. Ocean. Eng. 2013, 38, 144–157. [Google Scholar] [CrossRef]
- Barnes, C.R.; Tunnicliffe, V. Building the World’s First Multi-node Cabled Ocean Observatories (NEPTUNE Canada and VENUS, Canada): Science, Realities, Challenges and Opportunities. In Proceedings of the OCEANS 2008—MTS/IEEE Kobe Techno-Ocean, Kobe, Japan, 8–11 April 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Takagi, R.; Uchida, N.; Nakayama, T.; Azuma, R.; Ishigami, A.; Okada, T.; Nakamura, T.; Shiomi, K. Estimation of the Orientations of the S-net Cabled Ocean-Bottom Sensors. Seismol. Res. Lett. 2019, 90, 2175–2187. [Google Scholar] [CrossRef]
- Uchida, N.; Nakajima, J.; Wang, K.L.; Takagi, R.; Yoshida, K.; Nakayama, T.; Hino, R.; Okada, T.; Asano, Y. Stagnant forearc mantle wedge inferred from mapping of shear-wave anisotropy using S-net seafloor seismometers. Nat. Commun. 2020, 11, 5676. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, M.; Uehira, K.; Kanazawa, T.; Kunugi, T.; Shiomi, K.; Aoi, S.; Matsumoto, T.; Takahashi, N.; Chikasada, N.; Nakamura, T.; et al. S-Net project: Performance of a Large-Scale Seafloor Observation Network for Preventing and Reducing Seismic and Tsunami Disasters. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Aoi, S.; Youichi, A.; Takashi, K.; Takeshi, K.; Kenji, U.; Narumi, T.; Hideki, U.; Katsuhiko, S.; Takumi, M.; Hiroyuki, F. MOWLAS: NIED observation network for earthquake, tsunami and volcano. Earth Planets Space 2020, 72, 126. [Google Scholar] [CrossRef]
- Gainov, V.; Gurkin, N.; Lukinih, S.; Makovejs, S.; Akopov, S.; Ten, S.; Nanii, O.; Treshchikov, V.; Sleptsov, M. Record 500 km Unrepeatered 1 Tbit/s (10 × 100G) Transmission Over an Ultra-Low Loss Fiber. Opt. Express 2014, 22, 22308–22313. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Borel, P.I.; Geisler, T.; Jensen, R.; Leng, L.; Jiang, X.; Peckham, D.W.; Lingle, R.L.; Vaidya, D.; Yan, M.F.; et al. 800Gb/s (8 × 128Gb/s) Unrepeatered Transmission Over 515-km Large-Area Ultra-Low-Loss Fibre Using 2nd-Order Raman Pumping. Opt. Express 2016, 24, 25291–25297. [Google Scholar] [CrossRef]
- Etienne, S.; Bissessur, H.; Bastide, C.; Mongardien, D. Ultra-long 610 km unrepeatered transmission of 100 Gb/s using single fibre configuration. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015. Paper Th225. [Google Scholar]
- Huang, Y.K.; Ip, E.; Zhang, S.; Yaman, F.; Downie, J.D.; Wood, W.A.; Zakharian, A.; Hurley, J.; Mishra, S.; Aono, Y.; et al. 20.7-Tb/s repeater-less transmission over 401.1-km using QSM fiber and XPM compensation via transmitter-side DBP. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016. Paper PD14. [Google Scholar]
- Januario, J.C.; Rossi, S.M.; José, H.C.; Chiuchiarelli, A.; Souza, A.L.; Felipe, A.; Bordonalli, A.C.; Makovejs, S.; Mornatta, C.; Festa, A.; et al. Single-carrier 400G unrepeatered WDM transmission over 443.1 km. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. Paper M1F. [Google Scholar]
- Xu, J.; Sun, S.; Hu, Q.; Yu, J.; Liu, J.; Luo, Q.; Wang, W.; Huang, L.; Xiang, M.; Wu, J.; et al. Unrepeatered Transmission Over 670.64 km of 50G BPSK, 653.35 km of 100G PS-QPSK, 601.93 km of 200G 8QAM, and 502.13 km of 400G 64QAM. J. Light. Technol. 2019, 38, 522–530. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Hu, Q.; Zhou, H.; Li, M.; Huang, L.; Zheng, F.; Li, W.; Deng, L.; Zhang, L.; et al. Longest-Ever Unrepeatered Transmission Over 713.2km of 2.5 Gb/s with a Span Loss in Excess of 111dB. In Proceedings of the 2018 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR), Hong Kong, China, 29 July–3 August 2018. Paper Tu2I.5. [Google Scholar]
- Huang, Y.K.; Ip, E.; Aono, Y.; Tajima, T.; Zhang, S.; Yaman, F.; Inada, Y.; Downie, J.D.; Wood, W.; Zakharian, A.; et al. Real-time 8 × 200-Gb/s 16-QAM unrepeatered transmission over 458.8 km using concatenated receiver-side ROPAs. In Proceedings of the Optical Fiber Communication Conference 2017, Los Angeles, CA, USA, 19–23 March 2017. Paper Th2A59. [Google Scholar]
- Bissessur, H.; Bastide, C.; Etienne, S.; Dupont, S. 24 Tb/s Unrepeatered C-Band Transmission of Real-Time Processed 200 Gb/s PDM 16-QAM Over 349 km. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017. Paper Th4D2. [Google Scholar]
- Xia, T.J.; Wellbrock, G.A.; Huang, M.F.; Zhang, S.; Huang, Y.K.; Chang, D.I.; Burtsev, S.; Pelouch, W.; Zak, E.; de Pedro, H.; et al. Transmission of 400G PM-16QAM channels over long-haul distance with commercial all-distributed Raman amplification system and aged standard SMF in field. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014. Paper Tu2B1. [Google Scholar]
- DONET. Available online: https://www.seafloor.bosai.go.jp/DONET/ (accessed on 30 November 2024).
- Nakano, M.; Nakamura, T.; Kamiya, S.; Ohori, M.; Kaneda, Y. Intensive seismic activity around the Nankai trough revealed by DONET ocean-floor seismic observations. Earth Planet Space 2013, 65, 5–15. [Google Scholar] [CrossRef]
- DONET2. Available online: https://ja.dbpedia.org/page/DONET2 (accessed on 30 November 2024).
- Kawaguchi, K.; Araki, E.; Kogure, Y.; Takahashi, N.; Katayama, T.; Hishiki, K.; Fujiwara, N.; Iida, N.; Kaneda, Y. Development of DONET2-off Kii channel observatory network. In Proceedings of the 2013 IEEE International Under-water Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Yokobiki, T.; Choi, J.-K.; Nishida, S.; Matsumoto, H.; Araki, E.; Kawaguchi, K.; Takahashi, N.; Kodaira, S. Construction of DONET2. In Proceedings of the 2016 Techno-Ocean (Techno-Ocean), Kobe, Japan, 6–8 October 2016; pp. 435–438. [Google Scholar] [CrossRef]
- Smith, L.M.; Barth, J.A.; Kelley, D.S.; Plueddemann, A.; Rodero, I.; Ulses, G.A.; Vardaro, M.F.; Weller, R. The Ocean Observatories Initiative. Oceanography 2018, 31, 16–35. [Google Scholar] [CrossRef]
- Trowbridge, J.; Weller, R.; Kelley, D.; Dever, E.; Plueddemann, A.; Barth, J.A.; Orest, K. The Ocean Observatories Initiative. Front. Mar. Sci. 2019, 6, 74. [Google Scholar] [CrossRef]
- Cowles, T.; Delaney, J.; Orcutt, J.; Weller, R. The Ocean Observatories Initiative: Sustained Ocean Observing Across a Range of Spatial Scales. Mar. Technol. Soc. J. 2010, 44, 54–64. [Google Scholar] [CrossRef]
- Hansen, P.B.; Eskildsen, L. Remote Amplification in Repeaterless Transmission Systems. Opt. Fiber Technol. 1997, 3, 221–237. [Google Scholar] [CrossRef]
- Li, S.; Long, H.; Huang, L.; Huang, C.; Wu, J.; Liang, Y.; Duan, M.; Chen, F.; Wang, W. Unrepeatered transmission of single-carrier 800 Gb/s over 447.96 km with simplified third-order ROPA system. J. Phys. Conf. Ser. 2024, 2087, 012016. [Google Scholar] [CrossRef]
- Bissessur, H.; Bastide, C.; Dubost, S.; Calsat, A.; Hedaraly, F.; Plantady, P. Unrepeatered Transmission of 29.2 Tb/s over 295 km with Probabilistically Shaped 64 QAM. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018. [Google Scholar] [CrossRef]
- Chang, D.; Perrier, P.; Fevrier, H.; Xia, T.; Peterson, D.L.; Wellbrock, G.A.; Ten, S.; Towery, C.; Mills, G. Unrepeatered 100G Transmission Over 520.6 km of G.652 Fiber and 556.7 km of G.654 Fiber With Commercial Raman DWDM System and Enhanced ROPA. J. Light. Technol. 2015, 33, 631–638. [Google Scholar] [CrossRef]
- Zang, K.; Yu, C.X.; Xin, X.J.; Yuan, J.H.; Xie, W.J.; Wang, Y.C. Optimization on bandwidth in the third-order pumped distributed fiber Raman amplifier. Opt. Eng. 2013, 52, 076112. [Google Scholar] [CrossRef]
- Chang, D.-I.; Zak, E.; Pelouch, W.; Perrier, P.; Fevrier, H.; Deng, L.; Li, B.; Makovejs, S.; Hao, C.; Xu, J.; et al. 100G unrepeatered transmission over 626.8 km with a span loss in excess of 100 dB. In Proceedings of the Asia Communications and Photonics Conference (ACP) 2015, Hong Kong, China, 19 November–23 November 2015. Paper AM4A.2. [Google Scholar]
- Xiong, H.; Shan, Y.Y.; Sun, J.Q. Location optimization of remote gain unit in ultralong span repeaterless optical transmission system. Opt. Eng. 2017, 56, 1–4. [Google Scholar] [CrossRef]
- Soriano Sampaio Januario, J.C.; Chiuchiarelli, A.; Rossi, S.M.; Cruz, J.H., Jr.; Dias Reis, J.; Mornatta, C.; Festa, A.; Chrestani Bordonalli, A. System Design for High-capacity Unrepeatered Optical Transmission. J. Light. Technol. 2019, 37, 1246–1253. [Google Scholar] [CrossRef]
- Gainov, V.; Gurkin, N.; Lukinykh, S.; Nanii, O.; Treshchikov, V. Ultralong single-span lines with remote pumping of optical amplifiers. Tech. Phys. 2015, 60, 561–567. [Google Scholar] [CrossRef]
- Xu, J.; Fu, C.; Bu, Q.; Yu, C.; Jiang, Y.; Huang, L. Research on Remote Gain Unit of Ultra-Long Span Unrepeatered Optical Transmission System. Laser Optoelectron. Prog. 2012, 10, 102–107. [Google Scholar] [CrossRef]
- Agrawal, P.G. Optical Amplifers. In Fiber-Optic Communication Systems, 3rd ed.; Wiley: New York, NY, USA, 2002; pp. 226–273. ISBN 0-471-22114-7. [Google Scholar]
- Zibar, D.; Rosa Brusin, A.M.; De Moura, U.C.; Da Ros, F.; Curri, V.; Carena, A. Inverse System Design Using Machine Learning: The Raman Amplifier Case. J. Light. Technol. 2020, 38, 736–753. [Google Scholar] [CrossRef]
- Pelouch, W.S. Raman amplification: An enabling technology for long-haul coherent transmission systems. J. Light. Technol. 2016, 34, 6–19. [Google Scholar] [CrossRef]
- Singh, S.; Kaler, R.S. Performance optimization of EDFA–Raman hybrid optical amplifier using genetic algorithm. Opt. Laser Technol. 2015, 68, 89–95. [Google Scholar] [CrossRef]
- Singh, S.; Kaler, R.S. Optimizing the net gain of a raman-EDFA hybrid optical amplifier using a genetic algorithm. J. Opt. Soc. Korea 2014, 18, 442–448. [Google Scholar] [CrossRef]
- Mowla, A.; Granpayeh, N. Optimum design of a hybrid erbium-doped fiber amplifier/fiber Raman amplifier using particle swarm optimization. Appl. Opt. 2009, 48, 979–984. [Google Scholar] [CrossRef]
- Cai, J.-X.; Sun, Y.; Zhang, H.; Batshon, H.G.; Mazurczyk, M.V.; Sinkin, O.V.; Foursa, D.G.; Pilipetskii, A. 49.3 Tb/s transmission over 9100 km using C+L EDFA and 54 Tb/s transmission over 9150 km using hybrid-Raman EDFA. J. Light. Technol. 2015, 33, 724–2734. [Google Scholar] [CrossRef]
- Yuan, J.-G.; Liang, T.-Y.; Wang, W.; Gu, S. Impact analysis on performance optimization of the hybrid amplifier (RA + EDFA). J. Light Electron Opt. 2011, 122, 1565–1568. [Google Scholar] [CrossRef]
- HMN Technologies Co., Ltd. High Fiber Count Solution. Available online: https://www.hmntech.com/enjsrdB.jhtml (accessed on 30 April 2025).







| Fiber Type | G.654E |
| Attenuation | 0.1534 dB/km (including welding loss) |
| Chromatic Dispersion | 21.187 ps/(nm·km) |
| Dispersion Slope | 0.059 ps/(nm2·km) |
| Effective Area | 130 μm2 |
| PMD | 0.035 ps/km |
| Effective Group Index of Refraction | 1.4658 |
| TN51RPC | TN51ROP | TN97ERPC | TN97RPC | TN51HBA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Wavelength | Power | Wavelength | Power | Wavelength | Power | Wavelength | Power | Wavelength | Power |
| 1427–1457 nm | 18–28 dBm | 1476–1487 nm | 18–26.5 dBm | 1275 nm | 30–38.5 dBm | 1427–1457 nm | 18–28 dBm | 980 nm | 8–27 dBm |
| Repeatered | Unrepeatered | |
|---|---|---|
| Coverage | Very large (almost unlimited) | Relatively small (<690 km) |
| Number of fibers | Limited (≤16 fiber pairs) [43] | No less than 48 fiber pairs |
| Reliability | Relatively high (affected by repeaters) | Very high |
| Power supply mode | Mainly constant current | Both constant current and constant voltage |
| Cost | High | Low |
| Maintenance | Difficult | Relatively easy |
| Difficulty of construction | High | Low |
| Scalability | Relatively difficult | Relatively easy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, C.; Lyu, F.; Xu, R.; Li, J.; Wang, X.; Xu, L. Optimization of Unrepeatered Optical Communication Systems and the Applications in Cabled Ocean Observatories. Photonics 2025, 12, 930. https://doi.org/10.3390/photonics12090930
Shu C, Lyu F, Xu R, Li J, Wang X, Xu L. Optimization of Unrepeatered Optical Communication Systems and the Applications in Cabled Ocean Observatories. Photonics. 2025; 12(9):930. https://doi.org/10.3390/photonics12090930
Chicago/Turabian StyleShu, Chang, Feng Lyu, Rendong Xu, Jianping Li, Xichen Wang, and Liang Xu. 2025. "Optimization of Unrepeatered Optical Communication Systems and the Applications in Cabled Ocean Observatories" Photonics 12, no. 9: 930. https://doi.org/10.3390/photonics12090930
APA StyleShu, C., Lyu, F., Xu, R., Li, J., Wang, X., & Xu, L. (2025). Optimization of Unrepeatered Optical Communication Systems and the Applications in Cabled Ocean Observatories. Photonics, 12(9), 930. https://doi.org/10.3390/photonics12090930






