Cascaded Cavitation Bubble Excited by a Train of Microsecond Laser Pulses
Abstract
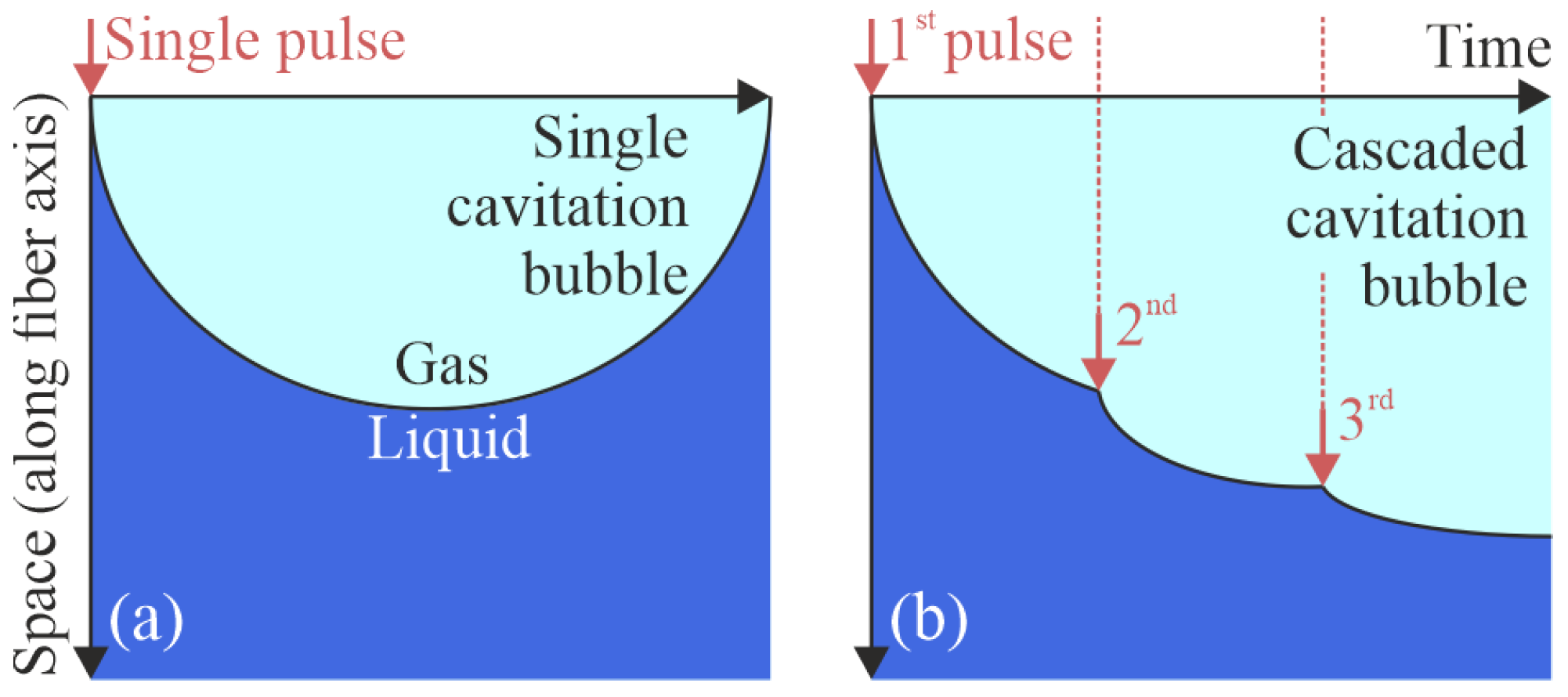
1. Introduction
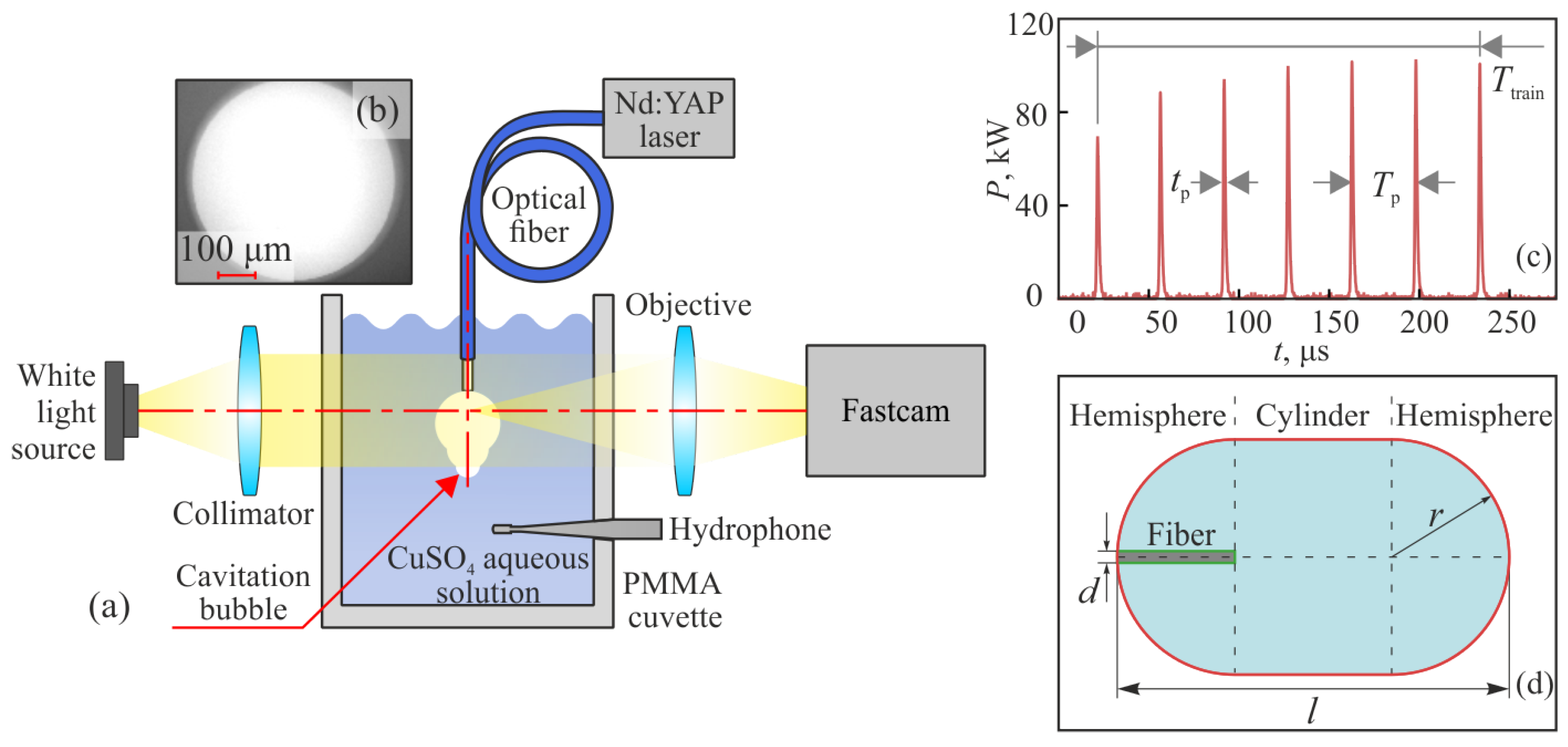
2. Materials and Methods
2.1. Experimental Setup
2.2. Sample Preparation
2.3. Numerical Simulations
2.4. Estimation of the Effective Radius of Cavitation Bubble
3. Results
3.1. Imaging of the Cavitation Process
3.2. Comparison of Numerical and Experimental Data
3.3. Acoustic Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391–399. [Google Scholar] [CrossRef]
- Lauterborn, W. Optische Kavitation. Phys. Bl. 1976, 32, 553–563. [Google Scholar] [CrossRef]
- Liang, X.X.; Linz, N.; Freidank, S.; Paltauf, G.; Vogel, A. Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation. J. Fluid Mech. 2022, 940, A5. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 1986, 169, 535–564. [Google Scholar] [CrossRef]
- Vogel, A.; Lauterborn, W.; Timm, R. Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 1989, 206, 299–338. [Google Scholar] [CrossRef]
- Lechner, C.; Lauterborn, W.; Koch, M.; Mettin, R. Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study. Phys. Rev. Fluids 2019, 4, 021601. [Google Scholar] [CrossRef]
- Rosselló, J.M.; Reese, H.; Ohl, C.D. Dynamics of pulsed laser-induced cavities on a liquid–gas interface: From a conical splash to a ‘bullet’ jet. J. Fluid Mech. 2022, 939, A35. [Google Scholar] [CrossRef]
- Ohl, S.W.; Reese, H.; Ohl, C.D. Cavitation bubble collapse near a rigid wall with an oil layer. Int. J. Multiph. Flow 2024, 174, 104761. [Google Scholar] [CrossRef]
- Lin, C.; Kelly, M. Cavitation and acoustic emission around laser-heated microparticles. Appl. Phys. Lett. 1998, 72, 2800–2802. [Google Scholar] [CrossRef]
- Long, J.; Eliceiri, M.; Vangelatos, Z.; Rho, Y.; Wang, L.; Su, Z.; Xie, X.; Zhang, Y.; Grigoropoulos, C. Early dynamics of cavitation bubbles generated during ns laser ablation of submerged targets. Opt. Express 2020, 28, 14300–14309. [Google Scholar] [CrossRef] [PubMed]
- Sieber, A.; Preso, D.; Farhat, M. Cavitation bubble dynamics and microjet atomization near tissue-mimicking materials. Phys. Fluids 2023, 35, 027101. [Google Scholar] [CrossRef]
- Cristoforetti, G.; Tiberi, M.; Simonelli, A.; Marsili, P.; Giammanco, F. Toward the optimization of double-pulse LIBS underwater: Effects of experimental parameters on the reproducibility and dynamics of laser-induced cavitation bubble. Appl. Opt. 2012, 51, B30–B41. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xu, R.Q.; Chen, J.P.; Shen, Z.H.; Jian, L.; Ni, X.W. Shock-wave propagation and cavitation bubble oscillation by Nd:YAG laser ablation of a metal in water. Appl. Opt. 2004, 43, 3251–3257. [Google Scholar] [CrossRef] [PubMed]
- Robles, V.; Gutierrez-Herrera, E.; Devia-Cruz, L.; Banks, D.; Camacho-Lopez, S.; Aguilar, G. Soft material perforation via double-bubble laser-induced cavitation microjets. Phys. Fluids 2020, 32, 042005. [Google Scholar] [CrossRef]
- Soyama, H.; Iga, Y. Laser Cavitation Peening: A Review. Appl. Sci. 2023, 13, 6702. [Google Scholar] [CrossRef]
- Streubel, R.; Barcikowski, S.; Gokce, B. Continuous multigram nanoparticle synthesis by high-power, high-repetition-rate ultrafast laser ablation in liquids. Opt. Lett. 2016, 41, 1486–1489. [Google Scholar] [CrossRef]
- Nagalingam, N.; Raghunathan, A.; Korede, V.; Poelma, C.; Smith, C.; Hartkamp, R.; Padding, J.; Eral, H. Laser-Induced Cavitation for Controlling Crystallization from Solution. Phys. Rev. Lett. 2023, 131, 124001. [Google Scholar] [CrossRef]
- Schoppink, J.; Fernandez Rivas, D. Jet injectors: Perspectives for small volume delivery with lasers. Adv. Drug Deliv. Rev. 2022, 182, 114109. [Google Scholar] [CrossRef]
- Zwaan, E.; Le Gac, S.; Tsuji, K.; Ohl, C.D. Controlled Cavitation in Microfluidic Systems. Phys. Rev. Lett. 2007, 98, 254501. [Google Scholar] [CrossRef]
- Yuan, F.; Sankin, G.; Zhong, P. Dynamics of tandem bubble interaction in a microfluidic channel. J. Acoust. Soc. Am. 2011, 130, 3339–3346. [Google Scholar] [CrossRef]
- Prentice, P.; Cuschieri, A.; Dholakia, K.; Prausnitz, M.; Campbell, P. Membrane disruption by optically controlled microbubble cavitation. Nat. Phys. 2005, 1, 107–110. [Google Scholar] [CrossRef]
- Dijkink, R.; Le Gac, S.; Nijhuis, E.; van den Berg, A.; Vermes, I.; Poot, A.; Ohl, C.D. Controlled cavitation–cell interaction: Trans-membrane transport and viability studies. Phys. Med. Biol. 2007, 53, 375–390. [Google Scholar] [CrossRef]
- Sankin, G.N.; Yuan, F.; Zhong, P. Pulsating Tandem Microbubble for Localized and Directional Single-Cell Membrane Poration. Phys. Rev. Lett. 2010, 105, 078101. [Google Scholar] [CrossRef]
- Rooney, J. Hemolysis Near an Ultrasonically Pulsating Gas Bubble. Science 1970, 169, 869–871. [Google Scholar] [CrossRef] [PubMed]
- Everbach, E.; Francis, C. Cavitational mechanisms in ultrasound-accelerated thrombolysis at 1 MHz. Ultrasound Med. Biol. 2000, 26, 1153–1160. [Google Scholar] [CrossRef] [PubMed]
- Marmottant, P.; Hilgenfeldt, S. Controlled vesicle deformation and lysis by single oscillating bubbles. Nature 2003, 423, 153–156. [Google Scholar] [CrossRef]
- Vogel, A.; Venugopalan, V. Mechanisms of Pulsed Laser Ablation of Biological Tissues. Chem. Rev. 2003, 103, 577–644. [Google Scholar] [CrossRef]
- Vogel, A.; Hentschel, W.; Holzfuss, J.; Lauterborn, W. Cavitation Bubble Dynamics and Acoustic Transient Generation in Ocular Surgery with Pulsed Neodymium:YAG Lasers. Ophthalmology 1986, 93, 1259–1269. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J. High-intensity focused ultrasound in the treatment of solid tumours. Nat. Rev. Cancer 2005, 5, 321–327. [Google Scholar] [CrossRef]
- Ho, D.; Scialabba, D.; Terry, R.; Ma, X.; Chen, J.; Sankin, G.; Xiang, G.; Qi, R.; Preminger, G.; Lipkin, M.; et al. The Role of Cavitation in Energy Delivery and Stone Damage During Laser Lithotripsy. J. Endourol. 2021, 35, 860–870. [Google Scholar] [CrossRef]
- Chen, J.; Ho, D.; Xiang, G.; Sankin, G.; Preminger, G.; Lipkin, M.; Zhong, P. Cavitation Plays a Vital Role in Stone Dusting During Short Pulse Holmium:YAG Laser Lithotripsy. J. Endourol. 2022, 36, 674–683. [Google Scholar] [CrossRef]
- Rastopov, S.; Sukhodol’sky, A. Cluster nucleation in the process of CW laser induced thermocavitation. Phys. Lett. A 1990, 149, 229–232. [Google Scholar] [CrossRef]
- Ramirez-San-Juan, J.; Rodriguez-Aboytes, E.; Martinez-Canton, A.; Baldovino-Pantaleon, O.; Robledo-Martinez, A.; Korneev, N.; Ramos-Garcia, R. Time-resolved analysis of cavitation induced by CW lasers in absorbing liquids. Opt. Express 2010, 18, 8735–8742. [Google Scholar] [CrossRef] [PubMed]
- Padilla-Martinez, J.; Berrospe-Rodriguez, C.; Aguilar, G.; Ramirez-San-Juan, J.; Ramos-Garcia, R. Optic cavitation with CW lasers: A review. Phys. Fluids 2014, 26, 122007. [Google Scholar] [CrossRef]
- Pecha, R.; Gompf, B. Microimplosions: Cavitation Collapse and Shock Wave Emission on a Nanosecond Time Scale. Phys. Rev. Lett. 2000, 84, 1328–1330. [Google Scholar] [CrossRef] [PubMed]
- Sankin, G.; Simmons, W.; Zhu, S.; Zhong, P. Shock Wave Interaction with Laser-Generated Single Bubbles. Phys. Rev. Lett. 2005, 95, 034501. [Google Scholar] [CrossRef] [PubMed]
- Sankin, G.; Zhong, P. Interaction between shock wave and single inertial bubbles near an elastic boundary. Phys. Rev. E 2006, 74, 046304. [Google Scholar] [CrossRef]
- Ju, H.; Roy, R.; Murray, T. Gold nanoparticle targeted photoacoustic cavitation for potential deep tissue imaging and therapy. Biomed. Opt. Express 2013, 4, 66–76. [Google Scholar] [CrossRef]
- Wei, C.w.; Xia, J.; Lombardo, M.; Perez, C.; Arnal, B.; Larson-Smith, K.; Pelivanov, I.; Matula, T.; Pozzo, L.; O’Donnell, M. Laser-induced cavitation in nanoemulsion with gold nanospheres for blood clot disruption: In vitro results. Opt. Lett. 2014, 39, 2599–2602. [Google Scholar] [CrossRef]
- Kim, H.; Kang, J.; Chang, J. Thermal therapeutic method for selective treatment of deep-lying tissue by combining laser and high-intensity focused ultrasound energy. Opt. Lett. 2014, 39, 2806–2809. [Google Scholar] [CrossRef]
- Tiwari, A.; Pantano, C.; Freund, J. Growth-and-collapse dynamics of small bubble clusters near a wall. J. Fluid Mech. 2015, 775, 1–23. [Google Scholar] [CrossRef]
- Bempedelis, N.; Ventikos, Y. Energy focusing in shock-collapsed bubble arrays. J. Fluid Mech. 2020, 900, A44. [Google Scholar] [CrossRef]
- Quinto-Su, P.A.; Venugopalan, V.; Ohl, C.D. Generation of laser-induced cavitation bubbles with a digital hologram. Opt. Express 2008, 16, 18964–18969. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Köhler, K.; Jungnickel, K.; Mettin, R.; Lauterborn, W.; Vogel, A. Dynamics of laser-induced bubble pairs. J. Fluid Mech. 2015, 771, 706–742. [Google Scholar] [CrossRef]
- Tomita, Y.; Sato, K. Pulsed jets driven by two interacting cavitation bubbles produced at different times. J. Fluid Mech. 2017, 819, 465–493. [Google Scholar] [CrossRef]
- Luo, J.; Niu, Z. Jet and Shock Wave from Collapse of Two Cavitation Bubbles. Sci. Rep. 2019, 9, 1352. [Google Scholar] [CrossRef]
- Fan, Y.; Bußmann, A.; Reuter, F.; Bao, H.; Adami, S.; Gordillo, J.; Adams, N.; Ohl, C.D. Amplification of Supersonic Microjets by Resonant Inertial Cavitation-Bubble Pair. Phys. Rev. Lett. 2024, 132, 104004. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Arba Mosquera, S. A Refined Model for Ablation Through Cavitation Bubbles with Ultrashort Pulse Lasers. Photonics 2024, 11, 1047. [Google Scholar] [CrossRef]
- Wang, D.; Bi, Y. Investigation of the influence of different liquid temperatures on the dynamics of long-pulse laser-induced cavitation bubbles. AIP Adv. 2024, 14, 025013. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, W.; Wang, K. Simulating laser-fluid coupling and laser-induced cavitation using embedded boundary and level set methods. J. Comput. Phys. 2023, 472, 111656. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, W.; Chen, J.; Xiang, G.; Zhong, P.; Wang, K. Vapour bubbles produced by long-pulsed laser: A race between advection and phase transition. J. Fluid Mech. 2024, 999, A103. [Google Scholar] [CrossRef]
- Wang, D.; Yang, F.; Gao, W.; Bi, Y.; Zhu, X.; Lin, Z. Exploratory study on the application of laser-induced cavitation bubble in the treatment of fallopian tube obstruction. PLoS ONE 2025, 20, e0317022. [Google Scholar] [CrossRef]
- Lim, K.Y.; Quinto-Su, P.A.; Klaseboer, E.; Khoo, B.C.; Venugopalan, V.; Ohl, C.D. Nonspherical laser-induced cavitation bubbles. Phys. Rev. E 2010, 81, 016308. [Google Scholar] [CrossRef]
- Vogel, A.; Noack, J.; Nahen, K.; Theisen, D.; Busch, S.; Parlitz, U.; Hammer, D.; Noojin, G.; Rockwell, B.; Birngruber, R. Energy balance of optical breakdown in water at nanosecond to femtosecond time scales. Appl. Phys. B 1999, 68, 271–280. [Google Scholar] [CrossRef]
- Li, M.; Huang, Z.; Yang, X. Collapsing dynamics and microjet formation of laser-induced cavitation bubble near corrugated solid wall. Appl. Phys. A 2025, 131, 242. [Google Scholar] [CrossRef]
- Park, S.H.; Phan, T.H.; Park, W.G. Numerical investigation of laser-induced cavitation bubble dynamics near a rigid surface based on three-dimensional fully compressible model. Int. J. Heat Mass Transf. 2022, 191, 122853. [Google Scholar] [CrossRef]
- Zhou, R.; Li, K.; Cao, Y.; Shi, W.; Yang, Y.; Tan, L.; Hu, R.; Jin, Y. Experimental Study of Laser-Induced Cavitation Bubbles near Wall: Plasma Shielding Observation. Water 2024, 16, 1324. [Google Scholar] [CrossRef]
- Fu, L.; Wang, J.; Wang, S.; Zhang, Z.; Vogel, A.; Liang, X.; Yao, C. Secondary cavitation bubble dynamics during laser-induced bubble formation in a small container. Opt. Express 2024, 32, 9747–9766. [Google Scholar] [CrossRef]
- Nagalingam, N.; Korede, V.; Irimia, D.; Westerweel, J.; Padding, J.T.; Hartkamp, R.; Eral, H.B. Unified framework for laser-induced transient bubble dynamics within microchannels. Sci. Rep. 2024, 14, 18763. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Liang, X.X.; Wang, S.; Wang, S.; Wang, P.; Zhang, Z.; Wang, J.; Vogel, A.; Yao, C. Laser induced spherical bubble dynamics in partially confined geometry with acoustic feedback from container walls. Ultrason. Sonochem. 2023, 101, 106664. [Google Scholar] [CrossRef] [PubMed]
- Soyama, H. Development of Laser Cavitation Peening Using a Normal-Oscillation Nd:YAG Laser. Coatings 2023, 13, 1395. [Google Scholar] [CrossRef]
- Soyama, H.; Kuji, C. Improving effects of cavitation peening, using a pulsed laser or a cavitating jet, and shot peening on the fatigue properties of additively manufactured titanium alloy Ti6Al4V. Surf. Coat. Technol. 2022, 451, 129047. [Google Scholar] [CrossRef]
- Fonseca, M.B.; An, L.; Cox, B.T. Sulfates as chromophores for multiwavelength photoacoustic imaging phantoms. J. Biomed. Opt. 2017, 22, 125007. [Google Scholar] [CrossRef]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V. Measuring optical properties of human liver between 400 and 1000 nm. Quantum Electron. 2019, 49, 13. [Google Scholar] [CrossRef]
- Gonçalves, T.M.; Martins, I.S.; Silva, H.F.; Tuchin, V.V.; Oliveira, L.M. Spectral Optical Properties of Rabbit Brain Cortex between 200 and 1000 nm. Photochem 2021, 1, 190–208. [Google Scholar] [CrossRef]
- Wei, H.; Xing, D.; He, B.; Gu, H.; Wu, G.; Chen, X. Using an oblique incident laser beam to measure the optical properties of stomach mucosa/submucosa tissue. BMC Gastroenterol. 2009, 9, 64. [Google Scholar] [CrossRef]
- OpenCFD Ltd. OpenFOAM User Guide; OpenCFD Ltd.: Reading, UK, 2024. [Google Scholar]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Bußmann, A.; Riahi, F.; Gökce, B.; Adami, S.; Barcikowski, S.; Adams, N.A. Investigation of cavitation bubble dynamics near a solid wall by high-resolution numerical simulation. Phys. Fluids 2023, 35, 016115. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; Denner, F.; Ohl, C.D. The acoustic pressure generated by the cavitation bubble expansion and collapse near a rigid wall. Phys. Fluids 2021, 33, 032118. [Google Scholar] [CrossRef]
- Olmes, A.; Lohmann, S.; Lubatschowski, H.; Ertmer, W. An improved method of measuring laser induced pressure transients. Appl. Phys. B 1997, 64, 677–682. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudasheva, N.A.; Kryuchkov, N.P.; Zotov, A.K.; Aleksandrova, P.V.; Pokhodyaev, O.I.; Feklisova, K.A.; Suchkov, Y.A.; Bondarenko, A.L.; Simkin, I.V.; Samsonov, V.A.; et al. Cascaded Cavitation Bubble Excited by a Train of Microsecond Laser Pulses. Photonics 2025, 12, 927. https://doi.org/10.3390/photonics12090927
Kudasheva NA, Kryuchkov NP, Zotov AK, Aleksandrova PV, Pokhodyaev OI, Feklisova KA, Suchkov YA, Bondarenko AL, Simkin IV, Samsonov VA, et al. Cascaded Cavitation Bubble Excited by a Train of Microsecond Laser Pulses. Photonics. 2025; 12(9):927. https://doi.org/10.3390/photonics12090927
Chicago/Turabian StyleKudasheva, Nadezhda A., Nikita P. Kryuchkov, Arsen K. Zotov, Polina V. Aleksandrova, Oleg I. Pokhodyaev, Kseniya A. Feklisova, Yurii A. Suchkov, Anatoly L. Bondarenko, Ivan V. Simkin, Vladislav A. Samsonov, and et al. 2025. "Cascaded Cavitation Bubble Excited by a Train of Microsecond Laser Pulses" Photonics 12, no. 9: 927. https://doi.org/10.3390/photonics12090927
APA StyleKudasheva, N. A., Kryuchkov, N. P., Zotov, A. K., Aleksandrova, P. V., Pokhodyaev, O. I., Feklisova, K. A., Suchkov, Y. A., Bondarenko, A. L., Simkin, I. V., Samsonov, V. A., Ivakhnenko, S. G., Dolganova, I. N., Yurchenko, S. O., Garnov, S. V., Zaytsev, K. I., Kochiev, D. G., & Yakovlev, E. V. (2025). Cascaded Cavitation Bubble Excited by a Train of Microsecond Laser Pulses. Photonics, 12(9), 927. https://doi.org/10.3390/photonics12090927




