Design and Optimization of an FSO Network Under Practical Considerations
Abstract
1. Introduction
1.1. Related Work
1.1.1. FSO Communications
1.1.2. HAPS-Assisted FSO Communications
1.2. Contributions
- An unsupervised learning technique is adopted for clustering, in which k-means is applied to assign ground nodes to HAPs in a way that minimizes the total cost of network deployment. This method also drastically simplifies the clustering process complexity [22,23], offering a scalable and automated solution compared with manual or heuristic-based methods [24].
- The work builds on [1] by relaxing the assumption of identical hardware across all HAPs. Instead, each HAP is allowed to have a distinct configuration (e.g., transceivers, beam divergence angles), enabling improved overall network performance through adaptive design.
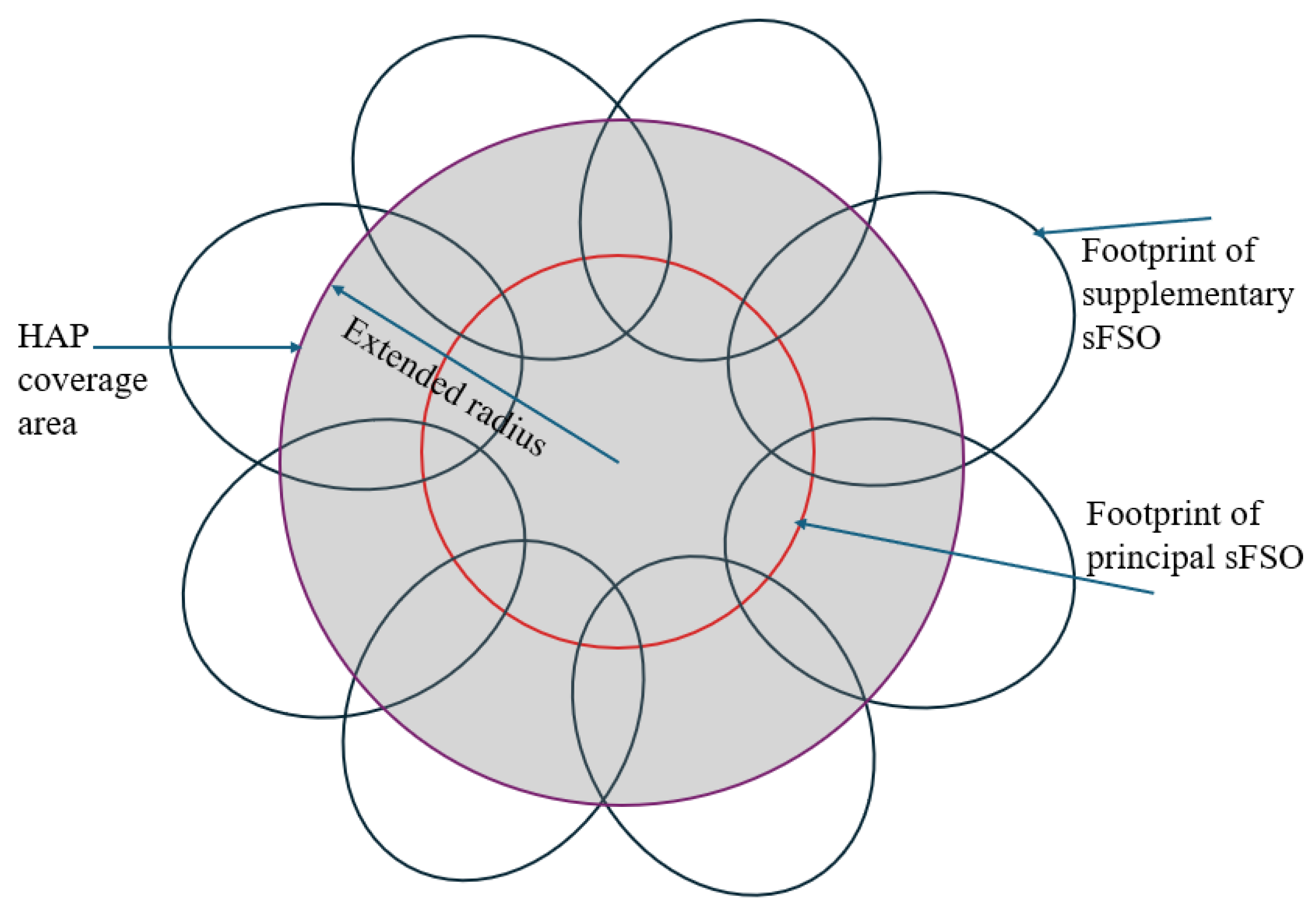
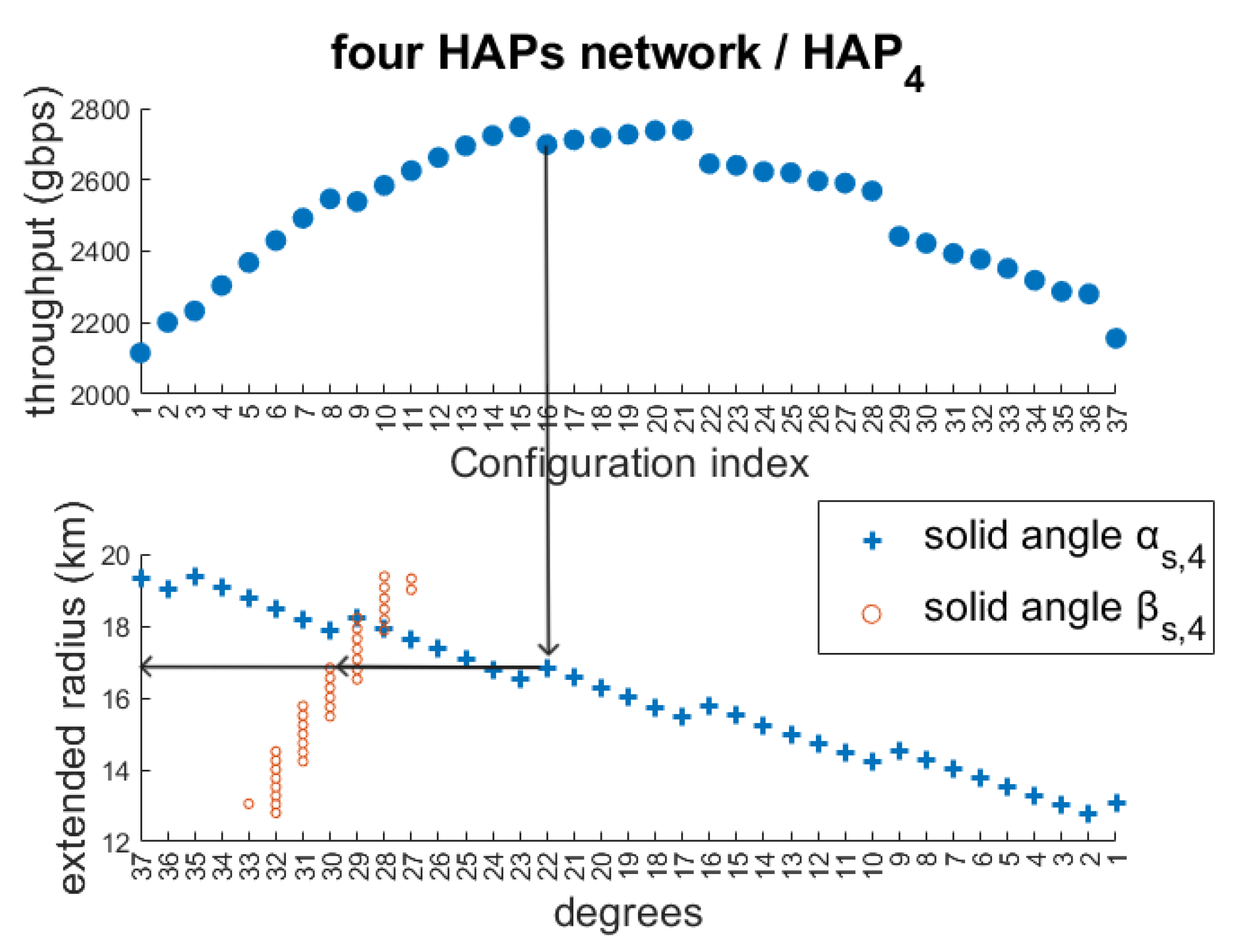
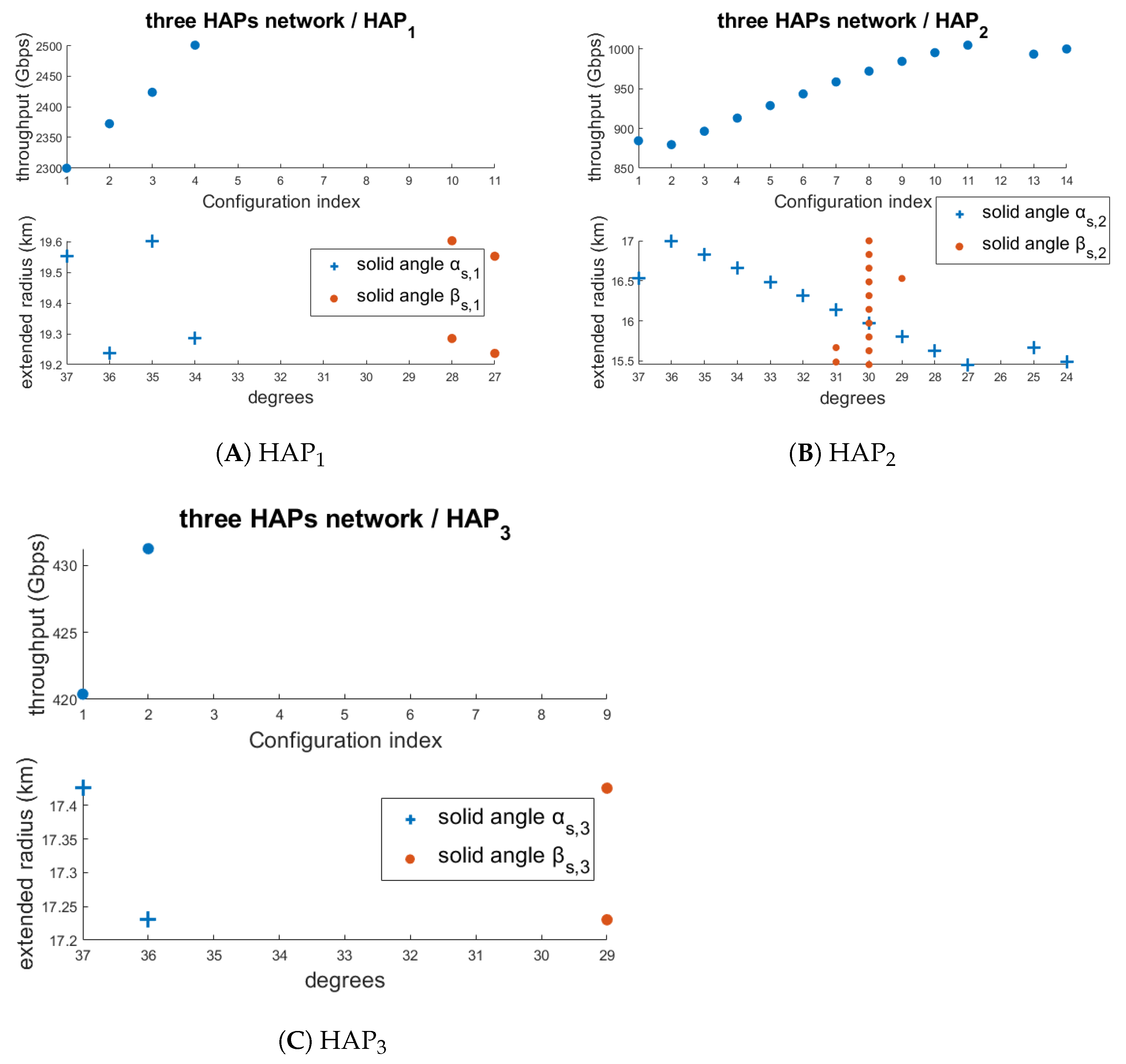
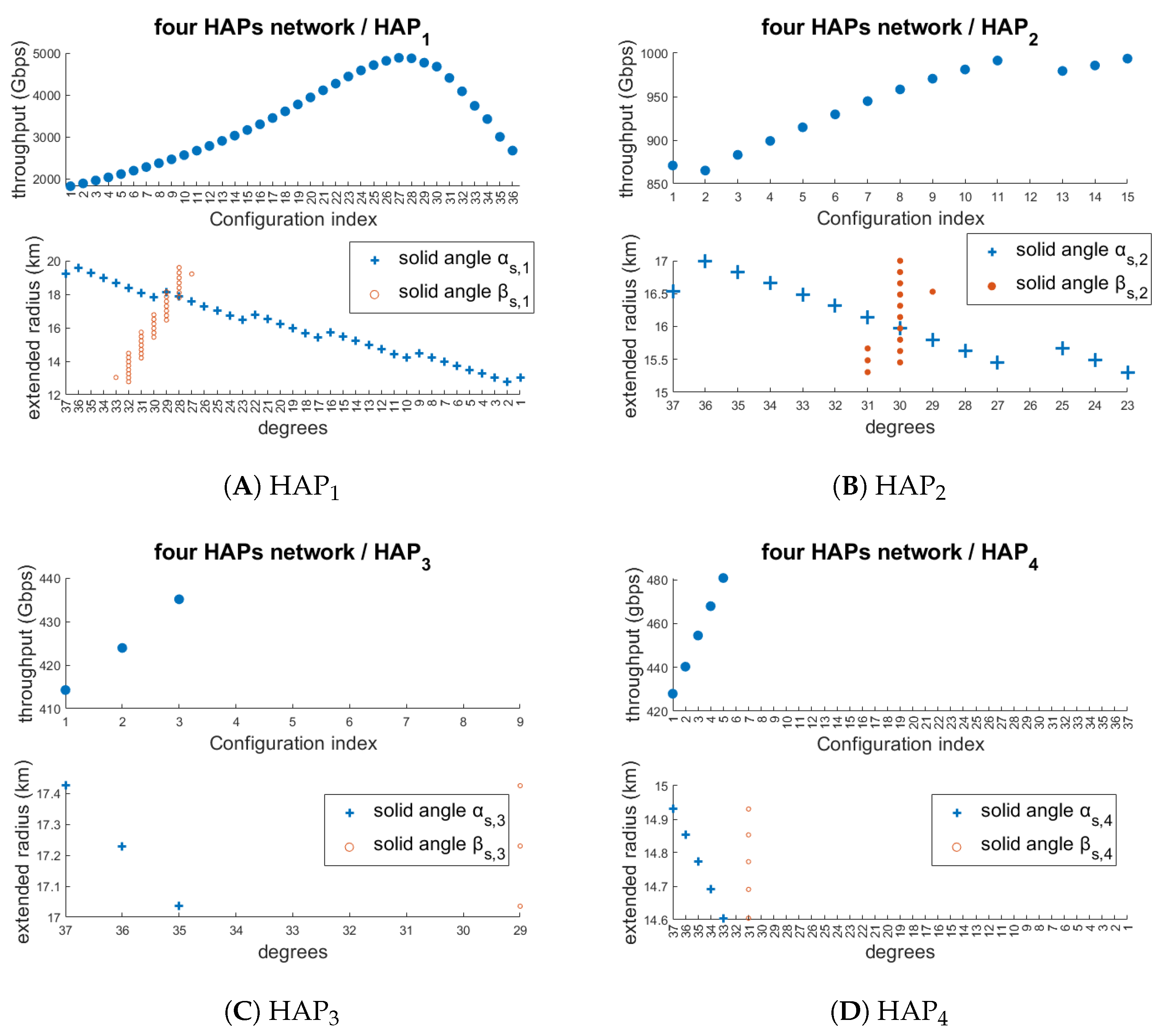
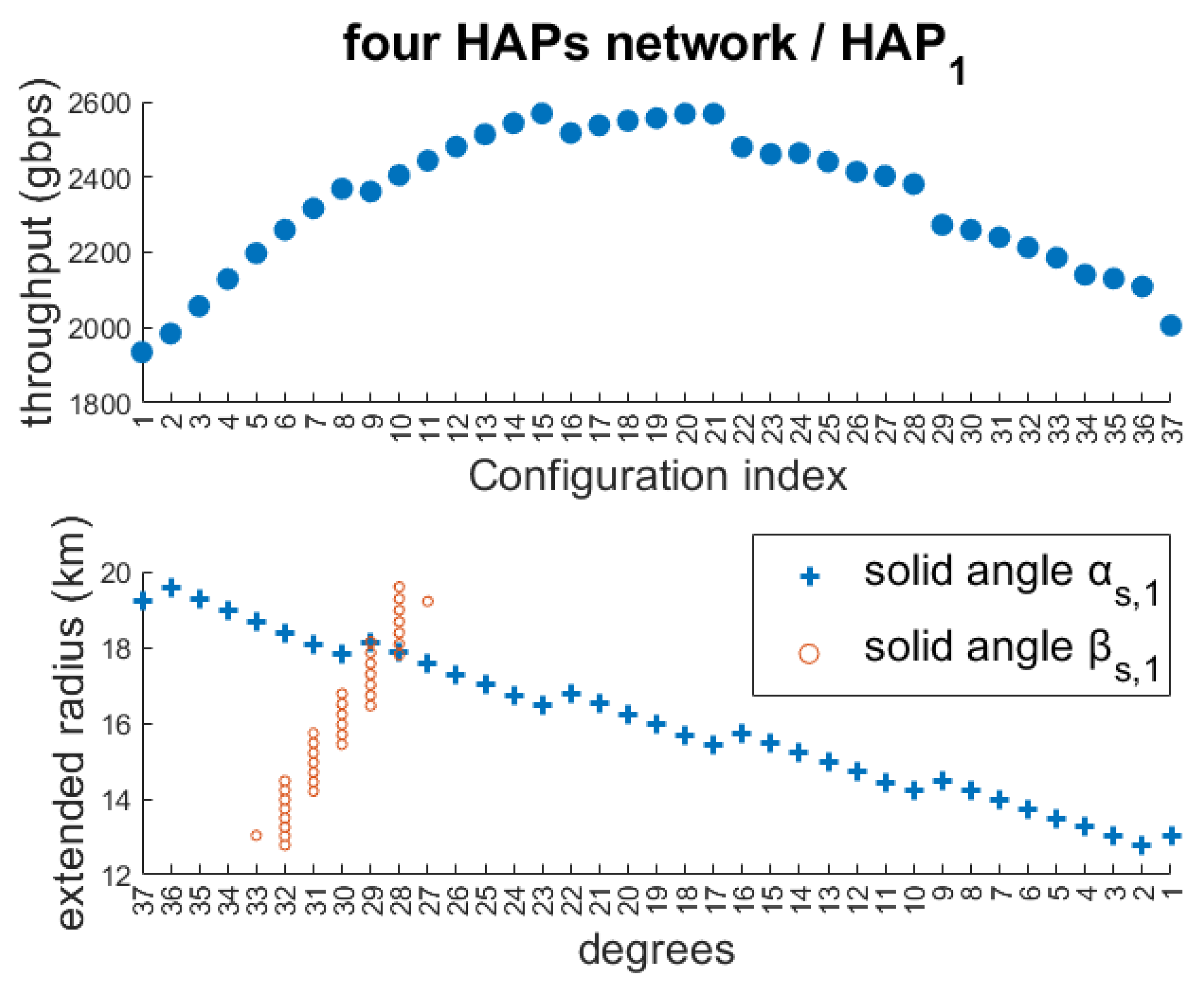
- A visual configuration tool is introduced in the form of a diagram that allows readers to extract all essential parameters of a single HAP—such as beam divergence angles, service radius, and cost contribution—by using only two vertical lines. This is an original and practical approach that helps network planners quickly interpret how configuration changes (e.g., widening a beam angle) affect the coverage and throughput.
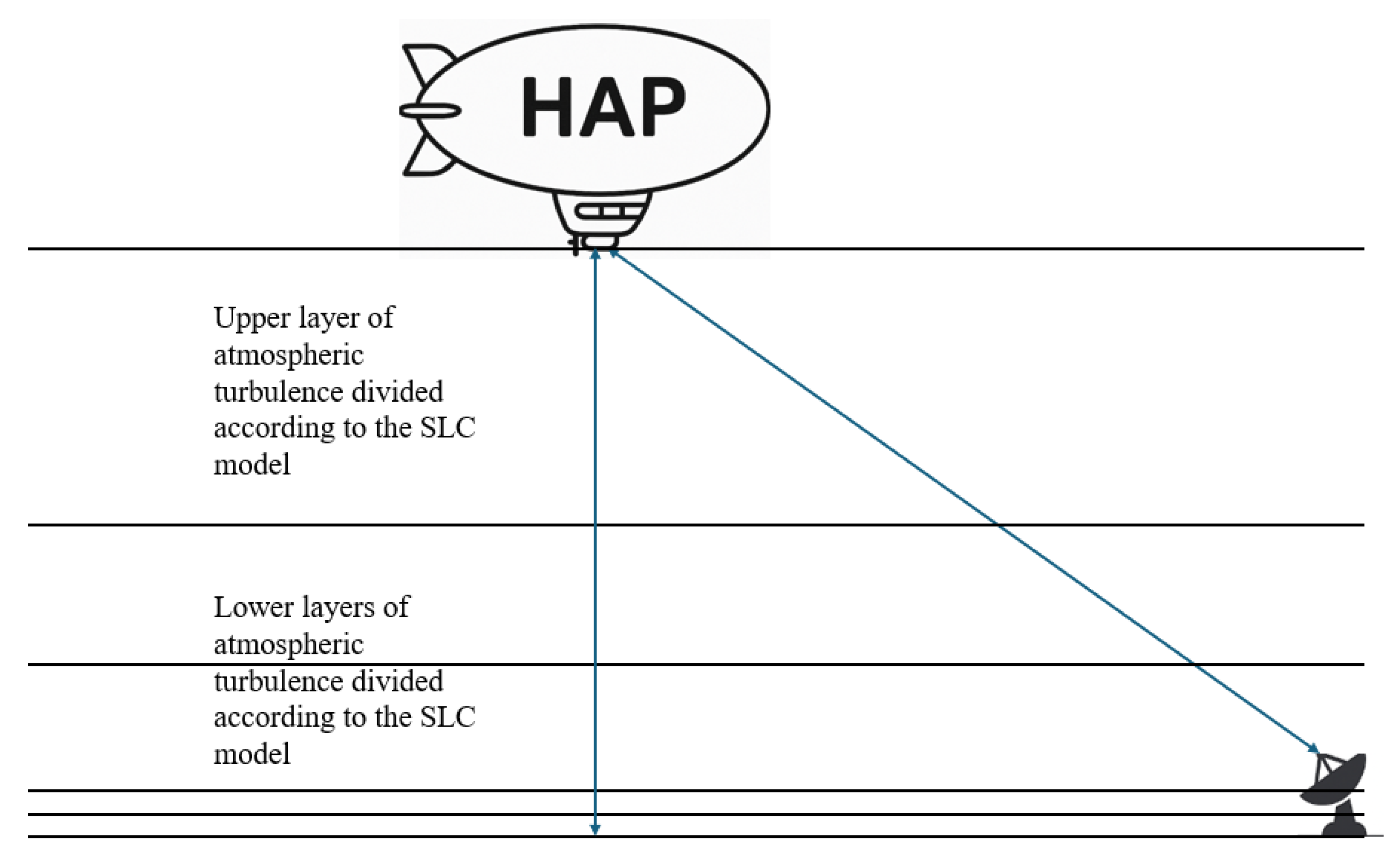
- A layered atmospheric modeling technique is employed to calculate the stochastic turbulence factor. While this stratification method is commonly found in underwater optical communication studies, to the best of the authors’ knowledge, it is applied here for the first time to HAP-based FSO channels.
- Extending the techno-economic modeling of [25] to HAP-assisted FSO communication scenarios, the analysis moves beyond strict cost minimization by evaluating and comparing both minimum-cost and slightly higher-cost network configurations. This approach enables the exploration of trade-offs between cost, throughput improvement, and resilience to future structural or environmental changes.
- Furthermore, in order to compute the network cost, we adopt a cost metric similar to that employed in [1]. For the sake of generality, the cost values are expressed in a dimensionless form, allowing for comparisons and applicability independent of any particular currency.
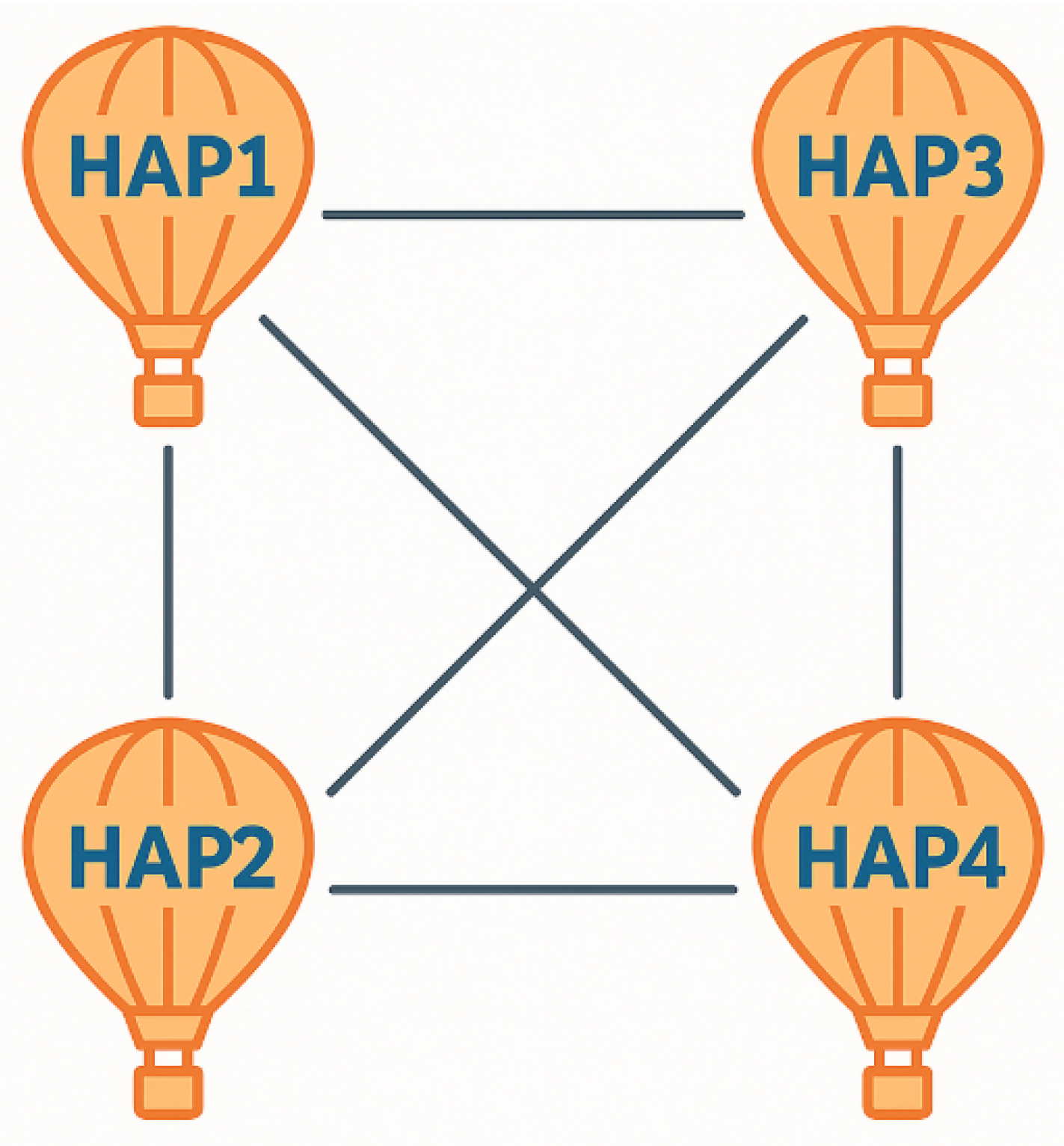
2. Dimensions and Cost of the HAP Network
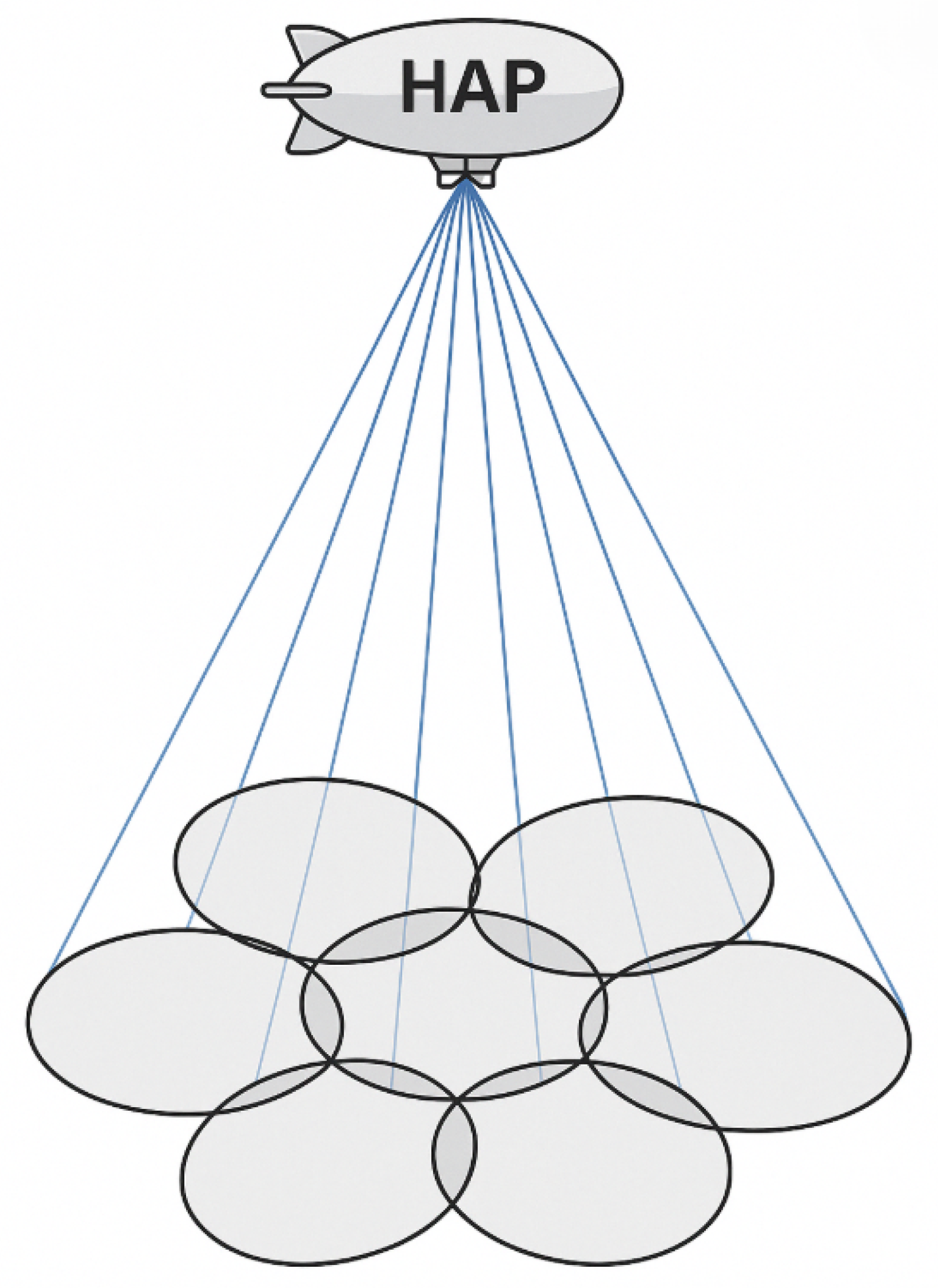
2.1. Network Description and Calculation of the Service Radius of a HAP
2.2. Cost Estimation of the HAP Network
3. Optimization of the Serving Network
3.1. Technical Parameters and Daily Energy Consumption
3.2. Optimization Problem
- 1.
- For a given distribution of ground nodes, the position of the HAPs are determined (e.g., k-means). Thus, for each N, we obtain a set of candidate HAP positions.where are the coordinates of the n-th HAP, .
- 2.
- For each candidate network with N HAPs, we define all possible combinations of configurations in term of the operating triplets for each HAP:
- 3.
- Among all feasible combinations of configurations , we select those that minimize the total network cost :
- 4.
- Finally, the configurations with minimized cost are further evaluated in terms of the network throughput. The throughput calculation takes into account the turbulence effect of the optical wireless channel. The exact analytical model is presented in Section 3.4.
3.3. Optimization
- Step 1:
- Create the ground node distribution and define system constants.
- Step 2:
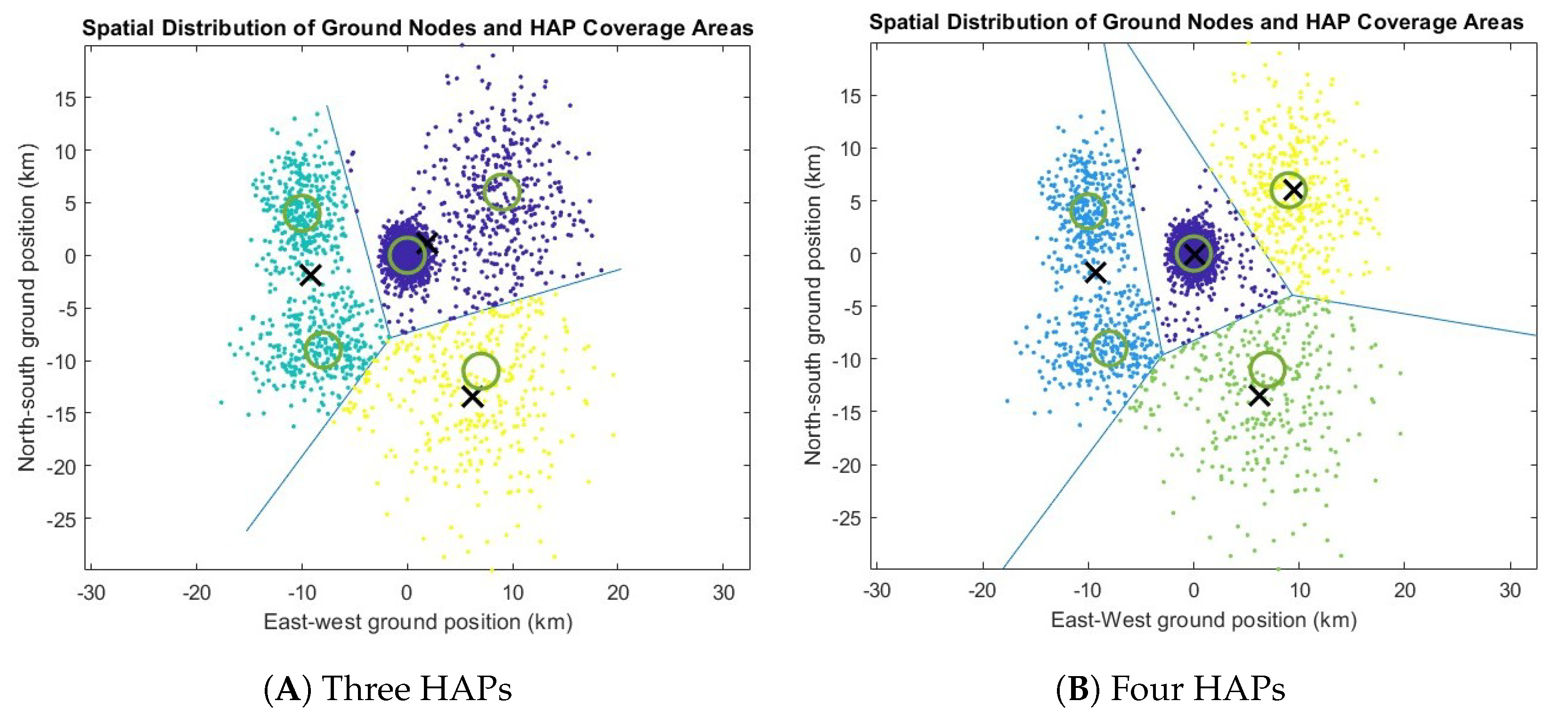
- Determine HAP positions and clustering of ground nodes per HAP (Clustering), for networks with one, two, three, and four HAPs, using the k-means.
- Step 3:
- Verification of technical and physical constraints for each network configuration and exclusion of those that do not satisfy them.
- Step 4:
- For each network and each HAP, computation of the total cost and extended coverage radius for all possible configurations using Algorithm 1.
- Step 5:
- Selection, for each network, of the configurations that satisfy the minimum-cost criterion.
| Algorithm 1 Find the optimal mFSO configuration for HAPi |
|
| Algorithm 2 Find beta_max [1] |
|
3.4. The Impact of Turbulence
3.5. Background Noise
3.6. Method for Calculating Turbulence Gain Based on SLC Models
4. Numerical Results
- Step 1:
- Four HAP network configurations are constructed, each with a different number of HAPs: the first network consists of four HAPs, the second of three, the third of two, and the last of a single HAP. In each case, the ground nodes are assigned to the HAPs that will serve them. The assignment is performed using the k-means clustering algorithm, an unsupervised learning method.
- Step 2:
- Networks that violate any of the constraints defined in this study (e.g., maximum link distance, number of sFSOs per HAP, etc.) are discarded.
- Step 3:
- For each remaining network, all feasible configurations, defined by the parameter sets , are examined, and only those with minimum cost are retained.
- Step 4:
- The minimum-cost configurations are then evaluated in terms of throughput under both day and night conditions.
- Step 5:
- Finally, the different networks are compared based on both cost and achieved throughput, for day and night scenarios.
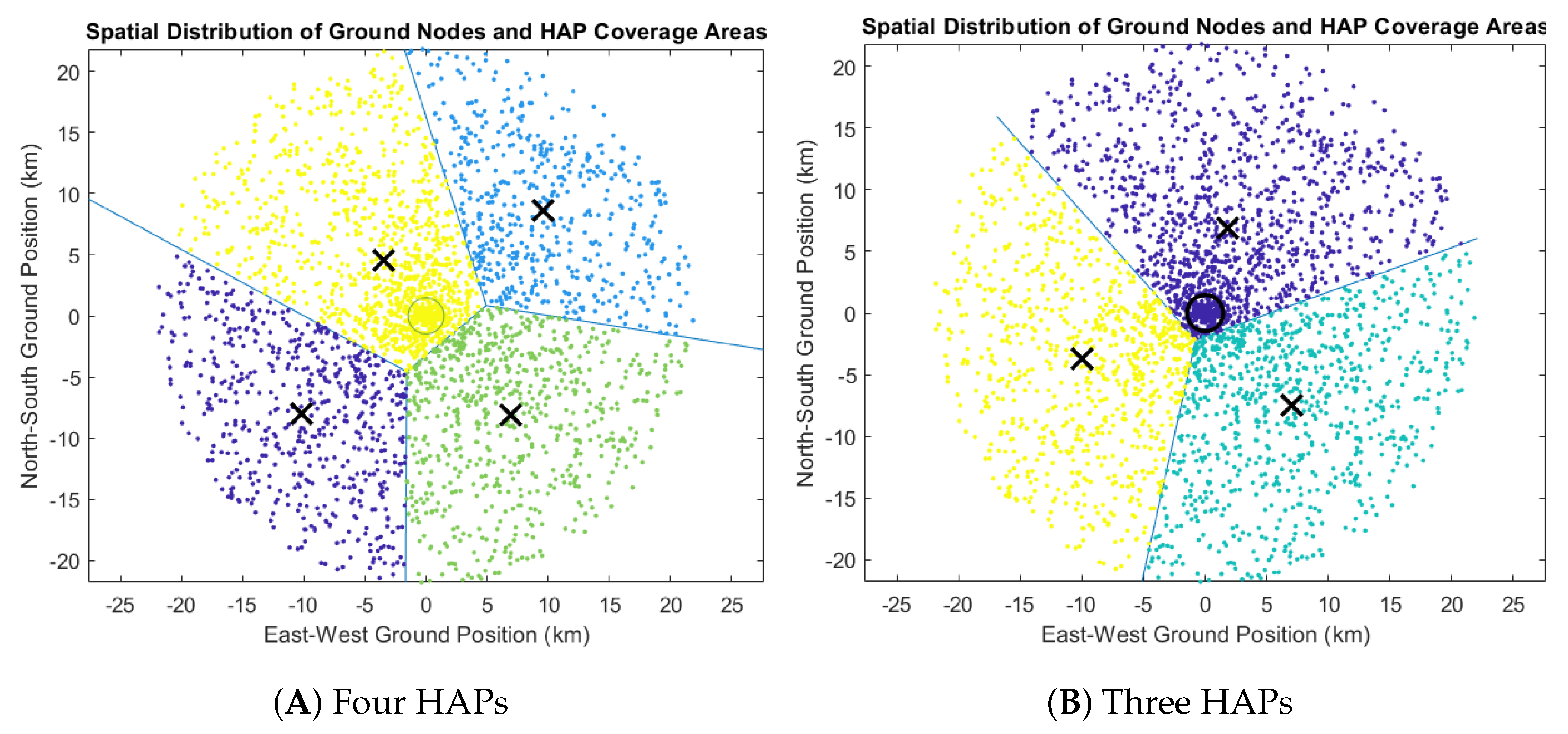
- ×:
- The location of the HAP;
- ⃝
- : The center of the distribution;
- ●:
- The location of the ground node. Different colors indicate which HAP serves each node.
4.1. Urban-Centered Distribution
4.2. Uniform Distribution of Ground Nodes in a Circular Area
4.3. Uniform Distribution of Ground Nodes in a Square Area
4.4. Comparison Between Scenarios and the Resulting Networks
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| APD | Avalanche Photo-Diode |
| AWGN | Additive White Gaussian Noise |
| BER | Bit Error Rate |
| DCSK | Differential Chaos Shift Keying |
| DNN | Deep Neural Network |
| EDFA | Erbium-Doped Fiber Amplifier |
| FBG | Fiber Bragg Grating |
| FSO | Free Space Optics |
| HAP | High Altitude Platform |
| iFSO | Inter-HAP FSO transceiver |
| LoS | Line-of-Sight |
| OOK | On–off Keying |
| PSD | Power Spectral Density |
| QoS | Quality of Service |
| RF | Radio Frequency |
| SAGI | Space–Air–Ground Integrated |
| SLC | Structure Layered Channel |
| SNR | Signal-to-Noise Ratio |
| sFSO | Serving FSO Transceiver |
| UAV | Unmanned Aerial Vehicle |
| WDM | Wavelength Division Multiplexing |
References
- Truong, D.L.; Dang, T.N. Optimal multiple FSO transceiver configuration for using on high-altitude platforms. IEEE Access 2023, 11, 47053–47069. [Google Scholar] [CrossRef]
- Bithas, P.S. Distributed HAPS-assisted communications in FSO/RF space-air-ground integrated networks. Opt. Quantum Electron. 2024, 56, 1020. [Google Scholar] [CrossRef]
- Mashiko, K.; Kawamoto, Y.; Kato, N.; Yoshida, K.; Ariyoshi, M. Combined control of coverage area and HAPS deployment in hybrid FSO/RF SAGIN. IEEE Trans. Veh. Technol. 2025, 74, 10819–10828. [Google Scholar] [CrossRef]
- Kashif, H.; Khan, M.N.; Altalbe, A. Hybrid optical-radio transmission system link quality: Link budget analysis. IEEE Access 2020, 8, 65983–65992. [Google Scholar] [CrossRef]
- Alimi, I.A.; Monteiro, P.P. Revolutionizing free-space optics: A survey of enabling technologies, challenges, trends, and prospects of beyond 5G free-space optical (FSO) communication systems. Sensors 2024, 24, 8036. [Google Scholar] [CrossRef]
- Gao, Z.; Eisen, M.; Ribeiro, A. Resource allocation via model-free deep learning in free space optical communications. IEEE Trans. Commun. 2021, 70, 920–934. [Google Scholar] [CrossRef]
- Zheng, G.; Han, Y. Free Space Optical Reliable Routing Algorithm based on Deep Reinforcement Learning. In Proceedings of the 5th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 8–10 December 2023; pp. 11–14. [Google Scholar]
- Lema, G.G. Free space optics communication system design using iterative optimization. J. Opt. Commun. 2024, 44, s1205–s1216. [Google Scholar] [CrossRef]
- Lionis, A.; Sklavounos, A.; Stassinakis, A.; Cohn, K.; Tsigopoulos, A.; Peppas, K.; Aidinis, K.; Nistazakis, H. Experimental machine learning approach for optical turbulence and FSO outage performance modeling. Electronics 2023, 12, 506. [Google Scholar] [CrossRef]
- Ren, W.; Sun, J.; Cong, H.; Jiang, Y. Sensitivity deterioration of free-space optical coherent/non-coherent OOK modulation receiver by ambient light noise. Sensors 2023, 23, 2140. [Google Scholar] [CrossRef]
- Gripeos, P.J.; Nistazakis, H.E.; Tsigopoulos, A.D.; Christofilakis, V.; Roditi, E. Time and spatial jitter influence on the performance of FSO links with DF relays and OC diversity over turbulence channels. Photonics 2021, 8, 318. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, J.; Long, J.; Wang, C.; Chen, J.; Lu, X. A Hybrid RF/FSO Transmission System Based on a Shared Transmitter. Sensors 2025, 25, 2021. [Google Scholar] [CrossRef]
- Singya, P.K.; Makki, B.; D’Errico, A.; Alouini, M.S. Hybrid FSO/THz-based backhaul network for mmWave terrestrial communication. IEEE Trans. Wirel. Commun. 2022, 22, 4342–4359. [Google Scholar] [CrossRef]
- Hayle, S.T.; Hsu, H.Y.; Wang, C.P.; Lu, H.H.; Lu, J.M.; Hsu, W.W.; Chung, Y.C.; Bai, Y.Y.; Okram, K. High-speed FSO-5G wireless communication system with enhanced loss compensation using high-power EDFA. Sci. Rep. 2025, 15, 379. [Google Scholar] [CrossRef] [PubMed]
- Narang, G.; Aggarwal, M.; Kaushal, H.; Kumar, A.; Ahuja, S.; Shukla, N.K. Performance evaluation of dual hop mixed FSO RF system using differential chaos shift keying with secrecy analysis. IEEE Trans. Veh. Technol. 2024, 73, 17347–17358. [Google Scholar] [CrossRef]
- Trung, H.D. Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors. Appl. Syst. Innov. 2021, 4, 65. [Google Scholar] [CrossRef]
- Le, H.T.; Nguyen, T.V.; Pham, H.T.; Dang, N.T. Harvested Energy Evaluation of Free-Space Optics RIS-Assisted Ground-HAP-UAV System Over Composite Channels. In Proceedings of the IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–5. [Google Scholar]
- Yahia, O.B.; Erdogan, E.; Kurt, G.K.; Altunbas, I.; Yanikomeroglu, H. HAPS selection for hybrid RF/FSO satellite networks. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2855–2867. [Google Scholar] [CrossRef]
- Elamassie, M.; Uysal, M. FSO-Based Multi-Layer Airborne Backhaul Networks. IEEE Trans. Veh. Technol. 2024, 73, 15004–15019. [Google Scholar] [CrossRef]
- Truong, D.L.; Dang, X.V.; Dang, T.N. Survivable free space optical mesh network using high-altitude platforms. Opt. Switch. Netw. 2023, 47, 100716. [Google Scholar] [CrossRef]
- Samy, R.; Yang, H.C.; Mahran, A.; Gebali, F.; Alouini, M.S. Enabling broadband internet access in remote and rural communities using HAP-based multi-hop FSO/RF transmissions. IEEE Commun. Mag. 2024, 63, 182–188. [Google Scholar] [CrossRef]
- McQueen, J.B. Some methods of classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. Adv. Res. Comput. Sci. Manag. Stud. 2013, 1, 90–95. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Kokkinis, D.; Ioannou, N.; Katsianis, D.; Varoutas, D. A Techno-Economic Modeling Approach to 6G Network Deployment: Exploring Costs and Use Case Feasibility. IEEE Access 2025, 13, 35597–35608. [Google Scholar] [CrossRef]
- Mahmood, A.S. An approach to investigating the feasibility of free-space optical communication technology deployment under scintillation effects. Opto-Electron. Rev. 2023, e147037. [Google Scholar] [CrossRef]
- Weichel, H. Laser Beam Propagation in the Atmosphere; SPIE Press: Bellingham, WA, USA, 1990; Volume 3. [Google Scholar]
- Elamassie, M.; Uysal, M. Free space optical communication: An enabling backhaul technology for 6G non-terrestrial networks. Photonics 2023, 10, 1210. [Google Scholar] [CrossRef]
- Bithas, P.S.; Nistazakis, H.E.; Katsis, A.; Yang, L. Hybrid FSO/RF communications in space–air–ground integrated networks: A reduced overhead link selection policy. Electronics 2024, 13, 806. [Google Scholar] [CrossRef]
- Miao, M.; Cai, W.; Li, X. Parameter Estimation of Gamma-Gamma Fading with Generalized Pointing Errors in FSO Systems. Wirel. Commun. Mob. Comput. 2021, 2021, 1301878. [Google Scholar] [CrossRef]


| Symbol | Description and Physical Meaning | Numerical Value |
|---|---|---|
| The number of inter-HAP links | 12 [1] | |
| Daily amortization cost of a HAP | 100 [1] | |
| Daily amortization cost of an FSO transceiver on HAP | 10 [1] | |
| Power consumption of the aeronautical section to support one unit of mass | 2 W/kg [1] | |
| Transmitted power from each sFSO | W [1] | |
| Power for thermal stabilization and management | W [1] | |
| Power consumption by Pointing Acquisition and Tracking System | W [1] | |
| Total power consumption by an iFSO | W [1] | |
| FSO transceiver mass | kg [1] | |
| Platform mass excluding FSO transceivers | kg [1] | |
| The number of wavelengths per FSO link according to used WDM technique | 80 [1] | |
| Elevation of HAPs | km [1] | |
| The number of HAPs per network | 1, 2, 3, 4 | |
| B | The bandwidth of the optical channel | Hz [10] |
| The power of background noise during daytime | W [10] | |
| The power of background noise during nighttime | W [10] | |
| Atmospheric attenuation coefficient | m−1 [1] | |
| Receiver telescope aperture radius of a ground node transceiver | m [1] | |
| The daily harvested solar energy | kWh [1] | |
| Detector’s sensitivity | dBm [1] | |
| k | The optical wavenumber |
| Urban Center | Suburb 1 | Suburb 2 | Suburb 3 | Suburb 4 | |
|---|---|---|---|---|---|
| Number of ground nodes | 1450 | 362 | 362 | 362 | 362 |
| Distribution center | (0, 0) | (9, 6) | (−10, 4) | (7, −11) | (−8, −9) |
| Dispersion on the x-axis | 1.000 | 3.482 | 2.075 | 5.204 | 3.482 |
| Dispersion on the y-axis | 1.388 | 5.204 | 3.482 | 7.225 | 2.881 |
| Three-HAPs Networks | Location (x, y), (km) | Number of Ground Nodes | Number of sFSOs | Operational Cost |
|---|---|---|---|---|
| (1.90, 1.12) | 1884 | 24 | 602.74 | |
| (−9.22, −1.91) | 682 | 9 | 302.74 | |
| (6.23, −13.40) | 332 | 10 | 322.74 | |
| Total network cost: 1228 | ||||
| Four-HAPs Networks | Location (x, y), (km) | Number of Ground Nodes | Number of sFSOs | Operational Cost |
|---|---|---|---|---|
| (0.11, −0.10) | 1541 | 20 | 522.74 | |
| (−9.31, −1.85) | 672 | 9 | 302.74 | |
| (6.27, −13.48) | 327 | 10 | 322.74 | |
| (9.51, 6.06) | 358 | 7 | 262.74 | |
| Total network cost: 1411 | ||||
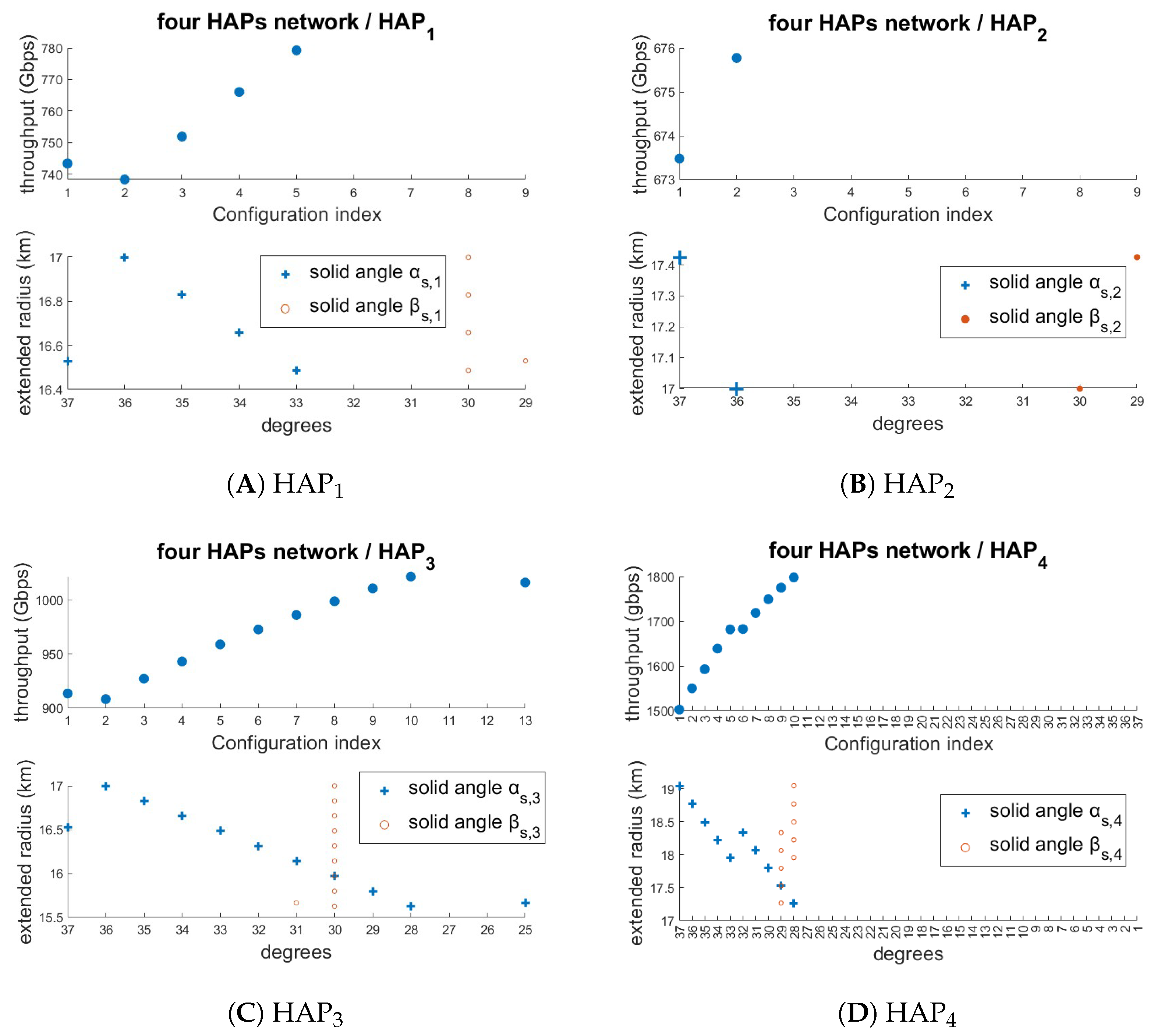
| Three-HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| 19.29 | 2501 | |||
| 15.45 | 1005 | |||
| 17.23 | 431 | |||
| Network throughput: 3937 Gbps Mean throughput per ground node: 431 | ||||
| Four-HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| 14.45 | 4886 | |||
| 16.52 | 994 | |||
| 15.31 | 435 | |||
| 14.61 | 480 | |||
| Network throughput: 6795 Gbps Mean throughput per ground node: 2.27 Gbps | ||||
| Four-HAPs Network | Location (x, y), (km) | Number of Ground Nodes | Number of sFSOs | Operational Cost |
|---|---|---|---|---|
| (−10.17, −7.97) | 576 | 9 | 302.74 | |
| (9.62, 8.67) | 528 | 10 | 322.74 | |
| (6.97, −8.06) | 704 | 9 | 302.74 | |
| (−3.42, 4.49) | 1192 | 15 | 422.74 | |
| Total network cost: 1351 | ||||
| Three-HAPs Network | Location (x, y), (km) | Number of Ground Nodes | Number of sFSOs | Operational Cost |
|---|---|---|---|---|
| (1.82, 6.88) | 1323 | 17 | 462.74 | |
| (6.99, −7.49) | 850 | 15 | 422.74 | |
| (−10.02, −3.69) | 827 | 14 | 402.74 | |
| Total network cost: 1288 | ||||
| Three-HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| 19.18 | 1794 | |||
| 19.05 | 1134 | |||
| 18.76 | 1099 | |||
| Network throughput: 4027 Gbps Mean throughput per ground node: 1.94 Gbps | ||||
| Four-HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| 16.49 | 779 | |||
| 17.00 | 676 | |||
| 15.63 | 1022 | |||
| 17.27 | 1798 | |||
| Network throughput: 4275 Gbps Mean throughput per ground node: 1.43 Gbps | ||||
|
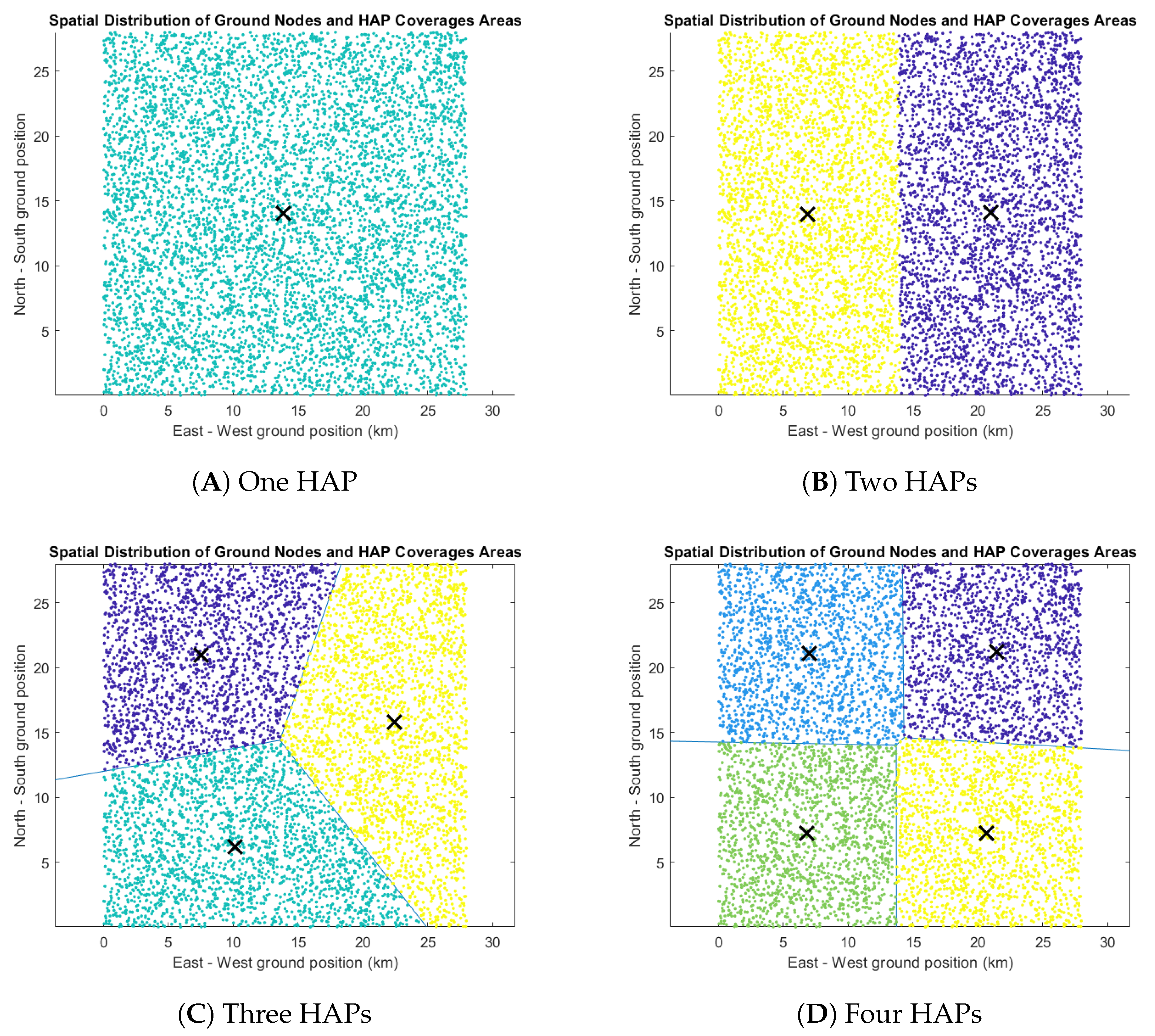
One HAP Network |
Location (x, y) (km) |
Number of Ground Nodes |
Number of sFSOs |
Operational Cost |
|---|---|---|---|---|
| HAP1 | (13.84, 14.04) | 6500 | 82 | 1763 |
| Total Network Cost: 1763 | ||||
|
Two HAPs Network |
Location (x, y) (km) |
Number of Ground Nodes |
Number of sFSOs |
Operational Cost |
|---|---|---|---|---|
| HAP1 | (20.98, 14.12) | 3211 | 41 | 942.74 |
| HAP2 | (6.86, 13.97) | 3289 | 42 | 962.74 |
| Total Network Cost: 1906 | ||||
|
Four HAPs Network |
Location (x, y) (km) |
Number of Ground Nodes |
Number of sFSOs |
Operational Cost |
|---|---|---|---|---|
| HAP1 | (21.44, 21.22) | 1536 | 20 | 522.74 |
| HAP2 | (7.03, 21.09) | 1647 | 21 | 542.74 |
| HAP3 | (6.79, 7.21) | 1662 | 21 | 542.74 |
| HAP4 | (20.64, 7.23) | 1655 | 21 | 542.74 |
| Total Network Cost: 2154 | ||||
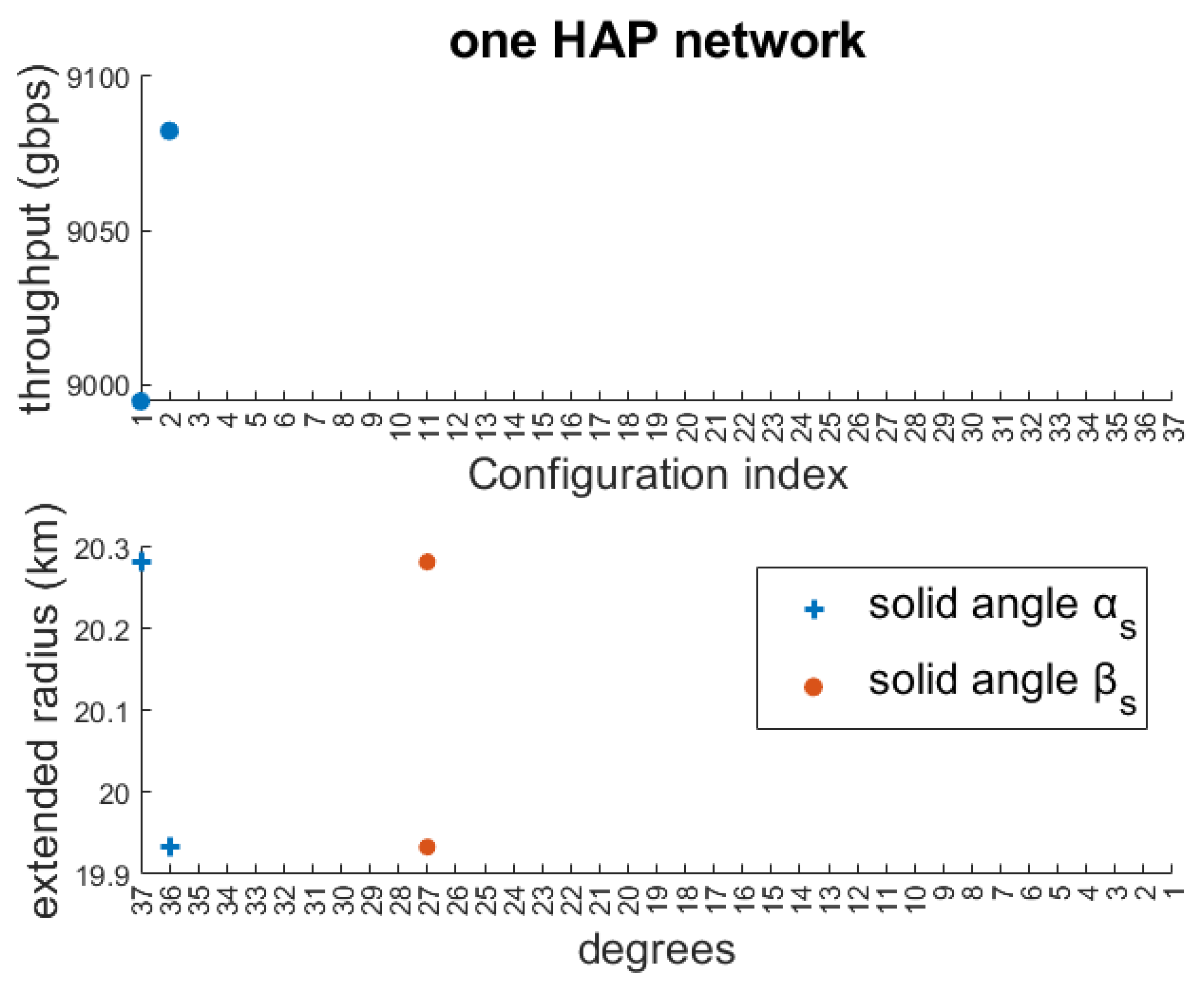
| One HAP Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| HAP1 | 19.93 | 9083 | ||
| Network throughput: 9083 Mean throughput per ground node: 1.40 Gbps | ||||
| Two HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| HAP1 | 16.64 | 4860 | ||
| HAP2 | 16.65 | 4977 | ||
| Network throughput: 9837 Mean throughput per ground node: 1.51 Gbps | ||||
| Four HAPs Network | (km) | (Gbps) | ||
|---|---|---|---|---|
| HAP1 | 16.46 | 2596 | ||
| HAP2 | 16.52 | 2742 | ||
| HAP3 | 16.52 | 2767 | ||
| HAP4 | 16.52 | 2749 | ||
| Network throughput: 10,827 Mean throughput per ground node: 1.67 Gbps | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melanitis, M.; Bithas, P.S.; Katsis, A.; Nistazakis, H.E. Design and Optimization of an FSO Network Under Practical Considerations. Photonics 2025, 12, 926. https://doi.org/10.3390/photonics12090926
Melanitis M, Bithas PS, Katsis A, Nistazakis HE. Design and Optimization of an FSO Network Under Practical Considerations. Photonics. 2025; 12(9):926. https://doi.org/10.3390/photonics12090926
Chicago/Turabian StyleMelanitis, Marios, Petros S. Bithas, Athanassios Katsis, and Hector E. Nistazakis. 2025. "Design and Optimization of an FSO Network Under Practical Considerations" Photonics 12, no. 9: 926. https://doi.org/10.3390/photonics12090926
APA StyleMelanitis, M., Bithas, P. S., Katsis, A., & Nistazakis, H. E. (2025). Design and Optimization of an FSO Network Under Practical Considerations. Photonics, 12(9), 926. https://doi.org/10.3390/photonics12090926







