High-Precision Angle Sensor Based on Angle Amplification via Double-Layer Regular Prism Structure
Abstract
1. Introduction
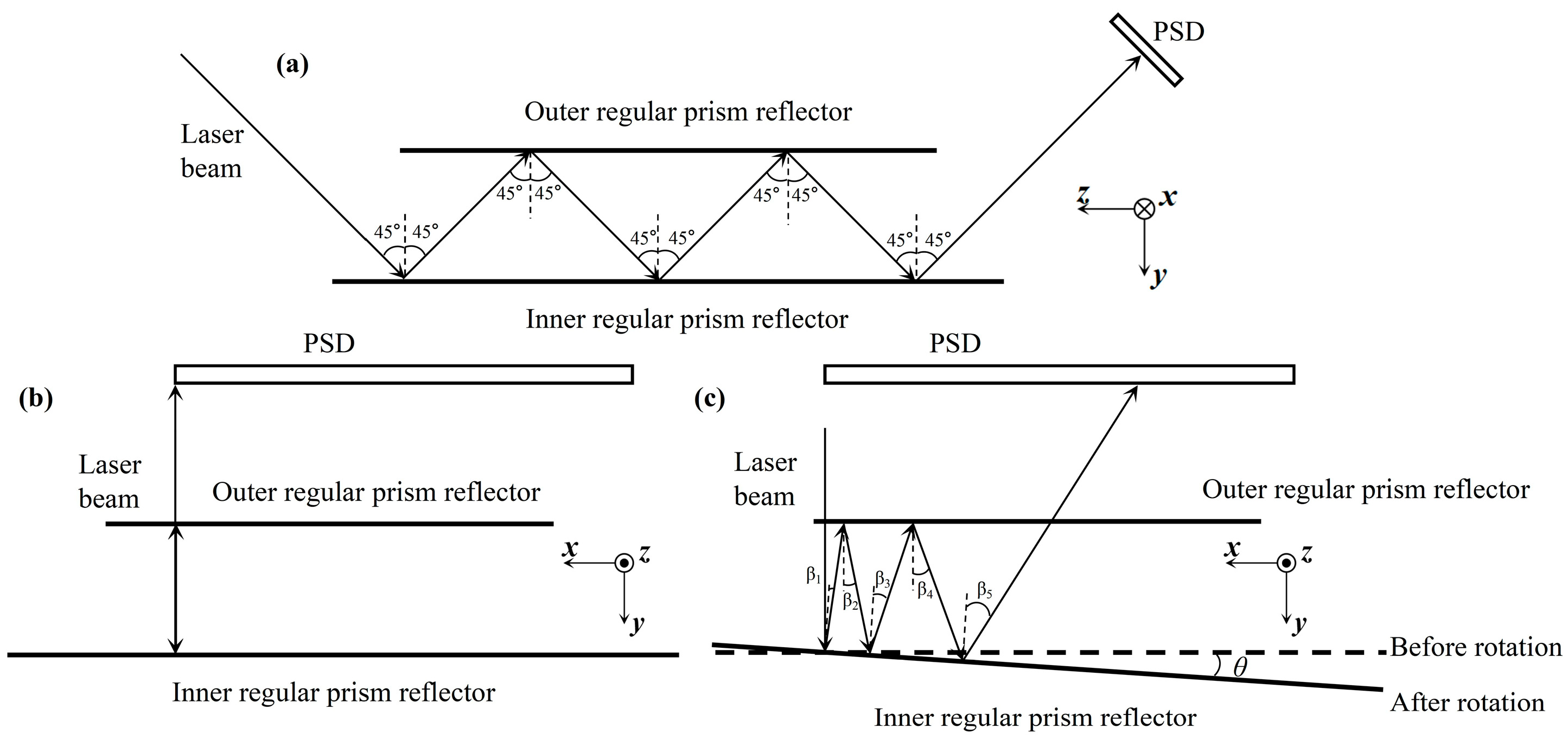
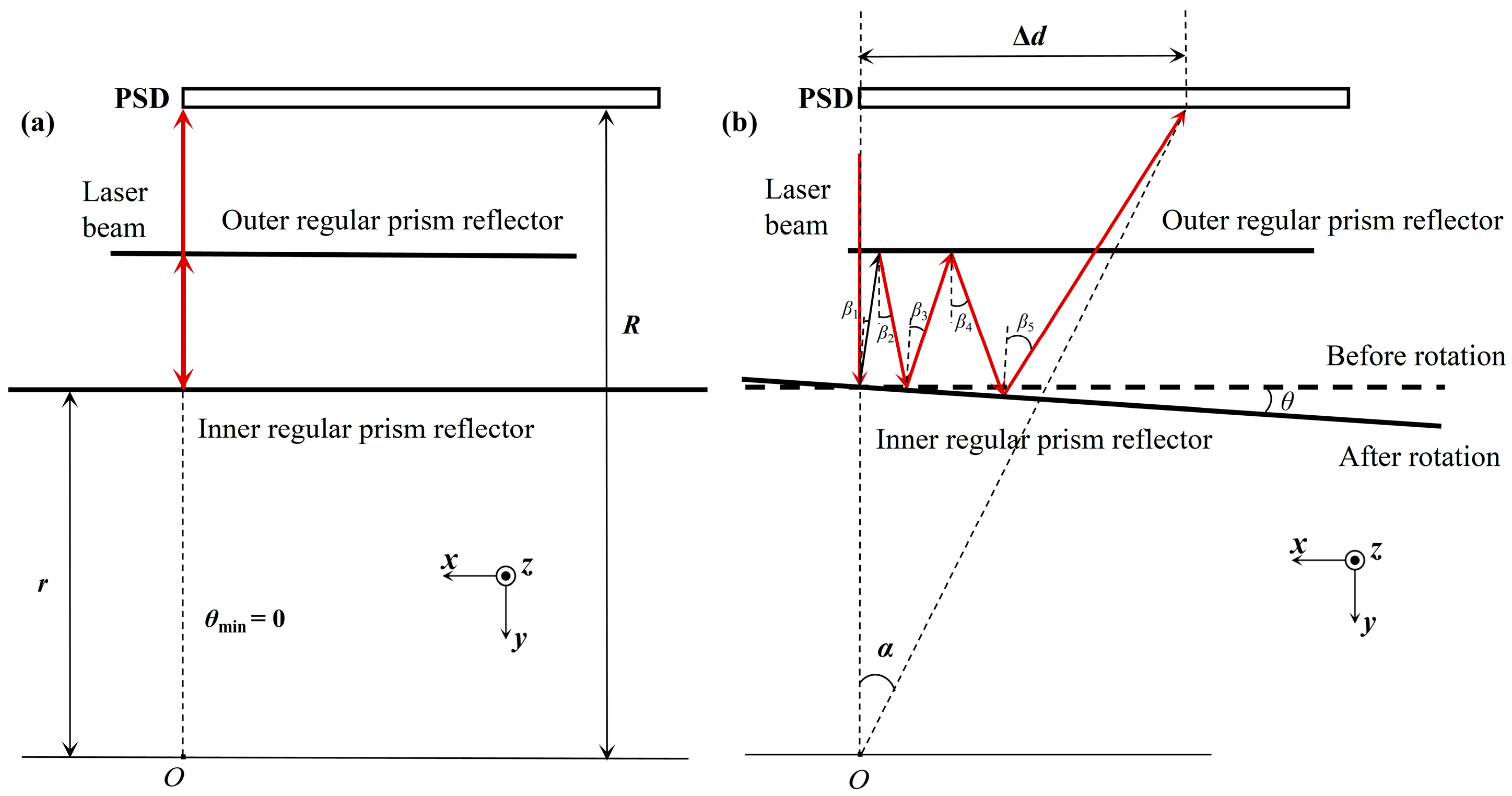
2. Principle of Angle Measurement
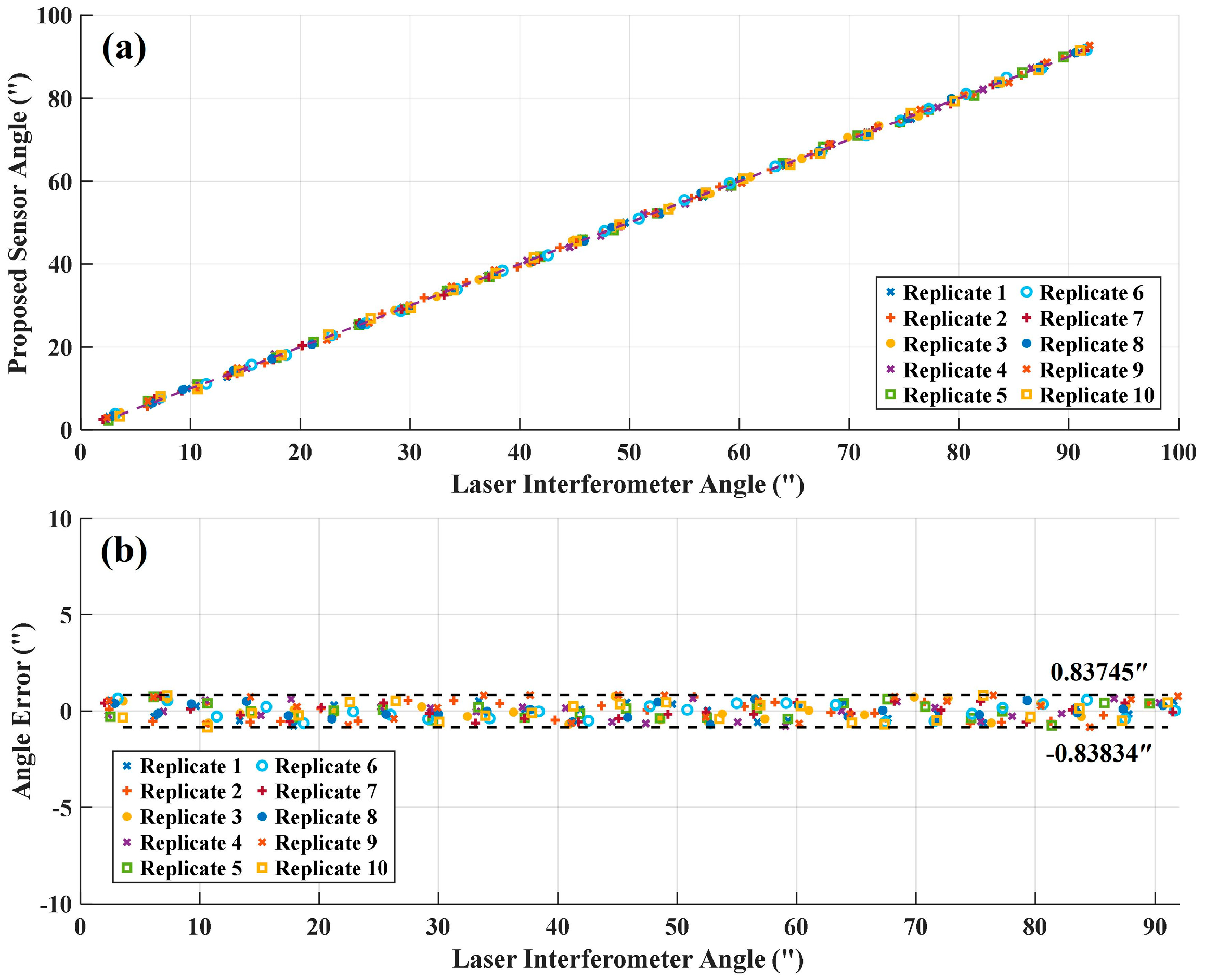
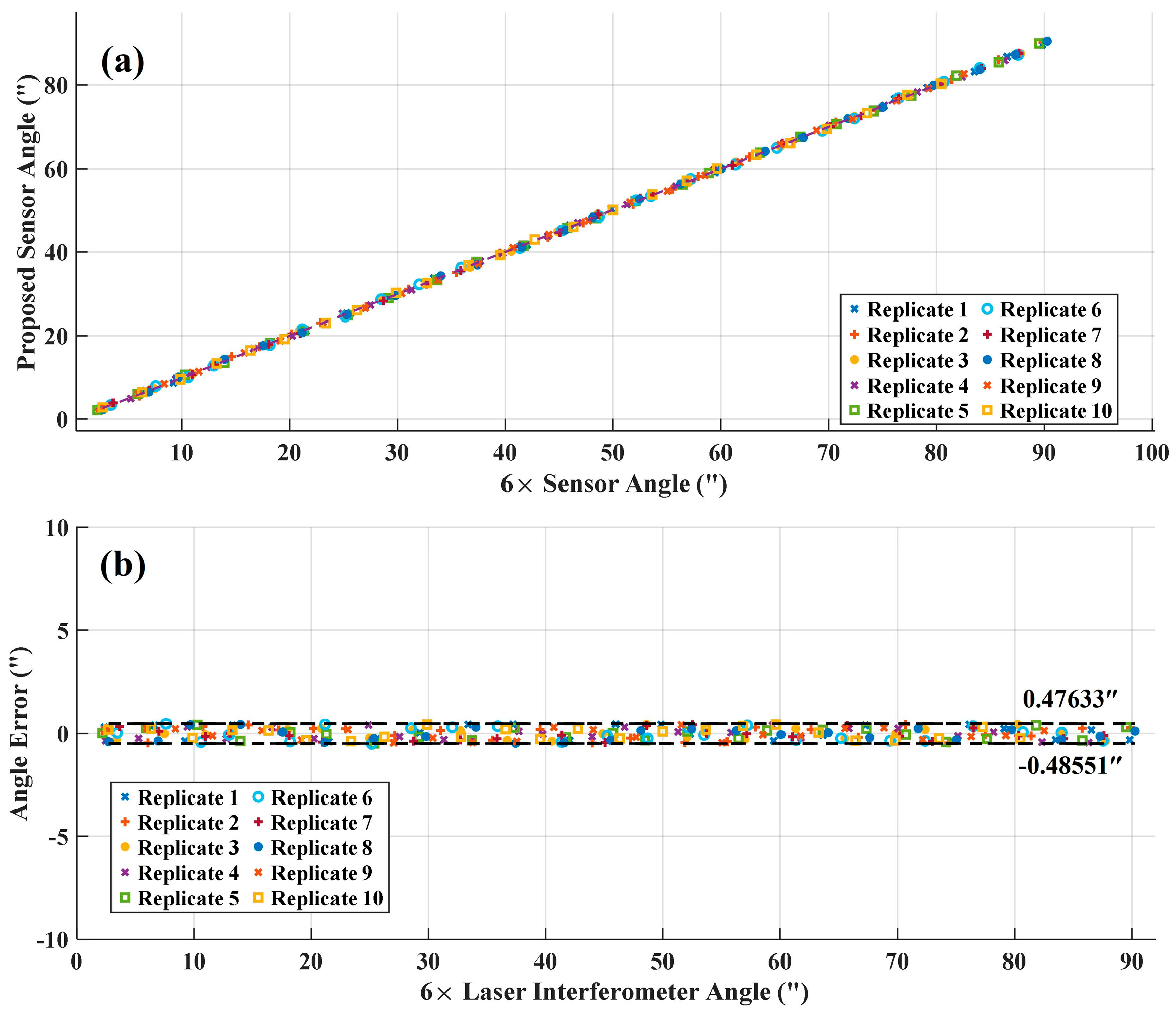
3. Experimental and Results
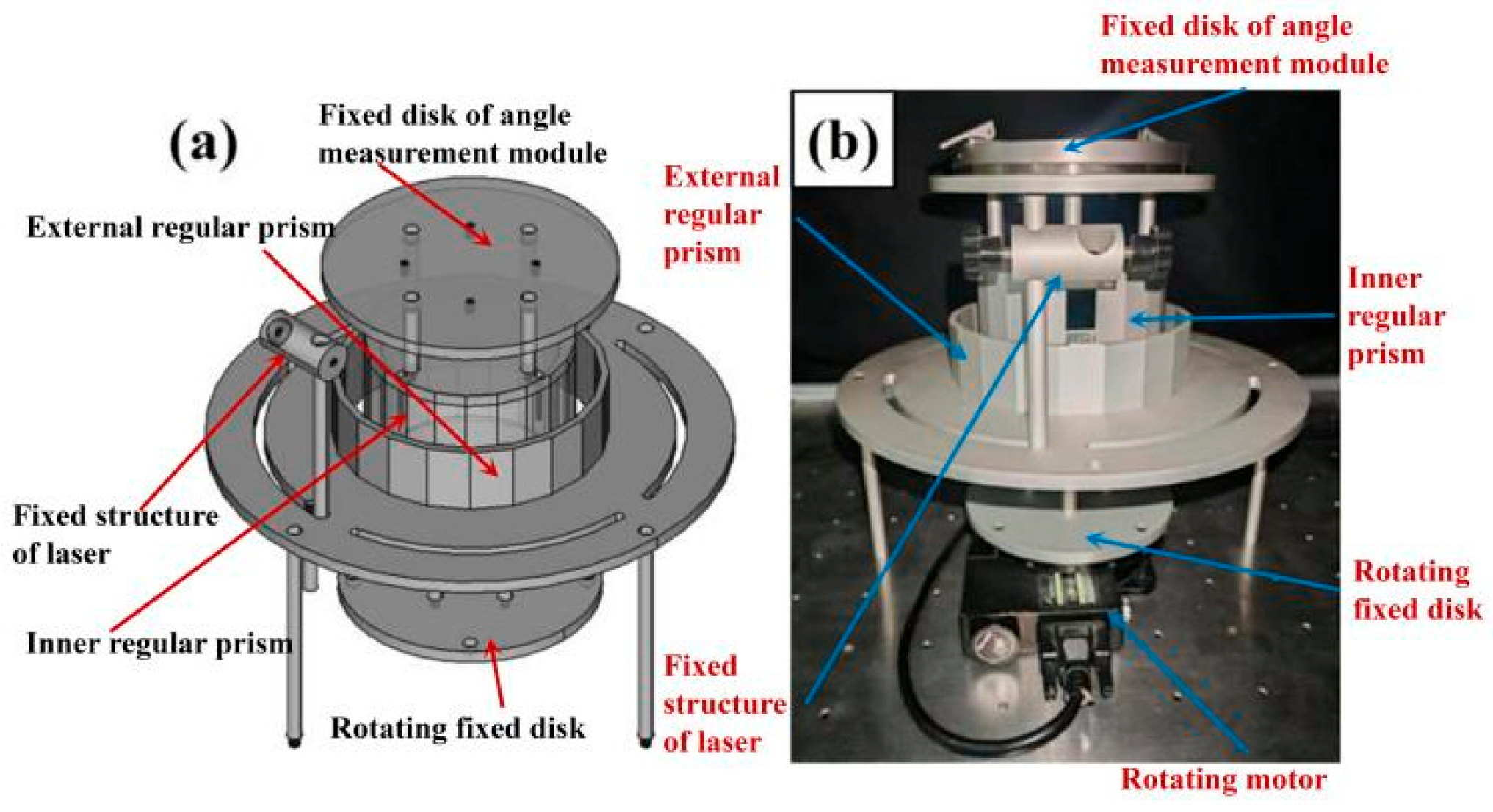
3.1. Hardware Implementation of the Sensor System
3.2. Expanding the Measurement Range with Coordinated Sensor Units
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, G. Improving the angle measurement accuracy of circular grating. Rev. Sci. Instrum. 2020, 91, 065108. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Meng, X.; Krolczyk, G.; Wei, H. A cluster-based method for quantitative characterization and uncertainty evaluation of areal step height in structured surface metrology. IEEE Trans. Instrum. Meas. 2022, 71, 3205662. [Google Scholar] [CrossRef]
- Kang, W.R.; Zheng, Z.Y.; Huang, H.C. Advancements in Digital Holography for Crystalline Material Characterization: A Review. Cryst. Res. Technol. 2025, 60, 2400264. [Google Scholar] [CrossRef]
- Wang, S.; Ma, R.; Cao, F.; Luo, L.; Li, X. A review: High-precision angle measurement technologies. Sensors 2024, 24, 1755. [Google Scholar] [CrossRef] [PubMed]
- Podlaskin, B.G.; Guk, E.G.; Obolenskov, A.G.; Sukharev, A.A. Improvement of the accuracy of a position-sensitive detector with a wide field of view. Tech. Phys. Lett. 2020, 46, 988–990. [Google Scholar] [CrossRef]
- Vittone, E.; Provatas, G.; Nizić, K.I.; Jaksic, M. IBIC analysis of a linear position sensitive detector: Model and experiment. Eur. Phys. J. Plus 2025, 140, 369. [Google Scholar] [CrossRef]
- Elrawashdeh, Z.; Revel, P.; Prelle, C.; Lamarque, F. High precision machining of a displacement sensor for helicoidal motions. Int. J. Precis. Eng. Manuf. 2022, 24, 409–422. [Google Scholar] [CrossRef]
- Guillen-Ruiz, L.E.; Anzueto-Sánchez, G.; Martínez-Rios, A.; Jiménez-Mares, M.C.; Martin-Vela, J.A. High-sensitivity displacement sensor using few-mode optical fibers and the optical vernier effect. Appl. Sci. 2024, 14, 9300. [Google Scholar] [CrossRef]
- Huang, H.C.; Liu, Z.; Ruggiero, M.T.; Zheng, Z.; Qiu, K.; Li, S.; Zhang, Z.; Zhang, Z. Terahertz Geoscience: THz Time-Domain Spectroscopy for Mineral Materials. Cryst. Growth Des. 2025, 25, 3578–3594. [Google Scholar] [CrossRef]
- Zhang, B.; Jiang, Z.; Yin, Z.; Cao, X.; Zhou, C.; Kang, X. Angle Sensor Based on Multiple Optical Arm Amplification. Int. J. Opt. 2025, 2025, 9979341. [Google Scholar] [CrossRef]
- Murai, T.; Uchiyama, S.; Nakamura, K.; Ido, Y.; Hata, Y.; Kato, H. Functional range of motion in the metacarpophalangeal joints of the hand measured by single axis electric goniometers. J. Orthop. Sci. 2018, 23, 504–510. [Google Scholar] [CrossRef] [PubMed]
- Nwaobi, O.M. Electric Goniometer for Positioning Children with Cerebral Palsy: Suggestion from the Field. Phys. Ther. 1986, 66, 1540–1541. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kumar, A.S.A.; George, B. A non-contact angle sensor based on eddy current technique. IEEE Trans. Instrum. Meas. 2019, 69, 1275–1283. [Google Scholar] [CrossRef]
- Kumar, A.S.A.; George, B.; Mukhopadhyay, S.C. Technologies and applications of angle sensors: A review. IEEE Sens. J. 2021, 21, 7195–7206. [Google Scholar] [CrossRef]
- Kim, J.A.; Lee, J.Y.; Kang, C.S.; Woo, J.H. High-precision two-dimensional angle sensor using a dot array of a diffractive optical element. Meas. Sci. Technol. 2021, 32, 105204. [Google Scholar] [CrossRef]
- Larichev, R.; Filatov, Y. A model of angle measurement using an autocollimator and optical polygon. Photonics 2023, 10, 1359. [Google Scholar] [CrossRef]
- Eves, B.J.; Leroux, I.D.; Cen, A.J. Phase shifting angle interferometer. Metrologia 2023, 60, 055006. [Google Scholar] [CrossRef]
- Kim, J.A.; Lee, J.Y.; Kang, C.S.; Woo, J.H. High precision vertical angle measurement system for calibration of various angle sensors and instruments. Meas. Sci. Technol. 2024, 35, 075011. [Google Scholar] [CrossRef]
- Coimbra, J.; Lorenzutti, P.; Leal Junior, A. Fiber Bragg grating-based sensor system for strain and angle assessment in passive orthosis. IEEE Sens. Lett. 2025, 9, 3500804. [Google Scholar] [CrossRef]
- Murashkina, T.I.; Badeeva, E.A.; Kukushkin, A.N.; Badeev, V.A.; Plotnikova, E.Y.; Vasil’ev, Y.A.; Istomina, T.V. A medical fiber optic tilt angle sensor. Biomed. Eng. 2025, 58, 300–303. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Cao, X.; Su, L.; Yin, Z.; Zhou, C.; Kang, X.; Liu, Y. High-Precision Angle Sensor Based on Angle Amplification via Double-Layer Regular Prism Structure. Photonics 2025, 12, 890. https://doi.org/10.3390/photonics12090890
Zhang B, Cao X, Su L, Yin Z, Zhou C, Kang X, Liu Y. High-Precision Angle Sensor Based on Angle Amplification via Double-Layer Regular Prism Structure. Photonics. 2025; 12(9):890. https://doi.org/10.3390/photonics12090890
Chicago/Turabian StyleZhang, Bai, Xixi Cao, Lihan Su, Zipeng Yin, Chunyan Zhou, Xueliang Kang, and Yiwei Liu. 2025. "High-Precision Angle Sensor Based on Angle Amplification via Double-Layer Regular Prism Structure" Photonics 12, no. 9: 890. https://doi.org/10.3390/photonics12090890
APA StyleZhang, B., Cao, X., Su, L., Yin, Z., Zhou, C., Kang, X., & Liu, Y. (2025). High-Precision Angle Sensor Based on Angle Amplification via Double-Layer Regular Prism Structure. Photonics, 12(9), 890. https://doi.org/10.3390/photonics12090890




