Quantifying Influence of Beam Drift on Linear Retardance Measurement in Dual-Rotating Retarder Mueller Matrix Polarimetry
Abstract
1. Introduction
2. Materials and Methods
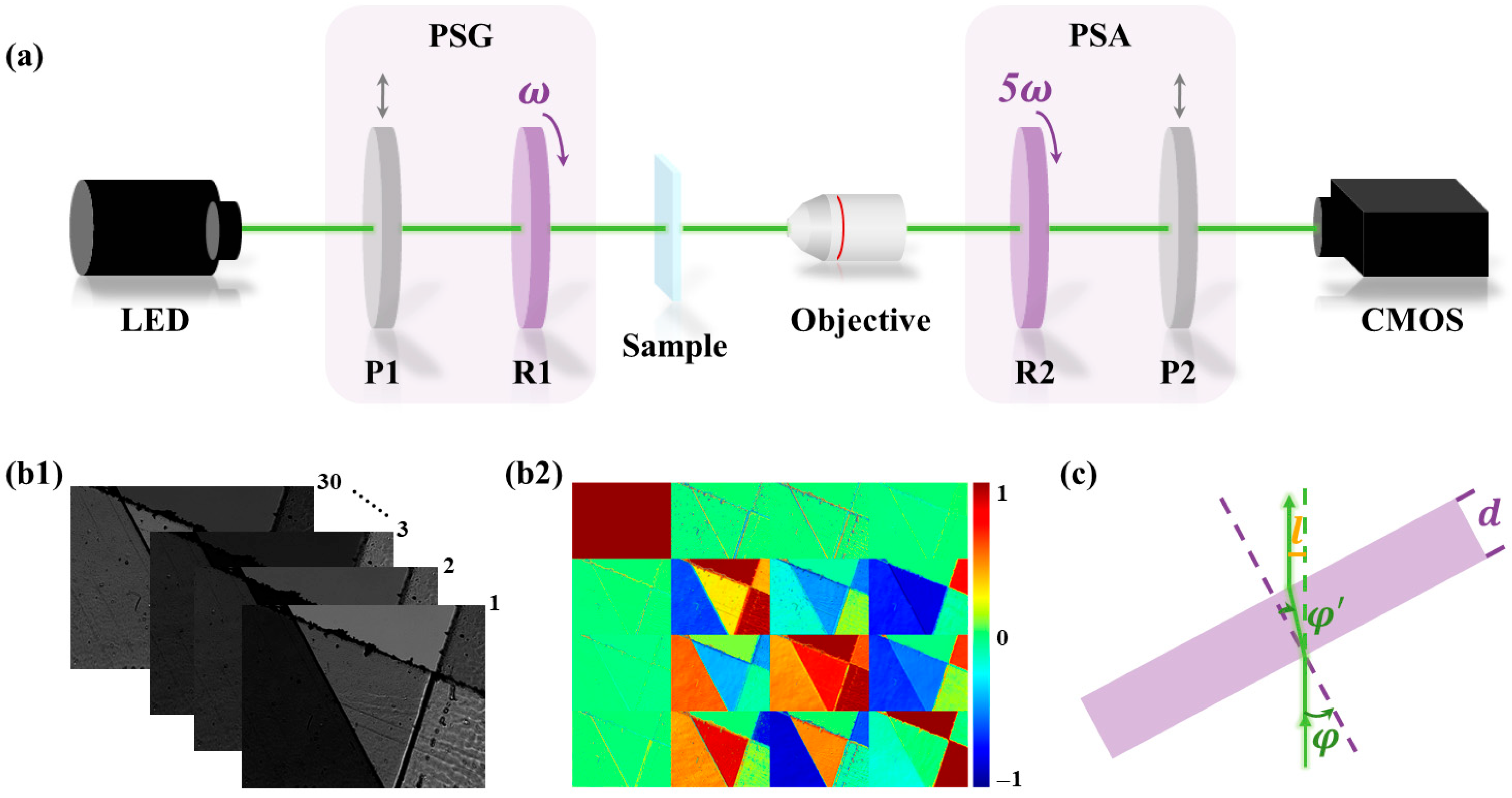
2.1. Experimental Setup
2.2. Linear Retardance Measurement Method
3. Results
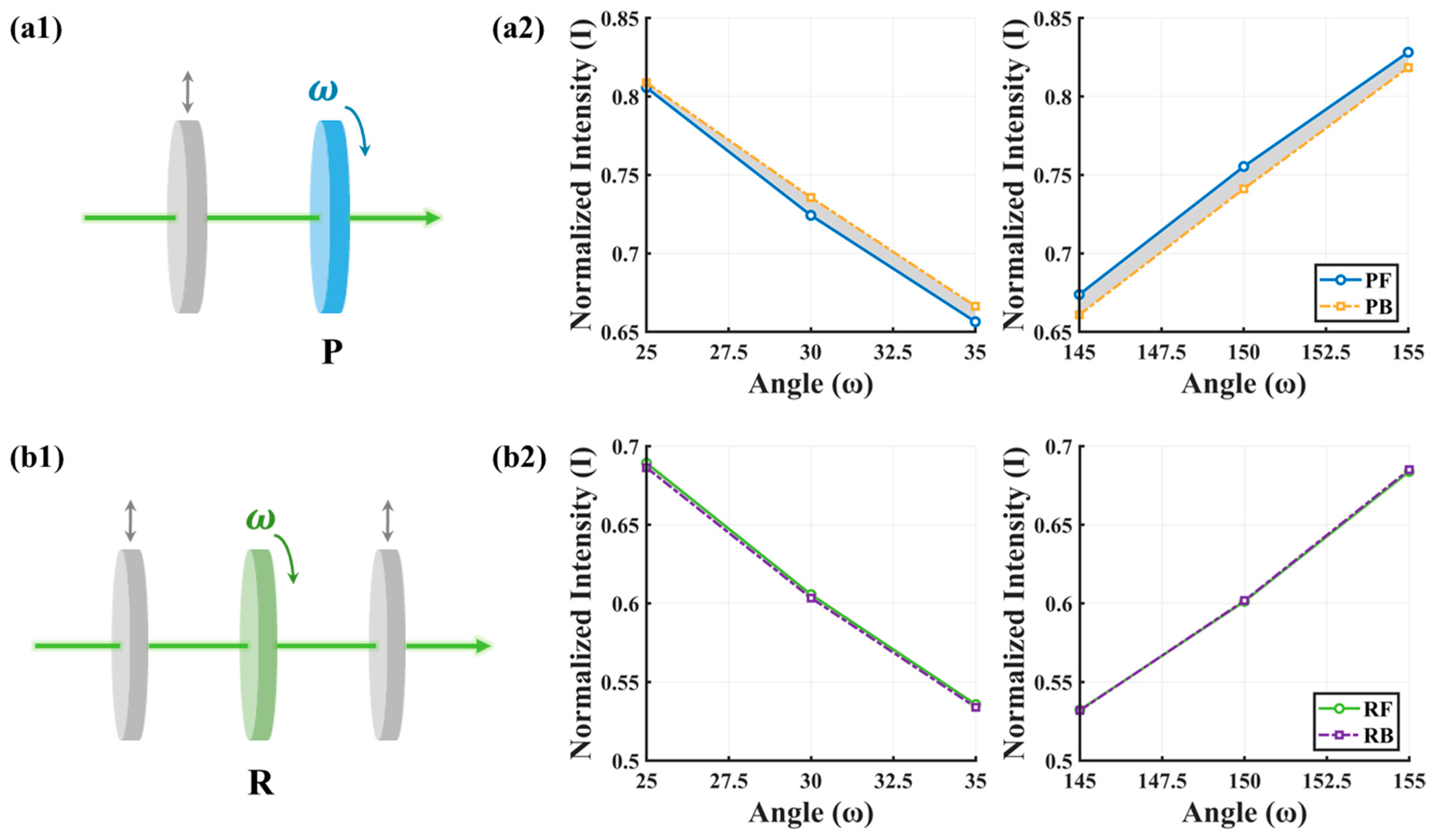
3.1. Beam Drift Magnitude Comparison
3.2. Influence on Linear Retardance Measurement
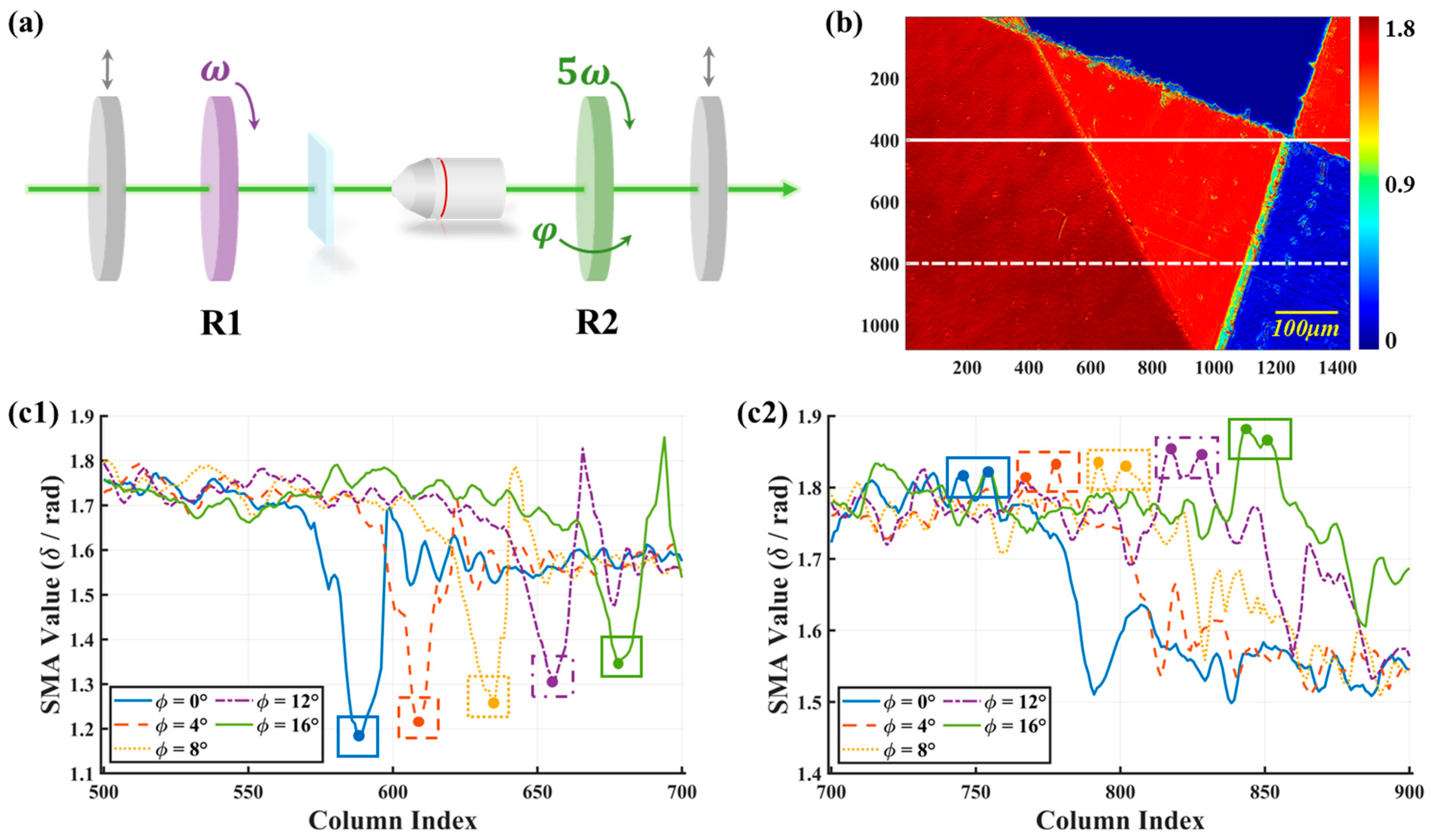
3.2.1. Phantom Experiment Results
3.2.2. Tissue Experiment Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tuchin, V.V. Polarized light interaction with tissues. J. Biomed. Opt. 2011, 21, 071114. [Google Scholar] [CrossRef] [PubMed]
- Ramella-Roman, J.C.; Saytashev, I.; Piccini, M. A review polarization-based imaging technologies for clinical and preclinical applications. J. Opt. 2020, 22, 123001. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Pezzaniti, J.L.; Russell, A.C. Mueller matrix imaging polarimetry. Opt. Eng. 1995, 34, 1558–1568. [Google Scholar] [CrossRef]
- Qi, J.; Elson, D.S. A high definition Mueller polarimetric endoscope for tissue characterization. Sci. Rep. 2016, 6, 25953. [Google Scholar] [CrossRef]
- Cameron, B.D.; Raković, M.J.; Mehrübeoǧlu, M.; Kattawar, G.W.; Rastegar, S.; Wang, L.V.; Coté, G.L. Measurement and calculation of the two-dimensional backscattering Mueller matrix of a turbid medium. Opt. Lett. 1998, 23, 485–487. [Google Scholar] [CrossRef]
- Alali, S.; Vitkin, I.A. Polarized light imaging in biomedicine: Emerging Mueller matrix methodologies for bulk tissue assessment. J. Biomed. Opt. 2015, 20, 061104. [Google Scholar] [CrossRef]
- Pierangelo, A.; Manhas, S.; Benali, A.; Fallet, C.; Antonelli, M.R.; Novikova, T.; Gayet, B.; Validire, P.; Martino, A.D. Ex vivo photometric and polarimetric multilayer characterization of human healthy colon by multispectral Mueller imaging. J. Biomed. Opt. 2012, 17, 066009. [Google Scholar] [CrossRef]
- Antonelli, M.R.; Pierangelo, A.; Novikova, T.; Validire, P.; Benali, A.; Gayet, B.; Martino, A.D. Mueller matrix imaging of human colon tissue for cancer diagnostics: How Monte Carlo modeling can help in the interpretation of experimental data. Opt. Express 2010, 18, 10200–10208. [Google Scholar] [CrossRef]
- Goldstein, D.H.; Chipman, R.A. Mueller matrix dual-rotating retarder polarimeter. Appl. Opt. 1992, 31, 6676–6683. [Google Scholar] [CrossRef]
- Smith, M.H. Optimization of a dual-rotating-retarder Mueller matrix polarimeter. Appl. Opt. 2002, 41, 2488–2493. [Google Scholar] [CrossRef]
- Twietmeyer, K.M.; Chipman, R.A. Optimization of Mueller matrix polarimeters in the presence of error sources. Opt. Express 2008, 16, 11589–11603. [Google Scholar] [CrossRef]
- Huang, T.; Meng, R.; Qi, J.; Liu, Y.; Wang, X.; Chen, Y.; Liao, R.; Ma, H. Fast Mueller matrix microscope based on dual DoFP polarimeters. Opt. Lett. 2021, 46, 1676–1679. [Google Scholar] [CrossRef] [PubMed]
- Chenault, D.B.; Pezzaniti, J.L.; Chipman, R.A. Mueller matrix algorithms. Proc. SPIE 1992, 1746, 231. [Google Scholar] [CrossRef]
- Li, X.; Goudail, F.; Chen, S.C. Self-calibration for Mueller polarimeters based on DoFP polarization imagers. Opt. Lett. 2022, 47, 1415–1418. [Google Scholar] [CrossRef] [PubMed]
- Xuan, T.; Zhai, H.; He, H.; He, C.; Liu, S.; Ma, H. Self-registration of constant-step rotating Mueller matrix polarimeters. Opt. Lett. 2022, 47, 5797–5800. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Ghosh, N.; Wood, M.F.G.; Vitkin, I.A. Mueller matrix decomposition for extraction of individual polarization parameters from complex turbid media exhibiting multiple scattering, optical activity, and linear birefringence. J. Biomed. Opt. 2008, 13, 044036. [Google Scholar] [CrossRef]
- Pierangelo, A.; Nazac, A.; Benali, A.; Validire, P.; Cohen, H.; Novikova, T.; Ibrahim, B.H.; Manhas, S.; Fallet, C.; Antonelli, M.R.; et al. Polarimetric imaging of uterine cervix: A case study. Opt. Express 2013, 21, 14120–14130. [Google Scholar] [CrossRef]
- Liang, Y.; Qu, Z.; Zhong, Y.; Song, Z.; Li, S. Analysis of errors in polarimetry using a rotating waveplate. Appl. Opt. 2019, 58, 9883–9895. [Google Scholar] [CrossRef]
- Hu, Z.; Zhao, Q.; Ma, H. Optimal configurations of Mueller polarimeter for Gaussian-Poisson mixed noise. Appl. Sci. 2022, 12, 6521. [Google Scholar] [CrossRef]
- Ren, L.; Yang, X.; Huang, S.; Zhong, Z.; Peng, J.; Ye, L.; Hou, Y.; Zhang, B. Towards high-performance polarimeters with large-area uniform chiral shells: A comparative study on the polarization detection precision enabled by the Mueller matrix and deep learning algorithm. Opt. Express 2024, 32, 16414–16425. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.R.; Lotz, C.; Becker, F.K.G.; Dembski, S.; Novikova, T. Digital histology of tissue with Mueller microscopy and FastDBSCAN. Appl. Opt. 2022, 61, 9616–9624. [Google Scholar] [CrossRef]
- Robinson, D.; Hoong, K.; Kleijn, W.B.; Doronin, A.; Rehbinder, J.; Vizet, J.; Pierangelo, A.; Novikova, T. Polarimetric imaging for cervical pre-cancer screening aided by machine learning: Ex vivo studies. J. Biomed. Opt. 2023, 28, 102904. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; He, H.; Chen, Z.; Wang, Y.; Ma, H. Modulus design multiwavelength polarization microscope for transmission Mueller matrix imaging. J. Biomed. Opt. 2018, 23, 016007. [Google Scholar] [CrossRef]
- Parazzoli, C.G.; Greegor, R.B.; Li, K.; Koltenbah, B.E.C.; Tanielian, M. Experimental verification and simulation of negative index of refraction using Snell’s law. Phys. Rev. Lett. 2003, 90, 107401. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the mean absolute error (MAE) and the root mean square error (RMSE) in assessing rounding model. Mater. Sci. Eng. 2018, 324, 012049. [Google Scholar] [CrossRef]
- Karunasingha, D.S.K. Root mean square error or mean absolute error? Use their ratio as well. Inform. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Chipman, R.A. Mechanics of polarization ray tracing. Opt. Eng. 1995, 34, 1636. [Google Scholar] [CrossRef]
- Kärcher, V.; Kim, V.V.; Reddy, A.N.K.; Zacharias, H.; Ganeev, R.A. Generation of complex vector and vortex extreme ultraviolet beams using the S-waveplate and spiral phase plate during high-order harmonics generation in argon. ACS Photonics 2023, 10, 4519–4528. [Google Scholar] [CrossRef]
- Chen, T.A.; Tang, Y.; Zhang, L.J.; Chang, Y.E.; Zheng, C. Correction of astigmatism and coma using analytic theory of aberrations in imaging spectrometer based on concentric off-axis dual reflector system. Appl. Opt. 2014, 53, 565–576. [Google Scholar] [CrossRef] [PubMed]
- de Gracia, P.; Dorronsoro, C.; Gambra, E.; Marin, G.; Hernández, M.; Marcos, S. Combining coma with astigmatism can improve retinal image over astigmatism alone. Vis. Res. 2010, 50, 2008–2014. [Google Scholar] [CrossRef] [PubMed]
- Rusdiana, S.; Yuni, S.M.; Khairunnisa, D. Comparison of rainfall forecasting in simple moving average (SMA) and weighted moving average (WMA) methods (Case study at village of Gampong Blang Bintang, Big Aceh District-Sumatera-Indonesia. J. Res. Math. Trends Technol. 2020, 2, 21–27. [Google Scholar] [CrossRef]
- Deng, L.; Chen, C.; Yu, W.; Shao, C.; Shen, Z.; Wang, Y.; He, C.; Li, H.; Liu, Z.; He, H.; et al. Influence of hematoxylin and eosin staining on linear birefringence measurement of fibrous tissue structures in polarization microscopy. J. Biomed. Opt. 2023, 28, 102909. [Google Scholar] [CrossRef]


| Region | Relative Error | ||
|---|---|---|---|
| 1 | 0.2425 | 0.2614 | 0.0781 |
| 2 | 0.2412 | 0.2669 | 0.1063 |
| 3 | 0.2516 | 0.2747 | 0.0918 |
| 4 | 0.2514 | 0.2689 | 0.0699 |
| 5 | 0.2237 | 0.2477 | 0.1073 |
| 6 | 0.2348 | 0.2538 | 0.0808 |
| 7 | 0.2501 | 0.2684 | 0.0732 |
| 8 | 0.2271 | 0.2433 | 0.0710 |
| 9 | 0.2387 | 0.2629 | 0.1011 |
| 10 | 0.2572 | 0.2730 | 0.0615 |
| average | 0.2418 | 0.2621 | 0.0841 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, K.; Zeng, N.; Deng, L.; Liu, S.; Ma, H.; He, C.; He, H. Quantifying Influence of Beam Drift on Linear Retardance Measurement in Dual-Rotating Retarder Mueller Matrix Polarimetry. Photonics 2025, 12, 868. https://doi.org/10.3390/photonics12090868
Deng K, Zeng N, Deng L, Liu S, Ma H, He C, He H. Quantifying Influence of Beam Drift on Linear Retardance Measurement in Dual-Rotating Retarder Mueller Matrix Polarimetry. Photonics. 2025; 12(9):868. https://doi.org/10.3390/photonics12090868
Chicago/Turabian StyleDeng, Kaisha, Nan Zeng, Liangyu Deng, Shaoxiong Liu, Hui Ma, Chao He, and Honghui He. 2025. "Quantifying Influence of Beam Drift on Linear Retardance Measurement in Dual-Rotating Retarder Mueller Matrix Polarimetry" Photonics 12, no. 9: 868. https://doi.org/10.3390/photonics12090868
APA StyleDeng, K., Zeng, N., Deng, L., Liu, S., Ma, H., He, C., & He, H. (2025). Quantifying Influence of Beam Drift on Linear Retardance Measurement in Dual-Rotating Retarder Mueller Matrix Polarimetry. Photonics, 12(9), 868. https://doi.org/10.3390/photonics12090868






