Adaptive Transmission Performance of Underwater Autoencoder Group Based on DNN Channel Estimation
Abstract
1. Introduction
2. Underwater Joint Channel Model
2.1. Attenuation Channel Model
2.2. Turbulence Channel Model
3. Underwater Adaptive Transmission Scheme
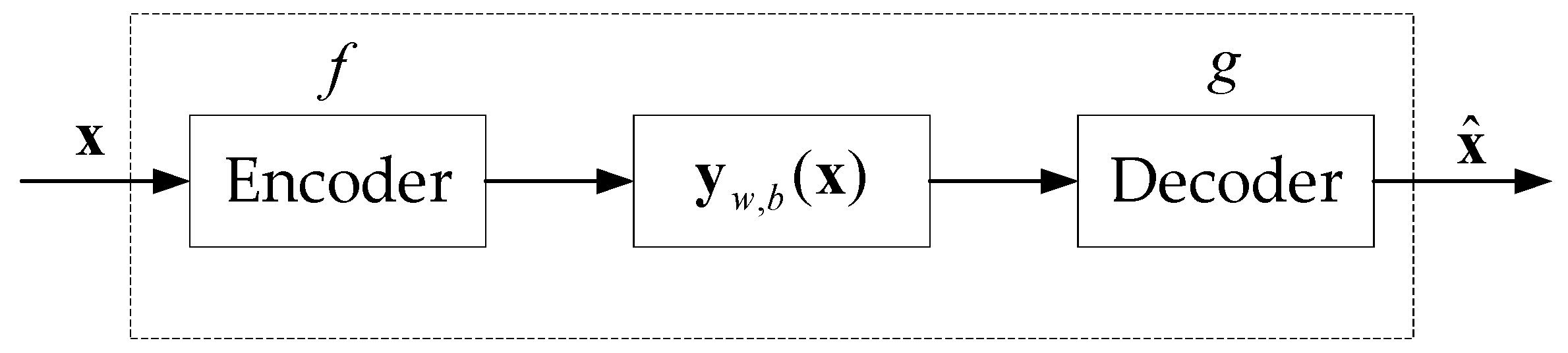
3.1. Underwater Autoencoders
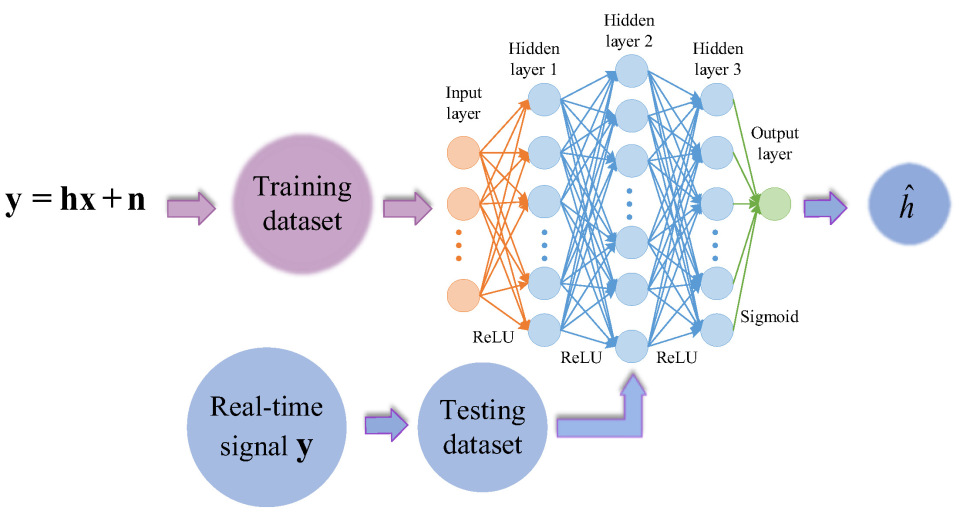
3.2. Underwater Channel Estimation Based on DNN
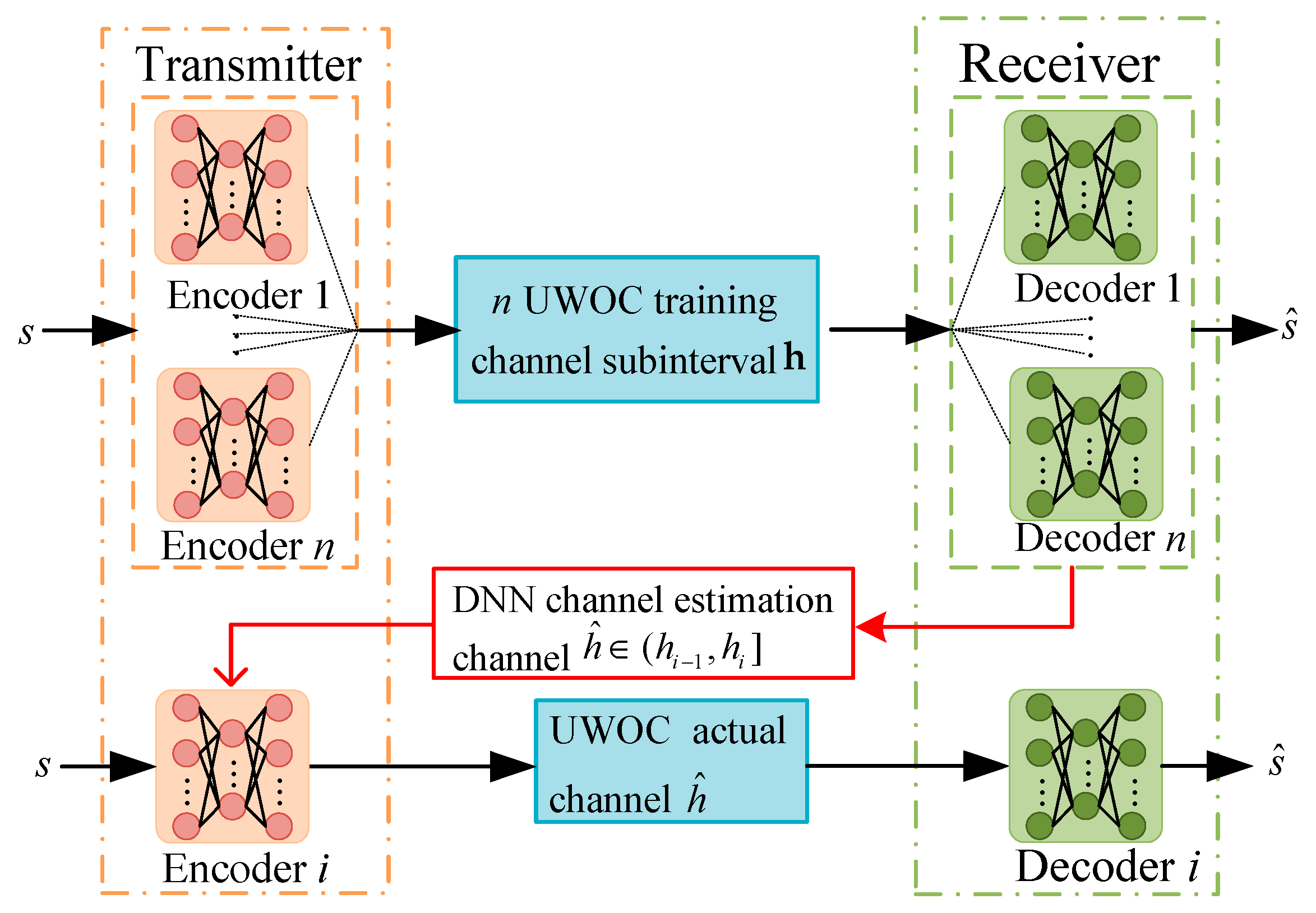
3.3. Adaptive Transmission of Autoencoder Groups
| Algorithm 1. Adaptive Transmission Using Real-Time Channel Estimation | |
| 1 | Input: n sub-intervals of channel fading, n pairs for encoder and decoder. |
| 2 | Output: The i-th pair of encoders and decoders used for sending and receiving data, estimated actual channel fading value . |
| 3 | Start |
| 4 | 1. (Offline) Training n pairs of encoders and decoders on n channel sub-intervals using a large training dataset consisting of all M possible one-hot vectors; |
| 5 | 2. (Online) Using DNN model to estimate the instantaneous underwater channel fading at the receiver and feed it back to the transmitter; |
| 6 | 3. (Online) if lies in the i-th sub-interval then |
| 7 | Select the i-th pair of encoder and decoder to send and receive data; |
| 8 | end if |
| 9 | 4. (Online) Estimate the real-time underwater channel fading; |
| 10 | if The estimated value has changed from the current sub-interval to another one then |
| 11 | Switch to the appropriate encoder and decoder in the group for data transmission. |
| 12 | end if |
| 13 | End |
4. Simulation Results and Analysis
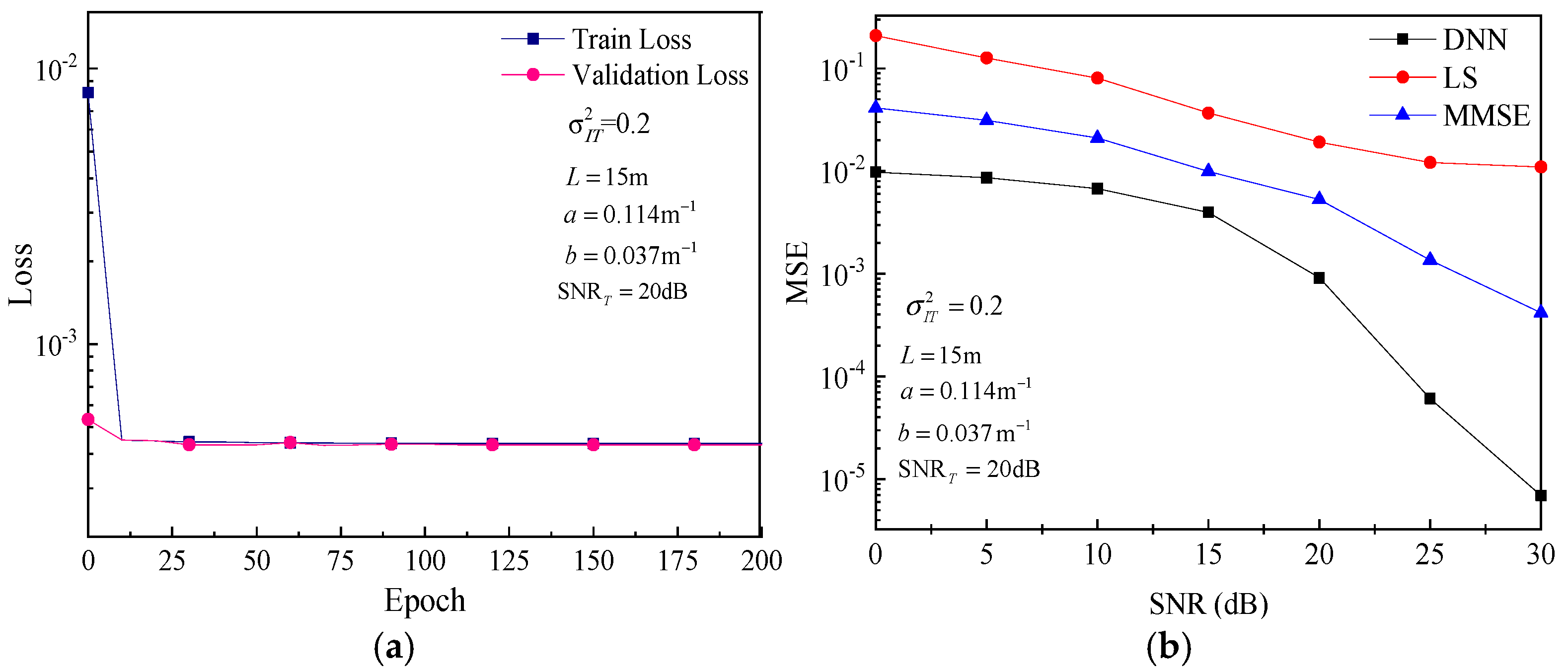
4.1. Performance Analysis of DNN Estimation Algorithm for Underwater Channel
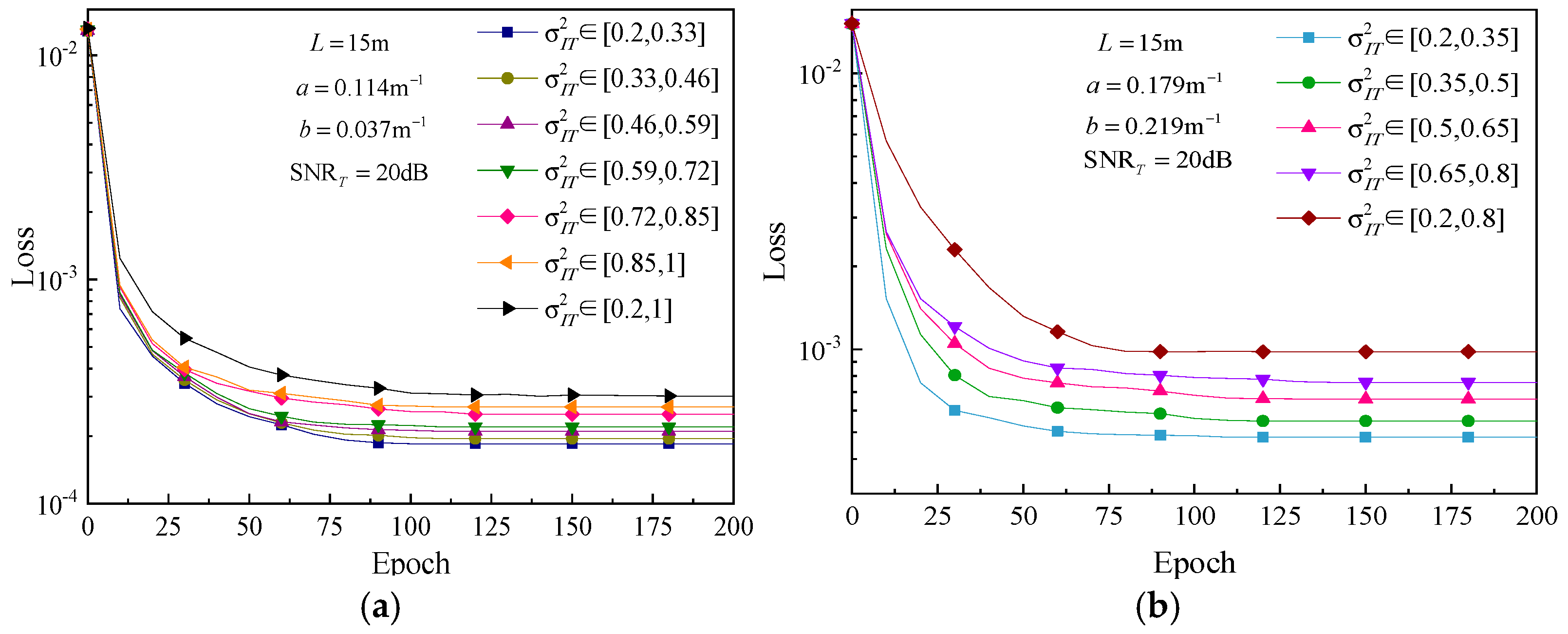
4.2. Performance Analysis of Autoencoder Transmission
4.2.1. Non-Adaptive Transmission
4.2.2. Adaptive Transmission
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Shamma’a, A.I.; Shaw, A.; Saman, S. Propagation of electromagnetic waves at MHz frequencies through seawater. IEEE Trans. Antennas Propag. 2004, 52, 2843–2849. [Google Scholar] [CrossRef]
- Sun, X.; Kang, C.H.; Kong, M.; Alkhazragi, O.; Guo, Y.; Ouhssain, M.; Weng, Y.; Jones, B.H.; Ng, T.K.; Ooi, B.S. A review on practical considerations and solutions in underwater wireless optical communication. J. Light. Technol. 2020, 38, 421–431. [Google Scholar] [CrossRef]
- Xu, J. Underwater wireless optical communication: Why, what, and how? Chin. Opt. Lett. 2019, 17, 100007. [Google Scholar] [CrossRef]
- Alipour, A.; Mir, A. On the performance of blue–green waves propagation through underwater optical wireless communication system. Photonic Netw. Commun. 2018, 36, 309–315. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Uysal, M. Visible light communication channel modeling for underwater environments with blocking and shadowing. IEEE Access 2017, 6, 1082–1090. [Google Scholar] [CrossRef]
- Ji, X.Y.; Yin, H.; Jing, L.; Liang, Y.; Wang, J. Performance analysis of underwater wireless optical communication system with strong turbulence channels based on strong fluctuation theory. Acta Opt. Sin. 2022, 42, 9–16. [Google Scholar] [CrossRef]
- Jamali, M.V.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical studies of fading in underwater wireless optical channels in the presence of air bubble, temperature, and salinity random variations. IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar] [CrossRef]
- Talaei Khoei, T.; Ould Slimane, H.; Kaabouch, N. Deep learning: Systematic review, models, challenges, and research directions. Neural Comput. Appl. 2023, 35, 23103–23124. [Google Scholar] [CrossRef]
- Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.H.F. Deep learning in physical layer communications. IEEE Wirel. Commun. 2019, 26, 93–99. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Karra, K.; Clancy, T.C. Learning to communicate: Channel auto-encoders, domain specific regularizers, and attention. In Proceedings of the 2016 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Limassol, Cyprus, 12–14 December 2016; pp. 223–228. [Google Scholar] [CrossRef]
- Mallik, W.; Jaiman, R.K.; Jelovica, J. Predicting transmission loss in underwater acoustics using convolutional recurrent autoencoder network. J. Acoust. Soc. Am. 2022, 152, 1627–1638. [Google Scholar] [CrossRef] [PubMed]
- Mirkarimi, F.; Tellambura, C.; Li, G.Y. Deep MMSE estimation for data detection. IEEE Commun. Lett. 2022, 27, 180–184. [Google Scholar] [CrossRef]
- Dörner, S.; Cammerer, S.; Hoydis, J.; Ten Brink, S. Deep learning based communication over the air. IEEE J. Sel. Top. Signal Process. 2017, 12, 132–143. [Google Scholar] [CrossRef]
- Aoudia, F.A.; Hoydis, J. End-to-end learning of communications systems without a channel model. In Proceedings of the 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 298–303. [Google Scholar] [CrossRef]
- Lu, H.; Jiang, M.; Cheng, J. Deep learning aided robust joint channel classification, channel estimation, and signal detection for underwater optical communication. IEEE Trans. Commun. 2020, 69, 2290–2303. [Google Scholar] [CrossRef]
- Gabriel, C.; Khalighi, M.A.; Bourennane, S.; Léon, P.; Rigaud, V. Monte-Carlo-based channel characterization for underwater optical communication systems. J. Opt. Commun. Netw. 2013, 5, 1–12. [Google Scholar] [CrossRef]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tutor. 2016, 19, 204–238. [Google Scholar] [CrossRef]
- Tang, S.; Dong, Y.; Zhang, X. Impulse response modeling for underwater wireless optical communication links. IEEE Trans. Commun. 2013, 62, 226–234. [Google Scholar] [CrossRef]
- Shi, J.; Huang, A.; Tao, L. Deep learning aided channel estimation and signal detection for underwater optical communication. Chin. J. Lasers 2022, 49, 110–117. [Google Scholar] [CrossRef]
- Ata, Y.; Kiasaleh, K. Analysis of optical wireless communication links in turbulent underwater channels with wide range of water parameters. IEEE Trans. Veh. Technol. 2023, 72, 6363–6374. [Google Scholar] [CrossRef]
- Andrews, L.C.; Beason, M.K. Laser Beam Propagation in Random Media: New and Advanced Topics; SPIE Publications: Bellingham, WA, USA, 2023. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. Available online: https://dl.acm.org/doi/abs/10.5555/2627435.2670313 (accessed on 21 August 2025).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Hu, J.; Bai, Z.; Yang, J.; Cai, Y.; Zhou, D.; Wang, Y.; Kwak, K. DNN and LS Based Channel Estimation in OTFS System. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 106–110. [Google Scholar] [CrossRef]



| Water Type | |||
|---|---|---|---|
| Pure sea water | 0.053 | 0.003 | 0.056 |
| Clear ocean water | 0.114 | 0.037 | 0.151 |
| Costal ocean water | 0.179 | 0.219 | 0.398 |
| Turbid harbor water | 0.295 | 1.875 | 2.17 |
| Simulation Parameters | Output Shape | Theoretical Parameters | |
|---|---|---|---|
| Transmitter | |||
| Input | 64 | M | |
| Dense (Reu layer) | 4160 | ||
| Dense (linear layer) | 455 | ||
| Normalization | 14 | ||
| Underwater channel | |||
| 14 | |||
| Additive white Gaussian noise | 14 | ||
| Receiver | |||
| Dense (ReLU layer) | 512 | ||
| Dense (Softmax layer) | 4160 |
| Parameter | Value |
|---|---|
| Optimizer | Adam |
| Loss function | MSE |
| Activation function | ReLU, Sigmoid |
| Number of training samples | |
| Number of test samples | |
| Number of input layer neurons | 7 |
| Number of neurons in hidden layer 1 | 500 |
| Number of neurons in hidden layer 2 | 250 |
| Number of neurons in hidden layer 3 | 120 |
| Number of output layer neurons | 1 |
| Maximum number of iterations epochs | 200 |
| Batch size quantity | 32 |
| Seawater Type | n | Channel Sub-Intervals |
|---|---|---|
| Clear seawater | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| Costal seawater | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Li, J.; Wang, R. Adaptive Transmission Performance of Underwater Autoencoder Group Based on DNN Channel Estimation. Photonics 2025, 12, 865. https://doi.org/10.3390/photonics12090865
Chen D, Li J, Wang R. Adaptive Transmission Performance of Underwater Autoencoder Group Based on DNN Channel Estimation. Photonics. 2025; 12(9):865. https://doi.org/10.3390/photonics12090865
Chicago/Turabian StyleChen, Dan, Jiongxuan Li, and Rui Wang. 2025. "Adaptive Transmission Performance of Underwater Autoencoder Group Based on DNN Channel Estimation" Photonics 12, no. 9: 865. https://doi.org/10.3390/photonics12090865
APA StyleChen, D., Li, J., & Wang, R. (2025). Adaptive Transmission Performance of Underwater Autoencoder Group Based on DNN Channel Estimation. Photonics, 12(9), 865. https://doi.org/10.3390/photonics12090865





