Abstract
Quartic solitons in ultrafast fibre lasers (intra-cavity optical fibre modulation systems) have been theoretically and experimentally analysed in recent years. However, there are few reports about extra-cavity modulating quartic solitons. In this situation, the purpose of this work is to investigate a quartic soliton’s extra-cavity modulation. In this paper, we theoretically simulate an extra-cavity-modulating quartic soliton with negative fourth-order dispersion at 1550 nm. The simulation relies on a physical model of a single-mode optical fibre system. Through controlling soliton parameters in an extra-cavity modulation system, a quartic soliton’s orthogonal polarisation modes will show unique characteristics depending on which kind of parameter is changed (seven parameters are considered for variation). For example, through the variation in the projection angle, only a horizontally polarised quartic soliton pulse is generated. These results explore the dynamics of quartic solitons in single-mode optical fibre modulation systems and are applicable to optical soliton transmission techniques in the field of optical fibre communication.
1. Introduction
Optical solitons have the characteristic of propagating over long distances without waveform distortions and exist in many types of nonlinear systems [1,2,3,4,5,6]. During past decades, the ultrafast fibre laser system was often selected as an ideal platforms with which to study optical soliton dynamics because it had the advantages of a compact and flexible structure, strong ability to resist electromagnetic interference, high heat dissipation efficiency, high laser beam quality, flexible parameter regulation and so on. Until now, optical solitons with specific properties (such as temporal pulse shape, optical spectrum and pulse chirp) have been theoretically studied and experimentally achieved, such as dispersion-managed solitons [7,8], dark solitons [9,10], dissipative solitons [11,12], noise-like pulses [13,14], dissipative soliton resonances [15,16], Kerr solitons [17,18], pure-quartic solitons [19,20,21,22,23,24,25] and so on. These research results effectively promote the exploration of optical solitons’ dynamic characteristics in optical fibre laser systems.
As a kind of intra-cavity modulation system, an ultrafast fibre laser can emit different optical solitons with appropriate intra-cavity parameter management. The controllable intra-cavity parameters include gain, loss, nonlinearity, dispersion, saturable energy, linear birefringence and some others. Gain can be varied through selecting a gain fibre with an appropriate length and absorption coefficient at a specific wavelength. Intra-cavity loss can be efficiently controlled by using an optical fibre attenuator. Nonlinearity is varied through controlling pump power or introducing a piece of optical fibre with high nonlinearity. Dispersion includes group-velocity dispersion and some other higher-order dispersions, which can be tuned with optical elements such as dispersion compensation fibres, chirped fibre Bragg grating, photonic crystal waveguide and spatial light modulators. Saturable energy depends on the saturable absorber that is adopted. The saturable absorber can be a real saturable absorber (such as SESAM, carbon nanotube, MXene, perovskite quantum dots and rare-earth-ion-doped fibre) or an artificial saturable absorber (such as nonlinear polarisation rotation). A change in linear birefringence in a fibre laser cavity can generate vector optical solitons when different intra-cavity parameters reach an equilibrium state. These vector solitons are group-velocity locked [26], polarisation locked [27] or polarisation rotated [28]. Different vector solitons have their own characteristics, including their orthogonal components’ central wavelengths, polarisation state, temporal pulse train and so on.
In addition to intra-cavity managing of optical solitons in ultrafast fibre laser cavities (oscillators or amplifiers), modulating optical solitons in extra-cavity optical fibre systems has also attracted some researchers’ attention [29,30,31,32]. For example, a dark bisoliton with a 1064 nm central wavelength was modulated in an extra-cavity manner based on an optical fibre system, and modulated orthogonal components showed unique properties in the time domain and frequency domain as different parameters varied [29]. Compared with intra-cavity modulation techniques, a larger tuning range in the time/frequency domain of optical solitons’ orthogonal components can be achieved with the adoption of extra-cavity modulation. So extra-cavity modulation systems can generate specific types of optical solitons, which is not easy for intra-cavtiy modulation systems. According to the structure, we classify extra-cavity modulation systems as single channel, dual-channel or multi-channel. In recent years, the extra-cavity modulation of optical solitons has already been studied by some researchers, and the relevant studies have potential applications in optical signal processing [33]. However, there are few reports about the extra-cavity modulation of quartic solitons. Recent studies indicate that quartic solitons can provide new ideas to develop high energy and high peak power laser pulses in ultrafast laser fields. For quartic solitons, fourth-order dispersion is introduced to compensate for higher-order nonlinear effects, which gives it the advantages of higher data rate and improved pulse quality in long-distance optical fibre transmission and high-power optical fibre transmission compared to conventional solitons. In this paper, we study the extra-cavity modulation of a quartic soliton with negative fourth-order dispersion at a 1550 nm wavelength regime. Through the control of several different extra-cavity parameters, the modulated quartic soliton can demonstrate different features in orthogonal polarisation direction and in the time domain and frequency domain. These results can provide meaningful values for developing fibre laser systems with quartic solitons.
2. Theoretical Physical Model
Figure 1 gives the physical model of our proposed modulation system. The fibre laser source can produce quartic soliton pulses. The quartic soliton pulses are modulated as follows: Firstly, the laser pulses are collimated by a collimator (COL1) and collected by another collimator (COL2). Through the mechanical rotation of three wave plates between the two COLs, the quartic soliton’s orthogonal phase difference can vary from zero to 2π, leading to the variation of the corresponding polarisation state. Secondly, the quartic soliton’s orthogonal electric fields are split by a polarisation beam splitter (PBS1) and combined by another polarisation beam splitter (PBS2). The two electric field amplitude modulators (AM1 and AM2) and two independent time delay lines (DL1 and DL2) are employed to independently change the orthogonal components’ amplitudes and orthogonal time delay, respectively. The fibres between PBS1 and PBS2 are polarisation-maintained (PM). Thirdly, the modulated quartic soliton’s polarisation state is further tuned by a polarisation controller (PC), then collimated by COL3 and split by PBS3. The orthogonally polarised components of modulated quartic solitons will demonstrate different characteristics as different parameters’ values change. It should be noted that the quartic soliton pulses can also be modulated directly in a single channel, but this method is usually used for modulating scalar soliton pulses.
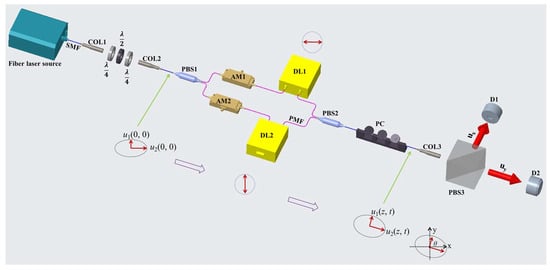
Figure 1.
Physical model of our simulation.
The governing equation of a quartic soliton with negative fourth-order dispersion is:
In this equation, u is an electric field. ξ, τ and δ4 can be expressed as following:
In Equations (2)–(4), z is the position variable and LD is the dispersion length (). ξ is the normalized propagation distance. t is the time variable. T0 is the initial pulse width. δ4 is related to β2, β4 and T0. β2 and β4 are second-order dispersion and fourth-order dispersion, respectively. In this work, β4 is as a negative number to get the quartic soliton solution of the governing equation. β4 can also be a positive number, but the relevant governing equation and soliton solution will be different.
The amplitudes after modulation and before the last PBS are expressed as follows:
In Equations (5) and (6), u1(z, t) and u2(z, t) are the quartic soliton’s electric field components in orthogonal directions after changing amplitude ratio, time delay, phase difference, propagation distances and fourth-order dispersion. u10 and u20 are constant amplitudes. ∆T is the time delay between the two orthogonal electric fields. z1 and z2 are the propagation distances. ∆φ is the orthogonal phase difference. λ is the central wavelength. The orthogonal electric fields are calculated with the following equation:
Here, θ is the modulated quartic soliton pulse’s projection angle on PBS3. ux(z, t) and uy(z, t) are the projected electric fields in a horizontal direction (x direction) and vertical direction (y direction). Modulated pulse shape intensities and optical spectral intensities are calculated with:
In Equations (8) and (9), Ij(z, t) and Ij(z, ω) are pulse shape intensities and optical spectral intensities in orthogonal polarisation directions. ω is angular frequency, i represents the unit complex number. Here, uj(z, ω) is a Fourier transform of uj(z, t). In our theoretical simulation, β2 and β4 are two important parameters that can induce variations in temporal pulse widths in orthogonal polarisations, finally influencing the achievable modulation bandwidth and the fidelity of the encoded information.
3. Simulation
In this part, we present the simulation results under variations in different soliton parameters. In the simulation, we assume T0 = 5 ps, λ = 1550 nm and β2 = −21 ps2/km.
Figure 2 shows extra-cavity-modulated orthogonal pulse shapes and the corresponding optical spectra when u2/u1 = 1/1.26, 1/1.13, 1/1, 1.13/1 and 1.26/1, θ = 20°, ∆T = 0 ps, ∆φ = 0, z1/LD = z2/LD = 0.1 and β4 = −1 ps4/km. In Figure 2a–e, as u2/u1 increases from 1/1.26 to 1/1, the horizontal/vertical pulse’s peak intensity decreases/increases. However, when u2/u1 increases from 1/1 to 1.26/1, both the orthogonal pulses’ peak intensities increase. These peak intensities’ variation tendencies are also applicable to corresponding optical spectra shown in Figure 2f–j. The relatively narrow (<1 nm) orthogonal optical spectrum bandwidths being shown in Figure 2f–j are accompanied by short temporal pulse widths (<1 ps). When u2/u1 = 1/1, orthogonal components still have different peak intensities in the time and frequency domains because θ ≠ 0°. Energy flow occurs between orthogonal directions in this situation, which comes from the projections of orthogonal electric fields on the axes of PBS3. It should be noted that the vertical component can have a higher peak intensity than the horizontal component in the time domain and frequency domain when u2/u1 increases further.
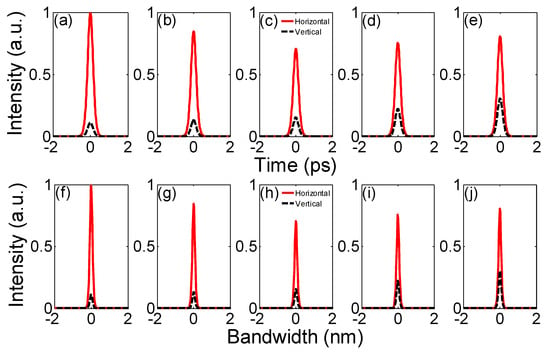
Figure 2.
Extra-cavity-modulated orthogonal pulse shapes (a–e) and optical spectral properties (f–j) as u2/u1 changes.
Figure 3 shows modulated quartic solitons’ temporal and frequency characteristics in output orthogonal polarisations when θ = 0°, 15°, 30°, 45° and 60°, u2/u1 = 1/1, ∆T = 0 ps, ∆φ = 0, z1/LD = z2/LD = 0.1 and β4 = −1 ps4/km. From these results, we can see orthogonal pulses and optical spectra are the same when θ = 0°, and the horizontal/vertical pulse’s peak intensity will increase/decrease as θ increases from 0° to 45°. When θ = 45°, the vertical mode disappears and only the horizontal mode exists, meaning only horizontally polarised quartic soliton pulses are generated in the case of symmetrical projection. When θ further increases to 60°, the horizontal/vertical pulse peak intensity decreases/increases. The orthogonal optical spectra have the same variation trends compared with the corresponding orthogonal pulses. It should be noted that θ can be increased further, and orthogonal pulses and optical spectra will overlap again when θ = 90°. The peak intensities of a vertical pulse and optical spectrum can be larger than a horizontal component’s when θ is larger than 90°.
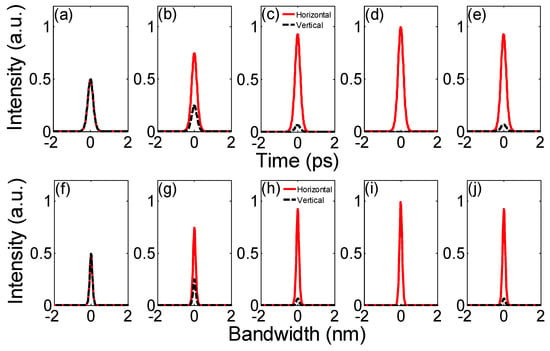
Figure 3.
Pulse shapes (a–e) and optical spectra properties (f–j) after PBS3 as θ changes.
Figure 4 shows extra-cavity-modulated quartic solitons’ orthogonal pulse shapes and optical spectra as ∆T = 0.1 ps, 0.2 ps, 0.3 ps, 0.4 ps and 0.5 ps, u2/u1 = 1/1, θ = 10°, ∆φ = 0, z1/LD = z2/LD = 0.1 and β4 = −1 ps4/km. In Figure 4a–e, the time delay between orthogonal pulses increases as ∆T increases, accompanied with amplitude variations. The peak intensity of a horizontally polarised pulse decreases with increased ∆T. And the situation is the contrary for a vertically polarised pulse. In Figure 4f–j, the orthogonal spectra-centering wavelengths are always centered at 1550 nm (see the zero point on the horizontal coordinate axis), with no obvious changes in peak intensities and 3 dB bandwidths as ∆T increases. The horizontal component always has a higher peak intensity than the vertical component either in time domain or frequency domain. When the time delay increases further, the vertical pulse’s peak intensity can be comparable to, but cannot exceed, the horizontal pulse’s peak intensity, while the vertical optical spectral peak intensity is always lower than the horizontal component’s.
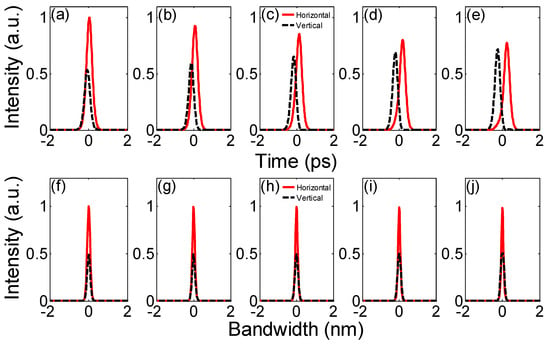
Figure 4.
Extra-cavity-modulated orthogonal pulse shapes (a–e) and optical spectra (f–j) of quartic solitons as ∆T changes.
Figure 5 shows the extra-cavity modulation results when ∆φ = π/9, 2π/9, π/3, 4π/9 and 5π/9, u2/u1 = 1/1, θ = 10°, ∆T = 0 ps, z1/LD = z2/LD = 0.1 and β4 = −1 ps4/km. In Figure 5a–e, the peak intensity of the horizontal/vertical pulse decreases/increases with increased ∆φ. It should be noted that the horizontal/vertical pulse’s peak intensity decreases/increases as ∆φ increases from 0 to π, and the orthogonal pulses overlap when ∆φ = π/2. After that, horizontal/vertical pulse peak intensity will increase/decrease when ∆φ increases from π to 2π. Orthogonal pulses will overlap again when ∆φ = 3π/2. And in Figure 5f–j, the optical spectral peak intensities have the same variation trends in orthogonal directions compared with the corresponding pulse shapes’ peak intensities. We can see that the vertical component has higher temporal and optical spectral peak intensities than the horizontal component when ∆φ = 5π/9. Orthogonal pulses and optical spectra are always different when u2/u1 = 1/1, except for some specific ∆φ values.
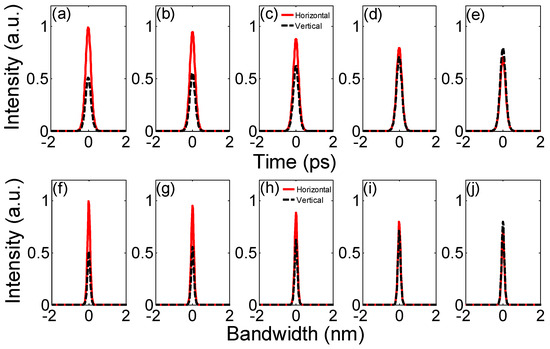
Figure 5.
Extra-cavity modulated orthogonal pulse shapes (a–e) and optical spectra (f–j) of quartic solitons as ∆φ changes.
Figure 6 shows the extra-cavity-modulated orthogonal components’ properties when z1/LD = z2/LD = 0.2, 0.3, 0.4, 0.5 and 0.6, u2/u1 = 1/1, θ = 10°, ∆T = 0 ps, ∆φ = π/9 and β4 = −1 ps4/km. Figure 6 shows that, as z1/LD or z2/LD increases, both pulse shapes in Figure 6a–e and optical spectra in Figure 6f–j have no obvious changes. These results mean that modulated quartic solitons are robust or insensitive to changes in soliton propagation distances when z1/LD = z2/LD. If z1/LD or z2/LD further increases, orthogonal pulse shapes and optical spectra still maintain their stability, demonstrating that a quartic soliton can keep its temporal and spectral properties in long-distance propagation when z1/LD = z2/LD. The horizontal pulse/optical spectrum’s peak intensity is always higher than that for vertical component because θ ≠ 0°.
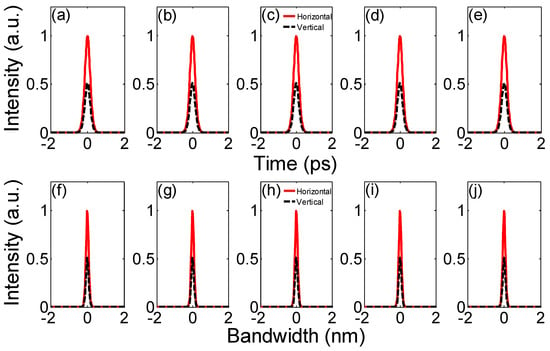
Figure 6.
Extra-cavity-modulated orthogonal components’ properties in the time domain (a–e) and frequency domain (f–j) as z1/LD or z2/LD changes (z1/LD = z2/LD).
Figure 7 shows pulse shapes and corresponding optical spectral properties in an output terminal when z1/LD = 0.1, z2/LD = 0.2, 0.3, 0.4, 0.5 and 0.6., u2/u1 = 1/1, θ = 10°, ∆T = 0 ps, ∆φ = π/9 and β4 = −1 ps4/km. Figure 7 shows that horizontal/vertical component time domain and frequency domain peak intensities decrease/increase as z2/LD increases, which is different from the simulation results shown in Figure 6. This variation trend in orthogonal polarisations means energy flow occurs between orthogonal components when orthogonal soliton components have different propagation distances. Horizontal component peak intensity is always at a higher level than that of vertical peak intensity, either in the time domain or frequency domain. If z2/LD increases further, orthogonal pulses and corresponding optical spectra will overlap when z2/LD = 1. And when z2/LD > 1, the vertical component’s pulse shape and optical spectrum have higher peak intensities than the horizontal peak intensities.
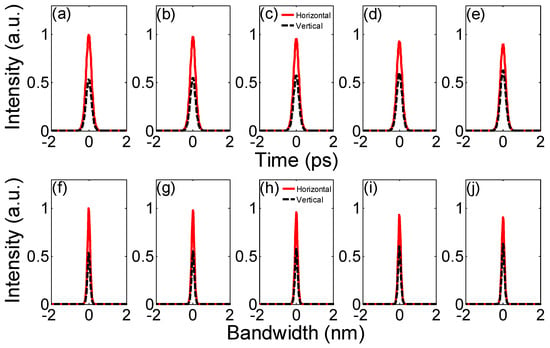
Figure 7.
Orthogonal pulse shapes (a–e) and optical spectral properties (f–j) after extra-cavity modulation as z2/LD changes (z1/LD ≠ z2/LD).
Figure 8 shows modulated quartic soliton properties in output orthogonal directions when β4 = −1 ps4/km, −2 ps4/km, −3 ps4/km, −4 ps4/km and −5 ps4/km, u2/u1 = 1/1, θ = 10°, ∆T = 0 ps, ∆φ = π/10 and z1/LD = z2/LD = 0.1. β4 can be varied with an intra-cavity spectral pulse shaper, which is located in the fibre laser source in Figure 1. In Figure 8a–e, orthogonal pulse peak intensities are almost unchanged when β4 changes. However, orthogonal pulse widths will increase as β4 varies from −1 ps4/km to −5 ps4/km, meaning that, in the design of long-distance optical fibre modulation system, β4 should be carefully controlled to avoid temporal pulse broadening. In Figure 8f–j, orthogonal optical spectral peak intensities increase with the increased absolute value of β4. The reason is that increased temporal pulse widths will induce decreased frequency domain bandwidths. According to the Parseval theorem, the total energy in the time domain and frequency domain are the same. Considering the total energy in one polarisation direction increases as increases, the corresponding peak intensity in Figure 8f–j will increase. And the horizontal component’s temporal peak intensity and optical spectral peak intensity are always higher than the vertical component’s, even if increases further.
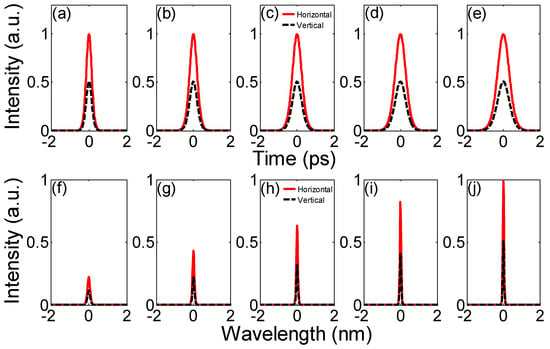
Figure 8.
Time domain (a–e) and frequency domain (f–j) properties of modulated quartic solitons as β4 changes.
4. Discussion
From the simulation results described above, we can see different soliton parameters will have different influences on the characteristics of pulse shapes and optical spectra in orthogonal polarisations. In previous works, studies about extra-cavity modulating optical fibre solitons focused on a normal or anomalous second-order dispersion regime, without consideration of higher-order dispersion [29,30,31,32]. In this manuscript, negative fourth-order dispersion is considered at an anomalous second-order dispersion regime. It is found that negative fourth-order dispersion can significantly influence the temporal pulse widths and optical spectral peak intensities of a modulated quartic soliton’s orthogonal components. In our future work, positive fourth-order dispersion will be considered to investigate extra-cavity-modulating self-similar quartic soliton pulses. Furthermore, the dual-channel structure can be replaced by a multi-channel structure to modulate soliton properties more flexibly, but it will also increase the complexity of the modulation system.
5. Conclusions
In the above-mentioned simulations, we mainly investigate extra-cavity-modulating a quartic soliton with negative fourth-order dispersion at 1550 nm wavelength regime. Different extra-cavity parameters were varied (including amplitude ratio, projection angle, time delay, orthogonal phase difference, propagation distances and fourth-order dispersion), to achieve the modulation of an input quartic soliton in a large adjustment range. The simulation results provided meaningful reference values for exploring quartic solitons’ dynamics in nonlinear optical fibre modulation systems. Additionally, research about extra-cavity modulation of a 1550 nm quartic soliton with negative fourth-order dispersion can find potential applications in C-band optical fibre soliton communication fields. These results also provide a new idea for modulating optical solitons with higher-order dispersions.
Author Contributions
Conceptualization, Y.Z.; methodology, D.T.; software, D.W., H.W. and Y.P.; validation, D.W.; formal analysis, J.Z.; investigation, D.T.; data curation, Y.Z.; writing—original draft preparation, D.W.; writing—review and editing, Y.Z.; supervision, Y.Z.; project administration, Y.Z. and D.W.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62105208; Collaborative Innovation Fund of Shanghai Institute of Technology, grant number XTCX2022-32 and College Students’ Innovation and Entrepreneurship Project of Shanghai Institute of Technology, grant numbers S202510259579, S202510259580, S202510259581, S202510259591, S202510259592, and X2025102591513.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Y.; Wang, M.H. Research progress on all-polarization-maintaining mode-locked fiber lasers. Photonics 2025, 12, 36. [Google Scholar] [CrossRef]
- Agrawal, G.P. Temporal reflection from ultrashort solitons in nonlinear dispersive medium: Impact of Raman scattering. Photonics 2024, 11, 1189. [Google Scholar] [CrossRef]
- Yang, Y.T.; Zeng, Q.; Yang, Y.Z.; Du, G.G.; Ji, J.H.; Song, Y.F.; Wang, Z.H.; Wang, K. Generation and dynamics of multiple pulses in an ultrafast fiber laser with a single-mode fiber-graded-index multimode fiber-single-mode fiber-based saturable absorber. Photonics 2024, 11, 52. [Google Scholar] [CrossRef]
- Yildirim, Y.; Biswas, A. Optical solitons for the concatenation model with differential group delay having multiplicative white noise by F-expansion approach. Phys. Lett. A 2024, 527, 129998. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A.; Moraru, L.; Moldovanu, S. Highly dispersive optical solitons in absence of self-phase modulation by Laplace-Adomian decomposition. Photonics 2023, 10, 114. [Google Scholar] [CrossRef]
- Zhong, W.P.; Belić, M.; Yang, Z.P. Optical wave packet compression using counterpropagating Scorer beams. Commun. Theor. Phys. 2025, 77, 055501. [Google Scholar] [CrossRef]
- Feng, N.; Yuan, Z.R.; Tang, H.T.; Zhou, R.L.; Nakkeeran, K.; Ji, E.C. Dispersion-managed all polarization-maintaining 2μm mode-locked fiber laser with nonreciprocal phase bias. Opt. Laser Technol. 2025, 183, 112340. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, H.D.; Zheng, J.W.; Li, J.B.; Zhang, F.; Fan, M.Q.; Xiang, X.J.; Tian, X.C.; Huang, Z.M.; Zhang, R.; et al. Transient behaviors in a spectrum-tailored all-PM NALM mode-locked fiber laser. Opt. Express 2024, 32, 25223–25234. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Jia, S.J.; Wang, S.B.; Farrell, G.; Li, Z.R.; Wang, P.F. Observation of mid infrared domain-wall dark pulses in an Er3+/Pr3+ co-doped InF3-glass based fiber laser. J. Light. Technol. 2025, 43, 4940–4944. [Google Scholar] [CrossRef]
- Lv, C.; Yin, B.; Ding, X.R.; Lv, Y.Z.; Wang, Y.M.; Sun, Z.G.; Xiao, S.Y.; Wang, M.G.; Pei, L.; Wu, S.H. Switchable dual-wavelength bright/dark pulses cylindrical vector beams fiber laser based on SMF-GIFMF-SMF as saturable absorber. Opt. Laser Technol. 2025, 184, 112513. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.W.; Lin, W.; Hu, X.; Xu, H.J.; Ma, Y.C.; Liang, Z.H.; Ling, L.; Xiong, Z.J.; Guo, Y.K.; et al. Polarization symmetry breaking of GHz dissipative solitons. Phys. Rev. Lett. 2025, 134, 213803. [Google Scholar] [CrossRef]
- Huang, X.Z.; Li, X.H.; Chen, E.C.; Pan, Z.W.; Guo, P.L.; Sun, L.X.; Wang, Y.S.; Zhao, W. Power-guided asymmetrical vector dissipative soliton molecules in a compact fiber resonator. IEEE J. Sel. Top. Quant. 2024, 30, 2100106. [Google Scholar] [CrossRef]
- Li, M.; Qin, L.; Li, X.W.; Zhang, J.X.; Zhang, Y.B.; Li, J.S.; Li, S.G.; Li, G. Study on characteristics of noise-like pulses and dissipative soliton resonance pulses in nonlinear multimode interference mode-locked fiber lasers. Opt. Laser Technol. 2025, 187, 112799. [Google Scholar] [CrossRef]
- Zhao, D.S.; Zhu, X.R.; Wu, Z.X.; Wang, J.W.; Li, X.; Tian, L.; Chen, L.R.; Zheng, Y.H. Direct generation and amplification of ultra-broadband noise-like pulse in an all-PM Tm-doped fiber laser system. J. Light. Technol. 2025, 43, 5843–5849. [Google Scholar] [CrossRef]
- Li, Y.; Mu, Y.; Xi, F.; Wang, X.; Li, X.H. 1.6 μm dissipative soliton resonance fiber laser based on nonlinear loop mirror. Opt. Laser Technol. 2025, 183, 112304. [Google Scholar] [CrossRef]
- Zou, J.H.; Pang, X.Y.; Luo, Z.Q. All-fiber mode-locked deep-red laser by a phase-biased NOLM. J. Light. Technol. 2025, 43, 4981–4987. [Google Scholar] [CrossRef]
- Yao, B.C.; Wang, W.T.; Xie, Z.D.; Zhou, Q.; Tan, T.; Zhou, H.; Guo, G.C.; Zhu, S.N.; Zhu, N.H.; Wong, C.W. Interdisciplinary advances in microcombs: Bridging physics and information technology. Elight 2024, 4, 19. [Google Scholar] [CrossRef]
- Yang, Q.F.; Hu, Y.W.; Torres-Company, V.; Vahala, K. Efficient microresonator frequency combs. Elight 2024, 4, 18. [Google Scholar] [CrossRef]
- Dai, X.L.; Qi, Y.Y.; Yu, Q.X.; He, C.J.; Yang, S.; Lu, Z.W. Comparative robustness analysis of quadratic solitons and pure-quartic solitons. Chaos Solitons Fract. 2025, 197, 116506. [Google Scholar] [CrossRef]
- Zou, D.F.; Guo, P.L.; Liu, R.M.; Zhang, A.Y.; Li, J.L.; Chen, G.J.; Dang, H.; Li, X.H.; Song, Y.J.; Shum, P.P. Quantum diffusion of pure-quartic solitons in a laser cavity. Opt. Express 2025, 33, 1427–1447. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; de Sterke, C.M.; Sipe, J.E.; Krauss, T.F.; Eggleton, B.J.; Husko, C. Pure-quartic solitons. Nat. Commun. 2016, 7, 10427. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Hudson, D.D.; Tam, K.K.K.; de Sterke, C.M.; Blanco-Redondo, A. The pure-quartic soliton laser. Nat. Photonics 2020, 14, 492–497. [Google Scholar] [CrossRef]
- Wang, Z.T.; Mao, Y.F.; Ling, X.H.; Zhang, L.F. Nonlinear evolution of modulational instability under the interaction of Kerr nonlinearity with pure higher, even-order dispersion. Opt. Express 2023, 31, 42338–42346. [Google Scholar] [CrossRef]
- Zhang, J.H.; Jia, Y.H.; Lan, W.Z.; Kudryashov, N.A.; Wang, X.Y.; Dai, C.Q. From metastable to stable states: Stability and explosion of pure-quartic soliton induced by the spectral filtering in fiber laser. Chaos Solitons Fract. 2025, 192, 116094. [Google Scholar] [CrossRef]
- Zhang, J.H.; Qin, H.Q.; Si, Z.Z.; Jia, Y.H.; Kudryashov, N.A.; Wang, Y.Y.; Dai, C.Q. Pure-quartic soliton attracted state and multi-soliton molecules in mode-locked fiber lasers. Chaos Solitons Fract. 2024, 187, 115380. [Google Scholar] [CrossRef]
- Song, Y.F.; Huang, S.P.; Wang, Z.H.; Lin, J.H.; Tung, J.C. High-performance tunable vector soliton pulse generation in Thulium-Holmium co-doped fiber lasers utilizing a HNLF-GIMF saturable absorber. J. Light. Technol. 2025, 43, 4988–4994. [Google Scholar] [CrossRef]
- Lan, H.W.; Chen, F.L.; Komarov, A.; Komarov, K.; Tang, X.H.; Tang, M.; Zhu, H.Y.; Zhao, L.M. Period-doubling bifurcation and polarization dynamics of vector solitons in a fiber laser. Phys. Rev. A 2024, 110, 053505. [Google Scholar] [CrossRef]
- Li, K.X.; Wang, X.D.; Geng, X.; Lu, M.X.; Fu, M.Z.; Fan, Y.H.; Li, S.W. Real-time observation of stationary and pulsating noise-like vector pulses in a fiber laser. Opt. Express 2023, 31, 23406–23418. [Google Scholar] [CrossRef]
- Wang, D.Y.; Zhang, Y.S.; Wang, H.M.; Tang, D.Q.; Zhan, J.X.; Zhou, Y. Extra-cavity modulating a dark bisoliton. Phys. Scr. 2025, 100, 015541. [Google Scholar] [CrossRef]
- Tang, D.Q.; Zhan, J.X.; Wang, D.Y.; Wang, H.M.; Peng, Y.Y.; Tiu, Z.C.; Zhou, Y. Extra-cavity modulating a soliton molecule with chirped Gaussian pulse shape. Photonics 2024, 11, 1098. [Google Scholar] [CrossRef]
- Wu, Z.C.; Hua, S.H.; Xu, C.Y.; Zhao, Y.Z.; Pan, J.X.; Luo, D.; Zhang, J.; Huang, T.Y. Extra-cavity manipulation from traditional scalar to flexible vector solitons. J. Opt. Soc. Am. B 2022, 39, 2181–2185. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.F.; Fang, Y.Z.; Liao, M.S. Generation of pseudo-high-order polarization-locked vector solitons. J. Technol. 2020, 20, 196–201. [Google Scholar]
- Kim, C.J.; Lu, X.D.; Kong, D.M.; Chen, N.; Chen, Y.T.; Oxenløwe, L.K.; Yvind, K.; Zhang, X.L.; Yang, L.; Pu, M.H.; et al. Parity-time symmetry enabled ultra-efficient nonlinear optical signal processing. Elight 2024, 4, 6. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).