Low-Light Image Enhancement with Residual Diffusion Model in Wavelet Domain
Abstract
1. Introduction
- We propose a low-light image enhancement method that utilizes the residual diffusion model in conjunction with the discrete wavelet transform. The residual diffusion model is employed to learn the mapping of low-frequency coefficients during the conversion from low-light to normal-light images.
- We designed a dual cross-coefficients recovery module to restore high-frequency coefficients. Additionally, we developed a perturbation compensation module to mitigate the impact of noise artifacts.
- Extensive experimental results on public low-light datasets demonstrate that our method outperforms previous diffusion-based approaches in both distortion metrics and perceptual quality, while also significantly increasing inference speed.
2. Related Work
2.1. Diffusion Models in Images Restoration
2.2. Low-Light Image Enhancement
3. Preliminaries: Diffusion Models
3.1. Forward Diffusion Process
3.2. Reverse Denoising Process
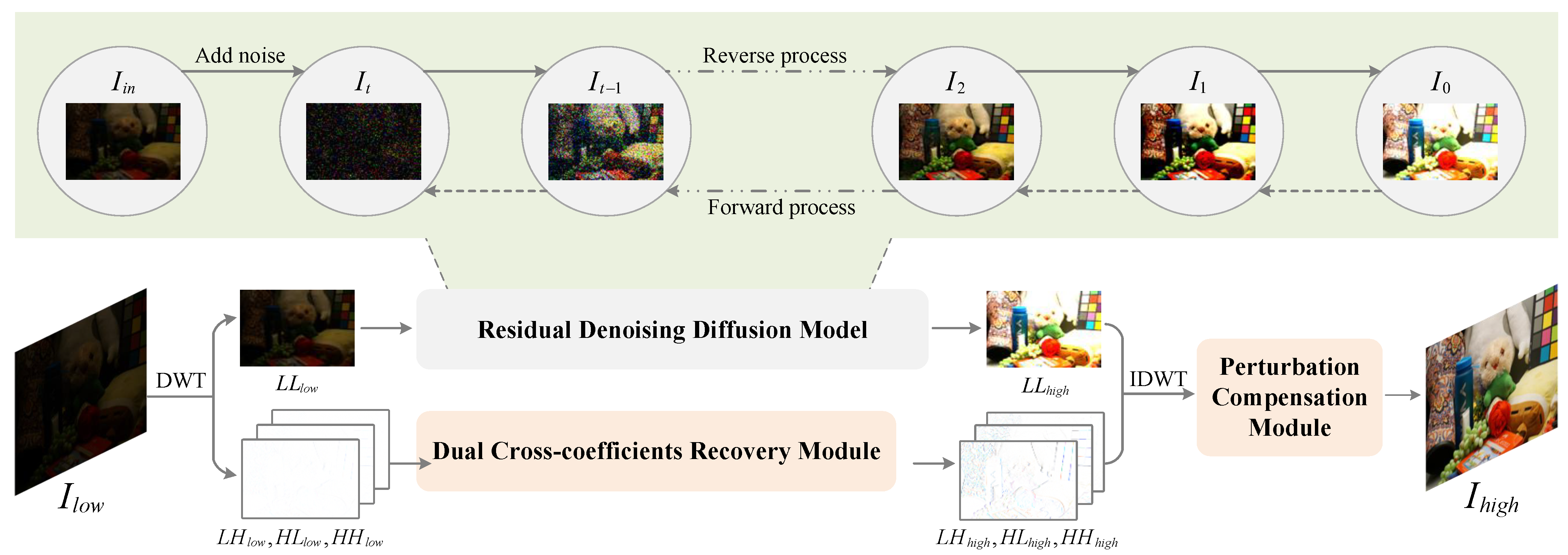
4. Method
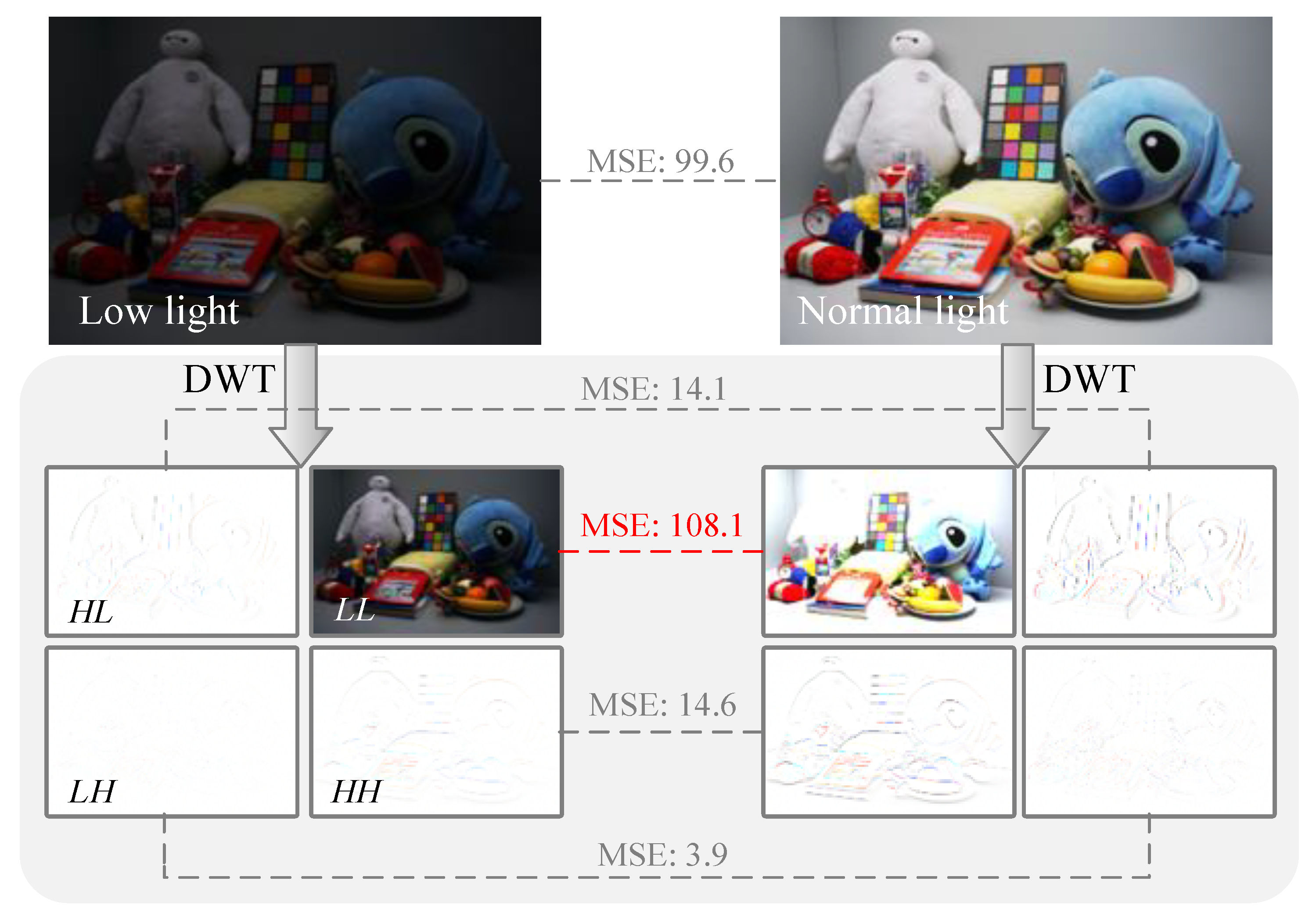
4.1. Discrete Wavelet Transform
4.2. Residual Denoising Diffusion Models
4.2.1. Forward Process
4.2.2. Reverse Process
4.3. Dual Cross-Coefficients Recovery Module
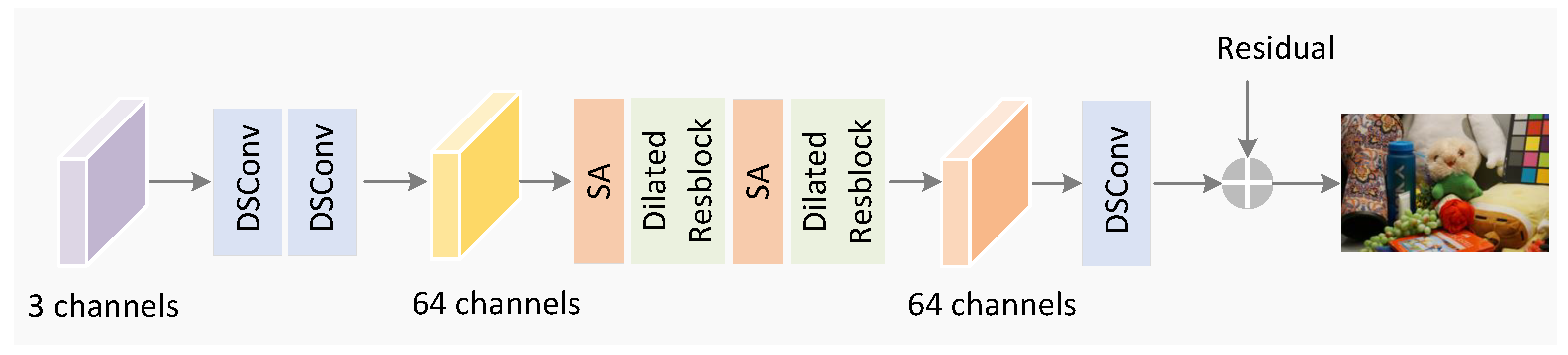
4.4. Perturbation Compensation Module
4.5. Training Loss
5. Experiments
5.1. Experimental Settings
5.2. Comparison with State-of-the-Art Approaches
5.3. Low-Light Object Detection
5.4. Ablation Study
5.4.1. Image Preprocessing
5.4.2. Loss Function
5.4.3. Module Architecture
5.4.4. Noise Factor and Sampling Steps
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, K.; Kapoor, R.; Sinha, S.K. Enhancement of low exposure images via recursive histogram equalization algorithms. Optik 2015, 126, 2619–2625. [Google Scholar] [CrossRef]
- Wang, Q.; Ward, R.K. Fast image/video contrast enhancement based on weighted thresholded histogram equalization. IEEE Trans. Consum. Electron. 2007, 53, 757–764. [Google Scholar] [CrossRef]
- Rahman, Z.U.; Jobson, D.J.; Woodell, G.A. Multi-scale retinex for color image enhancement. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; Volume 3, pp. 1003–1006. [Google Scholar]
- Cai, R.; Chen, Z. Brain-like retinex: A biologically plausible retinex algorithm for low light image enhancement. Pattern Recognit. 2023, 136, 109195. [Google Scholar] [CrossRef]
- Tang, Q.; Yang, J.; He, X.; Jia, W.; Zhang, Q.; Liu, H. Nighttime image dehazing based on Retinex and dark channel prior using Taylor series expansion. Comput. Vis. Image Underst. 2021, 202, 103086. [Google Scholar] [CrossRef]
- Wei, C.; Wang, W.; Yang, W.; Liu, J. Deep retinex decomposition for low-light enhancement. arXiv 2018, arXiv:1808.04560. [Google Scholar] [CrossRef]
- Jiang, Y.; Gong, X.; Liu, D.; Cheng, Y.; Wang, Z. EnlightenGAN: Deep Light Enhancement Without Paired Supervision. IEEE Trans. Image Process. 2021, 30, 2340–2349. [Google Scholar] [CrossRef]
- Wang, Z.; Cun, X.; Bao, J.; Zhou, W.; Liu, J.; Li, H. Uformer: A general u-shaped transformer for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 17683–17693. [Google Scholar]
- Cai, Y.; Bian, H.; Lin, J.; Wang, H.; Timofte, R.; Zhang, Y. Retinexformer: One-stage retinex-based transformer for low-light image enhancement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 12504–12513. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image super-resolution via iterative refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4713–4726. [Google Scholar] [CrossRef] [PubMed]
- Saharia, C.; Chan, W.; Chang, H.; Lee, C.; Ho, J.; Salimans, T.; Fleet, D.; Norouzi, M. Palette: Image-to-image diffusion models. In Proceedings of the ACM SIGGRAPH 2022 Conference Proceedings, Vancouver, BC, Canada, 8–11 August 2022; pp. 1–10. [Google Scholar]
- Yi, X.; Xu, H.; Zhang, H.; Tang, L.; Ma, J. Diff-retinex: Rethinking low-light image enhancement with a generative diffusion model. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 12302–12311. [Google Scholar]
- Yang, S.; Zhang, X.; Wang, Y.; Yu, J.; Wang, Y.; Zhang, J. Difflle: Diffusion-guided domain calibration for unsupervised low-light image enhancement. arXiv 2023, arXiv:2308.09279. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Ho, J.; Salimans, T. Classifier-free diffusion guidance. arXiv 2022, arXiv:2207.12598. [Google Scholar] [CrossRef]
- Jiang, H.; Luo, A.; Fan, H.; Han, S.; Liu, S. Low-light image enhancement with wavelet-based diffusion models. ACM Trans. Graph. (TOG) 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Wang, W.; Yang, H.; Fu, J.; Liu, J. Zero-reference low-light enhancement via physical quadruple priors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 26057–26066. [Google Scholar]
- Liu, J.; Wang, Q.; Fan, H.; Wang, Y.; Tang, Y.; Qu, L. Residual denoising diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2773–2783. [Google Scholar]
- Zheng, D.; Wu, X.M.; Yang, S.; Zhang, J.; Hu, J.F.; Zheng, W.S. Selective hourglass mapping for universal image restoration based on diffusion model. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 25445–25455. [Google Scholar]
- Wang, S.; Zheng, J.; Hu, H.M.; Li, B. Naturalness preserved enhancement algorithm for non-uniform illumination images. IEEE Trans. Image Process. 2013, 22, 3538–3548. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.P.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar]
- Guo, X.; Li, Y.; Ling, H. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans. Image Process. 2016, 26, 982–993. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning enriched features for real image restoration and enhancement. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020. Proceedings, Part XXV 16. pp. 492–511. [Google Scholar]
- Guo, C.; Li, C.; Guo, J.; Loy, C.C.; Hou, J.; Kwong, S.; Cong, R. Zero-reference deep curve estimation for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, online, 16–18 June 2020; pp. 1780–1789. [Google Scholar]
- Li, C.; Guo, C.; Loy, C.C. Learning to enhance low-light image via zero-reference deep curve estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4225–4238. [Google Scholar] [CrossRef]
- Liu, R.; Ma, L.; Zhang, J.; Fan, X.; Luo, Z. Retinex-inspired unrolling with cooperative prior architecture search for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10561–10570. [Google Scholar]
- Wu, W.; Weng, J.; Zhang, P.; Wang, X.; Yang, W.; Jiang, J. Uretinex-net: Retinex-based deep unfolding network for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 5901–5910. [Google Scholar]
- Ma, L.; Ma, T.; Liu, R.; Fan, X.; Luo, Z. Toward fast, flexible, and robust low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 5637–5646. [Google Scholar]
- Li, C.; Guo, C.L.; Zhou, M.; Liang, Z.; Zhou, S.; Feng, R.; Loy, C.C. Embedding fourier for ultra-high-definition low-light image enhancement. arXiv 2023, arXiv:2302.11831. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Wang, T.; Zhang, K.; Shen, T.; Luo, W.; Stenger, B.; Lu, T. Ultra-high-definition low-light image enhancement: A benchmark and transformer-based method. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 2654–2662. [Google Scholar]
- Van Den Oord, A.; Vinyals, O.; Kavukcuoglu, K. Neural discrete representation learning. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Hai, J.; Yang, R.; Yu, Y.; Han, S. Combining spatial and frequency information for image deblurring. IEEE Signal Process. Lett. 2022, 29, 1679–1683. [Google Scholar] [CrossRef]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Paszke, A. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yang, W.; Wang, S.; Fang, Y.; Wang, Y.; Liu, J. From fidelity to perceptual quality: A semi-supervised approach for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 14–19 June 2020; pp. 3063–3072. [Google Scholar]
- Chen, C.; Chen, Q.; Xu, J.; Koltun, V. Learning to see in the dark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3291–3300. [Google Scholar]
- Hai, J.; Xuan, Z.; Yang, R.; Hao, Y.; Zou, F.; Lin, F.; Han, S. R2rnet: Low-light image enhancement via real-low to real-normal network. J. Vis. Commun. Image Represent. 2023, 90, 103712. [Google Scholar] [CrossRef]
- Lee, C.; Lee, C.; Kim, C.S. Contrast enhancement based on layered difference representation of 2D histograms. IEEE Trans. Image Process. 2013, 22, 5372–5384. [Google Scholar] [CrossRef]
- Lee, C.; Lee, C.; Lee, Y.Y.; Kim, C.S. Power-constrained contrast enhancement for emissive displays based on histogram equalization. IEEE Trans. Image Process. 2011, 21, 80–93. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, F.; Cao, M.; Zhang, J.; Shao, Y.; Wang, Y.; Sang, N. Real-time exposure correction via collaborative transformations and adaptive sampling. In Proceedings of the of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 2984–2994. [Google Scholar]
- Loh, Y.P.; Chan, C.S. Getting to know low-light images with the exclusively dark dataset. Comput. Vis. Image Underst. 2019, 178, 30–42. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. Yolov11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Hou, R.; Chang, H.; Ma, B.; Shan, S.; Chen, X. Cross attention network for few-shot classification. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Yi, X.; Xu, H.; Zhang, H.; Tang, L.; Ma, J. Diff-Retinex++: Retinex-Driven Reinforced Diffusion Model for Low-Light Image Enhancement. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 6823–6841. [Google Scholar] [CrossRef] [PubMed]





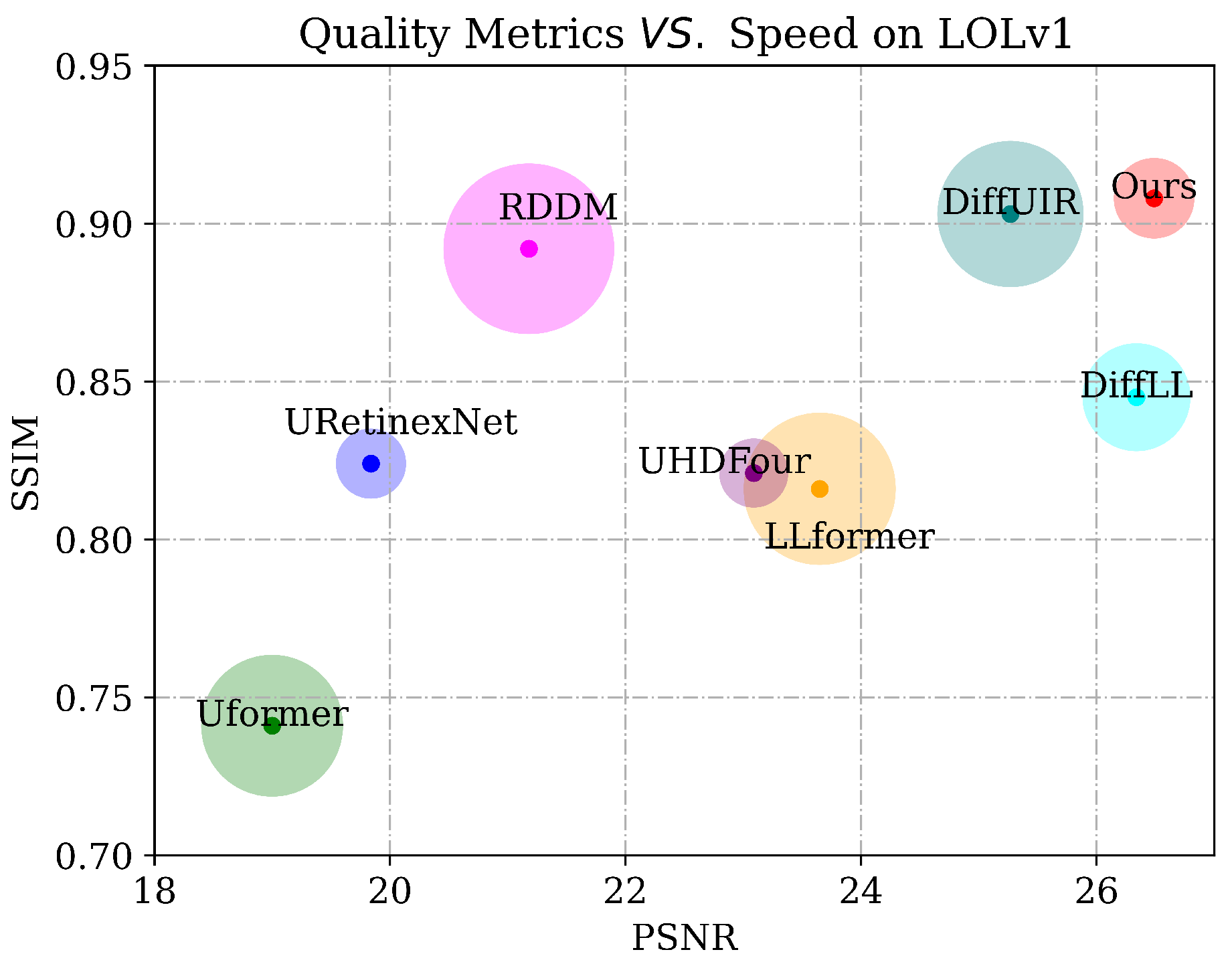

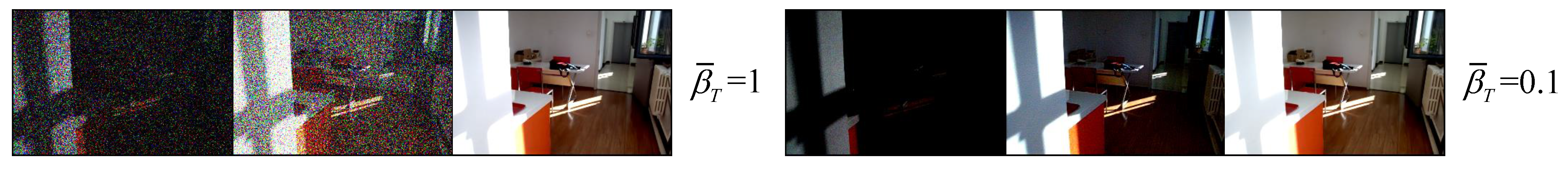
| Method | LOLv1 | LOLv2-real | LOLv2-syn | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | LPIPS↓ | PSNR↑ | SSIM↑ | LPIPS↓ | PSNR↑ | SSIM↑ | LPIPS↓ | |
| NPE [23] | 16.97 | 0.484 | 0.400 | 17.33 | 0.464 | 0.396 | 18.12 | 0.853 | 0.184 |
| SRIE [24] | 11.86 | 0.495 | 0.353 | 14.45 | 0.524 | 0.332 | 18.37 | 0.819 | 0.195 |
| LIME [25] | 17.55 | 0.531 | 0.387 | 17.48 | 0.505 | 0.428 | 15.86 | 0.761 | 0.241 |
| RetinexNet [6] | 16.77 | 0.462 | 0.417 | 17.72 | 0.652 | 0.436 | 21.11 | 0.869 | 0.195 |
| MIRNet [26] | 24.14 | 0.830 | 0.250 | 20.02 | 0.820 | 0.233 | 21.94 | 0.876 | 0.209 |
| Zero-DCE [27] | 14.86 | 0.562 | 0.372 | 18.06 | 0.580 | 0.352 | 19.65 | 0.888 | 0.168 |
| EnlightenGAN [7] | 17.61 | 0.653 | 0.372 | 18.68 | 0.678 | 0.364 | 19.76 | 0.877 | 0.158 |
| RUAS [29] | 16.41 | 0.503 | 0.364 | 15.35 | 0.495 | 0.395 | 16.55 | 0.652 | 0.364 |
| Uformer [8] | 19.00 | 0.741 | 0.354 | 18.44 | 0.759 | 0.347 | 22.79 | 0.918 | 0.142 |
| Restormer [33] | 20.61 | 0.797 | 0.288 | 20.51 | 0.854 | 0.232 | 23.76 | 0.904 | 0.144 |
| URetinexNet [30] | 19.84 | 0.824 | 0.237 | 21.09 | 0.858 | 0.208 | 20.93 | 0.895 | 0.192 |
| SCI [31] | 14.78 | 0.525 | 0.366 | 17.30 | 0.540 | 0.345 | 17.09 | 0.830 | 0.233 |
| LLformer [34] | 23.65 | 0.816 | 0.169 | 22.81 | 0.845 | 0.306 | 24.06 | 0.924 | 0.121 |
| UHDFour [32] | 23.09 | 0.821 | 0.259 | 21.79 | 0.854 | 0.292 | 23.68 | 0.897 | 0.179 |
| DiffLL [19] | 26.34 | 0.845 | 0.217 | 28.86 | 0.876 | 0.207 | 24.52 | 0.910 | 0.146 |
| RDDM [21] | 21.18 | 0.892 | 0.164 | 19.02 | 0.857 | 0.213 | 20.61 | 0.892 | 0.182 |
| DiffUIR [22] | 25.27 | 0.903 | 0.161 | 20.70 | 0.870 | 0.211 | 19.50 | 0.883 | 0.204 |
| CoTF [51] | 24.98 | 0.882 | 0.218 | 20.99 | 0.827 | 0.356 | 24.76 | 0.936 | 0.103 |
| Ours | 26.49 | 0.908 | 0.157 | 24.36 | 0.897 | 0.162 | 25.68 | 0.938 | 0.097 |
| Method | SID | LSRW | ||||
|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | LPIPS↓ | PSNR↑ | SSIM↑ | LPIPS↓ | |
| NPE [23] | 16.69 | 0.331 | 0.885 | 16.19 | 0.384 | 0.440 |
| SRIE [24] | 15.37 | 0.389 | 0.830 | 13.36 | 0.415 | 0.399 |
| LIME [25] | 16.50 | 0.219 | 0.982 | 17.34 | 0.520 | 0.471 |
| RetinexNet [6] | 15.64 | 0.690 | 0.827 | 15.61 | 0.414 | 0.454 |
| MIRNet [26] | 20.84 | 0.605 | 0.827 | 16.47 | 0.477 | 0.430 |
| Zero-DCE [27] | 18.05 | 0.314 | 0.896 | 15.87 | 0.443 | 0.411 |
| EnlightenGAN [7] | 15.36 | 0.453 | 0.755 | 17.11 | 0.463 | 0.406 |
| RUAS [29] | 18.44 | 0.581 | 0.911 | 14.27 | 0.461 | 0.501 |
| Uformer [8] | 22.04 | 0.740 | 0.446 | 16.59 | 0.494 | 0.435 |
| Restormer [33] | 22.42 | 0.601 | 0.646 | 16.30 | 0.453 | 0.427 |
| URetinexNet [30] | 17.97 | 0.300 | 0.897 | 18.27 | 0.518 | 0.419 |
| SCI [31] | 16.98 | 0.295 | 0.910 | 15.24 | 0.419 | 0.404 |
| LLformer [34] | 23.22 | 0.727 | 0.468 | 19.78 | 0.593 | 0.326 |
| UHDFour [32] | 24.71 | 0.741 | 0.417 | 17.30 | 0.529 | 0.443 |
| DiffLL [19] | 24.52 | 0.750 | 0.371 | 19.28 | 0.552 | 0.350 |
| RDDM [21] | 23.38 | 0.690 | 0.378 | 18.79 | 0.561 | 0.360 |
| DiffUIR [22] | 24.12 | 0.748 | 0.398 | 17.87 | 0.535 | 0.385 |
| CoTF [51] | 23.76 | 0.719 | 0.557 | 18.55 | 0.607 | 0.352 |
| Ours | 24.83 | 0.764 | 0.340 | 21.12 | 0.636 | 0.460 |
| Method | DICM | MEF | LIME | NPE | ||||
|---|---|---|---|---|---|---|---|---|
| NIQE↓ | BRI.↓ | NIQE↓ | BRI.↓ | NIQE↓ | BRI.↓ | NIQE↓ | BRI.↓ | |
| LIME [25] | 4.476 | 27.375 | 4.744 | 39.095 | 5.045 | 32.842 | 4.170 | 28.944 |
| Zero-DCE [27] | 3.951 | 23.350 | 3.500 | 29.359 | 4.379 | 26.054 | 3.826 | 21.835 |
| MIRNet [26] | 4.021 | 22.104 | 4.202 | 34.499 | 4.378 | 28.623 | 3.810 | 21.157 |
| EnlightenGAN [7] | 3.832 | 19.129 | 3.556 | 26.799 | 4.249 | 22.664 | 3.879 | 22.864 |
| RUAS [29] | 7.306 | 46.882 | 5.435 | 42.120 | 5.322 | 34.880 | 7.198 | 48.976 |
| SCI [31] | 4.519 | 27.922 | 3.608 | 26.716 | 4.463 | 25.170 | 4.124 | 28.887 |
| URetinexNet [30] | 4.774 | 24.544 | 4.231 | 34.720 | 4.694 | 29.022 | 4.028 | 26.094 |
| Uformer [8] | 3.847 | 19.657 | 3.935 | 25.240 | 4.300 | 21.874 | 3.510 | 16.239 |
| Restormer [33] | 3.964 | 19.474 | 3.815 | 25.322 | 4.365 | 22.931 | 3.729 | 16.668 |
| UHDFour [32] | 4.575 | 26.926 | 4.231 | 29.538 | 4.430 | 20.263 | 4.049 | 15.934 |
| RDDM [21] | 3.868 | 31.179 | 3.729 | 28.263 | 4.058 | 25.639 | 4.212 | 22.339 |
| Ours | 3.829 | 30.199 | 3.861 | 22.494 | 3.866 | 18.049 | 4.412 | 13.841 |
| Method | Params (M) | Mem. (G) | Time(s) |
|---|---|---|---|
| Uformer [8] | 5.29 | 4.223 | 0.269 |
| LLformer [34] | 24.52 | 2.943 | 0.310 |
| DiffLL [19] | 22.08 | 1.423 | 0.156 |
| RDDM [21] | 36.26 | 2.885 | 0.390 |
| DiffUIR [22] | 36.26 | 2.903 | 0.289 |
| Ours | 21.85 | 1.391 | 0.087 |
| Method | Bicycle | Boat | Bottle | Bus | Car | Cat | Chair | Cup | Dog | Motor | People | Table | All |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RetinexNet [6] | 0.497 | 0.348 | 0.124 | 0.545 | 0.431 | 0.304 | 0.272 | 0.237 | 0.321 | 0.305 | 0.308 | 0.252 | 0.329 |
| Zero-DCE [27] | 0.512 | 0.389 | 0.414 | 0.662 | 0.447 | 0.345 | 0.278 | 0.379 | 0.372 | 0.341 | 0.362 | 0.276 | 0.398 |
| URetinexNet [30] | 0.489 | 0.359 | 0.374 | 0.617 | 0.422 | 0.304 | 0.260 | 0.366 | 0.339 | 0.301 | 0.328 | 0.274 | 0.370 |
| SCI [31] | 0.484 | 0.373 | 0.415 | 0.642 | 0.460 | 0.348 | 0.294 | 0.403 | 0.368 | 0.338 | 0.359 | 0.290 | 0.398 |
| LLformer [34] | 0.493 | 0.378 | 0.396 | 0.642 | 0.451 | 0.344 | 0.288 | 0.414 | 0.394 | 0.353 | 0.359 | 0.285 | 0.400 |
| UHDFour [32] | 0.526 | 0.369 | 0.378 | 0.631 | 0.436 | 0.354 | 0.276 | 0.406 | 0.376 | 0.347 | 0.351 | 0.276 | 0.394 |
| DiffLL [19] | 0.503 | 0.348 | 0.419 | 0.630 | 0.443 | 0.374 | 0.267 | 0.378 | 0.386 | 0.336 | 0.344 | 0.260 | 0.391 |
| RDDM [21] | 0.502 | 0.379 | 0.276 | 0.589 | 0.447 | 0.331 | 0.298 | 0.325 | 0.378 | 0.348 | 0.334 | 0.283 | 0.374 |
| Ours | 0.513 | 0.394 | 0.437 | 0.676 | 0.456 | 0.362 | 0.283 | 0.406 | 0.380 | 0.357 | 0.360 | 0.290 | 0.410 |
| Method | PSNR↑ | SSIM↑ | LPIPS↓ | |
|---|---|---|---|---|
| Preprocessing | None | 21.28 | 0.889 | 0.169 |
| 26.41 | 0.899 | 0.196 | ||
| Loss Function | w/o | 25.14 | 0.904 | 0.158 |
| w/o | 25.13 | 0.882 | 0.189 | |
| w/o | 25.49 | 0.907 | 0.163 | |
| w/o MS-SSIM Loss | 25.76 | 0.908 | 0.162 | |
| Module Arch | baseline + | 24.59 | 0.900 | 0.165 |
| baseline + | 25.48 | 0.906 | 0.150 | |
| baseline + | 24.85 | 0.886 | 0.186 | |
| baseline + | 25.14 | 0.886 | 0.181 | |
| Noise and Step | , | 25.02 | 0.901 | 0.175 |
| , | 25.22 | 0.903 | 0.169 | |
| , | 25.31 | 0.900 | 0.181 | |
| , | 25.67 | 0.904 | 0.165 | |
| , | 26.47 | 0.905 | 0.160 | |
| Default Version | 26.49 | 0.908 | 0.157 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, B.; Bu, D.; Sun, B.; Wang, Y.; Jiang, W.; Sun, X.; Qian, H. Low-Light Image Enhancement with Residual Diffusion Model in Wavelet Domain. Photonics 2025, 12, 832. https://doi.org/10.3390/photonics12090832
Ding B, Bu D, Sun B, Wang Y, Jiang W, Sun X, Qian H. Low-Light Image Enhancement with Residual Diffusion Model in Wavelet Domain. Photonics. 2025; 12(9):832. https://doi.org/10.3390/photonics12090832
Chicago/Turabian StyleDing, Bing, Desen Bu, Bei Sun, Yinglong Wang, Wei Jiang, Xiaoyong Sun, and Hanxiang Qian. 2025. "Low-Light Image Enhancement with Residual Diffusion Model in Wavelet Domain" Photonics 12, no. 9: 832. https://doi.org/10.3390/photonics12090832
APA StyleDing, B., Bu, D., Sun, B., Wang, Y., Jiang, W., Sun, X., & Qian, H. (2025). Low-Light Image Enhancement with Residual Diffusion Model in Wavelet Domain. Photonics, 12(9), 832. https://doi.org/10.3390/photonics12090832





