Design and Optimization of Polarization-Maintaining Low-Loss Hollow-Core Anti-Resonant Fibers Based on a Multi-Objective Genetic Algorithm

Abstract

In this work, a novel polarization-maintaining hollow-core fiber structure featuring a semi-circular nested dual-ring geometry is proposed. To simultaneously optimize two inherently conflicting performance metrics, namely, birefringence and confinement loss, a multi objective genetic algorithm is employed for geometric parameter tuning, resulting in a set of Pareto-optimal solutions. At the target wavelength of 1550 nm, the first optimal design achieves birefringence exceeding $1\times {10}^{-4}$ over a 1275 nm bandwidth while maintaining confinement loss around ${10}^0$ dB/m; the second design maintains birefringence above $1\times {10}^{-4}$ across a 1000 nm spectral range, with confinement loss on the order of ${10}^{-1}$ dB/m. These optimized designs offer a promising approach for improving the performance of polarization-sensitive applications such as interferometric sensing and high coherence laser systems. The results confirm the suitability of multi-objective genetic algorithms for integrated multi-objective fiber optimization and provide a new strategy for designing low-loss and high-birefringence fiber devices.

1. Introduction

With the rapid advancement of communication infrastructure, emerging information technologies have imposed increasingly rigorous requirements on optical fiber transmission systems, particularly in terms of bandwidth, capacity, latency, and overall reliability. Conventional solid-core fibers [1] increasingly exhibit fundamental performance bottlenecks when applied in ultra-high-capacity and high-speed scenarios. These challenges mainly stem from inherent physical constraints such as chromatic dispersion [2], nonlinear effects [3], and transmission attenuation [4] which restrict their scalability and practical applicability in future optical networks. Hollow-core fibers (HCFs) [5] have garnered significant attention as alternative waveguides due to compelling advantages such as ultra-low loss [6], reduced group delay [7], broad operating bandwidths [3], and minimal nonlinear interactions [8]. Among various HCF configurations, anti-resonant fibers (ARFs) [9] have shown exceptional potential in diverse applications, including broadband data transmission [10], high-power laser guidance [11], and precision sensing [12], owing to their unique anti-resonant guiding mechanism [13]. In contrast to traditional fibers that rely on refractive index contrast for total internal reflection [14], ARFs confine light within an air core through engineered anti-resonant structures.

One of the critical advantages of ARFs lies in their potential for latency reduction [15]. In terms of attenuation, ARF transmission loss is influenced by multiple mechanisms, including confinement loss (CL), surface scattering, and bending-induced losses. Ongoing improvements in fabrication and structure design have significantly lowered ARF loss from initial values exceeding 500 dB/km to sub 0.1 dB/km levels [16], surpassing the material absorption limits of solid-core fibers and laying a strong foundation for the next generation of high-speed, long-haul, and low-latency optical communication systems. However, current ARF structures still face several critical design challenges. Chief among these are their inadequate polarization maintaining (PM) performance, low birefringence (BI), and difficulty in achieving low transmission loss simultaneously. These limitations hinder the adoption of ARFs in polarization sensitive applications, including high-precision fiber interferometry, polarization division multiplexing, and optical sensing [17].

Polarization-maintaining hollow-core fibers (PM-HCFs) are intended for for short-reach applications such as high-precision interferometric sensing, polarization control, and fiber-based spectroscopic systems, where birefringence is the primary performance metric. In these use cases, fiber lengths are typically below 20 m [18,19] and moderate confinement loss (e.g., 1–10 dB/m) is considered acceptable as long as sufficient birefringence is achieved. To meet the demands of such advanced systems, it is crucial to develop ARF structures capable of delivering both strong birefringence and moderate loss. Yet, a fundamental tradeoff arises, since enhancing BI often involves increasing structural asymmetry to differentiate polarization modes, while minimizing CL typically requires structural symmetry to reduce leakage pathways. This design conflict poses a significant obstacle to conventional optimization approaches. Thus, the structural design of ARFs represents a classical multi-objective optimization problem. Traditional single-objective methods are generally insufficient to address such competing performance criteria. In this context, multi-objective optimization strategies, particularly those leveraging Pareto front-based evolutionary algorithms, have proven promising for achieving balanced performance across both the birefringence and loss dimensions.

A variety of algorithm-driven strategies have emerged for the design and optimization of hollow core fibers. In 2019, Chugh et al. explored neural network models for predicting structural parameters in photonic crystal fibers [20]. This was extended by Hu et al. in 2020, who integrated geometric modeling with machine learning to evaluate over one million fiber designs [21]. Subsequently, in 2021, Meng et al. employed advanced classification techniques on a dataset of 290,000 structures to optimize twelve geometric types [22], and later expanded the dataset to 400,000 samples, combining it with optimization algorithms for refined structural tuning [23]. In 2023, the same group introduced a dual-layer neural architecture to accelerate geometry evaluation across twelve design parameters [24]. More recently, in 2024, Liu et al. proposed a surrogate assisted hybrid swarm optimization algorithm (HSOA), reducing the simulation burden to just 243 training points and 400 evaluation samples [25]; they further conducted exhaustive mathematical analyses of single-ring ARF geometries to identify optimal birefringent configurations.

Despite these advancements, prior work remains constrained by the use of complex fiber geometries, heavy reliance on large scale datasets, and limited effectiveness in handling inherently multi-objective problems using traditional single target strategies. Previous researchers have introduced multi-objective optimization algorithms into the parameter optimization of photonic crystal fibers [26,27,28]. Considering that such algorithms are well suited for handling the multi-objective nature of fiber design problems, this work applies a multi-objective genetic algorithm (MOGA) [29] to the optimization of polarization-maintaining hollow-core anti-resonant fibers (PM-HC-ARFs) [30]. At the operating wavelength of 1550 nm, two representative optimal designs are obtained, both exhibiting excellent tradeoffs between the target performance metrics.

In the first design, birefringence remains above $1.0\times {10}^{-4}$ across a wide spectral range of 1450–2725 nm, while confinement loss is maintained at the ${10}^1$ dB/m level. Specifically, at 1550 nm, the birefringence reaches $2.04\times {10}^{-4}$ and the confinement losses for the x- and y-polarized modes are 1.45 dB/m and 4.57 dB/m, respectively. In the second design, birefringence stays above $1.0\times {10}^{-4}$ over a slightly narrower range of 1400–2400 nm, with confinement loss reduced to the ${10}^{-1}$ dB/m level. At 1550 nm, the birefringence is $1.6\times {10}^{-4}$, while the corresponding losses for the two polarization states are 0.5 dB/m and 1.318 dB/m. These results validate the effectiveness and practicality of the proposed MOGA-based multi-objective optimization strategy in achieving simultaneous optimization of birefringence and confinement loss for advanced ARF structures.

2. Theory and Fiber Structure Design

In anti-resonant hollow-core fibers, the cladding tube walls function as spectral filters that inhibit optical leakage over specific wavelength intervals. This guiding mechanism is governed by the anti-resonance condition, which can be described using Fabry–Pérot interference theory. The corresponding anti-resonant wavelengths are calculated as follows [31]:

$${\lambda }_m={\displaystyle \frac{2t·n}{m}},m=1,2,3,\dots$$

(1)

where ${\lambda }_m$ is the m-th order anti-resonant wavelength, t denotes the thickness of the cladding tube wall, n is the refractive index of the wall material, and m is the resonance order. When the operational wavelength falls within a non-resonant interval, reflection at the wall boundaries prevents mode leakage, enabling efficient light confinement in the air core and supporting low-loss propagation.

The principal transmission loss mechanism in such fibers arises from structural leakage, which is quantified by the confinement loss. Based on the imaginary part of the complex effective refractive index, CL can be expressed as follows [32]:

$$\mathrm{CL}={\displaystyle \frac{40\pi }{ln10}}·{\displaystyle \frac{\mathrm{Im}\left(n_{\mathrm{eff}}\right)}{\lambda }}$$

(2)

where $\mathrm{Im}\left(n_{\mathrm{eff}}\right)$ is the imaginary component of the effective refractive index and $\lambda$ is the operating wavelength. This equation provides a theoretical tool for assessing leakage loss and serves as the basis for structural optimization.

To evaluate polarization-maintaining capability, birefringence is introduced to characterize the phase velocity difference between two orthogonally polarized modes [10]:

$$\mathrm{BI}=\left|n_{\mathrm{eff}}^x-n_{\mathrm{eff}}^y\right|$$

(3)

$n_{\mathrm{eff}}^x$ and $n_{\mathrm{eff}}^y$ are the effective indices for the x- and y-polarized fundamental modes, respectively. A higher BI value indicates stronger mode decoupling, enhancing the fiber’s robustness against polarization crosstalk in polarization-sensitive transmission systems.

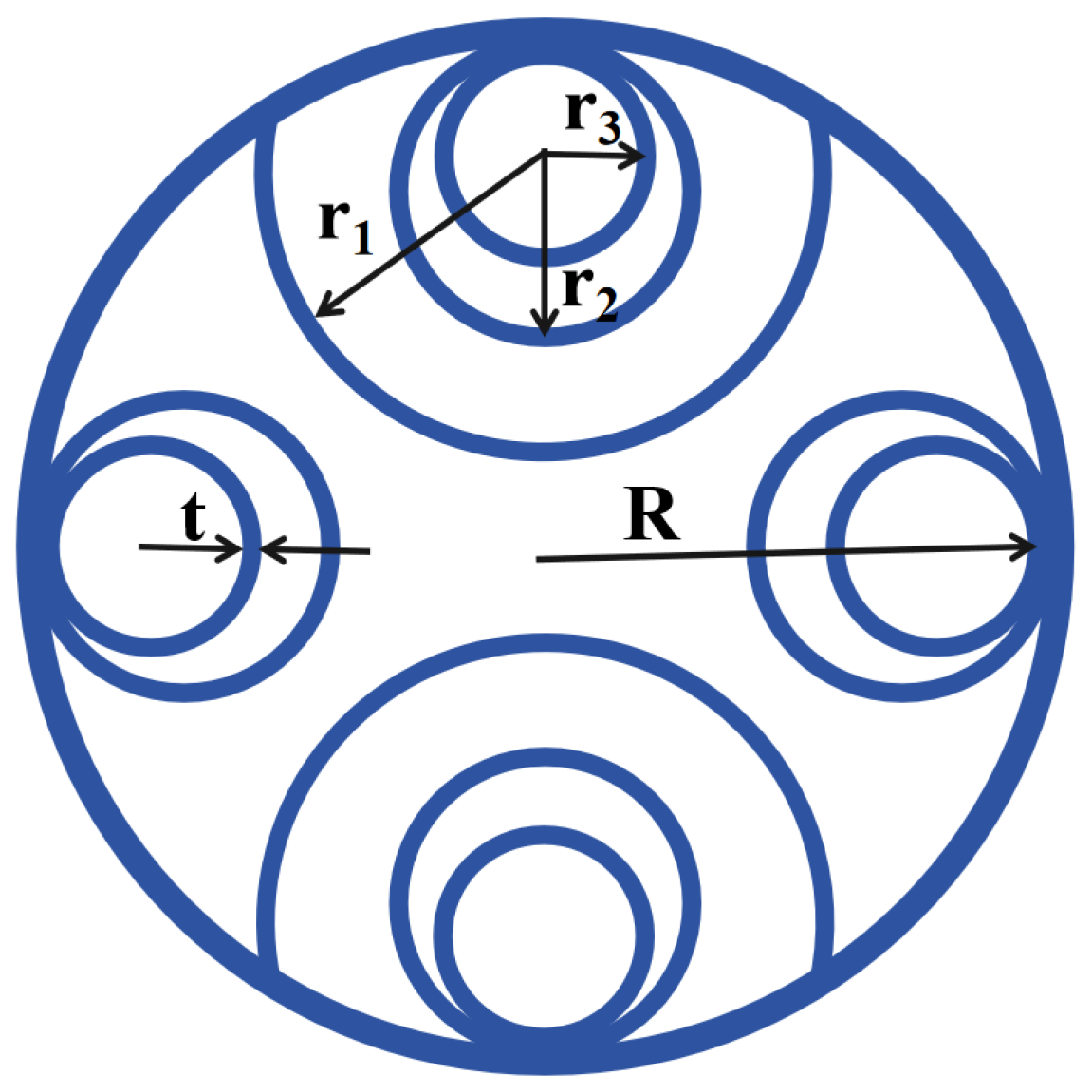
A novel polarization-maintaining hollow-core anti-resonant fiber structure is proposed and illustrated in Figure 1. The fiber features a symmetric cross-sectional geometry composed of a semi-circular cladding envelope, within which two nested concentric double-layer circular rings are embedded. The total cladding radius is denoted as R, and all glass wall layers share a uniform thickness denoted by t. The three concentric circular tubes are defined by their radii as $r_1$, $r_2$, and $r_3$, corresponding to the outer, middle, and inner layers, respectively. To describe the geometric proportions, the following normalized parameters are introduced: $A={\displaystyle \frac{r_1}{R}}$, $B={\displaystyle \frac{r_2}{r_1}}$, and $C={\displaystyle \frac{r_3}{r_2}}$, which characterize the size ratios between successive concentric rings. The design ranges for the structural parameters are specified as follows: the total cladding radius $R_{\mathrm{total}}$ is varied within $[30,40]\mathsf{\mu }\mathrm{m}$, the wall thickness t within $[0.1,1.0]\mathsf{\mu }\text{m}$, the geometric ratio A within the range $[0.5,0.6]$, B within $[0.4,0.55]$, and C within $[0.5,0.8]$. To balance computational efficiency and optimization accuracy, we set the population size to 30 and the number of generations to 10. We employed the tournament selection method for effective diversity and convergence, used single-point crossover to avoid local optima, and applied uniform mutation to explore the solution space and prevent premature convergence.

To systematically analyze the effects of different parameter combinations on birefringence and confinement loss, finite element method (FEM) simulations were conducted to compute the waveguide mode characteristics of the proposed structure. Simulation results indicated that under proper parameter configurations, the fiber structure enables effective light confinement and enhances the separation between polarization modes, significantly improving its polarization maintaining capability. Based on these findings, a multi-objective optimization strategy was further applied to explore the parameter space, yielding a Pareto front that reveals the tradeoff relationship between birefringence and loss. The final optimized design achieves a birefringence level exceeding ${10}^{-4}$ at 1550 nm while significantly suppressing transmission loss, demonstrating strong potential for high performance polarization maintaining fiber applications.

In this study, a multi-objective genetic algorithm is employed to perform bi-objective optimization for the proposed hollow-core anti-resonant fiber structure, as illustrated in the algorithm flowchart in Figure 2. The primary optimization objectives are to simultaneously enhance the fiber’s birefringence and suppress its transmission loss. Five key structural parameters are selected as optimization variables, including the cladding radius, wall thickness, and three geometric scaling factors. Each parameter is assigned a feasible design range based on fabrication constraints and prior knowledge.

During the optimization process, an objective function interface is first constructed and integrated with the multiphysics simulation model to evaluate the birefringence and confinement loss corresponding to each candidate parameter set. The algorithm then generates an initial population within the defined parameter space and constructs an initial Pareto front based on non-dominated sorting.

In the iterative stage, the MOGA explores new candidate solutions via localized search strategies and dynamically updates the non-dominated set. The search domain is progressively refined based on the convergence behavior of the Pareto front. For each generation, the objective values of candidate designs are computed through simulation and used to update the current Pareto-optimal solution set.

The Algorithm 1 does not require gradient information and involves only a limited number of control parameters, making it particularly suitable for complex, non-differentiable, or computationally expensive multiphysics models. The resulting Pareto front clearly reveals the tradeoff relationship between high birefringence and low loss, providing a solid theoretical and data-driven foundation for the structural design of high-performance polarization-maintaining hollow-core fibers.

Algorithm 1 Multi-Objective Genetic Algorithm for HC ARF Optimization

1: Input:   2:    Number of decision variables: $n=5$   3:    Number of objectives: $M=2$   4:    Variable bounds: $x_i\in [l{b}_i,u{b}_i],i=1,\dots ,5$   5:    Finite element simulation   6:    GA options: population size, max generations, mutation rate, etc.   7: Initialization:   8:    Generate initial population P within feasible domain   9:    Evaluate objective vector $f\left(x\right)=[f_1\left(x\right),f_2\left(x\right)]$ for all $x\in P$ 10:    Identify initial Pareto front via non dominated sorting 11: while termination condition not met do 12:     Perform selection, crossover, and mutation to produce new population 13:     Evaluate objective functions $f_1\left(x\right)$ (CL) and $f_2\left(x\right)$ ($-BI$) 14:     Update Pareto front using non dominated sorting 15:     Apply elitism and diversity preservation mechanisms 16: end while 17: Output: Pareto optimal set $X^{*}$ and corresponding objective values $f\left(X^{*}\right)$

3. Numerical Experiments

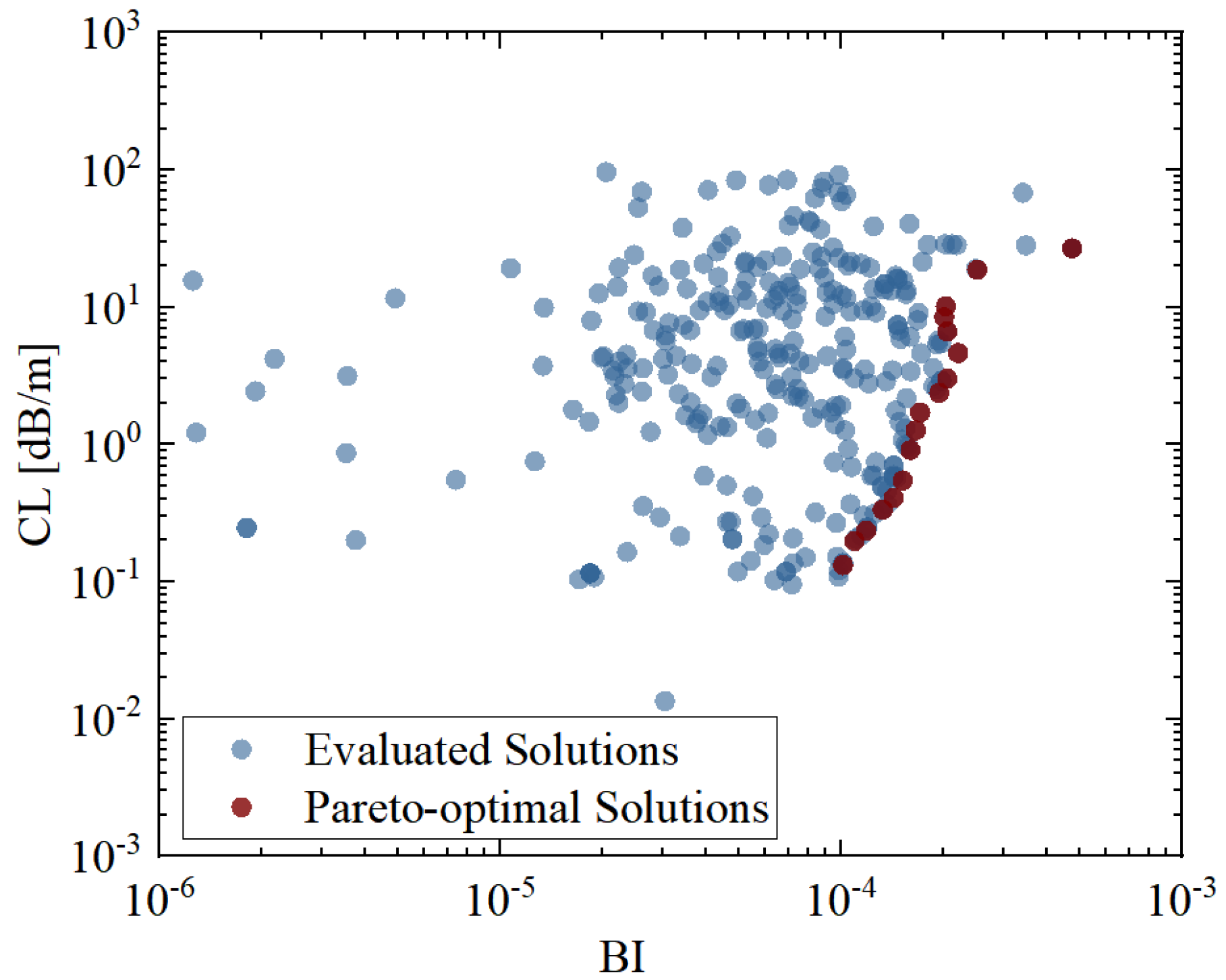
Figure 3 illustrates the tradeoff relationship between birefringence and confinement loss observed during the multi-objective optimization of the fiber design. The horizontal axis represents birefringence, which is to be maximized, while the vertical axis corresponds to confinement loss, which is to be minimized. Given the large disparity in magnitudes between the two objectives, logarithmic scaling is employed on both axes to enhance visualization clarity.

In the figure, blue dots denote all evaluated solutions generated during the search process, representing the exploration capability of the optimization algorithm across the design space. Among them, deep red dots highlight the Pareto-optimal solutions, forming a distinct non-dominated front. The Pareto-optimal set splits into two branches driven by distinct design mechanisms. In Branch A, BI is primarily increased by azimuthal asymmetry of the core boundary, which enhances polarization discrimination but perturbs anti-resonant guidance, leading to a concomitant rise of CL. In Branch B, BI is increased by nested-ring thickness/spacing detuning, which keeps the wall thickness close to the anti-resonant minima while introducing controlled anisotropy of modal overlap; in this way, leakage is suppressed and CL remains low. These two mechanisms explain the different BI–CL slopes observed in Figure 3 and the distinct performance of the two representative solutions.

Quantitatively, the Pareto front spans a birefringence range from approximately $1.01\times {10}^{-4}$ to $4.74\times {10}^{-4}$ and a confinement loss range from $0.1323\mathrm{dB}/\mathrm{m}$ to $26.8751\mathrm{dB}/\mathrm{m}$. Notably, several Pareto-optimal designs achieve high birefringence while maintaining low loss; for instance, a BI of $1.59\times {10}^{-4}$ corresponds to a CL of only $0.9108\mathrm{dB}/\mathrm{m}$. These results validate the effectiveness of the proposed optimization method in identifying high performance design tradeoffs. Such structures are particularly advantageous for applications requiring both strong polarization-maintaining capability and low transmission loss.

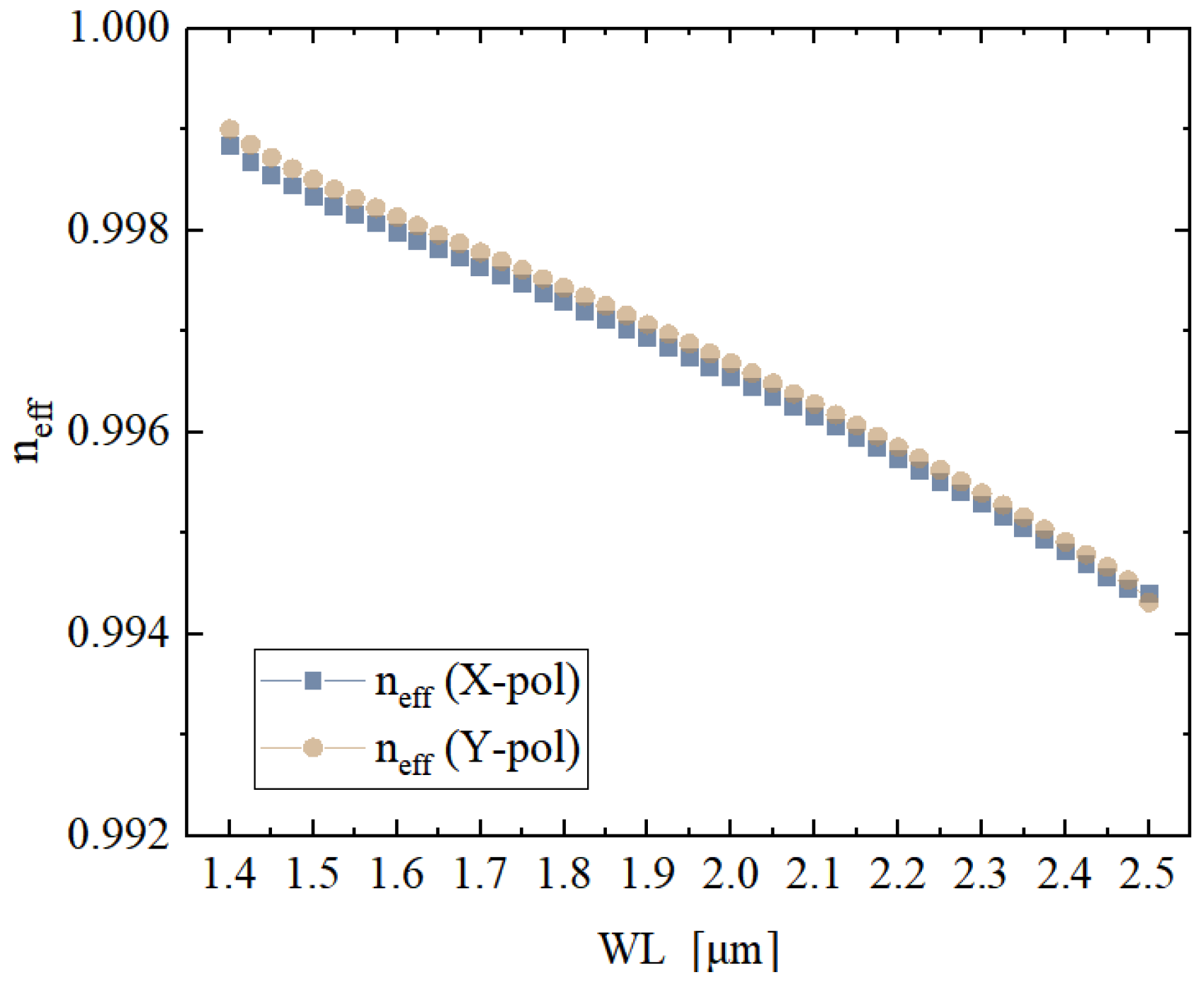
Figure 4 presents the wavelength-dependent effective refractive indices $n_{\mathrm{eff}}$ for the X- and Y-polarized fundamental modes of the proposed hollow-core anti-resonant fiber under the optimal design parameters: $R=32.943\mathsf{\mu }\mathrm{m}$, $t_1=0.653\mathsf{\mu }\mathrm{m}$, $A=0.558$, $B=0.518$, and $C=0.619$. The simulation spanned a broad spectral range from 1.4 μm to 2.85 μm. As observed, the effective refractive indices of the two orthogonal polarization modes differ significantly across the entire wavelength band, with both showing a monotonic decrease with increasing wavelength. This stable and pronounced birefringence indicates strong polarization-splitting characteristics on the part of the designed structure.

At the standard telecommunication wavelength of 1.55 μm, the refractive index difference between the x- and y-polarized modes reaches $2.04\times {10}^{-4}$, with the corresponding confinement loss measured at approximately 1.459 dB/m. The fiber maintains effective birefringence and low loss over a continuous operational bandwidth from 1450 nm to 2725 nm, yielding a total bandwidth of 1275 nm. These results demonstrate the structure’s capability to simultaneously offer broadband guidance, low transmission loss, and high phase birefringence.

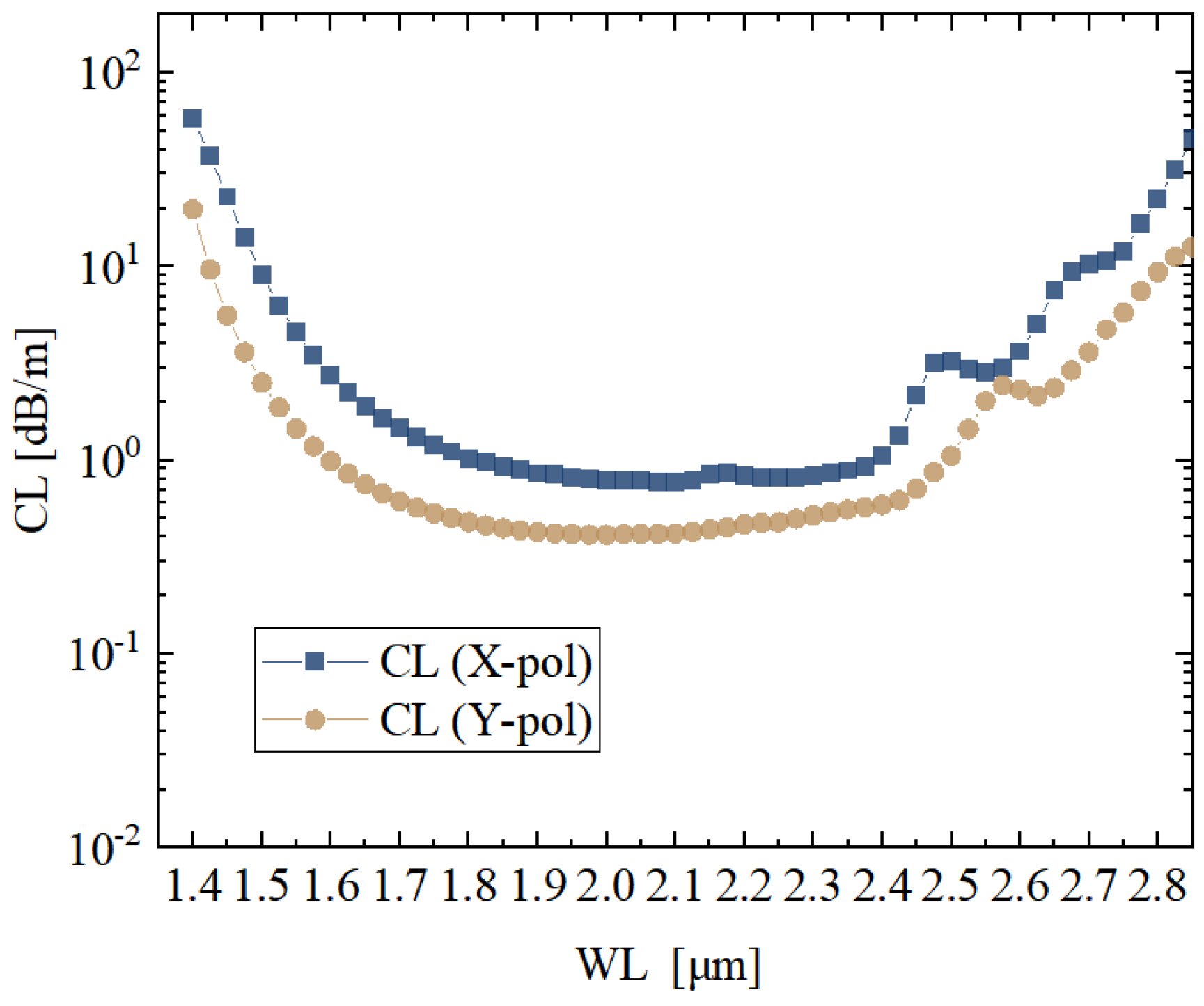
Figure 5 illustrates the wavelength-dependent confinement loss characteristics of the designed anti-resonant hollow-core fiber for both the X- and Y-polarized modes. A logarithmic scale is used on the vertical axis to clearly reveal the order of magnitude variation in loss over the broadband spectrum.

As the figure shows, in the primary operational range from 1.46 μm to 2.475 μm, the CL values for both polarization states remain below the ${10}^{-1}$ dB/m level, indicating excellent low loss transmission behavior across this spectral band. Specifically, at the central wavelength of 1.55 μm, the confinement loss for the X-polarized mode is approximately 1.459 dB/m.

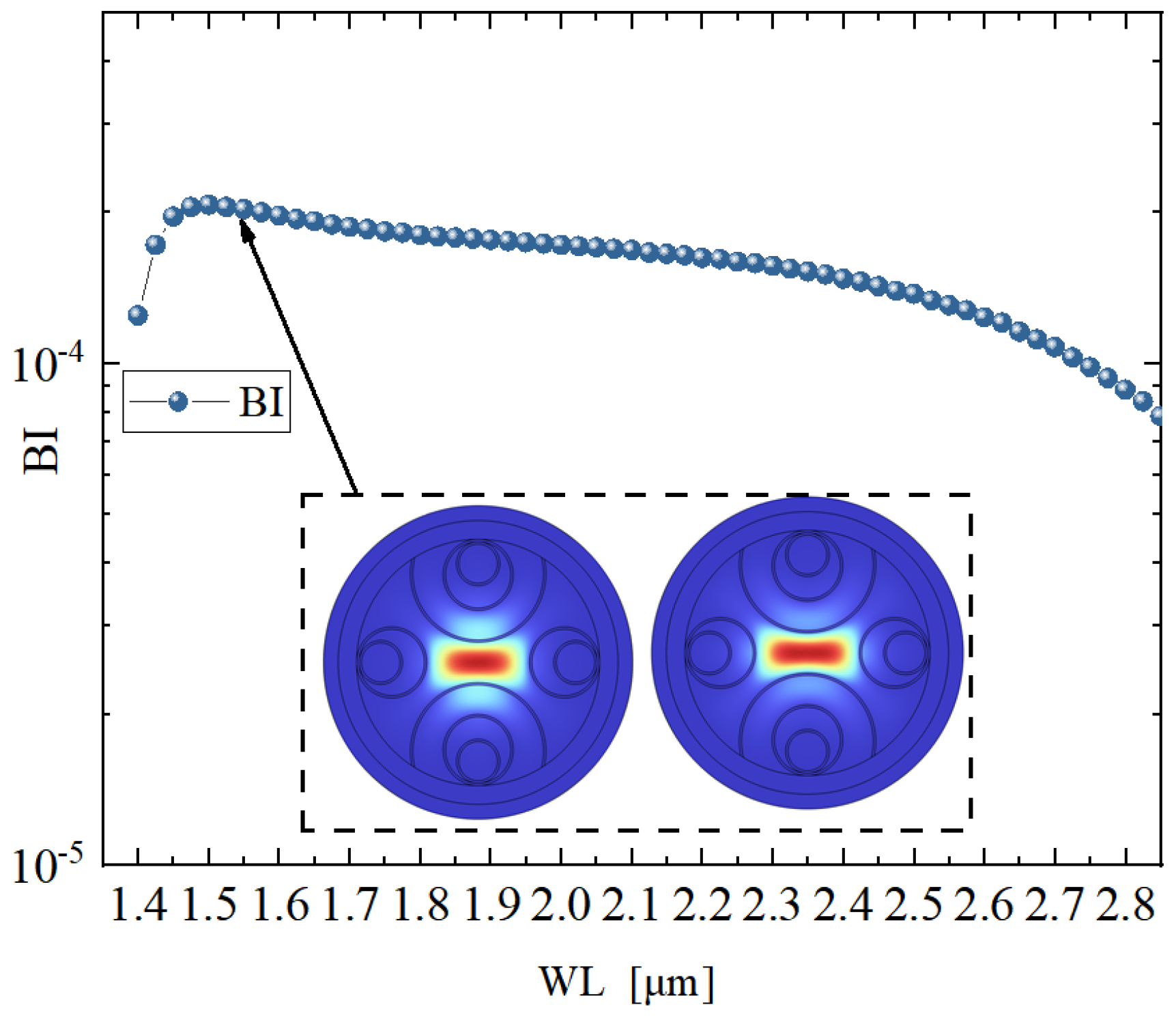
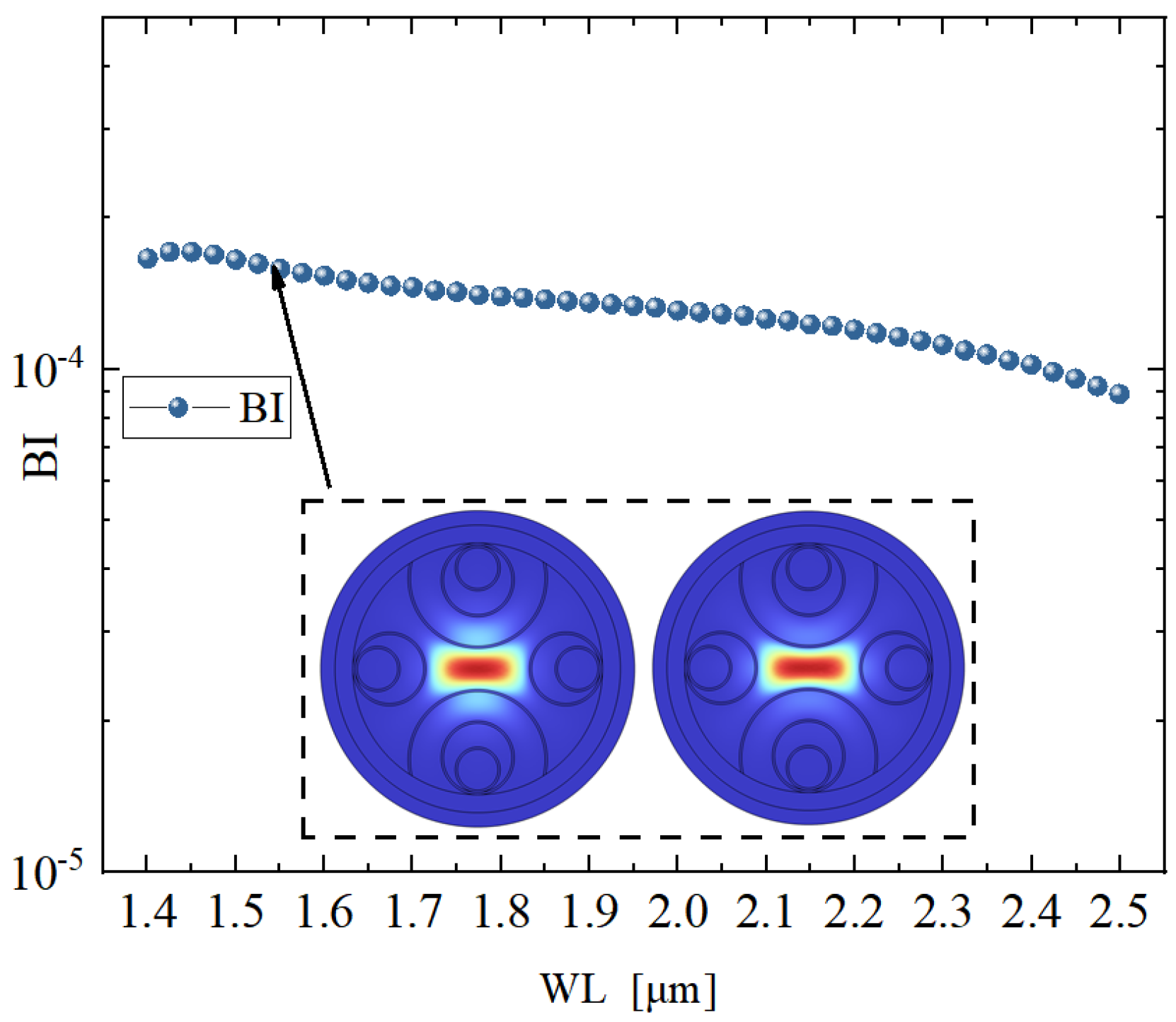
Figure 6 presents the variation of phase birefringence across a broad wavelength range for the proposed hollow-core anti-resonant fiber structure. As observed, the BI values remain consistently above the ${10}^{-4}$ level throughout the spectral span from 1.4 μm to 2.8 μm, demonstrating excellent high birefringence performance. Notably, in the wavelength interval from 1.5 μm to 1.6 μm, the BI exhibits minimal fluctuation, indicating superior polarization stability within this operational window.

The embedded mode field distributions in the figure further illustrate the transverse electric field profiles of the X- and Y-polarized fundamental modes at the representative wavelength of 1.55 μm. A clear spatial separation between the two polarization states can be identified, indicating strong modal localization and structural decoupling. This spatial differentiation effectively reduces polarization mode coupling and crosstalk, which is critical for achieving high-performance polarization-maintaining fiber operation.

Figure 7 illustrates the wavelength-dependent effective refractive indices $n_{\mathrm{eff}}$ for the X- and Y-polarized fundamental modes of the proposed anti-resonant hollow-core fiber under the optimized parameter configuration: $R=34.901\mathsf{\mu }\mathrm{m}$, $t_1=0.632\mathsf{\mu }\mathrm{m}$, $A=0.558$, $B=0.525$, and $C=0.615$. The simulation covered the spectral range from 1.35 μm to 1.875 μm.

As observed, the $n_{\mathrm{eff}}$ curves for both polarizations exhibit a monotonically decreasing trend with increasing wavelength, indicating stable dispersion characteristics across the operating band. More importantly, a consistent refractive index difference is maintained between the X- and Y-polarized modes throughout the full wavelength range, demonstrating robust polarization separation capability. This stable birefringence reflects a sustained phase propagation difference, i.e., a clear phase birefringence effect.

At the telecommunications wavelength of 1550 nm, the designed structure achieves a phase birefringence of $BI=1.59\times {10}^{-4}$ along with a confinement loss of $CL=0.5$ dB/m. According to the loss characteristics, the effective operational bandwidth spans from 1400 nm to 2400 nm, yielding a total bandwidth of 1000 nm. This combination of high birefringence and low transmission loss renders this fiber highly promising for applications such as short-wave near-infrared communications and polarization-sensitive sensing.

Figure 8 presents the variation of the confinement loss with the wavelength for the proposed anti-resonant hollow-core fiber, separately analyzing the X- and Y-polarized modes. The loss is expressed in dB/m and plotted on a logarithmic scale to clearly capture its magnitude variations across the spectral range.

As shown, in the main operating band between 1.35 μm and 1.6 μm, both polarization states exhibit consistently low confinement losses, indicating excellent low-loss transmission performance. Specifically, at the standard telecommunications wavelength of 1.55 μm, the confinement loss reaches approximately 0.5 dB/m.

Figure 9 shows the phase birefringence variation of the designed anti-resonant hollow-core fiber over the wavelength range from 1.4 μm to 2.5 μm. It can be observed that the BI consistently remains above the ${10}^{-4}$ level, with a slightly decreasing trend as the wavelength increases. Considering both birefringence and loss performance, the operational bandwidth is effectively defined as 1.4–2.4 μm. The sustained birefringence level across this broad spectrum confirms the fiber’s strong capability for polarization-maintaining operation.

The inset mode field distributions in the figure depict the transverse electric field profiles of the fundamental X- and Y-polarized modes at the working wavelength of 1.55 μm. The field profiles for both polarizations are well-defined, symmetric, and spatially distinct, further verifying the structure’s effective polarization separation and modal stability. The high consistency in modal shapes indicates weak coupling between polarization states under the optimized geometric configuration, which helps to suppress polarization crosstalk.

In summary, the two sets of design parameters demonstrated in this structure simultaneously achieve low confinement loss and high birefringence, ensuring robust polarization control. These characteristics make the proposed fiber well suited for applications in stable polarization-maintaining transmission, interferometric measurement, and high-sensitivity optical sensing.

4. Discussion

Table 1. Comparison of optimization methods for HC-ARF.

Ref.	CL [dB/m]	BI	Num. of Comps.	Num. of Obj.	Optimization Method
[24]	$>{10}^{-6}$	*	415,900	1	Neural Network
[23]	2 × 10−7	*	415,900	2	Optimization Algorithm
[22]	*	*	323,000	1	Classification-based
[33]	3 × 10−5	*	78,312	1	Neural Network
[34]	2 × 10−5	*	*	2	Optimization Algorithm
[25]	0.18	2 × 10−4	400	2	Surrogate Model & Optimization Algorithm
[35]	1 × 10−3	*	80,000	1	Classification-based
Prop.	1 × 100	1 × 10−4	300	2	Multi objective Optimization Algorithm

summarizes representative studies in recent years on the structural optimization of hollow-core anti-resonant fibers, comparing them in terms of confinement loss, birefringence, number of simulations, number of optimization objectives, and employed optimization methodologies. Most existing works focus on single-objective optimization, typically aiming to minimize CL [23,24,33], with only a few studies considering birefringence as a concurrent design target. Although some efforts [23,34] have attempted to introduce dual-objective optimization, these primarily adopt scalarization methods, converting multi-objective problems into equivalent single-objective tasks through weighted summation.

Furthermore, these approaches often rely on extensive simulation datasets (e.g., exceeding 400,000 evaluations) to train neural network models or perform structural classification. In contrast, the optimization process in this work employed only 300 finite element simulations to effectively explore the design space and identify a favorable tradeoff between CL and BI. The proposed multi-objective optimization framework achieves a minimum confinement loss of 1 dB/m and a birefringence level of $1\times {10}^{-4}$.

This notable outcome highlights the effectiveness of the developed optimization approach in balancing performance and computational efficiency under constrained simulation resources. Overall, compared to existing methods, the multi-objective strategy proposed in this study demonstrates significant advantages in achieving simultaneous confinement loss reduction and birefringence enhancement with reduced computational cost.

5. Conclusions

This work presents a novel polarization-maintaining hollow-core anti-resonant fiber design featuring a nested semicircular dual-ring structure and optimized through a multi-objective genetic algorithm. By simultaneously targeting high birefringence and low confinement loss, the proposed framework efficiently explores the structural parameter space and achieves a Pareto-optimal front with only 300 finite element simulations. Two representative optimal designs demonstrate strong tradeoff performance: one exhibits a birefringence of $2.04\times {10}^{-4}$ and confinement loss of 1.45 dB/m at 1550 nm, maintaining $BI>1.0\times {10}^{-4}$ across a 1275 nm bandwidth, while the other offers even lower loss (0.5 dB/m) with consistent birefringence over a 1000 nm range. Simulated mode profiles confirm robust polarization separation and low modal crosstalk. These findings highlight the potential of our optimization approach to guide the design of next-generation low-loss and high-birefringence fibers for practical applications in communication, sensing, and laser systems. Compared with existing methods that require extensive computation or rely on scalarized objective formulations, our MOGA-based approach demonstrates superior efficiency and design effectiveness. In conclusion, the proposed strategy offers a promising solution for the development of next-generation low-loss and high-birefringence fiber devices suitable for polarization-sensitive communications, interferometric sensing, and high-coherence laser delivery systems.