Structured Emission and Entanglement Dynamics of a Giant Atom in a Photonic Creutz Ladder
Abstract
1. Introduction
2. Theory
2.1. Creutz Ladder Model
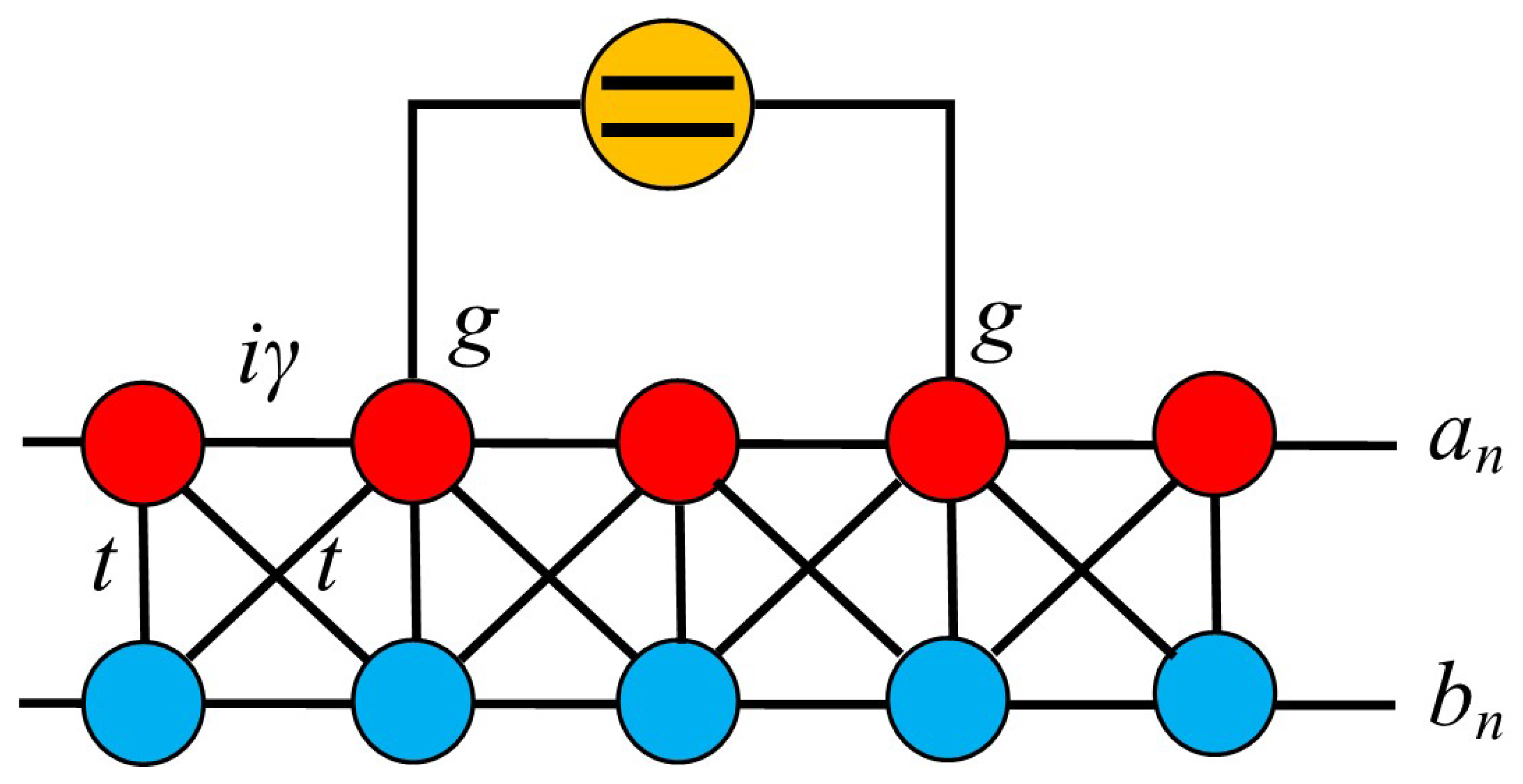
2.2. Giant Atom in a Creutz Ladder
2.3. Self-Energy and Bound States for a Giant Atom Coupled to a Creutz Ladder
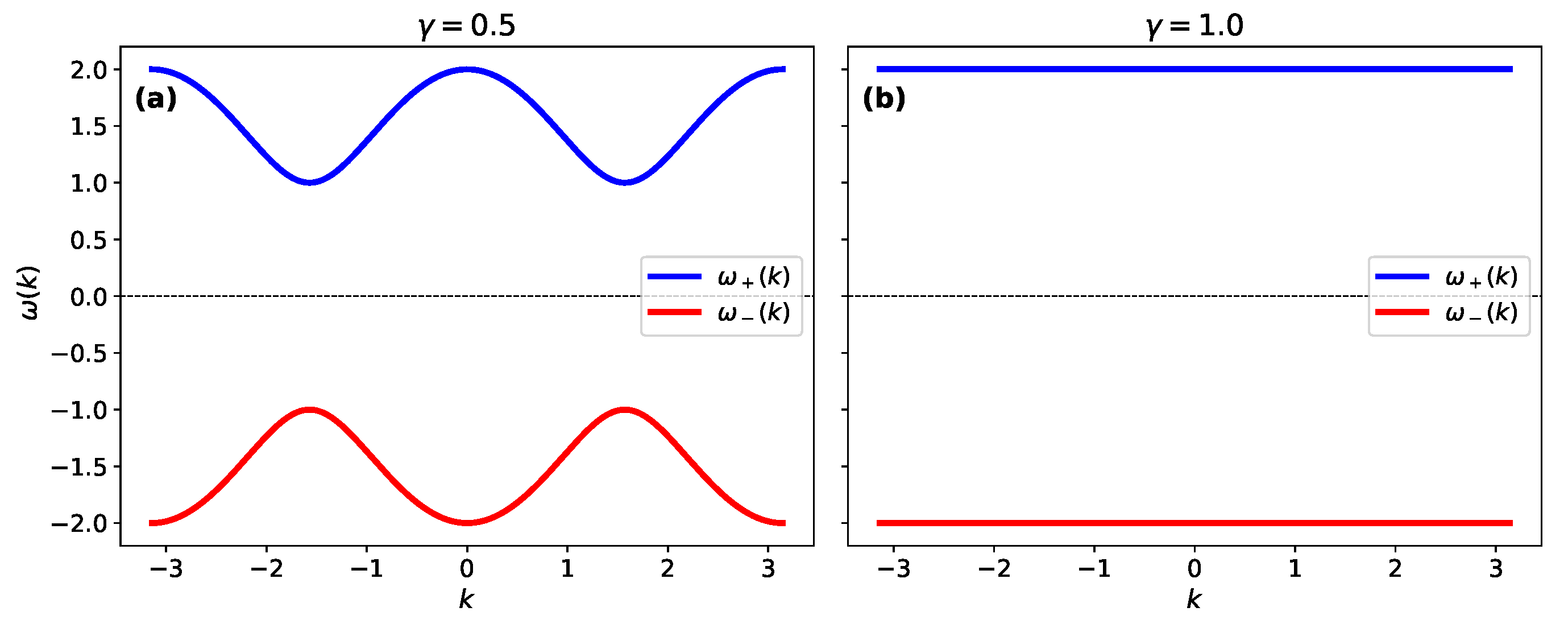
2.4. Flat-Band Limit
2.5. Bound States
3. Results and Discussion
| 0 | ||
| 1 | ||
| 2 |
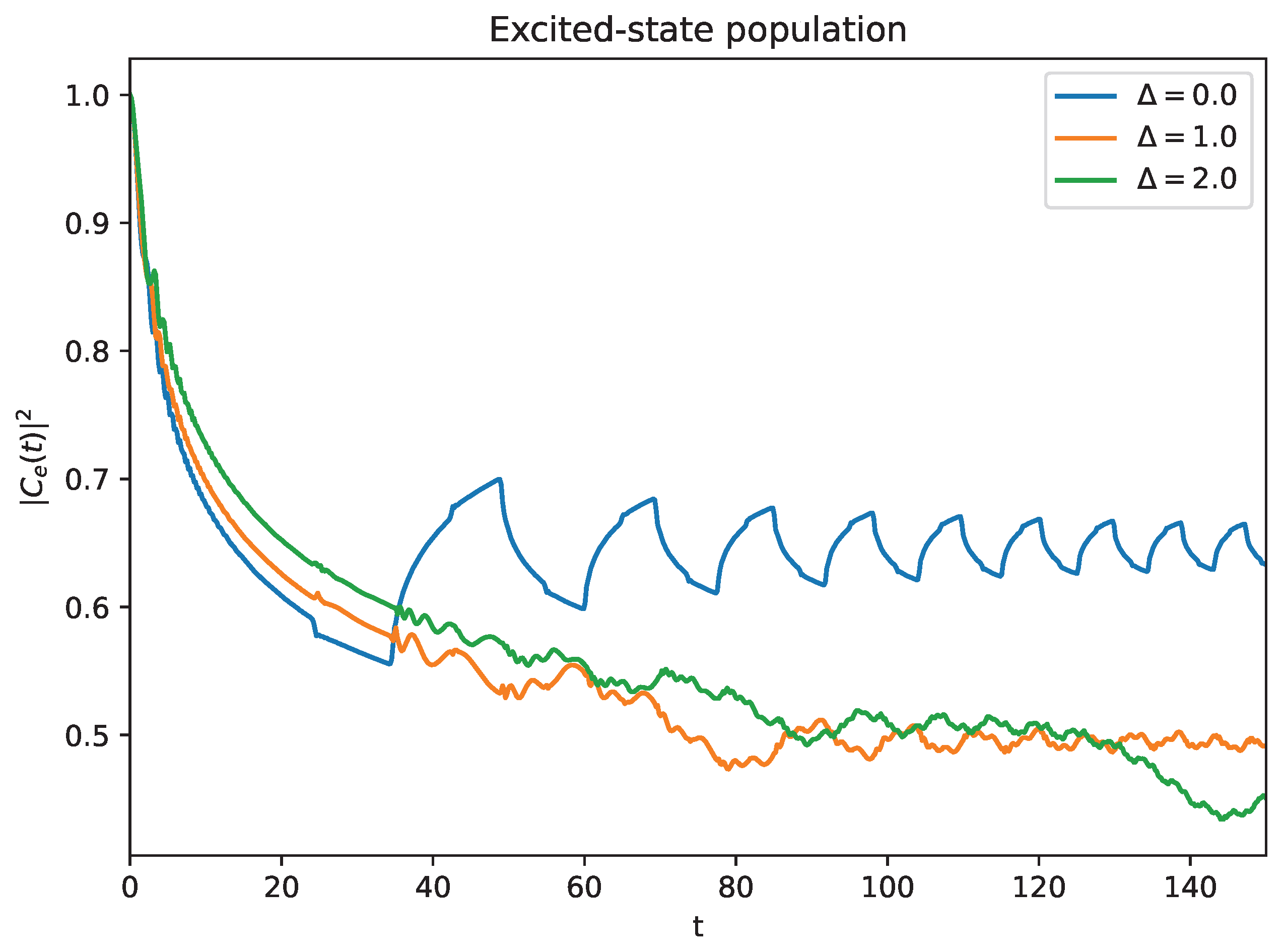
3.1. Population Dynamics
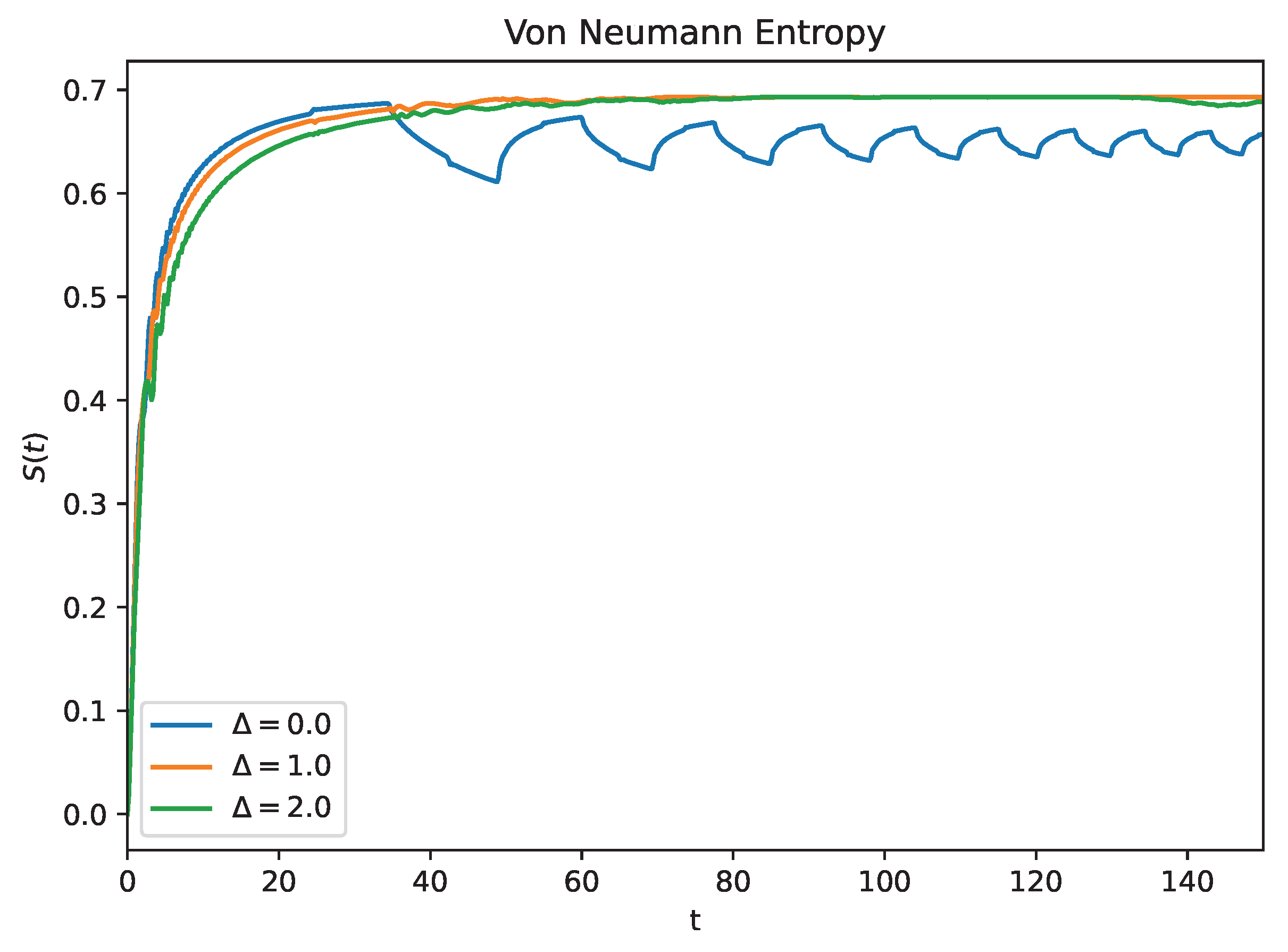
3.2. Entanglement Dynamics and Von Neumann Entropy
3.3. Atomic Mixedness and Purity Evolution
3.4. Effect of a Finite Temperature
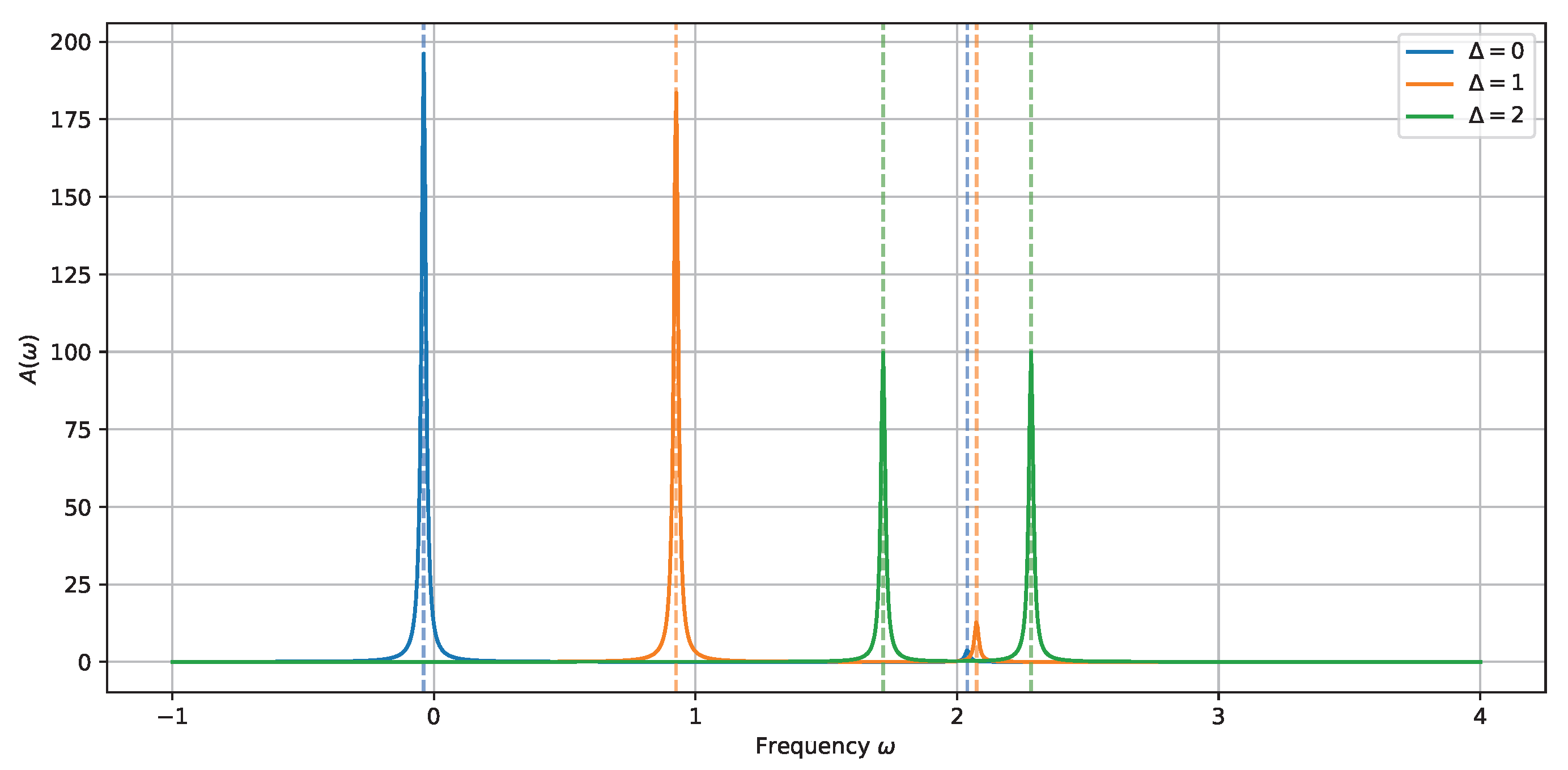
3.5. Photon Emission Profiles and Field Localization
3.6. Spacetime Evolution of the Photonic Field
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Chang, D.E.; Douglas, J.S.; González-Tudela, A.; Hung, C.-L.; Kimble, H.J. Colloquium: Quantum matter built from nanoscopic lattices of atoms and photons. Rev. Mod. Phys. 2018, 90, 031002. [Google Scholar] [CrossRef]
- Sheremet, A.S.; Petrov, M.I.; Iorsh, I.V.; Poshakinskiy, A.V.; Poddubny, A.N. Waveguide quantum electrodynamics: Collective radiance and photon-photon correlations. Rev. Mod. Phys. 2023, 95, 015002. [Google Scholar] [CrossRef]
- Ciccarello, F.; Lodahl, P.; Schneble, D. Waveguide quantum electrodynamics. Opt. Photonics News 2024, 35, 34. [Google Scholar] [CrossRef]
- Hood, J.D.; Goban, A.; Asenjo-Garcia, A.; Lu, M.; Yu, S.P.; Chang, D.E.; Kimble, H.J. Atom–atom interactions around the band edge of a photonic crystal waveguide. Proc. Natl. Acad. Sci. USA 2016, 113, 10507. [Google Scholar] [CrossRef] [PubMed]
- Owens, J.C.; Panetta, M.G.; Saxberg, B.; Roberts, G.; Chakram, S.; Ma, R.; Vrajitoarea, A.; Simon, J.; Schuster, D.I. Chiral cavity quantum electrodynamics. Nat. Phys. 2022, 18, 1048–1053. [Google Scholar] [CrossRef]
- Scigliuzzo, M.; Calajò, G.; Ciccarello, F.; Perez Lozano, D.; Bengtsson, A.; Scarlino, P.; Wallraff, A.; Chang, D.; Delsing, P.; Gasparinetti, S. Controlling atom-photon bound states in an array of Josephson-junction resonators. Phys. Rev. X 2022, 12, 031036. [Google Scholar] [CrossRef]
- Kim, E.; Zhang, X.; Ferreira, V.S.; Banker, J.; Iverson, J.K.; Sipahigil, A.; Bello, M.; González-Tudela, A.; Mirhosseini, M.; Painter, O. Quantum electrodynamics in a topological waveguide. Phys. Rev. X 2021, 11, 011015. [Google Scholar] [CrossRef]
- Krinner, L.; Stewart, M.; Pazmiño, A.; Kwon, J.; Schneble, D. Spontaneous emission of matter waves from a tunable open quantum system. Nature 2018, 559, 589–592. [Google Scholar] [CrossRef]
- Stewart, M.; Kwon, J.; Lanuza, A.; Schneble, D. Dynamics of matter-wave quantum emitters in a structured vacuum. Phys. Rev. Res. 2020, 2, 043307. [Google Scholar] [CrossRef]
- Kockum, A.F.; Delsing, P.; Johansson, G. Designing frequency-dependent relaxation rates and Lamb shifts for a giant artificial atom. Phys. Rev. A 2014, 90, 013837. [Google Scholar] [CrossRef]
- Andersson, G.; Suri, B.; Guo, L.; Aref, T.; Delsing, P. Non-exponential decay of a giant artificial atom. Nat. Phys. 2019, 15, 1123–1127. [Google Scholar] [CrossRef]
- Vadiraj, A.M.; Ask, A.; McConkey, T.G.; Nsanzineza, I.; Sandbo Chang, C.W.; Frisk Kockum, A.; Wilson, C.M. Engineering the level structure of a giant artificial atom in waveguide quantum electrodynamics. Phys. Rev. A 2021, 103, 023710. [Google Scholar] [CrossRef]
- Frisk Kockum, A.; Johansson, G.; Nori, F. Decoherence-free interaction between giant atoms in waveguide quantum electrodynamics. Phys. Rev. Lett. 2018, 120, 140404. [Google Scholar] [CrossRef] [PubMed]
- Kannan, B.; Ruckriegel, M.J.; Campbell, D.L.; Frisk Kockum, A.; Braumüller, J.; Kim, D.K.; Kjaergaard, M.; Krantz, P.; Melville, A.; Niedzielski, B.M.; et al. Waveguide quantum electrodynamics with superconducting artificial giant atoms. Nature 2020, 583, 775–779. [Google Scholar] [CrossRef]
- Carollo, A.; Cilluffo, D.; Ciccarello, F. Mechanism of decoherence-free coupling between giant atoms. Phys. Rev. Res. 2020, 2, 043184. [Google Scholar] [CrossRef]
- Soro, A.; Frisk Kockum, A. Chiral quantum optics with giant atoms. Phys. Rev. A 2022, 105, 023712. [Google Scholar] [CrossRef]
- Soro, A.; Muñoz, C.S.; Frisk Kockum, A. Interaction between giant atoms in a one-dimensional structured environment. Phys. Rev. A 2023, 107, 013710. [Google Scholar] [CrossRef]
- Du, L.; Guo, L.; Li, Y. Complex decoherence-free interactions between giant atoms. Phys. Rev. A 2023, 107, 023705. [Google Scholar] [CrossRef]
- Guo, L.; Frisk Kockum, A.; Marquardt, F.; Johansson, G. Oscillating bound states for a giant atom. Phys. Rev. Res. 2020, 2, 043014. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Y.; Purdy, T.; Taylor, J. Beyond spontaneous emission: Giant atom bounded in the continuum. Phys. Rev. A 2020, 102, 033706. [Google Scholar] [CrossRef]
- Terradas-Briansó, S.; González-Gutiérrez, C.A.; Nori, F.; Martín-Moreno, L.; Zueco, D. Ultrastrong waveguide QED with giant atoms. Phys. Rev. A 2022, 106, 063717. [Google Scholar] [CrossRef]
- Noachtar, D.D.; Knörzer, J.; Jonsson, R.H. Nonperturbative treatment of giant atoms using chain transformations. Phys. Rev. A 2022, 106, 013702. [Google Scholar] [CrossRef]
- Lim, K.H.; Mok, W.K.; Kwek, L.C. Oscillating bound states in non-Markovian photonic lattices. Phys. Rev. A 2023, 107, 023716. [Google Scholar] [CrossRef]
- Gustafsson, M.V.; Aref, T.; Frisk Kockum, A.; Ekström, M.K.; Johansson, G.; Delsing, P. Propagating phonons coupled to an artificial atom. Science 2014, 346, 207–211. [Google Scholar] [CrossRef]
- Aref, T.; Delsing, P.; Ekström, M.K.; Frisk Kockum, A.; Gustafsson, M.V.; Johansson, G.; Leek, P.J.; Magnusson, E.; Manenti, R. Quantum acoustics with surface acoustic waves. In Superconducting Devices in Quantum Optics; Hadfield, R.H., Johansson, G., Eds.; Springer: Berlin, Germany, 2016; pp. 217–244. [Google Scholar]
- Manenti, R.; Frisk Kockum, A.; Patterson, A.; Behrle, T.; Rahamim, J.; Tancredi, G.; Nori, F.; Leek, P.J. Circuit quantum acoustodynamics with surface acoustic waves. Nat. Commun. 2017, 8, 975. [Google Scholar] [CrossRef]
- Noguchi, A.; Yamazaki, R.; Tabuchi, Y.; Nakamura, Y. Qubit-assisted transduction for a detection of surface acoustic waves near the quantum limit. Phys. Rev. Lett. 2017, 119, 180505. [Google Scholar] [CrossRef]
- Satzinger, K.J.; Zhong, Y.P.; Chang, H.-S.; Peairs, G.A.; Bienfait, A.; Chou, M.-H.; Cleland, A.Y.; Conner, C.R.; Dumur, É.; Grebel, J.; et al. Quantum control of surface acoustic-wave phonons. Nature 2018, 563, 661–665. [Google Scholar] [CrossRef]
- Moores, B.A.; Sletten, L.R.; Viennot, J.J.; Lehnert, K.W. Cavity quantum acoustic device in the multimode strong coupling regime. Phys. Rev. Lett. 2018, 120, 227701. [Google Scholar] [CrossRef] [PubMed]
- Bolgar, A.N.; Zotova, J.I.; Kirichenko, D.D.; Besedin, I.S.; Semenov, A.V.; Shaikhaidarov, R.S.; Astafiev, O.V. Quantum regime of a two-dimensional phonon cavity. Phys. Rev. Lett. 2018, 120, 223603. [Google Scholar] [CrossRef]
- Sletten, L.R.; Moores, B.A.; Viennot, J.J.; Lehnert, K.W. Resolving phonon fock states in a multimode cavity with a double-slit qubit. Phys. Rev. X 2019, 9, 021056. [Google Scholar] [CrossRef]
- Bienfait, A.; Satzinger, K.J.; Zhong, Y.P.; Chang, H.-S.; Chou, M.-H.; Conner, C.R.; Dumur, É.; Grebel, J.; Peairs, G.A.; Povey, R.G.; et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 2019, 364, 368. [Google Scholar] [CrossRef]
- Bienfait, A.; Zhong, Y.P.; Chang, H.-S.; Chou, M.-H.; Conner, C.R.; Dumur, É.; Grebel, J.; Peairs, G.A.; Povey, R.G.; Satzinger, K.J.; et al. Quantum erasure using entangled surface acoustic phonons. Phys. Rev. X 2020, 10, 021055. [Google Scholar] [CrossRef]
- Andersson, G.; Ekström, M.K.; Delsing, P. Electromagnetically induced acoustic transparency with a superconducting circuit. Phys. Rev. Lett. 2020, 124, 240402. [Google Scholar] [CrossRef] [PubMed]
- Joshi, C.; Yang, F.; Mirhosseini, M. Resonance fluorescence of a chiral artificial atom. Phys. Rev. X 2023, 13, 021039. [Google Scholar] [CrossRef]
- González-Tudela, A.; Muñoz, C.S.; Cirac, J.I. Engineering and harnessing giant atoms in high-dimensional baths: A proposal for implementation with cold atoms. Phys. Rev. Lett. 2019, 122, 203603. [Google Scholar] [CrossRef]
- Du, L.; Zhang, Y.; Wu, J.H.; Kockum, A.F.; Li, Y. Giant atoms in a synthetic frequency dimension. Phys. Rev. Lett. 2022, 128, 223602. [Google Scholar] [CrossRef] [PubMed]
- Guimond, P.O.; Vermersch, B.; Juan, M.L.; Sharafiev, A.; Kirchmair, G.; Zoller, P. A unidirectional on-chip photonic interface for superconducting circuits. Npj Quantum Inf. 2020, 6, 32. [Google Scholar] [CrossRef]
- Gheeraert, N.; Kono, S.; Nakamura, Y. Programmable directional emitter and receiver of itinerant microwave photons in a waveguide. Phys. Rev. A 2020, 102, 053720. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Carceller, C.R.; Kjaergaard, M.; Sørensen, A.S. Charge-noise insensitive chiral photonic interface for waveguide circuit QED. Phys. Rev. Lett. 2021, 127, 233601. [Google Scholar] [CrossRef]
- Yin, X.-L.; Liu, Y.-H.; Huang, J.-F.; Liao, J.-Q. Single-photon scattering in a giant-molecule waveguide-QED system. Phys. Rev. A 2022, 106, 013715. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Liu, Z.; Li, X.; Chen, H.; Zhou, J.; Zhang, Y.; Liu, Y.; Zhang, L.; Liu, J.; et al. Observation of non-Hermitian skin effect and topology in a non-Hermitian lattice. Optica 2022, 9, 565–571. [Google Scholar]
- Kannan, B.; Almanakly, A.; Sung, Y.; Di Paolo, A.; Rower, D.A.; Braumüller, J.; Melville, A.; Niedzielski, B.M.; Karamlou, A.; Serniak, K.; et al. On-demand directional microwave photon emission using waveguide quantum electrodynamics. Nat. Phys. 2023, 19, 394. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Wang, Y.P.; Yao, J.; Shen, R.C.; Wu, W.J.; Qian, J.; Li, J.; Zhu, S.Y.; You, J.Q. Giant spin ensembles in waveguide magnonics. Nat. Commun. 2022, 13, 7580. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Grimsmo, A.L.; Kockum, A.F.; Pletyukhov, M.; Johansson, G. Giant acoustic atom: A single quantum system with a deterministic time delay. Phys. Rev. A 2017, 95, 053821. [Google Scholar] [CrossRef]
- Karg, T.M.; Gouraud, B.; Treutlein, P.; Hammerer, K. Remote Hamiltonian interactions mediated by light. Phys. Rev. A 2019, 99, 063829. [Google Scholar] [CrossRef]
- Ask, A.; Fang, Y.-L.L.; Kockum, A.F. Synthesizing electromagnetically induced transparency without a control field in waveguide QED using small and giant atoms. arXiv 2020, arXiv:2011.15077. [Google Scholar] [CrossRef]
- Du, L.; Li, Y. Single-photon frequency conversion via a giant Λ-type atom. Phys. Rev. A 2021, 104, 023712. [Google Scholar] [CrossRef]
- Feng, S.L.; Jia, W.Z. Manipulating single-photon transport in a waveguide-QED structure containing two giant atoms. Phys. Rev. A 2021, 104, 063712. [Google Scholar] [CrossRef]
- Cai, Q.Y.; Jia, W.Z. Coherent single-photon scattering spectra for a giant-atom waveguide-QED system beyond the dipole approximation. Phys. Rev. A 2021, 104, 033710. [Google Scholar] [CrossRef]
- Yin, X.-L.; Luo, W.-B.; Liao, J.-Q. Non-Markovian disentanglement dynamics in double-giant-atom waveguide-QED systems. Phys. Rev. A 2022, 106, 063703. [Google Scholar] [CrossRef]
- Gong, Z.; Bello, M.; Malz, D.; Kunst, F.K. Anomalous Behaviors of Quantum Emitters in Non-Hermitian Baths. Phys. Rev. Lett. 2022, 129, 223601. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Du, L.; Guo, L.; Wang, Z.; Zhang, Y.; Li, Y.; Wu, J.-H. Nonreciprocal and chiral single-photon scattering for giant atoms. Commun. Phys. 2022, 5, 215. [Google Scholar] [CrossRef]
- Du, L.; Chen, Y.-T.; Zhang, Y.; Li, Y. Giant atoms with time-dependent couplings. Phys. Rev. Res. 2022, 4, 023198. [Google Scholar] [CrossRef]
- Du, L.; Zhang, Y.; Li, Y. A giant atom with modulated transition frequency. Front. Phys. 2023, 18, 12301. [Google Scholar] [CrossRef]
- Santos, A.C.; Bachelard, R. Generation of maximally entangled long-lived states with giant atoms in a waveguide. Phys. Rev. Lett. 2023, 130, 053601. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, H.-B.; Liu, T.; Nori, F. Realizing quantum optics in structured environments with giant atoms. Phys. Rev. Res. 2024, 6, 013279. [Google Scholar] [CrossRef]
- Zhou, J.; Yin, X.-L.; Liao, J.-Q. Chiral and nonreciprocal single-photon scattering in a chiral-giant-molecule waveguide-QED system. Phys. Rev. A 2023, 107, 063703. [Google Scholar] [CrossRef]
- Gu, W.; Huang, H.; Yi, Z.; Chen, L.; Sun, L.; Tan, H. Correlated two-photon scattering in a one-dimensional waveguide coupled to two- or three-level giant atoms. Phys. Rev. A 2023, 108, 053718. [Google Scholar] [CrossRef]
- Xu, L.; Guo, L. Catch and release of propagating bosonic field with non-Markovian giant atom. New J. Phys. 2024, 26, 013025. [Google Scholar] [CrossRef]
- Longhi, S. Photonic simulation of giant atom decay. Opt. Lett. 2020, 45, 3017–3020. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Z. Single-photon scattering and bound states in an atom-waveguide system with two or multiple coupling points. Phys. Rev. A 2020, 101, 053855. [Google Scholar] [CrossRef]
- Wang, X.; Liu, T.; Kockum, A.F.; Li, H.-R.; Nori, F. Tunable chiral bound states with giant atoms. Phys. Rev. Lett. 2021, 126, 043602. [Google Scholar] [CrossRef]
- Longhi, S. Rabi oscillations of bound states in the continuum. Opt. Lett. 2021, 46, 2091–2094. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Z.; Wu, J.-H. Entanglement preparation and nonreciprocal excitation evolution in giant atoms by controllable dissipation and coupling. Phys. Rev. A 2021, 104, 013720. [Google Scholar] [CrossRef]
- Vega, C.; Bello, M.; Porras, D.; González-Tudela, A. Qubit-photon bound states in topological waveguides with long-range hoppings. Phys. Rev. A 2021, 104, 053522. [Google Scholar] [CrossRef]
- Smith, A.; Johnson, B.; Lee, C.; Kumar, D.; Nguyen, E.; Patel, F.; Garcia, G.; Chen, H.; Wang, I.; Zhao, J.; et al. Enhanced light–matter interaction in hybrid nanophotonic structures. Nanophotonics 2021, 10, 567–578. [Google Scholar]
- Wang, X.; Li, H.-R. Chiral quantum network with giant atoms. Quantum Sci. Technol. 2022, 7, 035007. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, L.; Li, Z.; Chen, X.; Yuan, L. Bound state in a giant atom-modulated resonators system. Npj Quantum Inf. 2022, 8, 80. [Google Scholar] [CrossRef]
- Cheng, W.; Wang, Z.; Liu, Y.X. Topology and retardation effect of a giant atom in a topological waveguide. Phys. Rev. A 2022, 106, 033522. [Google Scholar] [CrossRef]
- Gong, Z.; Bello, M.; Malz, D.; Kunst, F.K. Bound states and photon emission in non-Hermitian nanophotonics. Phys. Rev. A 2022, 106, 053517. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, W.; Gong, Z.; Zheng, T.; Wang, Z. Superconducting giant atom waveguide QED: Quantum Zeno and anti-Zeno effects in ultrastrong coupling regime. arXiv 2022, arXiv:2205.03674. [Google Scholar] [CrossRef]
- Du, L.; Guo, L.; Zhang, Y.; Kockum, A.F. Giant emitters in a structured bath with non-Hermitian skin effect. Phys. Rev. Res. 2023, 5, L042040. [Google Scholar] [CrossRef]
- Du, L.; Chen, Y.-T.; Zhang, Y.; Li, Y.; Wu, J.-H. Decay dynamics of a giant atom in a structured bath with broken time-reversal symmetry. Quantum Sci. Technol. 2023, 8, 045010. [Google Scholar] [CrossRef]
- Bello, M.; Cirac, J.I. Topological effects in two-dimensional quantum emitter systems. Phys. Rev. B 2023, 107, 054301. [Google Scholar] [CrossRef]
- Bag, R.; Roy, D. Quantum light-matter interactions in structured waveguides. Phys. Rev. A 2023, 108, 053717. [Google Scholar] [CrossRef]
- Jia, W.Z.; Yu, M.T. Atom-photon dressed states in a waveguide-QED system with multiple giant atoms. Opt. Express 2024, 32, 9495–9508. [Google Scholar] [CrossRef]
- Gao, Z.-M.; Li, J.-Q.; Li, Z.-W.; Liu, W.-X.; Wang, X. Circuit QED with giant atoms coupling to left-handed superlattice metamaterials. Phys. Rev. A 2024, 109, 013716. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Wang, L.; Chen, M.; Zhao, Q.; Li, H. Topological photonics in synthetic dimensions. Nat. Commun. 2024, 15, 1234. [Google Scholar] [CrossRef]
- Leonforte, L.; Sun, X.; Valenti, D.; Spagnolo, B.; Illuminati, F.; Carollo, A.; Ciccarello, F. Quantum optics with giant atoms in a structured photonic bath. Quantum Sci. Technol. 2024, 10, 015057. [Google Scholar] [CrossRef]
- Ingelsten, E.R.; Kockum, A.F.; Soro, A. Avoiding decoherence with giant atoms in a two-dimensional structured environment. Phys. Rev. Res. 2024, 6, 043222. [Google Scholar] [CrossRef]
- Du, L.; Kockum, A.F. Unconventional and robust light–matter interactions based on the non-Hermitian skin effect. Phys. Rev. Res. 2025, 7, 013140. [Google Scholar] [CrossRef]
- Chen, G.; Kockum, A.F. Simulating open quantum systems with giant atoms. Quantum Sci. Technol. 2025, 10, 025028. [Google Scholar] [CrossRef]
- Yannopapas, V. Non-Markovian Dynamics of Giant Atoms Embedded in an One-Dimensional Photonic Lattice with Synthetic Chirality. Photonics 2025, 12, 527. [Google Scholar] [CrossRef]
- Yannopapas, V. Entanglement Dynamics of Two Giant Atoms Embedded in a One-Dimensional Photonic Lattice with a Synthetic Gauge Field. Photonics 2025, 12, 612. [Google Scholar] [CrossRef]
- Creutz, M. End states, ladder compounds, and domain-wall fermions. Phys. Rev. Lett. 1999, 83, 2636. [Google Scholar] [CrossRef]
- Mukherjee, S.; Di Liberto, M.; Öhberg, P.; Thomson, R.R.; Goldman, N. Experimental Observation of Aharonov–Bohm Cages in Photonic Lattices. Phys. Rev. Lett. 2018, 121, 075502. [Google Scholar] [CrossRef]
- Zurita, J.; Creffield, C.E.; Platero, G. Topology and Interactions in the Photonic Creutz and Creutz-Hubbard Ladders. Adv. Quantum Technol. 2019, 3, 1900105. [Google Scholar] [CrossRef]
- Alaeian, H.; Chang, C.W.S.; Moghaddam, M.V.; Wilson, C.M.; Solano, E.; Rico, E. Creating Lattice Gauge Potentials in Circuit QED: The Bosonic Creutz Ladder. Phys. Rev. A 2019, 99, 053834. [Google Scholar] [CrossRef]
- Kang, J.H.; Han, J.H.; Shin, Y. Creutz Ladder in a Resonantly Shaken 1D Optical Lattice. New J. Phys. 2020, 22, 013023. [Google Scholar] [CrossRef]
- Kuno, Y. Extended Flat Band, Entanglement, and Topological Properties in a Creutz Ladder. Phys. Rev. B 2020, 101, 184112. [Google Scholar] [CrossRef]
- Kuno, Y.; Orito, T.; Ichinose, I. Flat-Band Many-Body Localization and Ergodicity Breaking in the Creutz Ladder. New J. Phys. 2020, 22, 013032. [Google Scholar] [CrossRef]
- Lahiri, S.; Basu, S. Higher Order Topology in a Creutz Ladder. J. Phys. Condens. Matter 2023, 35, 425902. [Google Scholar] [CrossRef]
- Hung, J.S.C.; Busnaina, J.H.; Chang, C.W.S.; Vadiraj, A.M.; Nsanzineza, I.; Solano, E.; Alaeian, H.; Rico, E.; Wilson, C.M. Quantum Simulation of the Bosonic Creutz Ladder with a Parametric Cavity. Phys. Rev. Lett. 2021, 127, 100503. [Google Scholar] [CrossRef]
- Zhang, S.M.; Xu, H.S.; Jin, L. Tunable Aharonov–Bohm Cages through Anti-PT-Symmetric Imaginary Couplings. Phys. Rev. A 2023, 108, 023518. [Google Scholar] [CrossRef]
- Leonforte, L.; Carollo, A.; Ciccarello, F. Vacancy-Like Dressed States in Topological Waveguide QED. Phys. Rev. Lett. 2021, 126, 063601. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Yuan, Z. Topological Properties of Non-Hermitian Creutz Ladder. Chin. Phys. B 2022, 31, 010310. [Google Scholar] [CrossRef]
- Hurtado-Aviles, E.A.; Vila, M.; Vilatela, J.J.; Martines-Arano, H.; Bornacelli, J.; García-Merino, J.A.; Cervantes-Sodi, F.; Torres-Torres, C. Structured light using carbon nanostructures driven by Kerr nonlinearities and a magnetic field. Phys. Chem. Chem. Phys. 2022, 24, 1081–1090. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Wang, K.; Liu, Y.-C. Selective coupling of a giant atom to flat and dispersive bands. Phys. Rev. A 2025, 111, 053706. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yannopapas, V. Structured Emission and Entanglement Dynamics of a Giant Atom in a Photonic Creutz Ladder. Photonics 2025, 12, 827. https://doi.org/10.3390/photonics12080827
Yannopapas V. Structured Emission and Entanglement Dynamics of a Giant Atom in a Photonic Creutz Ladder. Photonics. 2025; 12(8):827. https://doi.org/10.3390/photonics12080827
Chicago/Turabian StyleYannopapas, Vassilios. 2025. "Structured Emission and Entanglement Dynamics of a Giant Atom in a Photonic Creutz Ladder" Photonics 12, no. 8: 827. https://doi.org/10.3390/photonics12080827
APA StyleYannopapas, V. (2025). Structured Emission and Entanglement Dynamics of a Giant Atom in a Photonic Creutz Ladder. Photonics, 12(8), 827. https://doi.org/10.3390/photonics12080827





