An Improved PCA and Jacobian-Enhanced Whale Optimization Collaborative Method for Point Cloud Registration

Abstract

Scanned data often contain substantial outliers due to environmental interference, which drastically decreases the performance of traditional registration algorithms. To address this issue, this article proposes an improved principal component analysis (PCA) and Jacobian-enhanced whale optimization collaborative method for point cloud registration. First, an improved PCA point cloud initial registration algorithm is proposed by introducing the normal vector local information to set the screening conditions. This algorithm can streamline the original set of 48 candidate rotation matrices down to 4, achieving rapid point cloud registration at the data level between the scanned and model point clouds. Second, a Jacobian whale optimization algorithm for fine registration (JWOA-FR) is proposed by incorporating local gradient information. The algorithm employs gradient descent on optimal whale individuals to dynamically guide global search updates, thereby enhancing both registration accuracy and efficiency. Finally, a threshold is set to remove the outliers contained in the workpieces based on the information of the matched point pairs. The iterative closest point (ICP) algorithm is further used to improve registration accuracy for data without outliers. The experimental results showed that registration errors of large workpieces 1, 2, and 3 were 2.0755 mm, 2.3955 mm, and 2.5823 mm, respectively, after outlier removal, which indicates that the proposed method is applicable to data with outliers, and the registration accuracy meets the requirements.

1. Introduction

With the advancement of 3D laser scanning technology, scanners are constantly upgraded and replaced. Handheld and tracking scanners are better able to obtain the complete data of a measured workpiece. However, due to the limitations of the measurement environment, it is inevitable that there will be clutter in the final scan results. These clutter points are mostly not the usual noise points caused by uneven scanning, but outlier points in non-effective areas accidentally identified due to environmental factors. Moreover, the sources of these outliers are usually the tables or turntables where the workpieces are placed: these are very close to the workpieces, even connected, making it difficult for conventional denoising algorithms to achieve complete separation. If we directly apply this type of raw data containing substantial outliers and no overlap to registration, traditional algorithms are difficult to implement. As a core step in 3D reconstruction, quality inspection, robot orientation estimation, and related applications, the accuracy of point cloud registration directly affects subsequent steps.

Point cloud registration accuracy, core to the implementation of projects such as 3D reconstruction, quality inspection, and robot orientation estimation, will directly affect subsequent steps.

To solve this problem, scholars have proposed various improved registration methods or related denoising methods. Fortun D et al. [1] introduced an explicit local noise model combined with an expectation-maximization algorithm to efficiently solve the point cloud multi-view registration problem containing highly anisotropic noise in a single-molecule localization microscopy scenario. Zhao J et al. [2] proposed a novel geometric fast registration model based on three core modules: point extractor registration, dual attention transformation, and geometric feature matching. This model can be applied to the registration of noisy and incomplete skeletal data. Ervan O et al. [3] optimized point cloud registration from the perspective of sampling, using histograms to identify the most significant regions of the point cloud to create downsampled output data. Experimental results showed that the proposed method can improve registration accuracy and is robust to noise. Kim I et al. [4] integrated the concepts of random sampling consistency and Gaussian process regression to achieve the identification and removal of outliers by iteratively scoring them based on prediction confidence, as well as the ability to denoise by weighted prediction. Bao Y et al. [5] proposed an integrated processing method based on the Heber loss function for subway shield tunnel cross-section fitting and point cloud denoising, which can remove non-structural facilities and other noisy point clouds contained in the original tunnel point cloud data in order to prevent them from affecting the detection of the tunnel lining structure. Through the research of various scholars, it can be found that the application fields of point cloud registration algorithms have become increasingly broad, and the robustness of the algorithms has also been improving. In the field of outlier and noise removal, more and more applicable algorithms are being proposed. However, these algorithms are generally applicable to point clouds that contain outliers of 10% or less in the total data volume. Thus, their applicability of point cloud data with an outlier inclusion ratio of over 30% and no overlap is unknown.

It is difficult to correctly extract features from scanned point cloud data containing many outliers, and the relative initial pose between the scanned point cloud and the model point cloud is extremely poor, with no overlap. Therefore, this article is divided into two parts: initial registration and fine registration. The initial registration part requires the algorithm to quickly align the scanned point cloud data with the model point cloud and ensure the correct transformation direction. An improved PCA point cloud initial registration algorithm is proposed. By introducing local information of the normal vector combined with the global principal axis information to set up two screenings in advance, the 48 candidate matrices are reduced to 8 and then to 4. The improved algorithm can greatly reduce the initial registration time and is suitable for aligning point cloud data containing a large number of outliers.

In the fine registration section, we transform the point cloud registration into an optimization problem of rotational and translation parameters. In 2016, Mirjalili S et al. [6] proposed a novel nature-inspired metaheuristic optimization algorithm called the whale optimization algorithm (WOA) by mimicking the social behavior of humpback whales. This algorithm is suitable for solving continuous space optimization problems and is compatible with the logical properties of point cloud registration. WOA has become a classic swarm intelligence optimization algorithm, with continuous improvements and applications emerging. Ma Y et al. [7] combined the vehicle shape features with the improved WOA-Xception model to construct a nonlinear mapping model between the vehicle shape features and the wind noise level at the driver’s right ear, which was used for realizing the prediction of in-vehicle wind noise. Suthar B et al. [8] optimized load scheduling in an energy management system using fuzzy logic and WOA to reduce the cost of electricity for consumers. Wang Z et al. [9] introduced the Sobol sequence and a sine–cosine mechanism to propose an improved whale optimization algorithm that enhanced the accuracy detection of free-form surfaces. WOA can be applied to various optimization problems in different scenarios. Nevertheless, in order to achieve the desired results for specific problems, targeted improvements are still needed, along with an increase in iteration speed.

Based on this, a Jacobian whale optimization algorithm for fine registration is proposed in this article. The proposed algorithm introduces local Jacobian gradient information for optimization. When calculating the Jacobian matrix, an adaptive difference step size is set based on the iterations, and the results are used to perform gradient descent with momentum on the optimal individuals. By adjusting the optimal individuals, the search direction of the whale is dynamically adjusted while retaining the global update capability of the whale algorithm to avoid falling into local optima. The deep fusion optimization of the two can better accomplish the point cloud registration task. Subsequently, considering that the existence of outliers may still have a certain impact on the registration accuracy, we add the following step: search for matching point pairs through KD-tree, set a threshold to eliminate major outliers, and then use the ICP algorithm to further optimize the registration accuracy. In order to evaluate the performance of the proposed algorithm, comprehensive tests and comparisons were conducted on large-scale industrial workpieces obtained through actual scanning. The test data all contained more than 30% outlier point contamination. The results showed that the proposed algorithm is more feasible and effective.

In this article, for the registration of scanned point clouds containing numerous outliers, a point cloud collaborative registration method is proposed, combining improved PCA with Jacobian-enhanced whale optimization. The main steps of the proposed method are as follows. (1) In initial point cloud registration, set up the principal axis alignment check as well as the normal vector alignment check to eliminate the wrong candidates in advance and thereby improve the PCA registration algorithm. (2) Transform the fine point cloud registration into an optimization problem. Based on WOA, the Jacobian matrix is introduced to dynamically adjust the search direction using local gradient information. A Jacobian whale optimization algorithm for fine registration is proposed. (3) After completing the above algorithm, the KD-tree is used to search for matching pairs of the two. The points that are not matched in the transformed point cloud are removed as outliers. Finally, the ICP algorithm is utilized to further improve registration accuracy. The flowchart of the proposed registration method is shown in Figure 1.

The rest of this article is organized as follows. The initial registration of the scanned point cloud with the model point cloud and the proposed improved PCA algorithm are introduced in Section 2. The specific details of the proposed point cloud fine registration algorithm JWOA-FR are presented in Section 3. The algorithm comparison test experiments and the analysis of the registration results are given in Section 4. Finally, conclusions are provided in Section 5. Due to the relatively large number of abbreviations used in this article, a complete alphabetical listing is provided in Appendix A.

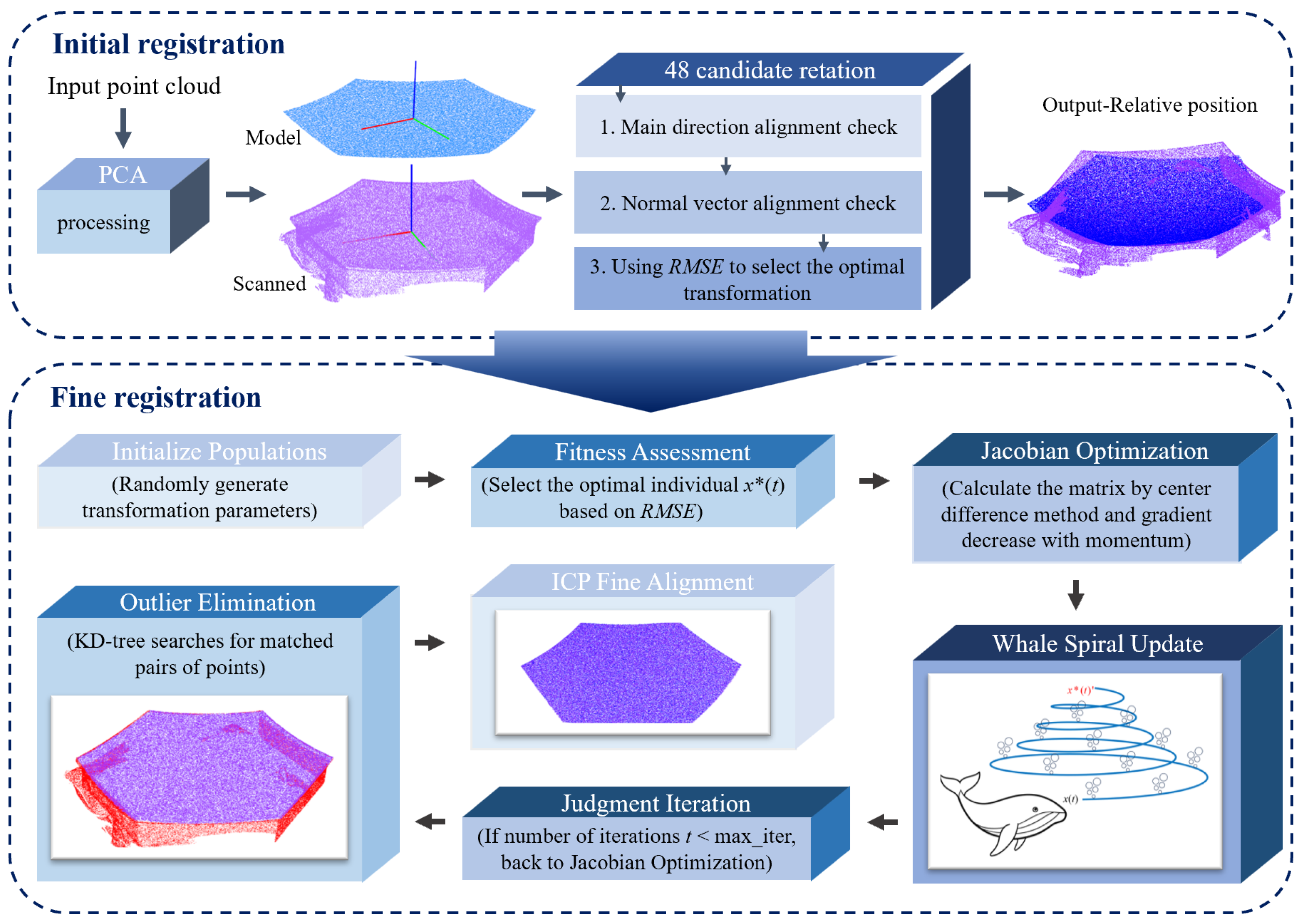
2. Point Cloud Initial Registration

There are existing point cloud initial registration algorithms based on feature descriptors, such as sample consensus initial alignment (SAC-IA) [10], 4-point congruent sets (4PCS) [11], and random sample consensus (RANSAC) [12]. They find matching point pairs for coordinate transformation by describing the local features of the scanned point cloud and the model point cloud. However, if the scanned point cloud has many stray points, strong local feature similarity, and poor relative initial orientation, the applicability of the above methods will be greatly diminished, resulting in poor registration outcomes [13]. From the data perspective, PCA [14,15] analyzes the main direction of two point clouds and retains the features that contribute the most to the point cloud, making it somewhat applicable to point cloud registration with outliers.

PCA acquires the eigenvalues and eigenvectors of the point cloud, i.e., principal components. According to the principal component directions and the three axes combined with positive and negative values, a total of 3! × 2³ = 6 × 8 = 48 candidate transformation matrices can be generated. The root mean square error (RMSE) is used as the evaluation index of point cloud registration accuracy, and the correspondence with the smallest error is the optimal transformation. However, fully evaluating the registration results of the 48 candidate transformations to determine the optimal transformation would be time-consuming. The calculation of RMSE is essentially to find the nearest neighbor pairs by KD-tree and then calculate the distance between them. The determination of its corresponding point pairs is also only a local optimal solution, which lacks a global nature. Therefore, an improved PCA point cloud initial registration algorithm is proposed: set two filtering criteria to preemptively eliminate incorrect candidates, namely the main direction alignment check and the normal vector alignment check, and finally determine the optimal transformation matrix using RMSE. The specific process is as follows.

2.1. PCA-Based Point Cloud Registration: A Brief Principle

The core of principal component analysis is to reduce the dimensionality of high-dimensional data through projection to extract the main information of the data. It focuses on the overall distribution of data. The essence of point cloud registration is the coordinate system transformation, which rotates and translates the scanned point cloud to the model point cloud according to the correspondence to realize effective region overlapping. Therefore, PCA-based point cloud registration can be specifically divided into three steps [16,17]: (1) perform PCA on the scanned point cloud and the model point cloud to extract the principal 3D components; (2) generate candidate rotation and translation matrices based on the principal axis direction of the point cloud; and (3) calculate the RMSE after registration to determine the optimal transformation matrix. The schematic diagram of the PCA spindle determination is shown in Figure 2.

2.2. Improved PCA Point Cloud Initial Registration Algorithm

If we follow the original algorithm’s process and calculate all candidate transformations completely, then the optimal transformations are determined based on the magnitude of the result error, causing excessive time consumption. At the same time, due to the presence of outliers in the scanned point cloud whose principal components are not identical to those of the model point cloud, the rotation matrix in the direction corresponding to the largest principal component cannot simply be taken as the optimal transformation. All possible cases still need to be considered. Therefore, this article proposes an improved PCA point cloud initial registration algorithm based on standard PCA. The proposed algorithm considers the local normal vector features of the point cloud, presets two filtering conditions to quickly eliminate erroneous candidates, and then determines the optimal transformation.

The proposed algorithm introduces local normal vector information to optimize registration based on global principal component analysis. Normal vectors represent the local features of the point cloud and ensure local surface geometric consistency. The local surface is fitted by searching the nearest points through KD-tree, and the plane normal vector is used as the local point normal vector. Then, by determining the uniform direction based on the neighboring points, we can obtain the final local normal vector information. If the scanned point cloud achieves the correct transformation, the normal vectors of corresponding points at its centroid should be approximately aligned with those of the model point cloud at the centroid. Therefore, the angle between their normal vectors can be calculated to determine the wrong candidate transforms and eliminate them early.

Also, the point cloud PCA information is prioritized to set the principal axis alignment check. For each candidate matrix, calculate the angle between the principal axis of the rotated scanned point cloud and the principal axis of the model point cloud. The one with a large angle will be eliminated in advance as incorrect. The translation matrix is obtained through difference calculation after rotational transformation of the centroid, which is also based on the rotation matrix. Therefore, there is no need to perform repeated filtering based on the translation matrix [18]. Through two-step screening, it is possible to combine the global principal direction information and the local normal vector information to exclude erroneous transformations in advance among the 48 candidate matrices. The optimal transformation determination time can be reduced by an order of magnitude as well as increase accuracy through the improved algorithm. The specific steps of the proposed algorithm are as follows.

Step 1: Scanned point cloud $S=\{s_1,s_2,\text{…},s_m\text{}}$, model point cloud $M=\{m_1,m_2,\text{…},m_n\text{}}$. Calculate their centroids as $\overline{S}$ and $\overline{M}$, respectively. After centering, calculate their covariance matrices $C_S$ and $C_M$, both 3 × 3 matrices.

$$\left\{\begin{array}{l}\overline{S}={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m{s}_i,\overline{M}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{m}_i}}\\ C_S={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m(s_i-\overline{S}){(s_i-\overline{S})}^T,C_M=\frac{1}{n}{\displaystyle \sum _{i=1}^n(m_i-\overline{M}){(m_i-\overline{M})}^T}}\end{array}\right.$$

(1)

Step 2: According to the spectral theorem, performing eigenvalue decomposition (EVD) [19] on the covariance matrices $C_S$ and $C_M$ can obtain their eigenvalues and eigenvectors, with the following formulas:

$$\left\{\begin{array}{l}{C}_S=\left[\begin{array}{ccc}{\nu }_{S1}& {\nu }_{S2}& {\nu }_{S3}\end{array}\right]\left[\begin{array}{ccc}{\lambda }_{S1}& & O\\ & {\lambda }_{S2}& \\ O& & {\lambda }_{S3}\end{array}\right]{\left[\begin{array}{ccc}{\nu }_{S1}& {\nu }_{S2}& {\nu }_{S3}\end{array}\right]}^T\\ C_M=\left[\begin{array}{ccc}{\nu }_{M1}& {\nu }_{M2}& {\nu }_{M3}\end{array}\right]\left[\begin{array}{ccc}{\lambda }_{M1}& & O\\ & {\lambda }_{M2}& \\ O& & {\lambda }_{M3}\end{array}\right]{\left[\begin{array}{ccc}{\nu }_{M1}& {\nu }_{M2}& {\nu }_{M3}\end{array}\right]}^T\end{array}\right.$$

(2)

where ${\lambda }_{S1}$, ${\lambda }_{S2}$, ${\lambda }_{S3}$ denotes the eigenvalue of the scanned point cloud S, and ${\lambda }_{S1}\ge {\lambda }_{S2}$ ≥ ${\lambda }_{S3}$; ${\nu }_{S1}$, ${\nu }_{S2}$, ${\nu }_{S3}$ is the 3 × 1 eigenvector corresponding to the eigenvalue. Similarly, the other parameters are the eigenvalues and eigenvectors corresponding to the model point cloud.

Step 3: The principal axis matrices $V_S$ and $V_M$ of the scanned and model point clouds are arranged by eigenvectors to form a 3 × 3 matrix. Rotate the principal axis of the scanned point cloud to align with the principal axis of the model point cloud using a rotation matrix $R=V_M{V}_S^T$. By combining the three feature vectors with the positive and negative directions, 3! × 2³ = 6 × 8 = 48 candidate rotation matrices can be generated. Translate the centroid of the scanned point cloud to the centroid of the model point cloud, resulting in a 3 × 1 translation matrix $T=\overline{M}-R\text{·}\overline{S}$. Generate candidate initial transformation matrices $H_i=\left[\begin{array}{cc}{R}_i& T_i\\ 0& 1\end{array}\right](i=1,2,\dots ,48)$.

Step 4: Perform the following two screenings on the 48 candidate transformation matrices:

(1)

Principal axis alignment check. Sort the three corresponding eigenvectors in descending order of their eigenvalues to determine the principal directions of the point cloud, denoted $P_S$ and $P_M$. After rotation, the scanned point cloud’s principal direction is $P_{Si}=R_i\text{·}{P}_S$. The angle between $P_{Si}$ and $P_{Mi}$ can be calculated using the dot product. Since the principal axes are all unit vectors, the angle has $P_{Si}\text{·}{P}_M=\left|P_{Si}\right|\left|P_M\right|\cos \theta =\cos \theta$. If the result is higher than the threshold, it will be rejected early. The 48 candidate matrices are reduced to 8.

(2)

Normal vector alignment check. In the transformed scanned and model point clouds, search for the k-nearest neighbors $\text{{}{s}_{i1},s_{i2},\text{…},s_{im}\text{}}$ and $\text{{}{m}_1,m_2,\text{…},m_k\text{}}$ corresponding to their centroid, respectively. The average normal vectors of the points in this neighborhood are denoted $N_{\overline{S_i}}$ and $N_{\overline{M}}$. Then, calculate the angle between the two normal vectors. If the angle exceeds the threshold, eliminate it in advance. Eight candidates are reduced to four.

Step 5: Use the candidate matrix that meets the screening to perform coordinate transformation on the scanned point cloud. The outliers in the scanned point cloud have no actual corresponding points in the model point cloud. Therefore, it is necessary to search for corresponding points in the scanned point cloud based on the model point cloud to calculate the RMSE and determine the registration accuracy. Select the transformation with the minimum registration error as the optimal one.

$$RMSE=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(D_i-{\widehat{D}}_i)}^2}}{n}}}$$

(3)

Here, n denotes the number of points in the model point cloud. $D_i$ represents the distance between the ith corresponding point pair after transformation. The default distance truth is $\widehat{D_i}=0$. Evaluating point cloud registration accuracy using RMSE is basically finding the closest point pairs using the algorithm and then calculating the average distance. Therefore, due to the inconsistency between the point distribution of the scanned point cloud and the model point cloud, there is no theoretical absolute true value for the distance between point pairs. However, it is undeniable that the RMSE is closely related to the alignment results, and the higher the registration accuracy, the smaller the value of the RMSE must be. Therefore, we are able to use the RMSE as an evaluation index to evaluate the registration results, which is also a common evaluation index in the field of point cloud registration at present.

The specific implementation process of the improved PCA point cloud initial registration algorithm is shown in Algorithm 1.

Algorithm 1: An improved PCA point cloud initial registration algorithm

Input: Scanned point cloud = {S}, Model point cloud = {M}

Output: Aligned point cloud = {A}, Rotation matrix = $R_a$, Translation matrix = $T_a$

1 Barycenter $\overline{S}={\sum }_{i=1}^m{s}_i÷m$, $\overline{M}={\sum }_{i=1}^n{m}_i÷n$;

2 Covariance matrix $C_S={\sum }_{i=1}^m(s_i-\overline{S}){(s_i-\overline{S})}^T$, $C_M={\sum }_{i=1}^n(m_i-\overline{M}){(m_i-\overline{M})}^T$;

3 Eigen Value Decomposition $C_S\to ({\nu }_{S1}$, ${\nu }_{S2}$, ${\nu }_{S3})$, $C_M\to ({\nu }_{M1}$, ${\nu }_{M2}$, ${\nu }_{M3})$;

4 Sort ν in descending order according to their eigenvalues to generate the point cloud main directions $P_S$ and $P_M$;

5 Generate 6 $\times$ 8 $=$ 48 combinations $P_{Si}(i=1,2,\text{…},48)$ of ν sorted by order [1, 2, 3] and sign [1, $-$1], candidate rotation matrix $R_i=P_M\times {P_{Si}}^T$;

6 for i = 0; i < 48; i ++ do

7   //---1. Main direction alignment check;

8   Aligned point cloud main direction $P_A=R_i\times P_S$;

9   if $P_A·P_M=\cos \theta <2.0f$ then

10     continue;

11   //---2. Normal vector alignment check;

12   Aligned point cloud barycenter $\overline{S_i}=R_i·S_i+T_i=\overline{M}$;

13   Search for the 30 nearest points of $\overline{S_i}$ and $\overline{M}$ in the point cloud by KD-tree;

14   Calculate the normal vector $N_{\overline{S_i}}$, $N_{\overline{M}}$ corresponding to the search point;

15   if$\arccos (N_{\overline{S_i}}·N_{\overline{M}})>10.0f$ then

16     continue;

17   //---3. Optimal transformation determination;

18   According to $R_i$, $T_i$, {S}$\to${$S_i$};

19   for const auto & p : $\left\{M\right\}$ do

20     Find the nearest point to point p in $\left\{S_i\right\}$ and calculate the distance;

21     error += distance;

22     points ++;

23   if points > 0 then

24     error /= points;

25     if error < ${\mathrm{error}}_a$ then

26       ${\mathrm{error}}_a=\mathrm{error}$;

27       $R_a=R_i$, $T_a=T_i$, {$S_i$}$\to${A};

28 return {A}, $R_a$, $T_a$

3. Point Cloud Fine Registration

Currently, the most classical point cloud fine alignment algorithm is still the iterative closest point algorithm, but it has a well-recognized drawback of being prone to local optimality [20]. When registering large amounts of point cloud data that contain a lot of noise, ICP is more dependent on the initial position. To address these issues, various improved ICP algorithms have been proposed. They have improved the original algorithm’s noise robustness and registration accuracy in varying degrees, but they still fail to fundamentally overcome its defect of being sensitive to initial position [21]. To this end, point cloud registration methods based on swarm intelligence optimization have been progressively developed.

Swarm intelligence optimization algorithms are inspired by the behavior of social organisms, simulating their behavioral processes to solve optimization problems [22]. Point cloud registration can be formulated as an optimization problem, seeking the optimal rotation and translation matrices to minimize the registration error between the scanned and the model point cloud. Consequently, it is theoretically feasible to utilize the swarm intelligence optimization algorithm in point cloud registration [23]. Among existing algorithms, the whale optimization algorithm is suitable for solving continuous space optimization problems, making it more compatible with the point cloud registration’s logical nature. WOA exhibits strong global search capabilities, but suffers from slow convergence and low optimization efficiency in the later stages [24]. Therefore, we introduce a Jacobian matrix [25] to dynamically adjust the search direction, avoid the aimless random search of WOA, and use the local gradient information to improve the iteration efficiency, The global search capability of WOA is also preserved to prevent the Jacobian optimization from converging to local optima. A Jacobian whale optimization algorithm for fine registration (JWOA-FR) is proposed.

After completing the above registration, since the algorithm also accounts for the global characteristics of the point cloud, the presence of outliers may affect the registration accuracy. Therefore, additional processing steps are incorporated. Employ KD-tree to search for matching point pairs between the model point cloud and the optimal transformation point cloud. Point pairs with distances exceeding the threshold are identified as outliers and subsequently removed. Upon completion of the outlier elimination, ICP is used to further improve the registration accuracy. The specific process is as follows.

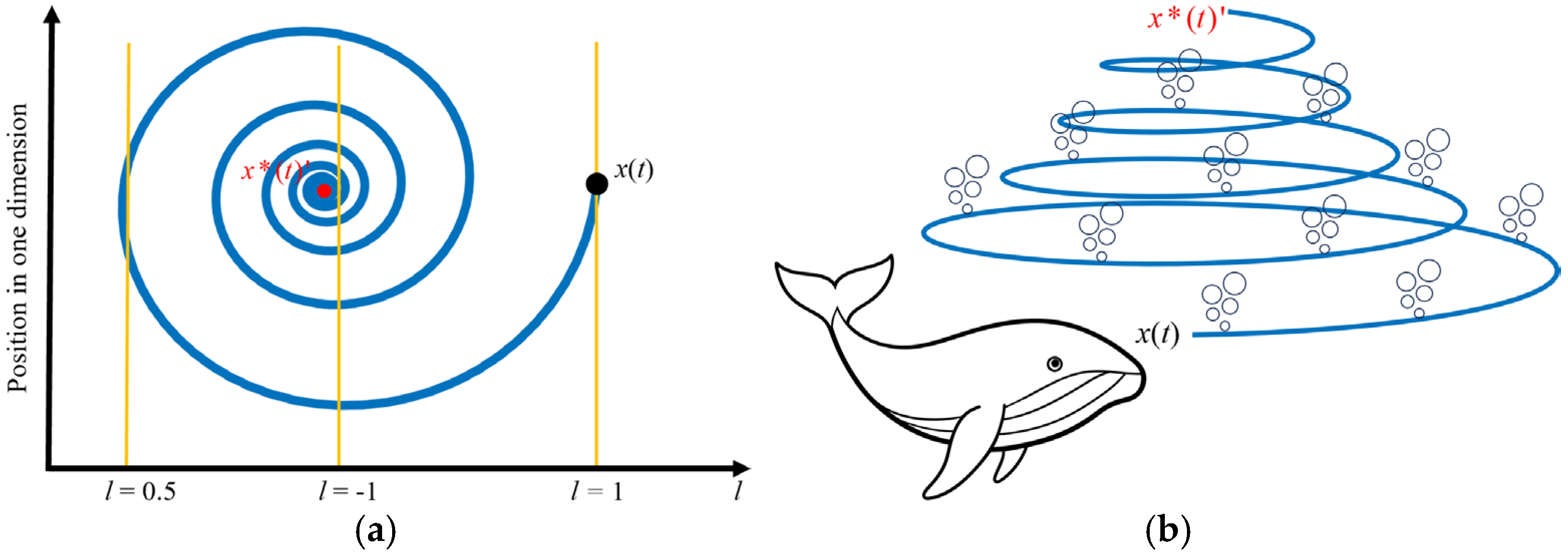
JWOA-FR: Jacobian Whale Optimization Algorithm for Fine Registration

After initial registration using the improved PCA algorithm, the initial transformation of the scanned point cloud was completed. Fine registration is also required to perform a secondary transformation of the scanned point cloud. Its ultimate goal is to locate the optimal transformation matrix $H_b$ (comprising rotation matrix $R_b$ and translation matrix $T_b$) that minimizes the RMSE between the model point cloud $M=\{m_1,m_2,\dots ,m_n\text{}}$ and the scanned point cloud after the initial registration $A=\{a_1,a_2,\dots ,a_m\text{}}$. The mathematical formulation is as follows:

$$\min E(R,T)={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=0}^n{‖m_i-(R\cdot a_i+T)‖}^2}$$

(4)

where $\left(R·a_i+T\right)$ denotes the nearest neighbor point in the scanned point cloud corresponding to $m_i$ after fine registration transformation and n is the number of points in the model point cloud. Due to the outliers in the scanned point cloud lacking corresponding points in the model point cloud, the RMSE calculation must use the model point cloud as the reference to search for corresponding points within the scanned point cloud. The specific JWOA-FR algorithm steps are as follows [26].

Step 1: Initialize population. Simulate each whale individual to represent a set of possible transformation parameters and randomly generate an initial population $X=\{x_1,x_2,\dots ,x_K\},x_i(i=1,2,\dots ,K)$, where $x_i$ is a six-dimensional solution vector corresponding to three rotation angles and three translations of the x, y, and z axes.

Step 2: Fitness assessment. For each individual, $x_i$ is decoded into transformation parameters ($R_i,T_i)$. Calculate the mean squared error $E_i$ and the fitness $Fitness\left(x_i\right)=-E_i$. Higher fitness indicates better registration, selecting the optimal individual x*(t) at the current iteration count t.

Step 3: Use the central difference method [27] to calculate the Jacobian matrix $J_t$ corresponding to the optimal individual x*(t). This is the partial derivative matrix of the error function E(R, T) concerning the transformation parameter x*(t), with dimensions n × 6, where n is the number of points in the model point cloud. The Jacobian’s differential step size is determined adaptively, varying with the iteration count t. Then, gradient descent with momentum m(t) is used, dominated by historical gradients, to accelerate parameter updates and suppress oscillations. The specific formula is as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial E}{\partial x*{(t)}_j}}\approx {\displaystyle \frac{E(x*{(t)}_j+\Delta x)-E(x*{(t)}_j+\Delta x)}{2\Delta x}},j=1,2,\dots ,6\\ m(t)=\beta m(t-1)+(1-\beta )\nabla E(x*(t)),\beta =0.9\\ \nabla E(x*(t))={\left[{\displaystyle \frac{\partial E}{\partial x*{(t)}_1}},{\displaystyle \frac{\partial E}{\partial x*{(t)}_2}},\dots ,{\displaystyle \frac{\partial E}{\partial x*{(t)}_6}}\right]}^T\\ x*{(t)}^{\prime }=x*(t)-\gamma m(t),\gamma =0.5\times \Delta x\end{array}\right.$$

(5)

where ${x^{*}\left(t\right)}_j$ is the jth rotational translation parameter of x*(t) and $∆x=0.1\times e^{-{\displaystyle \frac{t}{5}}}$ represents the set Jacobian step size that varies according to iterations. When the maximum number of iterations is set to 30, $∆x\approx 0.00025$, it means that as the iterations increase, the Jacobian step size becomes smaller with finer tuning. β = 0.9 denotes that 90% of the historical gradient is retained, which is an empirical value applicable to point cloud non-convex surface alignment, $\nabla E\left(x^{*}\right(t\left)\right)$ is the gradient of the error function at the parameter x*(t), and $\gamma =0.5\times ∆x$ denotes the adaptive learning rate set according to the difference in step size to avoid instability caused by excessive updates.

Step 4: Update populations according to the standard WOA

(1)

Encircle prey. Taking the current optimal individual $x^{*}{\left(t\right)}^{\prime }$ (updated via Jacobian iteration) as the target prey. Other whale individuals will move toward it to update their positions.

$$x(t+1)=x*{(t)}^{\prime }-U\cdot \left|C\cdot x*{(t)}^{\prime }-x(t)\right|$$

(6)

Here, $U=2u·r_1-u$ represents the encirclement intensity of whale individuals toward the optimal solution (prey): u linearly decreases from 2 to 0. When it satisfies $\left|U\right|<1$, whales approach the current optimal individual. $C=2·r_2$ is a random perturbation coefficient to avoid premature convergence of the algorithm and $r_1,r_2$ are random numbers in the interval [0, 1].

(2)

Bubble-net attack (spiral update). This phase simulates humpback whales’ behavior of creating spiral bubble nets to encircle prey, expressed as:

$$x(t+1)=\left|x*{(t)}^{\prime }-x(t)\right|\cdot e^{bl}\cdot \cos (2\pi l)+x*{(t)}^{\prime }$$

(7)

where $\left|x^{*}{\left(t\right)}^{\prime }-x\left(t\right)\right|$ denotes the distance between the current individual and the optimal solution, b is a spiral shape constant, and l is a random number in the interval [−1, 1]. The whale spiral update diagram is shown in Figure 3.

(3)

Random search. When $\left|U\right|\ge 1$, the whale conducts global exploration by randomly selecting an individual $x_{rand}\left(t\right)$ to search new regions, expressed as:

$$x(t+1)=x_{rand}(t)-U\left|C\cdot x_{rand}(t)-x(t)\right|$$

(8)

Step 5: After the whale optimization algorithm update is completed, if the current iteration count t is still below the required maximum iteration (max_iter), the process returns to Step 3 to continue the iterative optimization until max_iter is reached.

When the above algorithm completes registration, considering that the data with excessive outliers will still have a certain impact on the registration accuracy, we add two subsequent steps.

Step 6: Traverse the points of the model point cloud to search for corresponding points in the transformed scanned point cloud after JWOA-FR registration. Point pairs with a distance below the threshold dth are considered valid region points, while unmatched points are identified as outliers and subsequently removed.

Step 7: Use the ICP algorithm to register the scanned point cloud after outlier removal with the model point cloud. The algorithm is essentially a least-squares-based optimal matching algorithm that continuously searches for corresponding point pairs and the optimal coordinate transformation between two point clouds, minimizing the distance between the sets of corresponding points until a certain convergence condition is met and the iteration terminates. The maximum iterations of the algorithm are set as the convergence condition to complete the registration in this article.

4. Experiments and Results

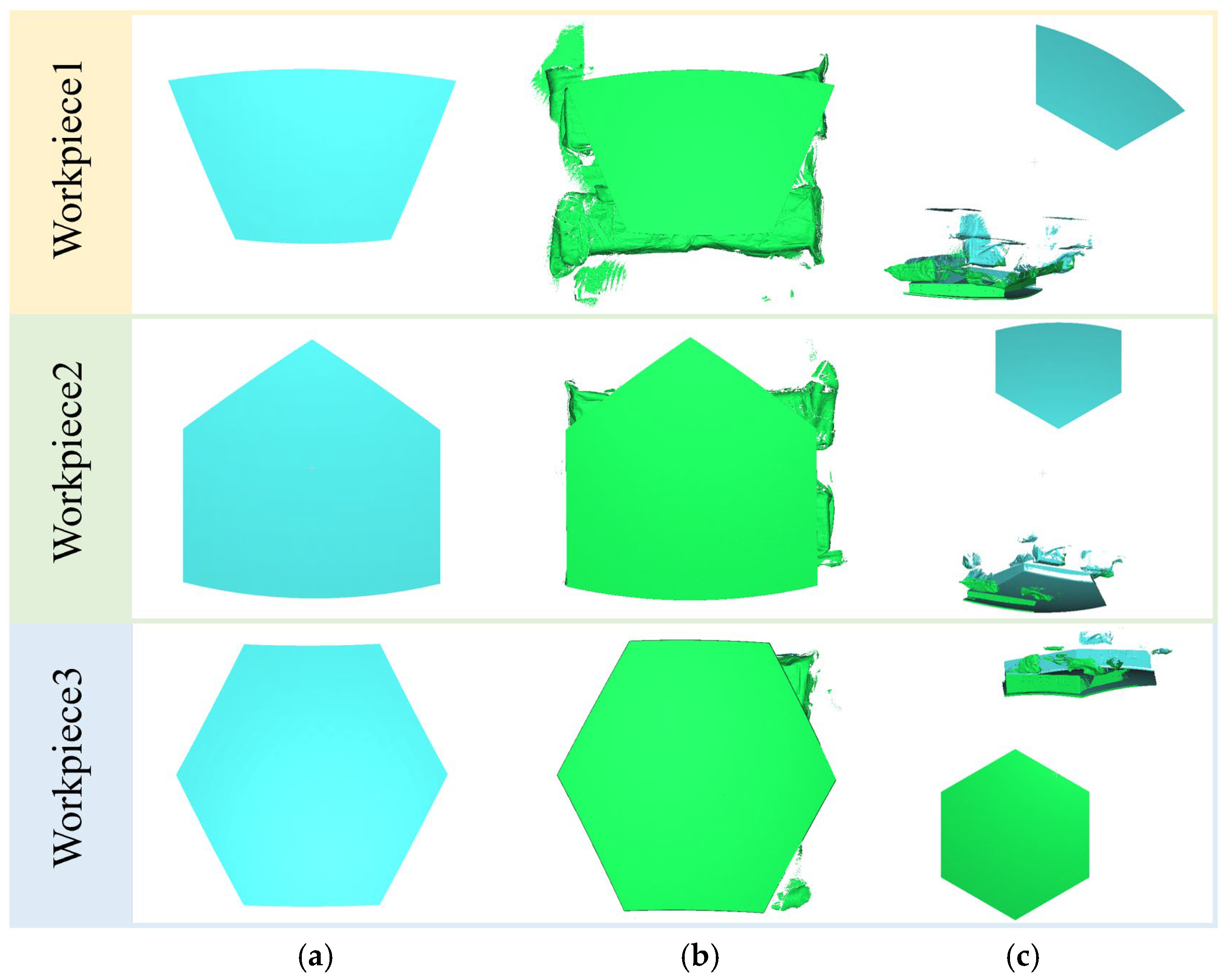
4.1. Experimental Environment and Scanned Data

All experiments were conducted on a computer with an AMD Ryzen 5 3550H processor with Radeon Vega Mobile Gfx 2.10 GHz (Lenovo, Beijing, China) and a Windows 11 system. The algorithm software is based on MATLAB R2019a and Visual Studio 2022, assembling the Point Cloud Library 1.13.0 (PCL) environment. We used CREAFORM’s MetraSCAN 3D optical CMM scanner series products (CREAFORM, Lévis, QC, Canada) combined with a robotic arm to build a scanning platform to obtain large-workpiece experimental test data, as shown in Figure 4.

Figure 5 presents the model data, scanned data, and relative position display diagrams of workpieces 1, 2, and 3 from left to right. It can be seen that the scanned point cloud contains numerous edge clutter points and has an extremely poor relative initial position with no overlap. The applicability of registration algorithms based on feature matching will be drastically reduced or even invalidated. Moreover, all three workpieces are large-scale curved surfaces (non-planar) with certain localized features. For this type of point cloud data, we conducted comparative registration tests using the proposed method to evaluate its performance. Section 4.2 is the relevant comparison of the initial registration algorithm with the performance test of the proposed algorithm. Section 4.3 presents the experiments and results analysis regarding the fine registration algorithm. Section 4.4 gives the visualization and analysis of the test results of the overall registration method.

4.2. Comparison of Initial Registration Algorithms

The positional coordinates of the scanned point cloud are based on the scanner’s coordinate system, and its initial position is usually far from the model data. Initial registration aims to quickly align the two point clouds with reasonable accuracy. The speed of the algorithm implementation is very important, while accuracy is secondary [28]. To validate the applicability of the proposed improved PCA algorithm, we compared it with the original PCA algorithm and the SAC-IA algorithm and the 4PCS algorithm for initial registration. Due to the impact of point cloud data volume on algorithm running speed, more downsampled point cloud data are used when comparing algorithm applicability.

Table 1. Comparison of classical sample alignment algorithms. Green part represents the model point cloud; blue part represents the scanned point cloud.

Algorithm	Workpiece 1	Workpiece 2	Workpiece 3
Initial position
Model/scanned points	54,118/148,111	88,444/137,087	98,026/146,568
SAC-IA
4PCS
PCA
Improved PCA

presents the registration results and accuracy of different algorithms for each workpiece (traversing the model point cloud to search for corresponding points in the scanned point cloud). In the registration results visualized in Table 1, green represents the model point cloud, and blue represents the scan point cloud.

In Table 1, it can be seen that the SAC-IA algorithm can make the scanned and modeled point clouds close together, but has a large difference in the rotation direction. The primary reason is that although this type of point cloud data contain local surface features, the low local feature differences make it difficult to match and locate. Moreover, during the actual testing process of the algorithm, it took a lot of time to run, and the results were unsatisfactory. In principle, the 4PCS algorithm searches for the best transformation by matching coplanar four-point sets, so it also suffers from matching inaccuracies caused by weak local features and excessive noise, resulting in poor performance. The PCA-based method for determining principal axes and rotation matrices is indeed unable to achieve perfect matching due to the influence of numerous outliers. Even so, the results obtained from the initial registration are adequate. Subsequently, only small displacements and rotations are needed to reach the registration optimization, which can also reduce the transformation parameter interval for fine alignment and the search consumption.

In the result diagram in Table 1, it can be observed that for workpiece 3, if the optimal transformation is determined solely based on the registration error among all candidate transformations, the registration direction of the scanned point cloud is opposite to that of the model point cloud in the actual registration result. This is because after using the matrix to perform inverse transformations, there is some overlap, resulting in the relatively small RMSE, but not the optimal solution we expect. Using the improved PCA algorithm, we can eliminate transformations with inconsistent orientations before calculating RMSE, ensuring that the rotation matrix for workpiece 3 is selected correctly. Also, workpieces 1 and 2 have correct choices that are consistent with the original PCA algorithm, indicating that it is also the smallest registration error among all the transformations. In contrast, the improved PCA algorithm not only achieves higher accuracy but also requires less runtime.

To verify the improvement of the improved algorithm registration speed, the following tests were performed. Under the condition of different downsampled point cloud data, we compared the runtime of the original PCA algorithm with the improved PCA algorithm.

Table 2. Comparison of PCA and improved PCA with different data volumes.

Test Object	Model Points/ Scanned Points	PCA		Improved PCA
		Candidate Matrix	Runtime (s)	Candidate Matrix (After Check 1)	Candidate Matrix (After Check 2)	Runtime (s)
Workpiece 1	54,118/148,111	48	454.05	8	4	6.93
	270,576/741,470	48	-	8	4	124.48
	541,120/1,484,222	48	-	8	4	294.55
Workpiece 2	88,444/137,087	48	720.38	8	4	8.12
	442,093/685,665	48	-	8	4	189.53
	884,178/13,771,191	48	-	8	4	443.70
Workpiece 3	98,026/146,568	48	786.19	8	4	4.69
	490,124/732,221	48	-	8	4	113.04
	980,242/1,462,181	48	-	8	4	284.77

shows the registration time spent on each workpiece and the changes in the number of candidate matrices eliminated in advance.

In Table 2, it can be seen that the initial 48 candidate matrices are screened by principal axis checking, with 8 candidate matrices remaining, and normal vector checking, with 4 remaining. The explanation with examples is as follows. Assume the principal directions of the two point clouds are u(x), u(y), u(z) and v(x), v(y), v(z), respectively. Through the principal axis alignment check, it can be confirmed that v(x) should be rotated to align with u(x) or −u(x), rather than corresponding to ±u(y) or ±u(z). At this point, there will be 2 × 2 ×2 = 8 remaining candidate matrices. Then, through the normal vector alignment check, it can be confirmed that v(x) should be rotated to align with u(x), eliminating the reverse transformations, leaving 4 candidates.

At the same time, it can be observed that after pre-filtering erroneous candidates, the minimum data volume experimental groups for workpieces 1, 2, and 3, which are in the hundreds of thousands, can all be processed within 10 s. Compared to the complete calculation of all candidates, the time required for optimization is minimized. Although the improved algorithm adds the calculation of local normal vectors and a screening process, the total time required is still much less than that of the original algorithm. This is because calculating the transformed point cloud and corresponding RMSE for the scanned point cloud based on each candidate matrix is the main source of runtime. Take the minimum data sample of workpiece 1 as an example. The runtime for PCA and the generation of all candidate matrices is 0.004 s. The runtime for local normal vector calculation is 0.430 s. The screening of each candidate matrix takes approximately 0.002 s. However, calculating the converted point cloud and corresponding RMSE based on the retained candidate matrix takes approximately 1.5 to 2 s. Of course, the algorithm runtime is also related to computer performance. On the experimental test computers in this study, the longest time taken by the improved algorithm in processing workpiece 2 was 443.70 s for millions of data points (maximum-data-volume experimental group). Nevertheless, this was still faster than the time spent by the original algorithm in the minimum-data-size experimental group, with respectable results. For the original PCA algorithm, the medium- and maximum-data-volume experimental groups will take longer to run, so the specific running times are not listed in Table 2.

4.3. Fine Alignment of Classical Sample

Through initial registration, a relatively good position has been obtained. However, since there are many outliers in the scanned point cloud itself, it is difficult to make the two correspond to each other completely, and fine registration is required. Using workpieces 1, 2, and 3 as examples, verify the applicability and iterative optimization strength of the proposed algorithm. Due to the large actual size of the workpiece, the point cloud data coordinates have a large absolute value range. Therefore, the point cloud data is first normalized to scale it to a uniform range, avoiding the instability caused by large numerical calculations and enabling the rotation parameters to be optimized on the same order of magnitude as the translation parameters. Similarly, using a test group of one hundred thousand units, adjust the set parameters according to the different workpiece conditions. The range of variation for the rotation angle and translation of workpieces 1 and 2 is set to [−π/4, π/4] and [−0.2, 0.2], respectively. Set [−π/8, π/8] and [−0.1, 0.1] for workpiece 3. Workpiece 1 is set to search for 100 whales, with a maximum iteration count of 30, workpiece 2 is set to 120 and 40, and workpiece 3 is set to 90 and 30. Figure 6 shows the first 10 iterations of three workpieces, including a diagram illustrating the changes in RMSE before and after Jacobian optimization.

In Figure 6, it can be observed that after each iteration, the Jacobian calculation can optimize the updated results. The normalized RMSE was able to be reduced by about 0.002–0.0001 per optimization. Although the data appear to show a small difference, this can help the whale update to adjust the search direction, allowing the RMSE to decrease more rapidly after the update. The algorithm is set as follows. The difference in step size of the Jacobian calculation is adaptively varied according to the number of iterations, with a large step for fast exploration at the beginning and a small step for fine-tuning at a later stage. The gradient descent with momentum m(t) is used later to mitigate the oscillations by dominating with the historical gradient. This setting is because the Jacobian adjusts parameters locally based on gradient information. If the step is too large, it may prematurely fall into a local optimum. If it is too small, it can lead to numerical instability. Moreover, the accumulation of historical gradient directions facilitates accelerated passage through regions of flattening change and avoids getting caught in local minima. It may not be too intuitive to see the advantages of Jacobian’s addition of the whale algorithm through Figure 6. As such, we provide

Table 3. Comparison of results under different fine registration algorithms.

Algorithm	Object (Workpiece)	Optimal Value for the Variable						Normalized RMSE	Actual RMSE/mm
		α/°	β/°	γ/°	Xt/mm	Yt/mm	Zt/mm			Runtime/s
JWOA-FR	1	2.25	2.01	6.06	−235.72	−170.01	230.12	0.0019	2.4919	28.53
	2	3.67	9.84	−10.67	34.64	−9.25	165.09	0.0019	2.3997	50.77
	3	1.46	5.21	12.87	−79.20	15.99	−116.13	0.0021	2.6204	30.45
E-WOA	1	4.08	4.44	2.68	−230.47	−154.63	244.26	0.0024	3.3004	30.07
	2	4.14	8.63	−9.59	61.69	−10.64	162.87	0.0023	4.0967	58.10
	3	−0.88	1.91	4.92	−69.33	−4.86	−123.12	0.0029	3.6054	35.47
WOA	1	−4.42	−6.45	15.92	−162.62	−191.16	244.90	0.0110	15.2069	35.95
	2	4.77	3.13	−2.04	4.74	30.92	196.84	0.0085	10.8118	61.58
	3	−1.17	−5.16	−8.07	−110.56	−68.34	−82.28	0.0101	12.6119	38.94
ICP	1	3.70	−1.39	0.40	−146.03	−211.93	232.34	0.0153	20.3383	31.73
	2	−5.74	6.39	3.90	15.97	−21.68	154.67	0.0050	6.1995	55.68
	3	2.64	0.75	−1.93	−53.12	−21.08	−120.75	0.0048	6.0463	34.97

, which compares the results of the registration data of different workpieces under the JWOA-FR, E-WOA [29], WOA, and ICP algorithms. The specific rotation and translation optimization parameters are expressed as $(\alpha ,\beta ,\gamma ,X_t,Y_t,Z_t)$. Figure 7 shows a line graph of the convergence state of each algorithm for different workpieces. The ICP algorithm retains the same preprocessing procedures and evaluation standards as other algorithms when used; that is, it applies normalized point cloud data for registration and traverses the model point cloud to calculate RMSE.

In Figure 7, it can be seen that the proposed JWOA-FR and E-WOA give better results, and the WOA and ICP algorithms give moderate results. In the iteration graph, an upper limit was set to achieve uniform visualization, so the specific results of the first few iterations of the ICP algorithm, which were relatively large, were not directly shown. For the results of workpiece 1, the normalized RMSE of ICP was 0.1264 after the first iteration. When 30 iterations had been completed, the data did not converge. In contrast, WOA converged faster. Through an initial population search, it achieves similar results to five iterations of the ICP algorithm in the first iteration. However, the registration accuracy still needs improvement. As can be seen in the convergence in Figure 7, the ICP algorithm has not reached convergence at 30 or 40 iterations. Therefore, we set the number of iterations to 100, at which point the ICP algorithm reached convergence. By this time, the actual registration errors of workpieces 1, 2, and 3 were 3.5849 mm, 3.0982 mm, and 3.6088 mm, respectively, which also failed to reach the optimal transformation.

Under the same set conditions, compare the runtime of the JWOA-FR, E-WOA, WOA, and ICP algorithms. It can be observed that the runtime differences among the four algorithms are not significant, with JWOA-FR being the most efficient and having the shortest runtime. This is because although JWOA-FR introduces the calculation of the Jacobian matrix, its calculation not only optimizes RMSE one step ahead, but also dynamically adjusts the whale search direction, ensuring fast convergence while maintaining registration accuracy, resulting in high overall execution efficiency. E-WOA is an enhanced whale optimization algorithm based on a pooling mechanism. This optimization can significantly improve algorithm performance and achieve rapid convergence in the initial stages. However, for the point cloud registration problem, the JWOA-FR algorithm proposed adds Jacobian pre-optimization of the optimal individual, which further improves registration accuracy. It is also the first among all algorithms to achieve optimal convergence.

Comparing the results of JWOA-FR and E-WOA in Table 3, the differences in convergence speed and RMSE results are not significant, but the differences in the obtained rotation and translation parameters are more obvious. In order to more intuitively demonstrate the differences, the registration results of the two methods are shown in

Table 4. Visualization of results with different fine registration algorithms. Green part represents the model point cloud; blue part represents the scanned point cloud.

Algorithm	Workpiece1	Workpiece2	Workpiece3
JWOA-FR
E-WOA
WOA
ICP

, and visualizations of the results from WOA and ICP are also provided. For workpieces 2 and 3, the proportion of outliers is lower than that of workpiece 1. The four algorithms have relatively small convergence differences and decent speed, but there is still a gap in registration accuracy. Table 4 shows that the proposed JWOA-FR is able to achieve higher matching between the scanned and modeled point clouds, the E-WOA results have a small deviation, and the WOA and ICP results have a large deviation.

4.4. Complete Testing of the Proposed Registration Method

Through the above comparative experiments, it was demonstrated that the proposed registration method is feasible and advantageous. Considering that outliers in the scanned point cloud may have a certain impact on registration accuracy, to further demonstrate the algorithm’s performance, we incorporated additional steps: (1) search for matching point pairs to eliminate outliers, and (2) improve registration accuracy with ICP. Point pairs with a distance larger than five times the point cloud scanned point spacing were considered outliers for removal. The average point spacing for workpiece 1 was 1.64 mm with a point pair threshold of 8.20 mm; for workpiece 2, it was 1.62 mm and 8.10 mm; and for workpiece 3, it was 1.60 mm and 8.00 mm. The visualization of the registration results for the overall processes of workpieces 1, 2, and 3, from top to bottom, is shown in Figure 8.

For workpiece 1, the number of original scanned data points was 148,111, with 92,546 outliers removed; for workpiece 2, 137,087 and 46,744; and for workpiece 3, 146,568 and 46,744. The data indicate that workpieces 2 and 3 contained 34.1% and 31.9% of the total number of outlier points and workpiece 1 contained 62.5% of the outlier points, whose application of algorithmic characterization was the most representative. After the overall registration was completed, the RMSE for workpieces 1, 2, and 3 were 2.0755 mm, 2.3955 mm, and 2.5823 mm, respectively. The final registration accuracy was improved compared to the processed JWOA-FR results, but the difference was not significant. This illustrates that our method is highly applicable to data with outliers. When the algorithm searches close to the optimal transformation, the impact of outliers on registration accuracy is minimal. The final registration accuracy of all workpieces was within 1–2 point spacing, meeting the requirements.

The laser scanner directly acquires and generates STL mesh data when scanning workpieces [30,31]. The scanned point cloud data is obtained by randomly collecting data points within its mesh surface, and the same applies to the model point cloud data. Therefore, two sets of point cloud data with identical distributions were not used for testing. The RMSE calculation is essentially averaging the distance between two point clouds by searching for the closest point pairs of the two clouds. Thus, the non-uniform distribution of points will inevitably result in errors, with no outcome being completely zero [32]. Scanner accuracy, workpiece processing errors, and computational errors in the transformation process are all objective sources of error in the registration process, which are difficult to analyze quantitatively.

5. Discussion

From the experimental results reported in the previous section, it can be seen that the improved PCA and Jacobian-enhanced whale optimization collaborative method for point cloud registration can achieve the registration of model data and scanned data containing a large number of outliers. This method demonstrates good applicability on the scanned data of large, low-feature workpieces. After removing outliers, the further improved registration accuracy was not significantly different from the registration results obtained directly by the proposed method, indicating that the proposed method has obvious advantages in data registration containing outliers.

This robustness is due to the fact that the proposed method consists of two parts: initial registration and fine registration. PCA analyzes the principal directions of both the scanned and the model point cloud at the data level, retaining features that contribute most significantly to the point distribution. It can be applied to point cloud data registration containing a large number of outliers. At the same time, the two additional screening conditions we added removed incorrect candidate matrices in advance, greatly optimizing the initial registration time and providing good initial transformation for fine registration. The fine registration part converts point cloud registration into an optimization problem of rotation and translation parameters, which is a relatively novel approach. This method also minimizes the impact of noise on point cloud registration and is more widely applicable. The Jacobian-based improvement makes the whale optimization algorithm more suitable for point cloud registration, efficiently completing the registration task.

Compare the proposed improved PCA point cloud initial registration algorithm with existing point cloud initial registration algorithms, such as SAC-IA and 4PCS [11]. We also conducted comparative tests. Existing methods find matching point pairs for coordinate transformation by describing the local features of the scanned and the model point cloud, but if the scanned point cloud has many stray points, strong local feature similarity, and poor relative initial orientation, the applicability of the above methods will be greatly diminished. Feature-based registration methods are more suitable for local-to-global registration, but they also require the ability to completely extract feature information [20]. Compared with the currently most classic ICP algorithm, the Jacobian-based whale optimization algorithm for fine point cloud registration demonstrates broader applicability, reduced sensitivity to initial pose, enhanced noise robustness, and promising application prospects.

This research addresses a more novel and practical point cloud registration problem. Currently, handheld scanners and tracking scanners can obtain complete workpiece scan data, but it is inevitable that environmental factors will cause scanning outliers. These outliers need to be manually deleted, which is troublesome and time-consuming. If the ideas presented in this paper can be applied to identify outliers in advance through registration and if this can be incorporated as a part of the scanner’s noise reduction function, it will be possible to obtain useful scan information more quickly, which is a future application direction worth considering.

6. Conclusions

This paper proposes an improved PCA with Jacobian-enhanced whale optimization collaborative method for point cloud registration on large-scale point cloud data containing numerous outlier points. To evaluate the performance of the proposed method, experimental tests and overall assessments were conducted separately for the initial and fine registration algorithms.

(1)

In the initial registration section, the registration effects of SAC-IA, 4PCS, PCA, and improved PCA on three workpieces were compared. For the initial alignment algorithm based on feature matching, numerous outliers and weak local features will affect the selection of corresponding point pairs, leading to poor results. Although this issue also affects the determination of the global principal components, the proposed algorithm can maximize the guarantee of the correct rotation and translation directions. We also tested the registration speed using workpieces with different data volumes. The improved PCA algorithm can reduce the 48 candidate matrices to 4, and the runtime can be shortened by an order of magnitude compared to the original algorithm, which is more effective.

(2)

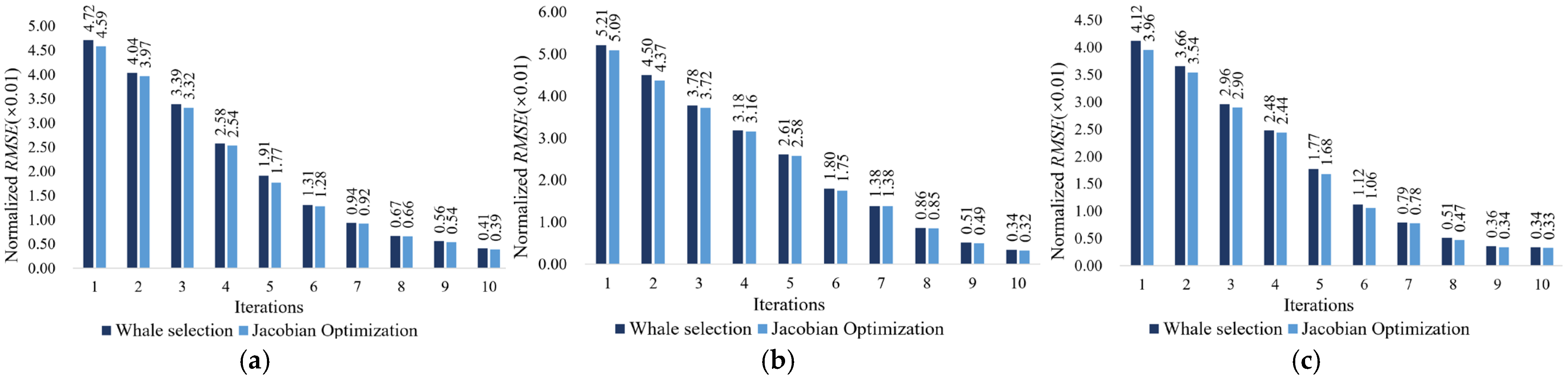
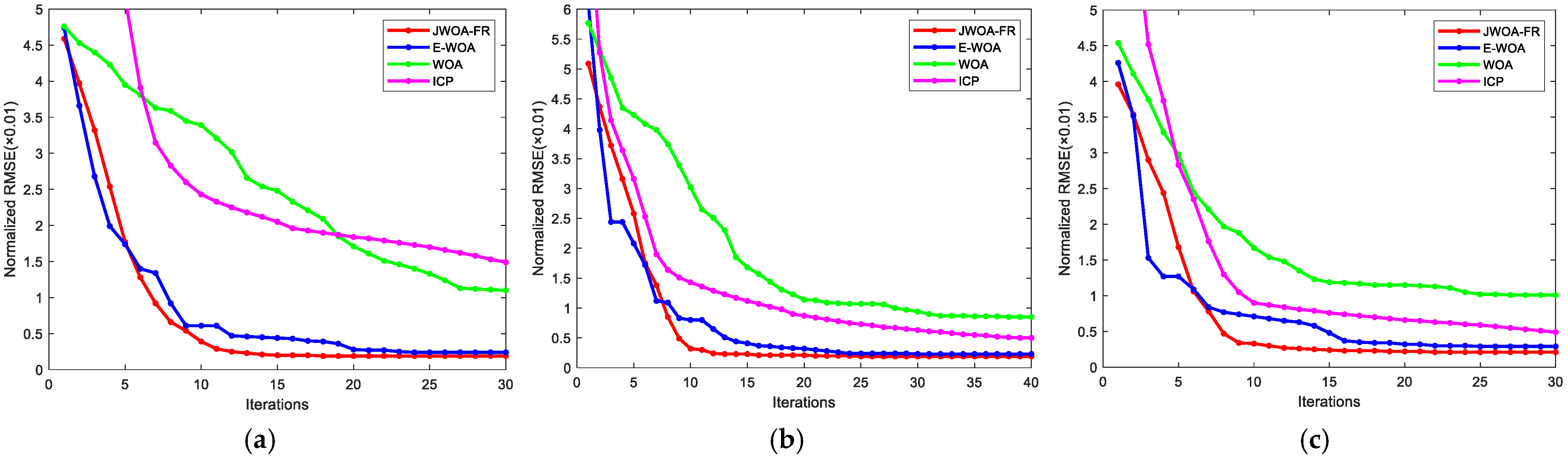
The fine registration section compared the registration data of different workpieces under JWOA-FR, E-WOA, WOA, and ICP algorithms. The results indicate that the proposed JWOA-FR is optimal in both iteration speed and registration accuracy, the E-WOA performs well, and the WOA and ICP have moderate results. The Jacobian calculation performs gradient descent on the optimal individual before each whale update iteration, ensuring that the algorithm reaches the optimal transformation stably and quickly. At this point, the RMSE of workpieces 1, 2, and 3 were 2.4919 mm, 2.3997 mm, and 2.6204 mm, respectively.

(3)

In the overall experimental section, the visualizations of the overall registration and the results of the subsequent added processing steps are presented. The number of outlier points eliminated in the workpieces accounted for more than 30% of the total data volume. Workpiece 1 had 62.5% of the outlier counts, which is a high contamination. After the overall registration was completed, the RMSEs for workpieces 1, 2, and 3 were 2.0755 mm, 2.3955 mm, and 2.5823 mm, respectively. The results indicate that our method is highly applicable to data with outliers. When the algorithm approaches the optimal transformation, the impact of outliers on registration accuracy is minimal, with the registration accuracy of all workpieces within 1–2 point distances meeting the requirements.