Generation of Four-Channel Multi-Polarization Bessel Vortex Beams with Equal Divergence Angle Based on Co-Aperture Metasurface
Abstract
1. Introduction
2. Theoretical Formulation and Metasurface Unit Design
2.1. Spin-Decoupling Theory
2.2. Theory of Multimode OAM Reflective Metasurface with Equal Divergence Angle
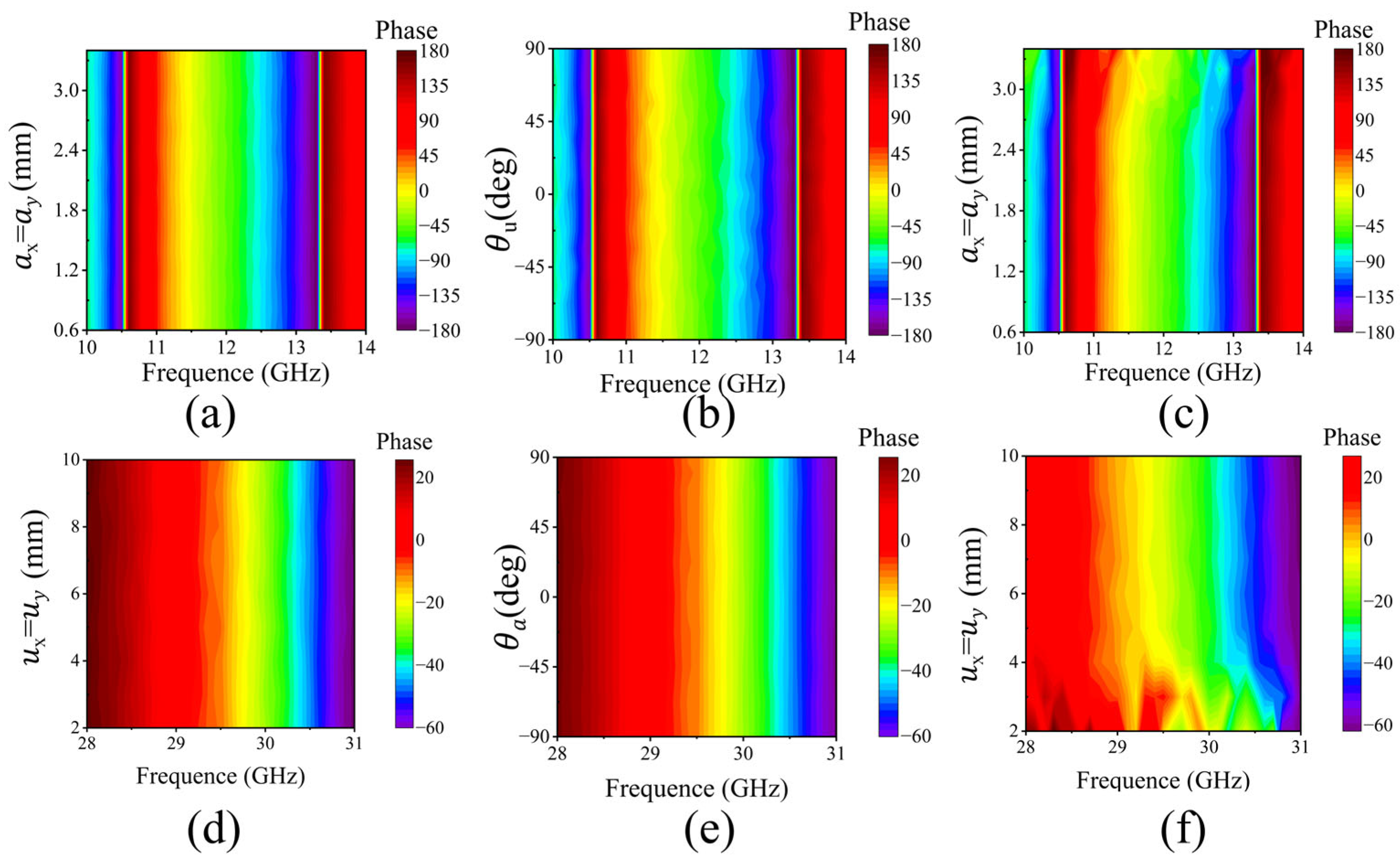
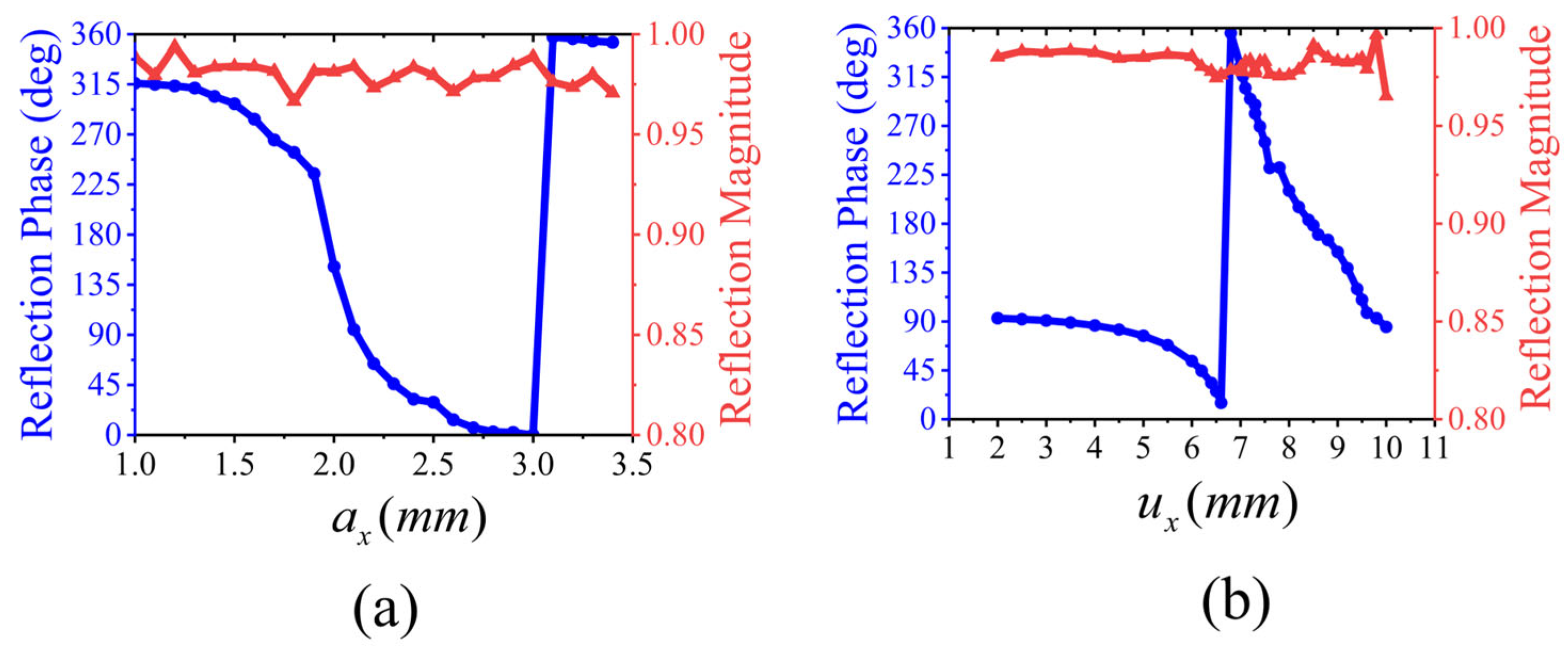
2.3. Multi-Polarization Element Design
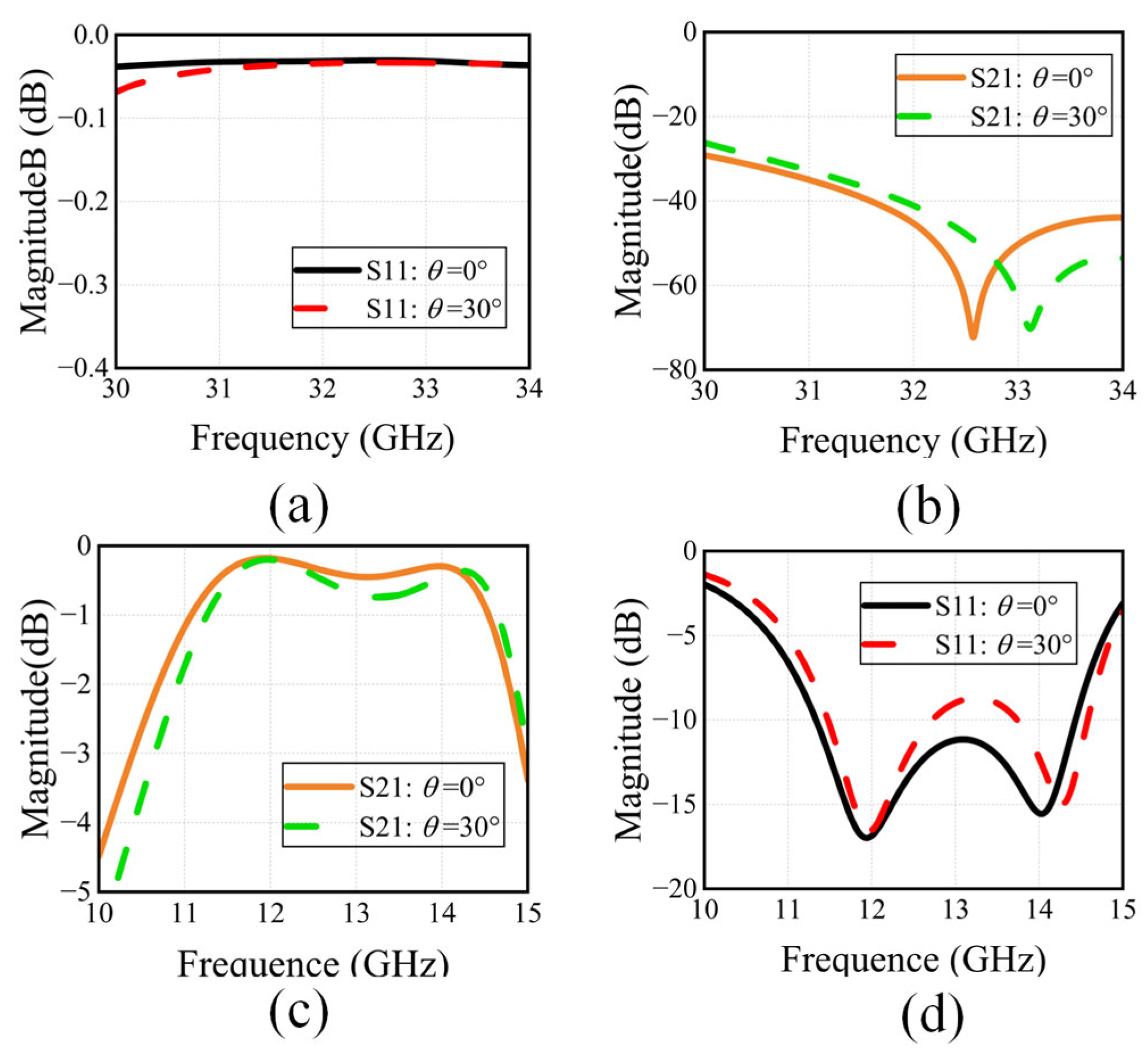
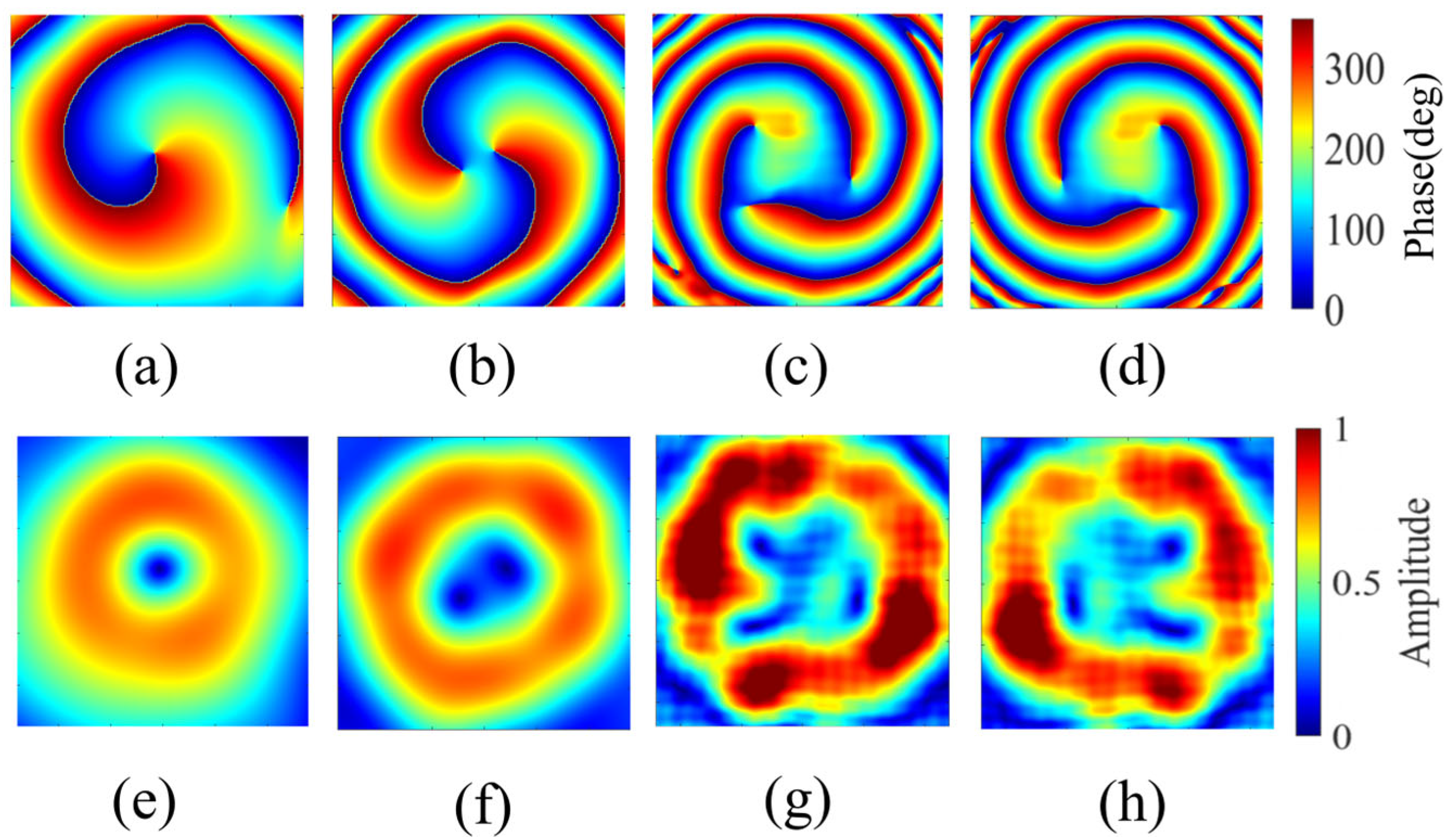
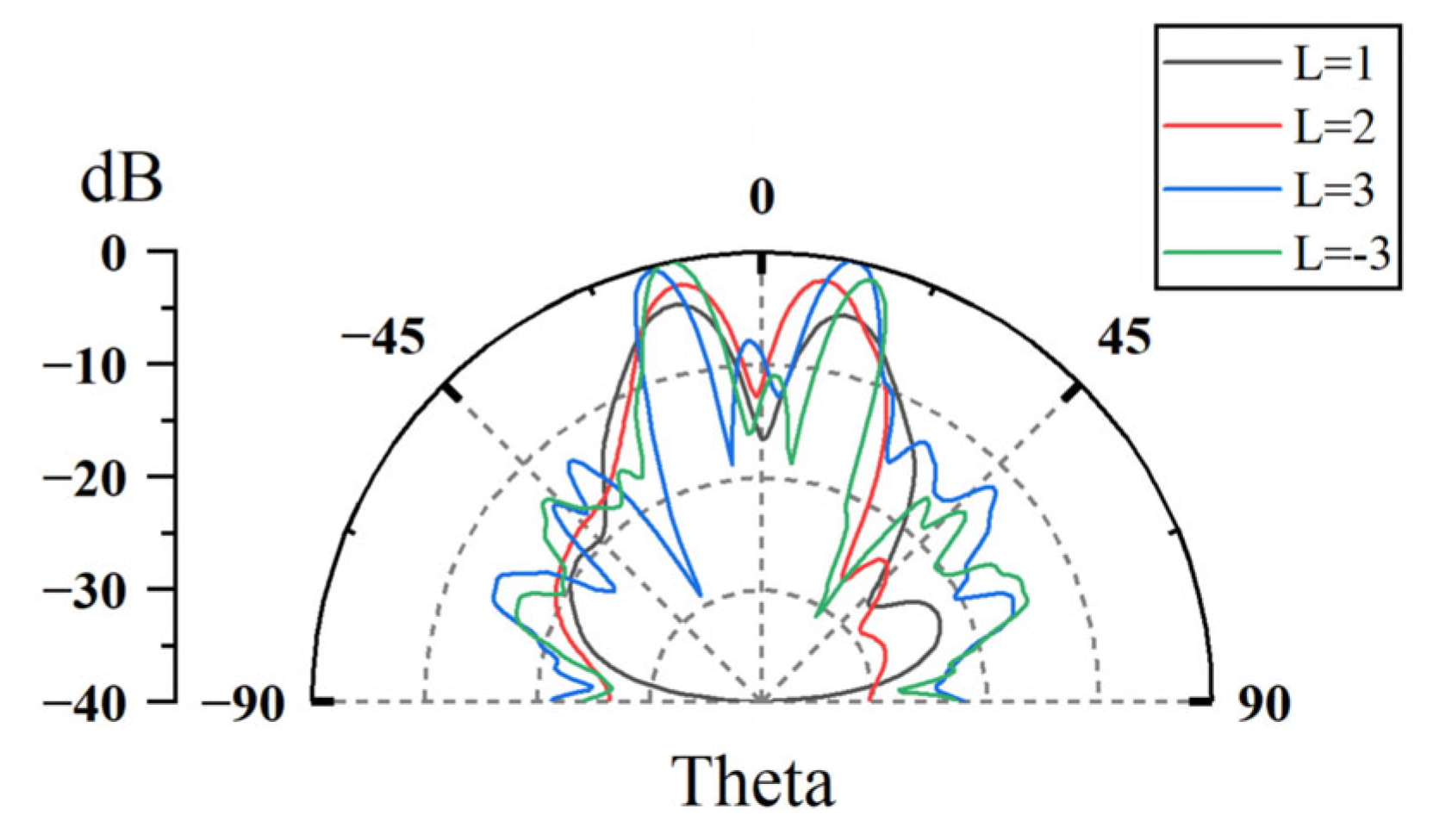
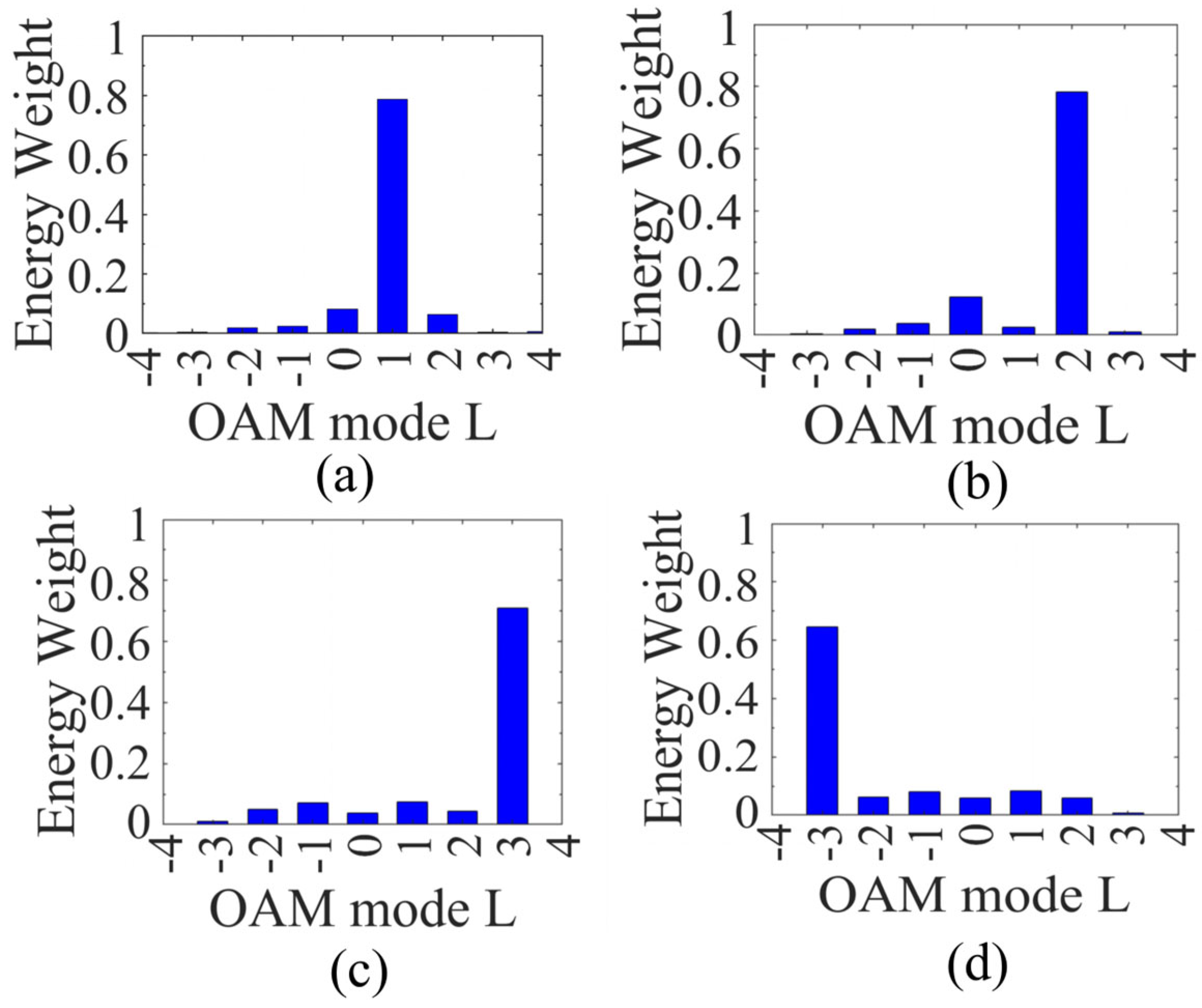
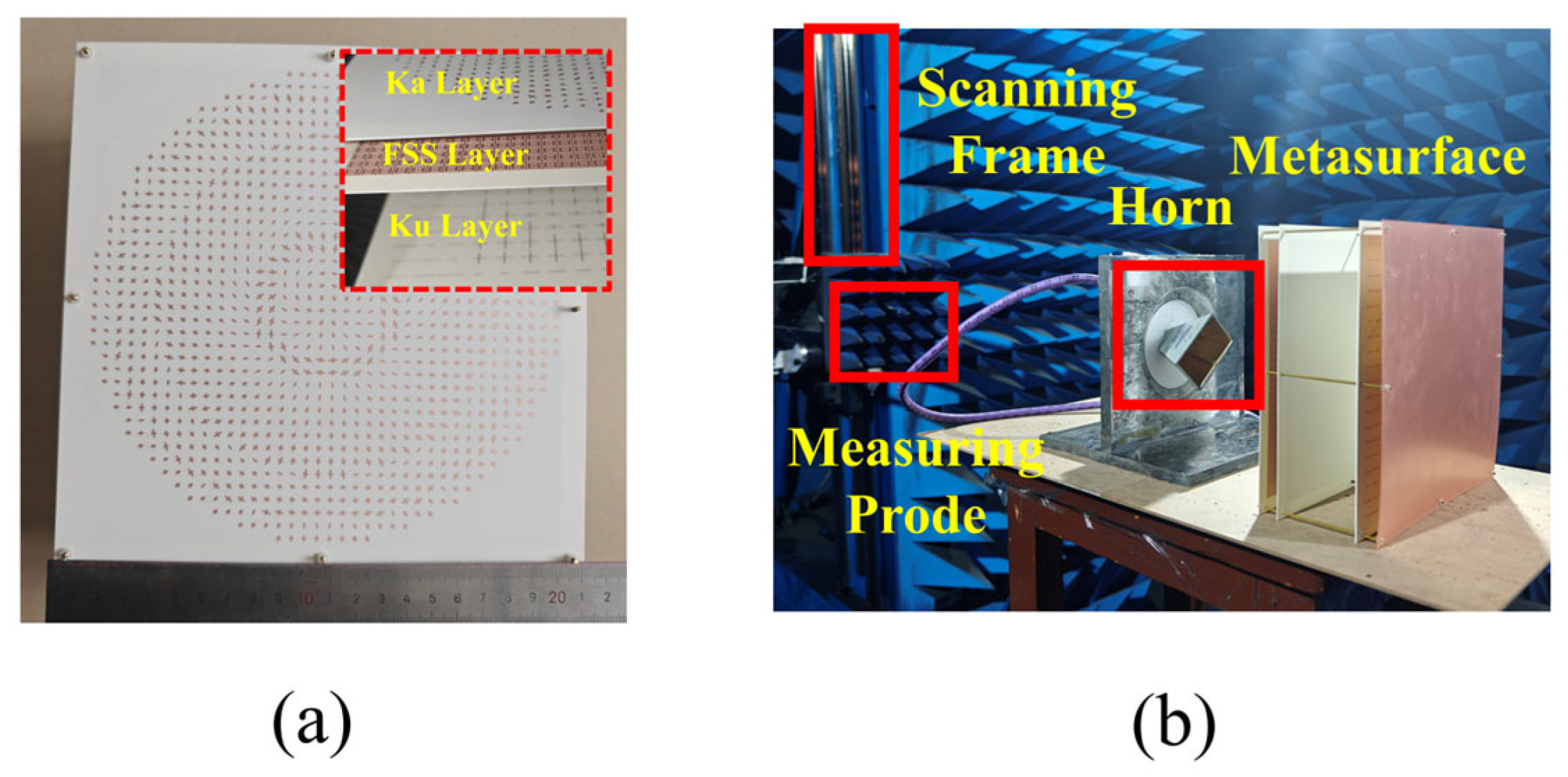
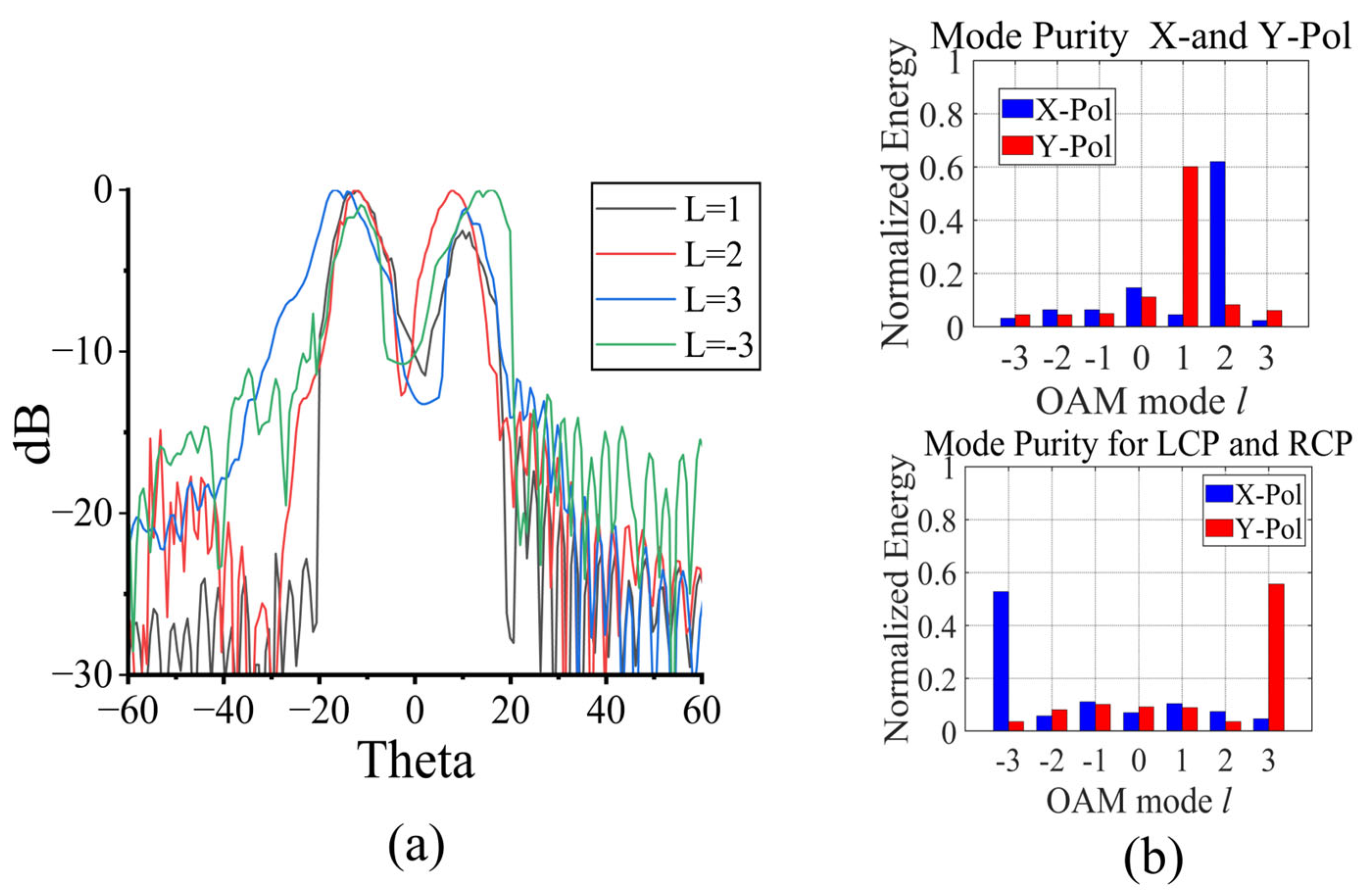
3. Reflective Metasurface Design and Empirical Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Xu, H.; Liu, T.; Zhang, F. Hybrid-phase assisted amplitude and phase control using full-space metasurface. Adv. Opt. Mater. 2024, 12, 2302153. [Google Scholar] [CrossRef]
- Abhyankar, G.G.; Gad, R.S.; Panem, C.; Chodankar, D.; Naik, G.M. Gaussian vortex beam modeling for multiplexing in data communication using OAM. J. Phys. Conf. Ser. 2021, 1921, 012054. [Google Scholar] [CrossRef]
- Mari, E.; Spinello, F.; Oldoni, M.; Ravanelli, R.A.; Romanato, F.; Parisi, G. Near-field experimental verification of separation of OAM channels. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 556–558. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Guo, Z. OAM radar based fast super-resolution imaging. Measurement 2022, 189, 110600. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; Wang, H.; Qin, Y.; Li, X. Orbital-angular-momentum-based electromagnetic vortex imaging. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 711–714. [Google Scholar] [CrossRef]
- Li, X.; Zhou, N.; Zhu, S.; Chen, X.; Zhao, M.; Zhang, A. Resolution analysis of coincidence imaging based on OAM beams with equal divergence angle. IEEE Trans. Antennas Propag. 2023, 71, 2891–2896. [Google Scholar] [CrossRef]
- Yang, L.-J.; Sun, S.; Sha, W.E.I.; Huang, Z.; Hu, J. Arbitrary vortex beam synthesis with donut-shaped metasurface. IEEE Trans. Antennas Propag. 2022, 70, 573–584. [Google Scholar] [CrossRef]
- Huang, S.; Miao, Z.; He, C.; Pang, F.; Li, Y.; Wang, T. Composite vortex beams by coaxial superposition of laguerre–gaussian beams. Opt. Lasers Eng. 2016, 78, 132–139. [Google Scholar] [CrossRef]
- Mallikharjuna Reddy, Y.; Ratna Kumari, U.V. 3D printable PLA spiral phase plate with horn feed for OAM beam generation for 6G communication. Int. J. Inf. Technol. 2024, 16, 2123–2128. [Google Scholar] [CrossRef]
- Yagi, Y.; Sasaki, H.; Kudo, R.; Lee, D. Parabolic reflector for UCA-based OAM multiplexing in sub-THz band and transmission experiment. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 991–996. [Google Scholar]
- Guo, Z.-G.; Yang, G.-M. Radial uniform circular antenna array for dual-mode OAM communication. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 404–407. [Google Scholar] [CrossRef]
- Zhang, B.; Luo, Y. Dynamic optical tuning and sensing in L-shaped dirac semimetal-based terahertz metasurfaces. Phys. Lett. A 2025, 541, 130419. [Google Scholar] [CrossRef]
- Chen, P.; Yi, Y.; Song, Q.; Yi, Z.; Yi, Y.; Cheng, S.; Zhang, J.; Tang, C.; Sun, T.; Zeng, Q. Simulation and Analysis of a Near-Perfect Solar Absorber Based on SiO2-Ti Cascade Optical Cavity. Photonics 2024, 11, 604. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.; Yi, Z.; Wang, J.; Cheng, S.; Li, B.; Wu, P. High Absorption Broadband Ultra-Long Infrared Absorption Device Based on Nanoring–Nanowire Metasurface Structure. Photonics 2025, 12, 451. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Yang, H.; Wang, J.; Li, B.; Zhang, H.; Yi, Y. TiN-Only Metasurface Absorber for Solar Energy Harvesting. Photonics 2025, 12, 443. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Y.; Yuan, Y.; Burokur, S.N. A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces. Appl. Sci. 2020, 10, 1015. [Google Scholar] [CrossRef]
- Yi, J.; Li, D.; Feng, R.; Ratni, B.; Jiang, Z.H.; De Lustrac, A.; Werner, D.H.; Burokur, S.N. Design and validation of a metasurface lens for converging vortex beams. Appl. Phys. Express 2019, 12, 084501. [Google Scholar] [CrossRef]
- Yi, J.; Guo, M.; Feng, R.; Ratni, B.; Zhu, L.; Werner, D.H.; Burokur, S.N. Design and Validation of an All-Dielectric Metamaterial Medium for Collimating Orbital-Angular-Momentum Vortex Waves at Microwave Frequencies. Phys. Rev. Appl. 2019, 12, 034060. [Google Scholar] [CrossRef]
- Han, L.; Zhu, Y.; Xu, Y.; Liu, Y.; Xie, W.; Xiong, B. Novel Folded Reflectarray and Transmitarray Antenna Generating Long Nondiffractive Bessel Beams Carrying OAM With Integrated Feed. IEEE Trans. Antennas Propag. 2024, 72, 4719–4728. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, Y.; Zhang, D.; Ding, X.; Ratni, B.; Burokur, S.N.; Lu, M.; Tang, K.; Wu, Q. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 2018, 26, 1351–1360. [Google Scholar] [CrossRef] [PubMed]
- Feng, R.; Ratni, B.; Yi, J.; Zhang, H.; de Lustrac, A.; Burokur, S.N. Versatile metasurface platform for electromagnetic wave tailoring. Photonics Res. 2021, 9, 1650–1659. [Google Scholar] [CrossRef]
- Guo, W.-L.; Wang, G.-M.; Luo, X.-Y.; Chen, K.; Li, H.-P.; Feng, Y. Dual-phase hybrid metasurface for independent amplitude and phase control of circularly polarized wave. IEEE Trans. Antennas Propag. 2020, 68, 7705–7710. [Google Scholar] [CrossRef]
- Yu, S.; Li, L.; Shi, G. Dual-polarization and dual-mode orbital angular momentum radio vortex beam generated by using reflective metasurface. Appl. Phys. Express 2016, 9, 082202. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, J.; Han, Y.; Sui, S.; Qiu, T.; Jia, Y.; Feng, M.; Wang, X.; Zheng, L.; Qu, S. Design of aperture-multiplexing metasurfaces via back-propagation neural network: Independent control of orthogonally-polarized waves. IEEE Trans. Antennas Propag. 2022, 70, 4569–4575. [Google Scholar] [CrossRef]
- Ji, C.; Song, J.; Huang, C.; Wu, X.; Luo, X. Dual-band vortex beam generation with different OAM modes using single-layer metasurface. Opt. Express 2019, 27, 34–44. [Google Scholar] [CrossRef]
- Guo, W.-L.; Yuan, F.; Xu, H.-X. Broadband spin-decoupled meta-devices enabled by a polarization conversion metasurface. IEEE Antennas Wireless Propag. Lett. 2024, 23, 920–924. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, X.; Qi, W.; Wu, H.; Chen, Q.; Geng, J.; Wang, W. Realization of Multimode OAM Beams with Almost the Same Divergence Angles. Int. J. Antenn. Propag. 2021, 2021, 6683622. [Google Scholar] [CrossRef]
- Qin, F.; Li, L.; Liu, Y.; Cheng, W.; Zhang, H. A Four-Mode OAM Antenna Array with Equal Divergence Angle. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1941–1945. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Zhang, Y.; Hong, W. Anisotropic impedance surface-enabled low-profile broadband dual- circularly polarized multibeam reflectarrays for ka-band applications. IEEE Trans. Antennas Propag. 2020, 68, 6441–6446. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Yue, T.; Hong, W. Low-profile and wideband dual-circularly polarized reflect-arrays based on rotated metal-backed dual-polarized aperture-coupled patch elements. IEEE Trans. Antennas Propag. 2020, 68, 2108–2117. [Google Scholar] [CrossRef]
- Lin, J.; Chen, C.; Ding, J.; Wang, S.; Chen, W. Dual-frequency multiple compact vortex beams generation based on single-layer bi-spectral metasurface. Appl. Phys. Lett. 2021, 119, 081905. [Google Scholar] [CrossRef]
- Jack, B.; Padgett, M.J.; Franke-Arnold, S. Angular diffraction. New J. Phys. 2008, 10, 103013. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.; Guo, X.; Qi, Z.; Zhu, H.; Li, Q. A reflective metasurface for generating dual-mode dual-polarized high-order bessel vortex beams with equal divergence angle. IET Microw. Antennas Propag. 2022, 16, 489–496. [Google Scholar] [CrossRef]
- He, X.; Deng, L.; Feng, B. Reflective metasurface for controlling the beam divergence angles of dual-mode OAM waves. In Proceedings of the 2020 IEEE 3rd International Conference on Electronic Information and Communication Technology (ICEICT), Shenzhen, China, 13–15 November 2020; IEEE: Shenzhen, China, 2020; pp. 636–639. [Google Scholar]
- Zhou, N.; Tian, C.; Zhu, S.; Li, C.; Zhao, M.; Chen, X.; Zhang, A. Metasurface modulator of frequency diverse multi-mode OAM beams with equal divergence angle for coincidence imaging. J. Phys. D Appl. Phys. 2023, 56, 445001. [Google Scholar] [CrossRef]
- Chen, R.; Yao, R.; Long, W.-X.; Moretti, M.; Li, J. UCA-based OAM non-orthogonal multi-mode multiplexing. IEEE Open J. Antennas Propag. 2021, 2, 181–190. [Google Scholar] [CrossRef]
- Wu, G.-B.; Chan, K.F.; Shum, K.M.; Chan, C.H. Millimeter-wave holographic flat lens antenna for orbital angular momentum multiplexing. IEEE Trans. Antennas Propag. 2021, 69, 4289–4303. [Google Scholar] [CrossRef]
- Xu, P.; Liu, H.; Li, R.; Zhang, K.; Li, L. Dual-band spin-decoupled metasurface for generating multiple coaxial OAM beams. IEEE Trans. Antennas Propag. 2022, 70, 10678–10690. [Google Scholar] [CrossRef]


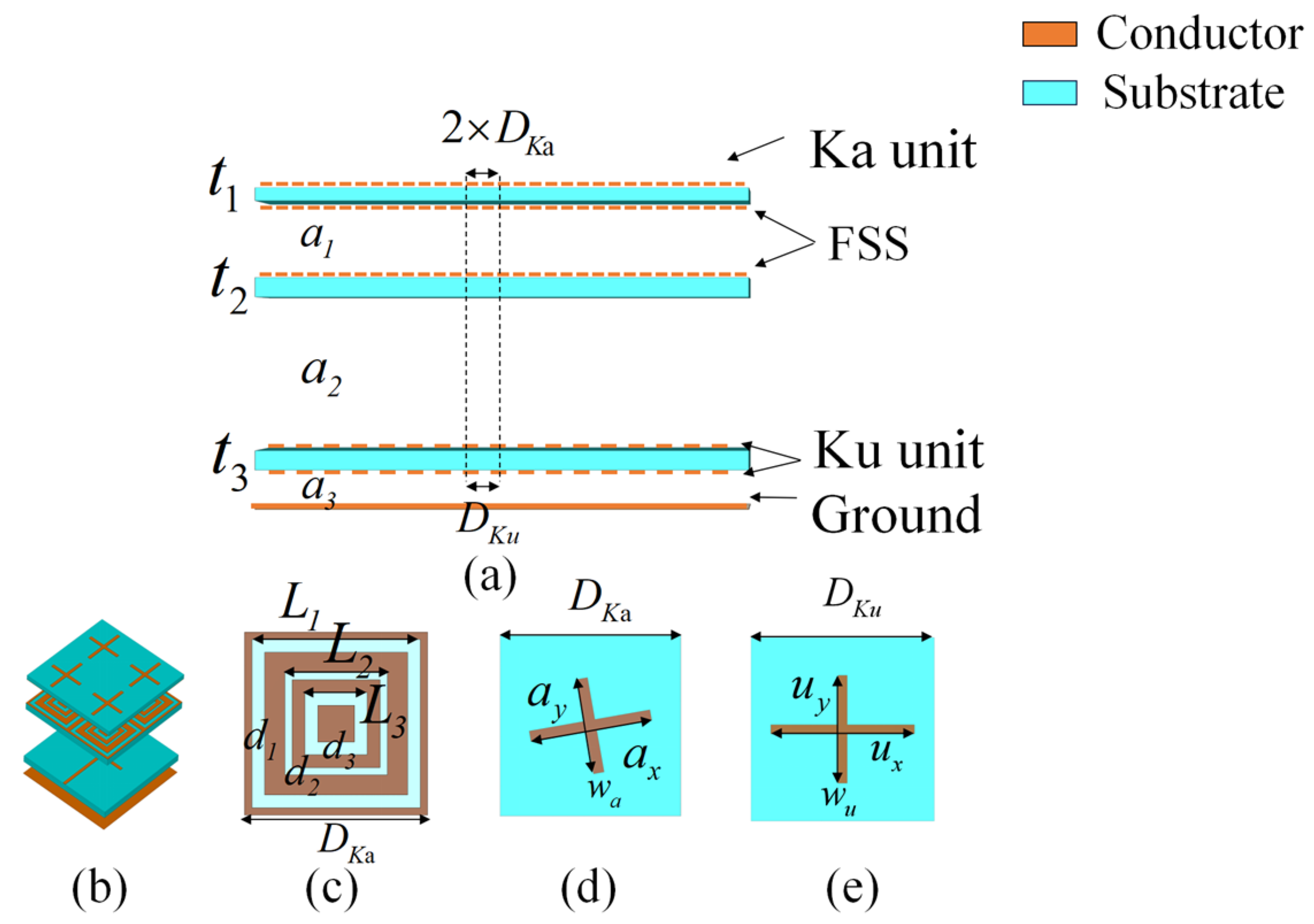



| Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Values (mm) | 0.508 | 0.762 | 0.762 | 2 | 6 | 1.5 | 0.5 |
| Parameters | |||||||
| Values (mm) | 4.5 | 2.8 | 1.5 | 0.35 | 0.2 | 0.45 | 0.3 |
| Ref. | Frequency | Band Width | Aperture Size | Polarization | OAM Mode | Mode Purity (Simulation) | Divergence Angle | Angle of Modes |
|---|---|---|---|---|---|---|---|---|
| [36] | 12.5 GHz 13.0 GHz 13.6 GHz | 0.9 GHz | 12 × 12 | LP | 1, 2, 3 | 60% 50% 45% | 12.5 | equal |
| [34] | 29.0 GHz | Central Frequency | 15 × 15 | DLP | 1, 2 | - | 3 | equal |
| [29] | 5.8 GHz | Central Frequency | 8 × 8 | LP | 1, 2, 3 | - | 12 | equal |
| [37] | 9 GHz | Central Frequency | 6 × 6 | CP | 0, ±1, 2 | - | 16.4 | equal |
| [38] | 60 GHz | Central Frequency | 10 × 10 | LP | ±1 | 95% | 10 | Unequal |
| [26] | 5.2 GHz 10.5–12 GHz | 1.5 GHz | 8.5 × 8.5 19 × 19 | LP CP | 1, 2 | 65%, 83% | 30, 12 | Unequal |
| [39] | 11.2–12.9 GHz 28.3–29.6 GHz | 1.7 GHz 1.3 GHz | 8.8 × 8.8 21 × 21 | DCP | ±1, ±2 | 96%, 93% | 12, 9 | Unequal |
| this work | 11.75–13.15 GHz 29.5–30.5 GHz | 1.4 GHz 1 GHz | 8 × 8 19 × 19 | DLP, DCP | 1, 2, ±3 | 80%, 79%, 70%, 65% | 9 | equal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhu, Y.; Chen, J.; Xie, W. Generation of Four-Channel Multi-Polarization Bessel Vortex Beams with Equal Divergence Angle Based on Co-Aperture Metasurface. Photonics 2025, 12, 816. https://doi.org/10.3390/photonics12080816
Wang Z, Zhu Y, Chen J, Xie W. Generation of Four-Channel Multi-Polarization Bessel Vortex Beams with Equal Divergence Angle Based on Co-Aperture Metasurface. Photonics. 2025; 12(8):816. https://doi.org/10.3390/photonics12080816
Chicago/Turabian StyleWang, Zhiwei, Yongzhong Zhu, Jun Chen, and Wenxuan Xie. 2025. "Generation of Four-Channel Multi-Polarization Bessel Vortex Beams with Equal Divergence Angle Based on Co-Aperture Metasurface" Photonics 12, no. 8: 816. https://doi.org/10.3390/photonics12080816
APA StyleWang, Z., Zhu, Y., Chen, J., & Xie, W. (2025). Generation of Four-Channel Multi-Polarization Bessel Vortex Beams with Equal Divergence Angle Based on Co-Aperture Metasurface. Photonics, 12(8), 816. https://doi.org/10.3390/photonics12080816





