High-Efficiency Mid-Infrared Transmission Modulator Based on Graphene Plasmon Resonance and Photonic Crystal Defect States
Abstract
1. Introduction
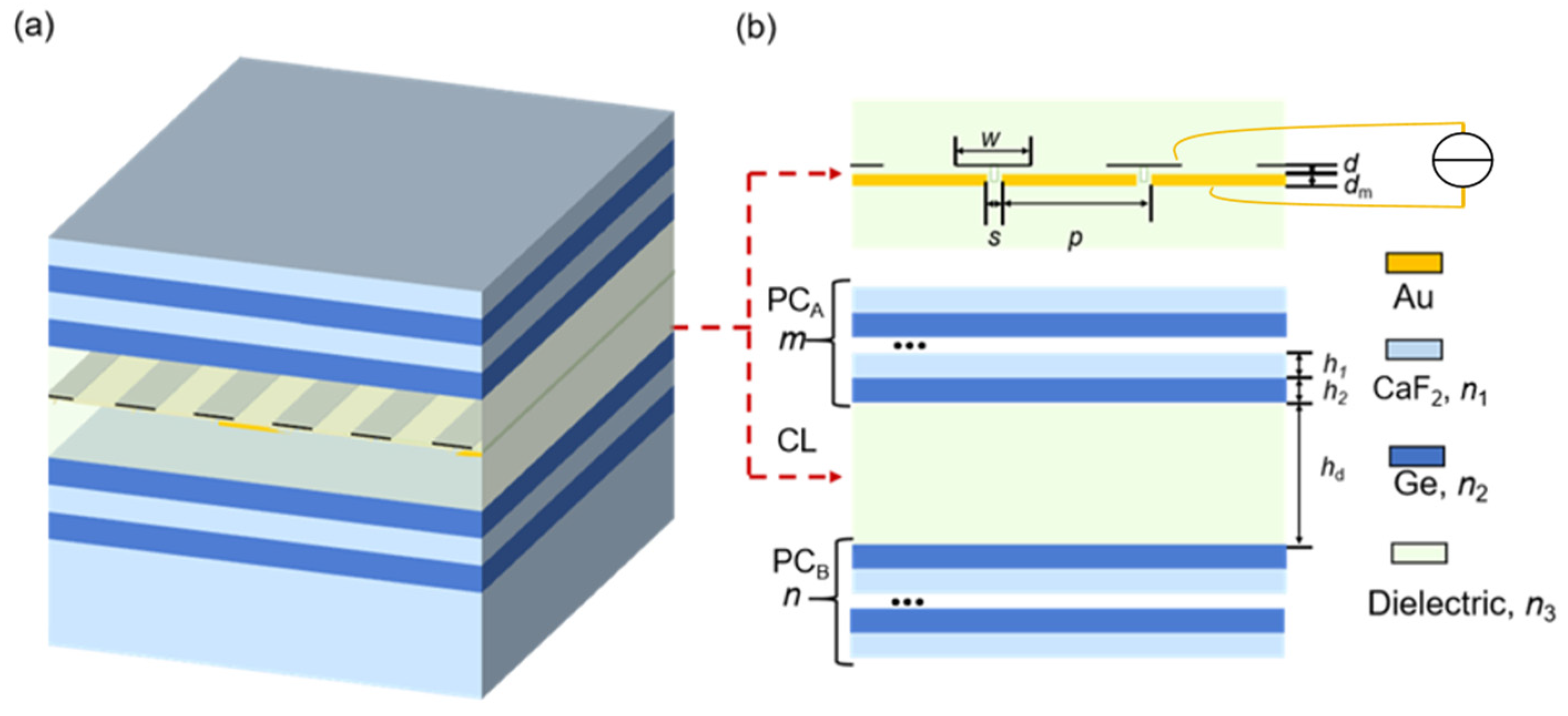
2. Design of the Structure
2.1. Overall Structural Design
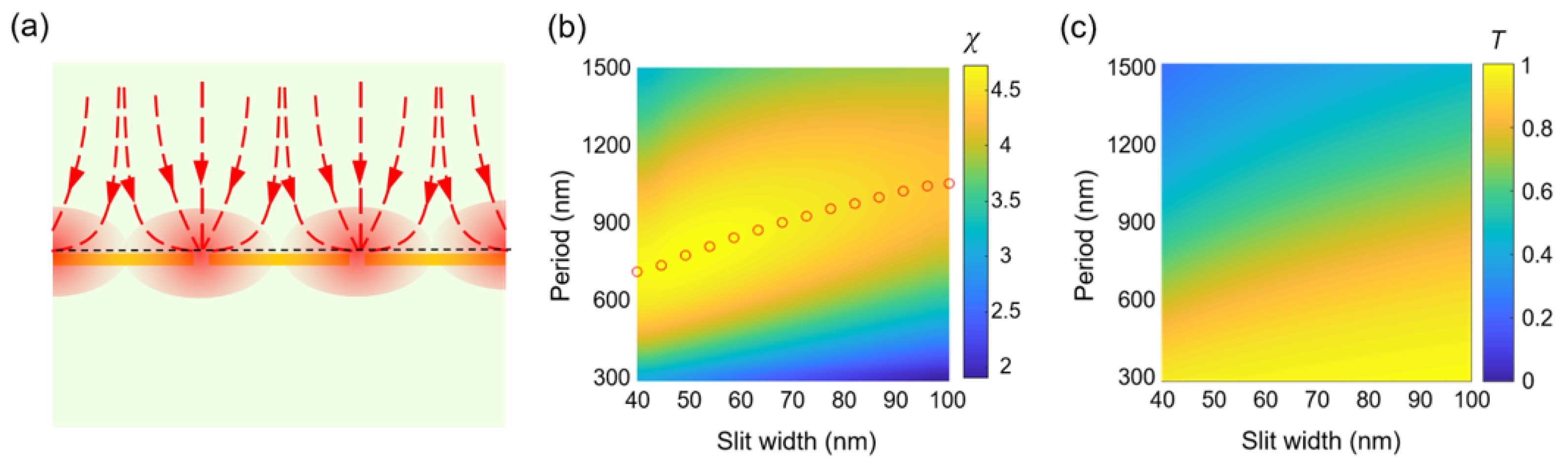
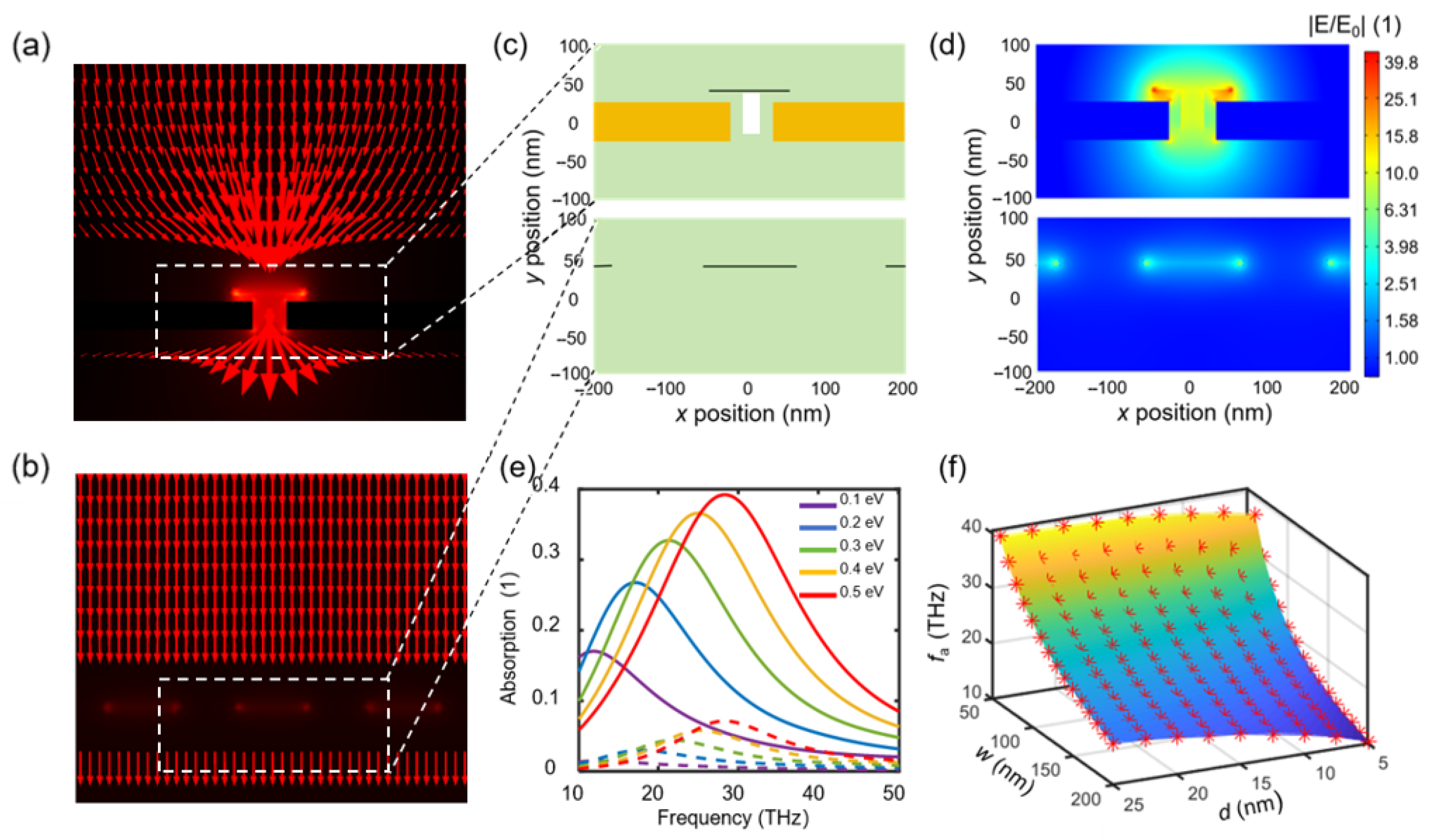
2.2. Design of the Antenna Enhanced Graphene Plasmonic Structure
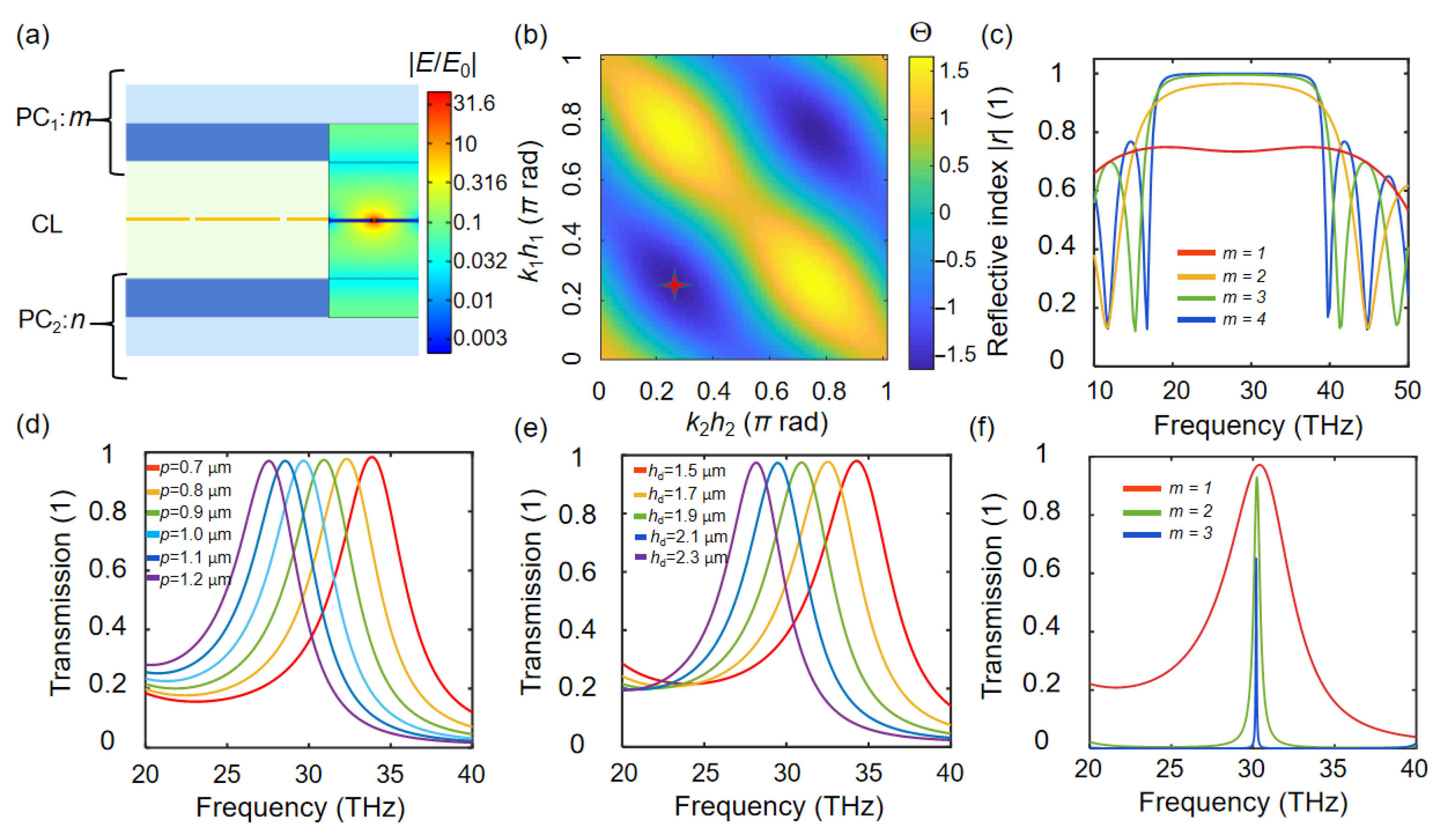
2.3. Design of the Photonic Crystal Cavity
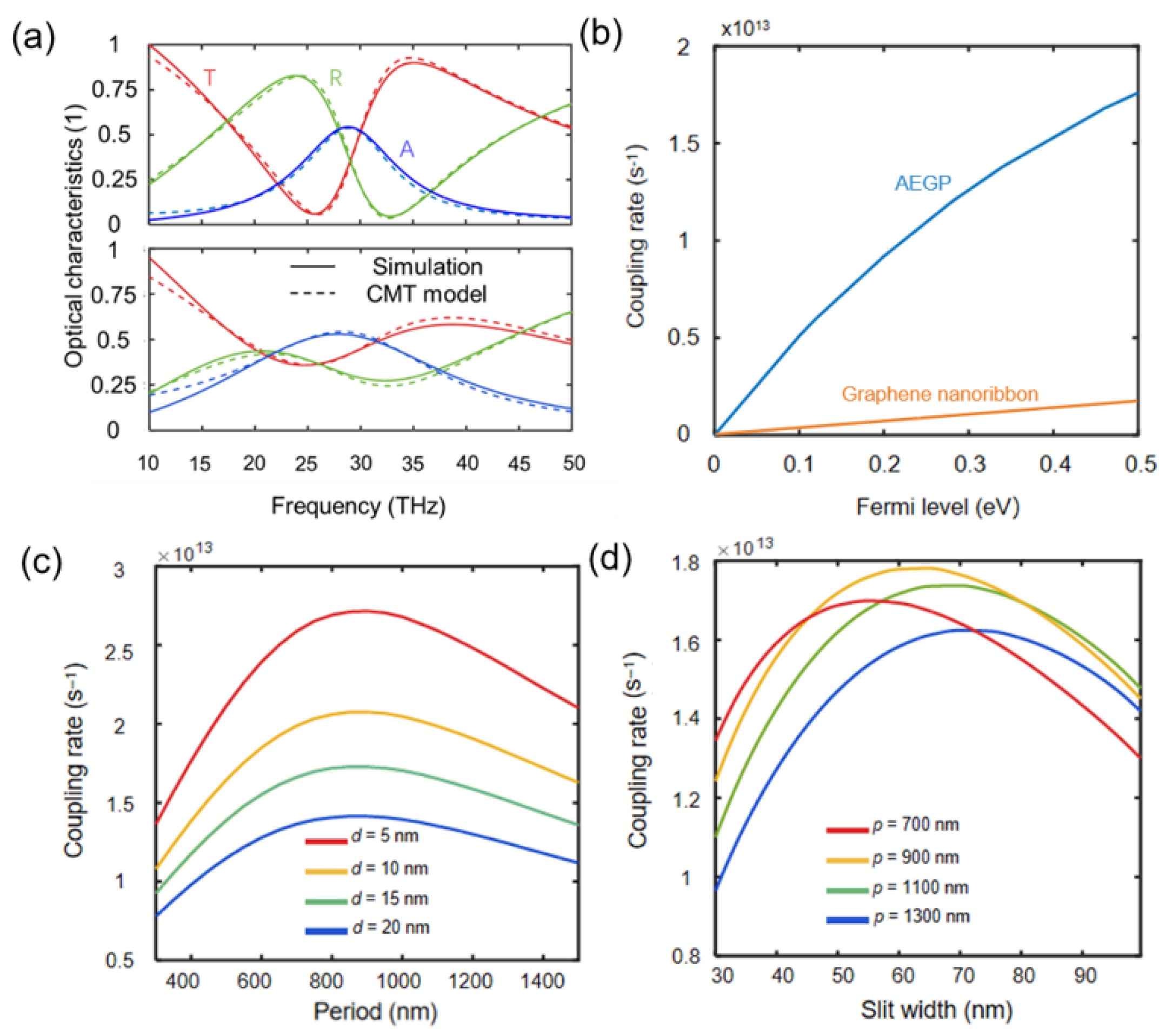
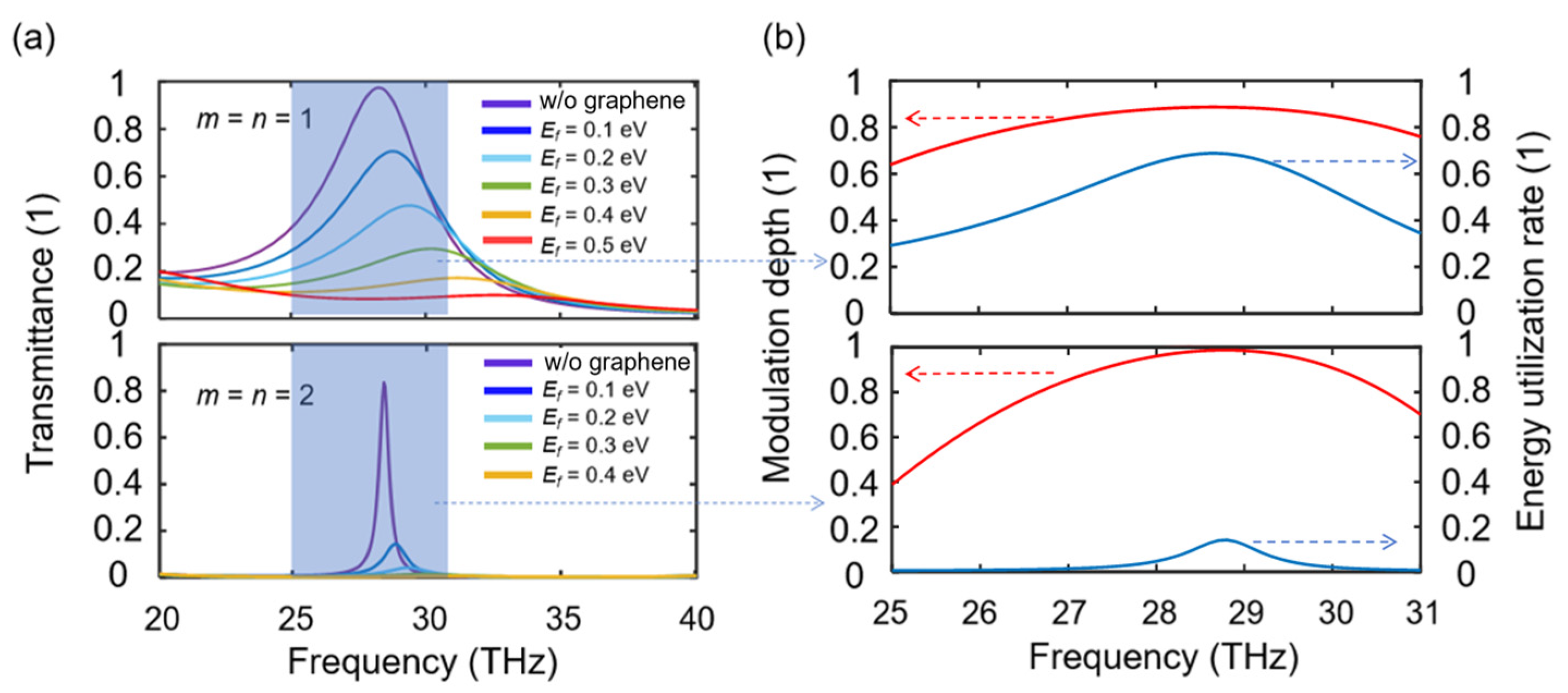
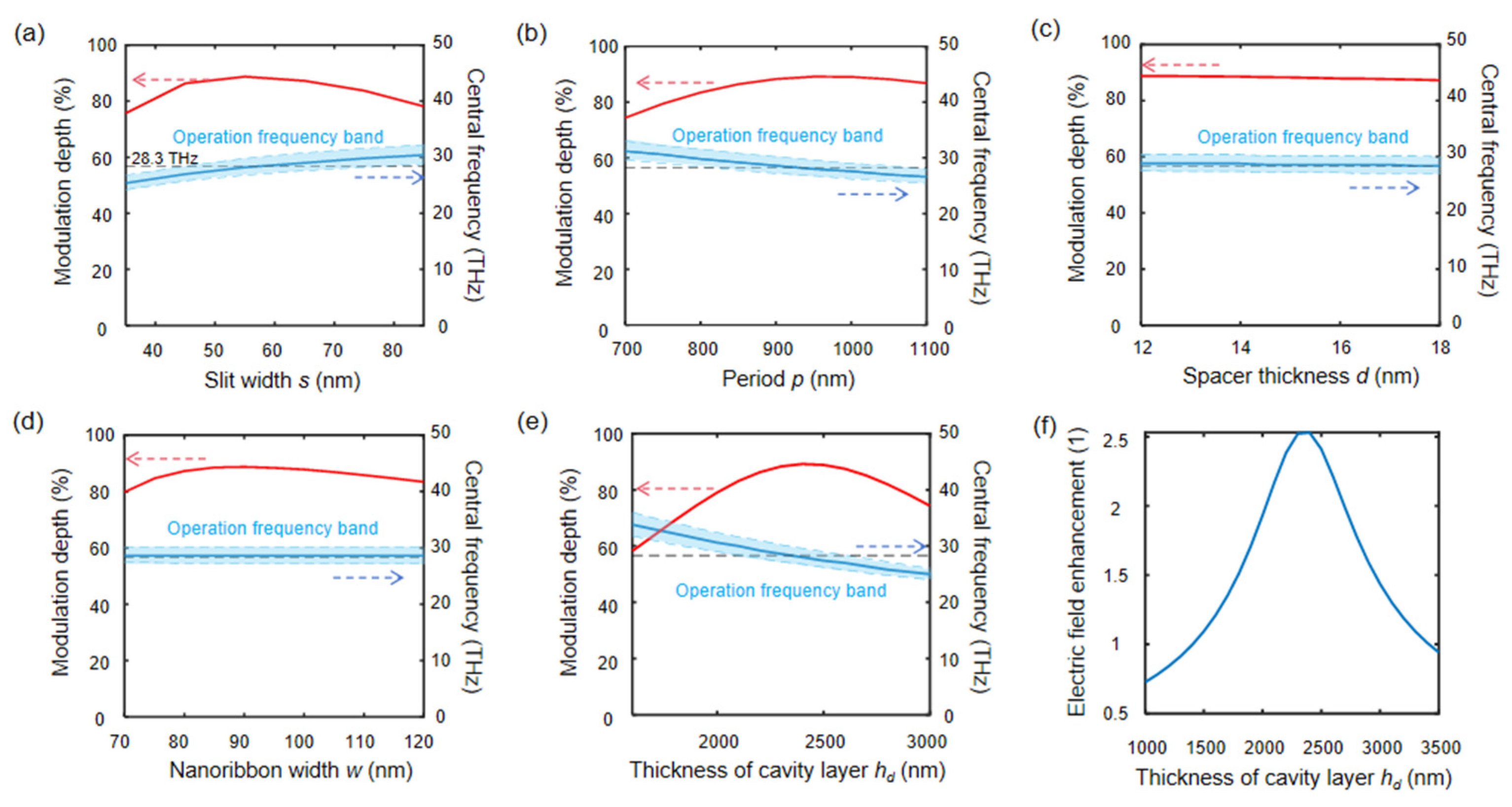
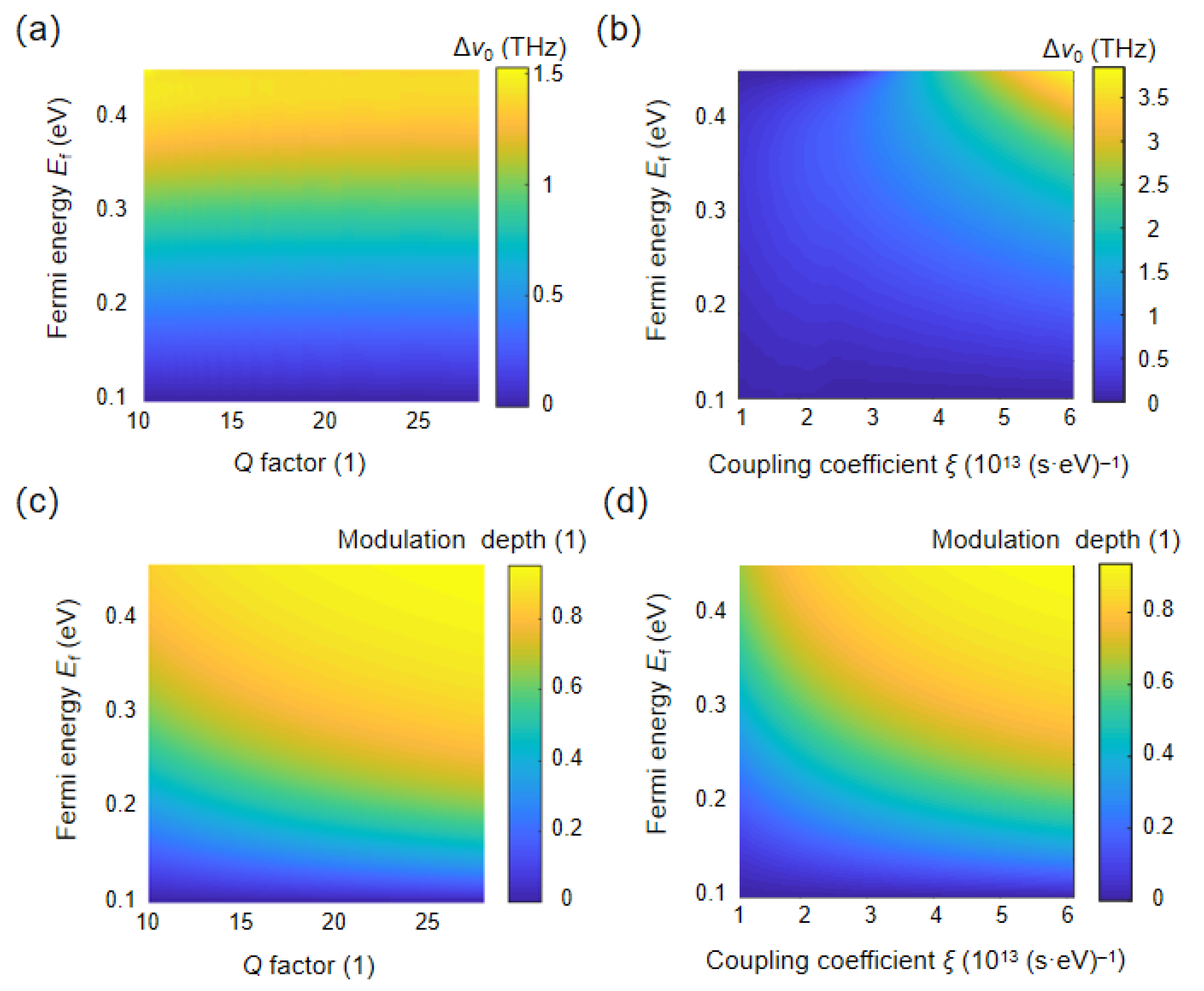
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.S. Modulators for Optical Communications. Proc. IEEE 1970, 58, 1440–1457. [Google Scholar] [CrossRef]
- Thylén, L.; Westergren, U.; Holmström, P.; Schatz, R.; Jänes, P. Recent Developments in High-Speed Optical Modulators. In Optical Fiber Telecommunications V A; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Academic Press: San Diego, CA, USA, 2008; pp. 183–220. [Google Scholar]
- Xu, M.; He, M.; Zhang, H.; Jian, J.; Pan, Y.; Liu, X.; Chen, L.; Meng, X.; Chen, H.; Li, Z.; et al. High-Performance Coherent Optical Modulators Based on Thin-Film Lithium Niobate Platform. Nat. Commun. 2020, 11, 3911. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, N.; Zhang, J.; Zhu, Z.; Liu, K. High Performance Electro-Optic Modulator Based on Thin-Film Lithium Niobate. Optoelectron. Lett. 2022, 18, 583–587. [Google Scholar] [CrossRef]
- Hou, S.; Hu, H.; Liu, Z.; Xing, W.; Zhang, J.; Hao, Y. High-Speed Electro-Optic Modulators Based on Thin-Film Lithium Niobate. Nanomaterials 2024, 14, 867. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Hu, H.; Xing, W.; Liu, Z.; Zhang, J.; Hao, Y. Improving Linewidth and Extinction Ratio Performances of Lithium Niobate Ring Modulator Using Ring-Pair Structure. Adv. Photonics Res. 2023, 4, 2300169. [Google Scholar] [CrossRef]
- Liu, J.J.; Stann, B.L.; Klett, K.K.; Cho, P.S.; Pellegrino, P.M. Mid and Long-Wave Infrared Free-Space Optical communication. In Laser Communication and Propagation Through the Atmosphere and Oceans VIII; SPIE: Washington, DC, USA, 2019; pp. 1–18. [Google Scholar]
- Grillot, F.; Poletti, T.; Pes, S. Progress in Mid-Infrared Optoelectronics for High-Speed Free-Space Data Throughput. APL Photonics 2025, 10, 010905. [Google Scholar] [CrossRef]
- Dong, W.; Qiu, Y.; Zhou, X.; Banas, A.; Banas, K.; Breese, M.B.; Cao, T.; Simpson, R.E. Tunable mid-infrared phase-change metasurface. Adv. Opt. Mater. 2018, 6, 1701346. [Google Scholar] [CrossRef]
- Guo, K.; Li, X.; Ai, H.; Ding, X.; Wang, L.; Wang, W.; Guo, Z. Tunable oriented mid-infrared wave based on metasurface with phase change material of GST. Results Phys. 2022, 34, 105269. [Google Scholar] [CrossRef]
- Dawood, N.Y.M.; Younis, B.M.; Areed, N.F.F.; Hameed, M.F.O.; Obayya, S.S.A. Mid-infrared optical modulator based on silicon D-shaped photonic crystal fiber with VO2 material. Appl. Opt. 2021, 60, 9488–9496. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, P.; Ai, W.; Liu, Y.; Li, Y.; Jiang, R.; Li, W.; Weng, X.; Bi, L.; Deng, L. Broadband switching of mid-infrared atmospheric windows by VO2-based thermal emitter. Opt. Express 2019, 27, 11537–11546. [Google Scholar] [CrossRef]
- Chen, J.H.; Jang, C.; Xiao, S.; Ishigami, M.; Fuhrer, M.S. Intrinsic and Extrinsic Performance Limits of Graphene Devices on SiO2. Nat. Nanotechnol. 2008, 3, 206–209. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A Graphene-Based Broadband Optical Modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Qu, S.; Ma, C.; Wang, S.; Liu, H.; Dong, L. Modulation Speed Limits of a Graphene-Based Modulator. Opt. Quantum Electron. 2018, 50, 105. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Schlather, A.E.; Liu, Z.; Ajayan, P.M.; García de Abajo, F.J.; Nordlander, P.; Zhu, X.; Halas, N.J. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 2014, 14, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.H.; Kholmanov, I.; Alici, K.B.; Purtseladze, D.; Arju, N.; Tatar, K.; Fozdar, D.Y.; Suk, J.W.; Hao, Y.; Khanikaev, A.B.; et al. Inductive tuning of Fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett. 2013, 13, 1111–1117. [Google Scholar] [CrossRef]
- Nong, J.; Tang, L.; Lan, G.; Luo, P.; Li, Z.; Huang, D.; Yi, J.; Shi, H.; Wei, W. Enhanced graphene plasmonic mode energy for highly sensitive molecular fingerprint retrieval. Laser Photonics Rev. 2021, 15, 2000300. [Google Scholar] [CrossRef]
- Lan, G.; Tang, L.; Dong, J.; Nong, J.; Luo, P.; Li, X.; Li, Z.; Zhang, Y.; Dai, Y.; Wang, W.; et al. Enhanced asymmetric light-plasmon coupling in graphene nanoribbons for high-efficiency transmissive infrared modulation. Laser Photonics Rev. 2024, 18, 2300469. [Google Scholar] [CrossRef]
- Fallahi, A.; Perruisseau-Carrier, J. Design of tunable biperiodic graphene metasurfaces. Phys. Rev. B 2012, 86, 195408. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhu, B.; Zhao, J.; Jiang, T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express 2014, 22, 22743–22752. [Google Scholar] [CrossRef]
- Tang, B.; Jia, Z.; Huang, L.; Su, J.; Jiang, C. Polarization-controlled dynamically tunable electromagnetically induced transparency-like effect based on graphene metasurfaces. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 1–6. [Google Scholar] [CrossRef]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 205418. [Google Scholar] [CrossRef]
- Kanayama, K.; Nagashio, K.; Nishimura, T.; Toriumi, A. Large Fermi Energy Modulation in Graphene Transistors with High-Pressure O2-Annealed Y2O3 Topgate Insulators. Appl. Phys. Lett. 2014, 104, 2024–2490. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J.; Zhang, Y.; Shan, Y.; Dai, Y.; Chen, A.; Shen, T.; Wu, S.; Liu, X.; Shi, L.; et al. Transmission-type optical modulator based on graphene plasmonic resonator integrated with off-resonant Au structure. Adv. Opt. Mater. 2020, 8, 2000264. [Google Scholar] [CrossRef]
- Kim, S.; Jang, M.S.; Brar, V.W.; Tolstova, Y.; Mauser, K.W.; Atwater, H.A. Electronically tunable extraordinary optical transmission in graphene plasmonic ribbons coupled to subwavelength metallic slit arrays. Nat. Commun. 2016, 7, 12323. [Google Scholar] [CrossRef] [PubMed]
- Ramanujam, N.R.; Amiri, I.S.; Taya, S.A.; Olyaee, S.; Udaiyakumar, R.; Pasumpon Pandian, A.; Joseph Wilson, K.S.; Mahalakshmi, P.; Yupapin, P.P. Enhanced sensitivity of cancer cell using one dimensional nano composite material coated photonic crystal. Microsyst. Technol. 2019, 25, 189–196. [Google Scholar] [CrossRef]
- van der Mee, C.; Contu, P.; Pintus, P. One-dimensional photonic crystal design. J. Quant. Spectrosc. Radiat. Trans. 2010, 111, 214–225. [Google Scholar] [CrossRef]
- Yue, Y.; Gong, J.P. Tunable one-dimensional photonic crystals from soft materials. J. Photochem. Photobiol. C 2015, 23, 45–67. [Google Scholar] [CrossRef]
- Fei, Z.; Goldflam, M.D.; Wu, J.S.; Dai, S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Post, K.W.; Zhu, S.; Janssen, G.C.A.M.; et al. Edge and Surface Plasmons in Graphene Nanoribbons. Nano Lett. 2015, 15, 8271–8276. [Google Scholar] [CrossRef]
- Lee, I.H.; Yoo, D.; Avouris, P.; Low, T.; Oh, S.H. Graphene acoustic plasmon resonator for ultrasensitive infrared spectroscopy. Nat. Nanotechnol. 2019, 14, 313–319. [Google Scholar] [CrossRef]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef]
- Suh, W.; Wang, Z.; Fan, S. Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities. IEEE J. Quantum Electron. 2004, 40, 1511–1518. [Google Scholar]
- Tang, L.L.; Nong, J.P.; Wei, W.; Zhang, S.; Zhu, Y.H.; Shang, Z.G.; Yi, J.M.; Wang, W. Mode Energy of Graphene Plasmons and Its Role in Determining The Local Field Magnitudes. Opt. Express 2018, 26, 6214–6221. [Google Scholar] [CrossRef]
- Russel, P.S.J.; Birks, T.A.; Lloyd-Lucas, F.D. Photonic bloch waves and photonic band gaps. In Confined Electrons and Photons; Burstein, E., Weisbuch, C., Eds.; Plenum: New York, NY, USA, 1995; pp. 585–633. [Google Scholar]
- Falkovsky, L.A.; Pershoguba, S.S. Optical Far-Infrared Properties of a Graphene Monolayer and Multilayer. Phys. Rev. B 2007, 76, 153410. [Google Scholar] [CrossRef]
| Structure | Central Wavelength | Tmax | Modulation Depth | Reference |
|---|---|---|---|---|
| Graphene nanoribbons and off-resonant Au structure | 12.5 μm | 95% (estimated) | 24% | [25] |
| Graphene nanoribbons and metallic slit arrays | 7.1 μm | 11% | 28.6% | [26] |
| Graphene nanoribbons and dielectric layer | 6.7 μm | 65% (estimated) | 41% | [19] |
| AEGP and PC | 10.6 μm | 67.6% | 88.5% | this work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Zang, Q.; Tang, L.; Wei, B.; Bai, X.; Zhang, H.; Liu, C.; Shi, H.; Shi, H.; Liu, Y.; et al. High-Efficiency Mid-Infrared Transmission Modulator Based on Graphene Plasmon Resonance and Photonic Crystal Defect States. Photonics 2025, 12, 800. https://doi.org/10.3390/photonics12080800
Dong J, Zang Q, Tang L, Wei B, Bai X, Zhang H, Liu C, Shi H, Shi H, Liu Y, et al. High-Efficiency Mid-Infrared Transmission Modulator Based on Graphene Plasmon Resonance and Photonic Crystal Defect States. Photonics. 2025; 12(8):800. https://doi.org/10.3390/photonics12080800
Chicago/Turabian StyleDong, Jiduo, Qing Zang, Linlong Tang, Binbin Wei, Xiangxing Bai, Hao Zhang, Chunheng Liu, Haofei Shi, Hongyan Shi, Yang Liu, and et al. 2025. "High-Efficiency Mid-Infrared Transmission Modulator Based on Graphene Plasmon Resonance and Photonic Crystal Defect States" Photonics 12, no. 8: 800. https://doi.org/10.3390/photonics12080800
APA StyleDong, J., Zang, Q., Tang, L., Wei, B., Bai, X., Zhang, H., Liu, C., Shi, H., Shi, H., Liu, Y., & Lu, Y. (2025). High-Efficiency Mid-Infrared Transmission Modulator Based on Graphene Plasmon Resonance and Photonic Crystal Defect States. Photonics, 12(8), 800. https://doi.org/10.3390/photonics12080800





