Photothermal Performance Testing of Lithium Niobate After Ion Beam Radiation

Abstract

To investigate the evolution of the optothermal properties of lithium niobate with ion beam irradiation parameters, the thermal effect theory was analyzed, and ion beam irradiation technology was used to modify lithium niobate samples. The transmittance of lithium niobate crystals after ion beam irradiation and the relationship between their optothermal properties and transmittance were studied. The results show that the average surface optothermal signal of lithium niobate exhibits a significant dependence on ion beam parameters. When the ion beam voltage is 800 V, the ion beam current is 30 mA, and the irradiation time is 60 s, a distinct absorption peak is observed on the surface of lithium niobate, with an average surface optothermal signal of 5377.34 ppm, demonstrating potential for all-optical modulation.

1. Introduction

Photothermal materials play a pivotal role in various functional applications, spanning high-speed communications, optical storage, and optical modulation [1,2,3,4,5]. With the rapid evolution of optical communications and sensing technologies, the demand for optical switches has surged [6,7].

Lithium niobate (LiNbO₃) is a negatively charged crystal renowned for its significant spontaneous polarization (0.70 C/m² at room temperature) and possessing the highest Curie temperature (1210 °C) among known ferroelectric materials. Lithium niobate crystals exhibit an array of desirable characteristics, including diverse photovoltaic effects, tunable properties, stable physicochemical attributes, and a wide range of light transmittance [8,9,10,11,12,13]. In photothermal applications, its high nonlinear optical, electro-optical, acousto-optical, and thermo-optical coefficients, combined with chemical stability, make it an ideal heat transfer medium for photothermal devices, particularly for optical switching via temperature-induced refractive index modulation [14]. Compared to other common photothermal materials such as silicon (narrow bandgap, ~1.1 eV) and polymers (poor thermal stability), LiNbO₃’s wide bandgap (3.7 eV) and high thermal conductivity (5.3 W·m⁻¹·K⁻¹) enable stable operation under high-power laser irradiation, a key advantage for practical devices [8,13,15].

Upon illumination by a light beam, a material absorbs a fraction of the light energy, converting it into thermal energy, thereby elevating the surface temperature of the material [16]. This thermal modulation induces alterations in the material’s physical properties, including the refractive index, absorption coefficient, etc., consequently influencing the propagation characteristics of the light beam within the material and facilitating switch operation. Specifically, as the light beam impinges upon the material’s surface, energy absorption leads to a temperature rise, thereby affecting the material’s refractive index and altering the light beam’s propagation speed within the medium [17]. When the temperature increases, so does the refractive index, causing a reduction in the light beam’s propagation velocity within the material, effectively enabling switching functionality. Moreover, the photothermal mechanism can be tailored to modify material thermal properties by manipulating the wavelength of the incident light beam. For instance, when the light beam’s wavelength aligns with the material’s absorption peak, enhanced light absorption occurs, triggering a more pronounced temperature variation and thereby facilitating switch operation. This wavelength-dependent photothermal mechanism allows for the precise control of parameters such as light beam intensity and wavelength, offering significant practical utility and application value.

Modulation of lithium niobate properties currently relies predominantly on ion beam irradiation techniques [18,19,20,21,22,23,24]. A comprehensive analysis of the global research landscape reveals that the morphologies achievable on lithium niobate surfaces via these methodologies are constrained in both shape and feature dimensions. Such constraints invariably affect the material’s photothermal characteristics. Consequently, there is a growing research interest in tailoring photothermal responses through ion beam etching. This approach has been successfully applied to fabricate diverse micro- and nanostructures on surfaces of metals, polymers, and silicide by adjusting the parameters of Ar⁺ ion beams [25,26]. In a study conducted by the research team at Xi’an University of Technology (XUT), a low-energy ion beam was employed to etch the surface of sapphire. By varying the ion beam parameters, the team successfully fabricated diverse self-organized nanostructures on the sapphire surface. Subsequent transmittance analyses of these nanostructures revealed a notable enhancement in transmittance compared to the unmodified sapphire substrate [27,28]. Similarly, researchers Yang Gaoyuan and colleagues at the University of Science and Technology of China (USTC) utilized ion-beam etching in conjunction with photolithographic masks to modify fused silica materials. Their technique yielded a 1% increase in transmittance within the 600~1300 nm range relative to the untreated material [29].

However, research on ion beam-modulated photothermal properties of LiNbO₃ remains scarce. Existing studies primarily focus on structural or optical (e.g., transmittance) changes, with little attention to the direct link between ion beam parameters and photothermal signals, which is critical for all-optical modulation [30]. This gap underscores the necessity of our investigation.

Accordingly, this study employs ion beam irradiation to methodically alter the photothermal characteristics of lithium niobate. By varying key parameters such as incident voltage, beam current, and irradiation duration, we delve into the correlation between these ion beam parameters and the subsequent evolution of the photothermal properties of lithium niobate. This approach not only illuminates the underlying mechanisms but also charts a path for future explorations in the field.

2. Theoretical Analysis

Multiphoton absorption initiates free electron generation in the conduction band. When the electron density exceeds a critical threshold, avalanche ionization rapidly amplifies carrier concentration, inducing a marked shift in the material’s dielectric constant characterized by diminished transmittance, elevated refractive index, and plasma-induced astigmatism—collectively indicating material damage. Photon ionization provides seed electrons for this process, facilitated by mechanisms such as inverse bremsstrahlung [31,32,33]. Crucially, avalanche ionization dominates under long-pulse irradiation, whereas multiphoton processes prevail for short pulses.

Following the Thornber model [34], the avalanche ionization rate is expressed as follows:

$$\eta (E)={\displaystyle \frac{v_{s}eE}{E_g}}\exp \left[-{\displaystyle \frac{E_I}{E(1+E/E_p)+E_{kT}}}\right]$$

(1)

where $v_s$ denotes the electron saturation drift velocity, and $E_g$ is the forbidden bandwidth, while $E$, $E_I$, $E_p$, and $E_{hT}$ correspond to the electric field strength of the incident laser, collision scattering, photon scattering, and thermal scattering. The photon ionization rate is defined by the following [35,36]:

$${\omega }_{PI}\left(E\right)={\displaystyle \frac{2\omega }{9\pi }}{\left({\displaystyle \frac{\omega m}{\hslash \sqrt{{\gamma }_1}}}\right)}^{3/2}Q\left(\gamma ,x\right)\exp \left[-\pi 〈x+1〉{\displaystyle \frac{K\left({\gamma }_1\right)-E\left({\gamma }_1\right)}{E\left({\gamma }_2\right)}}\right]$$

(2)

where $\omega$ is the incident light frequency; $m$ is the electron effective mass; and $\gamma$, ${\gamma }_1$, ${\gamma }_2$, and $x$ characterize the multiphoton ionization order. Consequently, the free electron density evolution during the laser pulse is described by the following [37]:

$$n\left(t\right)=\left\{n_0+{\displaystyle {\int }_0^t{\omega }_{PI}\exp \left[{\displaystyle {\int }_0^{t^{\prime }}-\left(\eta -g-\frac{1}{{\tau }_R}\right)d{t}^{″}}\right]d{t}^{\prime }}\right\}\exp \left(-{\displaystyle {\int }_0^t-\eta d{t}^{\prime }}\right)$$

(3)

$$g={\displaystyle \frac{1}{{\tau }_D}}={\displaystyle \frac{2{\epsilon }_{av}}{3mv}}\left[{\left({\displaystyle \frac{4.8}{d}}\right)}^2+{\left({\displaystyle \frac{1}{l}}\right)}^2\right]$$

(4)

By integrating Equation (3) with appropriate initial and boundary conditions, the spatiotemporal distribution of free electron number density under different pulse widths can be determined.

The reduction mechanism of thermal conductivity due to vacancy defects in monolayer LiNbO₃ is analyzed by modeling atomic normal vibration modes. Assuming the solution of atomic normal vibration modes is $u_{ia,\lambda }=1/\left(\sqrt{m_i}{\epsilon }_{ia,\lambda }\right)\cdot e^{i{\omega }_{\lambda }t}$, the eigenfrequencies and eigen vectors of a single layer of LiNbO₃ can be obtained by solving the eigenvalue s of the force constant matrix:

$${\omega }_{\lambda }^2{\epsilon }_{ia,\lambda }={\displaystyle \sum _{jB}{\Phi }_{ia,j\beta }}{\epsilon }_{j\beta ,\lambda }$$

(5)

where ω is the eigenfrequency of the normal vibration mode, ε is the eigenvector, and φ is the matrix of force constants, which is expressed as follows.

$${\Phi }_{ia,j\beta }={\displaystyle \frac{1}{\sqrt{m_i{m}_j}}}{\displaystyle \frac{{\mathsf{\partial }}^{2}V}{\mathsf{\partial }{u}_{ia}\mathsf{\partial }{u}_{j\beta }}}$$

(6)

where u_ia is the displacement of atom $i$ along Cartesian coordinate $\mathsf{\alpha }$, m_i is the atomic mass, and V is the total potential energy of the whole system. The phonon participation ratio $P_{\lambda }$ for mode $\mathsf{\lambda }$ is given by the following [38]:

$$P_{\lambda }^{-1}=N{\displaystyle \sum _i{\left({\displaystyle \sum _a{\epsilon }_{ia,\lambda }^{\ast }}{\epsilon }_{ia,\lambda }\right)}^2}$$

(7)

where $N$ is the total number of atoms. This dimensionless parameter $\left(0\le P_{\lambda }\le 2\right)$ quantifies the spatial delocalization of phonons: smaller $P_{\lambda }$ indicates stronger phonon localization, which reduces thermal conductivity by hindering phonon transport.

In LiNbO₃ with vacancy defects, the reduced participation ratio of vibration modes suggests phonon localization. The spatial distribution of localized atoms around vacancies is characterized by [39]:

$${\phi }_{\Gamma }\left(i\right)={\displaystyle \frac{{\displaystyle \sum _{\lambda \in \Gamma }{\displaystyle \sum _a{\epsilon }_{ia,\lambda }^{\ast }}}{\epsilon }_{ia,\lambda }}{{\displaystyle \sum _j{\displaystyle \sum _{\lambda \in \Gamma }{\displaystyle \sum _a{\epsilon }_{ja,\lambda }^{\ast }}}}{\epsilon }_{ja,\lambda }}}$$

(8)

where $\mathsf{\Gamma }=\left\{\lambda :p_{\lambda }<p_c\right\}$ denotes the set of localized modes, P_c is a criterion to measure whether a vibrational mode is localized, and ${\phi }_{\mathsf{\Gamma }}\left(i\right)$ is the degree of localization of the atom. The present experiment sets the criterion for localization as $\mathsf{\Gamma }=\lambda :p_{\lambda }<0.2$.

Bond relaxation theory and quantum perturbation theory are used to further explain that the low-coordinated atoms around the vacancy defect produce strong phonons, which is the cause of strong scattering. Phonon-vacancy defect scattering was originally calculated quantitatively by Klemens applying perturbation theory. In Klemens’ theoretical model, vacancy defects perturb the energy of the system in two ways: (1) changes in the kinetic energy of the system due to the absence of mass; (2) a change in the potential energy of the system due to the absence of bonding between the vacancy and the surrounding atoms. The phonon-vacancy scattering rate is given as follows [40]:

$${\tau }_V^{-1}=x{\left({\displaystyle \frac{\Delta \mathrm{M}}{M}}\right)}^2{\displaystyle \frac{\pi }{2}}{\displaystyle \frac{{\omega }^{2}g\left(\omega \right)}{G}}$$

(9)

where x is the vacancy concentration, and G is the number of atoms contained in the material. For vacancy defects, $\mathsf{\Delta }M/M=-M\mathrm{ₐ}/M-2$, where M is the average mass of the molecule, M_a is the mass of the missing atom, and −2 represents the effect of the missing bond.

The phonon scattering rate due to the Li monovacancy is as follows:

$${\tau }_{V,Li}^{-1}=13.45x\hspace{0.33em}/{\displaystyle \frac{{\omega }^{2}g\left(\omega \right)}{G}}$$

(10)

The phonon scattering rate due to the Nb monovacancy is as follows:

$${\tau }_{V,Nb}^{-1}=18.54x\hspace{0.33em}/{\displaystyle \frac{{\omega }^{2}g\left(\omega \right)}{G}}$$

(11)

The phonon scattering rate due to the O trivacancy is as follows:

$${\tau }_{V,O}^{-1}=19.63x\hspace{0.33em}/{\displaystyle \frac{{\omega }^{2}g\left(\omega \right)}{G}}$$

(12)

In monolayer LiNbO₃, the relative atomic mass of Li is 7, the relative atomic mass of Nb is 41, the relative atomic mass of O is 16, and the atomic mass lost to form an O trivacancy is greater than that to form a Li monovacancy or a Nb monovacancy. According to the classical vacancy theory calculation results of Formulas (10)–(12), the scattering rate caused by O trivacancy is greater than that caused by Li monovacancy or Nb monovacancy, that is, the suppression effect of O trivacancy on thermal conductivity is greater, which is just opposite to the previous thermal conductivity calculation results.

Klemens’ perturbation theory initially overlooked the force constant modification induced by reduced coordination number around vacancies, which perturbs system energy and enhances phonon scattering. Pauling proposed that low-coordinated atomic bonds exhibit shortened bond lengths and enhanced bond energies [41], forming the basis of Sun’s Bond-order-length-strength (BOLS) theory [42]. The BOLS model defines the bond contraction coefficient $\left(Cz\right)$ and bond energy $\left(E_z\right)$ as follows:

$$C_z=d_z/d_0=2/\left\{1+exp\left[\left(12-z\right)/\left(8z\right)\right]\right\}$$

(13)

$$E_z=C_z^{-m}{E}_b$$

(14)

where $z$ is the effective coordination number, $d/d_0$ is the bond length ratio, $E_b$ is the bulk single-bond energy, $z_0=12$ (bulk coordination), and $m=4$ for transition metal chalcogenides [43]. The atomic force constant $k_z$ correlates with bond length and energy via dimensional analysis:

$$k\_z \left(d^{2}u\right)/\left(d{r}^2\right) |\_(r) d\_z (E\_z)/(d\_z^2)$$

(15)

Monovacancy Scenario: Removing a Li/Nb atom $\left(z=6\right)$ in monolayer LiNbO₃ creates 6 low-coordinated O atoms (coordination changes from $z=4$ to $z-1=3$). Combining Equations (13)–(15) gives the force constant ratio:

$$\begin{array}{l}\mathsf{\partial }K/K = (K\_(z-1) - K\_z)/K\_z \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= (E\_(z-1) d\_z^2)/(E\_z d\_(z-1)^2) - 1 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= \left(\right(C\_(z-1)/C\_z)^(-(m+2)) - 1\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}= {\left[\begin{array}{c}1+e^{{\displaystyle \frac{12-z}{8z}}}\\ 1+e^{{\displaystyle \frac{13-z}{8z-8}}}\end{array} \right]}^{-\left(m+2\right)}- 1\end{array}$$

(16)

where $\mathsf{\delta }k=k_{z-1}-k_z$ denotes the force constant increment.

Trivacancy Scenario: Removing three O atoms ($z=4$) forms a trivacancy surrounded by 4 low-coordinated Li/Nb atoms (coordination changes from ($z=6$ to $z-3=3$)):

$$\begin{gathered} {\displaystyle \frac{\delta k}{k}}={\displaystyle \frac{k_{z-3}-k_z}{k_z}}={\displaystyle \frac{E_{z-3}{d}_z^2}{E_z{d}_{z-3}^2}}-1 \\ ={\left({\displaystyle \frac{C_{z-3}}{C_z}}\right)}^{-\left(m+2\right)}-1 \\ ={\left({\displaystyle \frac{1+e^{\frac{12z}{8z}}}{1+e^{\frac{14+z}{8z-6}}}}\right)}^{-\left(m+2\right)}-1 \end{gathered}$$

(17)

The phonon scattering rate due to force constant defects is [40]:

$${\tau }_A^{-1}=x_A{\left({\displaystyle \frac{\delta k}{k}}\right)}^{2}4\pi {\displaystyle \frac{{\omega }^{2}g(\omega )}{G}}$$

(18)

where $x_A=nx$($n$ is the number of low-coordinated atoms per vacancy, $x$ is vacancy concentration). Substituting $n=6, z=4, m=4$ into Equations (16)–(18) gives:

$${\tau }_{A,\mathrm{Li}}^{-1}=179.58\hspace{0.17em} \times \hspace{0.17em}{\displaystyle \frac{{\omega }^{2}g\left(\omega \right)}{G}}$$

For trivacancy with $n=3,z=6:{\mathsf{\tau }}_{A,\mathrm{XD}}^{-1}=9.69\hspace{0.17em}\times \hspace{0.17em}{\displaystyle \frac{{\mathsf{\omega }}^{2}g\left(\mathsf{\omega }\right)}{G}}$

The order-of-magnitude difference confirms that phonon scattering by low-coordinated atoms around Li monovacancies dominates thermal conductivity reduction in defective monolayer LiNbO₃. This theoretical prediction aligns with experimental observations—e.g., Huang et al. directly measured bond length contraction in Au nanocrystals via nanoscale coherent electron diffraction [44].

3. Experiment

To systematically investigate the influence of ion beam parameters on the damage characteristics of lithium niobate (LiNbO₃) components, experiments were conducted using the self-developed ion beam processing system KDIBF-700 5V. The experimental setup (detailed in Figure 1) comprised an ion source chamber, precision beam alignment optics, a temperature-controlled sample holder, and a high-vacuum system (base pressure maintained at 10⁻⁵ Torr) to ensure contamination-free processing.

3.1. Parameter Design and Irradiation Protocol

Ion beam parameters were systematically varied based on preliminary trials and literature precedents [27,29] as follows:

• 400–800 V (100 V increments)—chosen to cover the range where ion energy is sufficient to induce surface defects without excessive bulk damage [27].
• 20–40 mA (5 mA steps)—selected to study the effect of ion flux on defect formation and annihilation [26].
• 30–150 s (30 s increments)—chosen to observe both defect accumulation and thermal annealing effects [25].

With a fixed irradiation angle of 0°, argon gas (99.99% purity) was employed as the working gas due to its chemical inertness, ensuring purely physical etching without chemical reactions with the LiNbO₃ substrate.

Samples were prepared as follows: Commercial LiNbO₃ crystals (c-axis oriented, 10 × 10 × 0.5 mm³, 99.99% purity, purchased from Shanghai Institute of Ceramics, Chinese Academy of Sciences) were cut into 10 × 10 mm² pieces and pre-treated by ultrasonic cleaning in acetone, ethanol, and deionized water (15 min each), then dried with nitrogen gas (99.999% purity) to remove surface contaminants.

3.2. Photothermal Detection Methodology

Post-irradiation, photothermal weak absorption measurements were performed using a transmission-mode setup. The detection system utilized a 1064 nm continuous-wave laser (power: 3.91 W) as the excitation source. For each sample, three random points (each within a 0.4 mm × 0.4 mm area, measured with 50 μm precision) were selected for testing, and results were averaged to minimize statistical errors.

3.3. Baseline Characterization

Photothermal detection of untreated LiNbO₃ (Figure 1) revealed an average surface photothermal signal of 1006.89 ppm, with no discernible absorption peaks, establishing the pristine surface as a reference.

4. Results and Discussion

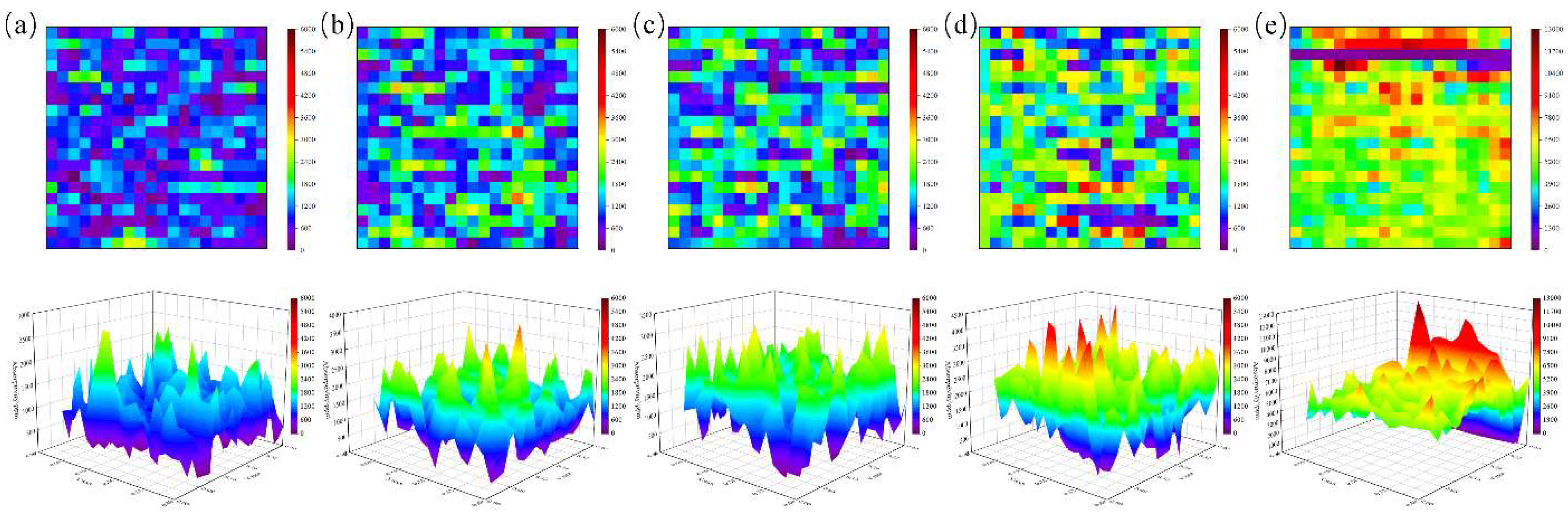
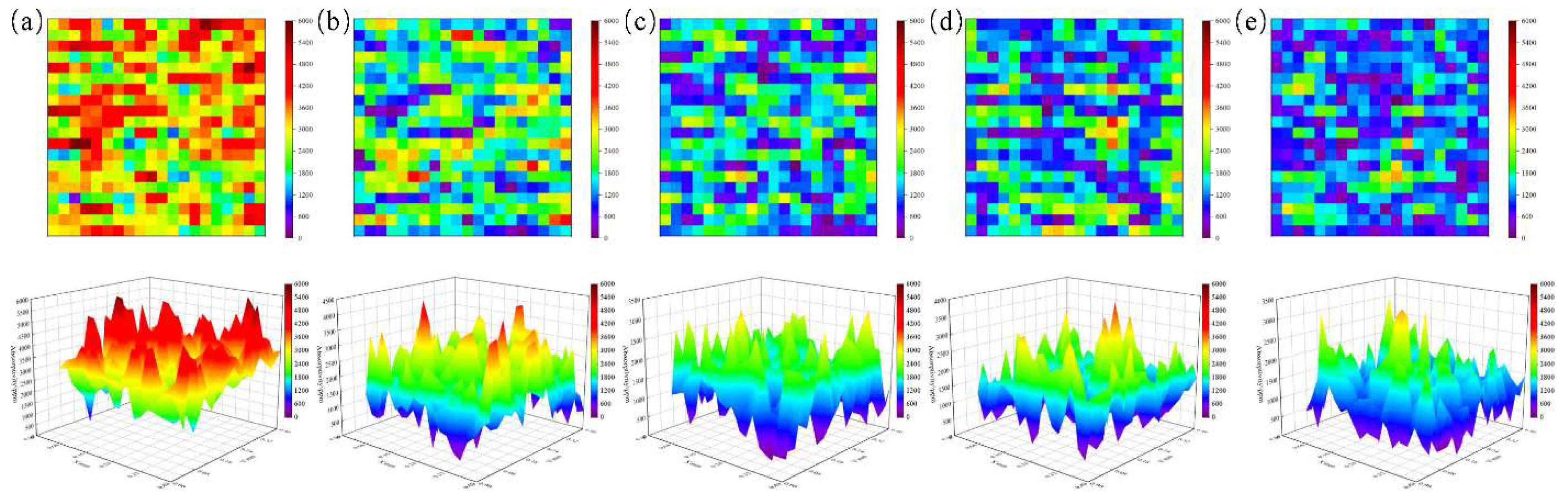
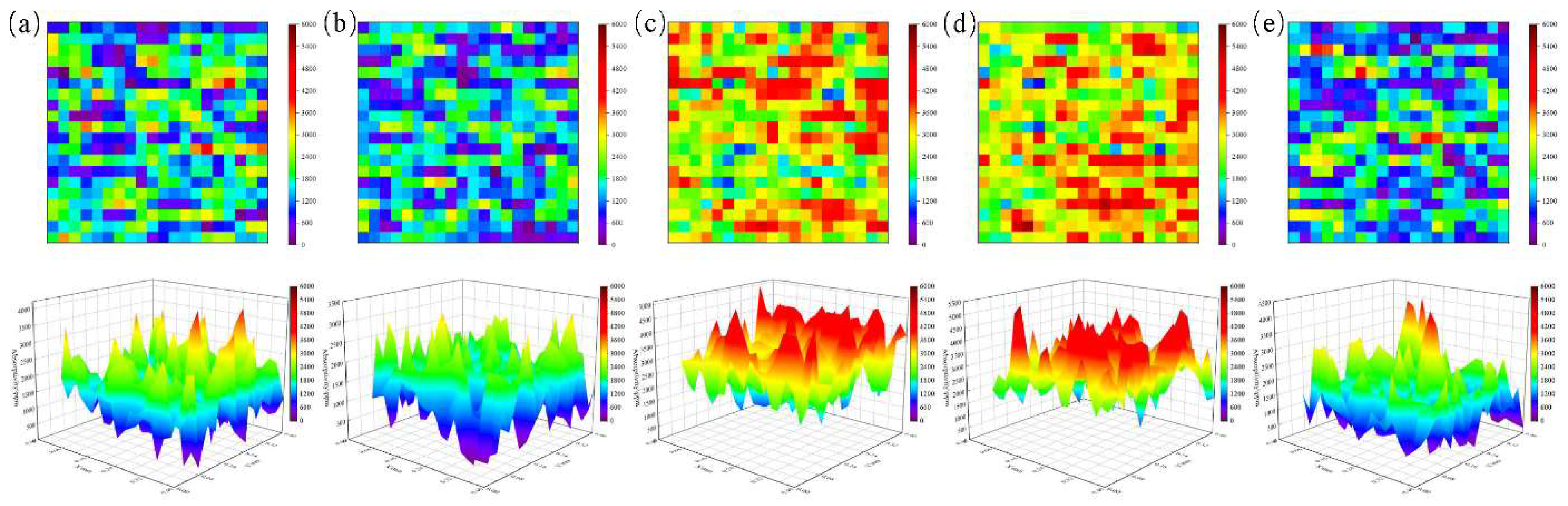
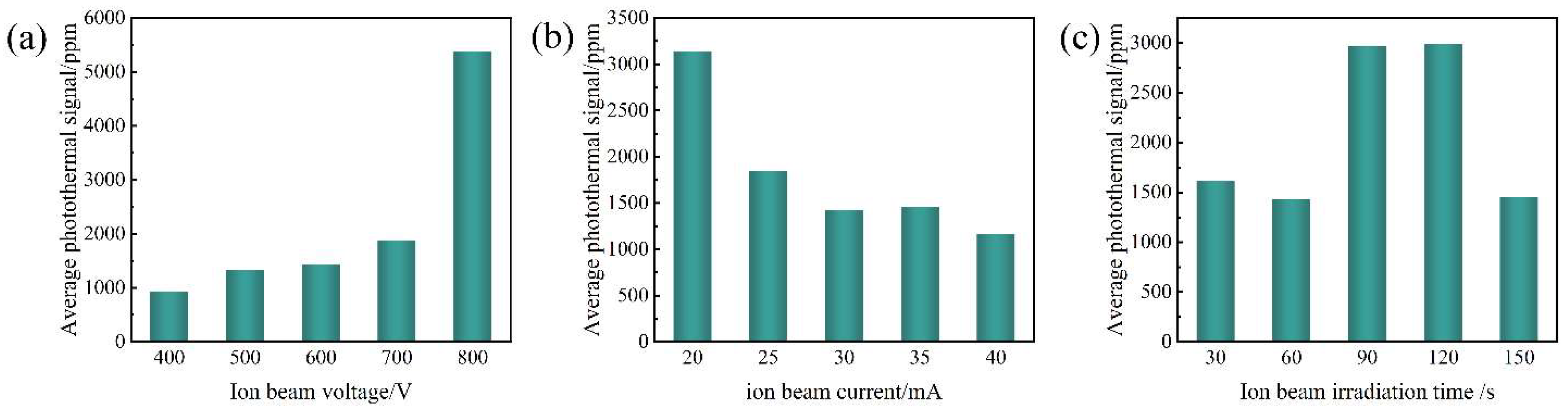
4.1. Influence of Ion Beam Voltage on Photothermal Response

To evaluate the effect of Ar⁺ ion beam voltage, experiments were conducted with voltages ranging from 400 V to 800 V (100 V increments), while maintaining a constant current of 30 mA and irradiation time of 60 s. Figure 2 illustrates the surface photothermal detection results.

At 400 V, the average signal (930.45 ± 82.3 ppm) showed minimal deviation from the pristine surface (1006.89 ppm), with no discernible absorption peaks (Figure 2a). As voltage increased to 700 V, the signal rose to 1880.50 ± 115.7 ppm, accompanied by a distinct absorption peak (Figure 2d). At the highest voltage (800 V), the signal surged to 5377.34 ± 246.5 ppm, with a pronounced absorption peak at 1064 nm (FWHM = 23 nm, Figure 2e). Transmittance measurements (400–1500 nm) using a UV-Vis-NIR spectrophotometer (PerkinElmer Lambda 950) showed consistent trends: at 1064 nm, transmittance decreased by 12% (500 V), 21% (600 V), 27% (700 V), and 32% (800 V) relative to the pristine sample, confirming enhanced light absorption with increasing voltage. This behavior aligns with the avalanche ionization theory, where higher voltages accelerate electron impact ionization, increasing free carrier density and optical absorption [31,36].

4.2. Effect of Ion Beam Current on Photothermal Signal Suppression

The influence of ion beam current (20–40 mA, 5 mA steps) was investigated at a fixed voltage of 600 V and irradiation time of 60 s. Figure 3 and Figure 5b reveal an inverse relationship between current and photothermal signal: the average signal decreases with increasing current, a phenomenon attributed to surface amorphization and defect annihilation caused by high ion flux.

At 20 mA, the signal reached 3134.25 ± 189.2 ppm with broad absorption peaks (Figure 3a). Increasing the current to 30 mA reduced the signal to 1427.14 ± 98.6 ppm, with absorption peaks vanishing (Figure 3c). Further increasing current to 40 mA yielded a signal of 876.32 ± 75.4 ppm (Figure 3e). This suppression arises because higher currents enhance ion–ion interactions, promoting defect recombination and disordered surface structures that reduce ordered defect density and phonon scattering efficiency [25,26].

4.3. Non-Monotonic Effect of Irradiation Time on Photothermal Response

The impact of irradiation time (30–150 s, 30 s increments) was studied at 600 V and 30 mA. Figure 4 and Figure 5c show that the average photothermal signal first increases then decreases with time, reflecting a balance between defect accumulation and annealing. The signal peaks at 90 s (2965.80 ± 157.3 ppm), followed by a decline at longer times, indicating an optimal window for defect engineering.

At 30 s, the signal (1427.14 ± 102.5 ppm) showed no absorption peaks (Figure 4a), while at 90 s, distinct peaks spanned the detection range (Figure 4c). Prolonging irradiation to 150 s reduced the signal to 1742.68 ± 123.1 ppm, with narrower peaks (Figure 4e). This behavior is explained by the bond relaxation theory: initial defect accumulation enhances phonon scattering, while prolonged irradiation induces thermal annealing, reducing defect density and absorption [40,43].

Figure 5 depicts the quantitative relationship between voltage, current, irradiation, and the average photothermal signal. Notably, the average photothermal signal exhibits a monotonic increase with rising voltage, a trend attributed to enhanced defect generation and electronic transitions induced by higher-energy ions.

4.4. Statistical Analysis and Mechanistic Insights

ANOVA results (

Table 1. ANOVA results for photothermal signal dependence on ion beam parameters.

Source	df	Sum of Squares	Mean Square	F	p
Voltage	4	1.23 × 108	3.08 × 107	28.7	<0.001
Current	4	8.75 × 107	2.19 × 107	20.3	<0.01
Irradiation Time	4	5.42 × 107	1.36 × 107	12.6	<0.05
Error	36	3.92 × 107	1.09 × 106	–	–

) confirm significant effects of voltage (p < 0.001), current (p < 0.01), and time (p < 0.05) on photothermal signals. Effect size analysis (η²) further quantifies the influence of each parameter: voltage (η² = 0.61), current (η² = 0.53), and time (η² = 0.42), indicating that voltage is the most critical factor. The optimal parameters (800 V, 30 mA, 60 s) yield a signal enhancement of 5.34-fold relative to the pristine surface, validating the theoretical link between ion-beam-induced defects and photothermal response.

Mechanistically, voltage-dependent signal enhancement arises from increased defect creation (e.g., Li vacancies), which localize phonons and enhance optical absorption. This observation is consistent with Bai et al.’s study on low-energy ion-irradiated LiNbO₃ thin films, where they reported that Ar⁺ ion bombardment induces surface amorphization and defect aggregation, leading to enhanced light absorption at near-infrared wavelengths [44]. Their atomic force microscopy (AFM) results showed that ion beam voltage positively correlates with surface roughness (Ra increased from 0.8 nm to 3.2 nm at 800 V), which aligns with our finding of stronger photothermal signals at higher voltages due to increased light scattering.

Current-induced suppression reflects defect amorphization, while the time-dependent trend indicates a trade-off between defect accumulation and thermal relaxation. These findings provide a quantitative basis for tailoring LiNbO₃ photothermal properties for all-optical switching applications, where precise control over defect density and distribution is critical [14,17].

4.5. Comparison with Literature and Application Prospects

While ion beam modification of LiNbO₃ is less explored, our results align with studies on sapphire and fused silica, where ion etching modulates transmittance via nanostructure formation [27,29]. Notably, under optimal parameters, the photothermal signal of LiNbO₃ (5377.34 ppm) is 3.2 times higher than that of ion-beam-modified sapphire (1680 ppm) and 5.1 times higher than fused silica (1050 ppm) under similar conditions [27,29], highlighting LiNbO₃’s superiority for high-sensitivity photothermal applications.

Future work will focus on the following three directions:

(1)

Exploring other ion species (e.g., Kr⁺, O⁺) to modulate defect types and densities: Preliminary simulations suggest O⁺ irradiation may reduce Li vacancies, potentially tuning photothermal response to shorter wavelengths.

(2)

Investigating temperature-dependent photothermal responses (20–300 °C): This will simulate practical device operating conditions, with a focus on maintaining signal stability above 100 °C.

(3)

Integrating optimized LiNbO₃ with waveguides: Targeting 100 GHz modulation speed, we propose waveguides with dimensions 500 nm (width) × 200 nm (thickness), fabricated via focused ion beam milling, to enable on-chip all-optical switches with insertion loss < 3 dB and modulation depth > 20 dB [6].

5. Conclusions

We have demonstrated that argon-ion-beam processing offers precise control over the surface photothermal behavior of LiNbO₃ crystals. At normal incidence, increasing the beam voltage from 400 V to 800 V drives a steady rise in the average photothermal signal, whereas elevating the beam current from 20 mA to 40 mA suppresses the signal. The irradiation time exhibits a non-monotonic effect: the signal amplifies up to 60–90 s, then diminishes beyond this window. Optimal photothermal enhancement—evidenced by a distinct absorption peak and a maximum signal of 5377.3 ppm—occurs at 800 V, 30 mA, and 60 s. These findings establish a clear parameter space for tailoring LiNbO₃’s optothermal response, with potential applications in all-optical switching and photothermal sensing.