Abstract
The suppression of Rayleigh backscattering noise in a resonant fiber optic gyro (RFOG) is accompanied by the emergence of residual amplitude modulation (RAM) effects, which impact the bias performance of the RFOG output. In this paper, we propose a double demodulation technique that integrates reciprocal modulation and RAM feedback. By utilizing reciprocal modulation–demodulation along with a RAM feedback control method, we effectively suppress both RAM and laser frequency noise. Furthermore, the inherent suppression characteristics of the double modulation–demodulation scheme facilitate effective backscatter noise reduction. As a result, the gyro angular random walk of the RFOG has improved to , and the long-term bias instability has been enhanced to 0.1°/h over a test duration of 10 h.
1. Introduction
The fiber optic gyroscope is an inertial angular rate sensor that operates based on the Sagnac effect. Current configurations of fiber optic gyroscopes are categorized into two main types: interferometric fiber optic gyroscopes (IFOGs) and resonant fiber optic gyroscopes (RFOGs) [1]. The key distinction between these two types lies in the use of a fiber ring resonator in the RFOGs, which enhances the Sagnac effect. This amplification enables the RFOGs to achieve measurement accuracy comparable to that of the IFOG while utilizing a shorter optical path [2,3,4], thus offering significant advantages in terms of size and weight reduction. As a result, RFOG technology has found widespread application in various engineering and technology fields. For example, Geng et al. enhanced the measurement sensitivity of RFOG, making it suitable for high-precision measurement environments [5]. Li et al. implemented RFOG technology in the field of inertial navigation, particularly in miniature unmanned aerial vehicles [6]. Furthermore, Sanders et al. successfully applied the improved hollow optical fiber technology in civil navigation [7]. Additionally, Li W et al. pioneered the integration of an all-polymer photonic wearable device for the assessment and identification of cardiorespiratory functions, thereby providing a novel direction for personalized medicine and chronic disease management [8].
The Resonant Fiber Optic Gyro (RFOG) can be categorized into two types based on the driving light sources employed: broadband source-driven RFOG and narrow-linewidth laser-driven RFOG [9,10]. The narrow-linewidth laser driving method is widely utilized in RFOG due to the unique monochromatic properties of lasers and their associated theoretical accuracy [11,12]; however, in practical applications, the performance of RFOG does not significantly surpass that of IFOG. This is primarily attributed to several factors influencing the accuracy of angular velocity measurements in RFOG, including the nonlinear Kerr effect, laser frequency noise, and Rayleigh backscattering noise. In recent years, numerous experts and scholars have made significant strides in enhancing the performance of RFOGs. Wu et al. employed a four-frequency sawtooth wave modulation technique to suppress optical noise, thereby improving the output performance of RFOG [13]. Liu et al. detected half-wave voltage fluctuations by applying an additional sawtooth modulation signal and established a dual-closed-loop control scheme to reduce the scale factor error in RFOG [14]. Wang et al. improved gyro bias performance by utilizing fibers with dual 90° polarization axis rotation joints within the resonator [15]. Suo et al. designed a dual-closed-loop resonant fiber gyroscope using a high-performance Kagome hollow photonic crystal fiber resonator, which enhanced the random walk coefficient performance metrics of RFOG output [16]. Zou et al. analyzed the resonance splitting phenomenon under sinusoidal modulation and proposed a sideband frequency locking scheme to improve the accuracy of RFOG output [17]. In addition, Hu et al. demonstrated the superiority of the fiber ring resonator (FRR) scheme by analyzing the sensitivity performance of RFOG driven by a broadband light source [18]. Xu et al. enhanced the angular random walk performance of RFOG for the first time by actively canceling the relative intensity noise (RIN) of a broadband light source through the innovative design of the optical path [19]. Shen et al. achieved miniaturization of high-performance RFOG by integrating key devices monolithically using optical integration technology [20].
Rayleigh backscattering noise is the primary source of RFOGs [21]. Currently, a carrier suppression separation phase modulation technique is employed to modulate and demodulate at different frequencies, aiming to eliminate Rayleigh backscattering noise [22,23]. However, the phase modulator introduces residual amplitude modulation (RAM) during the modulation process. The clockwise (CW) and counterclockwise (CCW) light entering the fiber ring resonator (FRR) is modulated and demodulated by different phase modulators (PMs), resulting in parasitic RAM that cannot be eliminated during subsequent frequency locking. This ultimately impacts the bias performance of the RFOG [24,25]. Additionally, when using semiconductor lasers, the white-noise linewidth is larger than other types of lasers, further deteriorating the performance of the RFOG [26].
RAM refers to the phenomenon in which the intensity of light output from the PM varies at the same frequency as the modulating signal. Research has shown that RAM is demodulated alongside the angular velocity signal, resulting in bias errors in the RFOG [27]. Descamps et al. elucidate the fundamental principles underlying RAM-induced output bias errors in RFOGs, analyze the modulated signal output under non-ideal modulation conditions, and propose a feedback loop aimed at mitigating RAM effects [28]. Li et al. proposed a reciprocal modulation–demodulation technology that simultaneously suppresses the RAM effect and Rayleigh backscattering noise effect. Compared to traditional separate modulation and demodulation in RFOG [29], the performance is enhanced by a factor of 15 [24]. However, the issue of suppressing Rayleigh backscattering noise has not been thoroughly addressed, leading to concerns regarding stability. In response to the Rayleigh backscattering noise problem, Lu Liu et al. introduced a single laser reciprocal modulation combined with a double demodulation technical solution, which effectively mitigates backscatter noise and provides long-term bias stability for RFOG [30]. Nonetheless, this double demodulation solution inadvertently amplifies the RAM effect deviation.
In response to the observed phenomena in the RFOG system, this article proposes and validates a novel double-demodulation scheme that integrates reciprocal modulation of a single laser source with RAM feedback. First, the fundamental principle of suppressing backscatter noise and the RAM effect of this RFOG solution is introduced. Second, various simulation models are established to compare and validate the performance of this technical solution. Finally, the product is subjected to a long-term test at room temperature for 10 h. The gyro angular random walk is measured to be better than . Furthermore, compared with the conventional reciprocal-modulation double-demodulation scheme, the long-term bias instability improves from 0.2°/h to 0.1°/h.
2. Separation Modulation–Demodulation Principle
As shown in Figure 1, the configuration diagram of the separate modulation and demodulation RFOG is presented. The laser output light wave is frequency-shifted by an acousto-optic modulator (AOM) and subsequently divided into two beams through a 3 dB coupler. These beams are modulated at frequencies and by PM1 and PM2, respectively, and enter the FRR, forming light waves in both clockwise (CW) and counterclockwise (CCW) directions. The CW light wave is detected by the photodetector PD2. After passing through the lock-in amplifier (LIA) operating at frequency , the signal is fed back to the AOM via a proportional-integral (PI) controller. This feedback mechanism adjusts the laser frequency to lock it to the resonant frequency of the FRR. Simultaneously, photodetector (PD1) detects the CCW beam, and after processing through the lock-in amplifier operating at frequency , it provides the angular velocity signal. This approach effectively suppresses Rayleigh backscattering noise.
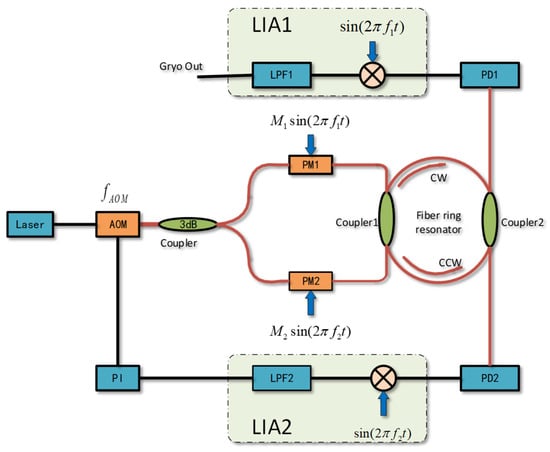
Figure 1.
Configuration of the separate modulation–demodulation of RFOG.
3. Double Demodulation with Reciprocal Modulation and RAM Feedback
Phase modulators mostly use electro-optic phase modulators based on lithium niobate (LiNbO3) crystals, which inherently exhibit the RAM effect during signal modulation [24]. As illustrated in Figure 1, upon frequency locking of the RFOG system, the demodulation output from the lock-in amplifier is proportional to the difference between the resonant frequencies. Consequently, the outputs of LIA1 and LIA2 are computed as presented in Equation (1) [24].
where is the laser frequency, and denote the resonant frequency of the FRR in the CW and CCW direction, and indicate the slope of the demodulation curve in the CW and CCW direction, and are the laser frequency noise in the CW and CCW directions, and is the output noise caused by the phase modulators PM1 and PM2. When the laser frequency is locked at the FRR resonant frequency in the CW direction, the demodulation output is ideally zero. Therefore, the CW direction beam exhibits the following relationship:
Based on the relationship between Equations (1) and (2), the demodulation voltage output in the CCW direction can be derived as presented in Equation (3).
Equation (3) demonstrates that the voltage output related to angular velocity contains noise signals in addition to the Sagnac effect, as indicated by the presence of the second and third terms. Under the influence of Rayleigh backscattering noise in the FRR, the demodulation slopes in the CW and CCW beam directions differ. Different phase modulation and demodulation schemes result in distinct RAM effects for CW and CCW beams, which cannot be eliminated even in a frequency-locked state. The difference in modulation and demodulation frequencies leads to variations in laser frequency noise in both the CW and CCW directions, which collectively influence the performance level of the gyroscope output.
In response to the aforementioned issues, we propose a double-demodulation scheme incorporating reciprocal modulation and RAM feedback. The configuration of the RFOG is illustrated in Figure 2. The laser beam is first frequency-shifted by an AOM and then phase-modulated at frequency by PM0. The beam is then split into two light waves using a 3 dB coupler. One wave beam passes through PM1 and PM3, and it is modulated twice with frequency and . Subsequently, the light enters the FRR, forming the CCW direction beam. The other wave is successively phase-modulated at frequencies at frequency and by PM2 and PM4 before entering the FRR to create a CW direction beam. The CW direction beam coming out of the FRR is detected by PD2 and passes through the lock-in amplifier LIA4. On the one hand, the signal is processed by the lock-in amplifier LIA5 with a frequency of and a phase of . After PID control, the system applies RAM feedback compensation for PM0 is achieved. On the other hand, the signal is demodulated using a frequency of and subsequently filtered by LPF2. The signal then passes through a PI controller, effectively locking the resonant frequency. PD1 detects the CCW direction beam emitted from the FRR. After passing through LIA3 and LIA1, the angular rate signal is extracted.

Figure 2.
Double demodulation with reciprocal modulation and RAM feedback.
The double-demodulation scheme, incorporating reciprocal modulation and RAM dual feedback, demonstrates a robust capability to suppress laser frequency noise, backscatter noise, and the RAM effect. The carrier suppression and double modulation and demodulation scheme, comprising PM1, PM2, PM3, PM4, LIA3, and LIA4, effectively suppresses Rayleigh backscattering noise within the FRR and enhances the long-term bias instability of the RFOG. Additionally, the RAM closed-loop control scheme, composed of PM0, PID module, and LIA5 module, suppresses the RAM noise of the main phase modulator. Finally, reciprocal modulation technology is integrated, consisting of the PM0, a PI module, and LIA2 module. By employing reciprocal signal processing, laser frequency noise is mitigated, and the RAM effect is further suppressed, thereby enhancing the gyro output bias performance.
3.1. Double Modulation–Demodulation Technology
According to the RFOG configuration scheme illustrated in Figure 2, the output optical electric field of the laser is expressed as shown in Equation (4).
where represents the light wave amplitude, is the center frequency of the laser. In the configuration diagram presented in Figure 2, PM1 and PM2 represent non-demodulated phase modulation signals. A carrier suppression scheme is implemented to mitigate the Rayleigh backscattering noise from the resonant cavity; thus, this process is excluded from the overall modulation and demodulation analysis. Disregarding the insertion loss of the phase modulator and coupler, the expression for the light field entering the FRR in the CW direction is provided in Equation (5).
where is the offset frequency of the acousto-optic modulator, and are the modulation index and frequency of PM0 and PM2, respectively, refers to the first kind of Bessel function with the order. The transfer function of the FRR resonant cavity is shown in Equation (6) [30]
For the present analysis, the impact of Rayleigh backscattering noise, represented by the second term in Equation (6), is not taken into account. Equation (7) delineates the transfer function of the FRR resonant cavity.
The voltage of the CW beam at detector PD2 is expressed in Equation (8).
where represents the photoelectric conversion factor of PD2, is the light velocity in vacuum and is the electric permittivity of the vacuum, and represent the other orders of modulation sidebands.
The output voltage of PD2 is demodulated at frequencies of and , with the resulting output voltage sent to the PI proportional and integral amplifier as described in Equation (9). The purpose of the second modulation is to reconstruct the FRR resonance curve; thus, we have , is the free spectral range of the FRR.
where are the phase components of the phase modulators PM1 and PM4.
The demodulated output curve in the simulation state is shown in Figure 2. In this simulation, the diameter of the FRR resonant cavity is set to 72 mm, the length is 125 m, and the precision is 25.8. The modulation parameters of the phase modulator are , , and . When frequency locking and RAM feedback are disabled, the demodulated voltage signals produced by amplifier LIA1 and amplifier LIA2 are illustrated in Figure 3. In the linear region of frequency deviation, completes the measurement output for angular velocity.

Figure 3.
Ideal demodulation output curve.
In practical engineering applications, the second term of Rayleigh backscattering noise in Equation (6) is significant and cannot be disregarded. To simplify the model’s calculation parameters, the effects of and are omitted. The voltage of the CW light wave at PD1 is shown in Equation (10).
In Equation (10), a phase difference exists between the voltage component of the primary light wave and that of the Rayleigh backscattering noise. Consequently, phase modulation and demodulation techniques operating at distinct frequencies are employed to effectively suppress the Rayleigh backscattering noise.
As depicted in Figure 4, a double modulation and demodulation simulation model was established both with and without backscatter noise. The resulting comparison diagrams for the PD1 output voltage and the demodulation output voltage are presented in Figure 4. According to Figure 4a, the voltage of Rayleigh backscattering noise at the PD1 terminal measures 0.185 V. Following the implementation of double modulation technology, the output voltage difference at the PD1 terminal, with and without Rayleigh backscattering noise, is 0.03 V, demonstrating effective suppression of Rayleigh backscattering noise. Figure 4b illustrates a comparison of the demodulated voltage output. The frequency deviation, when accounting for Rayleigh backscattering noise, is approximately 60 Hz. In contrast, the reciprocal modulation–demodulation method exhibits a deviation of 510 Hz, indicating an improvement in performance by more than seven times.

Figure 4.
Comparison of output with and without backscatter noise: (a) shows the photodetector output curve; (b) shows the demodulated output curve.
3.2. RAM Feedback Closed-Loop Control Technology
Experiments studies have demonstrated that the process of laser light ratio phase modulation is accompanied by the RAM effect. Consequently, the output light field of the laser signal, after passing through PM0, can be simplified to a signal containing primarily sinusoidal energy fluctuations, as illustrated in Equation (11).
In the formula, the second term represents the deviation effect induced by the RAM effect. Disregarding the initial phase of the modulator, the electrical signal following its passage through the amplifier LIA4 is illustrated in Equation (12)
Due to the minimal phase deviation induced by FRR, Equation (12) has been simplified and restructured into Equation (13).
where is the demodulation voltage amplitude.
The frequency of the demodulated signal is , with an initial phase of . Considering that the demodulated signal incorporates a component with a frequency of , the design of the low-pass filter bandwidth should be more than an order of magnitude lower than . The voltage output after passing through the low-pass filter is presented in Equation (14).
As indicated by Equation (14), the RAM error signal can be measured with high accuracy, and the RAM effect can be effectively suppressed using the PID controller.
Figure 5 illustrates the comparison between the demodulated signal and the normalized optical power in RAM feedback control. In Figure 5a, the green curve depicts the normalized optical power, while the blue curve shows the demodulated output of a quadrature signal with a frequency of . The slope of the blue curve corresponds proportionally to the peak value of fluctuations in the normalized optical power. Figure 5b demonstrates that the RAM feedback control method significantly reduces the normalized optical power peak deviation from approximately 0.2 to 0.035, thus effectively mitigating the RAM effect phenomenon.
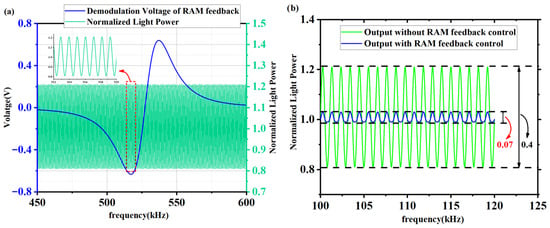
Figure 5.
Phase modulator intensity curve under RAM feedback control. (a) Comparison curve between RAM demodulation and normalized light power. (b) Normalized light power with or without RAM feedback control.
3.3. Reciprocal Modulation–Demodulation Technology
Given that the RAM effect cannot be entirely suppressed through RAM feedback control in practice [26], and considering the presence of laser frequency noise in the RFOG system, we propose a method that integrates reciprocal modulation–demodulation signal processing with RAM feedback control and double-demodulation scheme.
As demonstrated in Equation (3), the error term in the output voltage of the RFOG encompasses deviations due to the RAM effect, laser frequency noise, and demodulation slope deviations resulting from backscatter noise. In the absence of backscatter noise, the demodulation slopes in both the CW and CCW directions are consistent, allowing Equation (3) to be simplified as follows:
As demonstrated in Equation (15), the error component of the RFOG output voltage encompasses deviations due to laser frequency noise and RAM effects. When utilizing identical modulation and demodulation frequencies, the consistency of output errors arising from laser frequency noise and RAM effects in both the CW and CCW directions can be significantly ensured, as illustrated below.
The output voltage of the RFOG is determined by the results of Equations (15) and (16). Consequently, the output voltage information is derived as follows:
In summary, the intermodulation demodulation scheme effectively suppresses laser frequency noise and the RAM effect in the RFOG, thereby enhancing the bias performance of the gyro output.
4. Experiments
This section evaluates the performance of the double demodulation configuration scheme, which combines reciprocal modulation and RAM feedback, through experimental methods. Initially, digital simulations were conducted to assess various configuration schemes of the RFOG and to compare their performance differences. Subsequently, a test environment was established based on the RFOG configuration scheme illustrated in Figure 2, facilitating long-term testing of the bias characteristics of the RFOG.
4.1. Configuration Scheme Performance Comparison Simulation
Based on the RFOG configuration scheme illustrated in Figure 2, we examine the effects of narrow linewidth laser frequency noise, a constant RAM coefficient, and FRR backscatter noise. We conduct comparative simulation verifications of the proposed technical solutions, establishing separate modulation–demodulation technology, RAM feedback technology, reciprocal modulation–demodulation technology, reciprocal modulation with RAM feedback technology, reciprocal modulation with double-demodulation scheme, and double-demodulation scheme utilizing reciprocal modulation and RAM feedback to compare the performance of gyro bias.
- (1)
- Simulation base model
In the simulation model, we consider the same broadband laser source and FRR as utilized in the experiments. The operating wavelength of the laser is 1550 nm, with a linewidth of 3 kHz. The diameter of the FRR is 72 mm, and its length is 125 m, resulting in a fineness of 25.8. The backscattering coefficient is 60 dB. The simulation results of the system’s resonance curve are illustrated in Figure 6. These results indicate that the FSR of the system is approximately 1.66 MHz. The spectral full width at half maximum (FWHM) is measured at 63.4 Hz.

Figure 6.
Simulation results of the resonance curve.
Based on the sweep characteristics illustrated in Figure 6, the design of the signal processing module was conducted. The modulation frequencies for PM3 and PM4 are strategically set near (FSR/2) Hz to maximize the demodulation slope while minimizing the angular random walk coefficient (ARW) and avoiding integer multiplicity frequency aliasing. Considering engineering feasibility, the modulation frequencies for PM3 and PM4 have been established at 827 kHz and 827.15 kHz, respectively. Additionally, the modulation frequency for PM0 is set at 19 kHz, while the modulation frequencies for the carrier suppression phase modulators PM1 and PM2 are 200 Hz and 280 Hz.
- (2)
- Simulation Noise Parameter Settings
The noise settings for the simulation model are detailed as follows:
- (a)
- The relative intensity noise (RIN) of the output optical power from the broadband light source is configured to −135 dBc/Hz. The presence of RIN significantly impacts the normalized intensity of the FRR output in RFOGs. The mathematical modeling equation is presented as follows:where is the normalized intensity noise due to RIN and is the free spectral width.
- (b)
- The residual amplitude modulation (RAM) in the phase modulator is established at −30 dB. The presence of RAM introduces a parasitic amplitude modulation component in the phase modulator signal, which can be mathematically represented by the following equation:where is the modulation frequency.
- (c)
- The Rayleigh backscattering noise (RBN) in the ring fiber optic gyroscope (RFOG) is set to 0.3 dB/km. The presence of RBN leads to the emergence of the corresponding intensity of Rayleigh backscattering noise light, as represented by the mathematical formula provided below.where I is the input light intensity, and L is the fiber length.
In accordance with the aforementioned conditions, we conducted simulation verification of various technical solutions to assess the bias zero point and noise variance of the gyroscope output. The simulation duration was three hours, and the results are presented in Figure 7.

Figure 7.
Comparison of simulation output performance under different RFOG technology schemes: (a) illustrates the comparison of gyro zero position under different technology schemes; (b) shows the comparison of noise variance under different technology schemes.
Figure 7 presents a comparative analysis of the gyroscope output performance characteristics across various configuration schemes. The results depicted in the figure allow for the following conclusions to be drawn.
- (1)
- Figure 7a presents a comparison of the bias zero point of various RFOG technical solutions based on simulation results. Among these solutions, the separate modulation and demodulation approach exhibits the largest bias zero point. Both reciprocal modulation–demodulation technology and RAM feedback technology enhance the gyroscope bias zero-point performance to a certain extent. Notably, the reciprocal modulation and RAM feedback dual demodulation technology employed in this paper demonstrates the smallest bias zero-point position, thereby achieving a significant performance improvement.
- (2)
- Figure 7b presents a comparison of the noise standard deviation across various RFOG technical solutions. Notably, the gyro output noise of the separate modulation and demodulation solution is the highest, which poses challenges for its implementation in engineering applications. In contrast, reciprocal modulation–demodulation technology demonstrates a significant advantage over RAM feedback technology in processing gyro output noise. This paper employs a dual demodulation solution that integrates reciprocal modulation–demodulation with RAM feedback, resulting in a marked enhancement in gyro output noise performance, optimized to 0.6°/h, thereby offering substantial value for engineering applications.
4.2. Performance Comparison Verification Tests of Existing Methods
To compare the performance differences between the proposed RFOG configuration scheme and the existing scheme, we selected the angle random walk coefficient and zero-bias instability from the gyro performance metrics as evaluation criteria. These metrics are defined as follows:
- (1)
- Gyro angular random walk refers to the process of angular random walk that arises from integrating the white noise component present in the gyro output. This phenomenon is quantified by analyzing the segment of the Allan variance curve that exhibits a slope of −1/2. The angle random walk value is represented by the ordinate value at the moment of 1 in the Allan variance curve, which reflects the short-term noise performance metric of the gyro.
- (2)
- Zero-bias instability refers to the degree of dispersion of a gyroscope’s output around its mean value when the input is zero. It can be calculated by analyzing the minimum point of the Allan variance curve, reflecting the gyroscope’s long-term performance metric.
By comparing the proposed scheme with various techniques, including reciprocal modulation–demodulation phase [21], dual-channel error RAM feedback control [26], single-polarization (SP) fiber ring resonators [27], reciprocal modulation and double demodulation [28], and three-laser high-frequency (HP)/low-frequency (LP) modulation and demodulation [29], we have verified the superior performance of the proposed scheme. Under digital simulation conditions, we conducted a simulation with a sampling frequency of 200 Hz over a duration of 5 h, performing Allan variance analysis on the output signals of the gyroscope across different schemes. The results are illustrated in Figure 8.

Figure 8.
Allan variance analysis results of gyroscope output signal under different schemes.
According to the simulation test results in Figure 7, it can be seen that the RFOG configuration scheme proposed in this paper has better performance. Based on the Allan variance results in the figure, the angle random walk and zero bias instability of the gyro output signal are quantified and statistically analyzed, as shown in Table 1.

Table 1.
Angular random walks and zero-bias instability under different technical solutions.
Based on the experimental results presented in Figure 7 and Table 1, the following conclusions can be drawn:
- (1)
- The angular random walk coefficients exhibit significant performance improvements when employing reciprocal modulation and RAM feedback control. While the three-laser HP/LP modulation and demodulation also demonstrates considerable enhancements, it introduces considerable complexity into the system and poses challenges in eliminating laser interference. Consequently, this paper adopts a single-laser light source design that integrates reciprocal demodulation technology with RAM feedback control schemes based on double-demodulation schemes, resulting in enhanced performance of the angular random walk coefficients.
- (2)
- In terms of zero-bias instability, the dual-channel error RAM feedback control scheme significantly enhances zero-bias instability; however, it exhibits suboptimal performance regarding random walk coefficient metrics. The double demodulation control method, when integrated with reciprocal demodulation technology, improves gyroscope output performance, yet it still does not match the efficacy of the three-laser HP/LP modulation and demodulation scheme. This paper demonstrates a substantial enhancement in the output performance of the single-laser light source gyroscope through the optimized design of reciprocal demodulation technology, RAM feedback, and double-demodulation scheme, achieving performance levels that surpass those of the three-laser HP/LP modulation and demodulation scheme.
4.3. Product Performance Testing
In practical engineering applications, the bias instability of the reciprocal modulation–demodulation scheme is measured at 0.06°/h over a duration of half an hour [21]. However, as time progresses, low-frequency random noise signals tend to appear in the output [28]. The implementation of a reciprocal modulation combined with a double demodulation configuration significantly enhances long-term bias instability, with the measured bias instability over a 10 h period not exceeding 0.2°/h. Nonetheless, the introduction of the double demodulation further amplifies the RAM effect.
To further demonstrate the superiority of the RFOG scheme proposed in this paper, we established RFOG systems based on various technical schemes according to the parameter criteria of digital simulation. These systems were fixedly mounted on a high-precision rotary table, and data were recorded statically for a duration of 10 h. This setup allows for a comprehensive analysis of the performance of the RFOG systems under different conditions, as illustrated in Figure 9.

Figure 9.
Double demodulation RFOG test results of intermodulation modulation and RAM feedback. (a) Gyro output for more than 10 h of testing. (b) Allan deviation analysis of gyro data collected for more than 10 h.
Based on the product test results presented in Figure 8, the following conclusions can be drawn:
- (1)
- Figure 9a presents the angular velocity outputs of various RFOGs. The proposed scheme exhibits a significant improvement in zero-bias stability and noise performance compared to reciprocal-phase-modulation demodulation and reciprocal modulation with double demodulation. The measured zero-bias offset of the proposed scheme is 1°/h, with a standard deviation of approximately 1.5°/h.
- (2)
- Figure 9b displays the Allan standard deviation. The bias instability of the RFOG scheme proposed in this paper is 0.1°/h over a duration of 10 h, in contrast to the 0.2°/h bias instability observed for the reciprocal modulation and double demodulation RFOG scheme, indicating a 50% reduction in bias instability.
5. Conclusions
In conclusion, this study proposes an RFOG that utilizes a double-demodulation scheme, which incorporates reciprocal modulation and RAM feedback. Experimental results demonstrate its significant inhibitory effect on Rayleigh backscattering noise and RAM-related disturbances. Over a measurement period exceeding 10 h, the performance metrics indicate a gyro output bias zero point of 1° and a bias instability of 0.1°/h. This represents a more than twofold improvement compared to the bias zero point of 2.6°/h achieved by the reciprocal modulation–demodulation technology in RFOG [21]. In comparison to the reciprocal modulation combined with double-demodulation scheme, the long-term bias instability has enhanced from 0.2°/h to 0.1°/h. Considering that both the PID and PI controllers are utilized in this scheme, the design of the controller parameters relies heavily on the alignment between the mathematical model and the actual equipment. This dependency imposes limitations on the application and development of this scheme within the RFOG system, which accounts for the observed variability between the actual product test results and the simulated performance indices. However, the method proposed in this paper simultaneously suppresses laser frequency noise, Rayleigh backscattering noise, and RAM effects, significantly optimizing the gyroscope’s output bias performance, which holds substantial potential for the integrated and miniaturized design of RFOG in engineering applications.
Author Contributions
Conceptualization, Z.Y. and G.C.; methodology, Z.Y. and X.Y.; software, Z.Y. and X.Y.; validation, Z.Y. and X.T.; formal analysis, Z.Y.; investigation, X.Y.; resources, X.Y.; data curation, Z.Y. and X.Y.; writing—original draft preparation, Z.Y.; writing—review and editing, Z.Y.; visualization, Z.Y.; supervision, Z.Y.; project administration, X.T.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of Shanxi (Grant No. 202203021221110).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the privacy of the subjects involved in the study.
Acknowledgments
We thank the reviewers and editors for their insightful comments that helped to improve the quality of the paper a great deal.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Udd, E. An overview of the development of fiber gyros. In Proceedings of the Conference on Optical Waveguide and Laser Sensors, Online, 27 April–8 May 2020; SPIE-International Social Optical Engineering: Bellingham, WA, USA, 2020. [Google Scholar]
- Ma, H.; Zhang, J.; Wang, L.; Jin, Z. Development and Evaluation of Optical Passive Resonant Gyroscopes. J. Light. Technol. 2016, 35, 3546–3554. [Google Scholar] [CrossRef]
- Smiciklas, M.; Sanders, G.; Strandjord, L.; Williams, W.; Benser, E.; Ayotte, S.; Costin, F. Development of a Silicon Photonics-based Light Source for Compact Resonator Fiber Optic Gyroscopes. In Proceedings of the 2nd International Conference on DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 10–11 September 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Silver, J.M.; Del Bino, L.; Woodley, M.T.M.; Ghalanos, G.N.; Svela, A.Ø.; Moroney, N.; Zhang, S.; Grattan, K.T.V.; Del’hAye, P. Nonlinear enhanced microresonator gyroscope. Optica 2021, 8, 1219–1226. [Google Scholar] [CrossRef]
- Geng, J.; Yang, L.; Zhao, S.; Zhang, Y. Resonant micro-optical gyro based on self-injection locking. Opt. Express 2020, 28, 32907–32915. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wen, C.; Feng, C.; Qing, C.; Zhang, D.; Feng, L. Frequency Spectrum Separation Method of Suppressing Backward-Light-Related Errors for Resonant Integrated Optical Gyroscope. J. Light. Technol. 2021, 40, 1188–1194. [Google Scholar] [CrossRef]
- Sanders, G.A.; Taranta, A.A.; Narayanan, C.; Fokoua, E.R.N.; Mousavi, S.M.A.; Strandjord, L.K.; Smiciklas, M.; Bradley, T.D.; Hayes, J.; Jasion, G.T.; et al. Hollow-core resonator fiber optic gyroscope using nodeless anti-resonant fiber. Opt. Lett. 2020, 46, 46–49. [Google Scholar] [CrossRef]
- Li, W.; Long, Y.; Yan, Y.; Xiao, K.; Wang, Z.; Zheng, D.; Leal-Junior, A.; Kumar, S.; Ortega, B.; Marques, C.; et al. Wearable photonic smart wristband for cardiorespiratory function assessment and biometric identification. Opto-Electron. Adv. 2025, 8, 240254-1. [Google Scholar] [CrossRef]
- Hu, J.; Liu, S.; Liu, L.; Ma, H. Closed-Loop Resonant Fiber-Optic Gyroscope with a Broadband Light Source. J. Light. Technol. 2023, 41, 6088–6093. [Google Scholar] [CrossRef]
- Xu, K.; Zhou, Y.; Xue, F.; Wang, Y.; Liu, W.; Tang, J.; Liu, J. Resonant fiber optic gyroscope driven by a broadband light source based on an over-coupled state fiber ring resonator. Appl. Opt. 2024, 63, 4840–4847. [Google Scholar] [CrossRef]
- Liu, S.; Hu, J.; Wang, Y.; Wang, H.; Liu, L.; Ma, H. Improving the Performance of Broadband Source-Driven Resonant Fiber-Optic Gyroscopes. J. Light. Technol. 2024, 42, 6417–6423. [Google Scholar] [CrossRef]
- Ma, H.; Yan, Y.; Wang, L.; Chang, X.; Jin, Z. Laser frequency noise induced error in resonant fiber optic gyro due to an intermodulation effect. Opt. Express 2015, 23, 25474–25486. [Google Scholar] [CrossRef]
- Wu, F.; Li, J.; Lan, S.; Yan, B.; Zhou, J.; Yue, Y. Performance improvement of white-light-driven resonant fiber optic gyroscope using four-frequency sawtooth wave modulation technology. Opt. Commun. 2023, 550, 129827. [Google Scholar] [CrossRef]
- Liu, L.; Liu, S.; Wang, H.; Hu, J.; Li, B.; Ma, H. Improving the Scale Factor Thermal Stability of Resonant Fiber-Optic Gyroscopes by Tracking the Half-Wave Voltage of the Phase Modulator. J. Light. Technol. 2024, 43, 922–930. [Google Scholar] [CrossRef]
- Wang, X.; He, Z.; Hotate, K. Automated suppression of polarization fluctuation in resonator fiber optic gyro with twin 90° polarization-axis rotated splices. J. Light. Technol. 2012, 31, 366–374. [Google Scholar] [CrossRef]
- Suo, X.; Yu, H.; Li, J.; Wu, X. Transmissive resonant fiber-optic gyroscope employing Kagome hollow-core photonic crystal fiber resonator. Opt. Lett. 2020, 45, 2227–2230. [Google Scholar] [CrossRef]
- Zou, K.; Chen, K.; Shen, H.; Gong, Y.; Bi, R.; Shu, X. Research on resonance splitting under sinusoidal modulation in resonant optic fiber gyro. Opt. Laser Technol. 2021, 144, 107459. [Google Scholar] [CrossRef]
- Hu, J.; Li, B.; Liu, S.; Ma, H. Sensitivity analysis and comparison of broadband source-driven resonant fiber-optic gyroscopes. Appl. Opt. 2025, 64, 3974–3979. [Google Scholar] [CrossRef]
- Xu, C.; Yang, L.; Wang, Y.; Chen, Z.; Jin, T.; Zhang, Y. Suppression of RIN in broadband source-driven RFOG using a light intensity fluctuation offset technique. Opt. Commun. 2025, 580, 131588. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L.; Li, M.; Huang, F.; She, X.; Chen, K.; Bi, R.; Wang, L.; Shu, X. Multi-function integrated optic chip for miniaturized resonant fiber optic gyroscope. Opt. Commun. 2025, 583, 131774. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, L.S.; Li, H.; Jiao, H.; Liu, N.; Zhang, C. Resonant fiber optic gyroscope with three-frequency differential detection by sideband locking. Opt. Express 2020, 28, 8423–8435. [Google Scholar] [CrossRef]
- Liu, L.; Liu, S.; Ma, H.; Jin, Z. Evaluation and Measurement of the Lock-in Effect in Resonant Fiber Optic Gyroscopes. J. Light. Technol. 2023, 41, 5754–5762. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Ma, H.; Liang, S.; Feng, H.; Feng, C.; Jiao, H.; Feng, L. Resonant Fiber Optic Gyroscope With HOPLL Technique Based on Acousto-Optic Modulation. J. Light. Technol. 2021, 40, 1238–1244. [Google Scholar] [CrossRef]
- Li, H.; Lin, Y.; Liu, L.; Ma, H.; Jin, Z. Signal processing improvement of passive resonant fiber optic gyroscope using a reciprocal modulation-demodulation technique. Opt. Express 2020, 28, 18103–18111. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Liu, S.; Jin, Z.; Ma, H. Suppressing backscattering noise of a resonant fiber optic gyroscope using coherent detection. Appl. Opt. 2022, 61, 4421–4428. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Ma, H.; Jin, Z. Evaluation and Suppression of the Effect of Laser Frequency Noise on Resonant Fiber Optic Gyroscope. J. Light. Technol. 2021, 40, 2631–2638. [Google Scholar] [CrossRef]
- Wong, N.C.; Hall, J.L. Servo control of amplitude modulation in frequency-modulation spectroscopy: Demonstration of shot-noise-limited detection. J. Opt. Soc. Am. B Opt. Phys. 1985, 2, 1527–1533. [Google Scholar] [CrossRef]
- Descampeaux, M.; Feugnet, G.; Bretenaker, F. New method for residual amplitude modulation control in fibered optical experiments. Opt. Express 2021, 29, 36211–36225. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Ma, H.; Jin, Z. Reducing polarization-fluctuation induced drift in resonant fiber optic gyro by using single-polarization fiber. Opt. Express 2015, 23, 2002–2009. [Google Scholar] [CrossRef]
- Liu, L.; Liu, S.; Hu, J.; Ma, H.; Jin, Z. Resonant fiber optic gyroscope using a reciprocal modulation and double demodulation technique. Opt. Express 2022, 30, 12192–12203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).