Speckle-Correlation Holographic Imaging: Advances, Techniques, and Current Challenges
Abstract
1. Introduction
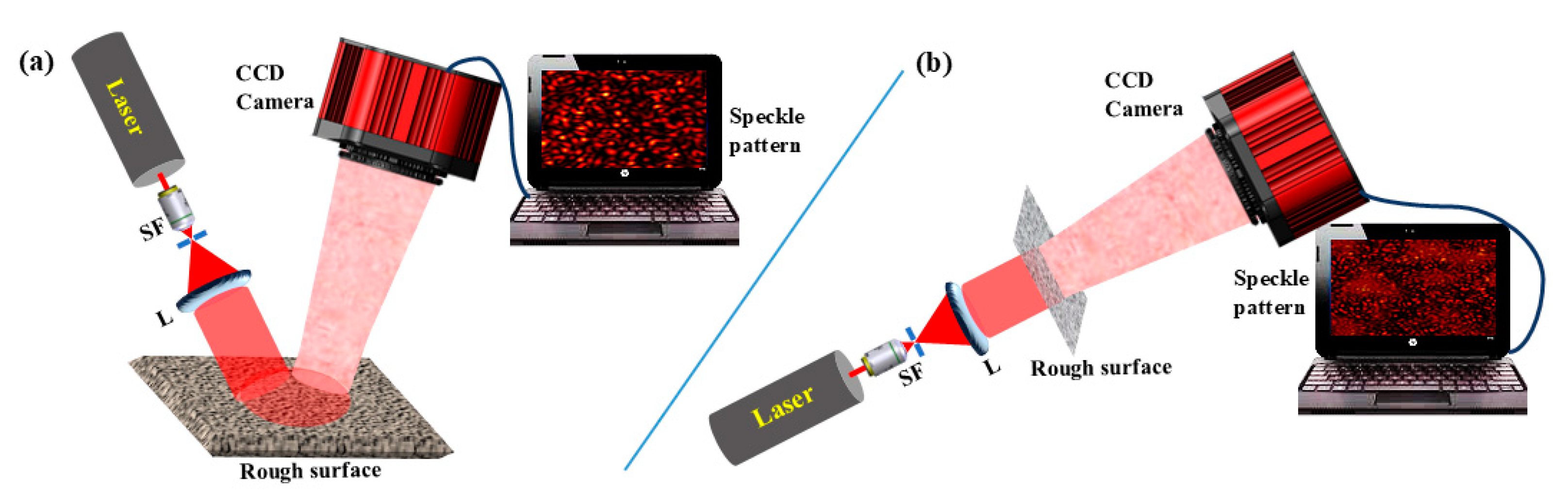
2. Laser Speckles
2.1. Origin of Speckles
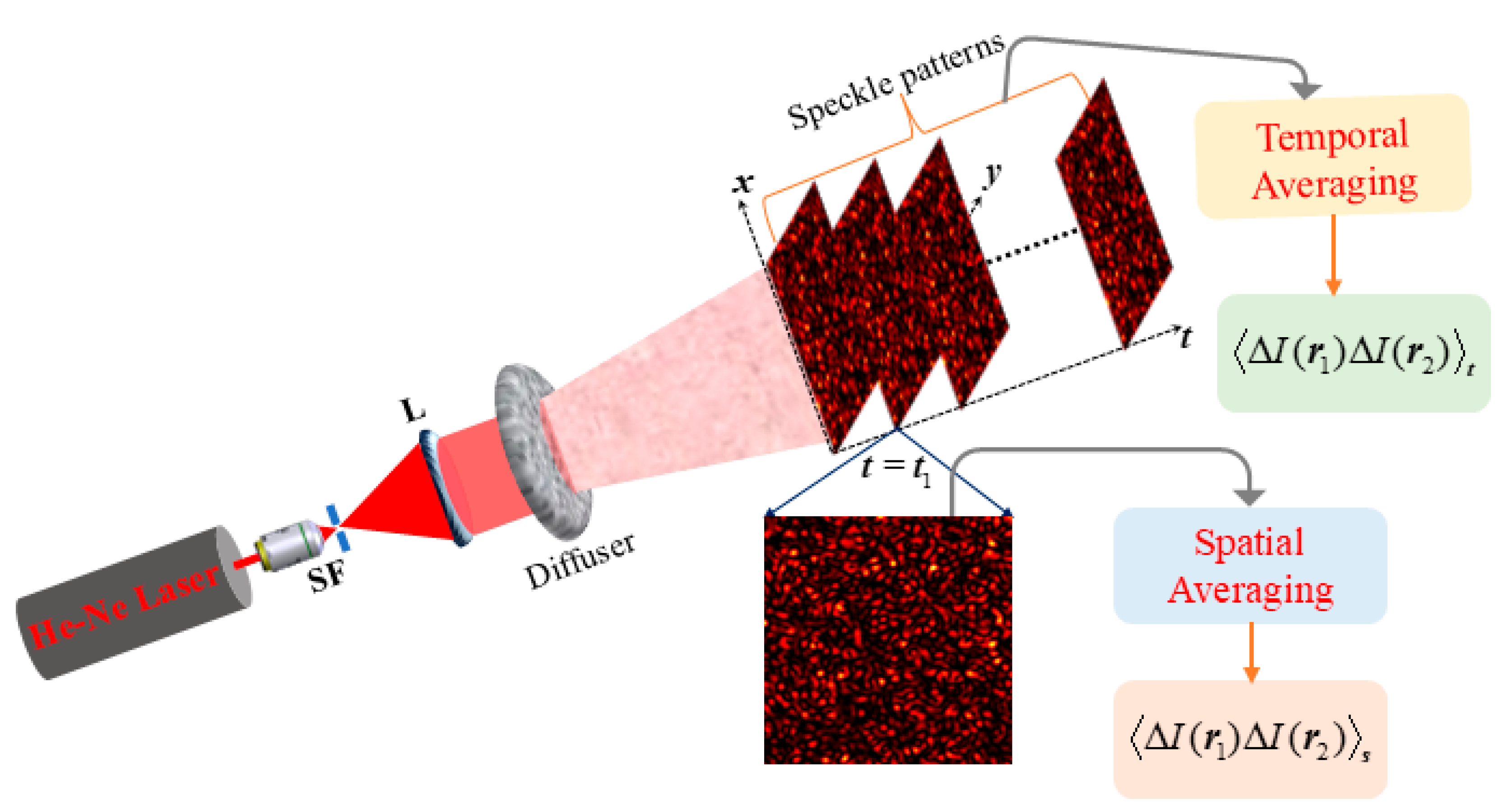
2.2. Speckle Correlation
2.3. Snapshot Speckle Correlation
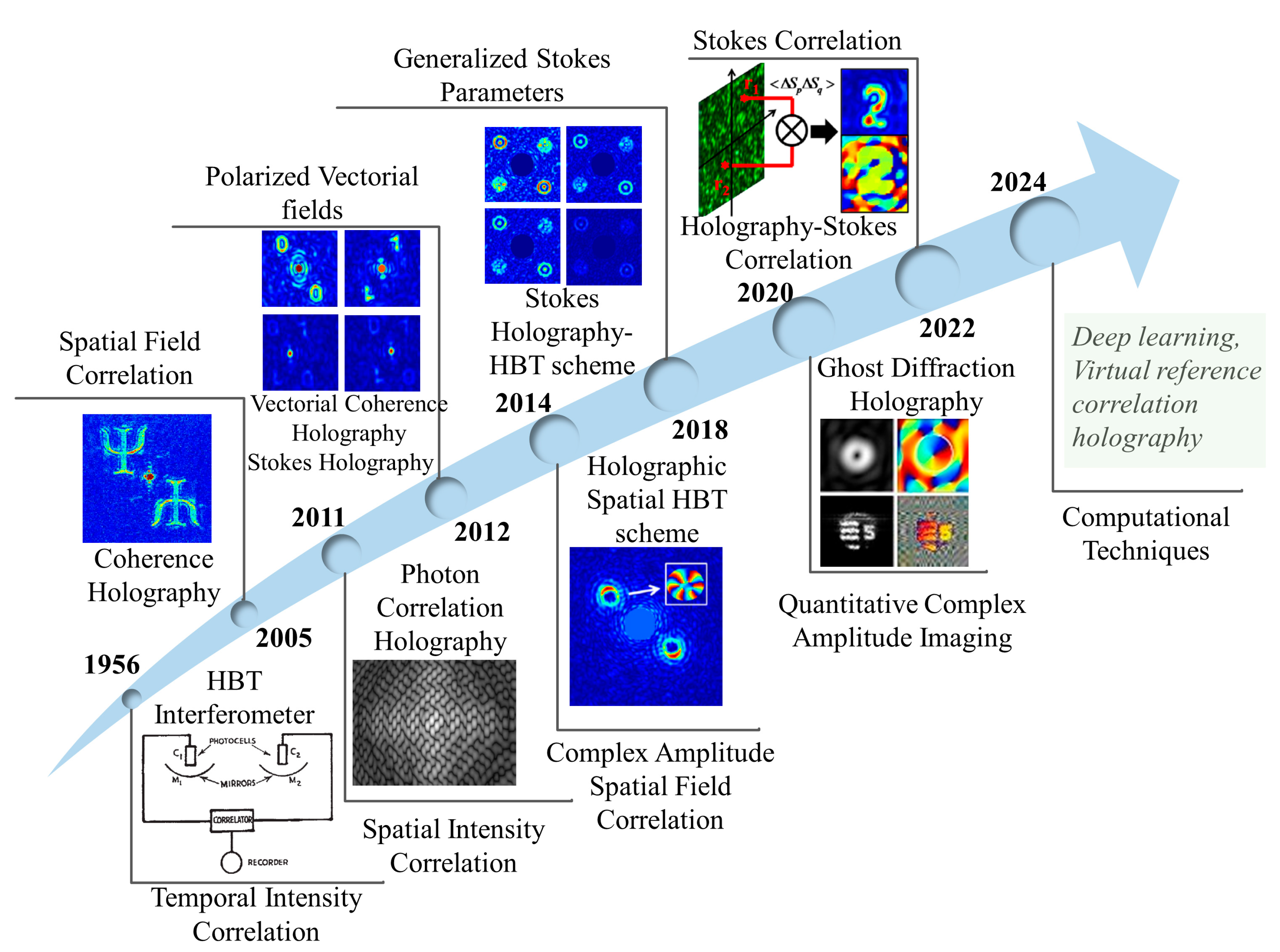
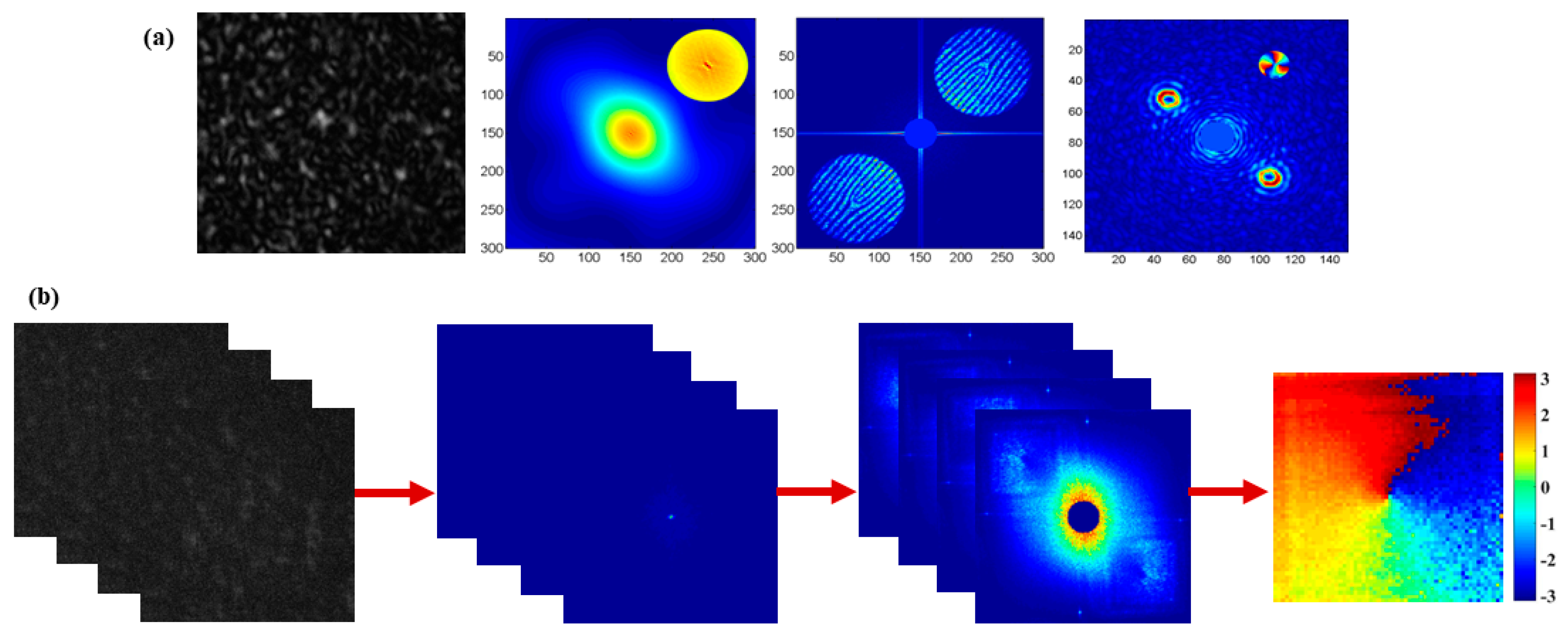
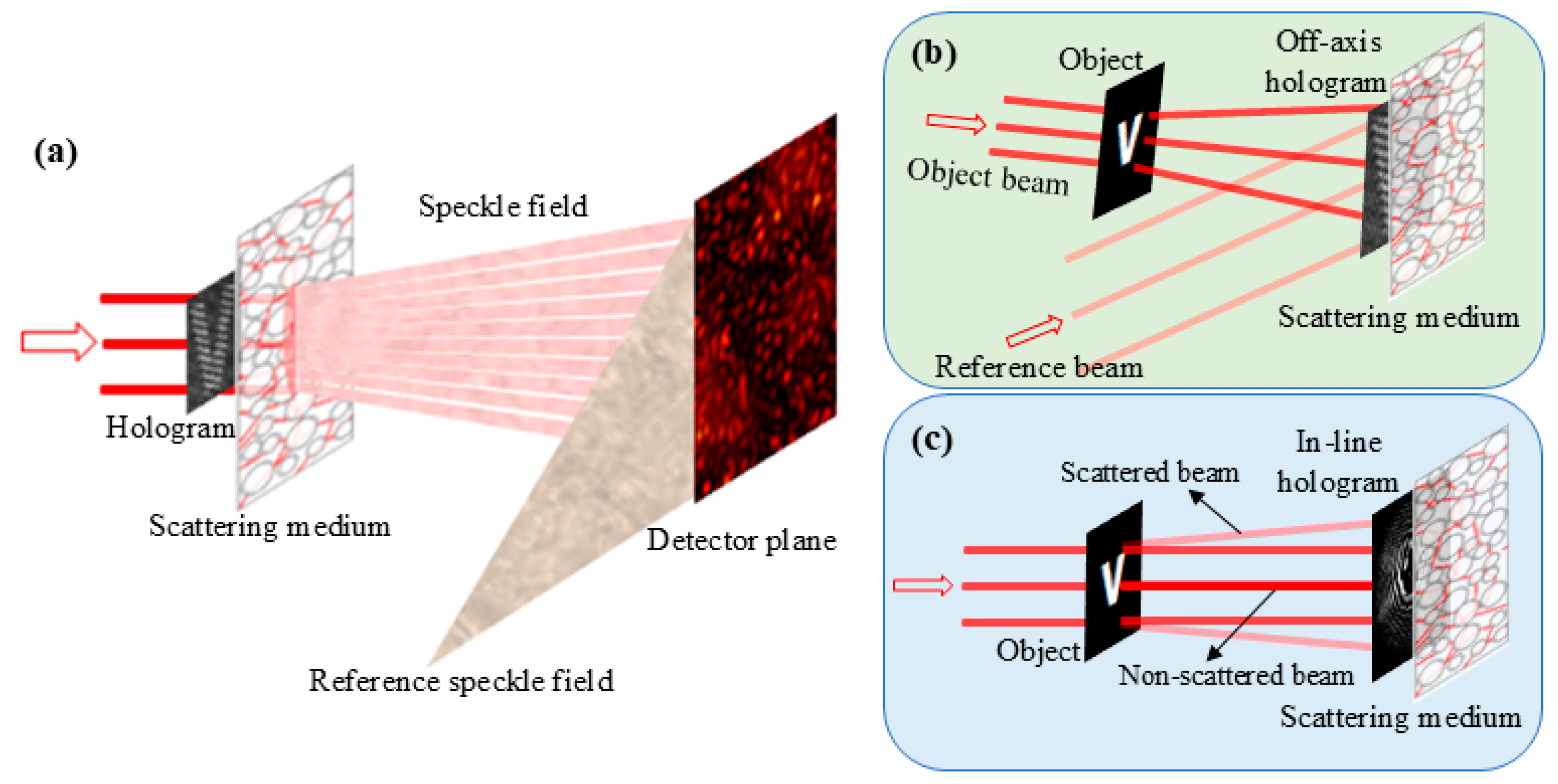
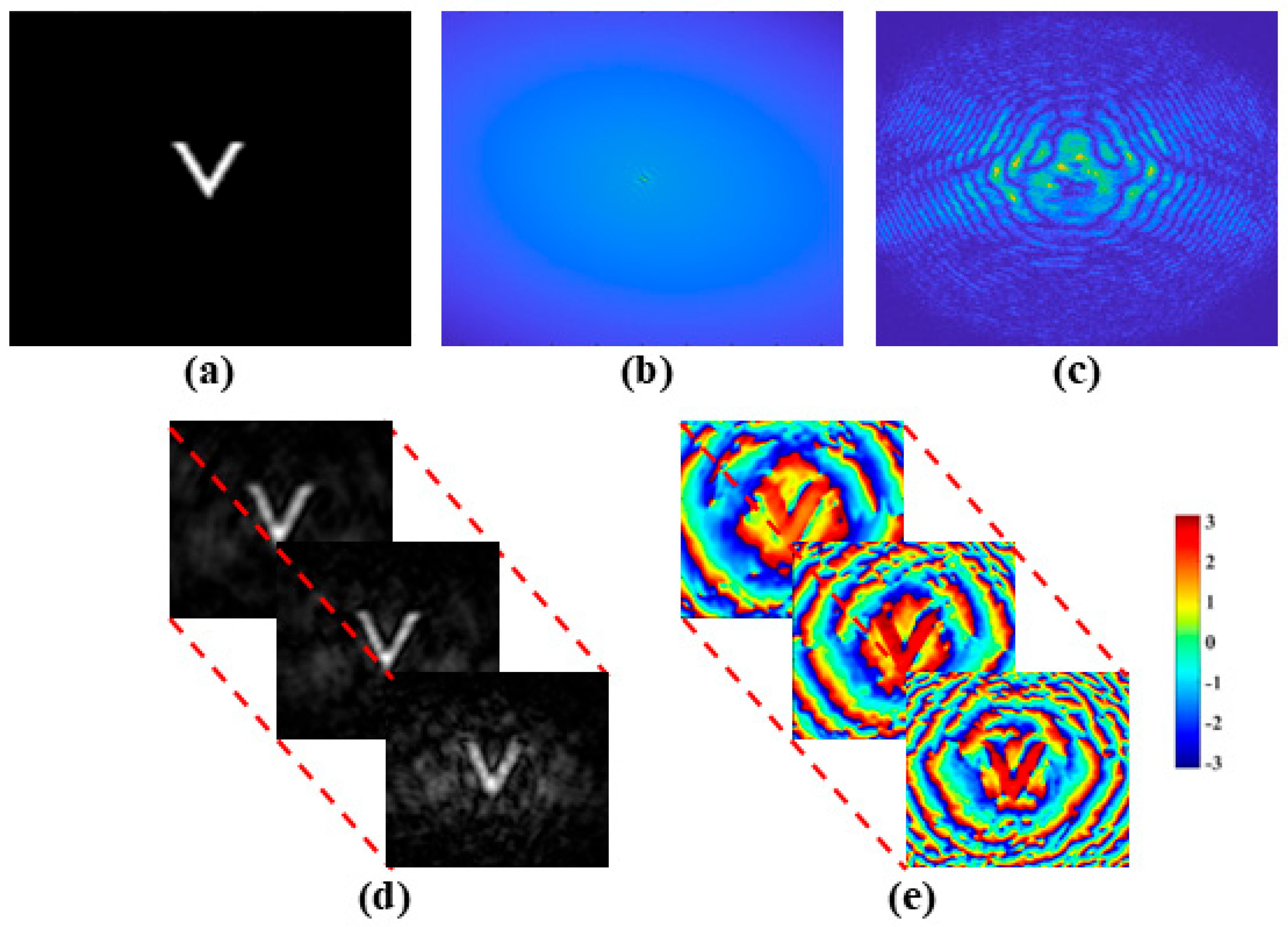
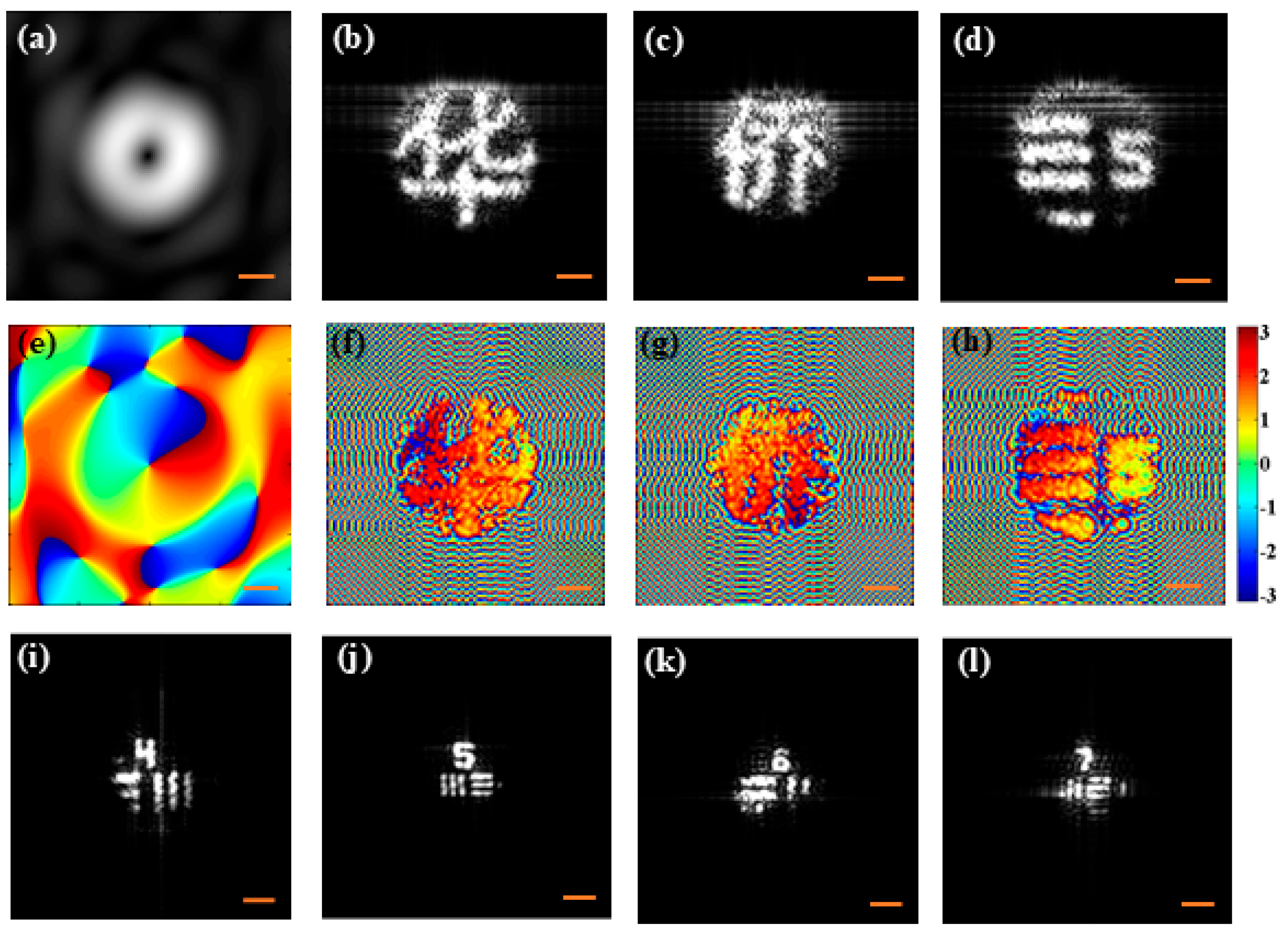
3. Correlation Holographic Imaging
4. Implementation
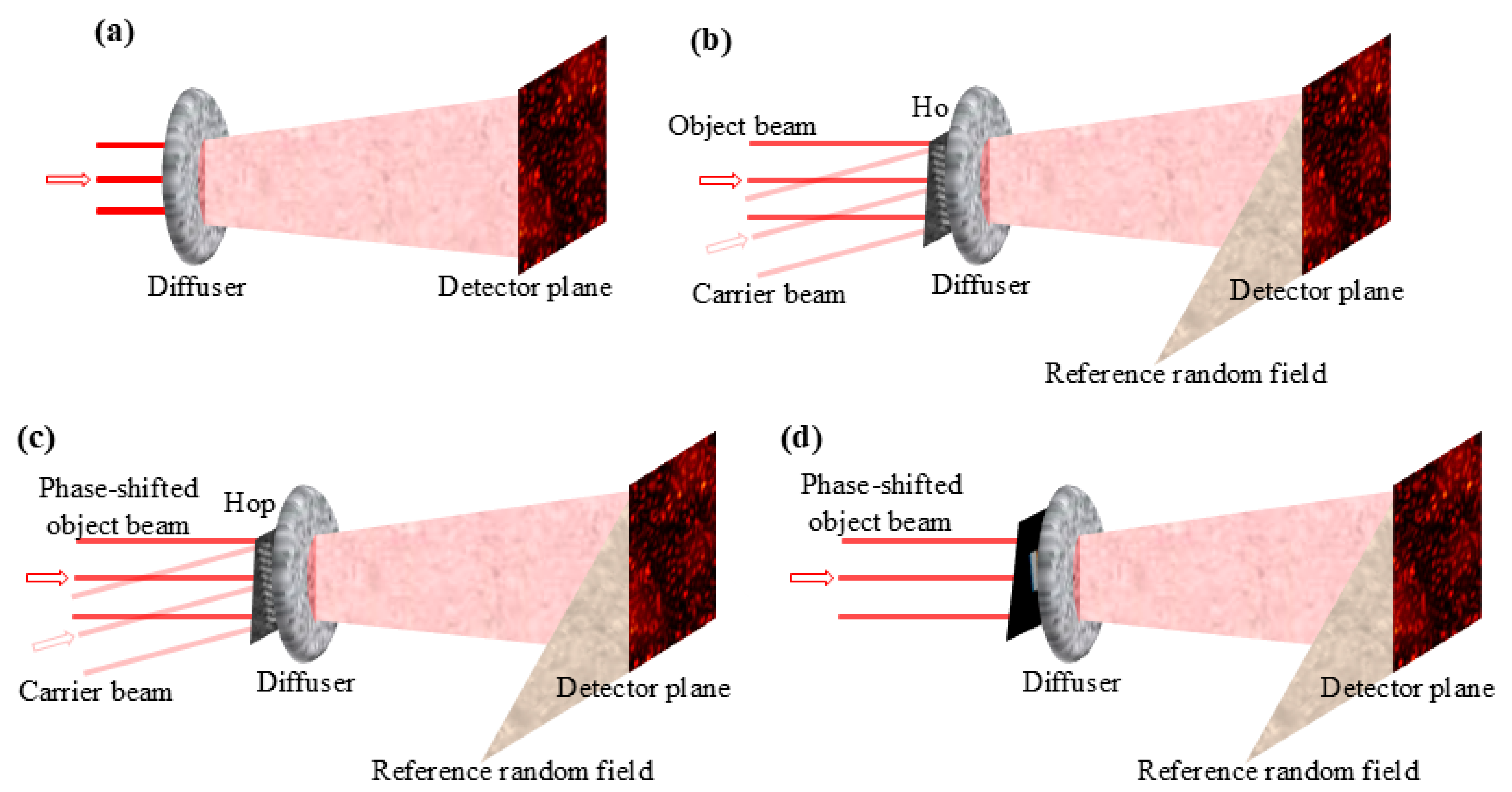
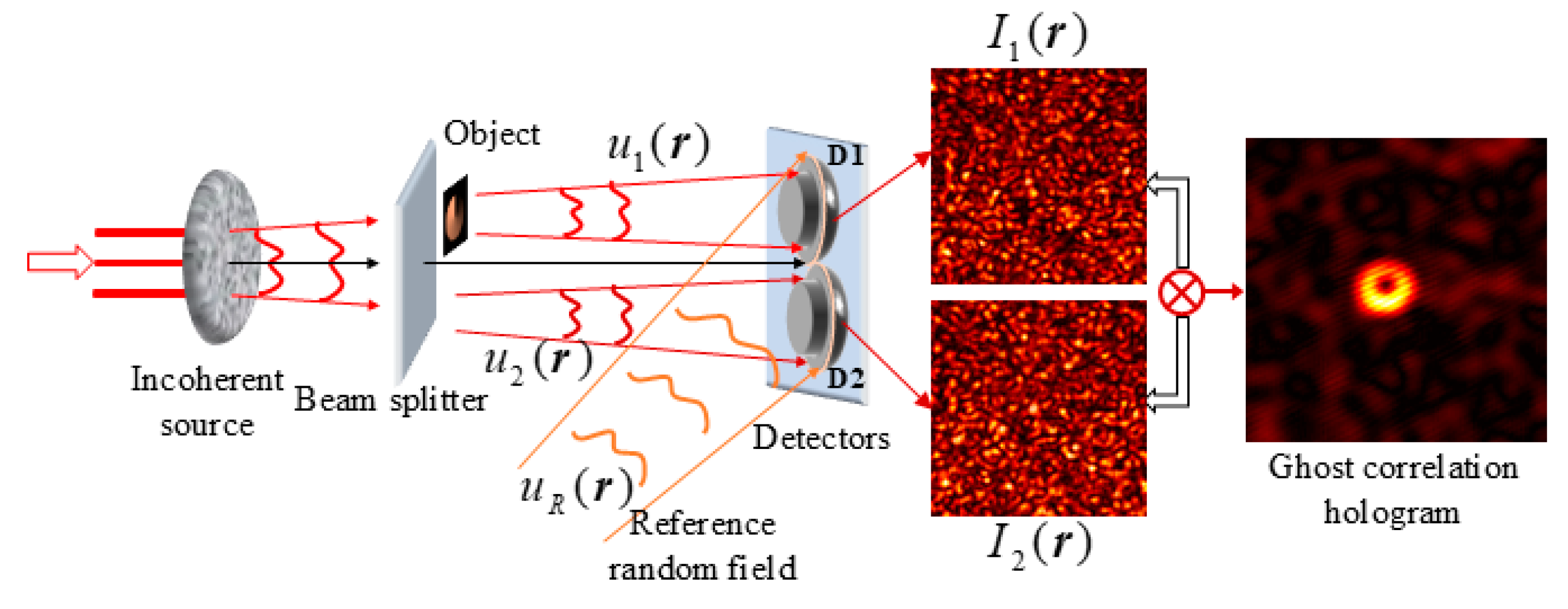
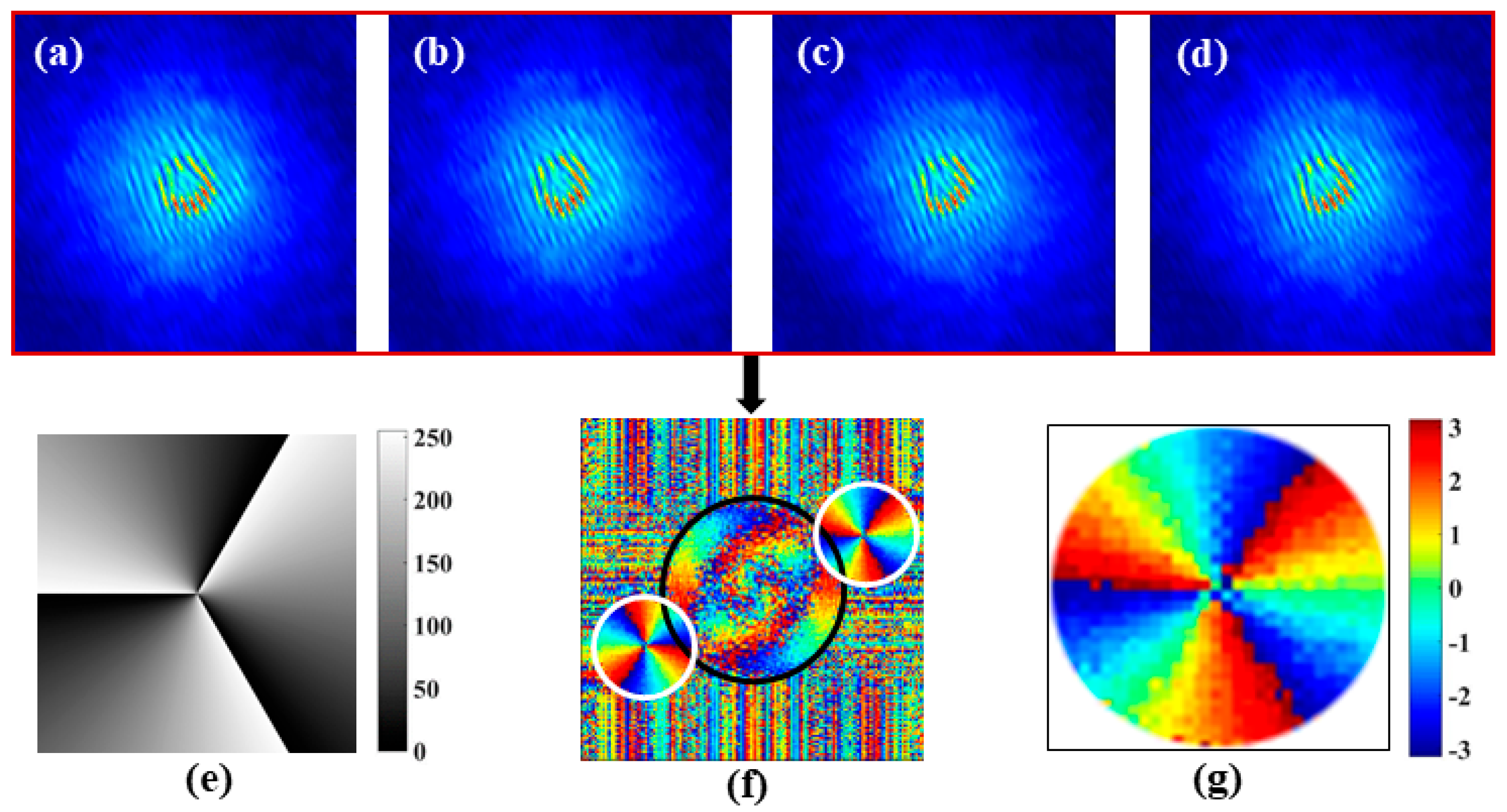
4.1. Correlation Holographic HBT Scheme
4.2. Imaging Through Scattering Media
4.3. Holographic Ghost Diffraction Imaging
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Angelsky, O.V.; Gbur, G.J.; Polyanskii, P.; Hanson, S.G.; Volyar, A.; Zimnyakov, D.A.; Mokhun, I. Emerging Correlation Optics. Appl. Opt. 2012, 51, CO1–CO2. [Google Scholar] [CrossRef][Green Version]
- Korotkova, O. Random Light Beams: Theory and Applications; CRC Press: New York, NY, USA, 2014; ISBN 9788578110796. [Google Scholar]
- Goodman, J.W. Statistical Optics; Wiley-Interscience: Hoboken, NJ, USA, 2000; ISBN 9788578110796. [Google Scholar]
- Dainty, J.C. Laser Speckle and Related Phenomena; Springer: New York, NY, USA, 1984; Volume 1, ISBN 3540074988. [Google Scholar]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications, 2nd ed; Goodman, J.W., Ed.; Roberts and Company: Greenwood Village, CO, USA, 2020. [Google Scholar] [CrossRef]
- Porcello, L.J.; Massey, N.G.; Innes, R.B.; Marks, J.M. Speckle Reduction in Synthetic-Aperture Radars. J. Opt. Soc. Am. 1976, 66, 1305–1344. [Google Scholar] [CrossRef]
- Dantas, R.G.; Costa, E.T.; Leeman, S. Ultrasound Speckle and Equivalent Scatterers. Ultrasonics 2005, 43, 405–420. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.M.; Xiang, S.H.; Yung, K.M. Speckle in Optical Coherence Tomography. J. Biomed. Opt. 1999, 4, 95–105. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Cadotte, D.W.; Vuong, B.; Sun, C.; Luk, T.W.H.; Mariampillai, A.; Yang, V.X.D. Review of Speckle and Phase Variance Optical Coherence Tomography to Visualize Microvascular Networks. J. Biomed. Opt. 2013, 18, 050901. [Google Scholar] [CrossRef]
- Garcia-Sucerquia, J.; Ramírez, J.A.H.; Prieto, D.V. Reduction of Speckle Noise in Digital Holography by Using Digital Image Processing. Optik 2005, 116, 44–48. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Chen, L.; Chen, H.H.; Wen, K.H.; Guo, J.W. Speckle Noise Reduction for Digital Holographic Images Using Swin Transformer. Opt. Lasers Eng. 2025, 184, 108605. [Google Scholar] [CrossRef]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for Reducing Speckle Noise in Digital Holography. Light. Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef]
- Pradeep, S.; Nirmaladevi, P. A Review on Speckle Noise Reduction Techniques in Ultrasound Medical Images Based on Spatial Domain, Transform Domain and CNN Methods. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Erode, India, 15 December 2020; Volume 1055, p. 012116. [Google Scholar] [CrossRef]
- Kumar, M.; Tounsi, Y.; Kaur, K.; Nassim, A.; Matoba, M. Speckle-Noise Reduction in Optical Techniques by Non-Local Means Methods. Full Field Opt. Metrol. Appl. 2022, 13, 13-1–13-21. [Google Scholar] [CrossRef]
- Bertolotti, J.; Katz, O. Imaging in Complex Media. Nat. Phys. 2022, 18, 1008–1017. [Google Scholar] [CrossRef]
- Sjödahl, M.; Benckert, L.R. Electronic Speckle Photography: Analysis of an Algorithm Giving the Displacement with Subpixel Accuracy. Appl. Opt. 1993, 32, 2278–2284. [Google Scholar] [CrossRef]
- Sjödahl, M. Accuracy in Electronic Speckle Photography. Appl. Opt. 1997, 36, 2875–2885. [Google Scholar] [CrossRef]
- Sjödahl, M. Some Recent Advances in Electronic Speckle Photography. Opt. Lasers Eng. 1998, 29, 125–144. [Google Scholar] [CrossRef]
- Angel, L.; Tebaldi, M.; Bolognini, N.; Trivi, M. Speckle Photography with Different Pupils in a Multiple-Exposure Scheme. J. Opt. Soc. Am. A 2000, 17, 107–119. [Google Scholar] [CrossRef]
- Dainty, J.C. Speckle Interferometry in Astronomy. In Sympposium on Recent Advances in Observational Astronomy; Universidad Nacional Autonoma de Mexico: Mexico City, Mexico, 1981; pp. 95–111. [Google Scholar]
- Creath, K. Phase-Shifting Speckle Interferometry. Appl. Opt. 1985, 24, 3053–3058. [Google Scholar] [CrossRef] [PubMed]
- Weigelt, G.P. Speckle Holography Measurements of the Stars Zeta Cancri and ADS 3358. Appl. Opt. 1978, 17, 2660–2662. [Google Scholar] [CrossRef]
- Yamaguchi, I. Advances in the Laser Speckle Strain Gauge. In Proceedings of the SPIE Photomechanics and Speckle Metrology, San Diego, CA, USA, 17–20 August 1987; Volume 814, pp. 141–148. [Google Scholar]
- Takai, N.; Asakura, T. Vectorial Measurements of Speckle Displacement by the 2-D Electronic Correlation Method. Appl. Opt. 1985, 24, 660–665. [Google Scholar] [CrossRef]
- Fischer, A. Fundamental Uncertainty Limit for Speckle Displacement Measurements. Appl. Opt. 2017, 56, 7013–7019. [Google Scholar] [CrossRef] [PubMed]
- Sjödahl, M. Calculation of Speckle Displacement, Decorrelation, and Object-Point Location in Imaging Systems. Appl. Opt. 1995, 34, 7998–8010. [Google Scholar] [CrossRef]
- Khodadad, D.; Hallstig, E.J.; Sjödahl, M. Dual-Wavelength Digital Holographic Shape Measurement Using Speckle Movements and Phase Gradients. Opt. Eng. 2013, 52, 101912. [Google Scholar] [CrossRef]
- Sirohi, R.S. Speckle Metrology; Taylor & Francis: Boca Raton, FL, USA, 2020. [Google Scholar]
- Boas, D.A.; Dunn, A.K. Laser Speckle Contrast Imaging in Biomedical Optics. J. Biomed. Opt. 2010, 15, 011109. [Google Scholar] [CrossRef] [PubMed]
- Briers, D.; Duncan, D.D.; Hirst, E.; Kirkpatrick, S.J.; Larsson, M.; Steenbergen, W.; Stromberg, T.; Thopson, O.B. Laser Speckle Contrast Imaging: Theoretical and Practical Limitations. J. Biomed. Opt. 2013, 18, 066018. [Google Scholar] [CrossRef]
- Richards, L.M.; Kazmi, S.M.S.; Davis, J.L.; Olin, K.E.; Dunn, A.K. Low-Cost Laser Speckle Contrast Imaging of Blood Flow Using a Webcam. Biomed. Opt. Express 2013, 4, 2269–2283. [Google Scholar] [CrossRef] [PubMed]
- Volpe, G.; Kurz, L.; Callegari, A.; Volpe, G.; Gigan, S. Speckle Optical Tweezers: Micromanipulation with Random Light Fields. Opt. Express 2014, 22, 18159–18167. [Google Scholar] [CrossRef]
- Chen, D.J.; Chiang, F.P. Optimal Sampling and Range of Measurement in Displacement-Only Laser-Speckle Correlation. Exp. Mech. 1992, 32, 145–153. [Google Scholar] [CrossRef]
- Fricke-Begemann, T. Three-Dimensional Deformation Field Measurement with Digital Speckle Correlation. Appl. Opt. 2003, 42, 6783–6796. [Google Scholar] [CrossRef]
- Li, J.H.; Genack, A.Z. Correlation in Laser Speckle. Phys. Rev. E 1994, 49, 4530–4533. [Google Scholar] [CrossRef]
- Fayard, N.; Cazé, A.; Pierrat, R.; Carminati, R. Intensity Correlations between Reflected and Transmitted Speckle Patterns. Phys. Rev. A 2015, 92, 033827. [Google Scholar] [CrossRef]
- Lee, K.R.; Park, Y.K. Exploiting the Speckle-Correlation Scattering Matrix for a Compact Reference-Free Holographic Image Sensor. Nat. Commun. 2016, 7, 13359. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Wang, W.; Duan, Z.; Miyamoto, Y. Coherence Holography. Opt. Express 2005, 13, 9629–9635. [Google Scholar] [CrossRef]
- Takeda, M.; Wang, W.; Naik, D.N. Coherence Holography: A Thought Synthesis and Analysis of Optical Coherence Fields. In Fringe 2009; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Naik, D.N.; Singh, R.K.; Ezawa, T.; Miyamoto, Y.; Takeda, M. Photon Correlation Holography. Opt. Express 2011, 19, 1408–1421. [Google Scholar] [CrossRef]
- Padgett, M.J.; Boyd, R.W. An Introduction to Ghost Imaging: Quantum and Classical. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160233. [Google Scholar] [CrossRef]
- Erkmen, B.I.; Shapiro, J.H. Ghost Imaging: From Quantum to Classical to Computational. Adv. Opt. Photonics 2010, 2, 405–450. [Google Scholar] [CrossRef]
- Li, P.; Chen, X.; Qiu, X.; Qiu, X.; Chen, B.; Chen, L.; Sun, B.; Sun, B. Ghost Imaging, Development, and Recent Advances [Invited]. Chin. Opt. Lett. 2024, 22, 112701. [Google Scholar] [CrossRef]
- Hoenders, B.J. Review of a Bewildering Classical-Quantum Phenomenon: Ghost Imaging. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2018; Volume 208, pp. 1–41. [Google Scholar]
- Brown, R.H.; Twiss, R.Q. Correlation between Photons in Two Coherent Beams of Light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q. Interferometry of the Intensity Fluctuations in Light. I. Basic Theory: The Correlation between Photons in Coherent Beams of Radiation. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 242, 300–324. [Google Scholar] [CrossRef]
- Dainty, J.C. Some Statistical Properties of Random Speckle Patterns in Coherent and Partially Coherent Illumination. Opt. Acta Int. J. Opt. 1970, 17, 761–772. [Google Scholar] [CrossRef]
- Ohtsubo, J.; Asakura, T. Statistical Properties of Speckle Intensity Variations in the Diffraction Field under Illumination of Coherent Light. Opt. Commun. 1975, 14, 30–34. [Google Scholar] [CrossRef]
- Prunty, A.C.; Snieder, R.K. Demystifying the Memory Effect: A Geometrical Approach to Understanding Speckle Correlations. Eur. Phys. J. Spéc. Top. 2017, 226, 1445–1455. [Google Scholar] [CrossRef]
- Bertolotti, J.; van Putten, E.G.; Blum, C.; Lagendijk, A.; Vos, W.L.; Mosk, A.P. Non-Invasive Imaging through Opaque Scattering Layers. Nature 2012, 491, 232–234. [Google Scholar] [CrossRef]
- Katz, O.; Heidmann, P.; Fink, M.; Gigan, S. Non-Invasive Single-Shot Imaging through Scattering Layers and around Corners via Speckle Correlations. Nat. Photonics 2014, 8, 784–790. [Google Scholar] [CrossRef]
- Goldfischer, L.I. Autocorrelation Function and Power Spectral Density of Laser-Produced Speckle Patterns. J. Opt. Soc. Am. 1965, 55, 247–253. [Google Scholar] [CrossRef]
- Bertolotti, J. Non-Invasive Imaging: Peeking through the Curtain. Nat. Photonics 2014, 8, 751–752. [Google Scholar] [CrossRef]
- Liu, W.; Liu, W.; Liu, W.; Gong, W.; Gong, W.; Liu, Z.; Liu, Z.; Liu, Z.; Sun, S.; Sun, S.; et al. Progress and Applications of Ghost Imaging with Classical Sources: A Brief Review [Invited]. Chin. Opt. Lett. 2024, 22, 111101. [Google Scholar] [CrossRef]
- Moreau, P.-A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Ghost Imaging Using Optical Correlations. Laser Photonics Rev. 2018, 12, 1700143. [Google Scholar] [CrossRef]
- Kumari, V.R.P.V.; Chen, Z.; Singh, R.K.; Pu, J.; Kumari, V.R.P.V.; Chen, Z.; Singh, R.K.; Pu, J. Ghost Diffraction Holography: A Correlation Assisted Quantitative Tool for Complex Field Imaging and Characterization. Hologr. Recent Adv. Appl. 2022. [Google Scholar] [CrossRef]
- Takeda, M.; Wang, W.; Naik, D.N.; Singh, R.K. Spatial Statistical Optics and Spatial Correlation Holography: A Review. Opt. Rev. 2014, 21, 849–861. [Google Scholar] [CrossRef]
- Takeda, M. Spatial Stationarity of Statistical Optical Fields for Coherence Holography and Photon Correlation Holography. Opt. Lett. 2013, 38, 3452–3455. [Google Scholar] [CrossRef]
- Takeda, M.; Wang, W.; Duan, Z.; Miyamoto, Y.; Rosen, J. Coherence Holography and Spatial Frequency Comb for 3-D Coherence Imaging. In Frontiers in Optics; Optica Publishing Group: Washington, DC, USA, 2008. [Google Scholar]
- Takeda, M.; Wang, W.; Naik, D.N. Coherence Holography: Principle and Applications. In Optical Imaging and Metrology: Advanced Technologies; Wiley: Hoboken, NJ, USA, 2012; pp. 239–253. [Google Scholar] [CrossRef]
- Singh, R.K.; Naik, D.N.; Itou, H.; Miyamoto, Y.; Takeda, M. Vectorial Coherence Holography. Opt. Express 2011, 19, 11558–11567. [Google Scholar] [CrossRef]
- Singh, R.K.; Naik, D.N.; Itou, H.; Miyamoto, Y.; Takeda, M. Stokes Holography. Opt. Lett. 2012, 37, 966–968. [Google Scholar] [CrossRef]
- Singh, R.K.; Vinu, R.V.; Sharma, M.A. Recovery of Complex Valued Objects from Two-Point Intensity Correlation Measurement. Appl. Phys. Lett. 2014, 104, 111108. [Google Scholar] [CrossRef]
- Singh, R.K.; Vinu, R.P.V.K.; Anandraj Sharma, M.S. Retrieving Complex Coherence from Two-Point Intensity Correlation Using Holographic Principle. Opt. Eng. 2014, 53, 104102. [Google Scholar] [CrossRef]
- Takeda, M.; Singh, A.K.; Naik, D.N.; Pedrini, G.; Osten, W. Holographic Correloscopy-Unconventional Holographic Techniques for Imaging a Three-Dimensional Object Through an Opaque Diffuser or Via a Scattering Wall: A Review. IEEE Trans. Ind. Inform. 2016, 12, 1631–1640. [Google Scholar] [CrossRef]
- Singh, R.K.; Sharma, A.M.; Das, B. Quantitative Phase-Contrast Imaging through a Scattering Media. Opt. Lett. 2014, 39, 5054–5057. [Google Scholar] [CrossRef]
- V, R.V.; Kim, K.; Somkuwar, A.S.; Park, Y.K.; Singh, R.K. Imaging through Scattering Media Using Digital Holography. Opt. Commun. 2019, 439, 218–223. [Google Scholar] [CrossRef]
- Somkuwar, A.S.; Das, B.; Vinu, R.V.; Park, Y.; Singh, R.K. Holographic Imaging through a Scattering Layer Using Speckle Interferometry. J. Opt. Soc. Am. A 2017, 34, 1392–1399. [Google Scholar] [CrossRef]
- Singh, A.K.; Pedrini, G.; Takeda, M.; Osten, W. Scatter-Plate Microscope for Lensless Microscopy with Diffraction Limited Resolution. Sci. Rep. 2017, 7, 10687. [Google Scholar] [CrossRef]
- Vinu, R.V.; Chen, Z.; Singh, R.K.; Pu, J. Ghost Diffraction Holographic Microscopy. Optica 2020, 7, 1697. [Google Scholar] [CrossRef]
- Vinu, R.V.; Huang, Y.; Du, X.; Chen, Z.; Pu, J.; Pu, J. Wide-Field Quantitative Ghost Phase Imaging with Phase-Shifting Holographic Ghost Diffraction. Opt. Express 2025, 33, 531–542. [Google Scholar] [CrossRef]
- Chen, Z.; Singh, R.K.; Chen, L.; Pu, J. Phase Shifting Digital Holography with the Hanbury Brown–Twiss Approach. Opt. Lett. 2020, 45, 212–215. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Chen, Z.; Singh, R.K.; Singh, R.K.; Singh, R.K.; Pu, J. Imaging of Polarimetric-Phase Object through Scattering Medium by Phase Shifting. Opt. Express 2020, 28, 8145–8155. [Google Scholar] [CrossRef]
- Chen, L.; Kumar Singh, R.; Vinu, R.V.; Chen, Z.; Pu, J. A Wavefront Division Multiplexing Holographic Scheme and Its Application in Looking through Diffuser. New J. Phys. 2021, 23, 113034. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Singh, R.K.; Vinu, R.V.; Pu, J. Increasing Field of View and Signal to Noise Ratio in the Quantitative Phase Imaging with Phase Shifting Holography Based on the Hanbury Brown-Twiss Approach. Opt. Lasers Eng. 2022, 148, 106771. [Google Scholar] [CrossRef]
- Vinu, R.V.; Singh, R.K. Synthesis of Statistical Properties of a Randomly Fluctuating Polarized Field. Appl. Opt. 2015, 54, 6491–6497. [Google Scholar] [CrossRef]
- Vinu, R.V.; Sharma, M.K.; Singh, R.K.; Senthilkumaran, P. Generation of Spatial Coherence Comb Using Dammann Grating. Opt. Lett. 2014, 39, 2407–2410. [Google Scholar] [CrossRef] [PubMed]
- Vinu, R.V.; Singh, R.K. Experimental Determination of Generalized Stokes Parameters. Opt. Lett. 2015, 40, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Wang, W.; Hanson, S.G. Polarization Speckles and Generalized Stokes Vector Wave: A Review. In Proceedings of the SPIE—The International Society for Optical Metrology, Florianapolis, Brazil, 13 September 2010; Volume 7387, p. 73870V. [Google Scholar]
- Roy, A.; Singh, R.K.; Brundavanam, M.M. Analysis of Polarization Speckle for Imaging through Random Birefringent Scatterer. Appl. Phys. Lett. 2016, 109, 201108. [Google Scholar] [CrossRef]
- Vinu, R.V.; Singh, R.K. Determining Helicity and Topological Structure of Coherent Vortex Beam from Laser Speckle. Appl. Phys. Lett. 2016, 109, 111108. [Google Scholar] [CrossRef]
- Huang, Y.; Vinu, R.V.; Chen, Z.; Sarkar, T.; Singh, R.K.; Pu, J. Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography. Appl. Sci. 2021, 11, 12167. [Google Scholar] [CrossRef]
- Sarkar, T.; Parvin, R.; Brundavanam, M.M.; Singh, R.K. Higher-Order Stokes-Parameter Correlation to Restore the Twisted Wave Front Propagating through a Scattering Medium. Phys. Rev. A 2021, 104, 013525. [Google Scholar] [CrossRef]
- Sarkar, T.; Chandra, S.; Sheoran, G.; Singh, R.K. Leveraging the Depolarization of Scattered Light for Holography with the Stokes Correlation. Appl. Phys. Lett. 2024, 124, 071103. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Sixty Years of Lasers. Nat. Rev. Phys. 2020, 2, 221. [CrossRef]
- Goodman, J.W. Statistical Properties of Laser Speckle Patterns. In Laser Speckle and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 1975; pp. 9–75. [Google Scholar] [CrossRef]
- Dainty, J.C. I The Statistics of Speckle Patterns. Progress Opt. 1977, 14, 1–46. [Google Scholar] [CrossRef]
- Basak, K.; Manjunatha, M.; Dutta, P.K. Review of Laser Speckle-Based Analysis in Medical Imaging. Med. Biol. Eng. Comput. 2012, 50, 547–558. [Google Scholar] [CrossRef]
- Khan, D.; Shirazi, M.A.; Kim, M.Y. Single Shot Laser Speckle Based 3D Acquisition System for Medical Applications. Opt. Lasers Eng. 2018, 105, 43–53. [Google Scholar] [CrossRef]
- Singh, P.; Diwakar, M.; Shankar, A.; Shree, R.; Kumar, M. A Review on SAR Image and Its Despeckling. Arch. Comput. Methods Eng. 2021, 28, 4633–4653. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Liu, L.; Chen, H.; Han, H.; Zhang, B.; Zhang, Q. Speckle Noise Reduction for Medical Ultrasound Images Based on Cycle-Consistent Generative Adversarial Network. Biomed. Signal Process Control 2023, 86, 105150. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, K.; Wang, M.; Ma, Y.; Peng, Y.; Chen, Z.; Zhu, W.; Shi, F.; Chen, X. Speckle Noise Reduction for OCT Images Based on Image Style Transfer and Conditional GAN. IEEE J. Biomed. Health Inform. 2022, 26, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Freund, I.; Rosenbluh, M.; Feng, S. Memory Effects in Propagation of Optical Waves through Disordered Media. Phys. Rev. Lett. 1988, 61, 2328–2331. [Google Scholar] [CrossRef] [PubMed]
- Judkewitz, B.; Horstmeyer, R.; Osnabrugge, G.; Papadopoulos, I.N.; Vellekoop, I.M. Generalized Optical Memory Effect. Optica 2017, 4, 886–892. [Google Scholar] [CrossRef]
- Edrei, E.; Scarcelli, G. Memory-Effect Based Deconvolution Microscopy for Super-Resolution Imaging through Scattering Media. Sci. Rep. 2016, 6, 33558. [Google Scholar] [CrossRef]
- Takasaki, K.T.; Fleischer, J.W. Phase-Space Measurement for Depth-Resolved Memory-Effect Imaging. Opt. Express 2014, 22, 31426. [Google Scholar] [CrossRef]
- Korotkova, O. Random Light Beams: Theory and Applications. In Random Light Beams: Theory and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–361. [Google Scholar] [CrossRef]
- Goodman, J.W. Some Fundamental Properties of Speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Kozma, A.; Christensen, C.R. Effects of Speckle on Resolution*. J. Opt. Soc. Am. 1976, 66, 1257–1260. [Google Scholar] [CrossRef]
- Feng, S.; Kane, C.; Lee, P.A.; Stone, A.D. Correlations and Fluctuations of Coherent Wave Transmission through Disordered Media. Phys. Rev. Lett. 1988, 61, 834–837. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Kelly, D.P.; Li, D. Three-Dimensional Static Speckle Fields. Part I. Theory and Numerical. J. Opt. Soc. Am. A 2011, 28, 1896–1903. [Google Scholar] [CrossRef]
- Singh, D.; Singh, R.K. Lensless Stokes Holography with the Hanbury Brown-Twiss Approach. Opt. Express 2018, 26, 10801–10812. [Google Scholar] [CrossRef]
- Sarkar, T.; Tiwari, V.; Chandra, S.; Bisht, N.S.; Singh, R.K. Holography with Higher-Order Stokes Correlation. Phys. Rev. A 2022, 106, 013508. [Google Scholar] [CrossRef]
- Manisha; Mandal, A.C.; Rathor, M.; Zalevsky, Z.; Singh, R.K. Randomness Assisted In-Line Holography with Deep Learning. Sci. Rep. 2023, 13, 10986. [Google Scholar] [CrossRef]
- Saluja, R.; Subrahmanyam, G.R.K.S.; Mishra, D.; Vinu, R.V.; Singh, R.K. Compressive Correlation Holography. Appl. Opt. 2017, 56, 6949–6955. [Google Scholar] [CrossRef]
- Kreis, T. Handbook of Holographic Interferometry; Wiley-VCH: Weinheim, Germany, 2005; ISBN 3527405461. [Google Scholar]
- Paturzo, M.; Pagliarulo, V.; Bianco, V.; Memmolo, P.; Miccio, L.; Merola, F.; Ferraro, P. Digital Holography, a Metrological Tool for Quantitative Analysis: Trends and Future Applications. Opt. Lasers Eng. 2018, 104, 32–47. [Google Scholar] [CrossRef]
- Rosen, J. Holography: Research and Technologies. Intechopen: London, UK, 2011. [Google Scholar] [CrossRef]
- Hassinen, T.; Tervo, J.; Setälä, T.; Friberg, A.T. Hanbury Brown-Twiss Effect with Electromagnetic Waves. Opt. Express 2011, 19, 15188–15195. [Google Scholar] [CrossRef]
- Kuebel, D.; Visser, T.D. Generalized Hanbury Brown-Twiss Effect for Stokes Parameters. J. Opt. Soc. Am. A 2019, 36, 362. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Measuring Complex Degree of Coherence of Random Light Fields with Generalized Hanbury Brown-Twiss Experiment. Phys. Rev. Appl. 2020, 13, 044042. [Google Scholar] [CrossRef]
- McCUTCHEN, C.W. Generalized Source and the van Cittert—Zernike Theorem: A Study of the Spatial Coherence Required for Interferometry. J. Opt. Soc. Am. 1966, 56, 727. [Google Scholar] [CrossRef]
- Shirai, T. Some Consequences of the van Cittert-Zernike Electromagnetic Fields. Opt. Lett. 2009, 34, 3761–3763. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Borghi, R.; Piquero, G. Use of the van Cittert-Zernike Theorem for Partially Polarized Sources. Opt. Lett. 2000, 25, 1291–1293. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; Martínez-Niconoff, G.; Martínez-Vara, P.; Olvera-Santamaría, M.A. The van Cittert-Zernike Theorem for Electromagnetic Fields. Opt. Express 2009, 17, 1746–1752. [Google Scholar] [CrossRef]
- Singh, R.K.; Naik, D.N.; Itou, H.; Brundabanam, M.M.; Miyamoto, Y.; Takeda, M. Vectorial van Cittert-Zernike Theorem Based on Spatial Averaging: Experimental Demonstrations. Opt. Lett. 2013, 38, 4809–4812. [Google Scholar] [CrossRef]
- Chandra, S.; Singh, R.K. Measurement of Coherence-Polarization Matrix from a Single-Frame Recording. Opt. Lasers Eng. 2025, 184, 108611. [Google Scholar] [CrossRef]
- Shirai, T.; Wolf, E. Correlations between Intensity Fluctuations in Stochastic Electromagnetic Beams of Any State of Coherence and Polarization. Opt. Commun. 2007, 272, 289–292. [Google Scholar] [CrossRef]
- Das, B.; Bisht, N.S.; Vinu, R.V.; Singh, R.K. Lensless Complex Amplitude Image Retrieval through a Visually Opaque Scattering Medium. Appl. Opt. 2017, 56, 4591–4597. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; He, H.; Vinu, R.V.; Luo, S.; Pu, J.; Chen, Z. Single-Shot Non-Invasive Imaging Through Dynamic Scattering Media Beyond the Memory Effect via Virtual Reference-Based Correlation Holography. Laser Photon Rev. 2024, 19, 2400978. [Google Scholar] [CrossRef]
- Mosk, A.P.; Lagendijk, A.; Lerosey, G.; Fink, M. Controlling Waves in Space and Time for Imaging and Focusing in Complex Media. Nat. Photonics 2012, 6, 283. [Google Scholar] [CrossRef]
- Yaqoob, Z.; Psaltis, D.; Feld, M.S.; Yang, C. Optical Phase Conjugation for Turbidity Suppression in Biological Samples. Nat. Photonics 2008, 2, 110–115. [Google Scholar] [CrossRef]
- Hillman, T.R.; Yamauchi, T.; Choi, W.; Dasari, R.R.; Feld, M.S.; Park, Y.; Yaqoob, Z. Digital Optical Phase Conjugation for Delivering Two-Dimensional Images through Turbid Media. Sci. Rep. 2013, 3, 1909. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Cui, M.; Yang, C. Digital Optical Phase Conjugation of Fluorescence in Turbid Tissue. Appl. Phys. Lett. 2012, 101, 81108. [Google Scholar] [CrossRef]
- Wang, L.; Ho, P.P.; Liu, C.; Zhang, G.; Alfano, R.R. Ballistic 2-D Imaging Through Scattering Walls Using an Ultrafast Optical Kerr Gate. Science 1991, 253, 769–771. [Google Scholar] [CrossRef]
- Paciaroni, M.; Linne, M. Single-Shot, Two-Dimensional Ballistic Imaging through Scattering Media. Appl. Opt. 2004, 43, 5100–5109. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Focusing Coherent Light through Opaque Strongly Scattering Media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, X.; Dai, Q. Non-Invasive Imaging through Strongly Scattering Media Based on Speckle Pattern Estimation and Deconvolution. Sci. Rep. 2018, 8, 9088. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, Y.-R.; Choi, W.; Kang, S.; Hong, J.H.; Park, J.-S.; Lim, Y.-S.; Park, H.-G.; Choi, W. Focusing of Light Energy inside a Scattering Medium by Controlling the Time-Gated Multiple Light Scattering. Nat. Photonics 2018, 12, 277–283. [Google Scholar] [CrossRef]
- Yang, W.; Li, G.; Situ, G. Imaging through Scattering Media with the Auxiliary of a Known Reference Object. Sci. Rep. 2018, 8, 9614. [Google Scholar] [CrossRef]
- Katz, O.; Small, E.; Silberberg, Y. Looking around Corners and through Thin Turbid Layers in Real Time with Scattered Incoherent Light. Nat. Photonics 2012, 6, 549–553. [Google Scholar] [CrossRef]
- Wu, T.; Katz, O.; Shao, X.; Gigan, S. Single-Shot Diffraction-Limited Imaging through Scattering Layers via Bispectrum Analysis. Opt. Lett. 2016, 41, 5003. [Google Scholar] [CrossRef]
- Edrei, E.; Scarcelli, G. Optical Imaging through Dynamic Turbid Media Using the Fourier-Domain Shower-Curtain Effect. Optica 2016, 3, 71–74. [Google Scholar] [CrossRef]
- Singh, A.K.; Naik, D.N.; Pedrini, G.; Takeda, M.; Osten, W. Looking through a Diffuser and around an Opaque Surface: A Holographic Approach. Opt. Express 2014, 22, 7694–7701. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-Transform Method of Fringe-Pattern Analysis for Computer-Based Topography and Interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Li, S.; Cropp, F.; Kabra, K.; Lane, T.J.; Wetzstein, G.; Musumeci, P.; Ratner, D. Electron Ghost Imaging. Phys. Rev. Lett. 2018, 121, 114801. [Google Scholar] [CrossRef]
- Khakimov, R.I.; Henson, B.M.; Shin, D.K.; Hodgman, S.S.; Dall, R.G.; Baldwin, K.G.H.; Truscott, A.G. Ghost Imaging with Atoms. Nature 2016, 540, 100–103. [Google Scholar] [CrossRef]
- Abouraddy, A.F.; Stone, P.R.; Sergienko, A.V.; Saleh, B.E.A.; Teich, M.C. Entangled-Photon Imaging of a Pure Phase Object. Phys. Rev. Lett. 2004, 93, 213903. [Google Scholar] [CrossRef]
- Ying, G.; Wei, Q.; Shen, X.; Han, S. A Two-Step Phase-Retrieval Method in Fourier-Transform Ghost Imaging. Opt. Commun. 2008, 281, 5130–5132. [Google Scholar] [CrossRef]
- Gong, W.; Han, S. Phase-Retrieval Ghost Imaging of Complex-Valued Objects. Phys. Rev. A 2010, 82, 23828. [Google Scholar] [CrossRef]
- Shirai, T.; Friberg, A.T. Ghost Mach-Zehnder Interferometry for Phase Measurement with Spatially Incoherent Light. J. Opt. 2020, 22, 045604. [Google Scholar] [CrossRef]
- Clemente, P.; Durán, V.; Tajahuerce, E.; Torres-Company, V.; Lancis, J. Single-Pixel Digital Ghost Holography. Phys. Rev. A 2012, 86, 41803. [Google Scholar] [CrossRef]
- Takeda, M.; Miyamoto, Y.; Ezawa, T.; Naik, D.N. 3-D Coherence Holography Using a Modified Sagnac Radial Shearing Interferometer with Geometric Phase Shift. Opt. Express 2009, 17, 10633–10641. [Google Scholar] [CrossRef]
- Takeda, M.; Miyamoto, Y.; Ezawa, T.; Naik, D.N. Real-Time Coherence Holography. Opt. Express 2010, 18, 13782–13787. [Google Scholar] [CrossRef]
- Sarkar, T.; Parvin, R.; Brundavanam, M.M.; Singh, R.K. Measuring Obscured OAM Spectrum Using Stokes Fluctuations in a Non-Interferometric Approach. Opt. Lasers Eng. 2022, 155, 107065. [Google Scholar] [CrossRef]
- Sarkar, T.; Singh, R.K. Stokes Correlation to Estimate Topological Charge from the Speckle Pattern. Appl. Phys. B 2023, 129, 13. [Google Scholar] [CrossRef]
- Hannonen, A.; Hoenders, B.J.; Elsässer, W.; Friberg, A.T.; Setälä, T. Ghost Polarimetry Using Stokes Correlations. J. Opt. Soc. Am. A 2020, 37, 714. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Wolf, E. Generalized Stokes Parameters of Random Electromagnetic Beams. Opt. Lett. 2005, 30, 198. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Alford, S.; Allan, B.; Anand, V.; Arnon, S.; Arockiaraj, F.G.; Art, J.; Bai, B.; Balasubramaniam, G.M.; Birnbaum, T.; et al. Roadmap on Computational Methods in Optical Imaging and Holography [Invited]. Appl. Phys. B 2024, 130, 166. [Google Scholar] [CrossRef] [PubMed]


| Basic Principle | Method | Applications |
|---|---|---|
| Spatial field correlation (second-order correlation) | Coherence holography [38] | 3D 1 object reconstruction [144], imaging through diffuser [145] |
| Spatial intensity correlation (fourth-order correlation) | Photon correlation holography [40] | 3D 1 object reconstruction using intensity correlation [135], holographic correloscopy for imaging through scattering medium [65] |
| Holographic spatial HBT system [63] | Complex-valued object imaging through scattering layer [67,68,74], QPI 1 through scattering medium [66], helicity estimation of coherent vortex beam [81] | |
| Ghost diffraction holography [70] | Quantitative ghost microscopy [70], phase-shifting-holographic ghost diffraction imaging [71] | |
| Polarized vectorial field correlation (CP-matrix elements, GSPs) | Vectorial coherence holography [61] Stokes holography [62] Higher-order Stokes correlation [104] | Polarization speckles [79], determination of CP 1 matrix elements and GSPs 1 [78,118], Stokes holography-HBT scheme [103], OAM 1 spectrum estimation [146,147] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
R. V., V.; Chen, Z.; Pu, J. Speckle-Correlation Holographic Imaging: Advances, Techniques, and Current Challenges. Photonics 2025, 12, 776. https://doi.org/10.3390/photonics12080776
R. V. V, Chen Z, Pu J. Speckle-Correlation Holographic Imaging: Advances, Techniques, and Current Challenges. Photonics. 2025; 12(8):776. https://doi.org/10.3390/photonics12080776
Chicago/Turabian StyleR. V., Vinu, Ziyang Chen, and Jixiong Pu. 2025. "Speckle-Correlation Holographic Imaging: Advances, Techniques, and Current Challenges" Photonics 12, no. 8: 776. https://doi.org/10.3390/photonics12080776
APA StyleR. V., V., Chen, Z., & Pu, J. (2025). Speckle-Correlation Holographic Imaging: Advances, Techniques, and Current Challenges. Photonics, 12(8), 776. https://doi.org/10.3390/photonics12080776






