Multipath Interference Impact Due to Fiber Mode Coupling in C+L+S Multiband Transmission Reach
Abstract
1. Introduction
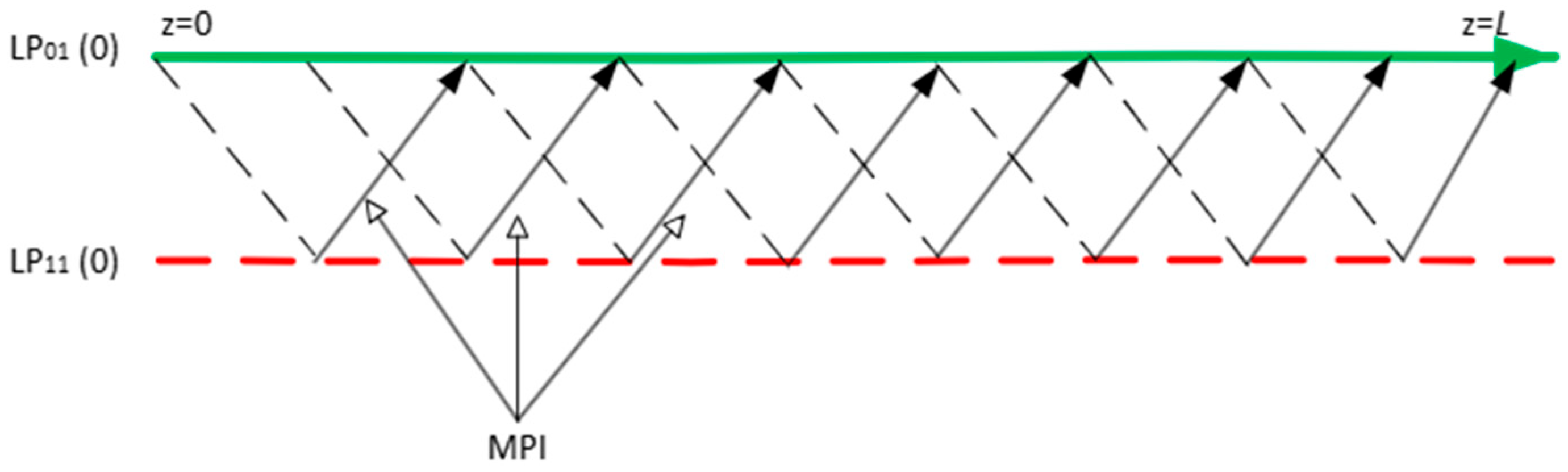
2. Characterization of Multipath Interference in G.654E SMF
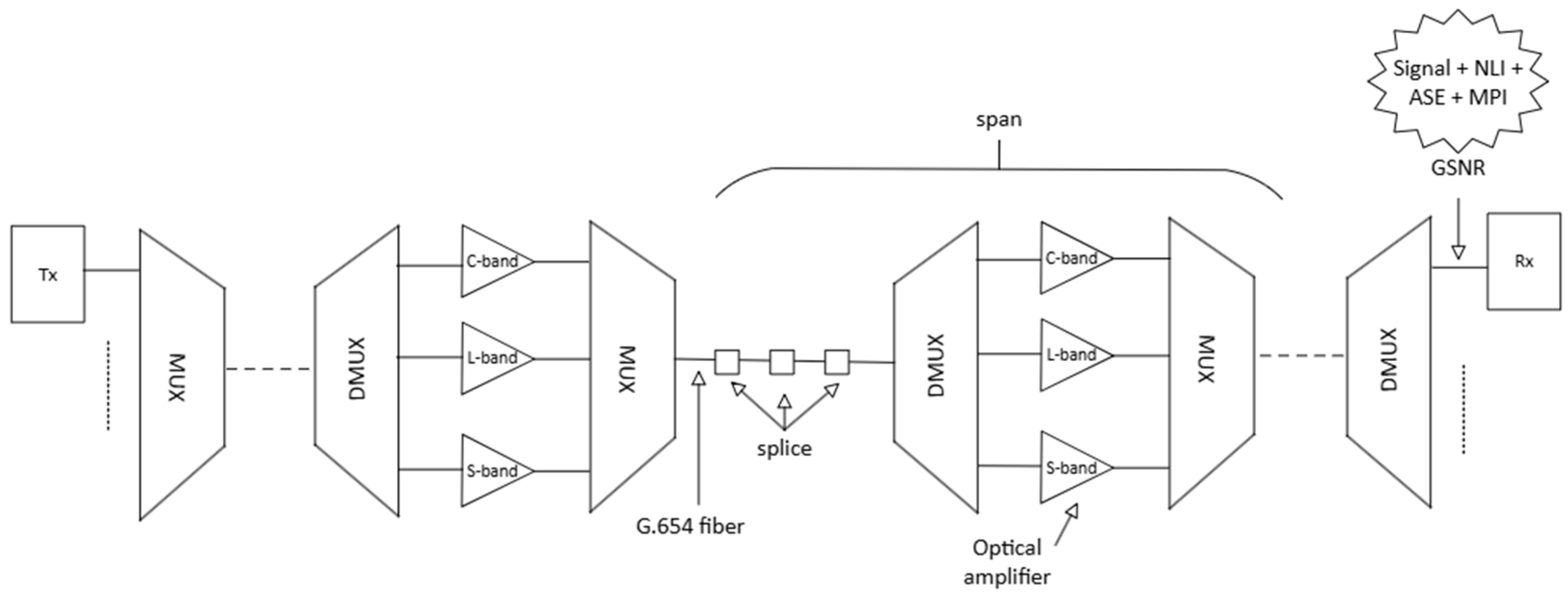
3. Quality of Transmission Model
4. Transmission Reach Assessment
4.1. System Parameters
4.2. Transmission Reach Assessment Without MPI
- (i)
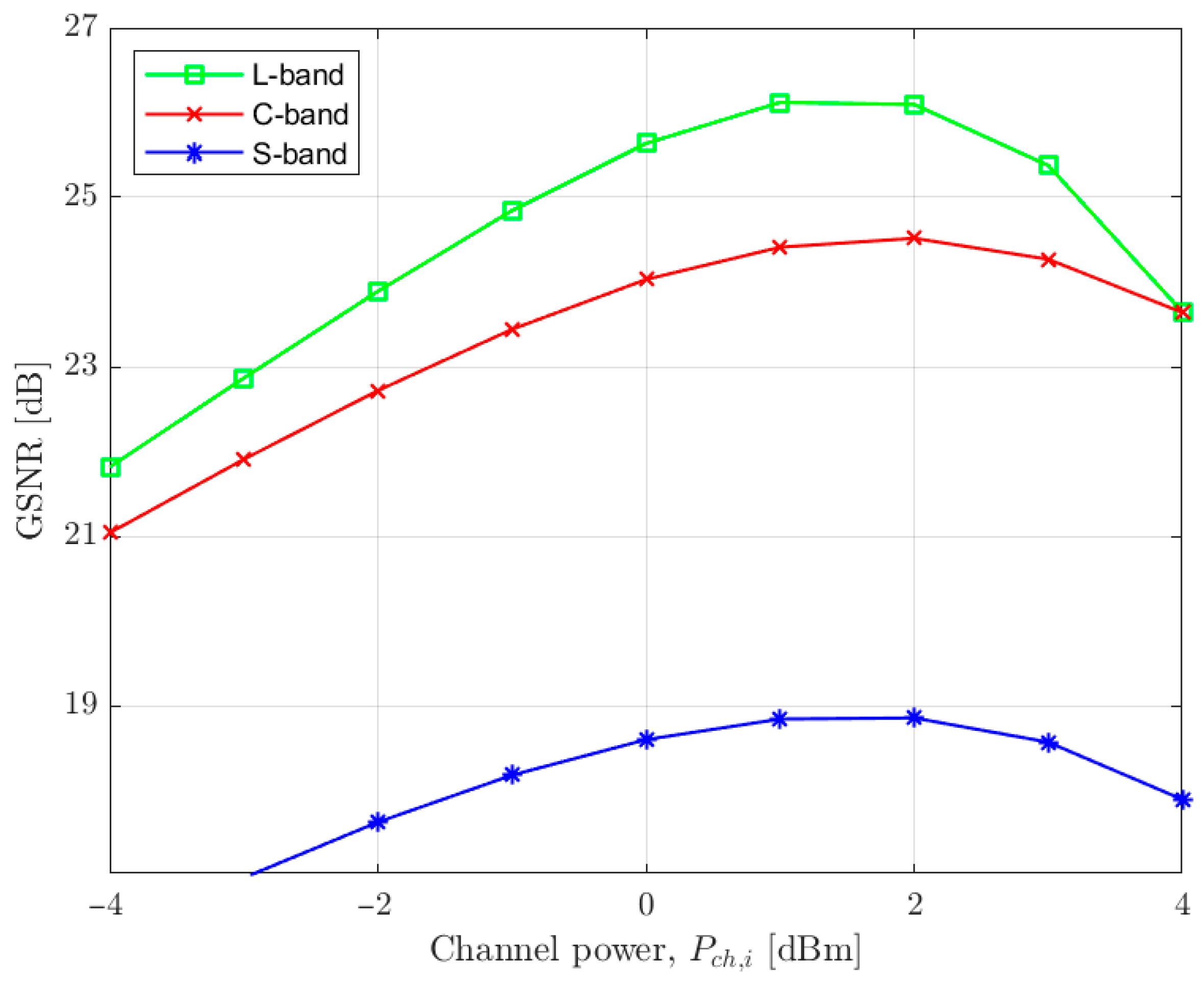
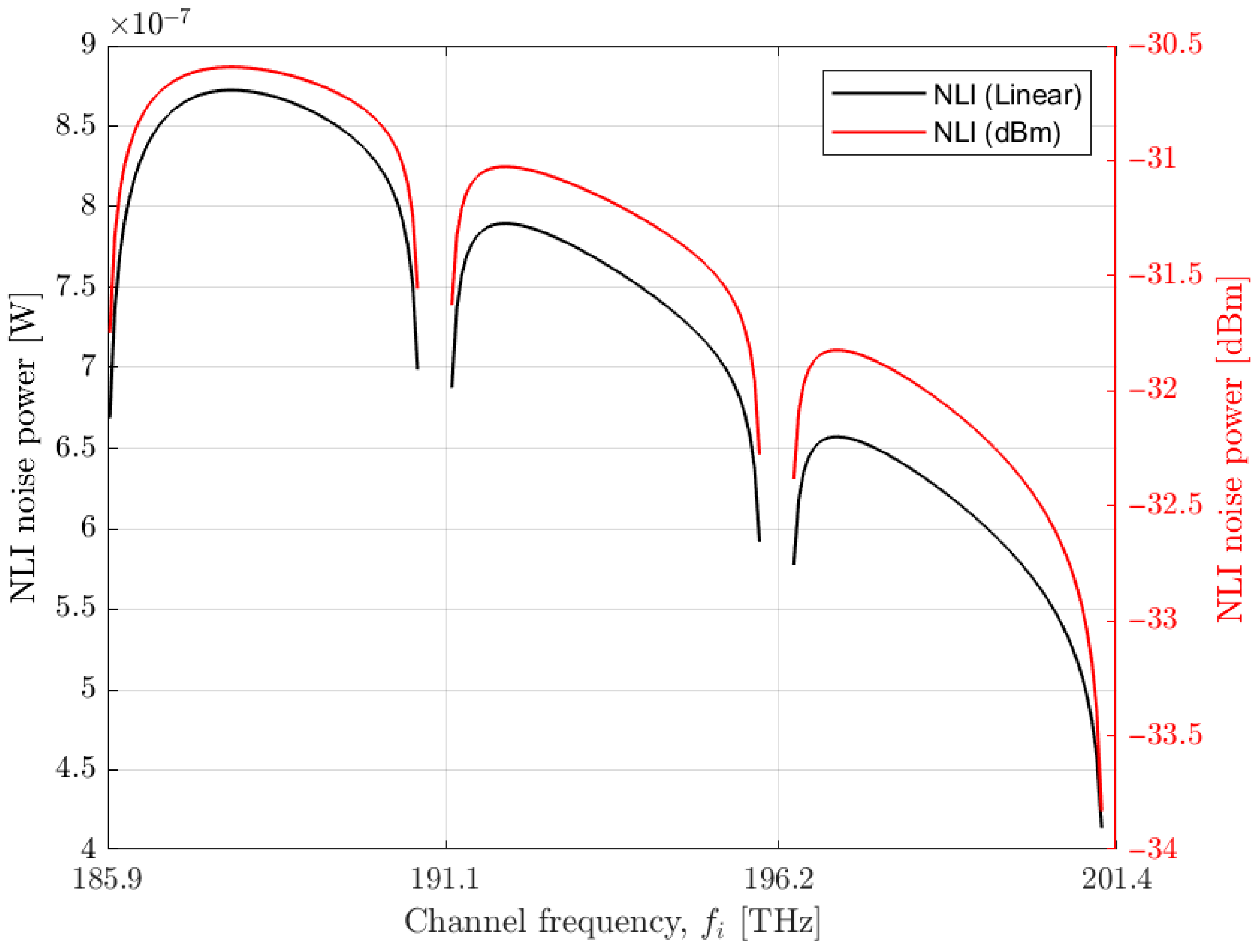
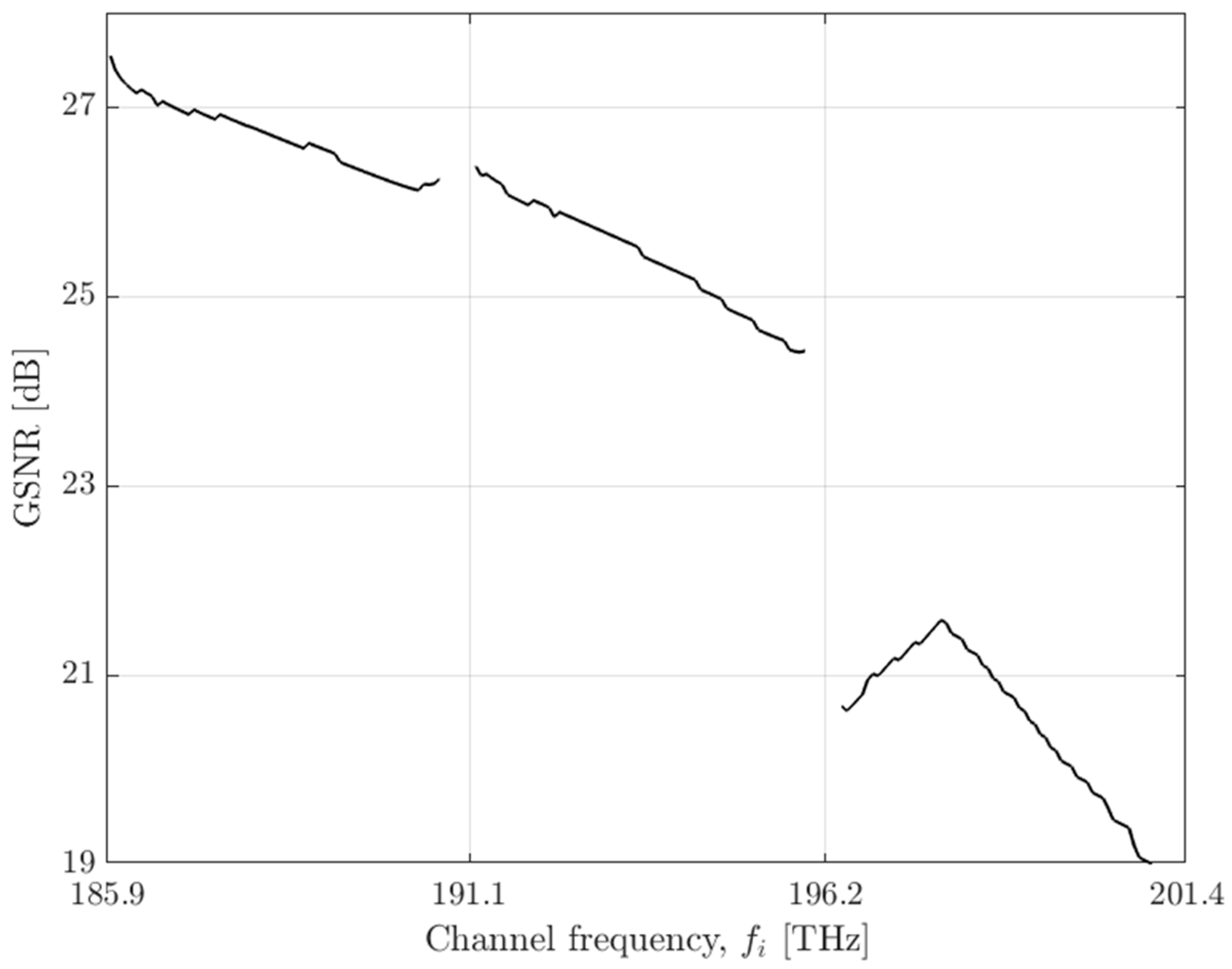
- In the first step, and assuming a single span, we assess the channel frequency for each band, considering a range of power channel values between −15 and 5 dBm, which minimizes the GSNR, given by Equation (4). The channel with the lowest GSNR is selected to represent each band, so that every channel within the band can, at least, propagate the estimated distance.
- (ii)
- In the second step, with the channel frequency assessed in step 1, we compute the GSNR as a function of the channel power, so that the power that maximizes the GSNR for each one of the bands can be found, which is called the optimum channel power. At the end of this step, we can show that the optimum channel power is 1 dBm.
- (iii)
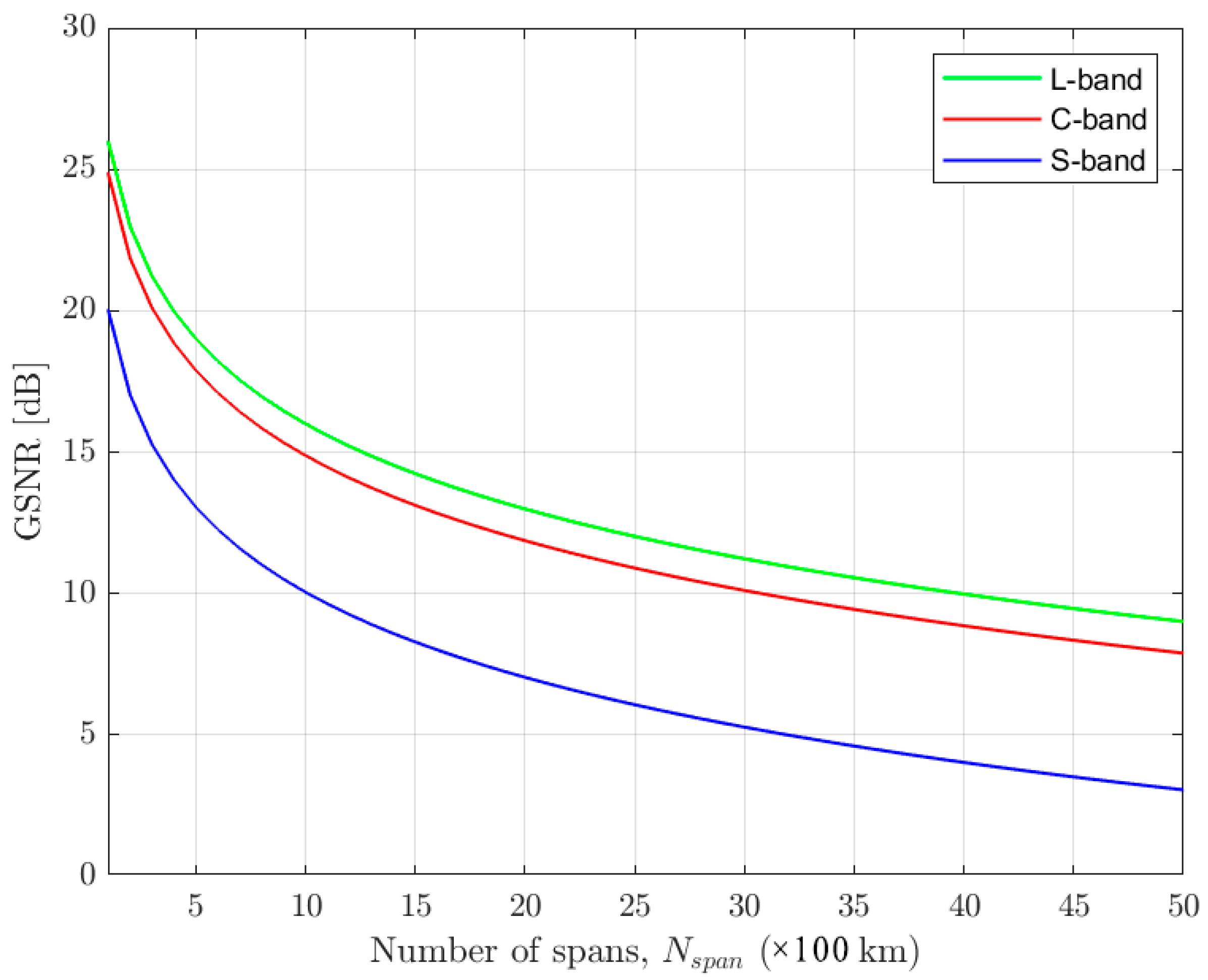
- In the third step, using the channel frequency found in step 1 and the optimum channel power found in step 2, we can compute the GSNR as a function of the number of spans.
- (iv)
- Finally, in step four, we compare the required signal-to-noise ratio (RSNR) for a particular modulation format and bit error rate (BER) with the GSNR computed in step 3 and estimate the maximum reach for each transmission band and modulation format. A fixed 2 dB system margin is assumed to account for performance-degrading effects [5].
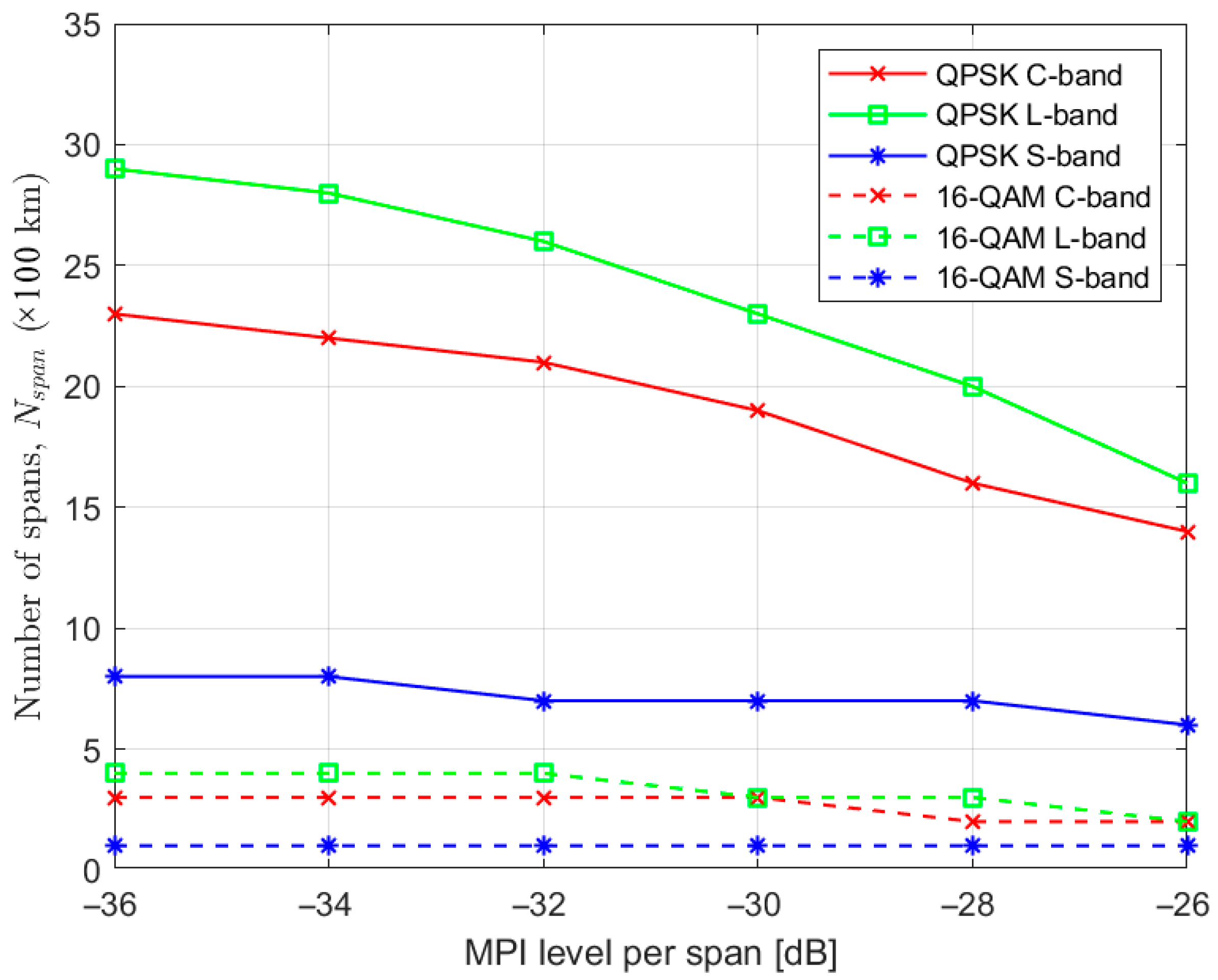
4.3. Transmission Reach Assessment with MPI
4.4. Impact of the Symbol Rate on the Transmission Reach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Winzer, P.; Neilson, D. From scaling disparities to integrated parallelism: A decathlon for a decade. J. Light. Technol. 2017, 35, 1099–1115. [Google Scholar] [CrossRef]
- Klaus, W.; Winzer, P.; Nakajima, K. The role of parallelism in the evolution of optical fiber communication systems. Proc. IEEE 2022, 110, 1619–1654. [Google Scholar] [CrossRef]
- Deng, N.; Zong, L.; Jiang, H.; Duan, Y.; Zhang, K. Challenges and enabling technologies for multi-band WDM optical networks. J. Light. Technol. 2022, 40, 3385–3394. [Google Scholar] [CrossRef]
- Cantono, M.; Schmogrow, R.; Newland, M.; Vusirikala, V.; Hofmeister, T. Opportunities and challenges of C+L transmission systems. J. Light. Technol. 2020, 38, 1050–1060. [Google Scholar] [CrossRef]
- Souza, A.; Costa, N.; Pedro, J.; Pires, J. Comparison of fast quality of transmission estimation methods for C+L+S optical systems. J. Opt. Commun. Netw. 2023, 15, F1–F12. [Google Scholar] [CrossRef]
- Puttnam, B.; Luis, R.S.; Phillips, I.; Tan, M.; Donodin, A.; Pratiwi, D.; Dallachiesa, L.; Huang, Y.; Mazur, M.; Fontaine, N.K.; et al. 402 Tb/s GMI data-rate OESCLU-band transmission. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024. paper Th4A.3. [Google Scholar]
- Radovic, M.; Sgambelluri, A.; Cugini, F.; Sambo, N. Power-aware high-capacity elastic optical networks. J. Opt. Commun. Netw. 2024, 16, B16–B25. [Google Scholar] [CrossRef]
- Ramos, J.Ó.; Cancela, L.; Rebola, J. Impact of the reconfigurable optical add-drop multiplexer architecture on the design of multi-band C+ L+ S optical networks. Opt. Fiber Technol. J. 2024, 85, 103815. [Google Scholar] [CrossRef]
- Semrau, D.; Killey, R.; Bayvel, P. A closed-form approximation of the Gaussian noise model in the presence of inter-channel stimulated Raman scattering. J. Light. Technol. 2019, 37, 1924–1936. [Google Scholar] [CrossRef]
- Yamamoto, Y. Practical Aspects of G.654.E Fibers for Terrestrial Long-Haul Transmission. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019. paper Tu3J.1. [Google Scholar]
- Recommendation ITU-T G.652; Characteristics of a Single-Mode Optical Fibre and Cable. August 2024. Available online: https://www.itu.int/ITU-T/recommendations/rec.aspx?id=13076&lang=en (accessed on 17 June 2025).
- Zhang, C.; Zhang, A.; Fan, Z.; Lv, K.; Feng, L.; Liu, Y. 400 Gb/s DWDM Field Trial over a Record Distance of 3820 km G.654.E Fiber Link with 107 GBaud Transceivers and C-band EDFAs. In Proceedings of the Asia Communications and Photonics Conference/ International Photonics and Optoelectronics Meetings (ACP/POEM), Wuhan, China, 4–7 November 2023. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Hirano, M. Ultra-low loss ITU-T 654.E Fiber ´PureAdvance´ for terrestrial optical transmission systems. Sumitomo Electr. Tech. Rev. 2023, 96, 35–39. [Google Scholar]
- Zhang, C.; Liu, X.; Li, J.; Zhang, A.; Liu, H.; Feng, L.; Lv, K.; Liao, S.; Chang, Z.; Zhang, J. Optical layer impairments and their mitigation in C+L+S+E+O multi-band optical networks with G.652 and loss-minimized G.654 fibers. J. Light. Technol. 2022, 40, 3415–3424. [Google Scholar] [CrossRef]
- Ramachandran, S.; Nicholson, J.; Ghalmi, S.; Yan, M. Measurement of multipath interference in the coherent crosstalk regime. IEEE Photon. Technol. Lett. 2003, 15, 1171–1173. [Google Scholar] [CrossRef]
- Arie, A.; Tur, M.; Goldstein, E. Probability-density function of noise at the output of a two-beam interferometer. J. Opt. Soc. Am. A 1991, 8, 1936–1942. [Google Scholar] [CrossRef][Green Version]
- Yu, C.; Wang, W.; Brorson, S. System degradation due to multipath coherent crosstalk in WDM network nodes. J. Light. Technol. 1998, 16, 1380–1386. [Google Scholar] [CrossRef]
- Travagnin, M. BER penalty induced by coherent MPI noise in FTTH optical links. J. Light. Technol. 2013, 31, 3021–3031. [Google Scholar] [CrossRef]
- Downie, J.; Mlejnek, M.; Roudas, I.; Wood, W.A.; Zakharian, A.; Hurley, J.E.; Mishra, S.; Yaman, F.; Zhang, S.; Ip, E.; et al. Quasi-Single-Mode Fiber transmission for optical communications. J. Sel. Top. Quantum Electron. 2017, 23, 31–42. [Google Scholar] [CrossRef]
- Mlejnek, M.; Roudas, I.; Downie, J.; Kaliteevskiy, N.; Koreshkov, K. Coupled-mode theory of multipath interference in quasi-single mode fibers. IEEE Photonics J. 2015, 7, 1–16. [Google Scholar] [CrossRef]
- Cancela, L.; Pires, J. Applying the skew-normal distribution to model coherent MPI and to evaluate its impact on PAM signals. Opt. Fiber Technol. J. 2020, 56, 102180. [Google Scholar] [CrossRef]
- Cancela, L.; Pires, J. MPI Impact in C+L+S Multiband Transmission Reach. In Proceedings of the Advanced Photonic Congress, Quebec City, QC, Canada, 28 July–1 August 2024. paper NeTu2C.4. [Google Scholar]
- Zheng, W.; Sardesai, H.; Taylor, M.; Craig, D.; Fowlkes, J.; Simpson, J. Measurement and system impact of multipath interference from dispersion compensating fiber modules. IEEE Trans. Instrum. Meas. 2004, 53, 15–23. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.; Newman, M. Power-law distributions in empirical data. Soc. Ind. Appl. Math. (SIAM) Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Lin, J.; Naghdi, B.; Wang, L.; Jiang, Z. Investigation of MPI Impact for Below Cut-Off Wavelength Transmission in G.654.E Fiber Link. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 24–27 October 2021. paper T4A.107. [Google Scholar]
- Semrau, D.; Killey, R.; Bayvel, P. Achievable rate degradation of ultra-wideband coherent fiber communication systems due to stimulated Raman scattering. Opt. Express 2017, 25, 13024–13034. [Google Scholar] [CrossRef]
- Mehrabi, M.; Beyranvand, H.; Emadi, M. Multi-band elastic optical networks: Inter-channel stimulated Raman scattering-aware routing, modulation level and spectrum assignment. J. Light. Technol. 2021, 39, 3360–3370. [Google Scholar] [CrossRef]
- Sadeghi, R.; Correia, B.; Souza, A.; Costa, N.; Pedro, J.; Napoli, A.; Curri, V. Transparent vs Translucent Multi-Band Optical Networking: Capacity and Energy Analyses. J. Light. Technol. 2022, 40, 3486–3498. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Hasegawa, T.; Osada, N. Low loss optical fibers for terrestrial long-haul networks, PureAdvance. Sumitomo Electr. Tech. Rev. 2021, 93, 19–24. [Google Scholar]
- Paz, E.; Saavedra, G. Maximum transmission reach for optical signals in elastic optical networks employing band division multiplexing. arXiv 2021, arXiv:2011.03671. [Google Scholar] [CrossRef]
- OpenZR+ MSA Specification, Version 3.0. Available online: https://openzrplus.org/wp-content/uploads/2024/04/openzrplus_rev3p0_final2.pdf (accessed on 17 June 2025).
- Zami, T.; Lavigne, B.; Bertolini, M. How 64 GBaud optical carriers maximize the capacity in core elastic WDM networks with fewer transponders per Gb/s. J. Opt. Commun. Netw. 2019, 11, A20–A32. [Google Scholar] [CrossRef]

| System Parameters | |||
|---|---|---|---|
| Bands | C+L+S | ||
| System bandwidth (THz) | 15.3 | ||
| Bandgaps (GHz) | 500 | ||
| Channel spacing (GHz) | 37.5 | 75 | 137.5 |
| Number of channels | 384 | 192 | 102 |
| Number of channels per band | 128 | 64 | 34 |
| Symbol rate (GBaud) | 32 | 64 (reference scenario) | 128 |
| Span length (km) | 100 | ||
| Splice loss (dB) | 0.0043 to 0.068 | ||
| Splice distance (km) | 4.2 | ||
| Band (de)multiplexer loss (dB) | 1 | ||
| Amplifier gain | compensate for span loss and ISRS effect | ||
| Amplifier noise figure | as in [5] | ||
| Channel launch power (dBm) | −2 | 1 | 4 |
| G.654E SMF Parameters | |
| Dispersion parameter (ps/nm/km) | 21 |
| Loss coefficient (dB/km) | 0.17 |
| Raman gain profile (W·THz·km)−1 | 0.018 |
| Core effective area (µm2) | 125 |
| Modulation Format | Bit Rate (Gbit/s) | ROSNR in the Reference Bandwidth of 12.5 Ghz (dB) [31] | RSNR in the Signal Bandwidth (dB) |
|---|---|---|---|
| QPSK | 200 | 16 | 8.9 |
| 16-QAM | 400 | 24 | 16.9 |
| Symbol Rate (GBaud) | No MPI | −36 dB/span | −34 dB/span | −32 dB/span | −30 dB/span | −28 dB/span |
|---|---|---|---|---|---|---|
| 32 | 33 | 30 | 28 | 26 | 23 | 20 |
| 64 | 33 | 29 | 28 | 26 | 23 | 20 |
| 128 | 31 | 28 | 27 | 25 | 22 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cancela, L.; Pires, J. Multipath Interference Impact Due to Fiber Mode Coupling in C+L+S Multiband Transmission Reach. Photonics 2025, 12, 770. https://doi.org/10.3390/photonics12080770
Cancela L, Pires J. Multipath Interference Impact Due to Fiber Mode Coupling in C+L+S Multiband Transmission Reach. Photonics. 2025; 12(8):770. https://doi.org/10.3390/photonics12080770
Chicago/Turabian StyleCancela, Luís, and João Pires. 2025. "Multipath Interference Impact Due to Fiber Mode Coupling in C+L+S Multiband Transmission Reach" Photonics 12, no. 8: 770. https://doi.org/10.3390/photonics12080770
APA StyleCancela, L., & Pires, J. (2025). Multipath Interference Impact Due to Fiber Mode Coupling in C+L+S Multiband Transmission Reach. Photonics, 12(8), 770. https://doi.org/10.3390/photonics12080770





