Impact of Corneal-Hydration-Induced Changes in Ablation Efficiency During Refractive Surgery

Abstract

(1) Background: A decrease in corneal hydration during refractive surgery is observed clinically as well as in laboratory settings, but the associated consequences are not yet fully understood. The purpose of this paper is to analyze the impact of the gain of ablation efficiency due to hydration changes during cornea refractive surgery. (2) Methods: We developed a simulation model to evaluate the influence of hydration changes on the ablation algorithms used in laser refractive surgery. The model simulates different physical effects of an entire surgical process, simulating the shot-by-shot ablation process based on a modeled beam profile. The model considers corneal hydration, as well as environmental humidity, along with the laser beam characteristics and ablative spot properties for evaluating any hydration changes and their effect on laser refractive surgery. (3) Results: Using pulse lists collected from actual treatments, we simulated the gain of efficiency during the ablation process. Ablation efficiency is increased due to dehydration effects during laser treatments. Longer treatments suffer larger dehydration effects and are more prone to overcorrections due to gain of efficiency than shorter treatments. (4) Conclusions: The improper use of a model that overestimates or underestimates the effects derived from the hydration dynamics during treatment may result in suboptimal refractive corrections. This model may contribute to improving emmetropization and the correction of ocular aberrations with improved laser parameters that can compensate for the changes in ablation efficiency due to hydration changes in the cornea.

1. Introduction

Laser refractive surgery is an ophthalmic technique used to reshape the cornea for the correction of refractive errors. In this technique, a laser beam is applied to the corneal surface for the ablation of tissue [1]. Using a flying-spot laser beam, better control is possible over the laser energy delivery at each corneal position and therefore provides the laser systems with a better capability to reproduce details accurately [2]. To implement the wavefront-based customized ablation, a surgical laser system must be capable of reproducing the details of complex wavefront-driven ablations while reducing the induction of high-order aberrations in the process [3,4]. It is well known that successful surgery depends on the correct design of an ablation profile, precise delivery of laser energy to the corneal position, and reliable understanding of the corneal tissue response.

Since the introduction of laser refractive surgery, technology has evolved significantly. Modern technology uses sophisticated algorithms, optimized tools in planning, and poses the challenge of improving surgery outcomes in terms of visual acuity and night vision. At the same time, patients are better informed about the potential of laser refractive surgery, raising the quality requirements demanded by the patients.

A decrease in corneal hydration during refractive surgery has been observed clinically [5,6,7,8,9], as well as in laboratory settings [10]. The changes in corneal hydration during the refractive surgery procedures and their associated consequences are not yet fully understood. Researchers have explored the qualitative relationship between the ablation rate of the cornea and the hydration level of the cornea.

Dougherty [5] delineates two ablation rates, a dry (essentially collagen) and a wet (water and collagen) ablation rate, with the former inversely proportional and the latter directly proportional to hydration. Dougherty [5] confirmed that the dry ablation rate correlates more with refractive outcome. Contrary to these results, Fisher et al. [10] predicted a direct proportionality and a non-linear relationship between hydration and ablation rate. They quantified corneal hydration using confocal micro-Raman spectroscopy. They demonstrated that in bovine eyes, significant changes in corneal hydration occurred under different drying conditions and treatment methodologies, with increased hydration reducing the relative concentration of collagen, thereby slowing the kinetics of the formation of the transient absorber and thereby reducing the degree of dynamic absorptivity.

Several researchers have explored various anatomical and physiological features of the human cornea based on the water content of the cornea. Patel et al. [11] estimated an equivalent percentage of water content in the anterior layers of the human cornea before and after excimer laser photoablation using a novel contact device, the VCH-1. With their setup, they were able to estimate water content with an error range of +/−0.6%. They found that the water content of the human cornea was not uniform, and intersubject and intracorneal variations should be considered, since they affect the optical performance of the eye. Müller et al. [12] analyzed the human corneal stroma in extreme hydration to discover if its structure is responsible for corneal stability. They found that the rigidity of the most anterior part of the corneal stroma in extreme hydration states points to an important role in maintaining the corneal curvature.

Maintaining safe corneal thickness during the refractive procedures is essential for the post-surgical corneal health. Online optical coherence pachymetry techniques cater to this concern. Neuhann et al. [13,14] evaluated the reliability and applicability of online optical coherence pachymetry under routine clinical conditions and found that OCP-online technology provided reliable intraoperative noncontact pachymetry measurements integrated into a clinical flow, indicating that the technology has the potential to improve the safety of corneal ablation procedures. Pfaeffl et al. [14,15] evaluated possible factors responsible for the difference between predicted and measured thickness parameters using online optical coherence pachymetry.

Modern refractive surgery techniques enable the correction of visual defects such as myopia [16], hyperopia [17], or astigmatism [18]. Achieving high precision in clinical outcomes and minimizing the need for retreatment remain primary objectives in refractive procedures. Accurate calibration of excimer lasers is essential in meeting these goals. Multiple factors influence laser-tissue interaction and surgical outcomes, including laser energy delivery [19,20], ablation decentration and registration [21,22], eye tracking [23,24], flap [25], physical characteristics of ablation [26,27,28,29,30,31,32], as well as corneal wound-healing and biomechanical response [33,34,35,36]. These parameters have been extensively investigated to explain discrepancies between the intended and actual refractive outcomes.

Among these, corneal hydration has emerged as a critical yet less quantified factor that influences ablation efficiency. Changes in stromal hydration during surgery can alter the ablation rate, potentially compromising precision. This underscores the need to explore a quantitative relationship between corneal hydration and the ablation rate. In this study, we investigate this relationship through a simulation model that accounts for key physical parameters of the refractive procedure. The model replicates the shot-by-shot laser ablation process using a spatially resolved laser beam profile. The aim is to assess how hydration-induced variations in ablation efficiency can be compensated by adjusting laser parameters, thereby contributing to more precise and predictable outcomes in refractive surgery.

2. Materials and Methods

2.1. Changes of Corneal Hydration with Time

The hydration model describes the variation of water content in the cornea over time. The hydration model is characterized by transient smoothing of the initial water content in the cornea asymptotic to the relative humidity of the environment tending towards stable equilibrium [37,38]. The variation of the water content of the cornea is dependent on the driving forces governed by the physical laws. The driving forces for achieving such an equilibrium state are the partial pressure difference due to the hydration state of the corneal surface and the surrounding environment, along with the difference in the temperature of the corneal surface and the surrounding environment [39].

For the sake of simplicity, in our model we have made some assumptions. We have assumed an asymptotic negative exponential behavior of corneal hydration based on our internal experimental results, as follows:

$$\mathrm{H}\left(\mathrm{t}\right)={\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}+\left({\mathrm{H}}_0-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}\right)\cdot {\mathrm{e}}^{-{\displaystyle \frac{\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}$$

(1)

where H(t) is the corneal hydration as a function of time, Henv is the asymptotic hydration (humidity of the environment), H₀ is the initial corneal hydration, t is the time, and τ_h is a positive time constant (the relaxation time for which the difference in hydration states drops to 1/e of its original value). The exponential model applied to fit our internal experimental data is commonly used to characterize corneal recovery from a swollen state—a relevant analogy that can be extended to the present context [40,41,42,43,44]. The parameters used in Equation (1) should not be interpreted as a true diffusion model due to the assumed approximations. We assume the difference in the hydration of the corneal surface and in the surrounding environment as the driving force for the variation in the water content. Although this is different compared to assuming the partial pressure difference, the fact that the hydration levels of the cornea and the relative humidity (RH) of the environment are proportional to the partial pressure makes our approximations reasonable. Furthermore, the same cannot be said when one excludes the effect of temperature in this physical phenomenon, but we exclude the temperature dependence, since we base our model and findings on the experimental data collected at normal temperature.

Due to this simplicity induced by the approximations, the exponential decay is independent from the exact time stamp considered and only depends on the Δt interval:

$$\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0+\mathsf{\Delta }\mathrm{t}\right)=\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-{\displaystyle \frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}$$

(2)

The model can be normalized to the initial hydration state in order to obtain the relative hydration state (H_r):

$${\mathrm{H}}_{\mathrm{r}}\left(\mathrm{t}\right)={\displaystyle \frac{{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}}{{\mathrm{H}}_0}}+\left(1-{\displaystyle \frac{{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}}{{\mathrm{H}}_0}}\right)\cdot {\mathrm{e}}^{-{\displaystyle \frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}$$

(3)

Or, using Equations (1) and (2), we obtain

$${\mathrm{H}}_{\mathrm{r}}\left({\mathrm{t}}_0+\mathsf{\Delta }\mathrm{t}\right)={\mathrm{H}}_{\mathrm{r}}\left({\mathrm{t}}_0\right)\cdot {\displaystyle \frac{{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}+\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-\frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}{{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}+\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)}}$$

(4)

2.2. Change in Ablation Efficiency Due to Variations in Corneal Hydration

From the variation of water content in the cornea over time, the change of ablation efficiency over time can be estimated.

The relative efficiency effect (Eff) is inversely proportional to the relative hydration effect. Therefore:

$$\mathrm{E}\mathrm{f}\mathrm{f}\left(\mathrm{t}\right)={\displaystyle \frac{1-\mathrm{H}\left(\mathrm{t}\right)}{1-{\mathrm{H}}_0}}$$

(5)

Combining with Equations (2) and (4),

$$\mathrm{E}\mathrm{f}\mathrm{f}\left({\mathrm{t}}_0+\mathsf{\Delta }\mathrm{t}\right)=\mathrm{E}\mathrm{f}\mathrm{f}\left({\mathrm{t}}_0\right)\cdot {\displaystyle \frac{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-\frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)}}$$

(6)

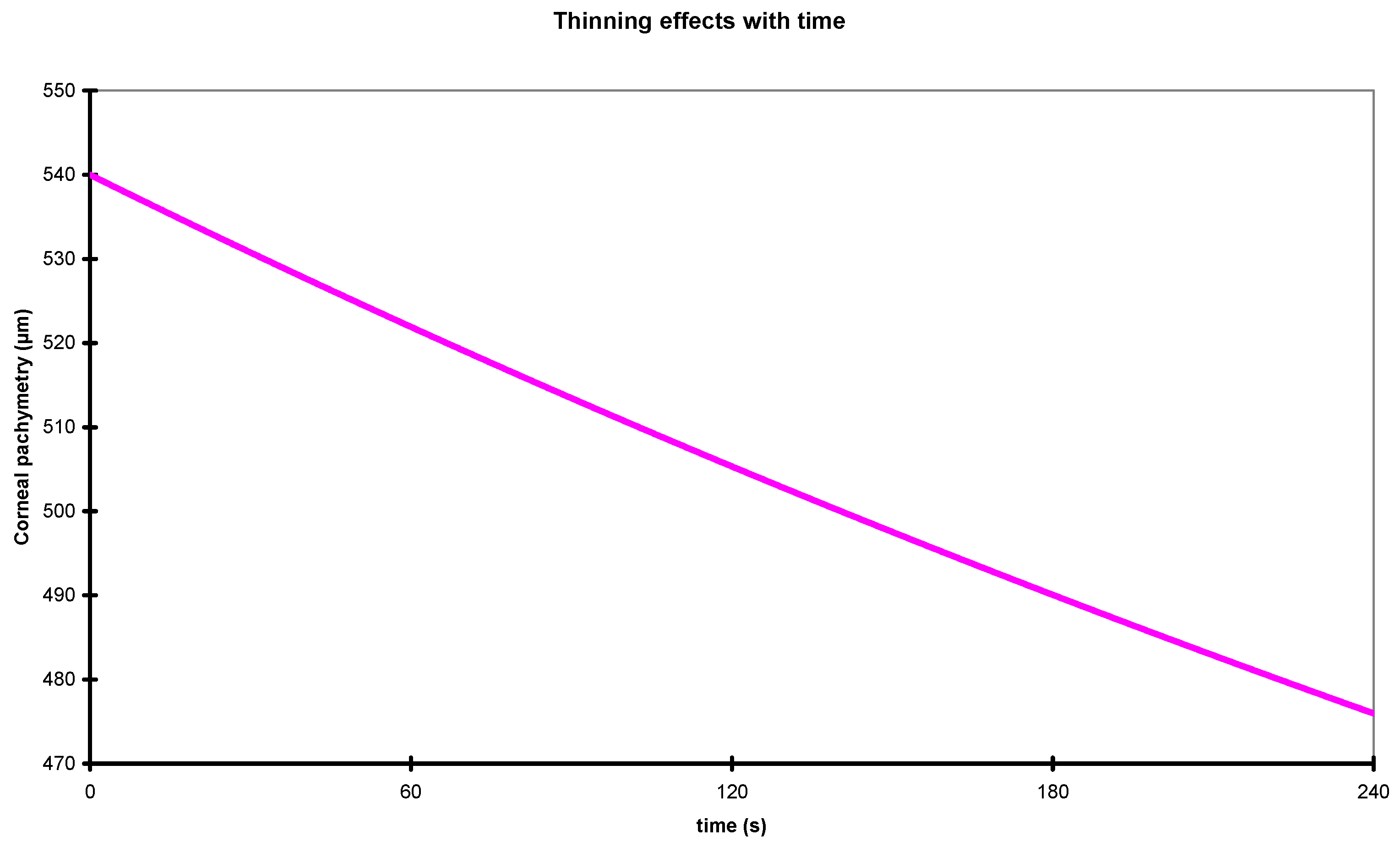
2.3. Corneal Thinning with Time

From the variation of water content in the cornea over time, the variation of corneal thickness over time can be estimated. The hydration model used is a simple diffusion model, which can be obtained from simple propagation models by assuming that the environment is much bigger than the tissue where the diffusion mainly occurs [45].

The hydration state at the time t is the ratio of the amount of water volume and the total corneal volume at this moment in time:

$$\mathrm{H}\left(\mathrm{t}\right)={\displaystyle \frac{\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)}{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)}}$$

(7)

Considering that dehydration simply means loss of water, and that the cornea is composed of water and solid cornea [solid components, primarily collagen and other extracellular matrix proteins] [46], which is invariant for hydration levels, the relative thinning effect (between initial state represented with “0” and current state at time “t”) produced by the relative hydration state is

$$\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)-\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)=\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(0\right)-\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(0\right)$$

(8)

Thus,

$$\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)\cdot \left(1-\mathrm{H}\left(\mathrm{t}\right)\right)=\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(0\right)\cdot \left(1-\mathrm{H}\left(0\right)\right)$$

(9)

$${\displaystyle \frac{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(\mathrm{t}\right)}{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left(0\right)}}={\displaystyle \frac{1-\mathrm{H}\left(0\right)}{1-\mathrm{H}\left(\mathrm{t}\right)}}$$

(10)

Or,

$$\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}{\mathrm{e}}_{\mathrm{r}}\left(\mathrm{t}\right)={\displaystyle \frac{1-{\mathrm{H}}_0}{1-{\mathrm{H}}_0\cdot {\mathrm{H}}_{\mathrm{r}}\left(\mathrm{t}\right)}}$$

(11)

Combining with Equations (2) and (4),

$$\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left({\mathrm{t}}_0+\mathsf{\Delta }\mathrm{t}\right)=\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\left({\mathrm{t}}_0\right)\cdot {\displaystyle \frac{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)}{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-\frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}}$$

(12)

2.4. Change in Ablation Efficiency Due to Variations in Corneal Hydration and Thickness

Since an incoming laser spot will have a different efficiency due to variations in corneal hydration and simultaneous change in corneal thickness due to the same variations in corneal hydration, the global gain in ablation efficiency (AblEff) is the combination of Equations (6) and (12):

$$\mathrm{A}\mathrm{b}\mathrm{l}\mathrm{E}\mathrm{f}\mathrm{f}\left({\mathrm{t}}_0+\mathsf{\Delta }\mathrm{t}\right)=\mathrm{A}\mathrm{b}\mathrm{l}\mathrm{E}\mathrm{f}\mathrm{f}\left({\mathrm{t}}_0\right)\cdot {\left({\displaystyle \frac{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-\frac{\mathsf{\Delta }\mathrm{t}}{{\mathsf{\tau }}_{\mathrm{h}}}}}{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)}}\right)}^2$$

(13)

2.5. Analysis of the Impact of the Change in Ablation Efficiency Due to Variations in Corneal Hydration and Thickness in Refractive Surgery Treatments

Considering a laser system for refractive surgery (without compensations for these hydration effects) with a known treatment time per corrected diopter, and assuming that the generic ablation algorithms for this laser system distribute the shots in a sequence that removes the tissue smoothly and progressively across the whole cornea over the course of ablation, the deviations between attempted and achieved corrections (in terms of the corneal hydration) can be calculated by averaging the efficiency (Equation (13)) over the course of the ablation.

A simple estimation of this effect is provided by

$$\mathrm{A}\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{A}\mathrm{b}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{A}\mathrm{b}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\cdot {\displaystyle \frac{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)\cdot {\mathrm{e}}^{-\frac{\mathrm{A}\mathrm{b}\mathrm{l}\mathrm{T}\mathrm{i}\mathrm{m}\mathrm{e}}{{\mathsf{\tau }}_{\mathrm{h}}}}}{1-{\mathrm{H}}_{\mathrm{e}\mathrm{n}\mathrm{v}}-\mathsf{\Delta }\mathrm{H}\left({\mathrm{t}}_0\right)}}$$

(14)

Here, the “AblTime” represents the time required to achieve the attempted ablation without compensations for the hydration effects.

Conversely, the nomogrammed correction to be planned in order to achieve the attempted correction while compensating the effects of corneal dehydration can be estimated as

$$NomogrammedAblation=AttemptedAblation\cdot {\displaystyle \frac{1-H_{env}-\Delta H\left(t_0\right)}{1-H_{env}-\Delta H\left(t_0\right)\cdot e^{-\frac{AblTime}{{\tau }_h}}}}$$

(15)

3. Results

For our simulations we have considered H_env (humidity of the environment) of 45%, H₀ (natural corneal hydration) of 80%, and τ_h (the relaxation time for which the difference in hydration states drops to 1/e of its original value) of 3000 s. Using pulse lists collected from actual treatments, we simulated the gain of efficiency during the ablation process.

3.1. Change in Ablation Efficiency Due to Variations in Corneal Hydration and Thickness

Figure 1 shows that corneal hydration decreased almost linearly with time.

As the corneal hydration decays with time, the ablation efficiency becomes higher (following Equation (13)). This change is shown in Figure 2.

As the corneal hydration decays with time, the cornea becomes thinner (following Equation (12)). This change is shown in Figure 3.

The ablation efficiency combined from the decay in corneal hydration and the derived corneal thinning is shown in Figure 4 (following Equation (14)).

3.2. Analysis of the Impact of the Change in Ablation Efficiency Due to Variations in Corneal Hydration and Thickness in Refractive Surgery Treatments

Assuming a refractive laser system that does not incorporate compensation for corneal hydration effects, and for which the treatment time per corrected diopter is known, we consider a generic ablation algorithm that distributes laser pulses in a smooth and progressive manner across the corneal surface. Under these conditions, deviations between the intended and achieved corrections can be estimated using Equation (14). The corresponding results are illustrated in Figure 5.

Same applies for the deviations between attempted and planned corrections estimated from Equation (15). The results are depicted in Figure 6.

4. Discussion

Achieving accurate clinical outcomes and reducing the likelihood of a retreatment procedure depends partly on accurately calibrated lasers. Parallel to clinical developments, increasingly capable, reliable, and safer laser systems with better resolution and accuracy are required.

Excessive dehydration of the cornea is an effect that should be avoided in commercial laser systems using sophisticated algorithms that cover most of the possible variables. This study provides analytical expressions for calculation of the dehydration of the cornea and derived effects related to the ablation process. The model directly considers applied corneal hydration, including the humidity of the environment. Separate analysis of the effect of each parameter was performed.

For our simulations we have considered H_env (humidity of the environment) of 45%, H₀ (natural corneal hydration) of 80%, and τ_h (the relaxation time for which the difference in hydration states drops to 1/e of its original value) of 3000 s, which seem to be consistent with the measurements reported in the recent literature [47,48,49].

For the sake of simplicity, we introduce some approximations in our approach in defining the driving forces for the physical basis of corneal dehydration. Hence, these parameters should not be taken as a true diffusion model. However, the direct relation of the hydration state of the cornea and the relative humidity of the environment with the partial pressure make our assumptions reasonably related to the physical phenomenon. In addition to this, another limitation of our model can be projected as not considering the effect of temperature on the physical phenomenon. We, however, base our model on internal experimental data collected at normal temperatures, giving us the possibility to exclude temperature as an affecting parameter. It should be mentioned here that the completeness of our model is affected by making such assumptions.

Modern high-speed excimer platforms may be associated with increased local thermal load, which may amplify dehydration dynamics. Shraiki and Arba-Mosquera [50] have evaluated algorithms and temperature changes in laser refractive surgery in the past, introducing a model that provides analytical expressions for the thermal load of the treatments, including cooling and heat propagation. Their proposed Virtual Laser System simulated temperature increase during the photoablation process, showing that ablation efficiency reduction in the periphery results in a lower peripheral temperature increase; steep corneas have lesser temperature increases than flat ones, and the maximum rise in temperature depends on the spatial density of the ablation pulses. A future expansion of this work could be to combine the two simulation models and incorporate the local increase in temperature in the analysis.

Our results (Figure 3) demonstrate time-dependent corneal thinning associated with a non-linear decrease in corneal hydration. This effect is particularly relevant at the periphery of the treatment zone in cases of hypercorrection during long-duration or high-diopter ablations. In such scenarios, localized corneal drying may occur, potentially affecting optical aberrations due to interactions with the laser beam profile at the treatment boundaries. The ablation efficiency combined from the decay in corneal hydration and the derived corneal thinning is shown in Figure 4, which seems to be consistent with the measurements reported by Dougherty et al. [5].

Our interpretation of the results of Dougherty [5] and Fisher et al. [10] is that, as Fisher [10] predicts, for natural corneal status, increased hydration reduces the relative concentration of collagen in the cornea. With the progressing refractive treatment, corneal tissue is removed, and a higher amount of water evaporates, leading to an increase in the relative concentration of collagen, and more importantly thinning of the cornea [5].

The hydration state of the cornea during surgery mainly depends on the duration of the surgery, the initial corneal hydration, and the humidity of the environment. Derived effects related to the ablation process can be easily determined.

Since τ_h = 3000 s represents a very slow process, even for long times (up to 600 s), the corneal hydration decays almost linearly with time. As the corneal hydration decays with time, the ablation efficiency becomes higher, and the corneal pachymetry becomes thinner. Qi et al. [49] used near-infrared absorption spectroscopy to measure the relative water content of the corneal stroma ex vivo. They have reported that the relative water content of fresh corneal stroma during dehydration under natural conditions (temperature, 25.8 ± 0.3 °C; humidity, 7.2% ± 0.9%) and the characteristic time τ when the relative water content dropped to 90% of the fresh corneal stroma was 140.1 ± 30.6 s. The change in the relative water content over time was found to be linear in this work, with a dehydration rate of 0.071% per second. In contrast, other studies that quantitatively analyze human corneal dehydration suggest that the process is non-linear, with a quadratic stromal thickness–time fitting curve more accurately reflecting the observed trend in water loss [51].

If no corneal hydration models (relative to the ablation process) are established for the system, deviations from the attempted corrections can be expected.

During the short surgical procedure, the transient process could accelerate the process of dehydration due to dynamic phenomena of fluid dynamics, for example vortex and increasing temperature induced by the laser beam during the short ablation of the cornea. Non-mechanical variables introduced by differing surgical techniques may influence the application of this model. A common procedural step involves wetting the corneal surface, either immediately before lifting the flap in LASIK or after epithelial removal in PRK, followed by drying the surface using Weck sponges. The interval between drying and the onset of laser ablation typically ranges from 5 to 10 s and varies by surgeon. This model can be adapted to account for such variability by incorporating the effect of delayed ablation onset. In this context, the pre-ablation waiting time can be treated as a discrete hydration phase, while changes occurring during laser application are modeled as a time-dependent accumulation, akin to a weighted integral over the duration of the laser treatment. These considerations also emphasize the need for standardized surgical protocols in refractive procedures. Minimizing variability introduced by technique-dependent factors is crucial for reducing confounding influences and supporting the development of robust, generalized optimization models.

The range for required time per corrected diopter of the excimer laser systems for refractive surgery available in the market runs from about 20 s/D to about 2 s/D, corresponding for a planned correction of 7 D to achieved ablations of about 7.6 D and about 7.1 D, respectively. For excimer laser systems treating with a speed of about 5 s/D and about 10 s/D, the overcorrections start being noticeable from about 10 D and about 7 D, respectively. Larger deviations occur for slower systems, as opposed to a nearly linear nature for faster systems.

For the range of excimer laser systems for refractive surgery available in the market treating with a speed from about 20 s/D to about 2 s/D, for achieving a correction of 10 D, ablations of about 9 D and about 9.9 D, respectively, should be planned. For excimer laser systems treating with a speed of about 5 s/D and 10 s/D, the nomogrammed underplans start being noticeable from about 10 D and about 7 D, respectively.

Assuming a refractive laser system with stochastic distribution of pulses (as commonly used in all flying-spots),

Table 1. Real-world examples of refractive corrections using laser systems with varying correction speeds. The table presents the calculated differences between attempted and achieved corrections, along with the corresponding nomogram factors, based on the proposed mathematical model assuming a stochastic distribution of laser pulses. Note that larger deviations are observed with slower systems and greater attempted corrections. The model is independent of the type of refractive correction; therefore, absolute values of the attempted corrections are provided.

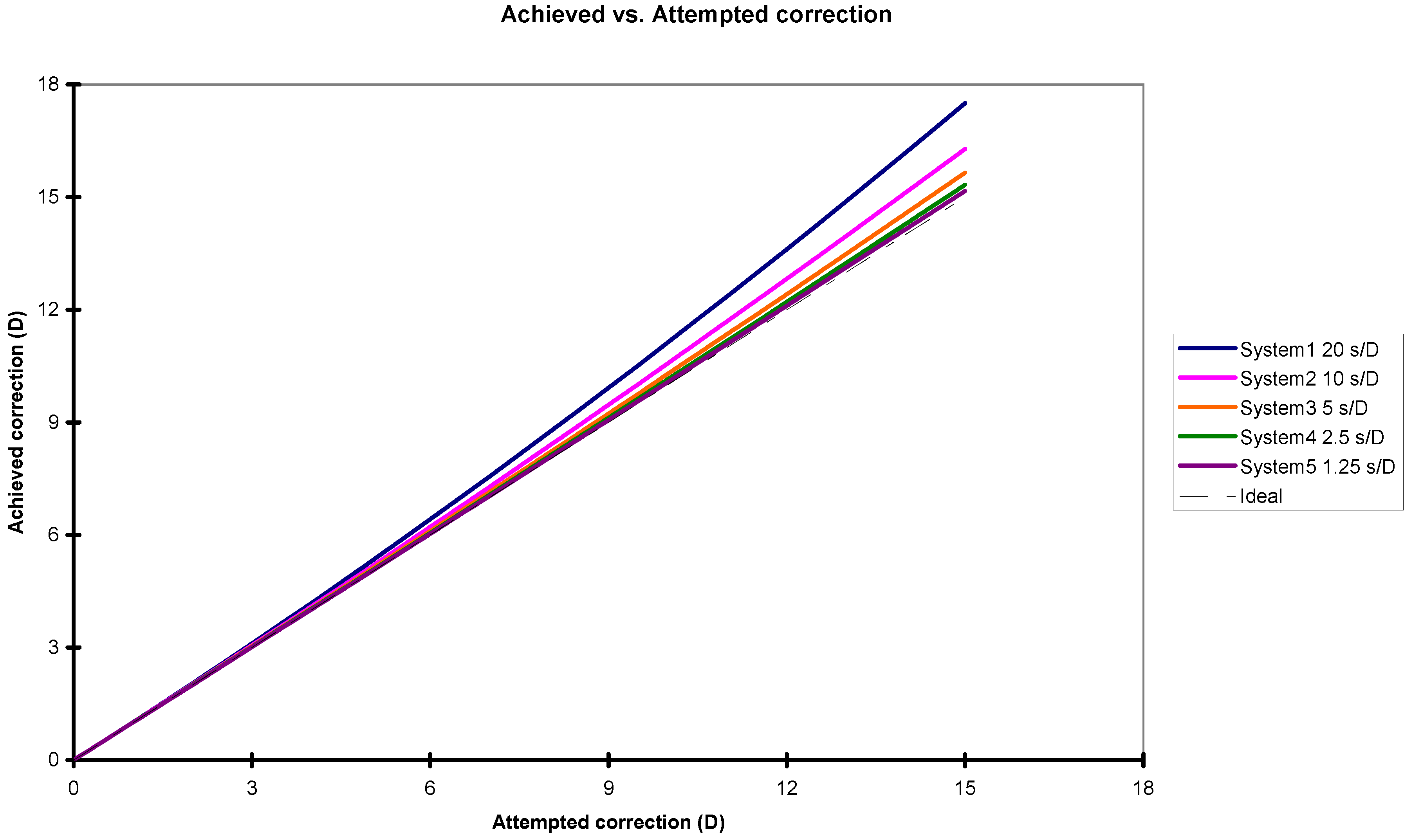
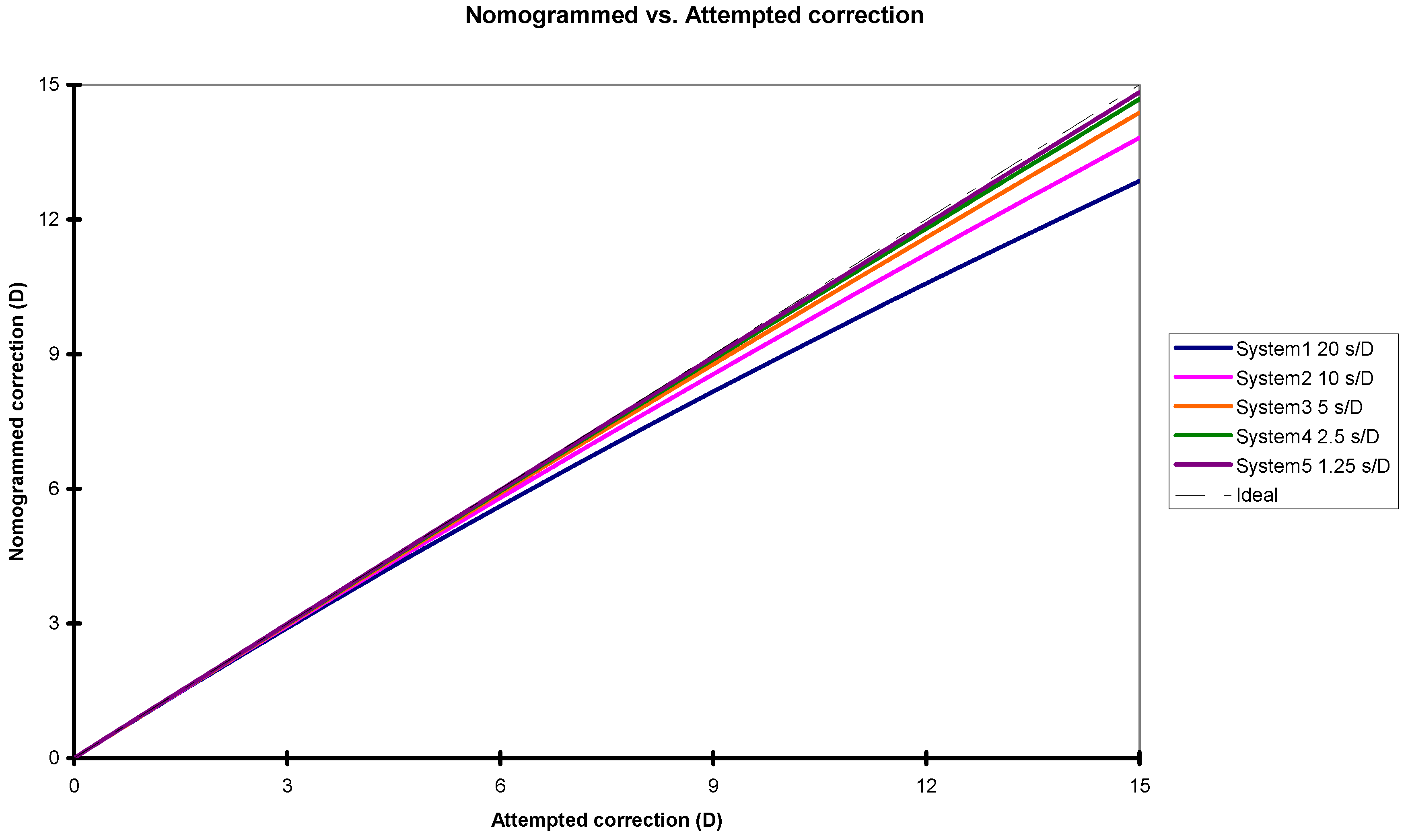
Attempted Correction (Diopter)	System Correction Speeds: 20 s/D		System Correction Speeds: 10 s/D		System Correction Speeds: 5 s/D		System Correction Speeds: 2.5 s/D		System Correction Speeds: 1.25 s/D
	Achieved Correction in D	Nomogram Factor in Percentage	Achieved Correction in D	Nomogram Factor in Percentage	Achieved Correction in D	Nomogram Factor in Percentage	Achieved Correction in D	Nomogram Factor in Percentage	Achieved Correction in D	Nomogram Factor in Percentage
1.00	1.01	−1.1%	1.01	−0.6%	1.00	−0.3%	1.00	−0.1%	1.00	−0.1%
2.00	2.05	−2.3%	2.02	−1.1%	2.01	−0.6%	2.01	−0.1%	2.00	−0.1%
3.00	3.10	−3.3%	3.05	−1.7%	3.03	−0.9%	3.01	−0.2%	3.01	−0.2%
4.00	4.18	−4.4%	4.09	−2.3%	4.05	−1.1%	4.02	−0.3%	4.01	−0.3%
5.00	5.29	−5.4%	5.14	−2.8%	5.07	−1.4%	5.04	−0.4%	5.02	−0.4%
6.00	6.41	−6.4%	6.21	−3.3%	6.10	−1.7%	6.05	−0.4%	6.03	−0.4%
7.00	7.56	−7.4%	7.28	−3.9%	7.14	−2.0%	7.07	−0.5%	7.04	−0.5%
8.00	8.73	−8.3%	8.37	−4.4%	8.19	−2.3%	8.09	−0.6%	8.05	−0.6%
9.00	9.92	−9.2%	9.47	−4.9%	9.23	−2.5%	9.12	−0.7%	9.06	−0.7%
10.00	11.13	−10.1%	10.57	−5.4%	10.29	−2.8%	10.15	−0.7%	10.07	−0.7%
11.00	12.36	−11.0%	11.69	−5.9%	11.35	−3.1%	11.18	−0.8%	11.09	−0.8%
12.00	13.61	−11.9%	12.82	−6.4%	12.42	−3.3%	12.21	−0.9%	12.10	−0.9%
13.00	14.89	−12.7%	13.96	−6.9%	13.49	−3.6%	13.25	−0.9%	13.12	−0.9%
14.00	16.18	−13.5%	15.12	−7.4%	14.57	−3.9%	14.28	−1.0%	14.14	−1.0%
15.00	17.50	−14.3%	16.28	−7.9%	15.65	−4.1%	15.33	−1.1%	15.16	−1.1%

presents real-world examples, including cases of hypercorrection in long or high-diopter treatments to illustrate the clinical relevance of the model and its potential (in form of nomogram parameters) to guide practical improvements in refractive outcomes.

The simple hydration model used here considers corneal hydration as an overall macroscopic quality, neglecting varying hydration states within the cornea. Particularly in the surgical situation, hydration gradients are very likely to exist within the volume of the cornea, as only part of the surface is exposed to air. Excimer laser ablation is a surface effect, so one expects surface hydration to be more important than volume hydration. The ablation itself is a dynamic process, with water from the cornea sometimes flowing to the surface. The model can be also generically expanded to other laser tissue interactions, for example to treatments based on an optical breakdown (like KLEx or Kerato Lenticule Extraction procedures). Although, in case of this extension of the model, not only the time before the treatment but likely also the applied suction has a dynamic effect on hydration, further affecting the breakdown threshold and corresponding bubble size. All of these probable factors affect the outcomes of the model. The simplifications considered in this work are justified for the situation of interest—the dehydration of the cornea during the short surgical procedure.

The corneal thinning with time predicted by this model seems to be consistent with the measurements reported in the recent literature [47,48]. Similarly, the calculated increase in ablation rate seems to be consistent with the measurements reported by Dougherty et al. [5].

It is known that acoustic/stress waves deposited after each pulse on the corneal surface tend to extract water content to the surface. Oshika et al. [6] hypothesized that this phenomenon was the cause of topographic “central islands” in early (wide-beam) laser systems. Thus, it is possible that the actual dehydration rate during laser ablation is significantly higher compared to that of a cornea resting in the atmosphere.

These physical effects are not independent from each other; they rather influence each other in a complex manner. Simple modeling of the local and global physical effects occurring during corneal ablation processes can be simulated at relatively low cost and potentially used for improving the quality of results.

5. Conclusions

From the hydration dynamics on the cornea during refractive surgery, several effects influencing the ablation process can be derived. These effects should be adequately analyzed and avoided in commercial laser systems using sophisticated algorithms that cover most of the possible variables. The improper use of a model that overestimates or underestimates the effects derived from the hydration dynamics during treatment may result in suboptimal refractive corrections. The model introduced in this study provides analytical expressions for the hydration dynamics during treatments and its derived effects. The model incorporates multiple physical effects—both local and global—and captures their interdependencies in a multifactorial manner, wherein variables such as hydration, ablation rate, and temperature rise dynamically influence one another; for example, hydration affects both ablation efficiency and thermal buildup, while ablation and temperature changes, in turn, alter hydration levels. Furthermore, due to its analytical approach, it is valid for different laser devices used in refractive surgery. To avoid the effects of changing corneal hydration and hence the pachymetry on the refractive outcomes, development of more accurate models is needed to realize the aim of achieving emmetropization and correction of ocular aberrations. We hope that this model will be an interesting and useful contribution to refractive surgery and will take us one step closer to this goal. As a future direction, comparative analysis with published experimental and clinical data should be conducted to evaluate the extent to which the model aligns with findings reported in the literature.