Abstract
We propose a simulation-based design for a flexible color filter (FCF) using a lithium niobate metamaterial (LNM) to investigate its color filtering potential. The FCF is composed of three periodically arranged half-ellipse LN arrays on a polydimethylsiloxane (PDMS) substrate, denoted as LNM-1, LNM-2, and LNM-3. The electromagnetic responses of the FCF can be controlled by adjusting the periods of the LNMs. Our simulations predict high-quality (Q) factors in transmission spectra, ranging from 100 to 200 for LNM-1, 290 to 360 for LNM-2, and 140 to 300 for LNM-3. When the FCF is exposed to the surrounding environments with different refractive indexes, it exhibits a theoretical figure of merit (FOM) up to 900 RIU−1 and a sensitivity reaching 130 nm/RIU. The electromagnetic field distributions reveal strong confinement within the LNM nanostructures, confirming an efficient light–matter interaction. These results indicate that the proposed LNM-based FCF presents a promising design concept for high-performance color sensing and filtering applications.
1. Introduction
Color filtering technologies have been fundamental to modern optical systems, from consumer electronics displays to advanced sensing applications [1]. The conventional filters leverage the selective absorption properties of organic molecules to achieve color separation, making them particularly attractive for mass production [2,3,4,5,6,7,8,9,10]. However, despite their commercial success, these traditional filters face several significant limitations that increasingly constrain their applications in emerging technologies [11]. Additionally, these conventional filters may not be tunable and require more arrays to realize all-optical realization. [12]. The integration capabilities also present substantial challenges in modern miniaturized devices, where their relatively thick functional layers often impose constraints on device miniaturization [13,14,15].
Currently, metamaterial-based color filtering technologies have been proposed as a promising alternative to address these fundamental limitations. These artificially engineered structures, typically consisting of subwavelength periodic arrays, offer control over light–matter interactions through careful geometric design rather than material properties alone [16,17,18,19,20,21,22]. Metamaterial color filters have demonstrated remarkable optical characteristics, including extraordinarily narrow spectral bandwidths, high transmission efficiency, and precise wavelength selectivity [23,24]. The ability to precisely control the optical response through nanoscale geometric parameters also offers unprecedented flexibility in design optimization [25].
In metallic metamaterials, surface plasmon polaritons originate from collective oscillation of free electrons driven by external optical fields. The optical field can be strongly confined to the metal–dielectric interface, generating specific reflection and transmission properties. However, metallic structures suffer from intrinsic ohmic losses that limit their Q-factors and efficiency [26]. All-dielectric metamaterials based on Mie scattering theory have been proposed to address these limitations [27]. The interaction between electromagnetic waves and displacement currents can stimulate both electric (E) and magnetic (H) dipole resonances. According to physical mechanisms such as surface plasmon and Mie scattering theories, metamaterials can control the frequency, amplitude, phase, and polarization from microwave to visible light through geometric designs [28,29,30]. By optimizing the geometric parameters of metamaterials, narrow-band color filtering with high transmission efficiency can be achieved [31].
Among various dielectric materials, we selected lithium niobate (LN) for this study due to a combination of favorable properties. While materials like silicon (Si) and titanium dioxide (TiO2) offer higher refractive indices, LN possesses excellent transparency with negligible material absorption across the entire visible spectrum, which is critical for achieving high-Q resonances in a transmissive or reflective color filter. Furthermore, LN is chemically stable and benefits from mature, well-established fabrication techniques that allow us to produce high-quality, single-crystal thin films with low defect densities. Although this work does not explicitly utilize LN’s strong electro-optic or nonlinear coefficients, its selection provides a clear and promising pathway for future work on actively tunable devices, positioning this passive filter design as a foundational platform for more advanced functionalities.
In this study, we present a flexible color filter (FCF) based on a lithium niobate metamaterial (LNM). An FCF is composed of three periodically half-ellipse LN arrays on a polydimethylsiloxane (PDMS) substrate. They are denoted as LNM-1, LNM-2, and LNM-3, respectively. The optical properties of the FCF can be precisely controlled by adjusting the periods of three LNMs along the y-axis direction. Three LNMs show the blue (B), green (G), and red (R) colors for LNM-1, LNM-2, and LNM-3, respectively. Such LNM-based FCFs reveal high quality (Q) factors, ultrahigh purity, and brightness characteristics. When an LNM-based FCF is exposed to different ambient environments, it exhibits ultrahigh and stable sensitivity in the background with the refractive index range from 1.0 to 1.4 [32,33,34,35,36]. This refractive index range is strategically chosen for its direct relevance to diverse real-world conditions anticipated for the FCF’s key applications. Specifically, values from 1.0 (approximating air or vacuum, a common reference for sensing in gaseous media) up to 1.4 cover a broad spectrum of environments. This includes crucial aqueous media, where water has a refractive index of approximately 1.33, which are fundamental to biomedical sensing of biological samples and environmental monitoring of substances in liquids. Investigating the device’s performance across this 1.0 to 1.4 span is therefore critical for validating its capability to function effectively and reliably in practical applications [37,38,39,40]. This design not only demonstrates excellent optical performance but also offers a straightforward tuning mechanism to adjust the RGB colors. These outstanding optical characteristics make the proposed LNM-based FCF particularly promising for various practical applications. In biomedical sensing, the high Q-factor and sensitivity enable real-time monitoring of subtle changes in biological samples, potentially revolutionizing disease diagnosis and drug development processes. The capability to operate across the entire visible spectrum makes it ideal for advanced spectroscopy applications, where precise wavelength selectivity is crucial for chemical and molecular analyses. In environmental monitoring, the device with a high figure of merit (FOM) allows for accurate detection of pollutants and contaminants in both aqueous and gaseous media. The narrow bandwidth of the spectrum and the tunable mechanism also make it suitable for display technologies, offering improved color purity and contrast ratio compared to conventional filtering methods.
2. Design and Method
The proposed LNM-based FCF is on a PDMS substrate, where the electromagnetic properties can be controlled through an electromechanical mechanism to perform optimization by stretching the PDMS substrate. The fundamental principle underlying the anticipated structural resilience lies in the strategic material distribution and geometric configuration of the composite system. During mechanical stretching operations, it is hypothesized that mechanical deformations would be primarily accommodated by the highly flexible PDMS material in the regions between the stiffer LN nanostructures. This selective deformation mechanism would create a protective environment where the high-modulus LN nanostructures remain largely undisturbed while the surrounding elastomeric matrix absorbs and distributes the applied mechanical stress [19].
The half-ellipse geometry of the LN nanostructures is expected to play a crucial role in this stress distribution paradigm. Unlike continuous thin films that would experience uniform strain distribution, the discrete nature of these nanostructures would create localized stress concentration points that are effectively isolated from one another by the intervening PDMS regions [41,42,43,44]. This segmentation could prevent the propagation of mechanical failures across the entire LN array, thereby enhancing the system’s overall reliability [31]. While a detailed mechanical simulation of the stress–strain behavior is a subject for future investigation, this qualitative analysis suggests that the design is well-suited for mechanical flexibility, which is essential for maintaining consistent optical performance.
The periodically half-ellipse LN arrays are strategically designed to enhance light–matter interactions and modify the local electromagnetic field distributions within the LNM nanostructures. The optical properties of the LNM-based FCF are simulated using the Ansys Lumerical simulation software (2020 R2, for x64 disk), a commercial-grade finite-different time-domain (FDTD) solver. The simulation environment is configured with a three-dimensional computational domain, where periodic boundary conditions are implemented along the x- and y-axis directions, while perfectly matched layer (PML) boundary conditions are applied in the z-axis direction to eliminate unwanted reflections. The mesh resolution is optimized through convergence testing, with a minimum mesh size of λ/20 in all directions to ensure computational accuracy. A frequency-domain resolution of 0.1 nm is set to accurately resolve transmission and reflection spectra.
It is important to acknowledge that these simulations assume perfect, idealized geometries and materials. In a practical fabrication scenario, deviations from the designed parameters are inevitable. For instance, variations of ±5–10 nm in the nanostructure dimensions, roughness at the edges of the slots, or non-uniformity in the PDMS substrate thickness could influence the device’s performance. Given the high-Q nature of the supported resonances, such imperfections would likely lead to resonance broadening (a decrease in the Q-factor) and a potential reduction in peak efficiency. A comprehensive tolerance analysis would be required in the experimental phase to quantify these effects, but the robustness of the underlying Mie and bound states in the continuum (BIC) resonances suggests that the fundamental filtering characteristics would be preserved.
Figure 1a shows the proposed LNM-based FCF composed of three periodically half-ellipse LN arrays on a PDMS substrate. The periods of LNMs are w1, w2, and w3 for LNM-1, LNM-2, and LNM-3, respectively. The incident wave is a transverse magnetic (TM) polarization state. Figure 1b–d are the detailed geometric parameters of the three LNMs, and each is responsible for one primary color. The horizontal period along the x-direction between LNM units is 80 nm for both LNM-1 and LNM-2 and 100 nm for LNM-3, and the thickness for all three LNMs is 200 nm. The short axis of the three LNMs is 60 nm for LNM-1 and LNM-2 and 80 nm for LNM-3. The long axis of the three LNMs is 240 nm for LNM-1, 300 nm for LNM-2, and 360 nm for LNM-3. Each LNM unit is composed of two half-ellipse LN nanostructures with a slot, whose width is 5 nm for LNM-1 and LNM-3 and 15 nm for LNM-2. By manipulating the w1, w2, and w3 values, the vertical period along the y-axis direction of LNMs, the resonant wavelength generated by plasmonic resonance can cover all the visible light spectra for both transmission and reflection with relatively small full width at half maximum (FWHM) and a high Q-factor.
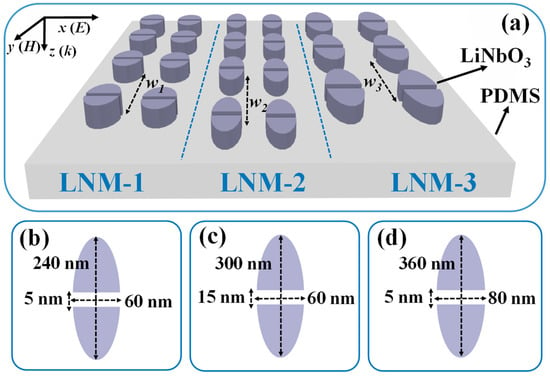
Figure 1.
Schematic drawings of (a) the proposed LNM-based FCF. Geometric parameters of (b) LNM-1, (c) LNM-2, and (d) LNM-3, respectively. The horizontal period along the x-direction between LNM units is 80 nm for both LNM-1 and LNM-2 and 100 nm for LNM-3, and the thickness of the LNM layers is 200 nm.
The optical responses of the proposed LNM-based FCF can be characterized by its transmission coefficient (T) and reflection coefficient (R), which are expressed by
where , , and represent the transmitted, reflected, and incident E-fields, respectively [36].
3. Results and Discussions
Figure 2a exhibits the reflection spectra of the LNM-based FCF, demonstrating their ability to cover the entire visible spectrum with high efficiency. LNM-1, LNM-2, and LNM-3 are designed for blue, green, red color filtering characteristics. By changing the vertical period along the y-axis direction of LNMs, i.e., w1 for LNM-1, w2 for LNM-2, and w3 for LNM-3, LNMs show strong reflection peaks from the wavelengths of 440 nm to 540 nm for LNM-1, 550 nm to 590 nm for LNM-2, and 620 nm to 740 nm for LNM-3. These optical characteristics prove the capability of the LNMs to selectively filter specific colors with high precision. The progressive redshift in resonance wavelengths from LNM-1 to LNM-3 is a direct result of the geometric tuning enabled by adjusting the vertical period along the y-axis direction of LNMs, which modifies the Mie scattering resonances and the associated electromagnetic field distributions. This geometric tunability is a key advantage of the LNM-based FCF design, as it allows for precise control over the optical response across the visible spectrum, making it highly adaptable for various applications in color filtering and sensing fields.
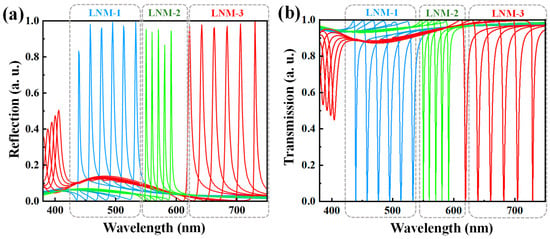
Figure 2.
(a) Reflection and (b) transmission spectra of LNM-1, LNM-2, and LNM-3 to exhibit the corresponding blue (B), green (G), and red (R) colors. For both (a) and (b), the w1 of LNM-1 is changed from 260 nm to 360 nm, the w2 of LNM-2 is changed from 360 nm to 400 nm, and the w3 of LNM-3 is changed from 400 nm to 500 nm.
Figure 2b shows the transmission spectra of the LNM-based FCF, enabling high-contrast color filtering with ultrahigh purity and brightness characteristics. The ability to span the entire visible spectrum in both reflection and transmission spectra highlights the robustness of these LNM-based FCFs. The redshift in resonant wavelengths is governed by the interaction between incident light and the periodic LNM nanostructures. In such all-dielectric systems, this interaction is fundamentally rooted in Mie scattering, where incident light excites a series of multipolar resonant modes within the individual nanostructures.
Our design elevates this fundamental interaction by engineering these modes to operate in the regime of quasi-BIC, which is the key to achieving the observed exceptionally sharp spectral features. A true BIC is a theoretical “dark” mode with an infinite quality (Q) factor, as it is perfectly confined and unable to couple with external radiation due to fundamental symmetry incompatibilities with the continuum of free-space modes. To make such a mode accessible, we introduce a controlled perturbation. In our design, the asymmetric slot within each half-ellipse nanostructure serves this purpose explicitly. This geometric asymmetry intentionally breaks the requisite symmetry that protects the BIC, creating a controlled leakage channel. This transformation from a perfect BIC into a quasi-BIC allows the previously confined mode to couple with incident light, manifesting as a high-Q resonance in the optical spectra. The degree of this asymmetry directly dictates the coupling strength and, consequently, the Q-factor of the resonance. The ability to precisely control the resonant wavelength and its Q-factor through geometric tuning is a significant advantage of this FCF design, enabling its application in advanced tunable optoelectronic devices.
Within the LNM nanostructure array, the interactions of Rayleigh–Wood Anomaly (RWA) modes have been observed to produce specific relationships between primary resonances and secondary RWA resonances throughout the visible spectrum. Through the coupling mechanism analysis, the coupling strength of RWAs has been determined to be dependent on the vertical period along the y-axis direction of LNMs between adjacent units, whereby both resonance positions and relative intensities are affected.
The operational parameters of the LNM-1, LNM-2, and LNM-3 designs are systematically optimized through simulations to leverage symmetry-protected BICs, with each configuration precisely targeting distinct spectral regimes. For LNM-1, a geometric scaling parameter w1 is calibrated to facilitate the evolution from fundamental Mie resonances to high-Q nonlocal BIC hybrid modes in the wavelength range of 400–500 nm. This enhancement is achieved by engineering destructive interference between competing radiative channels. Specifically, the structural asymmetry opens pathways for energy to radiate away from the resonator. By carefully tailoring the geometry, these pathways are forced to interfere destructively in the far-field region, effectively canceling radiation loss and trapping energy within the nanostructure. This process is equivalent to establishing near-orthogonality between the resonant mode and the continuum of free-space radiation channels, which is the mechanism that suppresses radiative losses and enables ultrahigh Q-factors.
For LNM-2 and LNM-3, analogous activation mechanisms are implemented by fine-tuning w2 and w3, respectively, where hybrid coupling between symmetry-protected BICs and propagating resonances produces spectrally separated responses in the green (520–580 nm) and red (620–750 nm) regions. The BIC-dominated regime emerges optimally when the ratio of the lattice period to the operational wavelength approaches 0.7–0.9. This parametric framework demonstrates the universal scalability of BIC physics across the visible spectrum, providing a robust platform for tailoring the optical response of all-dielectric metamaterials through geometric optimization.
The slot of the half-ellipse LN nanostructure plays a pivotal role in activating BICs. The slot creates a momentum mismatch that traps light as non-radiative BIC mode. This design suppresses energy leakage, achieving ultrahigh quality factors through destructive interference of radiative channels, enabling wavelength-specific light confinement without relying on BIC coupling. Such symmetry-engineered BICs provide a low-loss platform for nonlinear optics and sensing [40]. Second, by creating specific boundaries within the structure, the slot of the half-ellipse LN nanostructure confines the BIC mode to a designated region. This spatial confinement significantly enhances light–matter interaction strength, improving the optical response efficiency of the proposed device [41]. Third, precise control of the geometric dimensions of the half-ellipse LN nanostructure enables tailored momentum mismatch between the symmetry-protected BIC mode and the radiative channel. The radiative losses are suppressed through destructive interference, while non-radiative BIC confinement enhances near-field intensity and Q-factors exceeding 103. This geometric tuning bypasses RWA coupling limitations, achieving intrinsic Q-factor optimization via the BIC-dominated hybrid mode, as validated by pump–probe spectroscopy in recent low-loss metasurface studies [42].
The relationships between the Q-factor, FWHM, and the vertical period along the y-axis direction of LNMs are systematically analyzed in Figure 3. For reflection spectra (Figure 3a–c), LNM-1 (blue) exhibits a gradual decrease in the Q-factor from 155 to 90 as w1 varies from 260 nm to 360 nm, accompanied by an increase in FWHM from 2.6 to 5.5 nm (Figure 3a). Similarly, LNM-2 (green) demonstrates the Q-factor ranging from 260 nm to 330 nm as w2 varies from 360 nm to 420 nm with FWHM spanning from 1.65 to 2.22 nm, reflecting the superior performance in the green spectrum (Figure 3b). LNM-3 (red) shows a moderate Q-factor range from 100 to 200 as w3 increases from 400 nm to 500 nm, while FWHM shows its rise to 7 nm first, followed by its fall to 3.5 nm (Figure 3c). The above-mentioned characteristics highlight the tunability of the proposed LNM-based FCF for RGB-spectrum applications. These trends confirm that increasing w strengthens the coupling between adjacent resonant units and can cause redshifting. The inverse proportionality between the Q-factor and FWHM across all designs underscores the geometric tunability of LNM-based FCFs, enabling tailored performance for specific spectral bands.
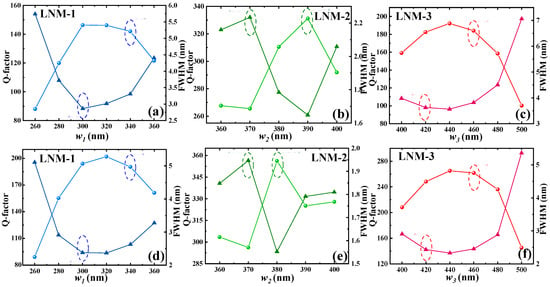
Figure 3.
Relationships of Q-factors and FWHM values of (a,d) LNM-1, (b,e) LNM-2, and (c,f) LNM-3 changing w1 from 260 nm to 360 nm for LNM-1, w2 from 360 nm to 400 nm for LNM-2, w3 from 400 nm to 500 nm for LNM-3, summarized by (a–c) reflection and (d–f) transmission spectra, respectively.
For transmission spectra (Figure 3d–f), the Q-factor and FWHM exhibit similar inverse relationships to those observed in the reflection spectra (Figure 3a–c), but with distinct numerical ranges that demonstrate enhanced performance in transmission spectra. For LNM-1, the Q-factor rises from 100 to 200 as w1 increases from 260 nm to 360 nm, with FWHM decreasing from 5.1 nm to 2.5 nm (Figure 3d), while LNM-2 achieves exceptional Q-factors from 290 to 360 (FWHM is between 1.95 nm to 1.55 nm) as w2 varies from 360 nm to 400 nm (Figure 3e). LNM-3 exhibits a broader tunability range, with Q-factors spanning from 140 to 300 and FWHM narrowing from 4.7 nm to 2.5 nm as w3 varies from 400 nm to 500 nm (Figure 3f). The enhanced Q-factors of these LNM-based FCFs in transmission spectra compared to reflection spectra suggest stronger light confinement within the nanostructures, driven by optimized w-dependent near-field interactions. The consistent variation in FWHM with increasing w across all designs further validates the role of geometric tuning in achieving high-purity spectral filtering characteristics.
The distinct trends in the Q-factor and FWHM for each LNM design, as shown in Figure 3, are a direct consequence of the tunable coupling between the intrinsic quasi-BIC resonance of the half-ellipse nanostructures and the collective lattice resonances, specifically the Rayleigh-Wood Anomaly (RWA). The vertical period (w) directly controls the spectral position of the RWA, which can introduce a significant radiative loss channel. The Q-factor of the device is critically dependent on the interference between the quasi-BIC mode and this RWA.
For LNM-1 and LNM-3, the Q-factors exhibit a distinct non-monotonic trend, decreasing to a minimum before rising again, while the FWHM shows the inverse behavior. This profile is a classic signature of a strong Fano-type interference. As the period (w1 or w3) is tuned, the RWA is swept across the spectral position of the main quasi-BIC resonance. The Q-factor is at its minimum (and FWHM is at its maximum) at the point of spectral degeneracy, where the coupling between the two modes is strongest, maximizing the radiative losses. As the RWA moves away from the resonance on either side, the coupling weakens, and the Q-factor recovers, returning to a state dominated by the intrinsic low-loss nature of the quasi-BIC.
The behavior of LNM-2 is qualitatively different and highlights its specialized design for superior performance. It does not exhibit the pronounced Q-factor dip seen in the other two designs; instead, it maintains an exceptionally high and more stable Q-factor across its entire tuning range. This unique stability is attributed to its distinct geometry, most notably the significantly wider slot of 15 nm compared to the 5 nm slot in LNM-1 and LNM-3. In the physics of BICs, the slot’s geometry directly defines the “asymmetry parameter” that transforms a perfect, non-radiating BIC into a quasi-BIC with a finite Q-factor. The wider slot in LNM-2 fundamentally alters this parameter, resulting in a much weaker coupling coefficient between the quasi-BIC mode and the radiative RWA channel. Because of this engineered weak coupling, the resonance of LNM-2 is less perturbed by the RWA, even as it sweeps past. The system remains in a robust, high-Q state, explaining its “strange” yet superior and more stable performance compared to LNM-1 and LNM-3.
To further contextualize the performance of our proposed LNM-FCF, a comparative analysis against several published and relevant works is presented. The key performance metrics, including the Q-factor, sensitivity, and the FOM, alongside other pertinent characteristics such as material systems and device flexibility are summarized in Table 1. This comparison aims to highlight the competitive advantages and unique contributions of our LNM-FCF within the current landscape of advanced optical filters and sensors. The LNM-FCF demonstrates a superior combination of a high experimental Q-factor (up to ~360), excellent sensitivity (130 nm/RIU), and an outstanding FOM (~900 RIU−1).

Table 1.
Comparison of the proposed LNM-FCF with literature works. “N/A” indicates that the value was not reported in the cited reference. An asterisk (*) denotes values obtained from simulations, and all other values are experimentally measured.
The transmission spectra of LNM-1, LNM-2, and LNM-3 exhibit significant wavelength shifts in their resonance dips as the refractive index (n) of the surrounding medium increases, as shown in Figure 4a. For LNM-1 (blue), the transmission spectra are shifted from the wavelength of 430 nm at n = 1.0 to 482 nm at n = 1.4, corresponding to a redshift of 52 nm. Similarly, LNM-2 (green) shows a resonant shift of 45 nm from the wavelength of 530 nm (n = 1.0) to 575 nm (n = 1.4), while LNM-3 (red) demonstrates the largest shift of 75 nm, moving from the wavelength of 620 nm to 695 nm. These redshifts arise from the increased effective n value, which modifies the phase-matching conditions for resonant modes. The intensity of each resonance remains stable while changing the n value, indicating robust light confinement despite environmental changes. The linear dependence of the resonant wavelength on the n value highlights greater sensitivity due to stronger field interactions and the tunability of these LNM-based FCFs for environmental sensing applications. The sensitivity and FOM are defined as
where ∆ is the shift in resonant wavelength, ∆ is the change in the refractive index of the surrounding medium, and FWHM is the full width at half maximum of the resonance dip.
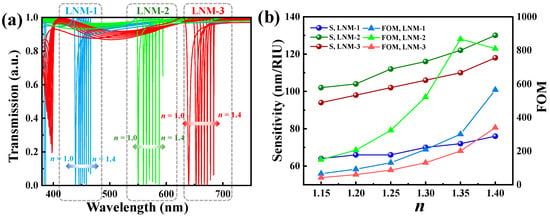
Figure 4.
(a) Transmission spectra of LNM-1, LNM-2, and LNM-3 exposed to the surrounding environment with different refractive indexes (n). (b) Relationships of sensitivities and FOM values of (a).
In Figure 4b, the trends of sensitivities show quite distinct and linear characteristics. LNM-2 achieves the highest sensitivity of 130 nm/RIU. In contrast, LNM-1 and LNM-3 exhibit sensitivities of 75 nm/RIU and 115 nm/RIU, respectively. The FOM can quantify the trade-off between sensitivity and resonance linewidth. The FOM peak is 900 RIU−1 for LNM-2 at n = 1.35, owing to its narrow FWHM of 3 nm and moderate sensitivity. The trend of the FOM for LNM-2, which peaks and then declines, is noteworthy. This behavior arises because, for refractive indices greater than 1.35, the resonance linewidth (FWHM) begins to broaden more rapidly than the linear increase in wavelength sensitivity (S). Such FWHM broadening at higher ambient refractive indices is a known phenomenon in high-Q resonant systems, where the delicate destructive interference sustaining the quasi-BIC mode becomes perturbed by the changing dielectric environment, leading to increased radiative losses [43].
The observed peak in the FOM for LNM-2 is directly linked to the physics of the quasi-BIC resonance upon which this design is based on. A quasi-BIC achieves its characteristically high Q-factor through the near-perfect destructive interference between different radiation pathways, a condition established by the specific geometry of the nanostructure, such as the half-ellipse slot. For LNM-2, the system is tuned so effectively that this interference condition appears to be maximally fulfilled not in air (n = 1.0) but in a background medium of n ≈ 1.35. At this optimal point, the peak FOM of 900 RIU−1 and a sensitivity of 130 nm/RIU imply an exceptionally narrow FWHM of approximately 0.144 nm (S/FOM). LNM-1 and LNM-3 show FOM values between 50–590 RIU−1 and 10–370 RIU−1, respectively. These results show the role of geometric design in balancing sensitivity and spectral resolution. The enhanced performance of LNM-2 in the green spectrum aligns with optimized BIC coupling efficiency at intermediate wavelengths.
The E- and H-field distributions of the LNM-based FCF at resonances in TM mode are shown in Figure 5. Figure 5a–c depict the E-field distributions of LNM-1, LNM-2, and LNM-3, where E-field energies concentrate predominantly on the upper and lower nanostructures of LNMs. The first and second rows of this figure represents the field distributions of LNMs in the lower- and upper-bound geometric parameter conditions (w), respectively. The difference in field distribution in the same LNM structure with different w values demonstrates the tunability of the proposed LNM-based FCFs. A progressive enhancement in field confinement is observed from LNM-1 to LNM-3, with the energy density becoming more localized at the edges of the nanostructures. This increasing confinement corresponds to the higher Q-factors observed in the spectral analysis. Figure 5d-f illustrate the H-field distributions of LNM-1, LNM-2, and LNM-3, demonstrating that H-field energies are concentrated in the slots and become more condensed in the middle slot of LNMs from LNM-1 to LNM-3. This complementary distribution of the E- and H-fields provides direct evidence of the BIC hybridization mechanism proposed earlier, where the slot acts as a coupling channel between propagating waves and bound states. The observed asymmetric field distribution pattern, with E-field density stronger than H-field density, confirms the formation of standing waves within the LNM nanostructure, a characteristic signature of the BIC resonator phenomenon that enables high spectral purity.
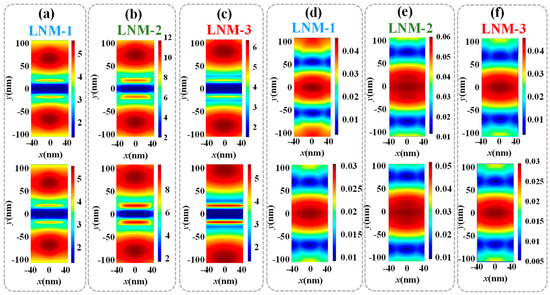
Figure 5.
(a–c) E-field and (d–f) H-field distributions of LNM-1, LNM-2, and LNM-3, respectively. The first and the second rows of this figure represents the field distributions of LNMs in the lower- and upper-bound geometric parameter conditions (w), respectively.
4. Conclusions
In conclusion, we propose an FCF composed of three LNMs to create RGB colors spanning the visible spectrum from 380 nm to 780 nm with ultrahigh purity and brightness characteristics. Through the manipulation of the FCF along the y-axis direction, LNMs show high Q-factors from 90 to 360. The electromagnetic field distributions reveal strong field confinement within the LNMs. When the LNM-based FCF is exposed to different backgrounds with n values from 1.0 to 1.4, it shows high sensitivity up to 130 nm/RIU and the FOM reaching 900 RIU−1. It indicates that the proposed LNM-based FCF possesses the potential for precise control in color sensing applications. The LNM-based FCF design shows significant promise for applications in color filters, particularly in scenarios requiring precise wavelength selectivity. Its conceptual combination of simplicity and high simulated performance makes it a promising candidate for further investigation of the next-generation optical devices.
Author Contributions
S.Z. (Siqiang Zhao), D.Z., Y.Z., S.Z. (Shuyan Zou), and Y.-S.L. carried out related simulations and data analysis. S.Z. (Siqiang Zhao) drafted the manuscript. Y.-S.L. supervised the simulations and the revising of the manuscript. Y.-S.L. also provided suggestions and guidance for the simulations and data analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Guangdong Science and Technology Program (2024A0505050007) and the Guangdong Basic and Applied Basic Research Foundation (2024A1515013019).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Horie, Y.; Han, S.; Lee, J.-Y.; Kim, J.; Kim, Y.; Arbabi, A.; Shin, C.; Shi, L.; Arbabi, E.; Kamali, S.M.; et al. Visible Wavelength Color Filters Using Dielectric Subwavelength Gratings for Backside-Illuminated CMOS Image Sensor Technologies. Nano Lett. 2017, 17, 3159–3164. [Google Scholar] [CrossRef]
- Nagasaki, Y.; Suzuki, M.; Takahare, J. All-Dielectric Dual-Color Pixel with Subwavelength Resolution. Nano Lett. 2017, 17, 7500–7506. [Google Scholar] [CrossRef] [PubMed]
- Vashistha, V.; Vaidya, G.; Hegde, R.-S.; Serebryannikov, A.-E.; Bonod, N.; Krawczyk, M. All-Dielectric Metasurfaces Based on Cross-Shaped Resonators for Color Pixels with Extended Gamut. ACS Photonics 2017, 4, 1076–1082. [Google Scholar] [CrossRef]
- Chen, H.-T.; Taylor, A.-J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, S.; Lu, X.; Saeidi, H.; Sengupta, K. A high-speed programmable and scalable terahertz holographic metasurface based on tiled CMOS chips. Nat. Electron. 2020, 3, 785–793. [Google Scholar] [CrossRef]
- Shrestha, V.R.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Aluminum Plasmonics Based Highly Transmissive Polarization-Independent Subtractive Color Filters Exploiting a Nanopatch Array. Nano Lett. 2014, 14, 6672–6678. [Google Scholar] [CrossRef]
- Song, M.; Wang, D.; Peana, S.; Choudhury, S.; Nyga, P.; Kudyshev, Z.; Yu, H.; Boltasseva, A.; Shalaev, V.; Kildishev, A. Colors with plasmonic nanostructures: A full-spectrum review. Appl. Phys. Rev. 2019, 6, 041308. [Google Scholar] [CrossRef]
- Li, Z.; Clark, A.W.; Cooper, J.M. Dual Color Plasmonic Pixels Create a Polarization Controlled Nano Color Palette. ACS Nano 2016, 10, 492–498. [Google Scholar] [CrossRef]
- Xu, R.; Lin, Y.-S. Characterizations of reconfigurable infrared metamaterial absorbers. Opt. Lett. 2018, 43, 4783–4786. [Google Scholar] [CrossRef]
- Grahn, P.; Shevchenko, A.; Kaivola, M. Electromagnetic multipole theory for optical nanomaterials. New J. Phys. 2012, 14, 093033. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, S.; Song, Q.; Liu, Y.; Wu, Y.; Wang, S.; Yu, J.; Han, J.; Tsai, D.-P. All-dielectric metasurface for high-performance structural color. Nat. Commun. 2020, 11, 1864. [Google Scholar] [CrossRef]
- Haddadin, Z.; Khan, S.; Poulikakos, L.V. Cutting Corners to Suppress High-Order Modes in Mie Resonator Arrays. ACS Photonics 2024, 11, 187–195. [Google Scholar] [CrossRef]
- Yang, B.; Liu, W.; Li, Z.; Cheng, H.; Choi, D.-Y.; Chen, S.; Tian, J. Ultrahighly Saturated Structural Colors Enhanced by Multipolar-Modulated Metasurfaces. Nano Lett. 2019, 19, 4221–4228. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-H.; Babicheva, V.E.; Yu, M.-W.; Lu, T.-C.; Lin, T.-R.; Chen, K.-P. Structural Colors Enabled by Lattice Resonance on Silicon Nitride Metasurfaces. ACS Nano 2020, 14, 5678–5685. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Lin, J.; Chen, K.; Lin, Y.-S.; Yang, B.-R. Full color metasurface with high-transmission and omnidirectional characteristics. Opt. Laser Technol. 2022, 150, 108004. [Google Scholar] [CrossRef]
- Lee, C.-R.; Lin, S.-H.; Wang, S.-M.; Lin, J.-D.; Chen, Y.-S.; Hsu, M.-C.; Liu, J.-K.; Mo, T.-S.; Huang, C.-Y. Optically controllable photonic crystals and passively tunable terahertz metamaterials using dye-doped liquid crystal cells. J. Mater. Chem. C 2018, 6, 4959–4966. [Google Scholar] [CrossRef]
- Lu, L.; Dong, Z.; Tijiptoharsono, F.; Ng, R.J.H.; Wang, H.; Rezaei, S.D.; Wang, Y.; Leong, H.S.; Lim, P.C.; Yang, J.K.W.; et al. Reversible Tuning of Mie Resonances in the Visible Spectrum. ACS Nano 2021, 15, 19722–19732. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Huang, W.; Chen, K.; Lin, Y.-S. Visible Metamaterial Using a Lithium Niobate Nanoring Structure for Stretchable Color Sensing Application. ACS Mater. Lett. 2023, 5, 1831–1840. [Google Scholar] [CrossRef]
- Zheng, D.; Wen, Y.; Xu, X.; Lin, Y.-S. Metamaterial grating for colorimetric chemical sensing applications. Mater. Today Phys. 2023, 33, 101056. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Y.-S.; Yang, B.-R. Tunable color switch using split-ring metamaterial. Opt. Laser Technol. 2020, 131, 106461. [Google Scholar] [CrossRef]
- Yang, W.; Lin, Y.-S. Tunable metamaterial filter for optical communication in the terahertz frequency range. Opt. Express 2020, 28, 17620–17629. [Google Scholar] [CrossRef]
- Lin, Y.-S.; Dai, J.; Zeng, Z.; Yang, B.-R. Metasurface Color Filters Using Aluminum and Lithium Niobate Configurations. Nanoscale Res. Lett. 2020, 15, 77. [Google Scholar] [CrossRef]
- Li, B.; Zeng, Q.; Lin, Y.-S. Tunable terahertz meta-resonator with switchable single-and dual-resonance characteristic. Mater. Today Commun. 2024, 41, 110197. [Google Scholar] [CrossRef]
- Wu, L.; Lin, Y.-S. Design and investigation of dual-axis electrostatic driving MEMS scanning micromirror. Int. J. Optomechatronics 2024, 18, 2350749. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, Y.-S. Angular-Dispersive Narrowband Absorption Induced by Quasi-BIC in SiO2-Au Metamaterial. Small Struct. 2024, 5, 2300529. [Google Scholar] [CrossRef]
- Xu, R.; Luo, J.; Sha, J.; Zhong, J.; Xu, Z.; Tong, Y.; Lin, Y.-S. Stretchable IR metamaterial with ultra-narrowband perfect absorption. Appl. Phys. Lett. 2018, 113, 101907. [Google Scholar] [CrossRef]
- Wu, L.; Guan, J.; Lin, Y.-S. Active logic modulator of terahertz metamaterial for future 6G communication system. Sens. Actuators A Phys. 2024, 379, 115992. [Google Scholar] [CrossRef]
- Jang, J.; Badloe, T.; Yang, Y.; Lee, T.; Mun, J.; Rho, J. Spectral Modulation through the Hybridization of Mie-Scatterers and Quasi-Guided Mode Resonances: Realizing Full and Gradients of Structural Color. ACS Nano 2020, 14, 15317–15326. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Elbahri, M. Review of Metasurface Plasmonic Structural Color. Plasmonics 2017, 12, 1463–1479. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, X.; Chen, Y.; Liu, Q.; Li, X.; Wang, Y.; Liu, N.; Duan, H. 3D-Integrated metasurfaces for full-colour holography. Light: Sci. Appl. 2019, 8, 86. [Google Scholar] [CrossRef]
- Qiu, C.-W.; Zhang, T.; Hu, G.; Kivshar, Y. Quo Vadis, Metasurfaces? Nano Lett. 2021, 21, 5461–5474. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lin, Y.-S. Multiplexed terahertz multifocal metalens based on stretchable single-, dual-, and quad-axis synthetic rectangular optical sparse aperture. Mater. Des. 2024, 237, 112631. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Pitchappa, P.; Manjappa, M.; Krishnamoorthy, H.N.S.; Chang, Y.; Lee, C.; Singh, R. Bidirectional reconfiguration and thermal tuning of microcantilever metamaterial device operating from 77 K to 400 K. Appl. Phys. Lett. 2017, 111, 261101. [Google Scholar] [CrossRef]
- Cong, L.; Pitchappa, P.; Wu, Y.; Ke, L.; Lee, C.; Singh, N.; Yang, H.; Singh, R. Active Multifunctional Microelectromechanical System Metadevices: Applications in Polarization Control, Wavefront Deflection, and Holograms. Adv. Opt. Mater. 2017, 5, 1600716. [Google Scholar] [CrossRef]
- Yi, Z.; Lin, H.; Niu, G.; Chen, X.; Zhou, Z.; Ye, X.; Duan, T.; Yi, Y.; Tang, Y.; Yi, Y. Graphene-based tunable triple-band plasmonic perfect metamaterial absorber with good angle-polarization-tolerance. Results Phys. 2019, 13, 102149. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High-Q Supercavity Modes in Subwavelength Dielectric Resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Zelmon, D.E.; Small, D.L.; Jundt, D. Infrared corrected Sellmeier coefficients for congruently grown lithium niobate and 5 mol% magnesium oxide-doped lithium niobate. J. Opt. Soc. Am. B 1997, 14, 3319–3322. [Google Scholar] [CrossRef]
- Park, J.; Li, M.; Wang, Z.; Li, Z.; Fan, J.A. Topology-Optimized Metasurface Resonant Waveguide Gratings. Nano Lett. 2024, 24, 4803–4810. [Google Scholar]
- Yoo, Y.J.; Lim, J.H.; Lee, G.J.; Jang, K.-I.; Song, Y.M. Ultra-thin films with highly absorbent porous media fine-tunable for coloration and enhanced color purity. Nanoscale 2017, 9, 2986–2991. [Google Scholar] [CrossRef]
- Yue, W.; Gao, S.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Highly reflective subtractive color filters capitalizing on a silicon metasurface integrated with nanostructured aluminum mirrors. Laser Photonics Rev. 2017, 11, 1600285. [Google Scholar] [CrossRef]
- Olson, J.; Manjavacas, A.; Basu, T.; Huang, D.; Schlather, A.E.; Zheng, B.; Halas, N.J.; Nordlander, P.; Link, S. High Chromaticity Aluminum Plasmonic Pixels for Active Liquid Crystal Displays. ACS Nano 2016, 10, 1108–1117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).