Quantum-Empowered Fiber Sensing Metrology
Abstract
1. Introduction
2. Preparation and Application of Quantum States in Optical Fibers
2.1. Properties of Quantum States
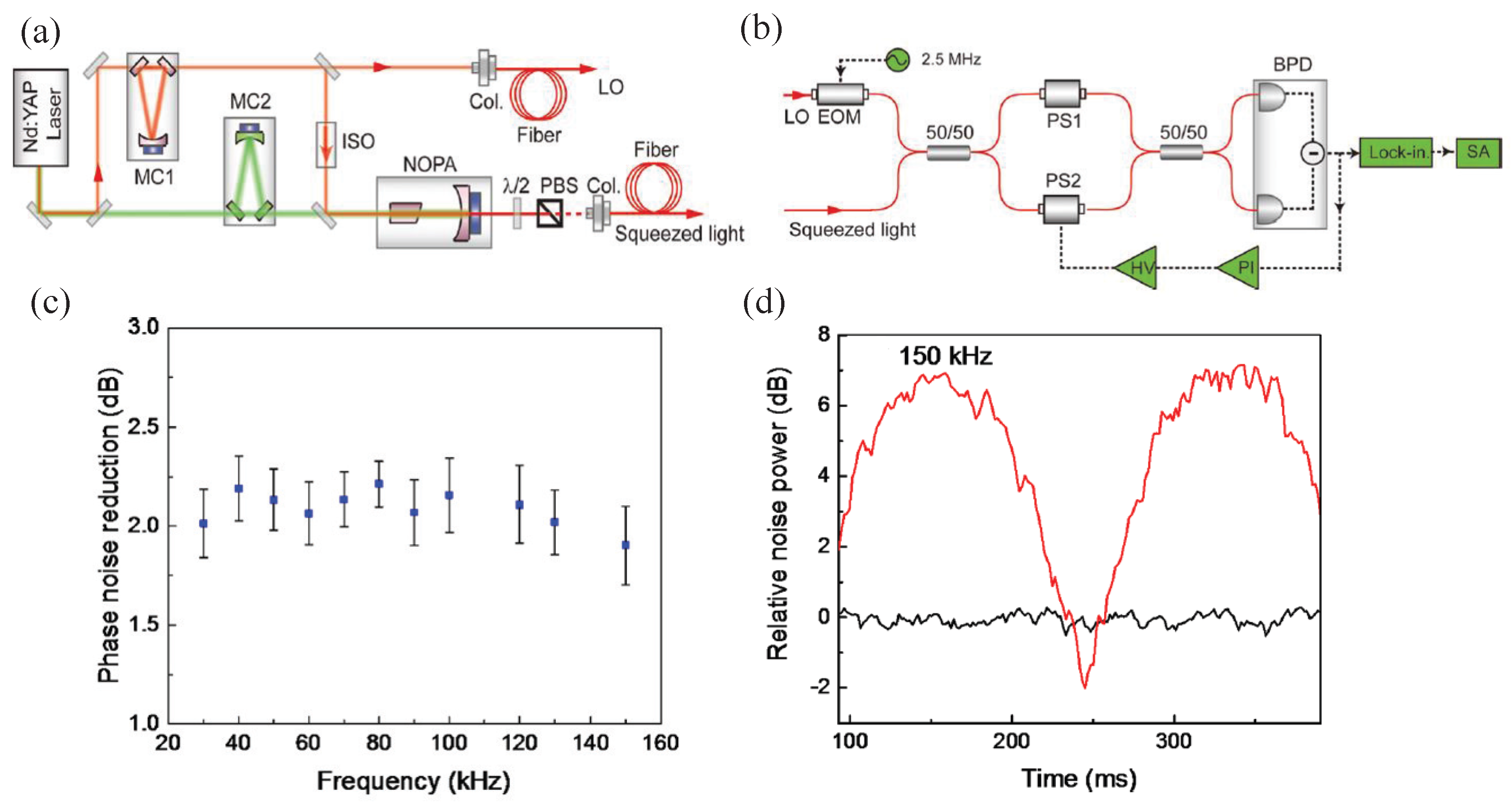
2.2. Generation of Quantum States in Optical Fibers Based on Four-Wave Mixing Process
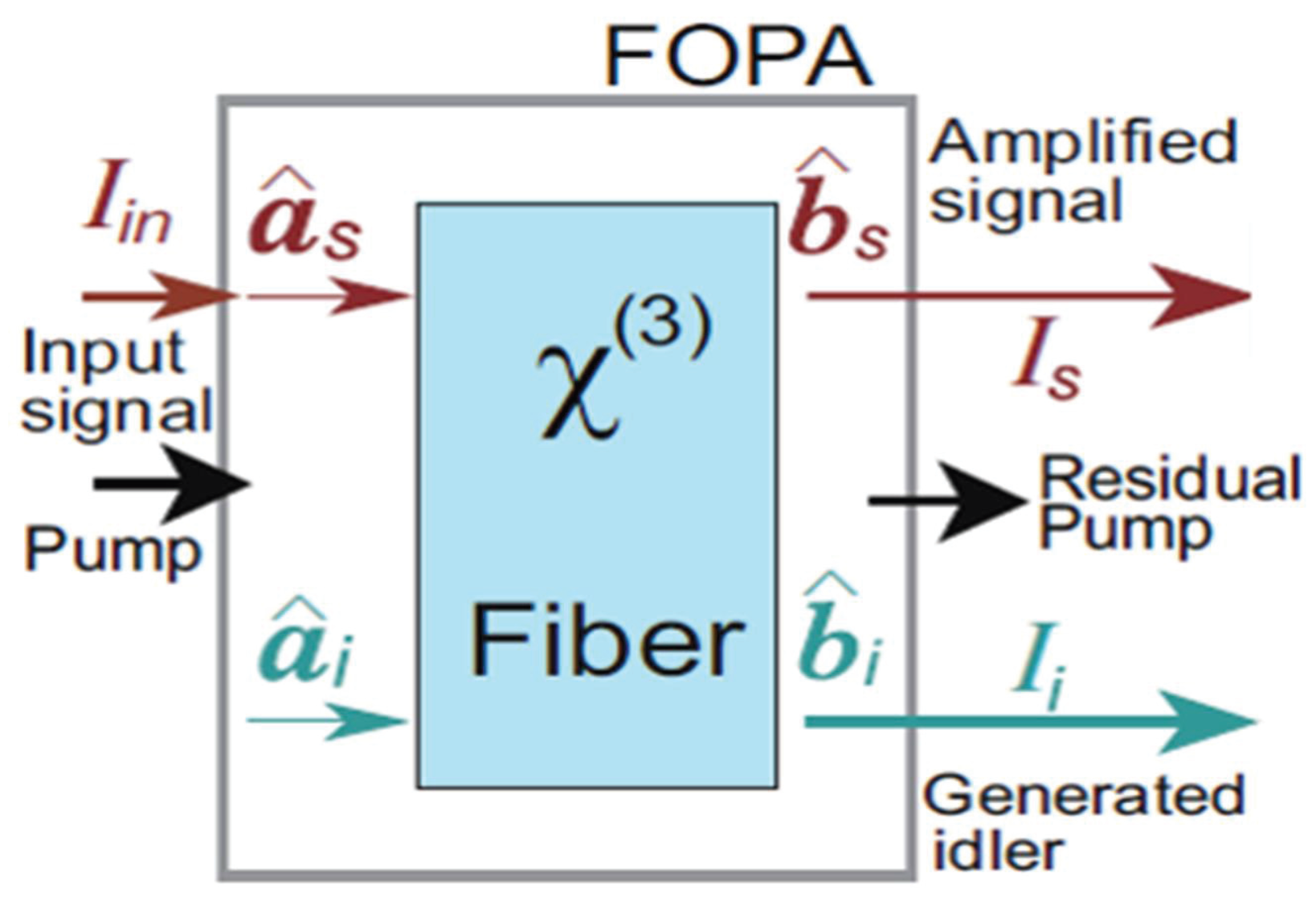
2.3. Generation of Quantum States in Optical Fibers Based on Kerr Effect
3. Optical Fiber Quantum Interferometer in Quantum Sensing
3.1. The All-Optical-Fiber Nonlinear Interferometer
3.2. The Optical Fiber Sagnac Interferometer
3.3. The Optical Fiber Mach–Zehnder Interferometer
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bashan, G.; London, Y.; Diamandi, H.H.; Zadok, A. Distributed cladding mode fiber-optic sensor. Optica 2020, 7, 85–92. [Google Scholar] [CrossRef]
- Tian, J.; Li, Z.; Sun, Y.; Yao, Y. High-sensitivity fiber-optic strain sensor based on the vernier effect and separated Fabry–Perot interferometers. J. Light. Technol. 2019, 37, 5609–5618. [Google Scholar] [CrossRef]
- Du, B.; He, J.; Xu, B.J.; Xu, X.Z.; Fu, C.L.; Li, P.F. High-density weak in-fibermicro-cavity array for distributed high-temperature sensing with millimeter spatial resolution. J. Light. Technol. 2022, 40, 7447–7455. [Google Scholar] [CrossRef]
- Qi, X.G.; Wang, S.; Jiang, J.F.; Liu, K.; Wang, X.; Yang, Y.G. Fiber optic fabry-perot pressure sensor with embedded MEMS micro-cavity for ultra-high pressure detection. J. Light. Technol. 2019, 37, 2719–2725. [Google Scholar] [CrossRef]
- Lu, H.L.; Yue, Y.L.; Jing Du, J.; Shao, L.P.; Wu, T.Y.; Pan, J.; Hu, J.H. Temperature and liquid refractive index sensor using P-D fiber structure-based Sagnac loop. Opt. Express 2018, 26, 18920–18927. [Google Scholar] [CrossRef]
- Ujah, E.; Lai, M.; Slaughter, G. Ultrasensitive tapered optical fiber refractive index glucose sensor. Sci. Rep. 2023, 13, 4495. [Google Scholar] [CrossRef]
- Costa, L.; Martins, H.F.; Martín-López, S.; Fernández-Ruiz, M.R.; González-Herráez, M. Fully distributed optical fiber strain sensor with 10−12ϵ/ sensitivity. J. Light. Technol. 2019, 37, 4487–4495. [Google Scholar] [CrossRef]
- Dong, S.; Dong, B.; Yu, C.; Guo, Y. High sensitivity optical fiber curvature sensor based on cascaded fiber interferometer. J. Light. Technol. 2018, 36, 1125–1130. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, C.B.; Liu, C.L.; Shi, C.; Wang, R.; Wang, X.K.; Ren, Z.; Ran, Z.; Liu, Z.H.; Zhang, Y. Multi-channel curvature sensor based on fiber bending loss wavelength and SPR. Opt. Lett. 2022, 47, 6017–6020. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Liu, Z.X.; Wang, B.; Kong, C.; Si, L.G.; Xiong, H.; Wu, Y. A proposed method to measure weak magnetic field based on a hybrid optomechanical system. Sci. Rep. 2017, 7, 12521. [Google Scholar] [CrossRef]
- Liu, Z.X.; Xiong, H. Highly sensitive charge sensor based on atom-assisted high-order sideband generation in a hybrid optomechanical system. Sensors 2018, 18, 3833. [Google Scholar] [CrossRef] [PubMed]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, T. Atomic super heterodyne receiver based on microwave-dressed Rydberg spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Sewell, R.I.; Koschorreck, M.; Napolitano, M.; Dubost, B.; Behbood, N.; Mitchell, M.W. Magnetic Sensitivity Beyond the Projection Noise Limit by Spin squeezing. Phy. Rev. Lett. 2012, 109, 253605. [Google Scholar] [CrossRef] [PubMed]
- Gross, C.; Zibold, T.; Nicklas, E.; Esteve, J.; Oberthaler, M.K. Nonlinear atom interferometer surpasses classical precision limit. Nature 2010, 464, 1165. [Google Scholar] [CrossRef]
- Anderson, B.E.; Gupta, P.; Schmittberger, B.L.; Horrom, T.; Hermann-Avigliano, C.; Jones, K.M.; Lett, P.D. Phase sensing beyond the standard quantum limit with a variation on the SU(1,1) interferometer. Optica 2017, 4, 752. [Google Scholar] [CrossRef]
- Pooser, R.C.; Lawrie, B. Ultrasensitive measurement of microcantilever displacement below the shot-noise limit. Optica 2015, 2, 393. [Google Scholar] [CrossRef]
- Zuo, X.J.; Yan, Z.H.; Feng, Y.N.; Ma, J.X.; Jia, X.J.; Xie, C.D.; Peng, K.C. Quantum Interferometer Combining Squeezing and Parametric Amplification. Phys. Rev. Lett. 2020, 124, 173602. [Google Scholar] [CrossRef]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Galiana, A.F. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Mehmet, M.; Luck, H.; Danzmann, K. Increasing the Astrophysical Reach of the Advanced Virgo Detector via the Application of Squeezed Vacuum States of Light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar] [CrossRef]
- Pooser, R.C.; Savino, N.; Batson, E.; Beckey, J.L.; Garcial, J.; Lawrie, B.J. Truncated Nonlinear Interferometry for Quantum-Enhanced Atomic Force Microscopy. Phys. Rev. Lett. 2020, 124, 230504. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M. Biological Measurement Beyond the Quantum Limit. Nat. Photonics 2013, 7, 229–233. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Mehmet, M.; Danzmann, K.; Schnabel, R. Detection of 15 dB Squeezed States of Light and their Application for the Absolute Calibration of Photoelectric Quantum Efficiency. Phys. Rev. Lett. 2016, 117, 110801. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yu, J.; Yan, Z.; Jia, X.; Zhang, J.; Xie, C.; Peng, K. Quantum Secret Sharing Among Four Players Using Multipartite Bound Entanglement of an Optical Field. Phys. Rev. Lett. 2018, 121, 150502. [Google Scholar] [CrossRef]
- Larsen, M.V.; Guo, X.S.; Breum, C.R.; Nielsen, J.S.N.; Andersen, U.L. Deterministic generation of a two-dimensional cluster state. Science 2019, 366, 369. [Google Scholar] [CrossRef]
- Kitagawa, M.; Yamamoto, Y. Number-phase minimum-uncertainty state with reduced number uncertainty in a Kerr nonlinear interferometer. Phys. Rev. A 1986, 34, 3974. [Google Scholar] [CrossRef]
- Korolkova, N.; Leuchs, G.; Loudon, R.; Ralph, T.C.; Silberhorn, C. Polarization squeezing and continuous-variable polarization entanglement. Phys. Rev. A 2002, 65, 052306. [Google Scholar] [CrossRef]
- Silberhorn, C.; Lam, P.K.; Weiss, O.; König, F.; Korolkova, N.; Leuchs, G. Generation of Continuous Variable Einstein-Podolsky-Rosen Entanglement via the Kerr Nonlinearity in an Optical Fiber. Phys. Rev. Lett. 2001, 86, 4267. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, Y.; Chen, M.Q.; Xia, F. Research Advances in Microfiber Humidity Sensors. Small 2018, 14, 1800524. [Google Scholar] [CrossRef]
- Cheol, J.; Shin, M.; Han, Y.G. Relative Humidity Sensor Based on an Optical Microfiber Knot Resonator with a Polyvinyl Alcohol Overlay. J. Light. Technol. 2016, 34, 4511. [Google Scholar] [CrossRef]
- Bo, L.; Wang, P.; Semenova, Y.; Farrell, G. Optical microfiber coupler based humidity sensorwith a polyethylene oxide coating. Microw. Opt. Technol. Lett. 2015, 57, 457–460. [Google Scholar] [CrossRef]
- Tan, Y.; Sun, L.P.; Jin, L.; Li, J.; Guan, B. Microfiber Mach-Zehnder interferometer based on long period grating for sensing applications. Opt. Express 2013, 21, 154–164. [Google Scholar] [CrossRef]
- Wu, Q.; Semenova, Y.; Wang, P.; Farrell, G. High sensitivity SMS fiber structure based refractometer–analysis and experiment. Opt. Express 2011, 19, 7937–7944. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Hu, H.; Zhao, Y.; Li, J.; Lei, M.; Zhang, Y. Highly-sensitive optical fiber temperature sensors based on PDMS/silica hybrid fiber structures. Sens. Actuators A Phys. 2018, 284, 22–27. [Google Scholar] [CrossRef]
- Eberle, T.; Steinlechner, S.; Bauchrowitz, J.; Handchen, V.; Vahlbruch, H.; Mehmet, M.; Muller-Ebhardt, H.; Schnabe, R. Quantum Enhancement of the Zero-area Sagnac Interferometer Topology for Gravitational Wave Detection. Phys. Rev. Lett. 2010, 104, 251102. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Dong, X.; Meng, Q.; Qi, F.; Zhao, C.L. Alcohol-filled side-hole fiber Sagnac interferometer for temperature measurement. Sens. Actuators A Phys. 2013, 193, 182–185. [Google Scholar] [CrossRef]
- Zhao, N.; Fu, H.; Shao, M.; Yan, X.; Li, H.D.; Liu, Q.P.; Gao, H.; Liu, Y.G.; Qiao, X.G. High temperature probe sensor with high sensitivity based on Michelson interferometer. Opt. Commun. 2015, 343, 131–134. [Google Scholar] [CrossRef]
- Goda, K.; Miyakawa, O.; Mikhailov, E.E.; Saraf, S.; Adhikari, R.; McKenzie, K.; Ward, R.; Vass, S.; Weinstein, A.J.; Mavalvala, N. A quantum-enhanced prototype gravitational-wave detector. Nat. Phys. 2008, 4, 472. [Google Scholar] [CrossRef]
- Xin, Y.; Zhao, M.; Zhao, H.; Gong, H.P.; Shen, C.Y.; Zhao, C.L.; Dong, X.Y. Alcohol-filled side-hole fiber based Mach-Zehnder interferometer for temperature measurement. Opt. Fiber Technol. 2018, 46, 72–76. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, L.; Huang, S.; Ma, T.; Liu, F.; Yonezawa, H.; Zhang, Y.; Xiao, M. Sensing and tracking enhanced by quantum squeezing. Photonics Res. 2019, 7, 6. [Google Scholar] [CrossRef]
- Hoff, U.B.; Harris, G.I.; Madsen, L.S.; Kerdoncuff, H.; Lassen, M.; Kerdoncuff, H.; Lassen, M.; Nielsen, B.M.; Bowen, W.P.; Andersen, U.L. Quantum-enhanced micro-mechanical displacement sensitivity. Opt. Lett. 2013, 38, 1413. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Wu, L.A.; Kimble, H.J. Precision measurement beyond the shot-noise limit. Phys. Rev. Lett. 1987, 59, 278. [Google Scholar] [CrossRef] [PubMed]
- O’brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef]
- Huo, M.R.; Qin, J.L.; Cheng, J.L.; Yan, Z.H.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Deterministic quantum teleportation through fiber channels. Sci. Adv. 2018, 4, eaas9401. [Google Scholar] [CrossRef]
- Liang, S.C.; Cheng, J.L.; Qin, J.L.; Li, J.T.; Shi, Y.; Yan, Z.H.; Jia, X.J.; Xie, C.D.; Peng, K.C. High-speed quantum radio-frequency-over-light communication. Phys. Rev. Lett. 2024, 132, 140802. [Google Scholar] [CrossRef]
- Clark, J.B.; Lecocq, F.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Observation of strong radiation pressure forces from squeezed light on a mechanical oscillator. Nat. Phys. 2016, 12, 683. [Google Scholar] [CrossRef]
- Li, B.B.; Bilek, J.; Hoff, U.B.; Madsen, L.S.; Forstner, S. Quantum enhanced optomechanical magnetometry. Optics 2018, 5, 850. [Google Scholar] [CrossRef]
- Heersink, J.; Gaber, T.; Lorenz, S.; Glockl, O.; Korolkova, N.; Leuchs, G. Polarization squeezing of intense pulses with a fiber optic Sagnac interferometer. Phys. Rev. A 2003, 68, 013815. [Google Scholar] [CrossRef]
- Barreiro, S.; Valente, P.; Failache, H.; Lezama, A. Polarization squeezing of light by single passage through an atomic vapor. Phys. Rev. A 2011, 84, 033851. [Google Scholar] [CrossRef]
- Su, X.; Zhao, Y.; Hao, S.; Xie, C.; Peng, K. Experimental preparation of eight-partite cluster state for photonic qumodes. Opt. Lett. 2012, 37, 5178. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.P.; Wang, Y.J.; Yang, W.H.; Zheng, Y.H.; Peng, K.C. Detection and perfect fitting of 13.2 dB squeezed vacuum states by considering green-light-induced infrared absorption. Opt. Lett. 2018, 43, 5411. [Google Scholar] [CrossRef] [PubMed]
- Morin, O.; Huang, K.; Liu, J.; Jeannic, H.L.; Fabre, C.; Laurat, J. Remote creation of hybrid entanglement between particle-like and wave-like optical qubits. Nat. Photonics 2014, 8, 570–574. [Google Scholar] [CrossRef]
- Eberle, T.; Handchen, V.; Schnabel, R. Stable control of 10 dB two-mode squeezed vacuum states of light. Opt. Express 2013, 21, 11546–11553. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, K.C. Quantum teleportation and dense coding by means of bright amplitude-squeezed light and direct measurement of a Bell state. Phys. Rev. A 2000, 62, 064302. [Google Scholar] [CrossRef]
- Sharping, J.E.; Fiorentino, M.; Kumar, P. Observation of twin-beam-type quantum correlation in optical fiber. Opt. Lett. 2001, 26, 367–369. [Google Scholar] [CrossRef]
- Guo, X.S.; Li, X.Y.; Liu, N.N.; Yang, L.; Ou, Z.Y. An all-fiber source of pulsed twin beams for quantum communication. Appl. Phys. Lett. 2012, 101, 261111. [Google Scholar] [CrossRef]
- Brida, G.; Genovese, M.; Berchera, I.R. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics 2010, 4, 227–230. [Google Scholar] [CrossRef]
- Lunghi, T.; Brask, J.B.; Lim, C.C.W.; Lavigne, Q.; Bowles, J.; Martin, A.; Zbinden, H.; Brunner, N. Self-testing quantum random number generator. Phys. Rev. Lett. 2015, 114, 150501. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, X.W.; Tian, C.X.; Xiao, L.S. Quantum random number generator based on twin beams. Opt. Lett. 2017, 42, 895–898. [Google Scholar] [CrossRef]
- Hald, J.; Sorensen, J.L.; Schori, C.; Polzik, E.S. Spin squeezed atoms: A new sub-Poissonian atomic beam. J. Mod. Opt. 2001, 47, 2599–2603. [Google Scholar] [CrossRef]
- Wolfgramm, F.; Cere, A.; Beduini, F.A.; Predojevic, A.; Koschorreck, M.; Mitchell, M.W. Squeezed-Light Optical Magnetometry. Phys. Rev. Lett. 2010, 105, 053601. [Google Scholar] [CrossRef]
- Bai, L.L.; Zhang, L.L.; Yang, Y.B.; Chuang, R.; Qin, Y.; He, J.; Wen, X.; Wang, J.M. Enhancement of spin noise spectroscopy of rubidium atomic ensemble by using the polarization squeezed light. Opt. Express 2022, 30, 1925–1935. [Google Scholar] [CrossRef]
- Wu, L.; Yan, Z.H.; Liu, Y.H.; Deng, R.J.; Jia, X.J.; Xie, C.D.; Peng, K.C. Experimental generation of tripartite polarization entangled states of bright optical beams. Appl. Phys. Lett. 2016, 108, 161102. [Google Scholar] [CrossRef]
- Josse, V.; Dantan, A.; Bramati, A.; Pinard, M.; Giacobino, E. Continuous variable entanglement using cold atoms. Phys. Rev. Lett. 2014, 92, 123601. [Google Scholar] [CrossRef] [PubMed]
- Korolkova, N.; Loudon, R.; Leuchs, G. Nonseparability and squeezing of continuous polarization variables. Phys. Rev. A 2005, 71, 032343. [Google Scholar] [CrossRef]
- Hudelist, F.; Kong, J.; Liu, C.J.; Jing, J.T.; Ou, Z.Y.; Zhang, W.P. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef]
- Du, W.; Wu, S.H.; Zhang, D.; Chen, J.; Yang, Y.Q.; Yang, P.Y.; Guo, J.X.; Bao, G.Z.; Zhang, W.P. Quantum Twin Interferometers. arXiv 2025, arXiv:2501.04244. [Google Scholar]
- Li, J.; Liu, Y.; Cui, L.; Huo, N.; Assad, S.M.; Li, X.; Ou, Z.Y. Joint measurement of multiple noncommuting parameters. Phys. Rev. A 2018, 97, 052127. [Google Scholar] [CrossRef]
- Guo, X.S.; Li, X.Y.; Liu, N.N.; Ou, Z.Y. Multimode theory of pulsed-twin-beams generation from a high-gain fiber-optical parametric amplifier. Phys. Rev. A 2013, 88, 023841. [Google Scholar] [CrossRef]
- Sharping, J.E.; Chen, J.; Li, X.Y.; Kumar, P. Quantum-correlated twin photons from microstructure fiber. Opt. Express 2004, 12, 3086–3094. [Google Scholar] [CrossRef]
- Takesue, H.; Inoue, K. 1.5-m band quantum-correlated photon pair generation in dispersionshifted fiber: Suppression of noise photons by cooling fiber. Opt. Express 2005, 13, 7832–7839. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.; Altepeter, J.B.; Huang, Y.P.; Oza, N.N.; Prem Kumar, P. Independent telecom-fiber sources of quantum indistinguishable single photons. New J. Phys. 2014, 16, 043019. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, W.; Huang, Y. Fiber-based frequency-degenerate polarization entangled photon pair sources for information encoding. Opt. Express 2016, 24, 25619–25628. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.M.; Levenson, M.D.; Perlmutter, S.H.; DeVoe, R.G.; Walls, D.F. Broad-band parametric deamplification of quantum noise in an optical fiber. Phys. Rev. Lett. 1986, 57, 691–694. [Google Scholar] [CrossRef]
- Li, X.Y.; Yang, L.; Ma, X.X.; Cui, L.; Ou, Z.Y.; Yu, D.Y. All-fiber source of frequency-entangled photon pairs. Phys. Rev. A 2009, 79, 033817. [Google Scholar] [CrossRef]
- Li, X.Y.; Ma, X.X.; Quan, L.M.; Yang, L.; Cui, L.; Guo, X.S. Quantum efficiency measurement of single-photon detectors using photon pairs generated in optical fibers. J. Opt. Soc. Am. B 2010, 27, 1857–1865. [Google Scholar] [CrossRef]
- Yang, L.; Ma, X.X.; Guo, X.S.; Cui, L.; Li, X.Y. Characterization of a fiber-based source of heralded single photons. Phys. Rev. A 2011, 83, 053843. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Cheng, J.R.; Huang, Y.D.; Peng, J.D. Noise performance comparison of 1.5 µm correlated photon pair generation in different fibers. Opt. Express 2010, 18, 17114–17123. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Cheng, J.R.; Huang, Y.D.; Peng, J.D. Polarization-entangled Bell states generation based on birefringence in high nonlinear microstructure fiber at 1.5 µm. Opt. Lett. 2009, 34, 2706–2708. [Google Scholar] [CrossRef]
- Guo, X.S.; Liu, N.N.; Liu, Y.H.; Li, X.Y.; Ou, Z.Y. Generation of continuous variable quantum entanglement using a fiber optical parametric amplifier. Opt. Lett. 2016, 41, 653. [Google Scholar] [CrossRef]
- Liu, Y.H.; Huo, N.; Li, J.M.; Li, X.Y. Long-distance distribution of the telecom band intensity difference squeezing generated in a fiber optical parametric amplifier. Opt. Lett. 2018, 43, 5559–5562. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Guo, X.S.; Li, X.Y. Time-domain measurement of twin beams produced by fiber amplifiers with an ultra-fast pulse train as a pump. Opt. Lett. 2023, 48, 444–447. [Google Scholar] [CrossRef] [PubMed]
- Li, J.M.; Liu, Y.H.; Huo, N.; Cui, L.; Feng, S.; Li, X.Y.; Ou, Z.Y. Measuring the continuous variable quantum entanglement with a parametric amplifier assisted homodyne detection. Phys. Rev. A 2020, 101, 053801. [Google Scholar] [CrossRef]
- Kong, J.; Hudelist, F.; Ou, Z.Y.; Zhang, W. Cancellation of internal quantum noise of an amplifier by quantum correlation. Phys. Rev. Lett. 2013, 111, 033608. [Google Scholar] [CrossRef]
- Guo, X.S.; Li, X.Y.; Liu, N.N.; Ou, Z.Y. Quantum information tapping using a fiber optical parametric amplifier with noise figure improved by correlated inputs. Sci. Rep. 2016, 6, 30214. [Google Scholar] [CrossRef]
- Kong, J.; Ou, Z.Y.; Zhang, W.P. Phase-measurement sensitivity beyond the standard quantum limit in an interferometer consisting of a parametric amplifier and a beam splitter. Phys. Rev. A 2013, 87, 023825. [Google Scholar] [CrossRef]
- Wang, H.L.; Shi, Y.P.; Fu, Z.X.; Chen, Z.H.; Jin, S.Z.; Zhao, C.L. Experimental implementation of quantum-enhanced tapered fiber sensor for simultaneous measurement of curvature and temperature. Opt. Fiber Technol. 2023, 81, 103545. [Google Scholar] [CrossRef]
- Rosenbluh, M.; Shelby, R.M. Squeezed optical solitons. Phys. Rev. Lett. 1991, 66, 153–156. [Google Scholar] [CrossRef]
- Schmitt, S.; Ficker, J.; Wolff, M.; Konig, F.; Sizmann, A.; Leuchs, G. Photon-number-squeezed solitons from an asymmetric fiber-optic Sagnac interferometer. Phys. Rev. Lett. 1998, 81, 2446–2449. [Google Scholar] [CrossRef]
- Hirosawa, K.; Furumochi, H.; Tada, A.; Kannari, F.; Takeoka, M.; Sasaki, M. Photon number squeezing of ultrabroadband laser pulses generated by microstructure fibers. Phys. Rev. Lett. 2005, 94, 203601. [Google Scholar] [CrossRef]
- Heersink, J.; Josse, V.; Leuchs, G.; Andersen, U.L. Efficient polarization squeezing in optical fibers. Opt. Lett. 2005, 30, 1192–1194. [Google Scholar] [CrossRef] [PubMed]
- Corney, J.F.; Drummond, P.D.; Heersink, J.; Josse, V.; Leuchs, G.; Andersen, U.L. Many-body quantum dynamics of polarization squeezing in optical fibre. Phys. Rev. Lett. 2006, 97, 023606. [Google Scholar] [CrossRef] [PubMed]
- Corney, J.F.; Heersink, J.; Dong, R.; Josse, V.; Drummond, P.D.; Leuchs, G.; Andersen, U.L. Simulations and experiments on polarization squeezing in optical fiber. Phys. Rev. A 2008, 78, 023831. [Google Scholar] [CrossRef]
- Rigas, I.; Klimov, A.B.; Sanchez-Soto, L.L.; Leuchs, G. Nonlinear cross-Kerr quasiclassical dynamics. New J. Phys. 2013, 15, 043038. [Google Scholar] [CrossRef]
- Dong, R.; Heersink, J.; Corney, J.F.; Drummond, P.D.; Andersen, U.L.; Leuchs, G. Experimental evidence for Raman-induced limits to efficient squeezing in optical fibers. Opt. Lett. 2008, 33, 116–118. [Google Scholar] [CrossRef]
- Kaiser, F.; Fedrici, B.; Zavatta, A.; dAuria, V.; Tanzilli, S. A fully guided-wave squeezing experiment for fiber quantum networks. Optica 2016, 3, 362–365. [Google Scholar] [CrossRef]
- Mondain, F.; Lunghi, T.; Zavatta, A.; Gouzien, E.; Doutre, F.; De Micheli, M.; Tanzilli, S.; D’Auria, V. Chip-based squeezing at a telecom wavelength. Photonics Res. 2019, 7, 36–39. [Google Scholar] [CrossRef]
- Taylor, M.A.; Janousek, J.; Daria, V.; Knittel1, J.; Hage, B.; Bachor, H.A.; Bowen, W.P. Subdiffraction-Limited Quantum Imaging within a Living Cell. Phys. Rev. X 2014, 4, 011017. [Google Scholar] [CrossRef]
- Mason, D.; Chen, J.X.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745. [Google Scholar] [CrossRef]
- Xiang, G.Y.; Higgins, B.L.; Berry, D.W.; Wiseman, H.M.; Pryde, G.J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 2011, 5, 43. [Google Scholar] [CrossRef]
- Liu, J.; Liu, W.; Li, S.; Wei, D.; Gao, H.; Li, F. Enhancement of the angular rotation measurement sensitivity based on SU(2) and SU(1,1) interferometers. Photonics Res. 2017, 5, 617. [Google Scholar] [CrossRef]
- Ou, Z.Y. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer. Phys. Rev. A 2012, 85, 023815. [Google Scholar] [CrossRef]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033–4054. [Google Scholar] [CrossRef]
- Manceau, M.; Leuchs, G.; Khalili, F.; Chekhova, M. Detection loss tolerant supersensitive phase measurement with an SU(1,1) interferometer. Phys. Rev. Lett. 2017, 119, 223601. [Google Scholar] [CrossRef]
- Du, W.; Jia, J.; Chen, J.F.; Ou, Z.Y.; Jing, J.T. Absolute sensitivity of phase measurement in an SU(1,1) type interferometer. Opt. Lett. 2018, 43, 1051–1054. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Huo, N.; Li, J.M.; Cui, L.; Li, X.Y.; Ou, Z.Y. Optimum quantum resource distribution for phase measurement and quantum information tapping in a dual-beam SU(1,1) interferometer. Opt. Express 2019, 27, 11292. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Li, J.M.; Cui, L.; Huo, N.; Assad, S.M.; Li, X.Y.; Ou, Z.Y. Loss-tolerant quantum dense metrology with SU(1,1) interferometer. Opt. Express 2018, 26, 27705. [Google Scholar] [CrossRef] [PubMed]
- Flurin, E.; Roch, N.; Mallet, F.; Devoret, M.H.; Huard, B. Generating entangled microwave radiation over two transmission lines. Phys. Rev. Lett. 2012, 109, 183901. [Google Scholar] [CrossRef]
- Linnemann, D.; Strobel, H.; Muessel, W.; Schulz, J.; Lewis-Swan, R.J.; Kheruntsyan, K.V.; Oberthaler, M.K. Quantum-enhanced sensing based on time reversal of nonlinear dynamics. Phys. Rev. Lett. 2016, 117, 013001. [Google Scholar] [CrossRef]
- Cheung, H.F.; Patil, Y.S.; Chang, L.; Chakram, S.; Vengalattore, M. Nonlinear phonon interferometry at the Heisenberg limit. arXiv 2016, arXiv:1601.02324. [Google Scholar]
- Chen, B.; Qiu, C.; Chen, S.Y.; Guo, J.X.; Chen, L.Q.; Ou, Z.Y.; Zhang, W.P. Atom-light hybrid interferometer. Phys. Rev. Lett. 2015, 115, 043602. [Google Scholar] [CrossRef]
- Grace, M.R.; Gagatsos, C.N.; Zhuang, Q.; Guha, S. Quantum-enhanced fiber-optic gyroscopes using quadrature squeezing and continuous-variable entanglement. Phys. Rev. Appl. 2020, 14, 034065. [Google Scholar] [CrossRef]
- Schubert, C.; Abend, S.; Gersemann, M.; Gebbe, M.; Schlippert, D.; Berg, P.; Rasel, E.M. Multi-loop atomic Sagnac interferometry. Sci. Rep. 2021, 11, 16121. [Google Scholar] [CrossRef]
- Zhang, W.X.; Zhang, R.; Zuo, Y.L.; Kuang, L.M. Enhancing the sensitivity of quantum fiber-optical gyroscopes via a non-Gaussian-state probe. Adv. Quantum Technol. 2025, 8, 2400270. [Google Scholar] [CrossRef]
- Krylov, D.; Bergman, K. Amplitude-squeezed solitons from an asymmetric fiber interferometer. Opt. Lett. 1998, 23, 1390. [Google Scholar] [CrossRef]
- Pizzaia, J.P.L.; Castellani, C.E.S.; Leal-Junior, A.G. Highly sensitive temperature sensing based on a birefringent fiber Sagnac loop. Opt. Fiber Technol. 2022, 72, 102949. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Chen, H. Enhanced sensitivity of temperature sensor by a PCF with a defect core based on Sagnac interferometer. Sens. Actuators B Chem. 2018, 254, 636–641. [Google Scholar] [CrossRef]
- Liu, Q.; Xing, L.; Wu, Z.X.; Cai, L.; Zhang, Z.; Zhao, J.C. High-sensitivity photonic crystal fiber force sensor based on Sagnac interferometer for weighing. Opt. Laser Technol. 2020, 123, 105939. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Cao, Z.; Xia, T.T.; Yang, C.K.; Liu, Z.Y.; Li, Z.H. Lateral force sensing based on Sagnac interferometry realized by a high-birefringence suspended-core fiber. J. Light. Technol. 2022, 40, 3935–3941. [Google Scholar] [CrossRef]
- Li, X.G.; Nguyen, L.V.; Zhao, Y.; Ebendorff-Heidepriem, H.; Warren-Smith, S.C. High-sensitivity Sagnac-interferometer biosensor based on exposed core microstructured optical fiber. Sens. Actuators B Chem. 2018, 269, 103–109. [Google Scholar] [CrossRef]
- Huang, B.S.; Sheng, X.; Gao, J.Q.; Gao, W.; Lou, S.Q. High sensitivity twist sensor based on suspended core fiber Sagnac interferometer with temperature calibration. Opt. Express 2023, 31, 38205. [Google Scholar] [CrossRef]
- Han, T.T.; Liu, Y.G.; Wang, Z.; Guo, J.Q.; Wu, Z.F.; Wang, S.X.; Li, Z.L.; Zhou, W.Y. Unique characteristics of a selective-filling photonic crystal fiber Sagnac interferometer and its application as high sensitivity sensor. Opt. Express 2013, 21, 122–128. [Google Scholar] [CrossRef]
- Mehmet, M.; Eberle, T.; Steinlechner, S.; Vahlbruch, H.; Schnabel, R. Demonstration of a quantum-enhanced fiber Sagnac interferometer. Opt. Lett. 2010, 35, 1665–1667. [Google Scholar] [CrossRef]
- Xin, J.; Liu, J.M.; Jing, J.T. Nonlinear Sagnac interferometer based on the four-wave mixing process. Opt. Express 2017, 25, 1350–1357. [Google Scholar] [CrossRef]
- Fink, M.; Steinlechner, F.; Handsteiner, J.; Dowling, J.P.; Scheidl, T.; Ursin, R. Entanglement-enhanced optical gyroscope. New J. Phys. 2019, 21, 053010. [Google Scholar] [CrossRef]
- Wang, H.L.; Chen, Z.H.; Ma, S.Y.; Wang, D.X.; Mao, T.H.; Zhang, Y.; Zhao, C.L. Quantum-Enhanced Strain and Curvature Sensing Based on a Birefringent Fiber Sagnac Interferometer. J. Light.Technol. 2025, 43, 966. [Google Scholar] [CrossRef]
- Duan, D.W.; Rao, Y.J.; Xu, L.C.; Zhu, T.; Wu, D.; Yao, J. In-fiber Mach–Zehnder interferometer formed by large lateral offset fusion splicing for gases refractive index measurement with high sensitivity. Sens. Actuators B Chem. 2011, 160, 1198–1202. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, J.; Wang, S.; Li, B.; Wang, M. Fiber Mach–Zehnder interferometer based on microcavities for high-temperature sensing with high sensitivity. Opt. Lett. 2011, 36, 3753–3755. [Google Scholar] [CrossRef] [PubMed]
- Li, E. Temperature compensation of multimode-interference-based fiber devices. Opt. Lett. 2007, 32, 2064. [Google Scholar] [CrossRef]
- Tripathi, S.M.; Kumar, A.; Varshney, R.K.; Kumar, Y.B.P.; Marin, E.; Meunier, J.P. Strain and temperature sensing characteristics of single-mode-multimode-single-mode structures. J. Light. Technol. 2009, 27, 2348–2356. [Google Scholar] [CrossRef]
- Wu, Q.; Semenova, Y.; Yan, B.B.; Ma, Y.Q.; Wang, P.F.; Yu, C.X.; Farrell, G. Fiber refractometer based on a fiber Bragg grating and single-mode-multimode-single-mode fiber structure. Opt. Lett. 2011, 36, 2197–2199. [Google Scholar] [CrossRef]
- Tian, Z.; Yam, S.S.H. In-line single-mode optical fiber interferometric refractive index sensors. J. Light. Technol. 2009, 27, 2296–2306. [Google Scholar] [CrossRef]
- Lu, P.; Men, L.Q.; Sooley, K.; Chen, Q.Y. Tapered fiber Mach-Zehnder interferometer for simultaneous measurement of refractive index and temperature. Appl. Phys. Lett. 2009, 94, 131110. [Google Scholar] [CrossRef]
- Wang, Q.; Wei, W.Q.; Guo, M.J.; Zhao, Y. Optimization of cascaded fiber tapered Mach-Zehnder interferometer and refractive index sensing technology. Sens. Actuators B Chem. 2016, 222, 159. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, Y.; Yu, J.; Guo, J.; Wu, Y.; Xiao, S.; Wei, D.; Zhang, Y.; Jia, X.; Xiao, M. Squeezing-enhanced fiber Mach-Zehnder interferometer for low-frequency phase measurement. Appl. Phys. Lett. 2017, 110, 021106. [Google Scholar] [CrossRef]
- Kang, G.H.; Feng, J.X.; Cheng, L.; Li, Y.J.; Zhang, K.S. Quantum-enhanced optical precision measurement assisted by low-frequency squeezed vacuum states. Chin. Phys. B 2023, 32, 104204. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, Y.; Hua, X.G.; Xia, F.; Zhao, Q. Beating the shot-noise limit with optical fiber quantum sensors for salinity measurement. Sens. Actuators B Chem. 2020, 320, 128353. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, Y.; Hu, X.G.; Yang, Y. Optical fiber quantum biosensor based on surface plasmon polaritons for the label-free measurement of protein. Sens. Actuators B Chem. 2020, 316, 128097. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, Y. Microfiber quantum sensors for protein measurement with quantum N00N state. Sens. Actuators B Chem. 2023, 383, 133616. [Google Scholar] [CrossRef]
- Alibart, O.; Fulconis, J.; Wong, G.K.L.; Murdoch, S.G.; Wadsworth, W.J.; Rarity, J.G. Photon pair generation using four-wave mixing in a microstructured fibre: Theory versus experiment. New J. Phys. 2006, 8, 67. [Google Scholar] [CrossRef]
- Chen, J.H.; Tan, J.; Wu, G.X.; Zhang, X.J.; Xu, F.; Lu, Y.Q. Tunable and enhanced light emission in hybrid WS2-optical-fiber-nanowire structures. Light Sci. Appl. 2019, 8, 8. [Google Scholar] [CrossRef]
- Zuo, Y.G.; Yu, W.T.; Liu, C.; Cheng, X.; Qiao, R.X.; Liang, J.; Zhou, X.; Wang, J.H.; Wu, M.H.; Zhao, Y.; et al. Optical fibres with embedded two-dimensional materials for ultrahigh nonlinearity. Nat. Nanotechnol. 2020, 15, 987. [Google Scholar] [CrossRef]
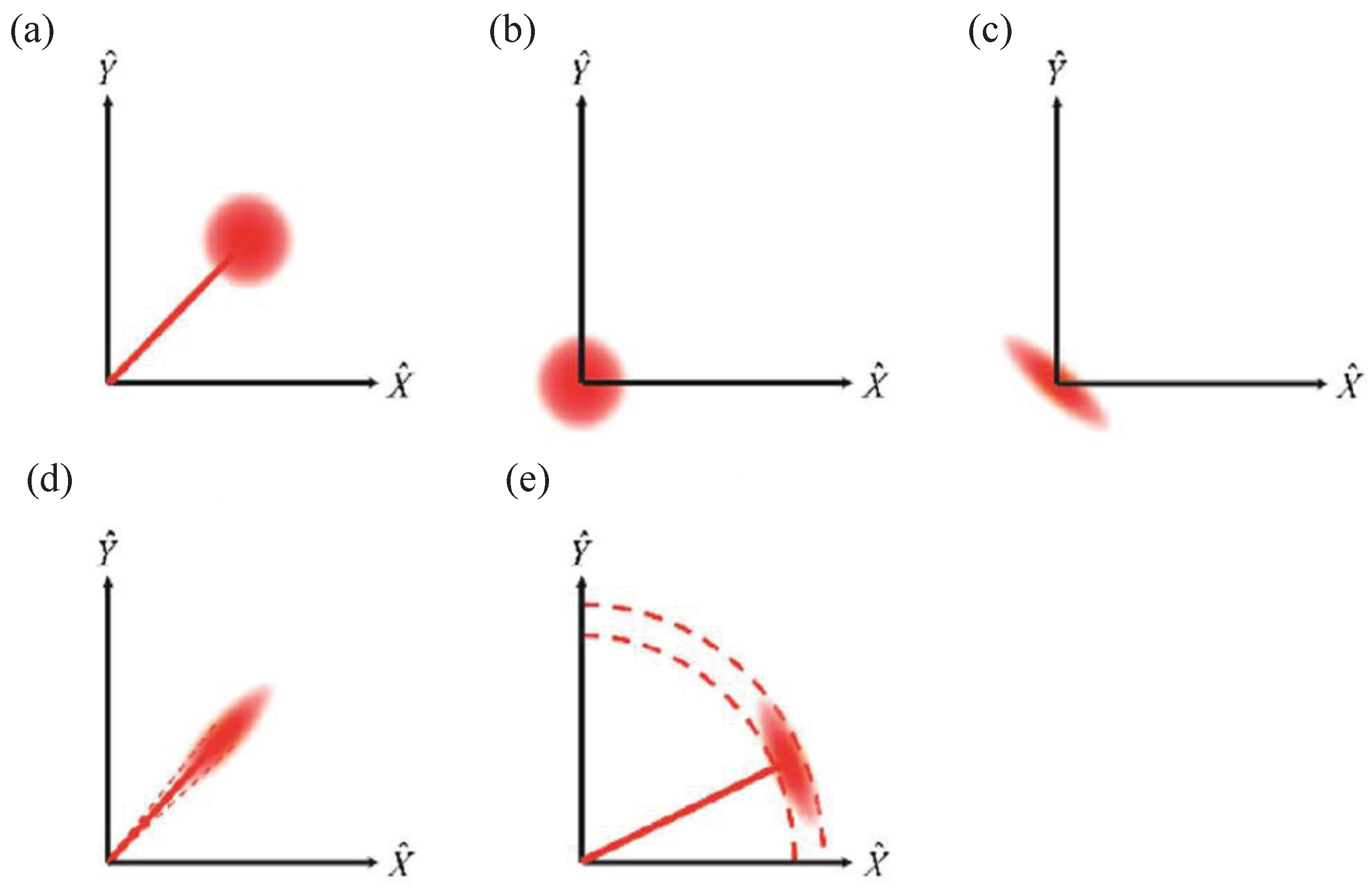
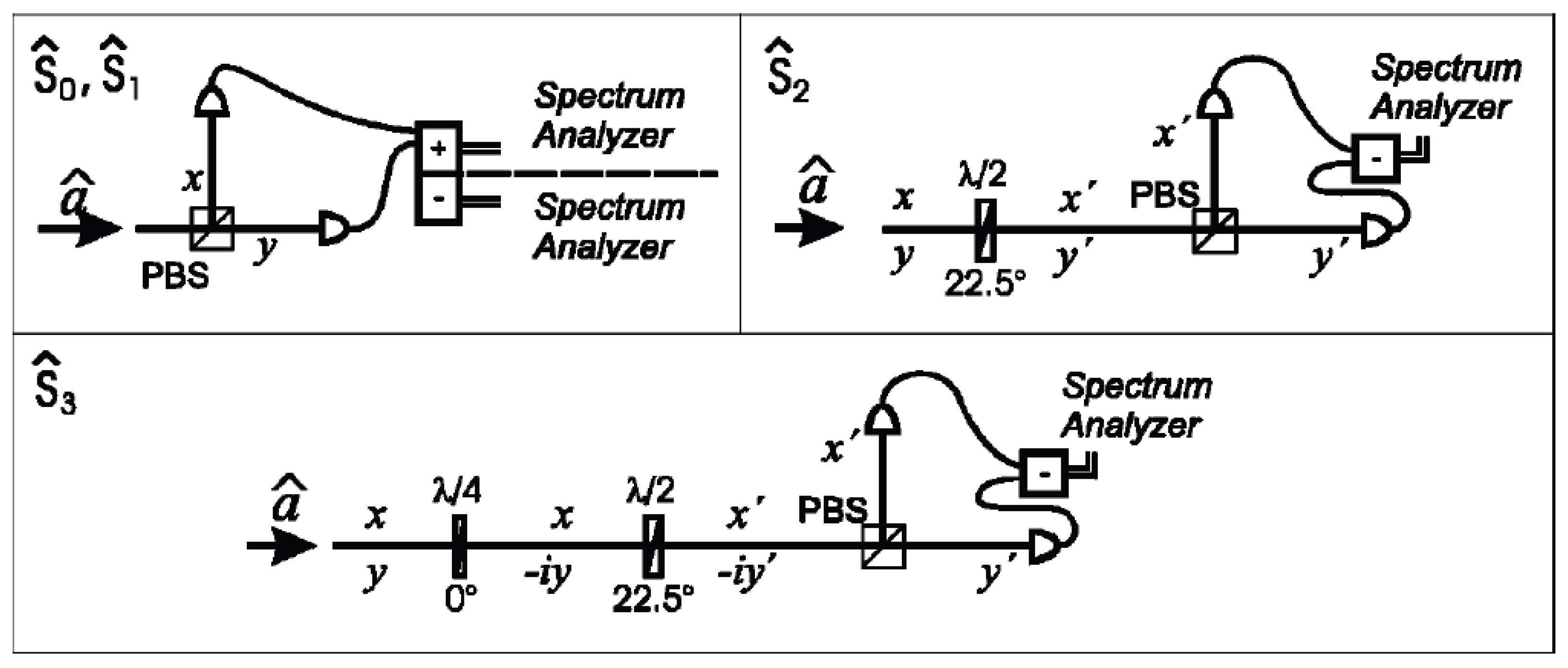
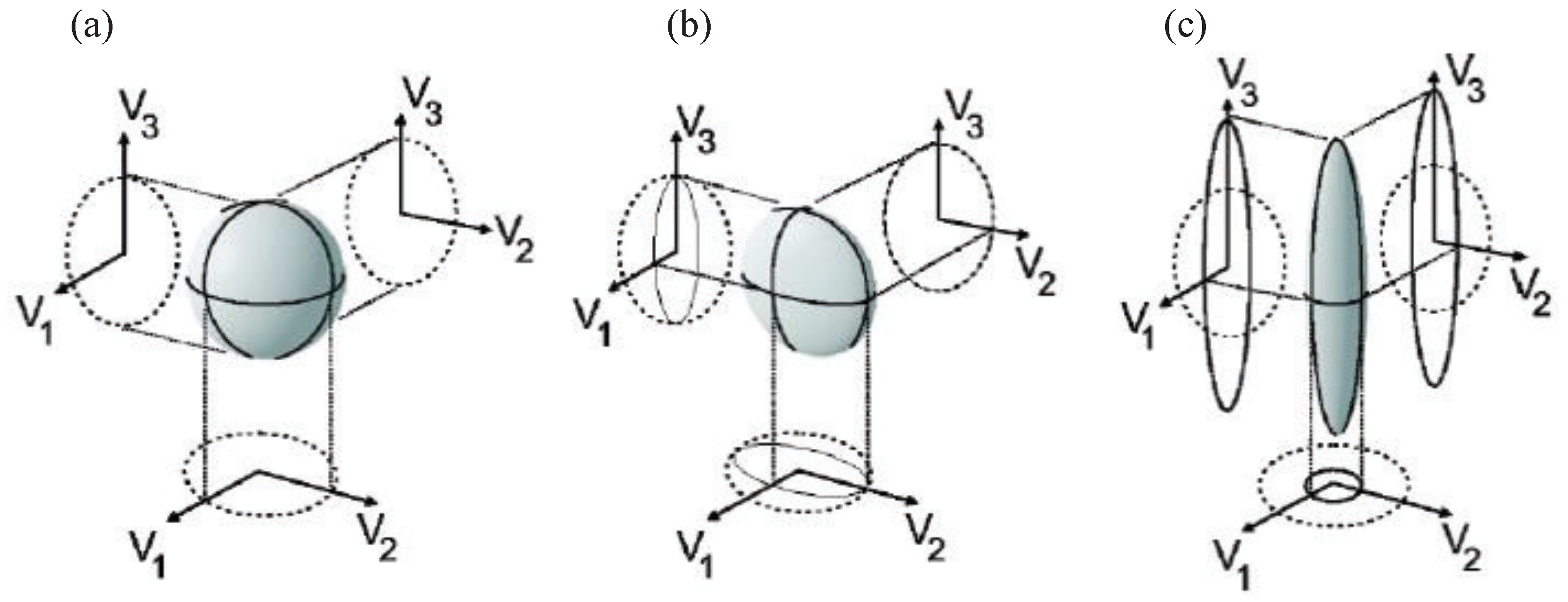

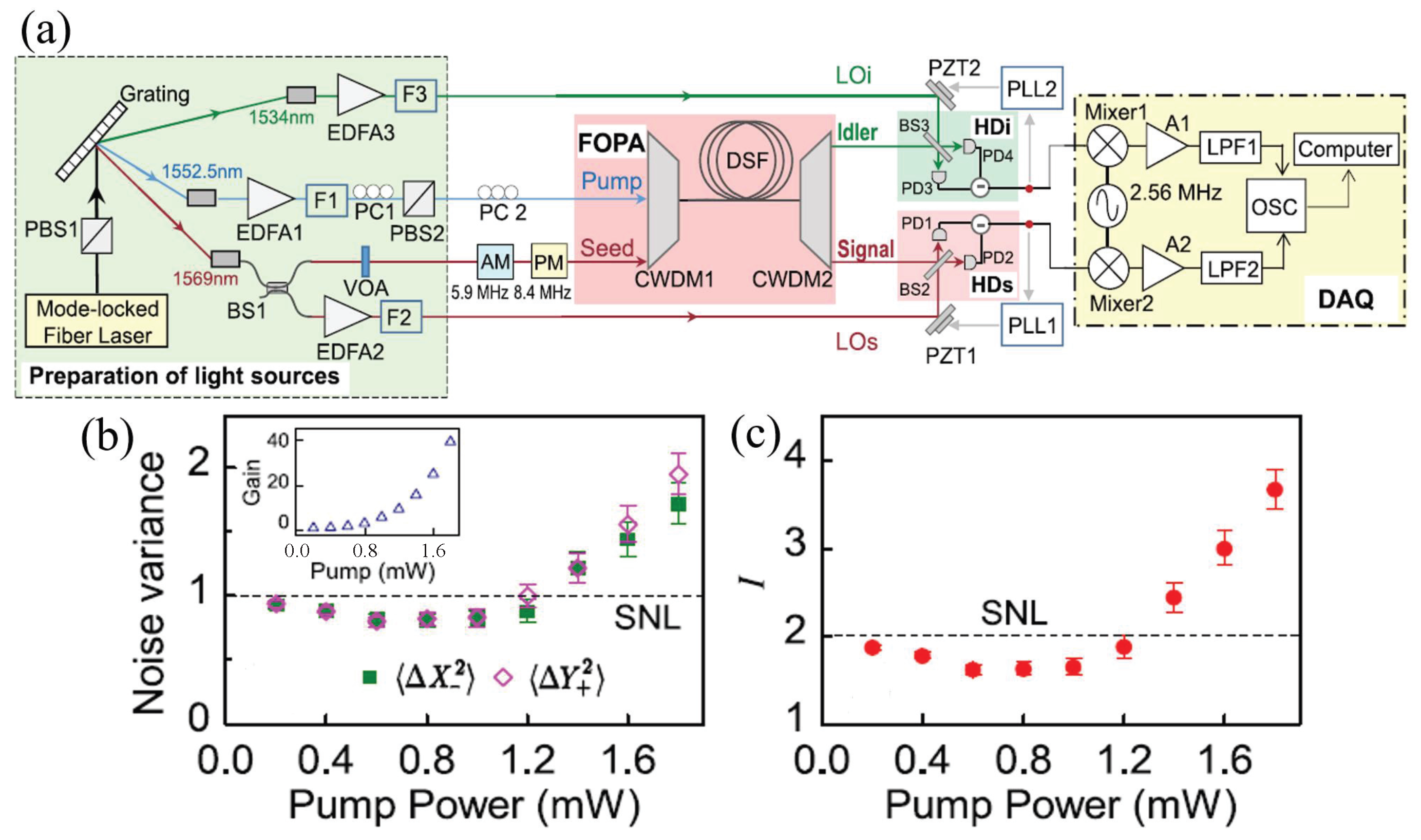
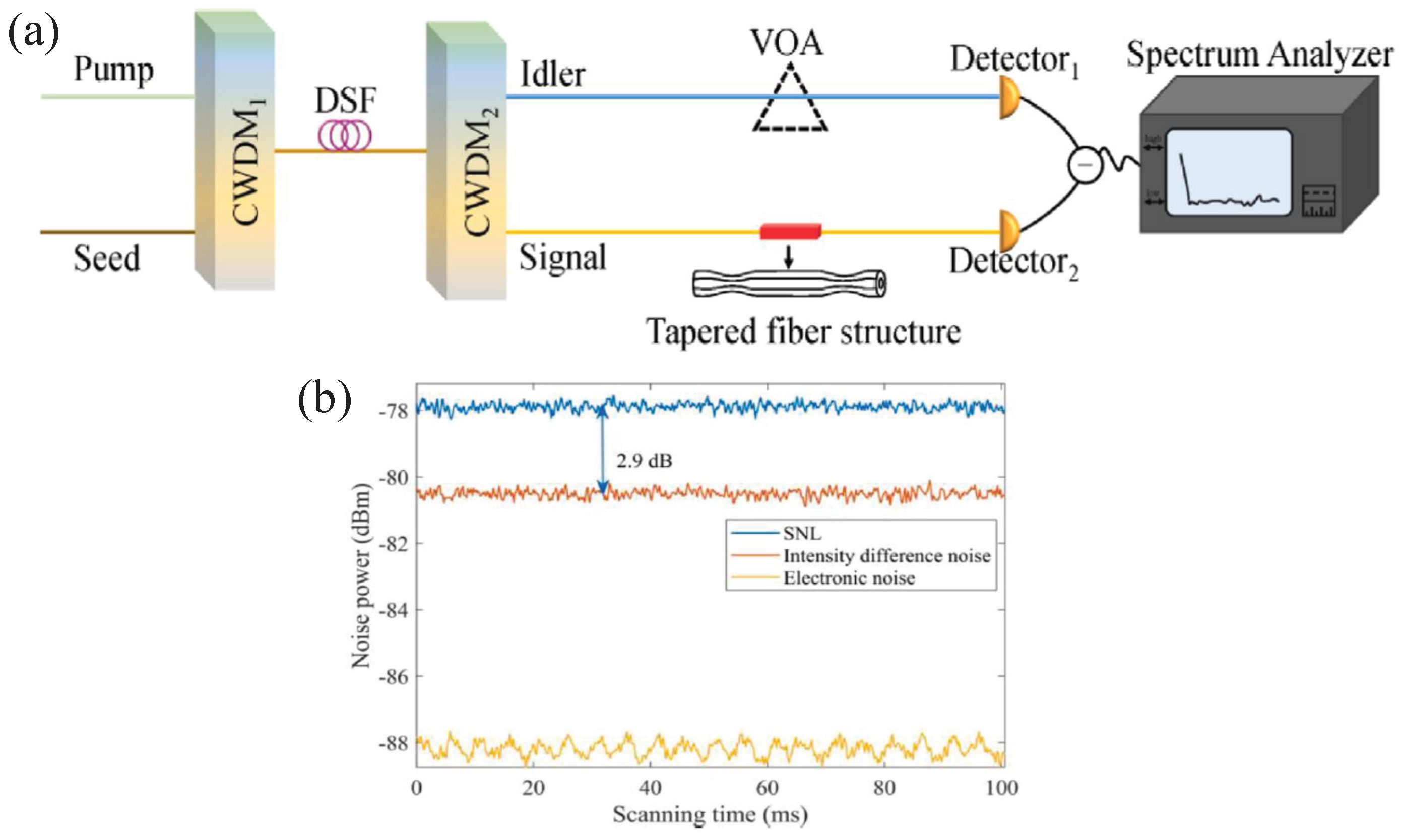

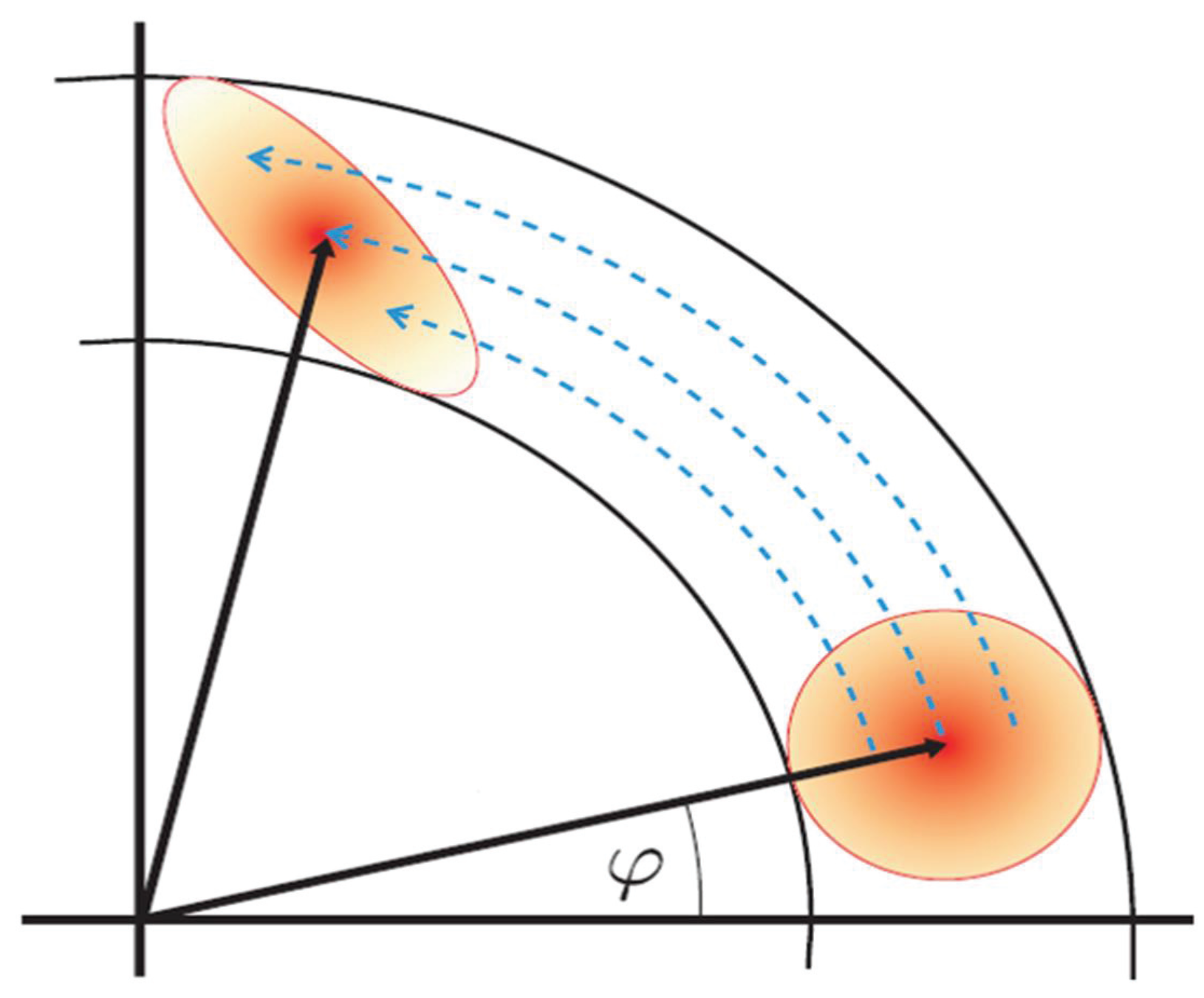
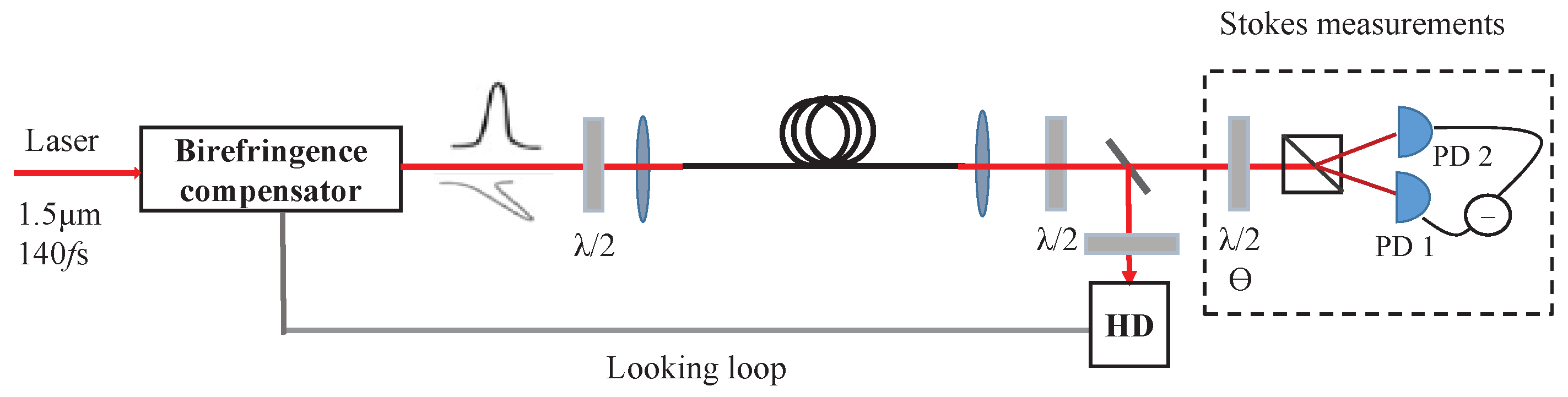


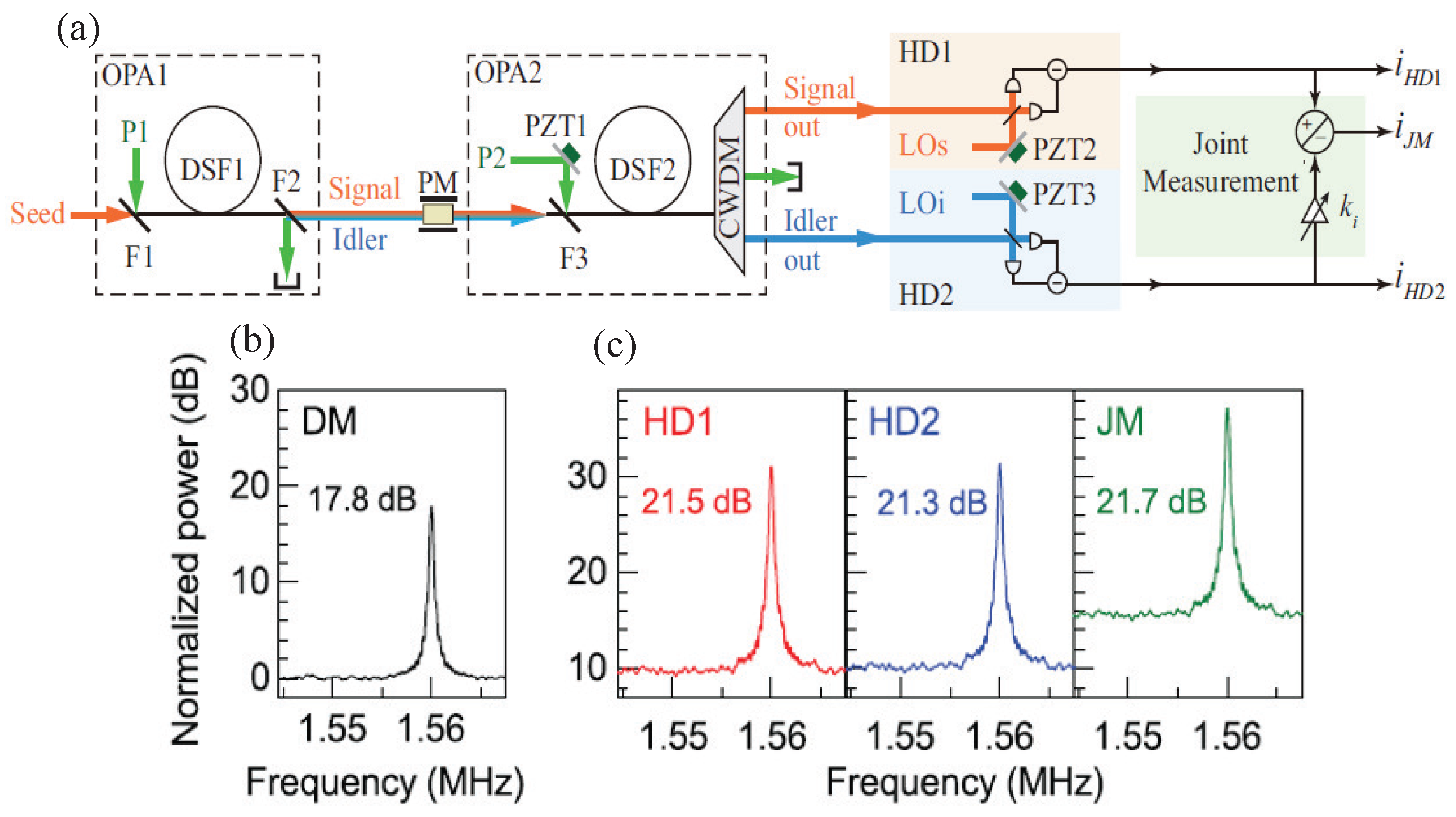
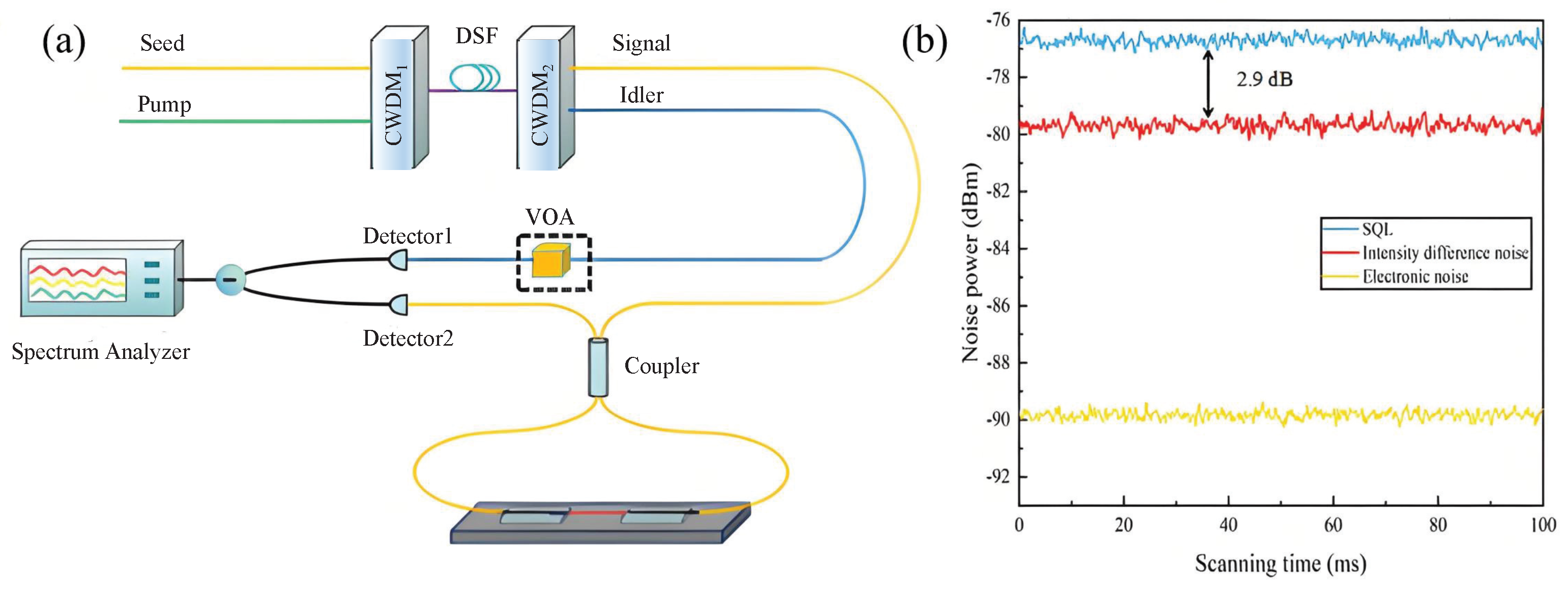
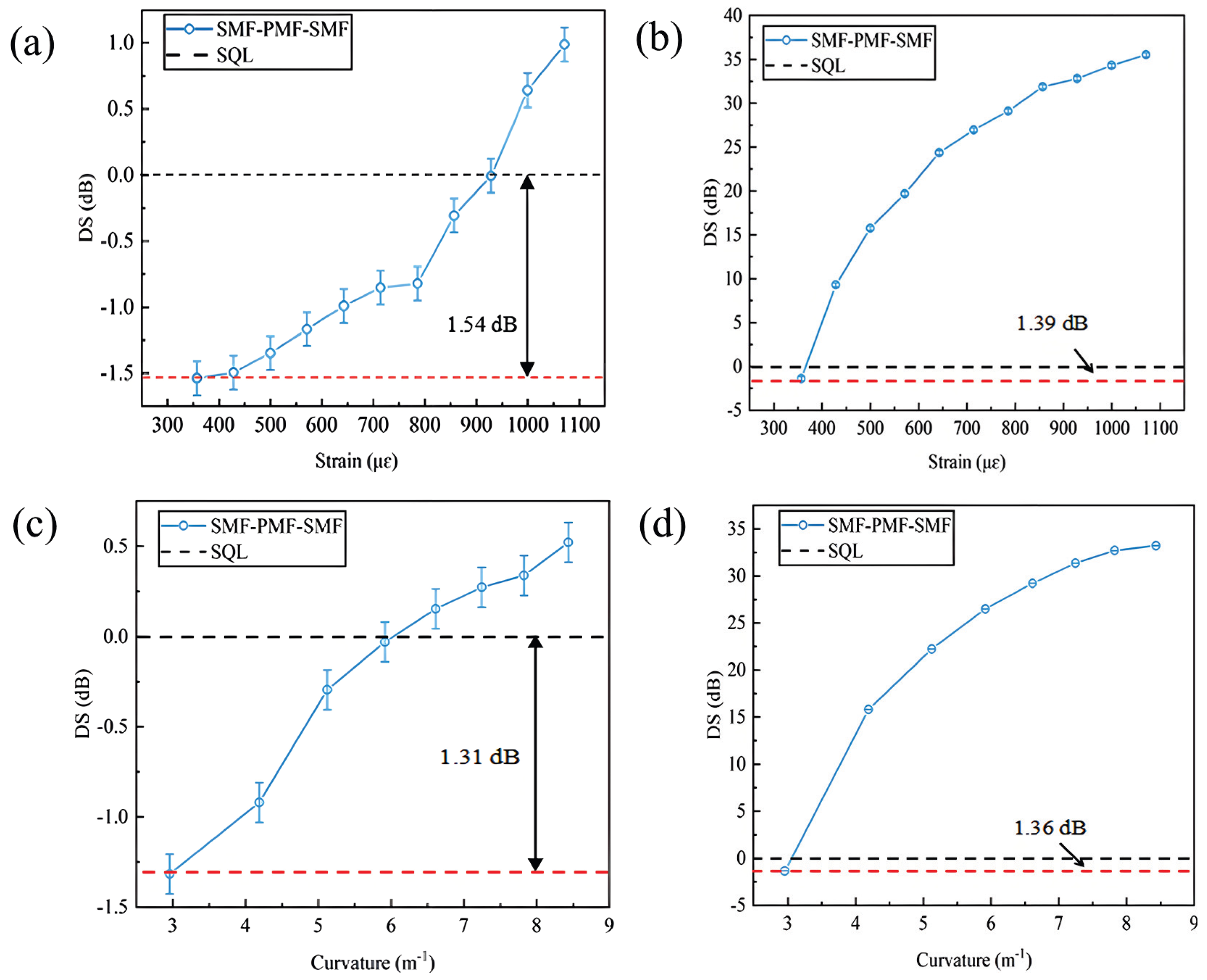
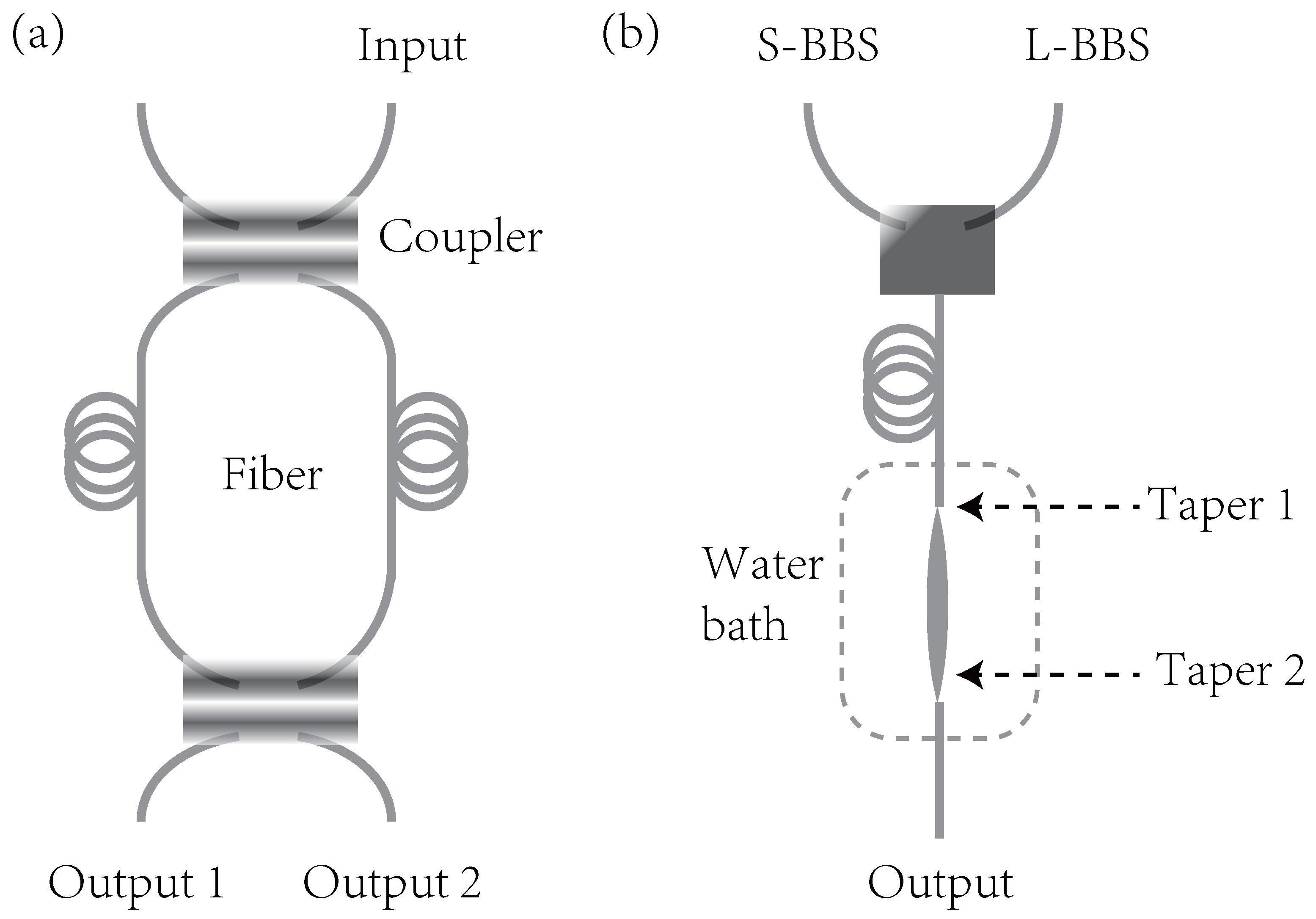
| Years | Quantum Devices | Quantum States | The Measured Physical Quantity | The Improvement of SNR (SNRI) Compared to SNL |
|---|---|---|---|---|
| 2010 [62] | OPO | the polarized squeezed state dB | optical magnetometer | dB |
| 2014 [67] | FWM in atomic ensemble | entanglement state | phase | dB |
| 2015 [18] | FWM in atomic ensemble | entanglement state | micro-electro-mechanical-systems cantilever displacement | 4 dB |
| 2019 [20] | DOPO | squeezed state dB | gravitational waves (LIGO) | 3 dB |
| 2020 [22] | FWM in atomic ensemble | entanglement state | atomic force microscope | 3 dB |
| 2020 [19] | DOPA | squeezed state dB | phase | dB |
| 2025 [68] | PA | dual pairs of entangled twin beams | distributed phase sensing | 3 dB/advances the record of SNR so far achieved in photon-correlated interferometers by three orders of magnitude |
| Years | Quantum Devices | Quantum States | Measurement Methods | The Measured Physical Quantity | The Improvement of SNR (SNRI) Compared to SNL |
|---|---|---|---|---|---|
| 2012 [57] | FOPA | the intensity difference squeezed state dB | differential detector | amplitude | |
| 2016 [81] | FOPA | quadrature amplitude entanglement 1 dB/ dB | homodyne detection | noise variances of the difference/sum of the quadrature amplitudes | |
| 2018 [82] | FOPA | the intensity difference squeezed state dB | homodyne detection | amplitude | |
| 2020 [84] | FOPA | the intensity difference squeezed state dB | PSA-assisted homodyne detection | amplitude | |
| 2023 [83] | FOPA | the intensity difference squeezed state dB | differential detector | amplitude | |
| 2023 [88] | FOPA | the intensity-difference squeezed state dB | temperature/ curvature | dB/ dB | |
| 2010 [124] | optical Sagnac interferometer | squeezed state injected dB | phase | dB | |
| 2018 [108] | NLI based on FOPA | entanglement state | phase amplitude and quadrature components at any angle | 20% | |
| 2019 [107] | NLI based on FOPA | entanglement state | joint measurement | dual-arm sensing (phase) | dB |
| 2019 [126] | optical fiber Sagnac interferometer | N00N state injected | phase shift caused by rotational motion | approximately dB | |
| 2023 [137] | optical fiber MZI | squeezed state injected | phase | 3 dB | |
| 2025 [127] | optical fiber Sagnac interferometer | generated by FOPA dB | strain/curvature | dB/ dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, X.; Tang, Z.; Li, B.; Chen, X.; Sun, J. Quantum-Empowered Fiber Sensing Metrology. Photonics 2025, 12, 763. https://doi.org/10.3390/photonics12080763
Zuo X, Tang Z, Li B, Chen X, Sun J. Quantum-Empowered Fiber Sensing Metrology. Photonics. 2025; 12(8):763. https://doi.org/10.3390/photonics12080763
Chicago/Turabian StyleZuo, Xiaojie, Zhangguan Tang, Boyao Li, Xiaoyong Chen, and Jinghua Sun. 2025. "Quantum-Empowered Fiber Sensing Metrology" Photonics 12, no. 8: 763. https://doi.org/10.3390/photonics12080763
APA StyleZuo, X., Tang, Z., Li, B., Chen, X., & Sun, J. (2025). Quantum-Empowered Fiber Sensing Metrology. Photonics, 12(8), 763. https://doi.org/10.3390/photonics12080763






