Quantitative Evaluation of Optical Clearing Agent Performance Based on Multilayer Monte Carlo and Diffusion Modeling
Abstract
1. Introduction
2. Materials and Methods
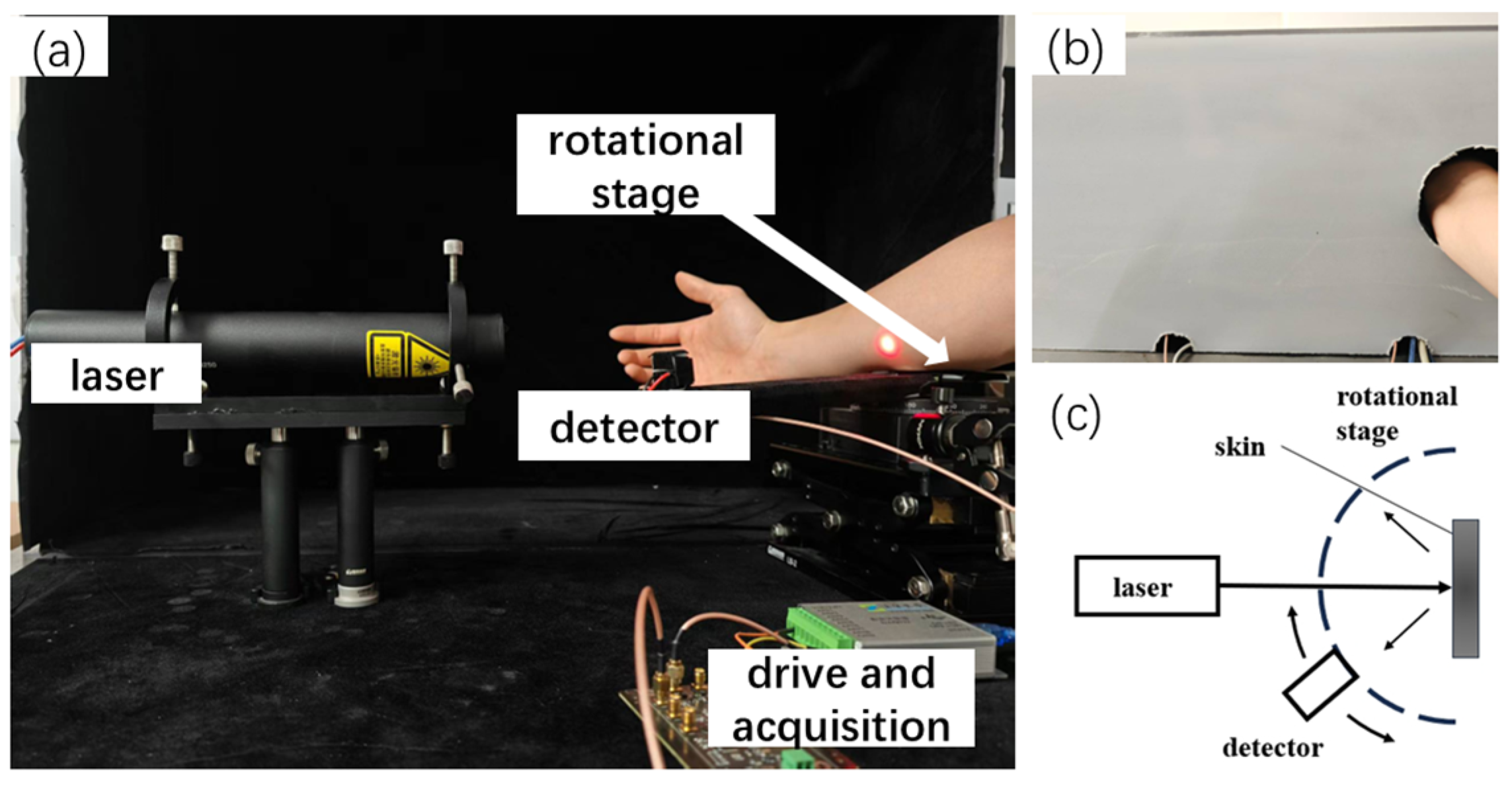
2.1. MC Simulation of Optical Ray Transmission Property in Skin Tissue
2.2. Effect of OCAs
2.2.1. Mie Scattering Theory for OCAs
2.2.2. Penetration of OCAs in Skin
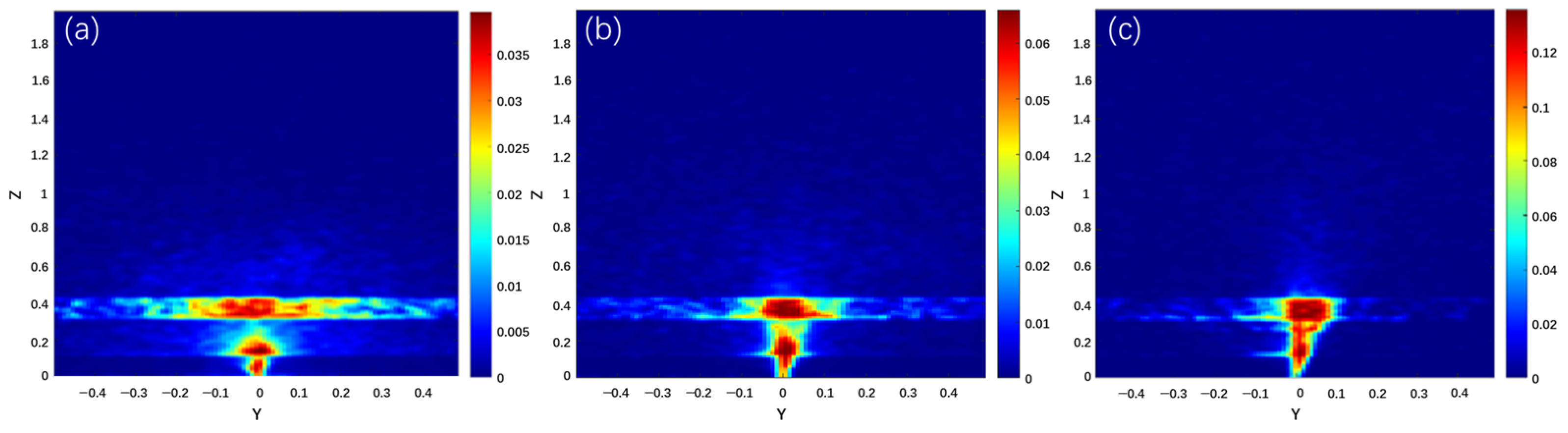
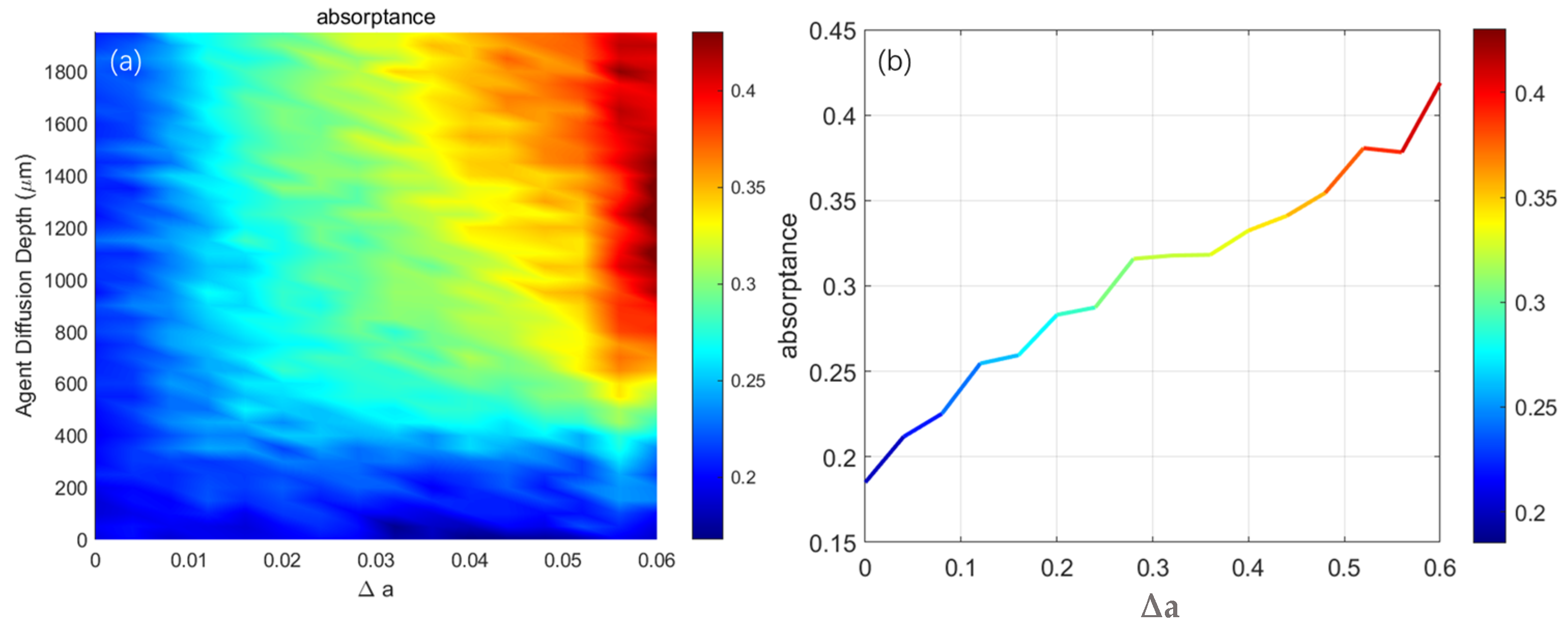
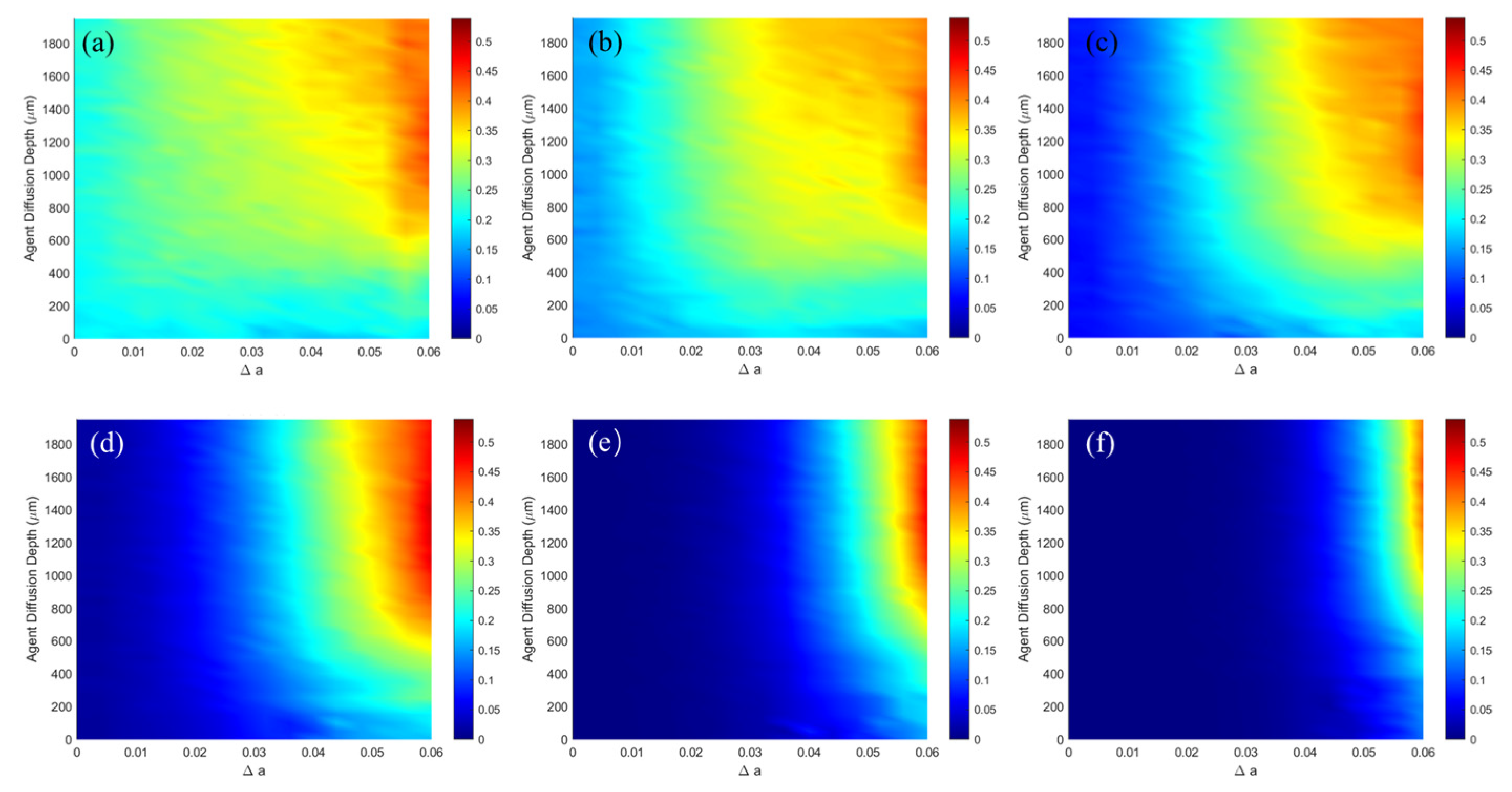
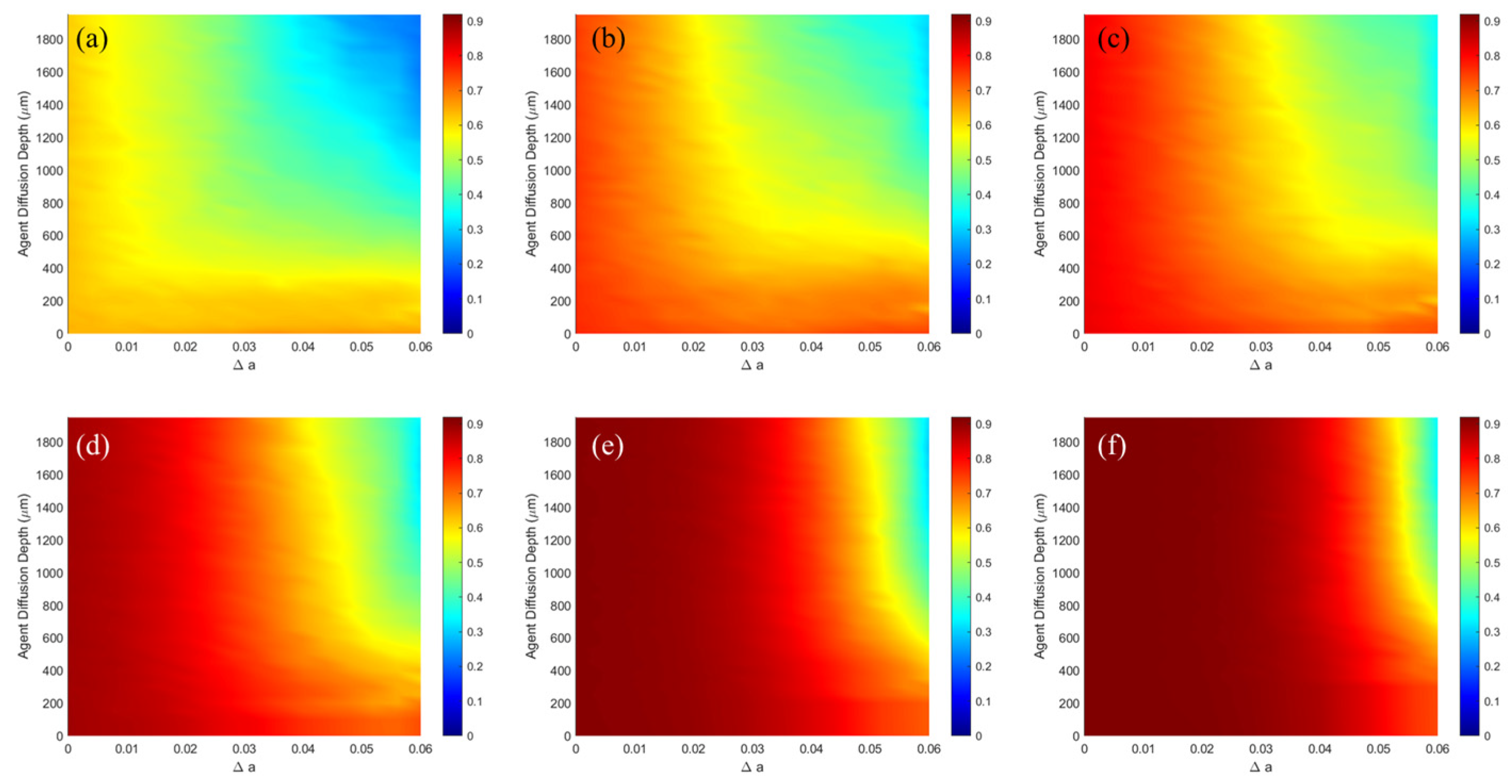
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saeedi, P.; Petersohn, I.; Salpea, P.; Salpea, P.; Malanda, B.; Karuranga, S.; Unwin, N.; Colagiuri, S.; Guariguata, L.; Motala, A.; et al. Global and regional diabetes prevalence estimates for 2019 and projections for 2030 and 2045: Results from the International Diabetes Federation Diabetes Atlas. Diabetes Res. Clin. Pract. 2019, 157, 107843. [Google Scholar] [CrossRef]
- Villena Gonzales, W.; Mobashsher, A.T.; Abbosh, A. The progress of glucose monitoring—A review of invasive to minimally and non-invasive techniques, devices and sensors. Sensors 2019, 19, 800. [Google Scholar] [CrossRef]
- Tomlins, P.H.; Wang, R.K. Theory, developments and applications of optical coherence tomography. J. Phys. D Appl. Phys. 2005, 38, 2519. [Google Scholar] [CrossRef]
- Althobaiti, M.; Al-Naib, I. Optimization of dual-channel near-infrared non-invasive glucose level measurement sensors based on Monte-Carlo simulations. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Joshi, A.M.; Jain, P.; Mohanty, S.P.; Agrawal, N. iGLU 2.0: A new wearable for accurate non-invasive continuous serum glucose measurement in IoMT framework. IEEE Trans. Consum. Electron. 2020, 66, 327–335. [Google Scholar] [CrossRef]
- Alsunaidi, B.; Althobaiti, M.; Tamal, M.; Albaker, W.; Al-Naib, I. A review of non-invasive optical systems for continuous blood glucose monitoring. Sensors 2021, 21, 6820. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Kim, M.; Jang, M.; Choi, Y.; Choi, W.; Kang, S.; Choi, W. Deep optical imaging within complex scattering media. Nat. Rev. Phys. 2020, 2, 141–158. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; An, J.; Ma, X.; Yang, J.; Luo, l.; Deng, Y.; Kim, J.S.; Sun, Y. Construction of a 980 nm laser-activated Pt (II) metallacycle nanosystem for efficient and safe photo-induced bacteria sterilization. Sci. China Chem. 2023, 66, 155–163. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Lu, S.; Wang, Z.; Liu, S.; Yu, X.; Li, X.; Sun, Y. Construction of emissive ruthenium (II) metallacycle over 1000 nm wavelength for in vivo biomedical applications. Nat. Commun. 2022, 13, 2009. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Ma, X.; Tuo, W.; Tu, L.; Li, X.; Sun, Y.; Stang, P.J.; Sun, Y. Long wavelength–emissive Ru (II) metallacycle–based photosensitizer assisting in vivo bacterial diagnosis and antibacterial treatment. Proc. Natl. Acad. Sci. USA 2022, 119, e2209904119. [Google Scholar] [CrossRef]
- Tuchin, V.V. Controlling of tissue optical properties. In Tissue Optics; SPIE: Bellingham, WA, USA, 2015; p. 329. [Google Scholar]
- Costantini, I.; Cicchi, R.; Silvestri, L.; Vanzi, F.; Pavone, F.S. In-vivo and ex-vivo optical clearing methods for biological tissues. Biomed. Opt. Express 2019, 10, 5251–5267. [Google Scholar] [CrossRef]
- Matryba, P.; Kaczmarek, L.; Gołąb, J. Advances in ex situ tissue optical clearing. Laser Photonics Rev. 2019, 13, 1800292. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2002, 32, 2309–2311. [Google Scholar] [CrossRef]
- Delbeck, S.; Vahlsing, T.; Leonhardt, S.; Steiner, G.; Heise, H.M. Non-invasive monitoring of blood glucose using optical methods for skin spectroscopy—Opportunities and recent advances. Anal. Bioanal. Chem. 2019, 411, 63–77. [Google Scholar] [CrossRef]
- Kong, L.; Zhao, Y.; Dong, L.; Jian, Y.; Jin, X.; Li, B.; Feng, Y.; Liu, M.; Liu, X.; Wu, H. Non-contact detection of oxygen saturation based on visible light imaging device using ambient light. Opt. Express 2013, 21, 17464–17471. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Feng, J.C.; Jia, K.B. Diffusion correlation spectroscopy for tissue blood flow detection and its clinical application. Laser Optoelectron. Prog. 2022, 59, 0617006-14. (In Chinese) [Google Scholar]
- Meglinski, I.V.; Matcher, S.J. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions. Physiol. Meas. 2002, 23, 741. [Google Scholar] [CrossRef]
- Ren, N.; Liang, J.; Qu, X.; Li, J.; Lu, B.; Tian, J. GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues. Opt. Express 2010, 18, 6811–6823. [Google Scholar] [CrossRef] [PubMed]
- Maeda, T.; Arakawa, N.; Takahashi, M.; et Aizu, Y. Monte Carlo simulation of spectral reflectance using a multilayered skin tissue model. Opt. Rev. 2010, 17, 223–229. [Google Scholar] [CrossRef]
- Egawa, M.; Hirao, T.; Takahashi, M. In vivo estimation of stratum corneum thickness from water concentration profiles obtained with Raman spectroscopy. Acta Derm.-Venereol. 2007, 87, 4–8. [Google Scholar] [CrossRef]
- Sheet, A.H.; Hamdy, O.; Abdel-Salam, Z.; Abdel-Harith, M. Combining laser-irradiation and glycerol immersion of skeletal muscles to improve their optical transparency. Opt. Laser Technol. 2022, 148, 107760. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, J.; Wan, J.; Huang, W.; Zhao, Y.; Yang, X. A versatile strategy for improving phototherapeutic efficacy on deep-sited tumor by tissue optical clearing technique. Nano Today 2021, 36, 101058. [Google Scholar] [CrossRef]
- Tuchina, D.K.; Genin, V.D.; Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical clearing of skin tissue ex vivo with polyethylene glycol. Opt. Spectrosc. 2016, 120, 28–37. [Google Scholar] [CrossRef]
- Jaafar, A.; Mahmood, M.H.; Holomb, R.; Himics, L.; Váczi, T.; Sdobnov, A.Y.; Tuchin, V.V.; Veres, M. Ex-vivo confocal Raman microspectroscopy of porcine skin with 633/785-NM laser excitation and optical clearing with glycerol/water/DMSO solution. J. Innov. Opt. Health Sci. 2021, 14, 2142003. [Google Scholar] [CrossRef]
- Genina, E.A.; Bashkatov, A.N.; Kozintseva, M.D.; Tuchin, V.V. OCT study of optical clearing of muscle tissue in vitro with 40% glucose solution. Opt. Spectrosc. 2016, 120, 20–27. [Google Scholar] [CrossRef]
- Liopo, A.; Su, R.; Tsyboulski, D.A.; Oraevsky, A.A. Optical clearing of skin enhanced with hyaluronic acid for increased contrast of optoacoustic imaging. J. Biomed. Opt. 2016, 21, 081208. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, B. In vivo experimental study on the enhancement of optical clearing effect by laser irradiation in conjunction with a chemical penetration enhancer. Appl. Sci. 2019, 9, 542. [Google Scholar] [CrossRef]
- Wen, X. Research on the Physical and Physiologyical Mechanisms of Skin Transparency; Huazhong University of Science and Technology: Wuhan, China, 2012. (In Chinese) [Google Scholar]
- Ueda, H.R.; Ertürk, A.; Chung, K.; Gradinaru, V.; Chédotal, A.; Tomancak, P.; Keller, P.J. Tissue clearing and its applications in neuroscience. Nat. Rev. Neurosci. 2020, 21, 61–79. [Google Scholar] [CrossRef]
- Mourant, J.R.; Freyer, J.P.; Hielscher, A.H.; Eick, A.A.; Shen, D.; Johnson, T.M. Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics. Appl. Opt. 1998, 37, 3586–3593. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, A.; Hamre, B.; Frette, Ø.; Stamnes, K.; Stamnes, J.J. Modeling optical properties of human skin using Mie theory for particles with different size distributions and refractive indices. Opt. Express 2011, 19, 14549–14567. [Google Scholar] [CrossRef]
- Tuchin, V.V. Tissue and blood optical immersion by exogenous chemical agents. Opt. Clear. Tissues Blood 2006, 2, 1–19. [Google Scholar]
- Sokolov, K.; Drezek, R.; Gossage, K.; Richards-Kortum, R. Reflectance spectroscopy with polarized light: Is it sensitive to cellular and nuclear morphology. Opt. Express 1999, 5, 302–317. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, V.V.; Maksimova, I.L.; Zimnyakov, D.A.; Kon, I.L.; Mavlutov, A.H.; Mishin, A.A. Light propagation in tissues with controlled optical properties. J. Biomed. Opt. 1997, 2, 401–417. [Google Scholar] [CrossRef]
- Graaff, R.; Aarnoudse, J.G.; Zijp, J.R.; Sloot, P.M.A.; De Mul, F.F.M.; Greve, J.; Koelink, M.H. Reduced light-scattering properties for mixtures of spherical particles: A simple approximation derived from Mie calculations. Appl. Opt. 1992, 31, 1370–1376. [Google Scholar] [CrossRef]
- Flock, S.T.; Jacques, S.L.; Wilson, B.C.; Star, W.M.; van Gemert, M.J.C. Optical properties of Intralipid: A phantom medium for light propagation studies. Lasers Surg. Med. 1992, 12, 510–519. [Google Scholar] [CrossRef]
- Martelli, F.; Zaccanti, G. Calibration of scattering and absorption properties of a liquid diffusive medium at NIR wavelengths. CW method. Opt. Express 2007, 15, 486–500. [Google Scholar] [CrossRef]
- Jeon, K.J.; Hwang, I.D.; Hahn, S.; eYoon, G. Comparison between transmittance and reflectance measurements in glucose determination using near infrared spectroscopy. J. Biomed. Opt. 2006, 11, 014022-7. [Google Scholar] [CrossRef] [PubMed]
- Shariati BK, B.; Ansari, M.A.; Khatami, S.S.; Tuchin, V.V. Multimodal optical clearing to minimize light attenuation in biological tissues. Sci. Rep. 2023, 13, 21509. [Google Scholar] [CrossRef] [PubMed]
- Gavrilova, A.A.; Pravdin, A.B.; Tuchin, V.V.; Altshuler, G.B.; Yaroslavsky, I.V. Assessment of diffusion coefficient of glycerol into the skin ex vivo. In Proceedings of the Fifth International Conference on Photonics and Imaging in Biology and Medicine, Wuhan, China, 1–3 September 2006; SPIE: Bellingham, WA, USA, 2007; Volume 6534, pp. 918–926. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, W.; Zhang, K.; Men, Z. DMSO synergized with sugars: Optical clearing agent modulation of optical coherence tomography of skin tissues. Appl. Opt. 2024, 63, 2279–2285. [Google Scholar] [CrossRef]
- Sandby-Møller, J.; Poulsen, T.; Wulf, H.C. Epidermal thickness at different body sites: Relationship to age, gender, pigmentation, blood content, skin type and smoking habits. Acta Derm.-Venereol. 2003, 83, 410–413. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, J.; Cui, H.; Mao, Z.; Li, P.; Luo, Q. Short-term and long-term effects of optical clearing agents on blood vessels in chick chorioallantoic membrane. J. Biomed. Opt. 2008, 13, 021106-8. [Google Scholar] [CrossRef] [PubMed]
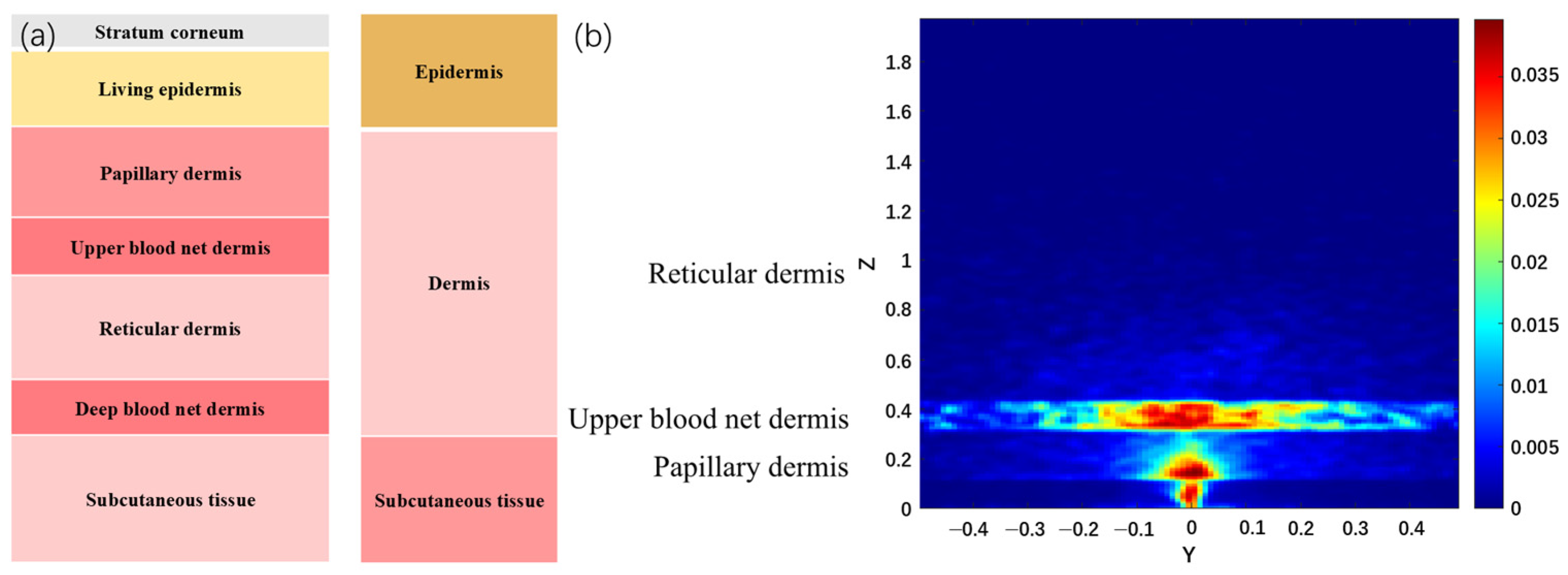




| NO. | Layer | Blood Content | μa (mm−1) | μs (mm−1) | g | n | t (mm) |
|---|---|---|---|---|---|---|---|
| 1 | Stratum corneum | 0 | 0.00586 | 100 | 0.86 | 1.5 | 0.02 |
| 2 | Living epidermis | 0 | 0.00482 | 45 | 0.80 | 1.34 | 0.08–0.1 |
| 3 | Papillary dermis | 0.04 | 0.03341 | 30 | 0.90 | 1.40 | 0.15–0.2 |
| 4 | Upper blood net dermis | 0.3 | 0.24130 | 35 | 0.95 | 1.39 | 0.08–0.1 |
| 5 | Reticular dermis | 0.04 | 0.03341 | 25 | 0.80 | 1.40 | 1.4–1.6 |
| 6 | Deep blood net dermis | 0.1 | 0.08078 | 30 | 0.95 | 1.38 | 0.08–0.12 |
| 7 | Subcutaneous tissue | 0.05 | 0.04127 | 5 | 0.75 | 1.44 | 6.0–6.5 |
| Skin | Diffuse | Stratum Corneum | Living Epidermis | Papillary Dermis | Upper Blood Net Dermis | Reticular Dermis | Deep Blood Net Dermis | Subcutaneous Tissue |
|---|---|---|---|---|---|---|---|---|
| Forearm | 62.31% | 0.32% | 0.90% | 6.87% | 16.96% | 8.34% | 0.03% | 0.34% |
| Palm | 87.55% | 2.19% | 0.01% | 1.11% | 3.58% | 1.51% | 0.01% | 0.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Hou, C.; Zhang, D.; Shi, Z.; Zhao, J.; Cui, G. Quantitative Evaluation of Optical Clearing Agent Performance Based on Multilayer Monte Carlo and Diffusion Modeling. Photonics 2025, 12, 751. https://doi.org/10.3390/photonics12080751
Fu L, Hou C, Zhang D, Shi Z, Zhao J, Cui G. Quantitative Evaluation of Optical Clearing Agent Performance Based on Multilayer Monte Carlo and Diffusion Modeling. Photonics. 2025; 12(8):751. https://doi.org/10.3390/photonics12080751
Chicago/Turabian StyleFu, Lu, Changlun Hou, Dongbiao Zhang, Zhen Shi, Jufeng Zhao, and Guangmang Cui. 2025. "Quantitative Evaluation of Optical Clearing Agent Performance Based on Multilayer Monte Carlo and Diffusion Modeling" Photonics 12, no. 8: 751. https://doi.org/10.3390/photonics12080751
APA StyleFu, L., Hou, C., Zhang, D., Shi, Z., Zhao, J., & Cui, G. (2025). Quantitative Evaluation of Optical Clearing Agent Performance Based on Multilayer Monte Carlo and Diffusion Modeling. Photonics, 12(8), 751. https://doi.org/10.3390/photonics12080751





