On-Chip Mid-Infrared Dual-Band Wavelength Splitting with Integrated Metalens and Enhanced Bandwidth
Abstract
1. Introduction
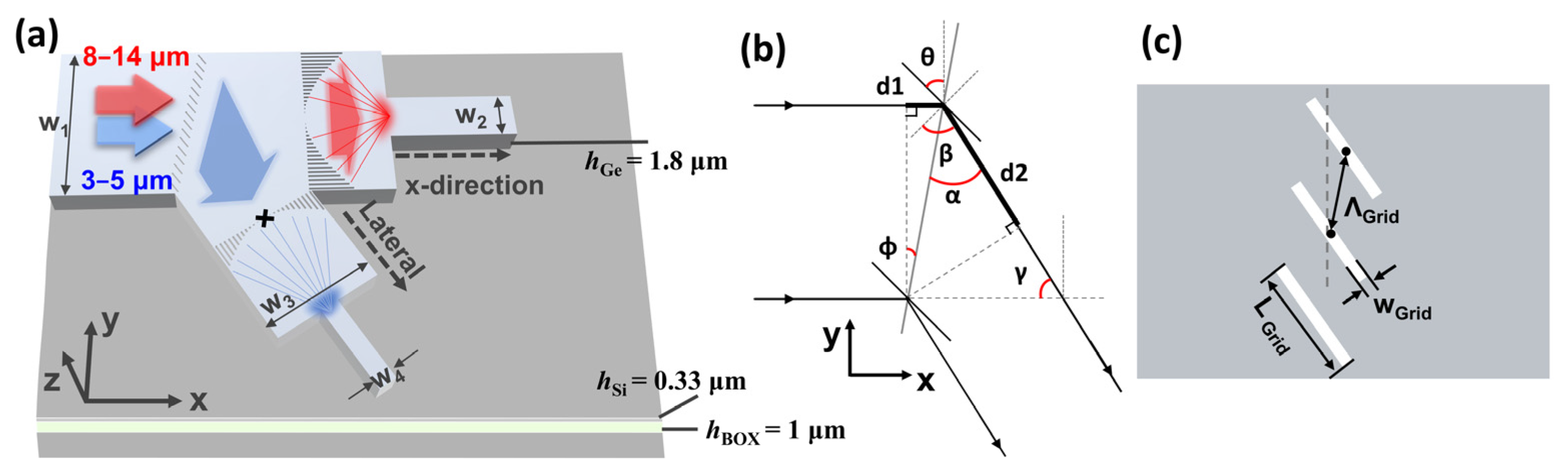
2. Design and Simulation of the Mid-IR Dual-Band Wavelength Splitting Device
3. Results and Discussion
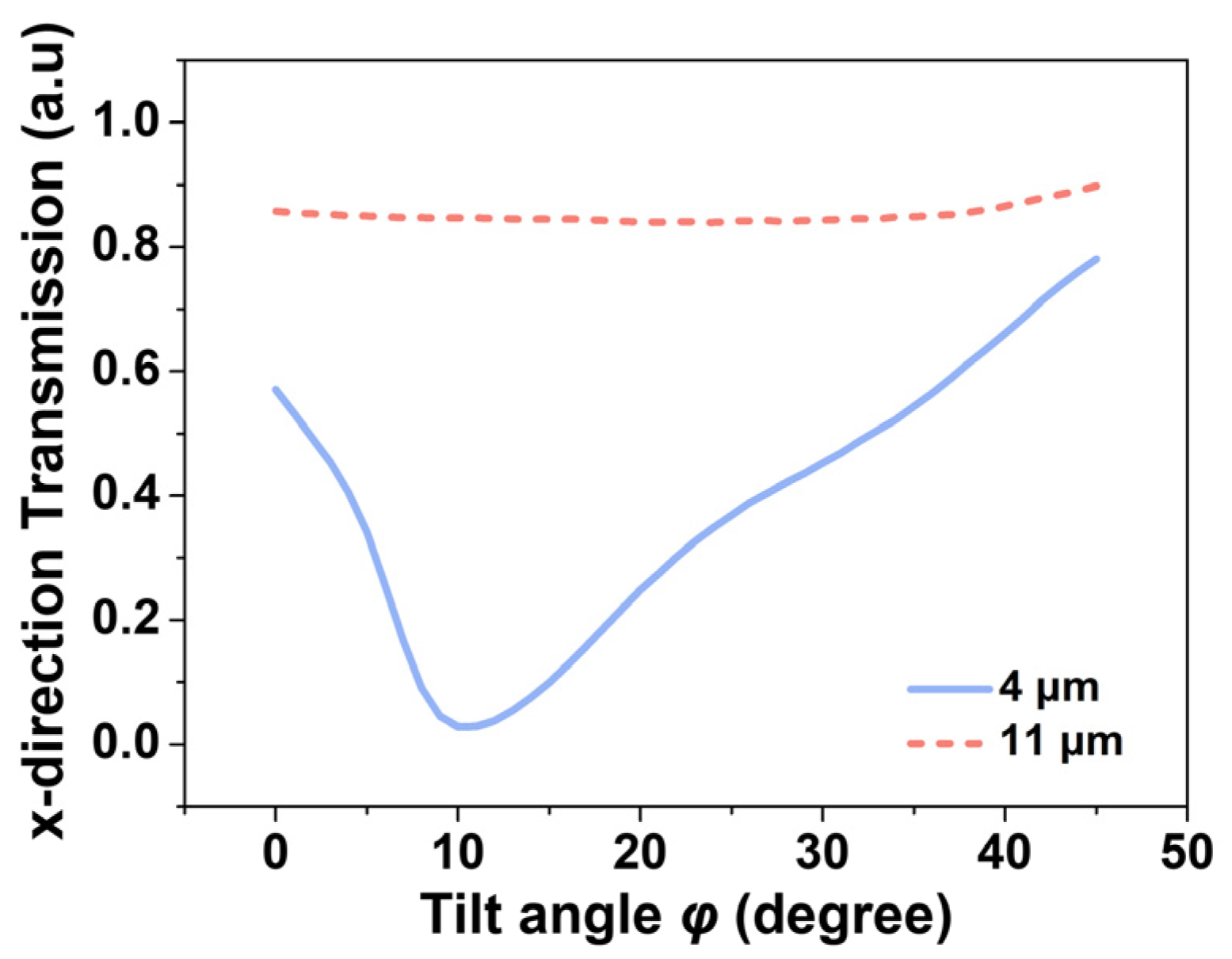
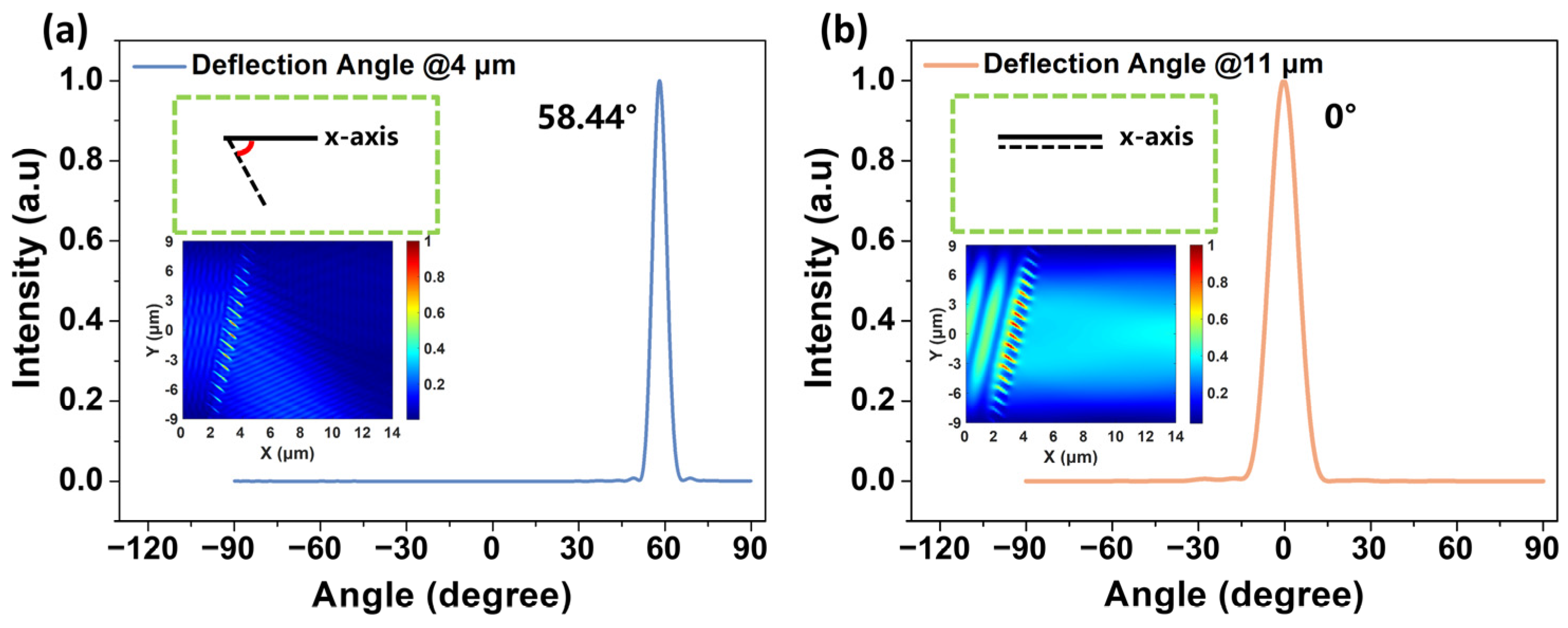
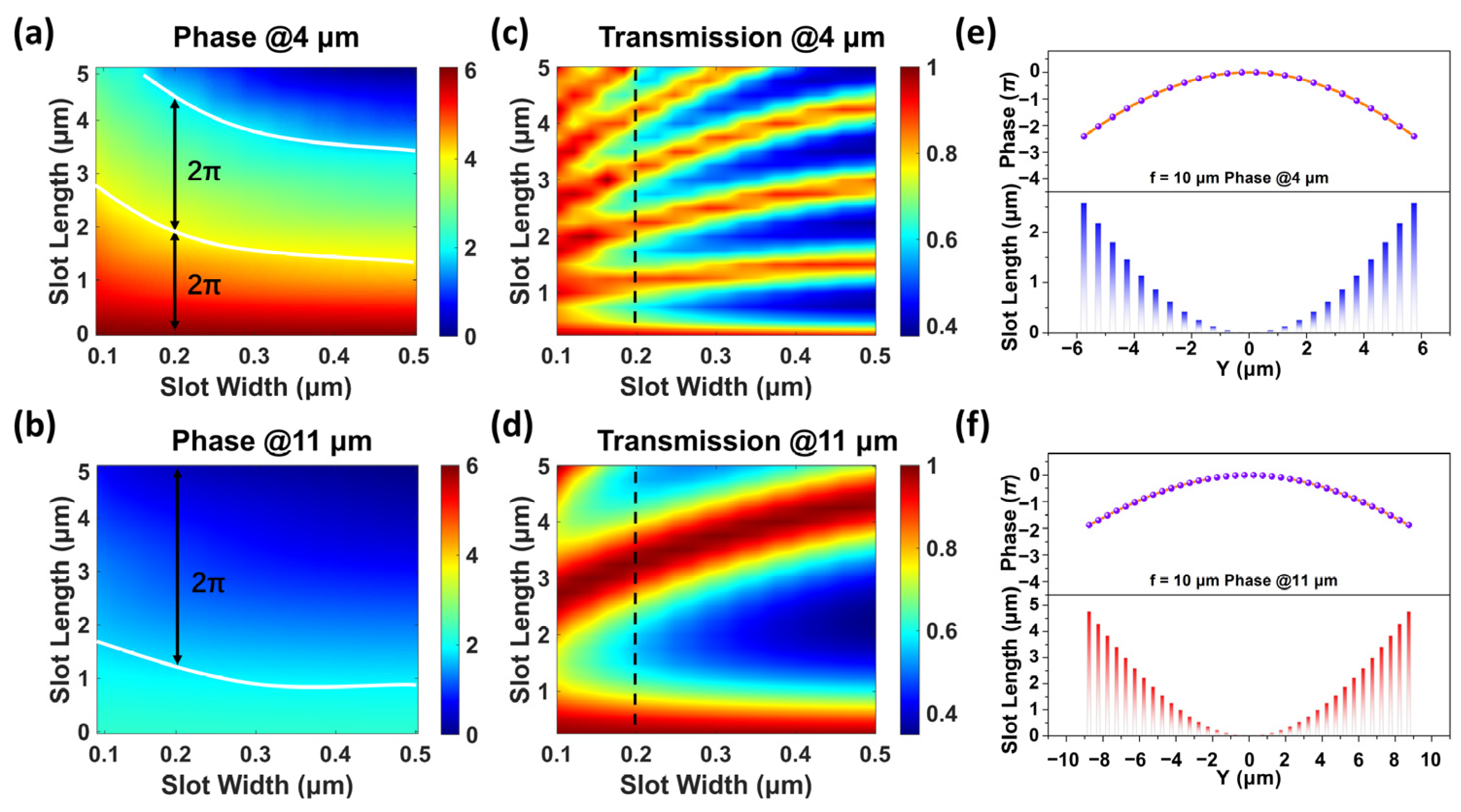
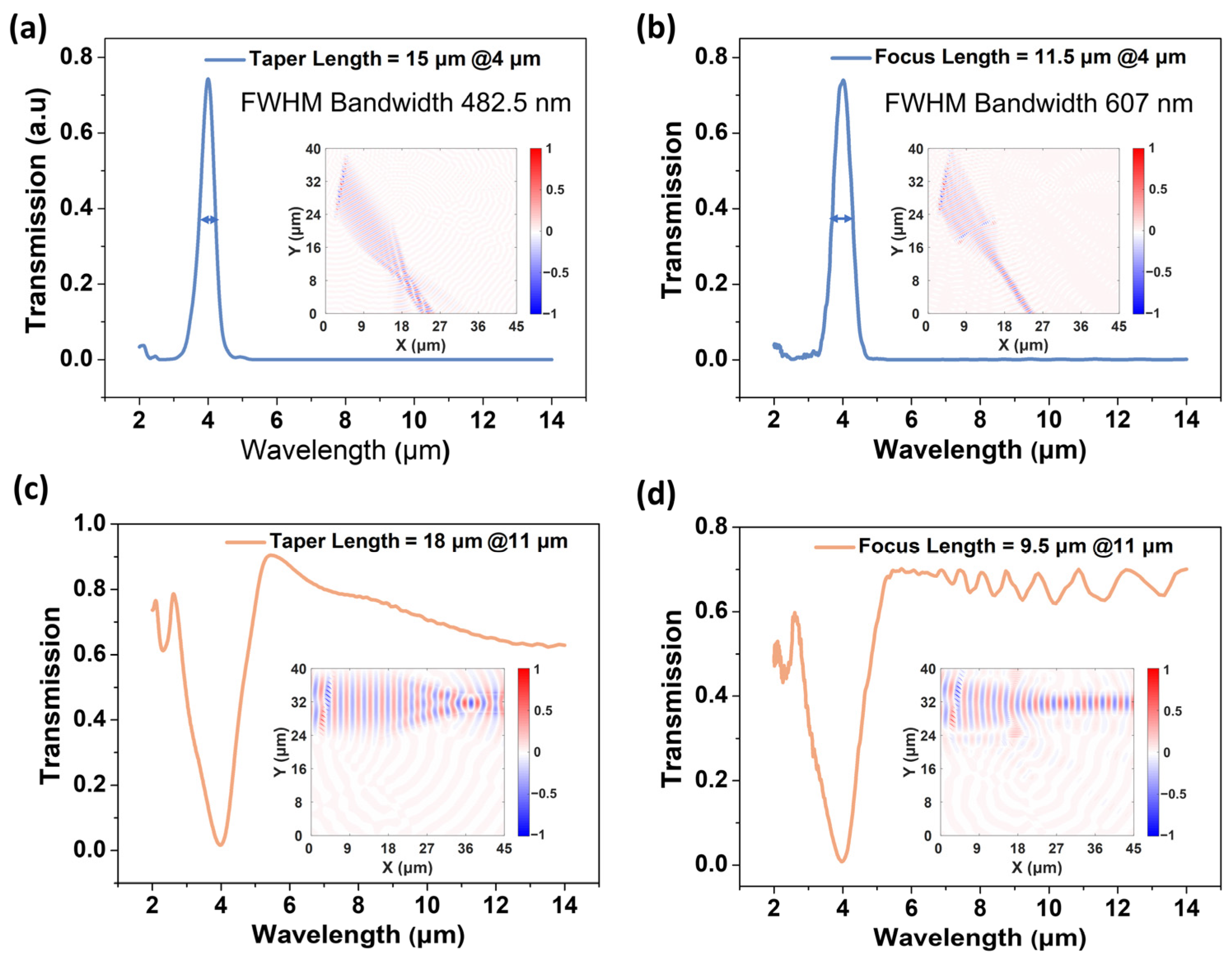
3.1. Tilt Grating for Mid-IR Dual-Band Splitting
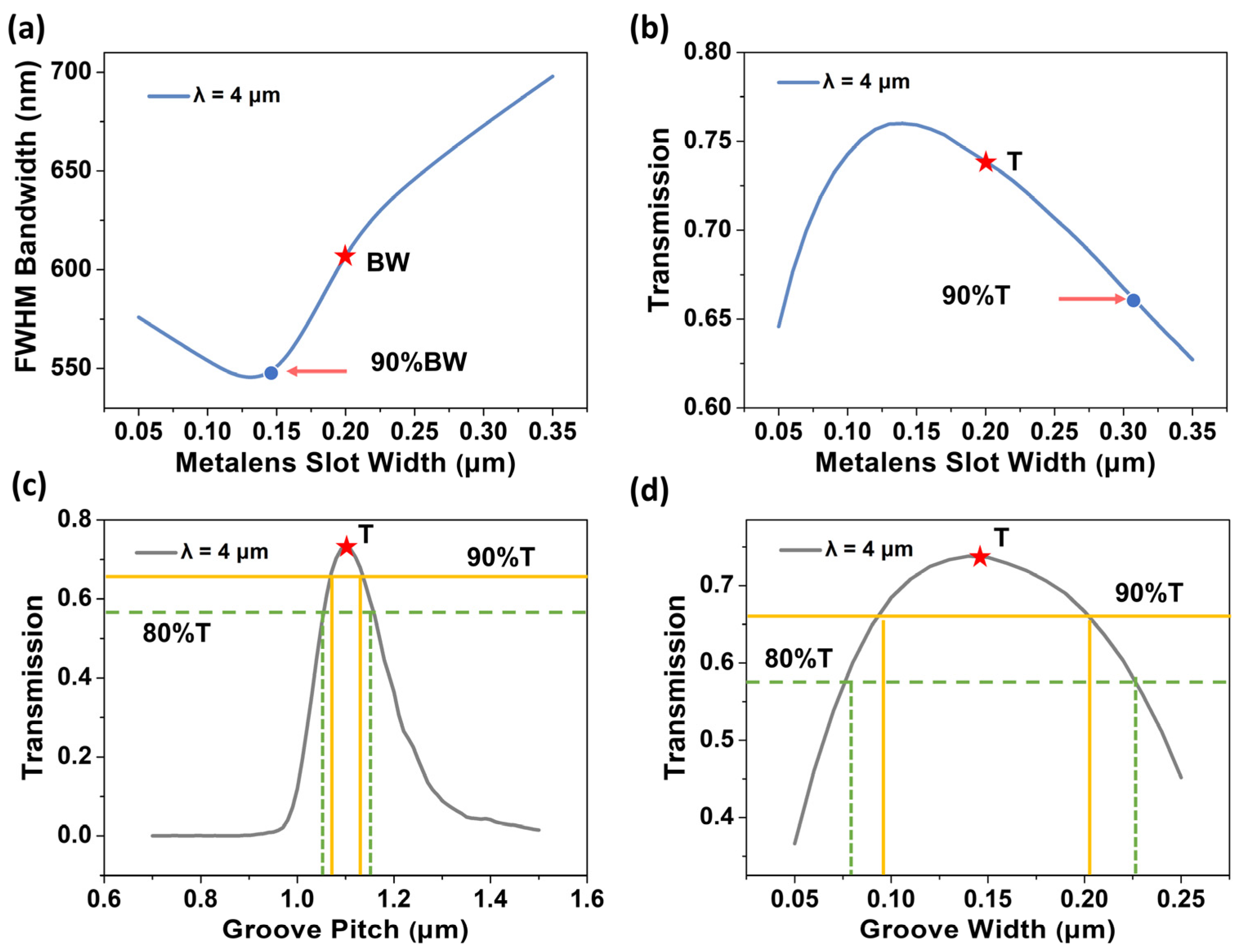
3.2. Light Coupling to Single-Mode Waveguide by Metalens
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petersen, C.R.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830–834. [Google Scholar] [CrossRef]
- Wang, L.; Mizaikoff, B. Application of multivariate data-analysis techniques to biomedical diagnostics based on mid-infrared spectroscopy. Anal. Bioanal. Chem. 2008, 391, 1641–1654. [Google Scholar] [CrossRef] [PubMed]
- Nikodem, M.; Krzempek, K.; Dudzik, G.; Abramski, K. Hollow core fiber-assisted absorption spectroscopy of methane at 3.4 µm. Opt. Express 2018, 26, 21843–21848. [Google Scholar] [CrossRef] [PubMed]
- Hinkov, B.; Pilat, F.; Lux, L.; Souza, P.L.; David, M.; Schwaighofer, A.; Ristanić, D.; Schwarz, B.; Detz, H.; Andrews, A.M. A mid-infrared lab-on-a-chip for dynamic reaction monitoring. Nat. Commun. 2022, 13, 4753. [Google Scholar] [CrossRef] [PubMed]
- Henderson, B.; Khodabakhsh, A.; Metsälä, M.; Ventrillard, I.; Schmidt, F.M.; Romanini, D.; Ritchie, G.A.; te Lintel Hekkert, S.; Briot, R.; Risby, T. Laser spectroscopy for breath analysis: Towards clinical implementation. Appl. Phys. B 2018, 124, 161. [Google Scholar] [CrossRef] [PubMed]
- Vlk, M.; Datta, A.; Alberti, S.; Yallew, H.D.; Mittal, V.; Murugan, G.S.; Jágerská, J. Extraordinary evanescent field confinement waveguide sensor for mid-infrared trace gas spectroscopy. Light Sci. Appl. 2021, 10, 26. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Ji, S.; Ren, Z.; Wu, W.; Zhang, Z.; Ni, Z.; Liu, L.; Zhang, Z.; Song, A.; Lee, C. Triboelectric-induced ion mobility for artificial intelligence-enhanced mid-infrared gas spectroscopy. Nat. Commun. 2023, 14, 2524. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Zhang, Z.; Wei, J.; Dong, B.; Lee, C. Wavelength-multiplexed hook nanoantennas for machine learning enabled mid-infrared spectroscopy. Nat. Commun. 2022, 13, 3859. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Luo, Z.; Gu, T.; Kimerling, L.C.; Wada, K.; Agarwal, A.; Hu, J. Mid-infrared integrated photonics on silicon: A perspective. Nanophotonics 2017, 7, 393–420. [Google Scholar] [CrossRef]
- Hu, T.; Dong, B.; Luo, X.; Liow, T.-Y.; Song, J.; Lee, C.; Lo, G.-Q. Silicon photonic platforms for mid-infrared applications. Photonics Res. 2017, 5, 417–430. [Google Scholar] [CrossRef]
- Alonso-Ramos, C.; Nedeljkovic, M.; Benedikovic, D.; Penadés, J.S.; Littlejohns, C.G.; Khokhar, A.Z.; Pérez-Galacho, D.; Vivien, L.; Cheben, P.; Mashanovich, G.Z. Germanium-on-silicon mid-infrared grating couplers with low-reflectivity inverse taper excitation. Opt. Lett. 2016, 41, 4324–4327. [Google Scholar] [CrossRef] [PubMed]
- Radosavljevic, S.; Kuyken, B.; Roelkens, G. Efficient 5.2 µm wavelength fiber-to-chip grating couplers for the Ge-on-Si and Ge-on-SOI mid-infrared waveguide platform. Opt. Express 2017, 25, 19034–19042. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Spring, A.M.; Qiu, F.; Yokoyama, S. A high efficiency silicon nitride waveguide grating coupler with a multilayer bottom reflector. Sci. Rep. 2019, 9, 12988. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Zhang, Y.; Zhao, Y.-Y.; Duan, X.-M. Efficient 4.95 µm–8.5 µm dual-band grating coupler with crosstalk suppression capability. Opt. Express 2022, 30, 2131–2142. [Google Scholar] [CrossRef] [PubMed]
- Smit, M.K. New focusing and dispersive planar component based on an optical phased array. Electron. Lett. 1988, 24, 385–386. [Google Scholar] [CrossRef]
- Karnik, T.S.; Diehl, L.; Dao, K.P.; Du, Q.; Pflügl, C.; Vakhshoori, D.; Hu, J. Monolithic beam combined quantum cascade laser arrays with integrated arrayed waveguide gratings. Opt. Express 2024, 32, 11681–11692. [Google Scholar] [CrossRef] [PubMed]
- Stanton, E.; Spott, A.; Davenport, M.; Volet, N.; Bowers, J. Low-loss arrayed waveguide grating at 760 nm. Opt. Lett. 2016, 41, 1785–1788. [Google Scholar] [CrossRef] [PubMed]
- Fotiadis, K.; Pitris, S.; Moralis-Pegios, M.; Mitsolidou, C.; De Heyn, P.; Van Campenhout, J.; Broeke, R.; Alexoudi, T.; Pleros, N. Silicon photonic 16× 16 Cyclic AWGR for DWDM O-band interconnects. IEEE Photonics Technol. Lett. 2020, 32, 1233–1236. [Google Scholar] [CrossRef]
- Gatkine, P.; Veilleux, S.; Hu, Y.; Bland-Hawthorn, J.; Dagenais, M. Arrayed waveguide grating spectrometers for astronomical applications: New results. Opt. Express 2017, 25, 17918–17935. [Google Scholar] [CrossRef] [PubMed]
- van Wijk, A.; Doerr, C.R.; Ali, Z.; Karabiyik, M.; Akca, B.I. Compact ultrabroad-bandwidth cascaded arrayed waveguide gratings. Opt. Express 2020, 28, 14618–14626. [Google Scholar] [CrossRef] [PubMed]
- Karnik, T.S.; Dao, K.P.; Du, Q.; Diehl, L.; Pflügl, C.; Vakhshoori, D.; Hu, J. High-efficiency mid-infrared InGaAs/InP arrayed waveguide gratings. Opt. Express 2023, 31, 5056–5068. [Google Scholar] [CrossRef] [PubMed]
- Brouckaert, J.; Bogaerts, W.; Dumon, P.; Van Thourhout, D.; Baets, R. Planar concave grating demultiplexer fabricated on a nanophotonic silicon-on-insulator platform. J. Light. Technol. 2007, 25, 1269–1275. [Google Scholar] [CrossRef]
- Malik, A.; Muneeb, M.; Shimura, Y.; Van Campenhout, J.; Loo, R.; Roelkens, G. Germanium-on-silicon planar concave grating wavelength (de) multiplexers in the mid-infrared. Appl. Phys. Lett. 2013, 103, 161119. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Nijem, J.; Naiman, A.; Zektzer, R.; Frydendahl, C.; Mazurski, N.; Levy, U. High-Q and high finesse silicon microring resonator. Opt. Express 2024, 32, 7896–7906. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Lipson, M. All-optical logic based on silicon micro-ring resonators. Opt. Express 2007, 15, 924–929. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, D.; Huang, K.; Zhou, Z.-Y.; Shi, B.-S. Characterizing mid-infrared micro-ring resonator with frequency conversion. Opt. Express 2024, 32, 21795–21805. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhang, C.; Liang, D.; Dai, D. Submicron-resonator-based add-drop optical filter with an ultra-large free spectral range. Opt. Express 2019, 27, 416–422. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Husseini, D.A.; Li, J.; Lin, Z.; Sukhishvili, S.; Coté, G.L.; Gutierrez-Osuna, R.; Lin, P.T. Mid-infrared serial microring resonator array for real-time detection of vapor-phase volatile organic compounds. Anal. Chem. 2022, 94, 11008–11015. [Google Scholar] [CrossRef] [PubMed]
- Ha, Y.; Wang, L.; Guo, Y.; Pu, M.; Zou, F.; Li, X.; Fan, Y.; Ma, X.; Luo, X. High-fidelity mode scaling via topological-optimized on-chip metalens for compact photonic interconnection. Light Adv. Manuf. 2023, 4, 222–232. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Cheng, H.; Zhang, Z.; Yang, G.; Zhang, K.; Wang, C. Compact and efficient grating coupler design combining a metalens and a topology-optimized mode converter. Opt. Lett. 2025, 50, 1077–1080. [Google Scholar] [CrossRef] [PubMed]
- Barulin, A.; Kim, Y.; Oh, D.K.; Jang, J.; Park, H.; Rho, J.; Kim, I. Dual-wavelength metalens enables Epi-fluorescence detection from single molecules. Nat. Commun. 2024, 15, 26. [Google Scholar] [CrossRef] [PubMed]
- Badloe, T.; Kim, Y.; Kim, J.; Park, H.; Barulin, A.; Diep, Y.N.; Cho, H.; Kim, W.-S.; Kim, Y.-K.; Kim, I. Bright-field and edge-enhanced imaging using an electrically tunable dual-mode metalens. ACS Nano 2023, 17, 14678–14685. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.; Zhu, J.; Ji, P.; Luo, X.; Dong, S.; Dun, X.; Wei, Z.; Wang, Z.; Cheng, X. Ultra-compact on-chip snapshot chiral spectral imaging with dispersion-engineered chiral metalens. npj Nanophotonics 2025, 2, 23. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.-T.; Wang, J.-H. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, T.; Soman, A.; Mao, D.; Kananen, T.; Gu, T. On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 2019, 10, 3547. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Shi, Y.; Dai, C.; Wan, C.; Wan, S.; Li, Z. On-chip metalenses based on one-dimensional gradient trench in the broadband visible. Opt. Lett. 2020, 45, 5640–5643. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Dong, B.; Qiao, Q.; Liu, X.; Liu, J.; Zhou, G.; Lee, C. Subwavelength on-chip light focusing with bigradient all-dielectric metamaterials for dense photonic integration. InfoMat 2022, 4, e12264. [Google Scholar] [CrossRef]
- Shanker, A.; Fröch, J.E.; Mukherjee, S.; Zhelyeznyakov, M.; Brunton, S.L.; Seibel, E.J.; Majumdar, A. Quantitative phase imaging endoscopy with a metalens. Light Sci. Appl. 2024, 13, 305. [Google Scholar] [CrossRef] [PubMed]
- LaFratta, C.N.; Baldacchini, T. Two-photon polymerization metrology: Characterization methods of mechanisms and microstructures. Micromachines 2017, 8, 101. [Google Scholar] [CrossRef]
- Singhal, A.; Dalmiya, A.; Lynch, P.T.; Paprotny, I. 2-photon polymerized IP-DIP 3D photonic crystals for Mid IR spectroscopic applications. IEEE Photonics Technol. Lett. 2023, 35, 410–413. [Google Scholar] [CrossRef]


| Type | Wavelength | Footprint | Bandwidth | Reference |
|---|---|---|---|---|
| AWG | 5.25 μm | 1.87 mm2 | 190 nm | [21] |
| EDG | 5.2 μm | 1.5 × 1.2 mm2 | 150 nm | [23] |
| MRRs | 3.42 μm | / | 100 nm | [29] |
| tilt grating—metalenses | 4 μm | 616.89 μm2 | 607 nm | This work |
| Type | Wavelength | Length 1 | Bandwidth |
|---|---|---|---|
| Tapered structure | 4 μm | 15 μm | 482.5 nm |
| Metalens structure | 4 μm | 11.5 μm | 607 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, D.; Zhang, Q.; Ye, Z.; Duan, X.-M.; Zhang, Y. On-Chip Mid-Infrared Dual-Band Wavelength Splitting with Integrated Metalens and Enhanced Bandwidth. Photonics 2025, 12, 736. https://doi.org/10.3390/photonics12070736
Hu D, Zhang Q, Ye Z, Duan X-M, Zhang Y. On-Chip Mid-Infrared Dual-Band Wavelength Splitting with Integrated Metalens and Enhanced Bandwidth. Photonics. 2025; 12(7):736. https://doi.org/10.3390/photonics12070736
Chicago/Turabian StyleHu, Deming, Qi Zhang, Zhibin Ye, Xuan-Ming Duan, and Yang Zhang. 2025. "On-Chip Mid-Infrared Dual-Band Wavelength Splitting with Integrated Metalens and Enhanced Bandwidth" Photonics 12, no. 7: 736. https://doi.org/10.3390/photonics12070736
APA StyleHu, D., Zhang, Q., Ye, Z., Duan, X.-M., & Zhang, Y. (2025). On-Chip Mid-Infrared Dual-Band Wavelength Splitting with Integrated Metalens and Enhanced Bandwidth. Photonics, 12(7), 736. https://doi.org/10.3390/photonics12070736





