Abstract
This paper studied the general mechanism of spatial-frequency-shift (SFS) super-resolution imaging based on multiplex illumination modulation. The theory of SFS joint intensity was first proposed. Experiments on parallel slots with discrete spatial frequency (SF) distribution and V-shape slots with continuous SF distribution were carried out, and their real-space images and k-space images were obtained. The influence of single illumination with different SFS and mixed illumination with various combinations on SFS super-resolution imaging was analyzed. The phenomena of sample SF coverage were discussed. The SFS super-resolution imaging characteristics based on low-coherence illumination and highly localized light fields were discovered. The phenomenon of image magnification during SFS super-resolution imaging process was discussed. The differences and connections between the SF spectrum of objects and the k-space images obtained in SFS super-resolution imaging process were explained. This provides certain support for optimization of high-throughput SFS super-resolution imaging.
1. Introduction
Due to the diffraction limit of optical microscopy systems, the resolution of optical microscopes is generally around half of the wavelength [1]. For example, in the visible light spectrum, the resolution is restricted to approximately 200 nm. Thus, many researchers have begun to study super-resolution microscopies to break the diffraction limit, including laser scanning confocal microscopy (LSCM) [2,3], stimulated emission depletion microscopy (STED) [4,5], single-molecule localization microscopy (SMLM) [6,7] and so on. Regardless of the type of super-resolution microscopy, it is necessary to detect the high spatial frequency (SF) information of the sample beyond the diffraction limit using an optical system with a cut-off SF. A common method is to modulate the SF of the illumination field interacting with the sample, which shifts the high SF information of the sample into the cut-off SF range of the optical system. Hence, super-resolution imaging in far-field detection based on spatial-frequency-shift (SFS) effect was developed, such as structured illumination microscope (SIM) [8,9,10,11,12,13], Fourier ptychographic microscopy (FPM) [14,15,16,17,18,19,20] and on-chip SFS super-resolution imaging [21,22,23,24]. The resolution improvement of the SFS super-resolution imaging technology based on illumination modulation depends on the transverse wave vector (kx) of the complex illumination field. The SIM and FPM depend on the illumination modulation with kx provided by the free-space propagation wave, which is always smaller than the free-space wave vector k0. To achieve a higher resolution, it is necessary to modulate and generate an illumination mode with a higher kx. Therefore, on-chip SFS super-resolution imaging technologies were proposed, which used illumination modulation with a higher transverse wave vector kx provided by the evanescent wave. However, such an illumination field has extremely high localization and weaker photon intensity. These two characteristics will lead to weaker intensities in both the k-space and real space in far-field detection, which will have a certain impact on the image quality and resolution of SFS super-resolution microscopic imaging. Based on the general SFS illumination mechanism, this work proposed the theory of joint intensity of real-space intensity and k-space intensity for SFS super-resolution imaging technology based on multiplex illumination modulation. The influence of the multiplexing of different illumination modes on super-resolution imaging was analyzed, providing certain theoretical support for the development of more effective illumination modulation methods and weak-signal demodulation techniques in SFS super-resolution microscopy.
2. Discussion and Results
2.1. Experimental Setup
We built a dual-channel optical SFS super-resolution microscopic imaging system, as shown in Figure 1 and Figure S1. The objective lens is 0.4 NA/×20. The pixel size of the camera in the real space is 1.85 μm. A programable LED array with a center wavelength of 530 nm and a full width at half maximum of 30 nm is set as the low-coherence illumination light source, which can provide vertical illumination and oblique illumination, leading to wide-field far-field imaging and SFS super-resolution imaging. All the LEDs are encoded, which means they can be lit individually or simultaneously with different combinations to generate the various modulated illumination modes. The LEDs illuminate the object through the waveguide, which can support evanescent illumination mode with high k. Then, through a beam splitter (BS), one path of the scattering field forms an image of the object, which is the real-space image of the object; the other path forms an image of the back focal plane (BFP) of the objective lens. The BFP of the objective lens possesses unique Fourier transform characteristics in optical systems. According to Fraunhofer’s diffraction theory, when the light passes through an object, the diffracted rays at different angles (corresponding to different SF) are converged by the objective lens to distinct positions on the BFP. This one-to-one mapping relationship establishes the BFP as the Fourier transform plane of the incident light: the light intensity distribution at each point on the BFP directly reflects the intensity of the corresponding SF component of the object, thereby constituting the SF power spectrum of the object. Consequently, the BFP image essentially represents the k-space image of the object.
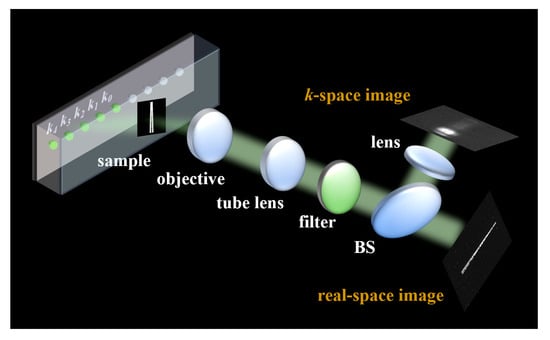
Figure 1.
Schematic of the dual-channel SFS super-resolution imaging system.
2.2. Theory of Joint Intensity
k-space intensity (KI) is the ratio of efficient photons in the object area (SFSeff) to all photons in the upper interface of the waveguide from the LED. As shown in Figure 2a, the divergence angle of LED is θ. When the oblique incident angle is smaller than the critical angle, the propagation wave is used to illuminate the object area, which is regarded as SFSkp. The KI is defined as SFSeff/SFSkp. When the oblique incident angle is larger than the critical angle, the highly localized evanescent wave is used to illuminate the object area, which is regarded as SFSkeva. The KI is defined as SFSeff/SFSkeva. In our experimental setup, five LEDs are used as the light source. The first LED is centrally positioned beneath the sample area, providing vertical illumination with a transverse wave vector of k0, which is the traditional illumination method. The other four LEDs are lined up in a row beginning with the first LED, providing oblique illumination. Therefore, the four LEDs induce different incident angles in the sample area. Total internal reflection occurs on the surface of the sample area when the incident angle exceeds the critical angle. The waveguide material is K9 glass with a refractive index of 1.52 at a wavelength of 530 nm (the influence of waveguide imperfections on SFS super-resolution imaging is detailed in Supplementary Materials S2). Then, the critical angle is 41°. To uniformly increase the incident angle from 0° to over 41°, the four incident angles φ are designated as 8°, 17°, 30°, 49°, providing transverse wave vectors of k1, k2, k3, k4. Notably, depending on whether the incident angle is larger than the critical angle, k1–k3 are the transverse wave vectors of propagation illuminations, while k4 is the transverse wave vector of evanescent illumination. As plotted in Figure 2b, as the SFS becomes deeper, the KI drops steeply, especially at the point from propagation wave illumination to evanescent wave illumination. The real-space intensity (RI) was detected in the object area by an optical power meter (S130C, Thorlabs, Newton, MA, United States), as plotted in Figure 2b. Notably, although the different LEDs have slightly different intensities, all data were averaged over 10 independent measurements to enhance the generalizability of the results. In the range of propagation illumination, as the SFS goes deeper, the RI decreases slightly. From propagation illumination to evanescent illumination, the RI drops extremely steeply. Once the LED is switched on and then illuminates the sample, the image sensor in the real-space path can collect the real-space image, and another image sensor in the k-space path can obtain the k-space image. The illumination from LEDs has the properties of both KI and RI. Although KI and RI are independent, the obtained image is influenced by illumination intensity, which is the combined effect of KI and RI. To analyze it, joint intensity (JI) is proposed, defined as JI = RI × KI. As shown in Figure 2c, the JI decreases as the SFS goes deeper. Specifically, the JI of the fourth SFS (the deepest SFS, provided by evanescent illumination in the x-axis) is 100-fold weaker than that of the first SFS (provided by propagation illumination).
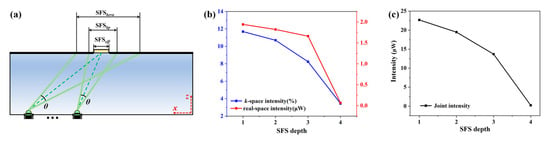
Figure 2.
(a) The schematic of KI. (b) The influence of KI and RI on SFS depth. (c) The influence of JI on SFS depth.
In our experiment, a series of parallel slots were used as objects to analyze the influence of illumination with multiplex SF modulation. The schematic of parallel slot distribution is illustrated in Figure 3j, where the periods of the slots are 860 nm, 815 nm, 659 nm, 491 nm, 351 nm, 304 nm, 243 nm and 237 nm. The origin of the coordinate system is set at the midpoint between the two slots. The object function of the slots can be expressed as
where p is the period of the slots, and lw is the line width of the slots. In the Fourier domain, this can be expressed as (a detailed derivation process is provided in the Supplementary Material S1)
where C is a constant. Notably, only the term of includes p, indicating that only this term determines the SF of the slots, further demonstrating that the expected resolution of SFS super-resolution imaging required for the slots to be distinguished can be analyzed based on the term, especially the p parameter.
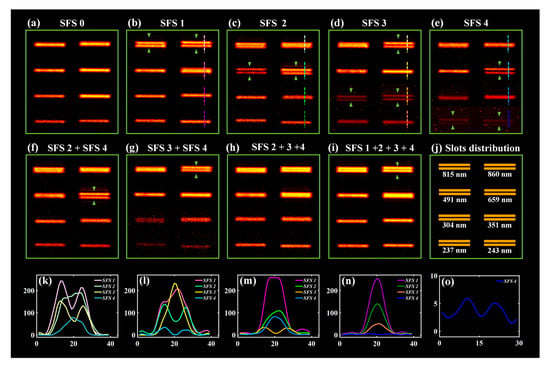
Figure 3.
(a–e) The experiment of parallel slots under single illumination from the SFS0 mode to the SFS4 mode. (f–i) The experiment of parallel slots under mixed illumination. (j) The schematic of parallel slots distribution. (k–o) The intensity profiles through the dot lines in (b–e).
Based on the periodicity of the cosine function, in the frequency domain, slots with high SF can cover some slots with low SF because high SF denotes a large period of cosine function in the frequency domain and a small spatial period of the slot structure in the spatial domain. In other words, in the spatial domain, if slots with small spatial periods can be resolved under the corresponding kx, some slots with large spatial periods may also be resolved simultaneously.
Imaging resolution refers to the smallest distinguishable detail that an optical microscope system can resolve. The LEDs are used as the light sources; thus, this is the partial coherence imaging. The resolution falls in a lager range between coherent imaging and incoherent imaging. The coherent imaging resolution is calculated by
The incoherent imaging resolution is calculated by
λ is the center wavelength of the illumination light. NA is the numerical aperture of the objective lens. NAillu = n cos(φ) is the expanded numerical aperture from the illumination modulation. n is the refractive index of the waveguide material, and φ is the incident angle. k0 = 2π/λ is the transverse wave vector provided by vertical illumination. kxi = 2π NAillu/λ is the transverse wave vector provided by oblique illumination. The expected resolutions are illustrated in Table 1. The LEDs can be modulated to generate single illumination and mixed illumination with various combinations. When a single LED illuminates the objects, the light field interacts with the sample; the scattering field of the illuminated object is calculated as
where the complex amplitude of the object is , and the electric field of the illumination field is .

Table 1.
The expected resolution of each SFS depth.
The light field, which encompasses the complex information of the object after being collected by the microscope, travels to the plane of the image sensor, which can be represented as
where the transfer function of the linear time-invariant imaging system is , and denotes the convolution calculation.
Then, the image sensor obtains the intensity of the above light field, which is denoted as
The Fourier transform of the intensity is calculated as
When multiple LEDs illuminate the object (multiplex SFS mode), which is a process of incoherent imaging with mixed SF, the image sensor records the superposition of intensities, which is expressed as
The corresponding Fourier form is calculated as
Based on Equation (9), when mixed illumination is executed, the real-space intensity recording by the image sensor depends on the sum of intensities of different SFS modes. Based on Figure 2c, the JI of the illumination with a highly localized field is greatly weaker than that of the illumination with a propagation field. Therefore, when mixed illumination with both a highly localized field and a propagation field is employed, its real-space images mostly show photon information in the spatial domain from the illumination provided by the propagation field. Moreover, based on Equation (10), the k-space images modulated by the illumination from multiplex LEDs also depend on the sum of JI, obviously dominantly influenced by the most intense JI.
2.3. Experimental Results and Discussion
As shown in Figure 3a, parallel slots cannot be resolved under vertical illumination. As shown in Figure 3b–e, parallel slots with corresponding periods matching the set SFS modes can be resolved under single oblique illumination with SFS1, SFS2, SFS3, SFS4, respectively, which are within the expected resolution ranges. Furthermore, based on the above analysis of the object function of slots, SF information of the SFS3 mode contains partial SF information of the SFS1 mode. And SF information of the SFS4 mode contains partial SF information of the SFS2 mode. Thus, under modulation by SFS3, as shown in Figure 3d, parallel slots with periods of 304 nm, 351 nm, 860 nm can be distinguished, covering the partial expected resolution under the SFS1 mode. Under modulation by SFS4, as shown in Figure 3e, slots with periods of 237 nm, 243 nm, 659 nm can be distinguished, covering the partial expected resolution under the SFS2 mode. Moreover, Figure 3k–n plot the intensity profiles of parallel slots through dot lines. The colors of the intensity profiles correspond to the colors of the dot lines in Figure 3b–e. For the same parallel slots, the photon intensity in the image plane drops with the SFS going deeper. The intensity profiles clearly illustrate that the slots with the expected periods are all distinguishable under the corresponding SFS modes. The intensity of real-space image analysis reveals significant variations across different SFS modes: SFS1 exhibits 1.71×, 6.86× and 40× stronger intensity compared to SFS2, SFS3 and SFS4 modes, respectively, in their resolved slots.
Interestingly, super-resolution imaging with multiplex SFS modes produces different properties compared to using the single SFS mode, including image intensity and resolution. As shown in Figure 3f, only parallel slots with the 659 nm period (they are the expected resolution of the SFS2 mode, and they can also be resolved under the SFS4 mode) are resolved under the mixed illumination of SFS2 and SFS4. This is because the JI of the illumination with SFS2 is 85-fold stronger than that of SFS4. The SFS4 mode is depressed, and the information of slots with the expected resolution of the SFS2 mode and the SFS4 mode is dominant. As shown in Figure 3g, under the mixed illumination of SFS3 and SFS4, parallel slots with the 860 nm period (they can be resolved under the SFS3 mode) are vaguely distinguished, while parallel slots within the expected SFS3 and SFS4 resolution cannot be distinguished. Because the JI of the illumination with SFS3 is 60-fold stronger than that of SFS4, the SFS3 mode and the SFS4 mode are mutually inhibitory to some extent, though the SFS3 mode is slightly dominant. As shown in Figure 3h, none of the parallel slots are distinguished under the mixed illumination of SFS2, SFS3 and SFS4. The JI of the illumination with SFS2 is 1.42-fold stronger than that of SFS3; thus, the SFS4 mode is inundated by the SFS2 mode and the SFS3 mode. And the SFS2 mode and the SFS3 mode are mutually constrained. As shown in Figure 3i, only parallel slots with the 860 nm period (they are the expected resolution of the SFS1 mode, and they can also be resolved under the SFS3 mode) can be slightly distinguished under the mixed illumination of SFS1, SFS2, SFS3 and SFS4. The JI of the illumination with SFS1 is 1.16-fold stronger than that of SFS2. Therefore, the SFS1 mode, the SFS2 mode and the SFS3 mode are mutually constrained to some extent, and the SFS4 mode is inundated by the SFS1 mode, the SFS2 mode and the SFS3 mode, though the SFS1 mode is slightly dominant.
The above parallel slots sample with different definite periods has a discrete SF distribution. Therefore, the experiment of the parallel slots sample can clearly calibrate the resolution of the imaging system. However, it fails to fully reflect the imaging resolution range of each SFS mode. Moreover, it cannot intuitively demonstrate the image magnification issue in the SFS super-resolution imaging process. Thus, V-shape slots with continuously changing periods were selected as the sample for our SFS super-resolution imaging. As shown in Figure 4b, the V-shape slots in the yellow box cannot be distinguished at all under wide-field vertical illumination. The image of V-shape slots obtained via field emission scanning electron microscopy (FESEM, Zeiss Ultra 55, Oberkochen, Germany) is shown in Figure 4a, whose resolution is within the range from 200 nm to 1200 nm. The following super-resolution images of V-shape slots obtained via modulated illuminations all illustrate the yellow box parts. In SFS super-resolution imaging, the modulated scattering photons carrying high SF information of the objects are collected by a microscope and then coupled into the image sensor. Hence, the high SF is shifted into the passband of the objective lens and reflected in the digital images provided by the image sensor. Objects with high SF information have sub-diffraction-limit structures in the spatial domain, and these fine structures are distorted the real size because of the optical magnification provided by the SFS method. In other words, SFS modulation provides extra magnification to the traditional microscope. Therefore, the magnification factor of SFS super-resolution imaging can be defined as

Figure 4.
(a) The FESEM image of V-shape slots. The scale bar is 1 μm. (b) The wide-field image of V-shape slots under vertical illumination. (c–f) The experiment of V-shape slots under single illumination from SFS1 to SFS4. The corresponding normalized intensity profile is provided in the inset. (g–j) The experiment of V-shape slots under mixed illumination. The corresponding normalized intensity profile is provided in the inset.
kc is the transverse wave vector of the cut-off SF of the objective lens, and kxi is the transverse wave vector of modulated illumination. The relationship between the pixel number (px_num) of SFS images and the real size of the objects lr is
where px_num denotes the center-to-center pixels of a pair of slots; px_size is the pixel size of the image sensor; and Mobj is the magnification of the objective lens.
As shown in Figure 4c, under the illumination with SFS1, the continuous area of V-shape slots around the orange arrow is resolved. The normalized intensity profile pointed by the orange arrow is plotted in the inset, indicating there are 11 pixels between two peeks (the distance between the middle of a pair of slots). Based on Equation (12), the period of the slots is 841 nm, which is within the expected resolution range. As shown in Figure 4d, under the illumination with SFS2, the continuous range of V-shape slots around the yellow arrow is resolved. The normalized intensity profile pointed by the yellow arrow shows 10 pixels, demonstrating that the period of the slots is 638 nm, which is also within the expected resolution range. Notably, it can be observed that there is a significant magnification in the distinguishable areas. As shown in Figure 4e, under the illumination with SFS3, two continuous areas are distinguished, where the resolutions are within the range of the SFS1 mode and the SFS3 mode. Compared with the orange area under the SFS1 mode, the orange area under the SFS3 mode has a more obvious magnified distortion. In other words, as the SFS becomes deeper, the magnification increases, which is consistent with Equation (11). The normalized intensity profile pointed by the green arrow is plotted in the inset, showing there are nine pixels between the peaks. After calculation, the resolution at the green point is 473 nm. The reason for the calculated resolution (473 nm) being slightly distant from the resolution range of SFS3 (274–459 nm) is imprecise computations due to the larger pixel size of the image sensor. As shown in Figure 4f, under the illumination with SFS4, similar phenomena are observed as with SFS3, but the intensity is smaller. And two continuous areas around the yellow and pink arrows are resolvable. The normalized intensity profile illustrates that there are eight pixels between the peaks at the pink point, indicating that the corresponding resolution is 344 nm, which is in line with expectations.
Furthermore, the multiplex SFS modes for V-shape slots are also studied. As shown in Figure 4g, under the mixed illumination of SFS2 and SFS4, the yellow area is magnified and distinguished. As shown in Figure 4h, under the mixed illumination of SFS3 and SFS4, the orange area is magnified and distinguished. As shown in Figure 4i, under the mixed illumination of SFS2, SFS3 and SFS4, the orange area is subtly magnified and slightly distinguished. As shown in Figure 4j, under the mixed illumination of SFS1, SFS2, SFS3 and SFS4, the orange area is subtly magnified and clearly distinguished. These results validate the conclusion from the parallel slots experiment, and furthermore, they demonstrate the situations encountered in objects with continuous SF.
While obtaining the real-space images of the object, its k-space images are also obtained. The parallel slots and V-shape slots are in the same substrate of the sample. Therefore, for the parallel slots and V-shape slots, the same k-space images are studied. Figure 5a shows the SF spectrum image of the object, which is obtained via Fourier transform from the SEM image of the object. The parallel slots and V-shape slots only contain SF information in the horizontal and vertical directions, as expected. The SEM image has a high resolution, resolving slots with both small and large periods. Thus, the SF spectrum image of the object contains low SF information and high SF information. The k-space image under wide-field vertical illumination is shown in Figure 5b, containing only cut-off SF information with four mutually perpendicular directions. The k-space images under single illumination with SFS1, SFS2, SFS3 and SFS4 are shown in Figure 5c–f. As the SFS goes deeper, the higher SF information shifts into the cut-off SF passband of the objective lens to the image sensor. The SF information in each SFS step corresponds to each part of the SF spectrum of the object in Figure 5a. Additionally, as the SFS goes deeper, the intensity of the k-space drops according to the JI. Furthermore, k-space images under multiplex SFS modes are studied, as shown in Figure 5g–j. The dominant role of SFS with a high JI can be observed, along with the mutual constraints and superposition effects of different SFS modes. These results in the k-space images are consistent with findings from the real-space images.
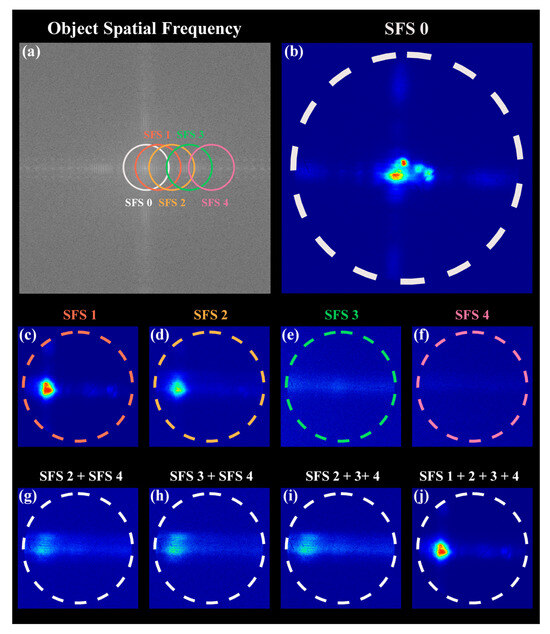
Figure 5.
(a) SF spectrum image of the object. The circles in different colors mark out the k-images that can be acquired in each SFS. (b) The k-space images obtained via wide-field vertical illumination in the experiment. (c–f) The k-space images obtained via single modulated illumination in the experiment. (g–j) The k-space images obtained via mixed modulated illumination in the experiment.
3. Conclusions
In conclusion, our work studied the mechanism of SFS super-resolution microscopic imaging based on illumination modulation. The SFS super-resolution imaging system was built to obtain real-space and k-space super-resolution images. The JI theory based on RI and KI was proposed to study its influence on SFS super-resolution imaging. As the SFS goes deeper, the JI drops. Especially at the point where the illumination changes from the propagation wave field to the evanescent field, the JI decreases significantly. Parallel slots with discrete SF distribution and V-shape slots with continuous SF distribution were used as the imaging objects. The effects of modulated illumination (different single SFS illumination and various mixed illumination) on SFS super-resolution imaging were explored. Partial coherent imaging illuminated by LEDs was observed. The phenomenon of high SF being able to cover part of low SF was revealed. The magnifying issue during SFS super-resolution imaging process was explained. The k-space images of parallel slots and V-shape slots were also studied. The effects of JI on the k-images were discussed. This also intuitively revealed that high SF information beyond the diffraction limit can be transferred into the objective lens passband through modulated illumination, thus achieving SFS super-resolution imaging. Any sample can be regarded as a superposition of numerous gratings with various frequencies, amplitudes and phases. Parallel slots and V-shape slots are the simplest gratings. Therefore, the theory of parallel slots and V-shape slots is possibly suitable for other complex samples. This work provides a certain basis for further optimization of SFS super-resolution microscopy imaging.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics12070717/s1, Note S1: Detailed derivation: Fourier expression of slots object; Note S2: The influence of waveguide imperfections on SFS super-resolution imaging; Figure S1: The 2D schematic of SFS super-resolution imaging system.
Author Contributions
Conceptualization, X.Y. and H.Z.; methodology, X.Y. and H.Z.; experiment, X.Y. and H.Z.; data analysis, X.Y.; investigation, F.L. and X.L.; writing—original draft preparation, X.Y.; writing—review and editing, X.Y. and Q.Y.; supervision, Q.Y.; funding acquisition, Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 62020106002, 92250304 and T2293751) and the National Key Research and Development Program of China (2021YFC2401403).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank the anonymous reviewers for their suggestions and insightful questions that helped to improve the clarity and scientific quality of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abbe, E. Beiträge zur Theorie des Mikroskops und der Mikroskopischen Wahrnehmung. Arch. Für Mikrosk. Anat. 1873, 9, 413–418. [Google Scholar] [CrossRef]
- Davidovits, P.; Egger, M.D. Scanning Laser Microscope for Biological Investigations. Appl. Opt. 1971, 10, 1615–1619. [Google Scholar] [CrossRef]
- Carlsson, K.; Aslund, N. Confocal Imaging for 3-D Digital Microscopy. Appl. Opt. 1987, 26, 3232–3238. [Google Scholar] [CrossRef] [PubMed]
- Hell, S.W.; Wichmann, J. Breaking the Diffraction Resolution Limit by Stimulated Emission: Stimulated-Emission-Depletion Fluorescence Microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, M.; Eggeling, C.; Jakobs, S.; Hell, S.W. Breaking the Diffraction Barrier in Fluorescence Microscopy at Low Light Intensities by Using Reversibly Photoswitchable Proteins. Proc. Natl. Acad. Sci. USA 2005, 102, 17565–17569. [Google Scholar] [CrossRef] [PubMed]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science 2006, 313, 1642–1645. [Google Scholar] [CrossRef]
- Dai, M.; Jungmann, R.; Yin, P. Optical Imaging of Individual Biomolecules in Densely Packed Clusters. Nat. Nanotechnol. 2016, 11, 798–807. [Google Scholar] [CrossRef]
- Gustafsson, M.G.L. Surpassing the Lateral Resolution Limit by a Factor of Two Using Structured Illumination Microscopy. J. Microsc. 2000, 198, 82–87. [Google Scholar] [CrossRef]
- Heintzmann, R. Saturated Patterned Excitation Microscopy with Two-Dimensional Excitation Patterns. Micron 2003, 34, 283–291. [Google Scholar] [CrossRef]
- Saxena, M.; Eluru, G.; Gorthi, S.S. Structured Illumination Microscopy. Adv. Opt. Photonics 2015, 7, 241–275. [Google Scholar] [CrossRef]
- Kner, P.; Chhun, B.B.; Griffis, E.R.; Winoto, L.; Gustafsson, M.G.L. Super-Resolution Video Microscopy of Live Cells by Structured Illumination. Nat. Methods 2022, 19, 1513–1521. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Shroff, H. Faster, Sharper, and Deeper: Structured Illumination Microscopy for Biological Imaging. Nat. Cell Biol. 2023, 25, 1230–1241. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Wang, Z.; Liu, M.; Wang, Z.; Li, D.; Zhang, X. Deep Learning Enables Structured Illumination Microscopy with Low Light Levels and Enhanced Speed. Nat. Commun. 2023, 14, 3675. [Google Scholar]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-Field, High-Resolution Fourier Ptychographic Microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef]
- Liu, M.; Wu, R.; Luo, Z.; Zhen, J.; Zhang, H.; Luo, J.; Yan, L.; Wu, Y. Fast Digital Refocusing Fourier Ptychographic Microscopy Method Based on Convolutional Neural Network. Opt. Express 2024, 32, 339–354. [Google Scholar] [CrossRef]
- Dong, Z.; Zhou, H.; Cao, R.; Zhang, O.; Zhao, S.; Lyu, P.; Alcalde, R.; Yang, C. Analytic Fourier Ptychotomography for Volumetric Refractive Index Imaging. arXiv 2025, arXiv:2504.16247. [Google Scholar] [CrossRef]
- Ou, X.; Zheng, G.; Yang, C. Embedded pupil function recovery for Fourier ptychographic microscopy. Opt. Express 2014, 22, 4960–4972. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Huang, X.; Zhang, Y.; Zuo, C. High-speed Fourier ptychographic microscopy based on optimized illumination scanning. Photonics Res. 2023, 11, 1234–1245. [Google Scholar]
- Zhang, Y.; Wang, H.; Tian, L.; Dai, Q. Deep learning-enabled Fourier ptychographic microscopy for high-resolution imaging. Light Sci. Appl. 2023, 12, 156. [Google Scholar]
- Jiang, S.; Guo, K.; Liao, J.; Zheng, G. Fourier ptychographic microscopy for gigapixel imaging with sub-wavelength resolution. Adv. Photonics 2023, 5, 036001. [Google Scholar]
- Liu, X.; Kuang, C.; Hao, X.; Pang, C.; Xu, P.; Li, H.; Liu, Y.; Yu, C.; Xu, Y.; Nan, D.; et al. Fluorescent Nanowire Ring Illumination for Wide-Field Far-Field Subdiffraction Imaging. Phys. Rev. Lett. 2017, 118, 076101. [Google Scholar] [CrossRef]
- Pang, C.; Li, J.; Tang, M.; Wang, J.; Mela, I.; Ströhl, F.; Hecker, L.; Shen, W.; Liu, Q.; Liu, X.; et al. On-Chip Super-Resolution Imaging with Fluorescent Polymer Films. Adv. Funct. Mater. 2019, 29, 1900126. [Google Scholar] [CrossRef]
- Tang, M.; Han, Y.; Ye, D.; Zhang, Q.; Pang, C.; Liu, X.; Shen, W.; Ma, Y.; Kaminski, C.F.; Liu, X.; et al. High-Refractive-Index Chip with Periodically Fine-Tuning Gratings for Tunable Virtual-Wavevector Spatial Frequency Shift Universal Super-Resolution Imaging. Adv. Sci. 2022, 9, 2103835. [Google Scholar] [CrossRef]
- Ye, D.; Tang, M.; Liu, X.; Ma, Y.; Liu, X.; Yang, Q. Low loss and omnidirectional Si3N4 waveguide for label-free spatial frequency shift super-resolution imaging. J. Phys. D Appl. Phys. 2021, 54, 315101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).