Abstract
In response to the increasing demands for reliable, fast, and secure communications beyond 5G scenarios, the high-capacity networks have become a focal point. Quantum communication is at the forefront of this research, offering unmatched throughput and security. A free space optics (FSO) communication system integrated with fiber-end is designed and investigated using the Bennett–Brassard 1984 quantum key distribution (BB84-QKD) protocol. Simulation results show that reliable transmission can be achieved over a 10–15 km fiber length with a signal power of −19.54 dBm and high optical-to-signal noise of 72.28–95.30 dB over a 550 m FSO range under clear air, haze, fog, and rain conditions at a data rate of 1 Gbps. Also, the system using rectilinearly and circularly polarized signals exhibits a Stokes parameter intensity of −4.69 to −35.65 dBm and −7.7 to −35.66 dBm Stokes parameter intensity, respectively, over 100–700 m FSO range under diverse weather conditions. Likewise, for the same scenario, an FSO range of 100 m incorporating 2.5–4 mrad beam divergence provides the Stokes power intensity of −6.03 to −11.1 dBm and −9.04 to −14.12 dBm for rectilinearly and circularly polarized signals, respectively. Moreover, compared to existing works, this work allows faithful and secure signal transmission in free space, considering FSO–fiber link losses.
1. Introduction
In daily life, communication services are used to conduct our routine activities, including transaction services, navigation, and even observing the universe. Physics principles can be applied to enable communication through various mediums such as free-space, cables, or radio frequencies. Recently, communication networks have matured while maintaining low costs. However, challenges such as availability, direction, security, and bandwidth still arise. Communication links are typically secured using computational hardness, satellites, and high resolution images, among other techniques. Some of these issues can be mitigated by incorporating quantum principles into communication, opening new opportunities [1,2].
Quantum technologies are evolving to meet the increasing demand for confidential information services and high quality. Wireless networks are rapidly advancing to cater to these needs. Research efforts are now shifting towards future wireless networks like sixth-generation (6G) networks and beyond, driven by the global roll-out of fifth-generation (5G) networks [3]. Global mobile data is projected to grow by 55% annually until 2030, resulting in exabytes of data per month. This immense data volume necessitates extensive processing and learning capabilities to manage the network at various levels [4]. Satellites can cover vast geographic areas with minimal infrastructure to meet the growing demand for ultra-broadband services [5].
Photonics and quantum-based technology will play a crucial role in 6G communication, including quantum computing communication, secure key distribution, timing, and random number generation [6]. Quantum communication uses principles of quantum mechanics to transmit information through quantum states [7]. Integrating communication networks with quantum system resources promises to revolutionize science and technology. Quantum communication systems are essential for developing quantum technologies such as distributed quantum computing and quantum sensing, in addition to secure long-distance quantum communications [8]. The forthcoming quantum revolution will redefine quantum technologies, enabling new capabilities, enhanced security, precision, and accuracy [9]. Quantum communication is already being implemented in various fields, which will benefit future 6G communication [10]. There is significant interest in quantum communication systems and networks due to the intriguing properties of quantum signals, including superposition, entanglement, and quantum interference [11].
The ultimate goal for quantum communications is the quantum internet. This will support remote quantum computing and secure communication while revealing new applications across the universe. Entanglement is a key component of the quantum internet, allowing users to store and distribute it among themselves. Recent efforts to achieve long-distance and stable entangled states have been limited. Enhancing quantum channel efficiency through high-dimensional quantum communication is crucial, as these channels are more robust to noise and have higher information capacity. However, their utilization is challenging due to real-life limitations and unresolved theoretical issues. Qubit-based protocols like entanglement swapping and quantum teleportation are complex to generalize and prove [12].
Quantum key distribution (QKD) allows the propagation of robust information—keys that are theoretically secure and ensured by quantum mechanical limits. However, due to the inescapable loss of a significant number of photons in the quantum channel, the key rate of most QKD protocols, is severely confined by the secret key capacity of repeater-less QKD [13]. Also, a quantum repeater protocol utilizing the idea of post-matching retains the same efficiency as the single-photon interference protocol, minimizing the phase-stability requirement and enabling the generation of a maximally entangled state in principle. It highlights the potential for developing a large-scale quantum communication network [14].
1.1. Related Works
The Quantum Communication Testbed (QCT) is described in [15]. In QCT, quantum communication is examined in a scenario similar to that of former commercial realizations: quantum key distribution (QKD) exchanges over a free-space optics (FSO) range of 600 m. Additionally, the Bennett–Brassard 1984 (BB84) algorithm is used in this work; process the data between the photonic components and the control computer. A global-scale FSO/QKD design for low Earth orbit and geosynchronous satellites is also proposed in [16]. It incorporates a continuous variable (CV) QKD protocol along with dual-threshold/direct-detection receivers. The system is analyzed by considering atmospheric attenuation, spreading loss, and turbulence. The FSO/QKD system design criteria are discussed along with the feasibility of a QKD network that incorporates an unauthorized receiver attack and a beam-splitting attack. Furthermore, Monte Carlo simulations are conducted to verify the performance of the proposed system and the secret-key rate. In [17], the performance of line-of-sight (LoS) QKD using a digital signal processing key and incorporating finite length analysis is investigated. Results show that the proposed system achieves long-distance, high-speed secret key agreement while providing information-theoretic security. This paper demonstrates that differential phase shift QKD offers higher security against active attacks. Furthermore, LoS-QKD or FSO physical layer security may provide the optimal solution for long-haul communication and secure key rate. Considering a wiretapping ratio of 10−4 to 10−6, the LoS-QKD can be implemented for satellite-to-ground secret key realization. According to [18], the performance of a QKD/FSO system is analyzed considering pointing error models. A few selected numerical results are presented to demonstrate mathematical formalism and to validate the accuracy of the analytical expressions. Monte Carlo simulations are utilized to validate the accuracy of the derived expressions numerically. Furthermore, in [19], multiple-input, multiple-output quantum communication is discussed to improve the QKD throughput. This paper develops a new mathematical model to analyze the impact of crosstalk and interference on the proposed scenario. Results depict the atmospheric effects on system performance at a wavelength of 1550 nm, with a refractive index structure of 5 × 10−16 cm−2/3, considering aerosol scattering and absorption coefficients. Additionally, utilizing multiple simultaneous wavelengths to achieve a specified performance is presented to reduce the atmospheric effect. In [20], a QKD system implementation framework that employs the Kumar-MacDonald-Bourgoin 2009 (KMB09) protocol in multi-dimensional space is discussed. Especially for states with more than two-photon dimensions, the protocol can be realized in terms of success rate or efficiency. In the case of two- and four-dimensional versions of the KMB09 protocol, the system efficiency was 0.25 and 0.3683, respectively. Additionally, this work can be extended to evaluate the error rate resulting from eavesdropping in QKD setups. According to [21], a multi-photon quantum communication-multiple beam system is proposed that accounts for geometrical losses. Considering a strong turbulence channel, the proposed system diminishes channel loss better than a single-beam system. By improving the transmission distance between sender and receiver, it also enhances the secret key rate compared to the single-beam system. The system shows superior performance over the single-beam system by minimizing channel loss by 8 dB and operating well under strong-turbulence conditions. A novel implementation of the BBM92 protocol for continuous-variable QKD satellite systems is presented in [22]. The proposed system is simple in design and may be more cost-effective than discrete-variable systems. Channel loss, receiver noise, and atmospheric turbulence-induced fading are considered in the analysis. The impact of signal geometric spread on legitimate users and the possibility of eavesdropping using the Gaussian beam model are also discussed. For dual ground stations, ref. [23] presents a quantum communication technique based on entanglement for CV-QKD. It provides a quantitative assessment of CV-QKD in the context of low earth orbit satellite scenarios. The system shows that an extremely selective post-selection strategy can lead to a beneficial QKD rate.
1.2. Motivation and Contributions
New methods must be identified to ensure the data security and safety in the post-quantum era. Recently, the proposed methods for this era have been categorized based on the underlying mathematical challenges. Quantum cryptography is a promising candidate, leading to the development of new algorithms that resist quantum computing while maintaining efficient data transmission. QKD systems use quantum mechanical principles to withstand threats from quantum computers, thereby ensuring future communication security. In recent times, there has been a notable surge of interest in quantum communication and quantum capacity for beyond 5G networks. An inquiry is underway to explore the feasibility of extending quantum communication to offer high-capacity services. However, capacity is also an important metric for beyond 5G networks.
Based on the existing works, the primary constraints in QKD-based systems are as follows:
- Several existing approaches [15,24,25,26,27] indicate a limited FSO transmission range under the impact of different atmospheric conditions.
- Existing schemes suffer from low throughput [28,29,30], high computational complexity [18,22,24,25,31] and high sensitivity under severe weather conditions (in FSO) as well as non-linearities and attenuation (in fiber).
- Current schemes are ineffective in handling high-speed transmission over an integrated fiber–FSO link considering free-space beam divergence, additional losses, and geometric losses.
- Several existing methods result in unsatisfactory system performance in terms of optical signal-to-noise ratio (OSNR) and signal quality at the receiver.
The novelty of this work lies in evaluating the system’s performance in terms of rectilinearly and circularly polarized signals, Stokes parameters, OSNR, and received power for the varying fiber–FSO range and beam divergence. These important parameters directly influence the system security, performance as well as reliability of quantum communication under different atmospheric conditions. The proposed design facilitates the keys distribution with verifiable privacy, ensuring security through the fundamental laws of physics.
The major contributions of this work are as follows:
- An integrated fiber–FSO-based QKD system using the BB84 protocol for beyond fiber-to-the-x scenarios is designed.
- In various existing BB84-QKD schemes, the effect of guided (fiber) and unguided (FSO) channels on different polarization states (rectilinear and circular) has not been explored. Polarization integrity can be verified at the receiver in terms of signal quality, and quantum bit error rate (QBER). Thus, the system’s performance is investigated for different polarization states over an integrated fiber–FSO link under distinct weather conditions in terms of Quality-factor (Q-factor), OSNR, signal power, noise, and QBER.
- In addition, to provide a complete description of the polarization state in the proposed system and to allow real-time monitoring and compensation of polarization distortions with minimal errors in QKD, Stokes parameters are evaluated.
- Further, in FSO links, the transmitted beam naturally diverges over distance, decreasing OSNR, reducing received power, increasing alignment losses, increasing atmospheric exposure, and thus reducing signal quality. Large beam divergence can distort polarization and consequently, reduce detection efficiency. Therefore, the impact of varied beam divergence is investigated under diverse weather conditions.
- The performance and reliability of the proposed system are verified through a comparative analysis with existing QKD-based systems, based on various performance parameters.
2. Proposed Design
Figure 1a depicts the schematic design of a quantum communication system over a quantum channel. Figure 1b depicts the proposed FSO–fiber system using the BB84-QKD protocol. The BB84 protocol is the first quantum protocol introduced to assure unlimited security. Figure 1c illustrates the proposed methodology used in the system.
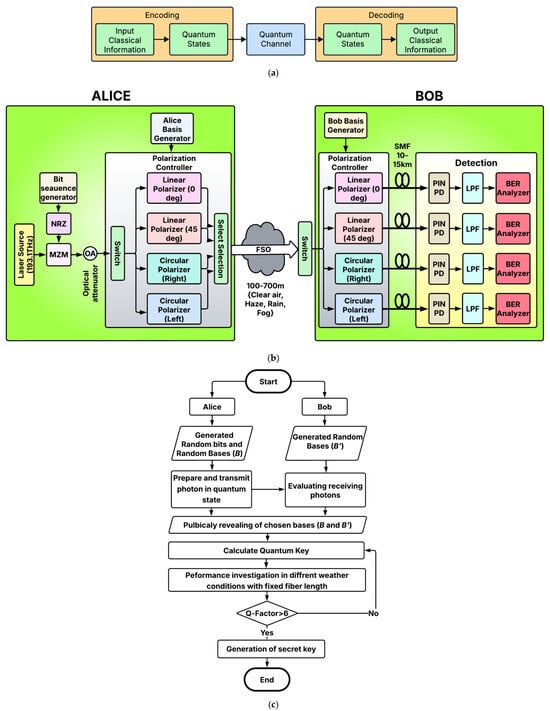
Figure 1.
Block diagram of (a) a basic quantum communication system, (b) the proposed FSO–fiber system using the BB84-QKD protocol under diverse weather scenarios, and (c) the proposed methodology.
Figure 1a shows a basic quantum communication network transferring data over a quantum channel. However, this scheme not only considers security from the physical layer point of view but also the network one. In the proposed system using the BB84 protocol, a discrete-variable (DV) QKD setup is designed in OptiSystem v22. Here, weak coherent pulses (laser source with optical attenuator) are used with polarization encoding (e.g., horizontal, vertical, right circular and left circular). The system’s performance is evaluated over an FSO link under different weather scenarios along with the optical fiber link considering the impact of non-linearities. Quantum channels allow for the transfer of quantum states between two locations, following a three-stage process: quantum state preparation (encoding classical information using multiple quantum states), quantum state transmission (sending quantum signals through a quantum channel), and quantum state decoding (using quantum measurements to produce specific classical information output). In an FSO system using this protocol, Alice prepares quantum bits (meaning ‘qubits’) via encoding photons emitted from a laser source (frequency = 193.1 THz) followed by an optical attenuator (OA) into one of four states: horizontal (), vertical (), circular right (), and circular left (). An OA (attenuation = 0.1 dB) is used to obtain one light photon at the Alice end. Alice selects one of two random bases (B), i.e., rectilinear () or circular (), as defined below [32].
The incoming laser signal with 5 dBm power is connected to a LiNbO3 mach-zehnder modulator (MZM). Also, the non-return-to-zero (NRZ) pulse train is fed into the MZM to generate optically modulated signals [33]. After this, Alice transmits the encoded quantum bits using a quantum FSO channel under diverse weather conditions. Bob evaluates incoming photons utilizing a randomly selected basis (B’). Finally, if Bob measures the ‘qubits’ like Alice, he will receive a correctly encoded bit; otherwise, the bits are discarded. Again, a switch is used to send the input signals to one of the output ports by using the Selection parameter, while the select component parameter helps send the input signals to the output port. It is followed by a single mode fiber (SMF) to four end-users. A PIN photodetector (PD) is utilized to achieve electrical signals followed by a low pass filter (LPF) to recover the transmitted signal. The bit error rate (BER) analyzer is used to analyze the system’s performance in terms of Q-factor, eye-patterns, and error-rate [33,34,35]. Figure 2 depicts the generated polarized states in the proposed FSO system using the BB84 protocol.
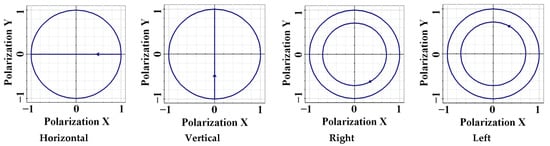
Figure 2.
Generated polarized states in the proposed system.
Table 1 shows the concept of the BB84 protocol with random bits at Alice.

Table 1.
Concept of the BB84-QKD protocol [32].
As per Table 1, bits are only accepted if Alice and Bob use the same basis. All mismatched bases are marked as “Discard” and matched bases (at both the Alice and Bob ends) are marked as “Match”, indicating correctly received bits. Table 2 depicts the various simulation parameters used in the system.

Table 2.
System parameters [33].
3. Results and Discussion
In this work, OptiSystem v.22 and MATLAB R2024b are used to design and investigate the system’s performance. The OptiSystem simulator can simulate the entire QKD system using an integrated fiber–FSO link (transmitter-to-receiver), while Monte Carlo simulation is bounded to the FSO channel. OptiSystem also enables protocol-specific as well as component-wise system performance analysis at a faster rate. This tool is more efficient for design optimization and multi-scenario performance evaluation, and it simulates FSO–fiber QKD links in a single platform considering real-world link impairments. On the other hand, the Monte Carlo simulation conducted in [36,37,38], does not provide direct QKD performance metrics, and it requires external tools to interpret photon distributions. In contrast, OptiSystem enables the direct evaluation of key parameters like QBER, OSNR, Stokes parameters, received power, and key rate for the end-to-end QKD system.
3.1. Channel Model
Compared to classical communication, the analysis of FSO loss in terms of secure communication is considered a crucial step for QKD transmission, as quantum data are significantly weaker and cannot be smoothly amplified. The efficiency of a quantum channel can simply be obtained by reducing the FSO channel attenuation and background noise for faithful QKD links. The factors that produce channel losses are geometric loss, detector loss, atmospheric loss, etc., defined as below [39]:
- Geometric loss: Diffraction, or geometric loss, refers to the channel loss owing to the beam spread effect when a signal propagates from one point to another point. Mathematically, geometric loss is defined as [40]:
- Atmospheric loss: When a QKD signal passes via the Earth’s atmosphere, turbulence, absorption, and scattering are the three primary effects that should be considered. For low atmospheric windows (at 1550 nm), absorption loss can be hugely reduced. Absorption and scattering due to dust, haze, and water vapor particles contribute to atmospheric losses. The QKD/FSO link under different weather conditions can be represented as [39]:
Moreover, large-sized raindrops induce optical signal reflection and refraction. Mathematically, the rain attenuation coefficient, , is given as [43]:
where is the rain rate, and are coefficients depending on operating frequency and system temperature. To calculate fog attenuation, the Kruse and Kim models are used. The fog attenuation coefficient is given as [43]:
where is visibility range and is operating wavelength. Further, the scattering size distribution coefficient , as per the Kruse model, is expressed as [43]:
As per Kim’s model, the value of , is given as [43]:
In addition to this, to measure the haze attenuation, the Beer–Lambert Law is extensively utilized as below [40]:
where is the haze attenuation coefficient, and it is defined by the Kruse and Kim models as [43]:
Furthermore, the Gamma-Gamma model is generally used to measure the impact of atmospheric loss under weak-to-strong turbulence as below [44]:
where Means a Gamma function, means a modified Bessel function of order , and denote the large and small scale effective eddies (irradiance fluctuations), respectively, and means attenuation turbulence.
and
where is the spherical wave diameter and, is Rytov variance parameter.
Also, to evaluate the atmospheric turbulence strength, an index of refraction structure parameter, is used as [45]:
where is atmospheric pressure, is average temperature, and is temperature structure parameter. For weak-to-strong atmospheric turbulence, varies from 10−17 to 10−13 m−2/3. Table 3 presents the various atmosphere parameters for different weather conditions.

Table 3.
Atmospheric parameters for rain, haze, and fog conditions [46,47,48,49].
In this work, the system’s performance is investigated for the following four cases:
- Maximum achievable fiber transmission distance considering distinct weather conditions.
- Maximum achievable FSO distance considering distinct weather conditions.
- Impact of various weather conditions on system performance using diverse polarization states.
- Effect of beam divergence on the system’s performance under diverse weather conditions.
3.2. Maximum Achievable Fiber Transmission Distance Considering Distinct Weather Conditions
Figure 3a–c illustrate the maximum obtained fiber range at the distribution end to several end users in terms of quality factor at 1 Gbps under diverse weather conditions. In optical communication systems, the quality factor, or Q-factor, is a primary performance metric correlated with the signal quality as well as BER. It is defined as [50]:
where and are the mean voltages levels of bit ‘0’ and bit ‘1’, respectively. and are the standard deviations of bit ‘0’ and bit ‘1’, respectively. Also, the relationship between the BER and the Q-factor is given as . A higher Q-factor indicates a lower BER and better signal quality. While a lower Q-factor results in a higher BER, indicating increased noise.
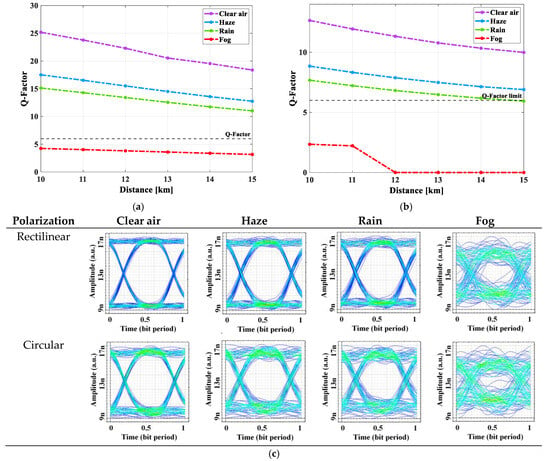
Figure 3.
Fiber range versus Q-factor considering distinct weather conditions over an FSO range of 400 m for (a) rectilinearly and (b) circularly polarized signals and (c) eye patterns at 10 km fiber range.
In an integrated fiber–FSO link, the polarization variations depend on the fiber length and absorption, turbulence-induced beam spreading, and atmospheric conditions (in FSO). Assume at the initial time, (), that the polarization bases of Alice and Bob are perfectly aligned and QBER = 0. Next, at time , the output state of an integrated fiber–FSO link is , while the state transforms into after time is caused by polarization variation. Mathematically, it is written as [51,52]:
where is perpendicular to , and are the complex amplitudes of , which are projected onto and separately, with . Thus, the QBER in terms of and , is expressed as [51]:
In this system, a polarization analyzer observes the output state of the integrated fiber–FSO link under the Stokes vector representation comprising four parameters () [51]. Meanwhile, the FSO link efficiency , considering the atmospheric conditions, is defined as [53]:
where indicates the detection efficiency, atmospheric attenuation, and pointing loss; is long-term beam width; and means the radius of the receiver telescope. As a function of polarization misalignment with Bob’s polarization axis rotated by angle (), the is defined as [53]. Moreover, in the QKD systems, rectilinear polarization usually shows better performance as compared to circular polarization owing to better alignment, high detection efficiency, and ease of implementation.
The system fiber range is obtained for both rectilinearly and circularly polarized signals over a fixed 400 m FSO link range, as shown in Figure 3a,b, respectively. It is realized that a maximum fiber range of >15 km is achieved under clear air, rain, and haze scenarios, while under foggy conditions, a distance of <10 km is achieved for both rectilinearly and circularly polarized signals. This is due to the presence of fiber non-linearities and FSO link noise. Moreover, the minimum acceptable Q-factor of 6 is achieved under clear air, rainy, and hazy conditions, whilst the worst signal quality as well as a lower Q-factor value is achieved under foggy conditions. In addition to this, it is depicted that rectilinearly polarized signals show better performance than circularly polarized signals due to the fixed alignment of the transmitter and receiver, i.e., the point-to-point link in the former, under the controlled environment conditions. It is noted that foggy conditions lead to significantly higher attenuation of incoming signals than haze, rain and clear air. Over the fixed FSO range of 400 m, the received power becomes negligible under foggy weather, with the increase in fiber distance due to the impact of fiber non-linearities and excessive attenuation under the fog (=20 dB/km) scenario compared to other conditions. Beyond a distance of 12 km, a negligible or no signal is detectable, resulting in a low Q-factor (<5) and, consequently, poor system performance under foggy conditions. However, the optical signals remain detectable under clear air (=0.22 dB/km), haze (=4.2 dB/km), and rain (=5.8 dB/km) weather conditions due to considerably lower attenuation than foggy weather conditions. This leads to a gradual degradation of received power under foggy weather conditions, while higher Q-factor values are under clear air, followed by haze and rain.
Figure 3c illustrates the corresponding eye patterns obtained for both types of polarized signals under diverse weather scenarios. Here, the open-eye patterns under clear air, rain, and haze scenarios indicate good signal integrity. However, the system operating under foggy conditions illustrates a closed-eye pattern indicating signal degradation owing to noise, jitter, and inter-symbol interference. Table 4 depicts the results obtained over an FSO range of 400 m under diverse weather conditions with fixed 10 km fiber.

Table 4.
Obtained results for different polarized signals under different weather conditions over a 400 m FSO range and fixed fiber length of 10 km.
3.3. Maximum Achievable FSO Distance Considering Distinct Weather Conditions
Figure 4 depicts the simulation results of the proposed system under different weather conditions over varying FSO ranges at a data rate of 1 Gbps, in terms of OSNR. OSNR is a measure of signal quality in the proposed system. It is defined as the ratio of optical signal power to the optical noise power. Higher OSNR indicates a high-quality signal and better system performance. In general, OSNR (in dB) is given as [33,34,35]:
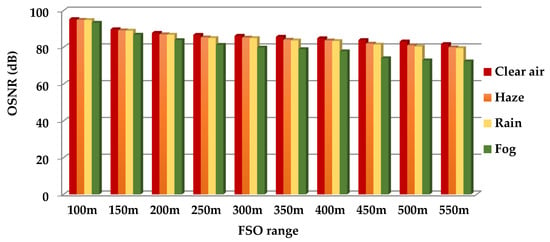
Figure 4.
FSO range versus OSNR under distinct weather conditions.
It was realized that as the signal travels through an FSO range of 100–550 m, the OSNR typically decreases with the increasing range. Also, the different weather conditions raise the attenuation, thereby reducing the signal power and diminishing the system’s performance. This signal loss across an FSO link is due to free-space path loss, the presence of turbulence, scintillation effects, pointing errors, geometric loss, and additional losses.
Here, four different weather conditions, viz. air, fog, haze, and rain, are considered. Notably, the system under clear air conditions significantly outperforms the other weather conditions, achieving maximum OSNR of 95.30 and 81.75 dB at 100 and 550 m ranges, respectively. The system performing under haze and rain conditions offers a maximum OSNR of 94.90–79.96 dB at 100 m and 94.80–79.52 dB at 550 m, respectively. On the other hand, the lowest OSNR value is observed under foggy conditions, i.e., 93.32–72.28 dB for the 100–550 m range, compared to other weather scenarios. This is illustrated by the fact that foggy weather (attenuation = 20 dB/km) causes maximum interference, which contradicts with the objective of extending the transmission range, whereas the clear air scenario maximizes the desired signal power, and thus it improves the system power gain and overall performance.
Figure 5 presents received optical spectra at an FSO range of 700 m under distinct weather conditions. The laser source emitting photons at a 193.1 THz frequency with a 5 dBm input power is shown in the figure. It is clearly seen that received power reduces to −18 dB under clear air, −19 dBm under haze, −22 dBm under rain, and −30 dB under foggy conditions with respect to an input power of 5 dBm. A significant power loss is seen under foggy conditions due to large scattering effects by fog droplets, which causes more absorption of laser light and reduced visibility. Visibility range can be mapped to attenuation coefficients (for different weather conditions) using empirical models like Kim and Kruse for link design, as shown in Equations (7) and (8).
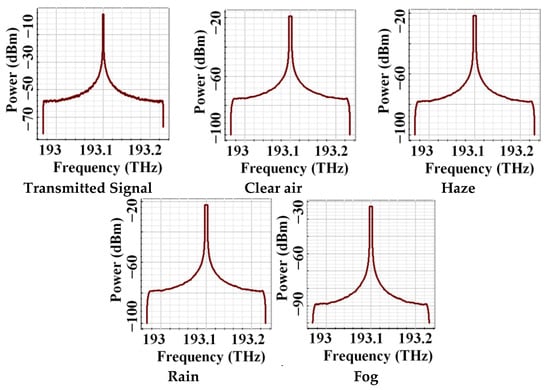
Figure 5.
Obtained optical spectra for the input laser source at an FSO range of 700 m under distinct weather conditions.
3.4. Impact of Various Weather Scenarios on System Performance Using Diverse Polarization States
Figure 6a and Figure 6b depict the received power intensity of the Stokes parameter in a polarized meter over an FSO range of 100–700 m under diverse weather conditions for rectilinearly and circularly polarized signals, respectively. Stokes parameters are used to describe polarization purity, degree of polarization, and how an atmospheric condition affects polarization. For rectilinearly polarized signals, Stokes parameter intensity ranges from −4.69 to −18.8 dBm under clear air, −5.09 to −21.59 dBm under haze, −5.25 to −22.7 dBm under rain, and −6.67 to −35.65 dBm under the fog scenario, over an FSO range of 100–700 m. As seen for circularly polarized signals, the Stokes parameter intensity decreases from −7.7 to −21.81 dBm under clear air, −8.1 to −24.62 dBm under haze, −8.26 to −25.72 dBm under rain, and −9.68 to −35.66 dBm under the fog scenario.
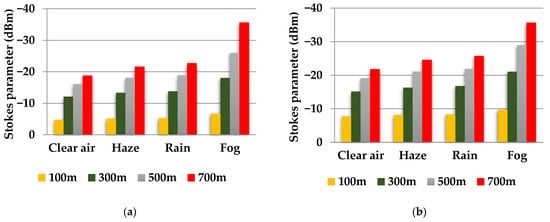
Figure 6.
FSO range versus Stokes parameter intensity for (a) rectilinearly and (b) circularly polarized signals under diverse weather conditions.
It should also be noted that linearly polarized signals (H/V) perform better than circularly polarized signals (R/L) due to the matched polarization conditions, less cross-polarization loss, higher received power, less multipath fading, and higher link reliability in the former, considering diverse weather conditions. In addition, maximum signal loss is observed under the fog scenario, followed by rain, haze, and a minimum in clear air. This is due to the presence of a higher impact of atmospheric attenuation, beam divergence, scintillation, pointing errors, and geometric loss under foggy conditions than others.
3.5. Effect of Beam Divergence on the System’s Performance in Varied Weather Conditions
Figure 7a and Figure 7b depict the obtained Stokes parameter intensity evaluated from a polarized meter over a 100 m FSO range with 2.5–4 mrad beam divergence under diverse weather conditions for rectilinearly and circularly polarized signals, respectively.
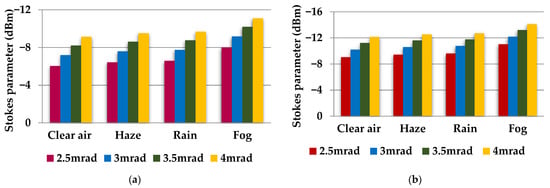
Figure 7.
Beam divergence versus Stokes parameter intensity for (a) rectilinearly and (b) circularly polarized signals under diverse weather conditions.
Notably, the maximum Stokes parameter intensity value is observed under clear air, followed by haze, rain, and the lowest in the fog scenario for both rectilinearly and circularly polarized signals. Also, a higher value for beam divergence spreads the optical beam due to diffraction, thus minimizing the power intensity at the Bob side. For this, a larger aperture receiver antenna is required to collect sufficient beams, which results in a complex system design. Figure 7a illustrates Stokes intensities ranging from −6.03 to −9.13 dBm under clear air, −6.43 to −9.52 dBm under haze, −6.59 to −9.68 dBm under rain, and −8.01 to −11.1 dBm under foggy conditions at 2.5–4 mrad divergence for rectilinearly polarized signals. In addition, the system using circularly polarized signals offers −9.04 to −12.14 dBm under clear air, −9.44 to −12.54 dBm under haze, −9.6 to −12.7 dBm under rain, and −11.02 to −14.12 dBm under the fog scenario for the same divergence, as depicted in Figure 7b.
Again, QBER is defined as the ratio of the number of incorrect bits received to the total number of bits at the Bob end. In general, QBER is given as [33]:
Assume that a total of 13 bits is transmitted at the Alice end as 1100010010011 and 1××1××1×××11× bits are received at the Bob end, where × means discarded bits. Out of these 13 bits, a total of 5 bits is correctly received out of which 2 and 3 bits are correctly received for rectilinear and circular polarization, respectively. Thus, the calculated and values are given as ~15% and ~23%, respectively.
Table 5 illustrates the comparison analysis of the proposed system with existing FSO/fiber-link-based QKD designs. It is seen that this work shows reliable data transmission over an integrated FSO–fiber link range at 1 Gbps under distinct weather scenarios.

Table 5.
Comparison analysis with existing works.
A comparison with existing works [24,25,27]—simulated sing OptiSystem/Monte Carlo approaches—reveals that the proposed system successfully achieves a reliable transmission distance of 700 m and 15 km over FSO and fiber, respectively. Although the existing works in ref. [26,28,30,33,54] offer extended fiber/FSO transmission distance than the proposed system, but they do not account for severe divergence and additional and geometric losses. Also, these existing works operate at either high input power or low data rate to attain long-reach QKD communication. Moderate to high system complexity and cost further degrade the system’s ability to support a large number of users. Thus, the proposed work presents a high-performance quantum FSO–fiber system-based BB84-QKD system at a data rate of 1 Gbps, achieving high OSNR over 700 m FSO with 15 km fiber, considering diverse link impairments as well as atmospheric conditions. While this system illustrates promising performance, it still faces limitations due to severe weather conditions (e.g., fog), larger beam misalignment, and polarization drift. These issues can be addressed in the future via adaptive beam tracking and polarization stabilization schemes to achieve resilience under real-world scenarios [55,56,57,58,59].
4. Conclusions
The aim of quantum communication lies in harnessing the quantum nature of data, which introduces both novel challenges and opportunities for constructing the infrastructure of 5G and subsequent networks. In this work, a quantum FSO–fiber communication system using the BB84-QKD protocol is simulated at a transmission rate of 1 Gbps. It is concluded that the system offers maximum OSNR of 95.30, 94.90, 94.8, and 93.32 dB under clear air, haze, rain, and fog scenarios, respectively, over a 100–550 m FSO range. The extended free-space transmission range of 100–700 m allows superior performance for the rectilinearly polarized signals with Stokes intensities of −6.67 to −4.69 dBm as compared to the circularly polarized signals, which offer lower Stokes intensities of −9.68 to −7.7 dBm under diverse weather conditions. At a fixed FSO range of 400 m, considering diverse weather conditions, the maximum 10–15 km fiber range is successfully achieved with signal power of −19.54 and −22.55 dBm for rectilinearly and circularly polarized signals, respectively. In addition, the system maintains Stokes intensities of −8.01 to −6.03 dBm and −11.02 to −9.04 dBm for rectilinearly and circularly polarized signals, respectively, for the divergence angle of 2.5–4 mrad over the 100 m FSO range. The comparative analysis of the proposed work with existing FSO-QKD systems highlights the reliability of the former for future quantum communication networks. Additionally, this investigation encompasses various aspects of quantum channels, including throughput, network capacity, energy efficiency, and data security. By integrating capacity into quantum networks, they can potentially provide enhanced mobile broadband, reliable low-latency communication, massive machine-type transmission, and tactile internet capabilities.
Author Contributions
M.K. and S.K.M. discussed and agreed upon a plan; M.K., drafted designs for the manuscript and wrote the original manuscript; S.K.M. edited the manuscript. All authors reviewed and commented on the original draft of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
S.K.M. wants to thank CTTC for providing the resources to conduct this research. This work is part of the project SOFIA PID2023-147305OB-C32 funded by MI-CIU/AEI/10.13039/501100011033 and by FEDER/UE.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chehimi, M.; Elhattab, M.; Saad, W.; Vardoyan, G.; Panigrahy, N.K.; Assi, C.; Towsley, D. Reconfigurable Intelligent Surface (RIS)-Assisted Entanglement Distribution in FSO Quantum Networks. IEEE Trans. Wirel. Commun. 2025, 24, 3132–3148. [Google Scholar] [CrossRef]
- Gümüş, K.; Frazão, J.d.R.; van Vliet, V.; van der Heide, S.; van den Hout, M.; Liga, G.; Gültekin, Y.C.; Albores-Mejia, A.; Bradley, T.; Alvarado, A.; et al. Rate-Adaptive Reconciliation for Experimental Continuous-Variable Quantum Key Distribution with Discrete Modulation over a Free-Space Optical Link. J. Light. Technol. 2024, 43, 3564–3573. [Google Scholar] [CrossRef]
- Zhou, X.; Shen, A.; Hu, S.; Ni, W.; Wang, X.; Hossain, E.; Hanzo, L. Towards Quantum-Native Communication Systems: New Developments, Trends, and Challenges. arXiv 2023, arXiv:2311.05239. [Google Scholar]
- Nawaz, S.J.; Member, S. Quantum Machine Learning for 6G Communication Networks: State-of-the-Art and Vision for the Future. IEEE Access 2019, 7, 46317–46350. [Google Scholar] [CrossRef]
- Chou, H.; Ha, V.N.; Al-hraishawi, H.; Garces-socarras, L.M.; Gonzalez-rios, J.L.; Merlano-duncan, J.C.; Chatzinotas, S. Satellite-Based Quantum Network: Security and Challenges over Atmospheric Channel. arXiv 2023, arXiv:2308.00011. [Google Scholar]
- Yuan, H.; Fowler, D.S.; Maple, C.; Epiphaniou, G. Analysis of Outage Performance in a 6G-V2X Communications System Utilising Free—Space Optical Quantum Key Distribution. IET Quantum Commun. 2023, 4, 191–199. [Google Scholar] [CrossRef]
- Chakraborty, M.; Mukherjee, A.; Nag, A.; Chandra, S. Hybrid Quantum Noise Model to Compute Gaussian Quantum Channel Capacity. IEEE Access 2024, 12, 14671–14689. [Google Scholar] [CrossRef]
- Doolittle, B.; Leditzky, F.; Chitambar, E. Operational Nonclassicality in Quantum Communication Networks. arXiv 2024, arXiv:2403.02988. [Google Scholar]
- Joshi, S.K.; Gündoğan, M.; Brougham, T.; Lowndes, D.; Mazzarella, L.; Krutzik, M.; Villoresi, P.; Mohapatra, S.; Dequal, D.; Vallone, G.; et al. Advances in Space Quantum Communications. IET Quantum Commun. 2021, 2, 182–217. [Google Scholar] [CrossRef]
- Fowler, D.S.; Maple, C.; Epiphaniou, G. A Practical Implementation of Quantum-Derived Keys for Secure Vehicle-to-Infrastructure Communications. Veehicles 2023, 5, 1586–1604. [Google Scholar] [CrossRef]
- Rezai, M.; Salehi, J.A. Quantum CDMA Communication Systems. IEEE Trans. Inf. Theory 2021, 67, 5526–5547. [Google Scholar] [CrossRef]
- Cozzolino, D.; Lio, B.D.; Bacco, D.; Oxenløwe, L.K. High-Dimensional Quantum Communication: Benefits, Progress, and Future Challenges. Adv. Quantum Technol. 2019, 2, 1900038. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Li, C.L.; Yin, H.L.; Chen, Z.B. Asynchronous Quantum Repeater Using Multiple Quantum Memory. Rep. Prog. Phys. 2024, 87, 127901. [Google Scholar] [CrossRef]
- Williams, C.J.; Tang, X.; Hiekkero, M.; Rouzaud, J.; Lu, R.; Goedecke, A.; Migdall, A.; Mink, A.; Nakassis, A.; Pibida, L.; et al. A High Speed Quantum Communication Testbed. Proc. SPIE 2002, 4821, 421–426. [Google Scholar]
- Vu, M.Q.; Member, S.; Le, H.D.; Pham, T.V.; Pham, A.T.; Member, S. Design of Satellite-Based FSO/QKD Systems Using GEO/LEOs for Multiple Wireless Users. IEEE Photonics J. 2023, 15, 7303314. [Google Scholar] [CrossRef]
- Endo, H.; Sasaki, T.; Takeoka, M.; Fujiwara, M. Line-of-Sight Quantum Key Distribution with Differential Phase Shift Keying Line-of-Sight Quantum Key Distribution with Differential Phase Shift Keying. New J. Phys. 2022, 24, 025008. [Google Scholar] [CrossRef]
- Zhao, H.; Alouini, M. On the Performance of Quantum Key Distribution FSO Systems Under a Generalized Pointing Error Model. IEEE Commun. Lett. 2019, 23, 1801–1805. [Google Scholar] [CrossRef]
- Arnon, S. Quantum Key Distribution by a Free-Space MIMO System. J. Light. Technol. 2006, 24, 3114–3120. [Google Scholar] [CrossRef]
- Kamran, M.; Khan, D.; Malik, T.; Arfeen, A. Quantum Key Distribution over Free Space Optic (FSO) Channel Using Higher Order Gaussian Beam Spatial Modes. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 3335–3351. [Google Scholar] [CrossRef]
- Harun, N.Z.; Zukarnain, Z.A.; Hanapi, Z.M.; Ahmad, I.; Khodr, M.F. MQC-MB: Multiphoton Quantum Communication Using Multiple-Beam Concept in Free Space Optical Channel. Symmetry 2020, 13, 66. [Google Scholar] [CrossRef]
- Vu, M.Q.; Le, H.D.; Pham, T.V.; Pham, A.T. Toward Practical Entanglement-Based Satellite FSO/QKD Systems Using Dual-Threshold/Direct Detection. IEEE Access 2022, 10, 113260–113274. [Google Scholar] [CrossRef]
- Hosseinidehaj, N.; Malaney, R. Quantum Key Distribution over Combined Atmospheric Fading Channels. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 7413–7419. [Google Scholar]
- Alshaer, N.; Moawad, A.; Ismail, T. Reliability and Security Analysis of an Entanglement-Based QKD Protocol in a Dynamic Ground-to-UAV FSO Communications System. IEEE Access 2021, 9, 168052–168067. [Google Scholar] [CrossRef]
- Alshaer, N.; Ismail, T. Performance Evaluation and Security Analysis of UAV-Based FSO/CV-QKD System Employing DP-QPSK/CD. IEEE Photonics J. 2022, 14, 7324911. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Le, H.T.; Pham, H.T.T.; Mai, V.; Dang, N.T. Enhancing Design and Performance Analysis of Satellite Entanglement-Based CV-QKD/FSO Systems. IEEE Access 2023, 11, 112097–112107. [Google Scholar] [CrossRef]
- Atieh, A.; Buhari, A.; Raytchev, M. QKD Over FSO Under Different Weather Conditions Using OptiSystem Software. In Proceedings of the 2023 Photonics North (PN), Montreal, QC, Canada, 12–15 June 2023; p. 10223140. [Google Scholar]
- Berikaa, E.; Cavaliere, F.; Zhang, J.; Gutiérrez-castrejón, R.; Giorgi, L.; Errico, A.D. Adapting the Classical Optical Communication Simulation Framework for Continuous-Variable Quantum Key Distribution Simulations. In Proceedings of the 25th International Conference on Optical Network Design and Modelling (ONDM 2021), Gothenburg, Sweden, 28 June–1 July 2021; pp. 1–4. [Google Scholar]
- Kundu, N.K.; McKay, M.R.; Murch, R.; Mallik, R.K. Intelligent Reflecting Surface-Assisted Free Space Optical Quantum Communications. IEEE Trans. Wirel. Commun. 2023, 23, 5079–5093. [Google Scholar] [CrossRef]
- Roy, A.; Kar, S.; Thakur, M.; Riaz, S.N.; Sarkar, S. Fabrication of Measurement Device Independent Quantum Key Distribution Protocol on Optisystem. In Proceedings of the 2023 8th International Conference on Computers and Devices for Communication, CODEC 2023, Kolkata, India, 14–16 December 2023; p. 10466195. [Google Scholar]
- Al-Mohammed, H.A.; Yaacoub, E.; Abualsaud, K.; Al-Maadeed, S.A. Using Quantum Key Distribution with Free Space Optics to Secure Communications in High-Speed Trains. IEEE Access 2024, 12, 43560–43574. [Google Scholar] [CrossRef]
- Trinh, P.V.; Pham, T.V.; Dang, N.T.; Nguyen, H.V.; Ng, S.X.; Pham, A.T. Design and Security Analysis of Quantum Key Distribution Protocol over Free-Space Optics Using Dual-Threshold Direct-Detection Receiver. IEEE Access 2018, 6, 4159–4175. [Google Scholar] [CrossRef]
- Mallick, B.; Parida, P.; Nayak, C.; Khalifa, T.; Panda, M.K.; Ali, N.; Patil, G.U.; Prasad, B. Multi-Channel Multi-Protocol Quantum Key Distribution System for Secure Image Transmission in Healthcare. IEEE Access 2025, 13, 62476–62505. [Google Scholar] [CrossRef]
- Mantey, S.T.; Fernandes, M.A.; Fernandes, G.M.; Silva, N.A.; Guiomar, F.P.; Monteiro, P.; Pinto, A.N.; Muga, N.J. On the Coexistence of Quantum and Classical Signal Transmission Over Turbulent FSO Channels. J. Light. Technol. 2025, 43, 1043–1050. [Google Scholar] [CrossRef]
- Arya, V. Realization of 32 × 4 × 40 Gbps PDM/MDM-FSO System Using Orbital Angular Momentum Beams. J. Opt. Commun. 2025, 8, 1–8. [Google Scholar] [CrossRef]
- Galaktionov, I.; Sheldakova, J.; Nikitin, A.; Samarkin, V.; Parfenov, V.; Kudryashov, A. Laser Beam Focusing through a Moderately Scattering Medium Using a Bimorph Mirror. Opt. Express 2020, 28, 38061. [Google Scholar] [CrossRef]
- Berrocal, E.; Sedarsky, D.L.; Paciaroni, M.E.; Meglinski, I.V.; Linne, M.A. Laser Light Scattering in Turbid Media Part I: Experimental and Simulated Results for the Spatial Intensity Distribution. Opt. Express 2007, 15, 10649. [Google Scholar] [CrossRef]
- Szymanski, W.W.; Mazzucco, R. Laser Beam Propagation in Multiply Scattering Droplet Aerosols-Comparison of Theoretical Models and Experimental Data. J. Aerosol Sci. 1999, 30, 6–7. [Google Scholar] [CrossRef]
- Zhang, C.; Tello, A.; Zanforlin, U.; Buller, G.S.; Donaldson, R. Link Loss Analysis for a Satellite Quantum Communication Down-Link. In Proceedings of the Emerging Imaging and Sensing Technologies for Security and Defence V; and Advanced Manufacturing Technologies for Micro- and Nanosystems in Security and Defence III, Online, 21–25 September 2020; pp. 18–29. [Google Scholar]
- Behera, S.R.; Sinha, U. Estimating the Link Budget of Satellite-Based Quantum Key Distribution (QKD) for Uplink Transmission through the Atmosphere. EPJ Quantum Technol. 2024, 11, 1–26. [Google Scholar] [CrossRef]
- Ahmad Anas, S.B.; Hamat, F.H.; Hitam, S.; Sahbudin, R.K.Z. Hybrid Fiber-to-the-x and Free Space Optics for High Bandwidth Access Networks. Photonic Netw. Commun. 2012, 23, 33–39. [Google Scholar] [CrossRef]
- Yu, S.; Ding, J.; Fu, Y.; Ma, J.; Tan, L.; Wang, L. Novel Approximate and Asymptotic Expressions of the Outage Probability and BER in Gamma–Gamma Fading FSO Links with Generalized Pointing Errors. Opt. Commun. 2019, 435, 289–296. [Google Scholar] [CrossRef]
- Niaz, A.; Qamar, F.; Ali, M.; Farhan, R.; Islam, M.K. Performance Analysis of Chaotic FSO Communication System under Different Weather Conditions. Trans. Emerg. Telecommun. Technol. 2019, 30, 1–13. [Google Scholar] [CrossRef]
- Yeh, C.H.; Xie, Y.R.; Luo, C.M.; Chow, C.W. Integration of FSO Traffic in Ring-Topology Bidirectional Fiber Access Network with Fault Protection. IEEE Commun. Lett. 2020, 24, 589–592. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Vallejo, L.; Bohata, J.; Ortega, B.; Ghassemlooy, Z.; Zvanovec, S. Wideband QAM-over-SMF/Turbulent FSO Downlinks in a PON Architecture for Ubiquitous Connectivity. Opt. Commun. 2020, 475, 126281. [Google Scholar] [CrossRef]
- Al Naboulsi, M. Fog Attenuation Prediction for Optical and Infrared Waves. Opt. Eng. 2004, 43, 319. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002; ISBN 0 521 78252 X. [Google Scholar]
- Kim, I.I.; McArthur, B.; Korevaar, E.J. Comparison of Laser Beam Propagation at 785 Nm and 1550 Nm in Fog and Haze for Optical Wireless Communications. In Optical Wireless Communications III; SPIE Press: Bellingham, WA, USA, 2001; Volume 4214, pp. 26–37. [Google Scholar]
- Andrews, L.C.; Beason, M.K. Laser Beam Propagation in Random Media: New and Advanced Topics; SPIE Press: Bellingham, WA, USA, 2023; ISBN 9781510656505. [Google Scholar]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Academic Press: Cambridge, MA, USA, 2008; ISBN 9780123743022. [Google Scholar]
- Ding, Y.-Y.; Chen, H.; Wang, S.; He, D.-Y.; Yin, Z.-Q.; Chen, W.; Zhou, Z.; Guo, G.-C.; Han, Z.-F. Polarization Variations in Installed Fibers and Their Influence on Quantum Key Distribution Systems. Opt. Express 2017, 25, 27923. [Google Scholar] [CrossRef] [PubMed]
- Khanna, A.; Majumder, S.; Jain, A.; Singh, D.K. Quantum BER Estimation Modelling and Analysis for Satellite-Based Quantum Key Distribution Scenarios. IET Quantum Commun. 2024, 5, 157–163. [Google Scholar] [CrossRef]
- Bonato, C.; Tomaello, A.; Deppo, V.D.; Naletto, G.; Villoresi, P. Feasibility of Satellite Quantum Key Distribution. New J. Phys. 2009, 11, 045017. [Google Scholar] [CrossRef]
- Roy, A.; Maitra, A.; Pal, S.K. Experimental Simulation of Two Pulses and Three Pulses Coherent One Way Quantum Key Distribution Protocol in Noisy/Noiseless and Wired/Wireless Environment. arXiv 2024, arXiv:2409.14909. [Google Scholar]
- Singh, H.; Sohi, B.A.S.; Gupta, A. Designing and Performance Evaluation of Metamaterial Inspired Antenna for 4G and 5G Applications. Int. J. Electron. 2021, 108, 1035–1057. [Google Scholar] [CrossRef]
- Singh, H. Transmission Line Modeling of Metamaterial for Different Fractional Band Width. Mater. Today Proc. 2021, 37, 3615–3619. [Google Scholar] [CrossRef]
- Silberschmidt, V.; Singh, H.; Rajput, S.; Sharma, A. Metaheuristics-Based Materials Optimization Enhancing Materials Applications; Elsevier: Amsterdam, The Netherlands, 2025; Volume i, ISBN 9780443291623. [Google Scholar]
- Singh, H. A Review on High Frequency Communication. In Proceedings of the 2021 2nd International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 7–9 October 2021; pp. 1722–1727. [Google Scholar]
- Dutta, T.; Safinezhad, A.; Zhuldybina, M.; Llamas-Garro, I.; Velázquez-González, J.S.; Sharma, A.K.; Ung, B.; Mishra, S.K. Advances in Integrated Quantum Photonics for Quantum Sensing and Communication. J. Mater. Chem. C 2025, 13, 11521–11561. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).