Abstract
Vehicular visible light communication (VVLC) with ultralow electromagnetic interference has great potential to propel the growth of the Internet of Vehicles (IoV). However, ensuring quick response times and minimal delays in VVLC is a significant challenge brought on by fast-moving vehicles. In response to this problem, we propose a heuristic optical flow scheduling algorithm. First, the optical flow scheduling problem of VVLC is built as a multi-objective optimization model considering the makespan, delay, schedulable ratio, and bandwidth utilization with non-conflict constraints. Second, an improved artificial plant community (APC) algorithm with enhanced global and local search capabilities is proposed to achieve low-delay communication for time-sensitive optical flows. Finally, a series of benchmark experiments are conducted to show that the proposed algorithm can efficiently schedule optical flows with minimal delay. The cost of this algorithm is very low, and it is suitable for deployment on edge computing platforms such as vehicles.
1. Introduction
In order to develop the Internet of Vehicles (IoV) and Vehicle-to-Everything (V2X) technology, vehicular visible light communication (VVLC) [1,2] is a major part of the rapid growth of edge computing, artificial intelligence (AI), and optical wireless communication (OWC) [3,4]. In this context, edge-enabled visible light communication (VLC) platforms are vital for accelerating the advancement of intelligent business applications involving predictive vehicular maintenance, smart transportation, and traffic monitoring [5]. Extremely low electromagnetic interference characteristics, high security, fast response speeds, short delays, and effective bandwidth usage are easy to achieve through VVLC. However, because of the high-speed mobility of vehicles, the heterogeneity and limited processing and communication capabilities of vehicular edge nodes, and the explosive growth of real-time IoV applications, ensuring quick response times and minimal delay in VVLC systems continues to be an important challenge [6,7].
Some researchers have proposed various hardware upgrade plans, i.e., time-sensitive networking (TSN) or time-sensitive optical networking (TSON), as possible approaches to satisfying the demanding real-time delay requirements of edge-enabled VVLC systems [7]. As an enhancement to optical Ethernet, TSON has recently garnered significant attention from researchers due to its ability to ensure bounded low delay and minimal jitter for time-sensitive optical flows while also accommodating best-effort traffic [8]. Furthermore, it is also widely agreed that TSN can accelerate the evolution to improved computing connection and next-generation operational efficiency [9,10]. A comprehensive set of OWC standards, including scheduled traffic enhancements, frame preemption, network management, and clock synchronization, has been established in the past decade. Among them, guaranteeing low delay through time-triggered communication based on static schedules is verified to be effective in many IoV systems [11,12].
In recent years, a lot of soft scheduling methods have been developed to establish global static schedules instead of costly hardware upgrades [8,13,14]. Queuing theory has been utilized to study end-to-end transmission delay, while network calculus has been used to evaluate the worst-case delay for time-sensitive optical flows [7]. However, one fundamental limitation of these methods is that statistical studies of transmission delay are based on hypothetical flow arrival patterns [11]. As a result, these methods are not appropriate for delay analysis in the high-speed, mobile Internet of Vehicles. Time-sensitive optical flow scheduling is often defined as a multi-objective optimization problem which cannot be solved by traditional algorithms in a finite time to obtain all exact solutions [8,14]. Although many AI solvers are capable of producing feasible scheduling solutions, their time complexity increases rapidly with the number of optical flows [3,6,13].
To support services requiring rapid response times, low delay, and efficient bandwidth utilization in the high-speed, mobile Internet of Vehicles, it is crucial to meet the demands for low-delay communication in edge-enabled VVLC systems [2,4]. Consequently, a key challenge is how to develop an efficient schedule algorithm on a vehicle computing platform with limited resources for large-scale, time-sensitive optical flows [2,14]. In this article, we propose an improved artificial plant community algorithm to address the scheduling challenges associated with time-sensitive optical flows in edge-enabled VVLC systems. Our primary contributions are as follows.
- We conduct a theoretical analysis of the multi-objective optimization problem among multiple VVLC flows, considering the makespan, delay, schedulable ratio, and bandwidth utilization with non-conflict constraints. Additionally, we provide constraints to measure conflicts between different optical flows, thereby improving the reliability of scheduling schemes.
- To address the multi-objective optimization problem in time-sensitive VVLC flows, an improved artificial plant community (APC) algorithm [15] is proposed, with enhanced global search and local search capabilities. By randomly seeding, the global search ability is improved, and by giving the optimal plant individuals more fruiting opportunities, the local search ability is enhanced. This heuristic method intelligently determines whether efficient schedules may be used or searches for optimal scheduling solutions.
- To test the performance, we propose a benchmark test set and conduct a series of benchmark experiments for VVLC flow scheduling. The outcomes of the experiments show that the proposed APC algorithm can efficiently ensure a low makespan and delay, a high schedulable ratio and bandwidth utilization, quick response times, and low computation overheads.
The rest of this article is organized as follows. Section 2 presents a summary of relevant work. In Section 3, we explain the problems to be solved. Section 4 provides an overview and thorough description of the proposed scheduling methods. Section 5 offers a benchmark test set and performance ratings. This article concludes in Section 6.
2. Related Works
The rapid development of time-sensitive applications has put forward increasingly high requirements for the Internet of Vehicles, such as a larger data transmission volume, higher security, faster transmission speed, and lower electromagnetic interference [2]. Recently, wireless optical communication, a technology that utilizes light waves to transmit data, has attracted attention [4,16]. Compared to traditional electromagnetic wave communication, wireless optical communication has higher spectral efficiency and security, while providing greater bandwidth and speed [17]. Among them, visible light communication uses flickering signals emitted by objects such as fluorescent lamps or light-emitting diodes (LEDs) to transmit information [18]. The frequency of visible light ranges from 400 THz (wavelength: 780 nm) to 800 THz (wavelength: 375 nm). When VLC was used for vehicles, VVLC was born [1,2].
However, VVLC is different from the static environment of traditional indoor visible light communication, as vehicles often move at high speeds, leading to rapid changes in network topology [9,10]. The rapid development of time-sensitive applications has often focused on TSON hardware upgrading and scheduling to address these challenges. Current TSON traffic scheduling methods include two main approaches, i.e., Quality of Service (QoS) [19,20] and Time-Aware Shaper (TAS) [12]. The QoS model seeks to assure the QoS of time-sensitive optical flows; for example, network calculus can be applied to optimize delay and packet loss [20]. The TAS model seeks to solve the scheduling problem using the satisfaction modulo theories; i.e., off-the-shelf solvers are used to calculate static TAS schedules [12]. In TSON, interactions with other concurrently scheduled optical flows also affect flow delay. The multi-objective optimization of optical flow scheduling and routing is employed in an effort to address this problem, where both the optical flow routes and schedules are determined simultaneously, although updates are required when network structures change or new optical flows are introduced [21,22].
In addition to expensive hardware upgrade solutions, software improvement methods have attracted much attention for their low cost and minimal impact on the structure of the original system. Time-sensitive software-defined networks (SDNs) enable the scheduling of both time-sensitive and best-effort flows within the same SDN framework [23]. In this architecture, a logically centralized controller is used to address the global scheduling problem. In addition, integer linear programming (ILP) is often utilized to address routing and scheduling challenges, allowing terminals to schedule user packets with great precision [24]. Many AI algorithms are used to optimize scheduling with a focus on minimizing time complexity, i.e., deep reinforcement learning (DRL) [3,6,25], particle swarm optimization (PSO) [14], the cat swarm optimization (CSO) algorithm [20], ant colony optimization (ACO) [21], the genetic algorithm (GA) [26], artificial bee colony (ABC) [27], and the marine predators algorithm (MPA) [28]. Recently, the joint optimization of optical flow scheduling and routing has been proposed, which takes into account the schedules of different optical flows at routing nodes in order to achieve end-to-end low delay [29].
The computational constraints of vehicles are also an important factor that makes challenges difficult to solve. As the VVLC progresses towards enhanced operational efficiency and computing connectivity, a significant volume of time-sensitive tasks must be offloaded to edge nodes for processing and analysis [30]. Due to the limited computing power, storage capacity, and energy supply of the computing platform carried by the vehicle, it is required that the solving algorithm on VVLC has higher solving efficiency and lower computing cost. Heuristic algorithms often have simple parameters and low computational costs and are suitable for searching solutions with comparatively less time complexity [8,31,32]. Considering the high mobility of vehicles, the delays resulting from computation between time-sensitive optical flows on the same port have been infrequently noticed [29]. Many studies primarily focus on scheduling analysis within simple network topologies, such as automotive in-vehicle networks and business networks, without considering the delay caused by computing power [25,27,33].
According to a survey of existing VVLC studies, the models and benchmark test sets in this field are also incomplete. In several studies, the scheduling and routing of optical flows in TSON are typically treated as programming issues with restrictions or as optimization problems aimed at minimizing end-to-end delays [14,20]. While other researchers have focused on delay guarantees via scheduling and routing algorithms, they frequently lack a theoretical analysis of the key aspects contributing to TSON flow delays and fail to address application difficulties with computing power [11,12]. It is important to theoretically examine the multi-objective optimization of time-sensitive optical flows and to conduct benchmark tests to justify scheduling applications. In addition, the testing indicators chosen by different scholars also vary greatly, such as only focusing on total bandwidth utilization or energy consumption [34].
Therefore, the following research gaps are also the research motivation of this article. Firstly, it is challenging to meet the stringent delay requirements of time-sensitive VVLC applications in high-speed moving vehicles while also fulfilling performance requirements for delay and total bandwidth utilization. Secondly, it is challenging to design an efficient algorithm to solve the multi-objective optimization of multiple optical flows on edge devices of vehicles with limited computing and storage resources. Optimizing scheduling for a large number of time-sensitive optical flows in edge-enabled VVLC systems presents a significant challenge, especially the mandatory decentralized resolution for these optical flows leading to an exponential increase in problem scale. Thirdly, it is challenging to provide a benchmark test set and test an effective scheduling algorithm on the delay requirements for time-sensitive optical flows and solving performance in edge-enabled VVLC systems.
3. Problem Description
In edge-enabled VVLC systems, multiple time-sensitive optical flows are inevitably scheduled and forwarded through the same VVLC data routing. To ensure efficient forwarding, dedicated time slots are typically reserved in advance for time-sensitive optical flows, while the remaining bandwidth is allocated for best-effort traffic. Optimizing optical flow scheduling in edge-enabled VVLC requires a mathematical analysis of the multi-objective optimization of multiple time-sensitive optical flows and the residual bandwidth utilization issues.
3.1. Notation Definition
In VVLC, numerous applications require end-to-end communication with strict guarantees for delay and reliability. These optical flows, characterized by bounded low delay and minimal jitter, are referred to as time-sensitive optical flows. However, meeting the requirements of one time-sensitive optical flow may compromise the requirements of another. Therefore, a mathematical model of the multi-objective optimization of multiple optical flows is necessary before designing an efficient scheduling algorithm.
The main notations for the optical flow scheduling problem of VVLC are defined in Table 1. The implementation of optical flow scheduling is directly impacted by the multi-objective optimization of optical flows. For many time-sensitive optical flows between an LED node and an end node, optimal optical flow scheduling typically requires satisfying two requirements, i.e., minimizing the forwarding delay of the optical flows and strictly maintaining the original periodicity of the optical flows during scheduling.

Table 1.
Definition of main notations.
3.2. Optical Flow Scheduling Model of VVLC
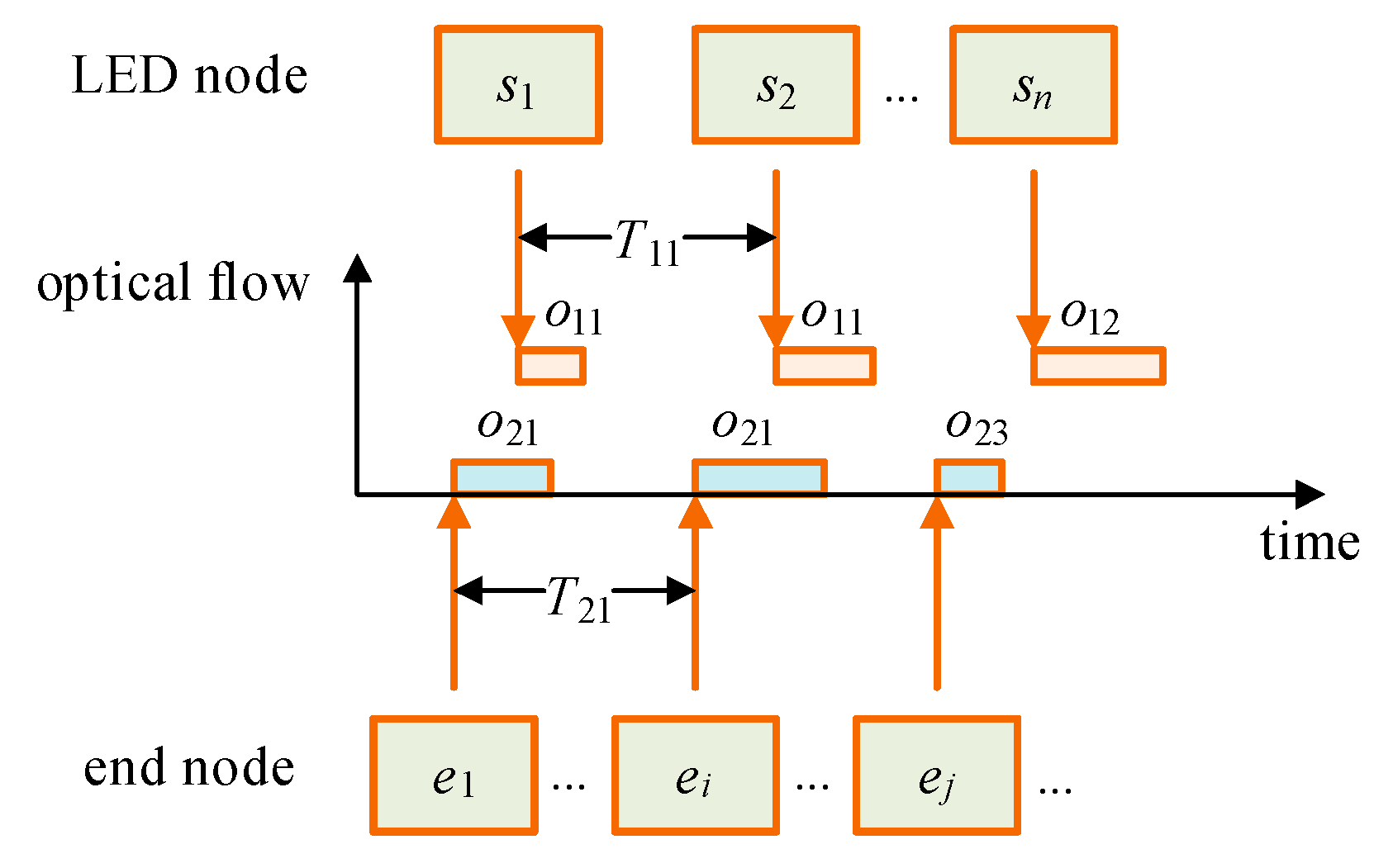
The optimal scheduling for two time-sensitive optical flows is shown in Figure 1. There is a set of LED nodes and a set of terminal nodes . For ideal scheduling, each packet in an optical flow must be prepared before the reserved time slot, with delay kept as low as possible. On the time axis in Figure 1, optical flows and have two different periods, i.e., and . At the same time, the reserved time slots for packets should not overlap in the time domain.
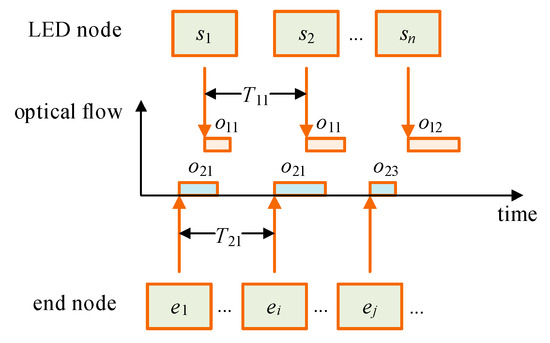
Figure 1.
Time-sensitive flows in VVLC.
Figure 1 is a typical VVLC network, which implements flow scheduling for time-sensitive TSON applications. It can be characterized as a graph G = {V, E}, where V represents the collection of vertices, i.e., LED nodes and end nodes, and E represents the set of directed edges, i.e., time-sensitive optical flows. Each directed edge represents a physical link between LED nodes and end nodes. Considering dynamic node positions and link instability in realistic VVLC scenarios, each directed edge can be described as a probabilistic channel model.
An end-to-end unicast or multicast network flow from one end node to another via LED nodes , expressed as , can be considered as a tuple. A tuple is denoted by a set , where is the directed subgraph that describes a probabilistic channel model from to via LED nodes, where the symbol above the arrow represents the probability of the link; is the set of emerged time offsets when a flow passes through the egress ports of all LED nodes; and is the set of all packets in the flow. For an intermediate LED node , the set of input flows is expressed as a probabilistic channel model , and the set of output flows is a probabilistic channel model , where the symbol above the arrow represents the probability of the link.
To ensure the efficiency of optical flow scheduling, time slots must first be allocated to all packets in each time-sensitive optical flow. The remaining time slots can then be utilized by best-effort optical flows, but this mandatory allocation method inevitably leads to the fragmentation of the residual time slots. In traditional scheduling methods such as priority strategy (PS) and round-robin, the schedulability of optical flows is determined solely by the remaining bandwidth, as it is continuously concentrated in the time domain. In contrast, for optical flow scheduling, the remaining bandwidth is typically dispersed in the time domain. If the length of a packet to be scheduled does not align with the size of a residual time slot, that time slot may be wasted or only partially used. Therefore, to enhance the utilization of the remaining bandwidth, it is essential to consider the characteristics of VVLC optical flows.
According to transfer power for a single packet in an optical flow and transfer time for a single packet in an optical flow , transfer energy consumption of a single packet in an optical flow can be obtained as their product .
Similarly, according to the packet processing power of an optical flow and the packet processing time of an optical flow , processing energy consumption of a single packet in an optical flow can be obtained as their product .
Then, according to transfer energy consumption and processing energy consumption, the energy consumption of an optical flow can be calculated as their sum, as shown in Equation (1).
Jitter is defined as the difference between the highest and minimum delays; hence, larger jitter indicates less consistent performance, as defined in Equation (2).
3.3. Conflicts Between Optical Flows
To simplify the analysis, it is assumed that the smallest time unit is 1, and all time variables in VVLC are integers. It is assumed that there is , so the conflicting constraint for the flows and can be defined as an optimization objective function. There is
where and denote the departure time of the first packets in the flows and , respectively; and represent the arrival time of the first packets; and are the periods of and , respectively; and denote the accumulated delays; denotes the accumulated jitters; and and are the processing times of packets in and , respectively. and refer to the transfer times for packets in and at the egress port, respectively.
Ideal VVLC scheduling can effectively diminish delays and jitters by ensuring that the th packet in optical flow is forwarded within the time slot , thereby maintaining uniform delay for all packets within the same optical flow. However, whether multiple optical flows can be ideally scheduled simultaneously requires further analysis, as loss between optical flows may arise.
Conflict between two optical flows and will arise if there exists insufficient transfer time, which can be defined by two positive integers (a, b).
This can be described as insufficient transfer time (ITT) conflict, which means that the departure time of the first packet in an optical flow is earlier than the sufficient transfer time .
In addition, conflict between two optical flows and may also arise if there exists departure time synchronization.
This can be described as departure time synchronization (DTS) conflict, which represents time synchronization between the departure time of the first packet in an optical flow and the departure time of the first packet in another optical flow .
In the absence of both DTS and ITT, multiple optical flows can be scheduled concurrently, enabling optimal scheduling. According to Bezout’s theorem [28], for any two flows and
, if and , then make true. Therefore, is true and ITT occurs. If , make true, and therefore, DTS occurs.
For the flows and , if DTS occurs, then the number of pairs of packets with DTS can be expressed as a set, that is,
where is a particular number of pairs of packets with DTS from and . For the flows and , if their periods and are coprime , DTS conflict occurs, and if or , ITT conflict occurs.
Given two flows and , if DTS occurs, make Bezout’s equation [28], , true. The complete solution of the equation can be achieved as follows:
Suppose all the conditions for two optical flows with DTS or ITT are satisfied. If DTS occurs, then make true. There is , and thus , which implies . Consequently, multi-objective optimization of two time-sensitive optical flows is available if the following conditions are satisfied:
where there are two time-sensitive optical flows, namely , and there is transfer time constraint, namely . Therefore, if DTS occurs, the condition cannot be satisfied. Similarly, it can be shown that if ITT occurs, the condition is also not satisfied.
For time-sensitive optical flows, if , DTS occurs, and if , ITT occurs. When any two optical flow periods are coprime, the most unfavorable situation for K time-sensitive optical flows occurs, leading to DTS for the of optical flows. A system of linear equations with an integer solution space can be used to describe this scenario. Furthermore, non-collision multi-objective optimization of K time-sensitive optical flows is possible if the following conditions are met:
where there is ; there are two time-sensitive optical flows, namely ; and there is transfer time constrain for non-collision multi-objective optimization, namely . If both the conditions are satisfied, then there must exist a set that ensures the satisfaction of non-collision multi-objective optimization.
3.4. Multi-Objective Optimization Model of VVLC
Multi-objective optimization indicates that optical flows in VVLC are sent over the same directed edge with non-conflict. Here, the multi-objective optimization model of optical flow scheduling regards the main business objectives, i.e., makespan, delay, schedulable ratio, and bandwidth utilization.
Objective 1 is the makespan, which represents the minimum of the maximum completion time of the optical flow scheduling system—specifically, the end time of the last optical flow should be as short as possible.
Objective 2 is the accumulated delay, which aims to minimize the delay time of the optical flow scheduling system as much as possible.
Objective 3 is the schedulable ratio, which indicates the proportion of optical flows that can be successfully scheduled in a VVLC system. The larger the value, the better, with a maximum value of 1. Each optical flow has different waiting times during the scheduling process due to different scheduling orders. Considering the highly dynamic environment of VVLC, if an optical flow can complete scheduling within a short waiting time (such as five optical flow scheduling cycles), it is considered a successful scheduling. Otherwise, if the waiting time is too long or exceeds the time limit (such as more than five optical flow scheduling cycles), it will be considered a scheduling failure. Assuming that in a VVLC system, the total number of optical flows that need to be scheduled is , and the total number of successfully scheduled optical flows is , then objective 3 can be achieved.
Objective 4 is the bandwidth utilization, which refers to the ratio between the actual bandwidth used in the VVLC network and the maximum transmission rate of the network. Similarly, the larger the value, the better, with a maximum value of 1.
According to objective 1 regarding the makespan in Equation (8), objective 2 regarding the accumulated delay in Equation (9), objective 3 regarding the schedulable ratio in Equation (10), and objective 4 regarding bandwidth utilization in Equation (11), the multi-objective optimization model of optical flow scheduling in VVLC can be built as
3.5. Integer Solution Space of VVLC
Due to the fact that the objective function in Equation (14) contains multiple conflicting objectives, it is difficult to solve. This equation can be simplified to facilitate the solution and improve the solution speed on edge computing devices. For time-sensitive optical flows, when two optical flows have coprime periods, it is the worst schedule and will result in DTS for the of optical flows. Then, Equation (14) can be expressed as an integer solution space for a collection of linear equations. There is
where
The integer solution space for Equation (15) can be described as a schedule with both a nonhomogeneous specific solution and a homogeneous general solution. There is
To solve Equation (15), for the scenario where DTS occurs between two optical flows (), the integer solution can be derived using a recursive method, which can be given as
It can be used to determine the form of the integer solution space for n − 1 linear equations. To solve n linear equations, there is
Therefore, the solution can be calculated as
The solution space of Equation (15) can be determined by Equation (19). In particular, Equation (19) has an integer solution space when there is a full synchronization of ITT between optical flows. There is
where represents the overlap length in the time domain, and must be nonzero; if it is zero, it indicates the presence of a complete optical flow collision of DTS. According to Equation (21), can be obtained:
Then, the nonhomogeneous particular solutions to the coefficient variables and are represented by , and . The solutions for and are given as
For K time-sensitive optical flows, it is prone to a complete optical flow collision of DTS between of optical flows when two optical flows have coprime periods. This happens at intervals of . Since and are coprime, Equation (21) can be rewritten as follows:
Finally, the integer solution space of Equation (18) can be obtained:
where and represent the particular solutions of the th equation in Equation (26) and the corresponding coefficient variable in the th recursive calculation, respectively.
4. An Improved Artificial Plant Community Algorithm
Since the objective function in Equation (14) contains multiple conflicting objectives, traditional algorithms struggle to solve it. Time-sensitive optical flows have strict delay limits, but the vehicle edge computing platform only has very limited computing resources and storage resources. The allocation of time slots for time-sensitive optical flows is challenging to achieve these delay constraints on vehicle edge computing platforms. To solve this issue, an improved artificial plant community algorithm is specifically designed for VVLC optical flow scheduling.
4.1. Methodologies
The proposed APC algorithm for VVLC optical flow scheduling has three basic operations, i.e., seeding, growing, and fruiting. Correspondingly, an artificial plant individual has three forms, i.e., a seed, an individual, and a fruit. A seed has a certain probability of growing into an individual, but it may also die. A growing individual can bear more fruits, which may grow as seeds around the individual or have a certain probability of spreading to distant places as seeds. These three basic operations bring global search ability, the ability of survival of the fittest, and local search ability to artificial plant communities, respectively.
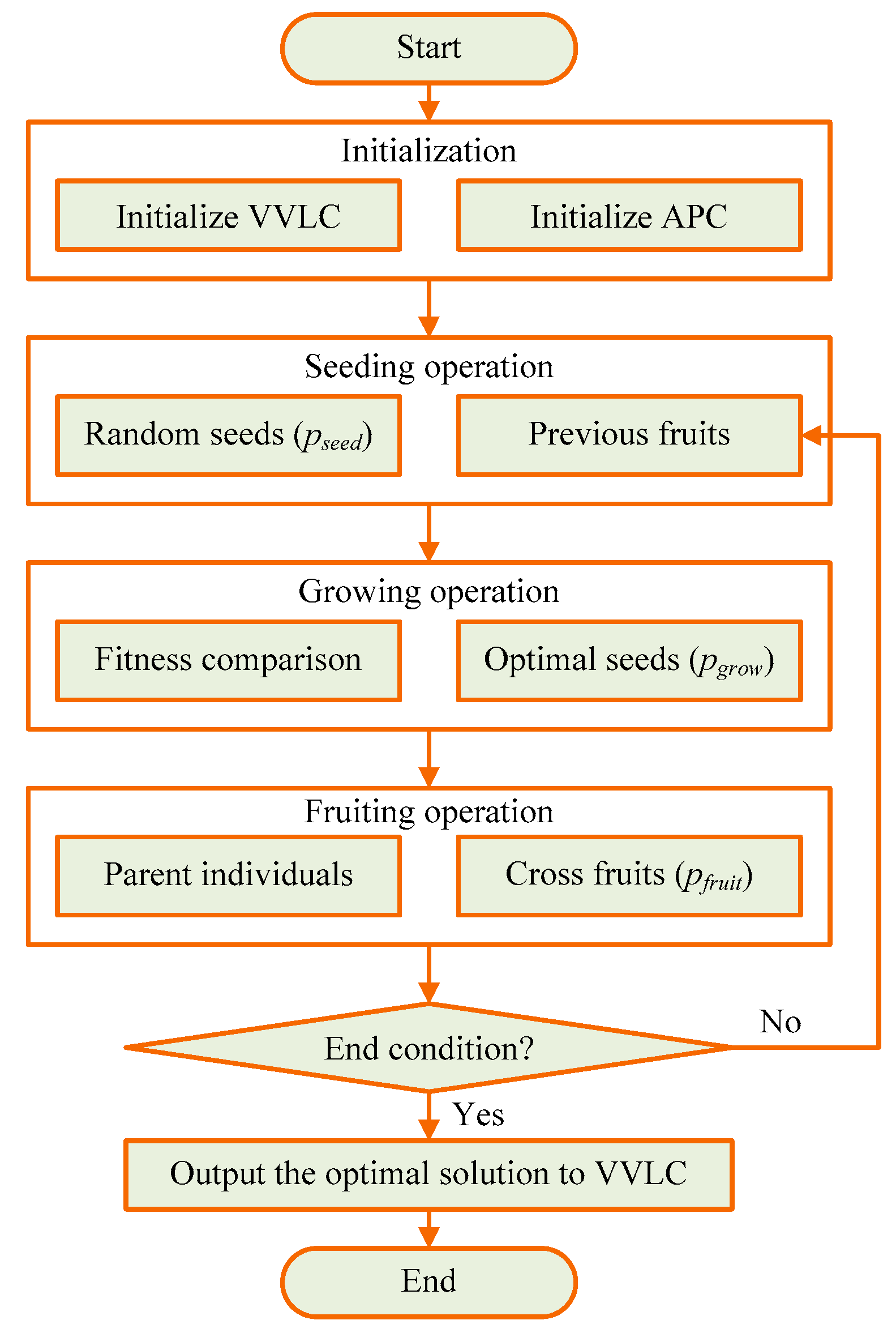
The APC algorithm employs five main steps to solve the optical flow scheduling problem, i.e., initialization, seeding, growing, fruiting, and end justification.
Step 1. Initialization
This step involves initializing primary solving system parameters, i.e., the optical flow scheduling problem and the APC algorithm.
The parameters that need to be initialized for an optical flow scheduling problem include the VVLC nodes, a set of optical flows , the period of an optical flow , the LED node number in TSON, the end node number in TSON, the optical flow number from a node to a node , the bandwidth of an optical flow , the bandwidth of the directed edge, the transfer time for a single packet in an optical flow , the packet processing time of an optical flow in the LED node, and the delay constraints for the optical flows in .
The parameters that should be initialized for an APC algorithm include the population size , the seeding probability , the growing probability , and the fruiting probability . The fitness function , of APC can choose the optimization objective function in Equation (14) or the integer solution objective function in Equation (15).
where is a coefficient that constrains fitness within a range, making it easy to solve, such as the range [0, 100]. is a positive constant to obtain a positive fitness value for an APC algorithm, and .
Step 2. Seeding of APC
The seeding step provides global search ability for the APC algorithm, where it will randomly generate seeds in the whole solution space. The global search ability is determined by a seeding probability ].
In each iteration, the population of the seeds consists of two parts: one is random seeds to provide the global search capability with a seeding probability , and the other is the previous fruits to provide the local search capability with a probability .
The population size of seeds is . At the first iteration , there are no fruits: . All seeds are randomly generated with a population size of .
Step 3. Growing of the APC
The growing process can help provide the ability of survival of the fittest for the APC algorithm, where it will select the optimal seeds to grow by a growing probability ]. According to the fitness function in Equation (22), the population size of the growing individuals will decrease. Hence, the population size of growing individuals is .
Step 4. Fruiting of the APC
The fruiting stage can help provide local search ability for the APC algorithm, where the growing individuals will produce more solutions . The population of fruits also includes two parts: one is the growing individuals with a population size —that is, the single sex reproduction of the parent—and the other part is the crossing fruits of growing individuals with a population size —that is, cross-generational reproduction—because growing individuals may have been preserved many generations ago. The latter is determined by a fruiting probability ], which determines how much original information a growing individual can retain. It is assumed that there are two parents, and , and they can generate two fruits. There is
where the symbol ‘//’ represents concatenating two strings.
Considering two parts of the fruit, namely the complete copy of the growing individuals in Equation (27) and the crossover of the growing individuals in Equation (30), the total population size of the fruit has doubled. Therefore, the equation for the overall fruit can be rewritten as
Step 5. End Justification
The end justification can consider the maximum number of iterations , the error threshold , or the maximum solving period . If the APC algorithm detects that any of the end conditions are met, then the iteration can be stopped, and the optimal solution can be output. Otherwise, the fruits will be returned to step 2 as the seeds for the next iterative computation until the end justification is met.
Figure 2 presents the flowchart of the proposed APC algorithm. If the error threshold is met, an optimal scheduling mechanism can be achieved. Otherwise, the artificial plant community will return and restart the next round of iterative calculations, including seeding, growing, and fruiting. It can be seen that the computational complexity of this algorithm is , where is the number of optical flows. Its convergence speed is linearly proportional to the number of optical flows, and it still has a good convergence speed when the number of optical flows is large.
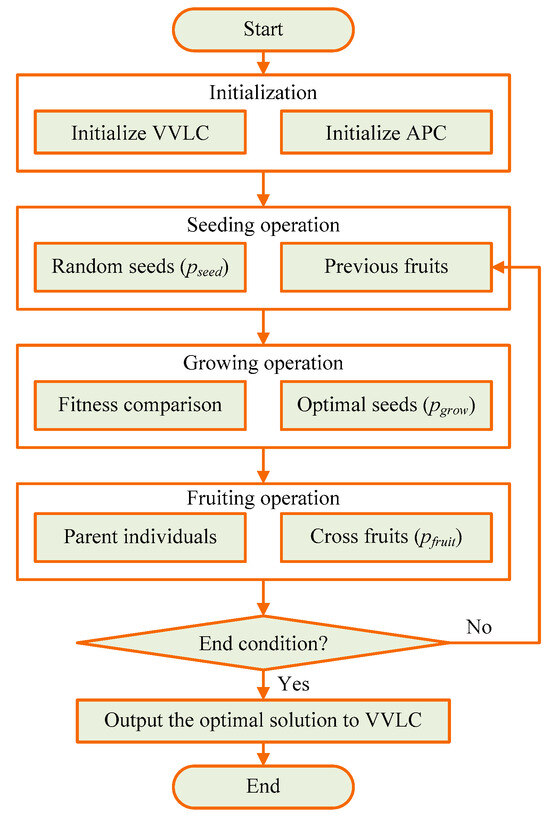
Figure 2.
The flowchart of the proposed APC algorithm.
Based on the engineering application of VVLC, two types of APC scheduling will be considered in the following two subchapters, i.e., static APC scheduling and dynamic APC scheduling.
4.2. Static APC Scheduling
A static environment is just a special case of dynamic APC scheduling, but considering the scheduling in this special case can help to reduce the computing overheads, reduce the energy consumption of edge computing devices, and improve their operation duration. For example, in the event of a vehicle malfunction, traffic accident, waiting at a red light, or maintaining a fixed speed with surrounding vehicles, it is possible to maintain a static LED/end node and stable communication link within a given time. At this time, the algorithm can be refined to reduce computation and energy consumption, which is extremely helpful for faulty vehicles or vehicles with insufficient power. For static scheduling, some assumptions are made to simplify analysis.
First, it is assumed that all LED nodes and end nodes are static, and their positions are fixed at a certain time. All LED/end nodes act as rational, self-interested agents, each one aiming to maximize its own data transmission.
Second, it is assumed that the communication links between all LED nodes and end nodes are static, and their communication parameters are fixed at a certain time.
Third, the movement of vehicles does not affect the positions and communication links of LED/end nodes at a certain time. Hence, optical flow delay coexists alongside uncertain delay.
Finally, the total bandwidth utilized by all time-sensitive optical flows is static and cannot exceed the bandwidth of a directed edge. If a packet is dropped at any node, the corresponding LED/end node needs a delay to reschedule it for the next communication.
If Equation (8) is met, for a given optical flow set containing time-sensitive optical flows, the static scheduling algorithm can help us search for the optimal solutions. Once is obtained, the static schedules can be directly computed. For instance, when the th packet of optical flow in a queue is ready for transfer, the queue’s outlet will open during the time slot . If Equation (8) is not met, it is very difficult for traditional scheduling methods to solve, since relaxed delay jitter constraints must be generated. On the one hand, to resolve loss between optical flows, it is not easy for traditional scheduling methods to search the relaxed constraints on delay jitters. The final static schedule is determined for a cycle that corresponds to the least common multiple of the periods of the optical flows in the set . On the other hand, if either DTS or ITT is unavoidable, it is necessary to divide the optical flow set into several subsets. To minimize the occurrence of DTS and ITT, it is challenging for traditional scheduling methods to realize non-conflict scheduling in each subset, even if all relevant conditions are satisfied.
To address the challenges in static scheduling, an improved version of the APC algorithm described in Section 4.1 is introduced here, and static APC scheduling calculation is outlined in Algorithm 1. This static APC scheduling strategy not only decreases scheduling time complexity, but it also makes it easier to meet delay or jitter criteria. The optical flow set needs to be divided into several subsets, and optical flows that match the criteria for multi-objective optimization should be combined into a single subset. This static APC scheduling will search for each subset of to include as many combinable optical flows as possible.
In Algorithm 1, the inputs include a set of optical flows , the period of an optical flow , the LED node number in TSON, the end node number in TSON, optical flow number from a node to a node , the bandwidth of an optical flow , the bandwidth of the directed edge, the transfer time for a single packet in an optical flow , the packet processing time of an optical flow in the LED node, and the delay constraints for the optical flows in .
| Algorithm 1. Static APC scheduling | |
| Input: , , , , , , . | |
| Set: , . | |
| Output: . | |
| 1: | |
| 2: | then |
| 3: | |
| 4: | else |
| 5: | |
| 6: | } |
| 7: | |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | |
| 13: | |
| 14: | then return to line 5 |
| 15: | end if |
| 16: | end for |
| 17: | |
The APC algorithm initially sets the population size , the seeding probability , the growing probability , the fruiting probability , the fitness function , the maximum number of iterations , the error threshold , and the maximum solving period . For an LED/end node, a packet from a queue is selected for transfer if the queue is ready and the node is free. If a packet in queue is marked as ready for transfer, the strategy is denoted as ; otherwise, it is . This strategy is subject to the constraint , or 1.
4.3. Dynamic APC Scheduling
If the vehicle’s motion and communication status at each moment are considered static, such as meeting the four assumptions in Section 4.2, static APC scheduling is very effective. However, if the vehicle is moving at high speed and the assumptions in Section 4.2 are no longer met, the optimal solution for static scheduling may not be applicable for the next VVLC. On the one hand, the optimal solution derived from the previous transmission of a time-sensitive optical flow within its reserved time slot may become overweight in the next transmission. On the other hand, time-sensitive optical packets may be subject to interference from other emerging transmissions. To address the challenges posed by highly dynamic environments to VVLC, a dynamic APC scheduling strategy is proposed here (Algorithm 2).
| Algorithm 2. Dynamic APC Scheduling | |
| , , , , , , . | |
| , . | |
| . | |
| 1: | |
| 2: | |
| 3: | |
| 4: | |
| 5: | i |
| 6: | |
| 7: | |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | |
| 13: | |
| 14: | then return to line 2 |
| 15: | end for |
| 16: | |
The dynamic APC scheduling strategy is intended to search for the optimal solution to meet the delay requirements of time-sensitive optical flows by frequently examining the dynamic environment. The mandated assignment of bandwidth to these optical flows will result in the fragmentation of residual time slots, which makes it difficult to improve overall bandwidth utilization. The dynamic APC scheduling method employs a heuristic search to dynamically fit the requirements inside the remaining slots.
The dynamic APC scheduling method for time-sensitive optical flows at LED/end nodes is determined not only by the current available time slots and packets queued for transmission but also by the upcoming transmission requirements displayed by the surrounding nodes. Furthermore, the number of packets in a queue ready for transmission may be affected by the present status as well as the optical flows arriving from surrounding nodes in subsequent periods. To overcome this complexity, the proposed APC algorithm solves with minimal computation and parameters, making it more suitable for VVLC with limited computing and storage resources than traditional algorithms.
5. Simulation Results and Analysis
In this section, a benchmark experiment is provided to show how the proposed APC algorithm searches for the solution. Some SOTA algorithms are also introduced to evaluate and compare the performance of VVLC scheduling.
5.1. Experiment Setup
The benchmark experiment is based on the test set in [32], which replicates actual business scenarios by referring to the flow features defined in IEC/IEEE 60802 [35]. Reference [32] divides flows into three even groups with the periods 0.5 ms, 2 ms, and 5 ms, where the packet sizes of these flows range from 64 to 512 bytes. IEEE standard for short-range optical wireless communications was defined in IEEE Std 802.15.7a™-2024 [36], where an interframe space (IFS) is defined to provide spacing between adjacent frames. The standard provides three types of interframe space: long (LIFS), short (SIFS), and reduced (RIFS). Correspondingly, there are three cycles: 400, 120, and 40 optical clocks. PHY I operating modes are also defined in the standard to provide two optical clock rates, i.e., 200 and 400 kHz. Therefore, it can be calculated that there are six cycles, 2.0, 1.0, 0.6, 0.3, 02, and 0.1 ms. Additionally, the standard defined the average brightness per display frame time, and one frame time = 1/60 s, where a time slot contains 260 bytes of header and data. Considering IEEE Std 802.15.7a™-2024 [36] and the delay of time-sensitive optical flows [1,2], our benchmark experiment made some necessary adjustments to the benchmark data set in [32], such as using six optical flow cycles for dynamic scheduling, smaller packet size, and the optical flow number ranging from 100 to 500. Our benchmark test set is shown in Table 2.

Table 2.
Benchmark test set.
The benchmark test set in Table 2 is more suitable for the dynamic scheduling of time-sensitive optical flows, since packet sizes range from 32 to 256 bytes, with periods of 2.0, 1.0, 0.6, 0.3, 0.2, and 0.1 ms. The ratio of fluxes with different times is roughly 1:1:1:1, and packet arrival times are produced at random. Table 2 can be used to assess the algorithm’s performance under varied business situations, i.e., examining delay throughout five to one hundred optical flows on a single directed edge. To validate the algorithm’s performance, objective 1 regarding makespan in Equation (10), objective 2 regarding accumulated delay in Equation (11), objective 3 regarding the schedulable ratio in Equation (12), and objective 4 regarding bandwidth utilization in Equation (13) are employed to assess optical flow scheduling.
Experiments were run on an AMD Ryzen 3 4300U with Radeon Graphics, a 2.70 GHz CPU, 8.00 GB of RAM, and a 64-bit Windows 10 operating system and MATLAB R2018a simulation software.
In the benchmark experiment, the proposed APC was tested and compared with some SOTA algorithms, including DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. For the sake of fair comparison, all algorithms employed a basic version and the same population size. For the APC algorithm, the population size S = 100, the seeding probability , the growing probability , and the fruiting probability .
For DRL [3,6,25], the parameters included a convolutional neural network with eight convolution cores, eight input channels (cin = 8), and eight output channels (cout = 8). The learning rate of the offset item was twice that of the weight. The extension edge was set to 0, the weight was initialized to Gaussian, and the value of the constant offset item was 0. The PSO [14] set the population size to S = 100, the location limitation to 0.5, the speed limitation to [−0.5, 0.5], the self-learning factor to c1 = 1.5, and the social learning factor to c2 = 1.5. The parameters of ACO [21] were set as follows: population size S = 100 ants, the importance of heuristic factors = 5.0, the pheromone volatilization factor = 0.1, and the pheromone importance = 1.0. The GA [26] set the population size to S = 100, the chromosome length to Lind = 20, the crossover probability to px = 0.7, and the mutation probability to pm = 0.01. For ABC [27], the parameters included the population size of bees S = 100, the searching capability limit = 100, and the neighborhood size NI = 10.
5.2. Benchmark Test of the APC Algorithm
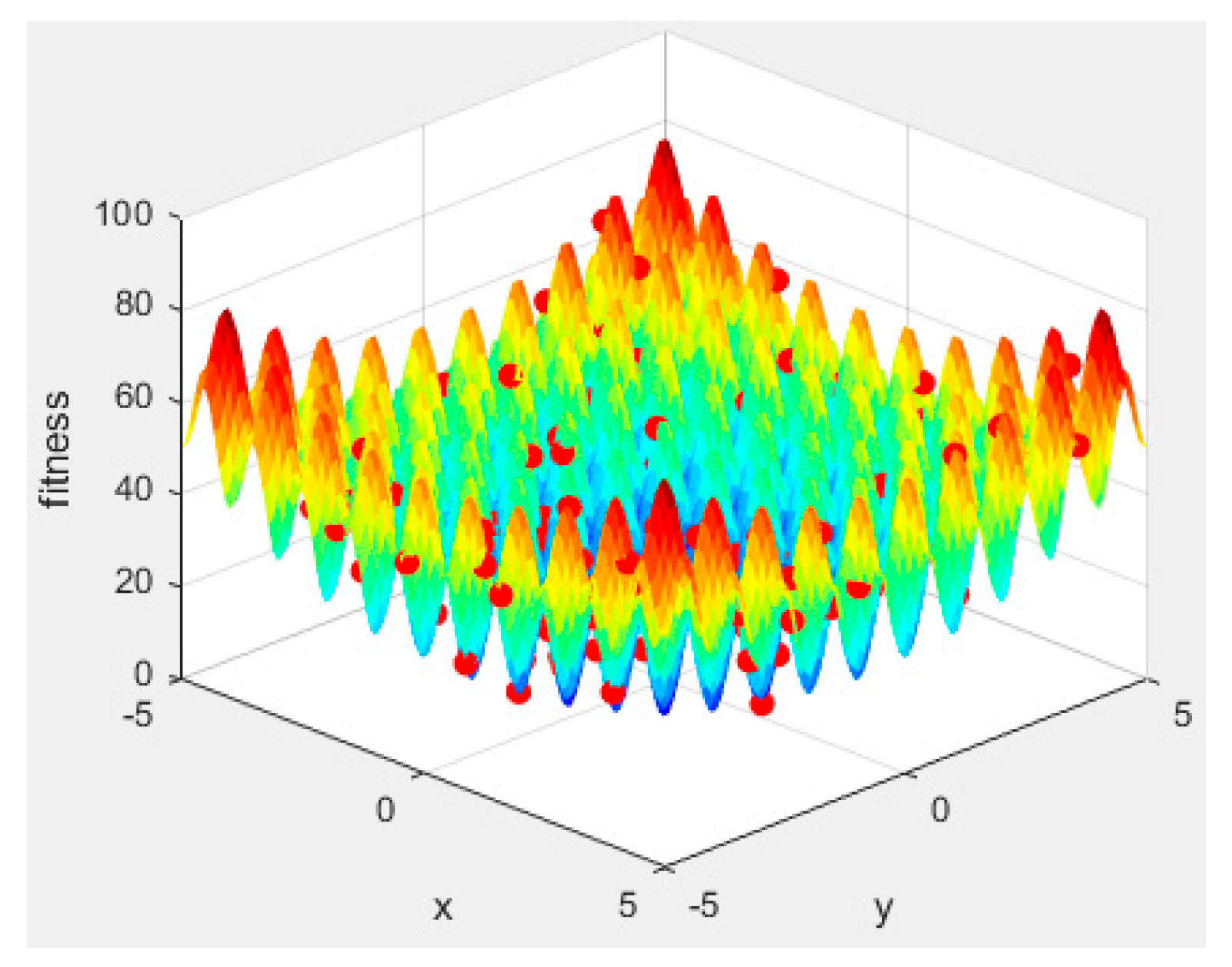
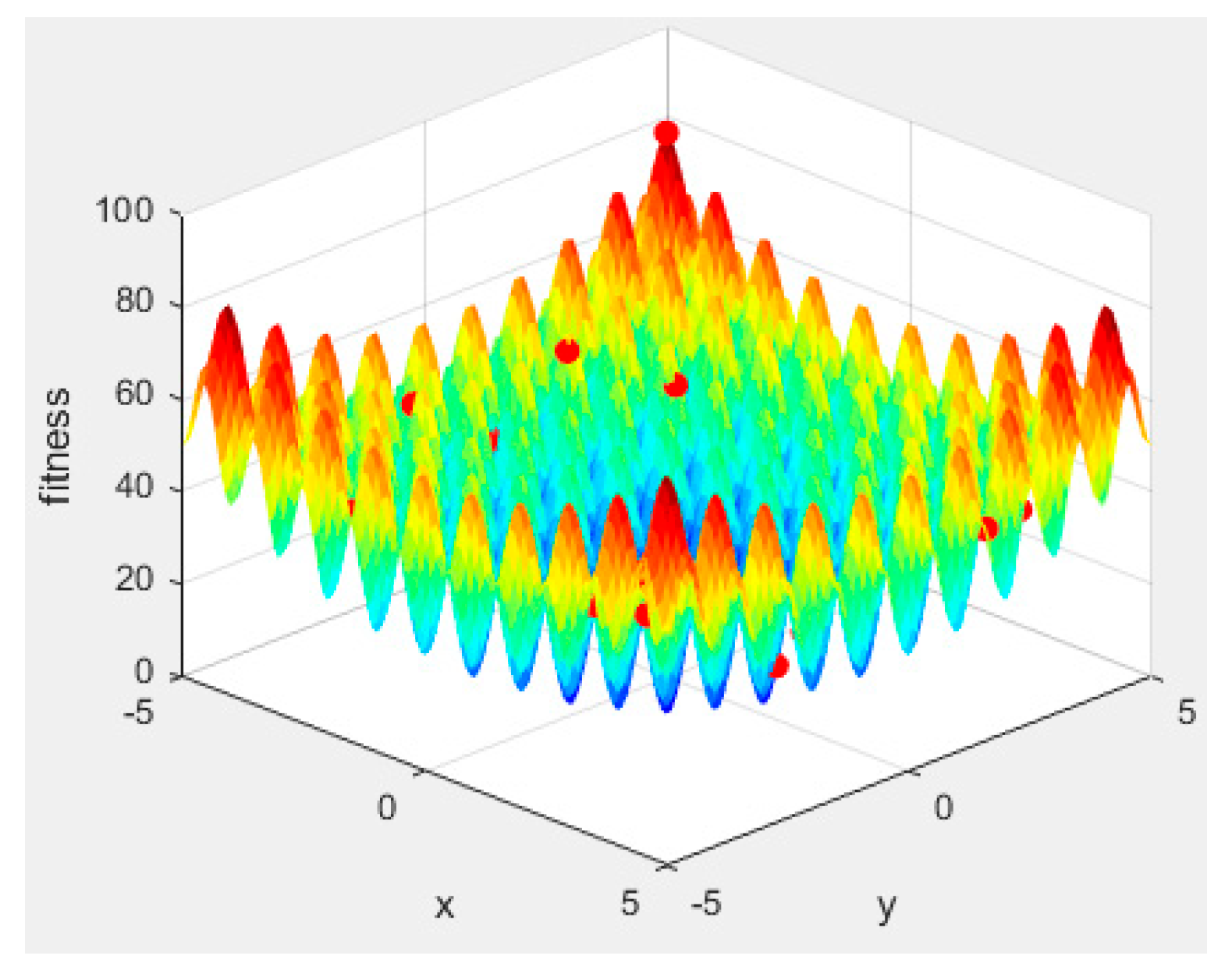
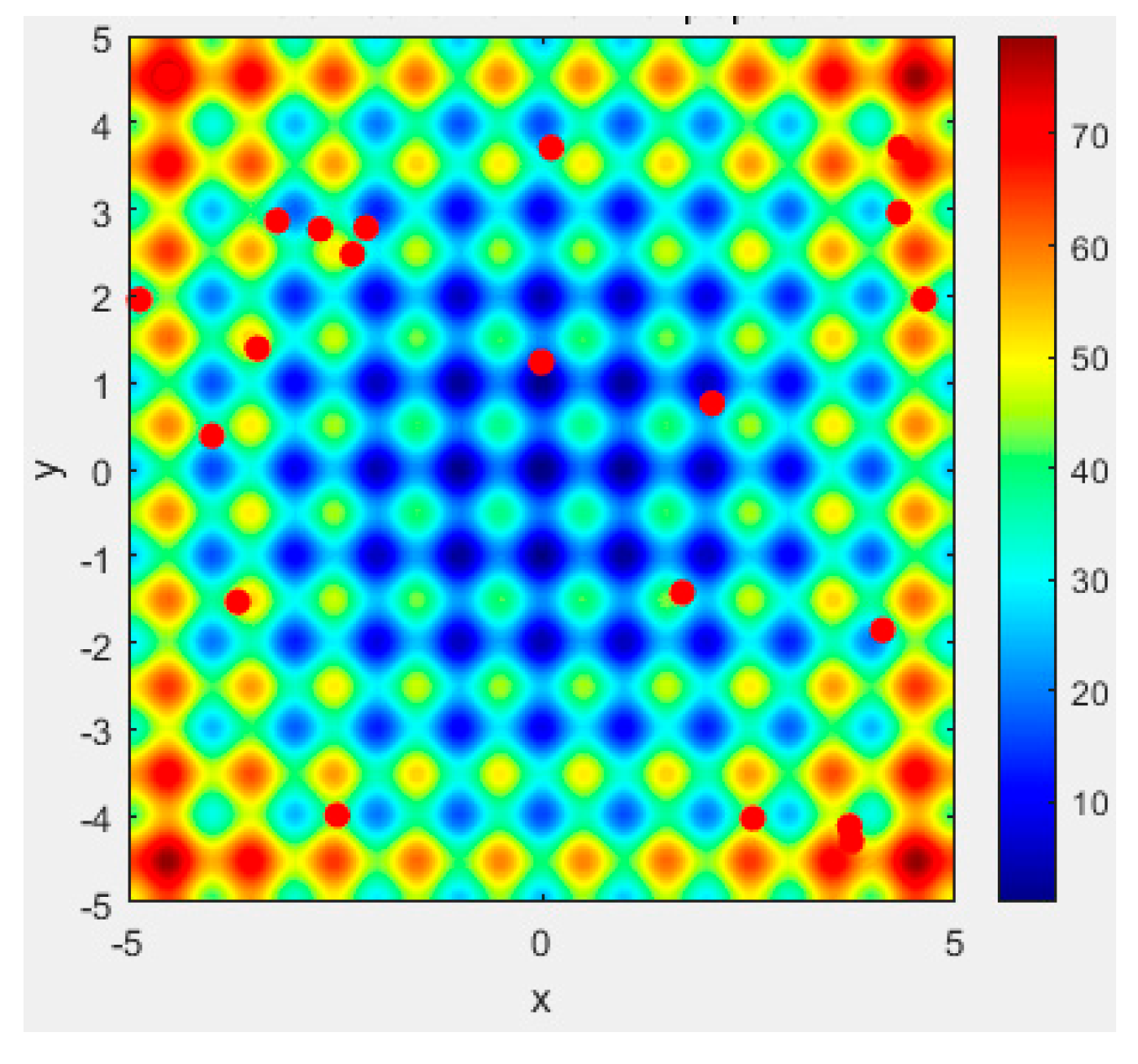
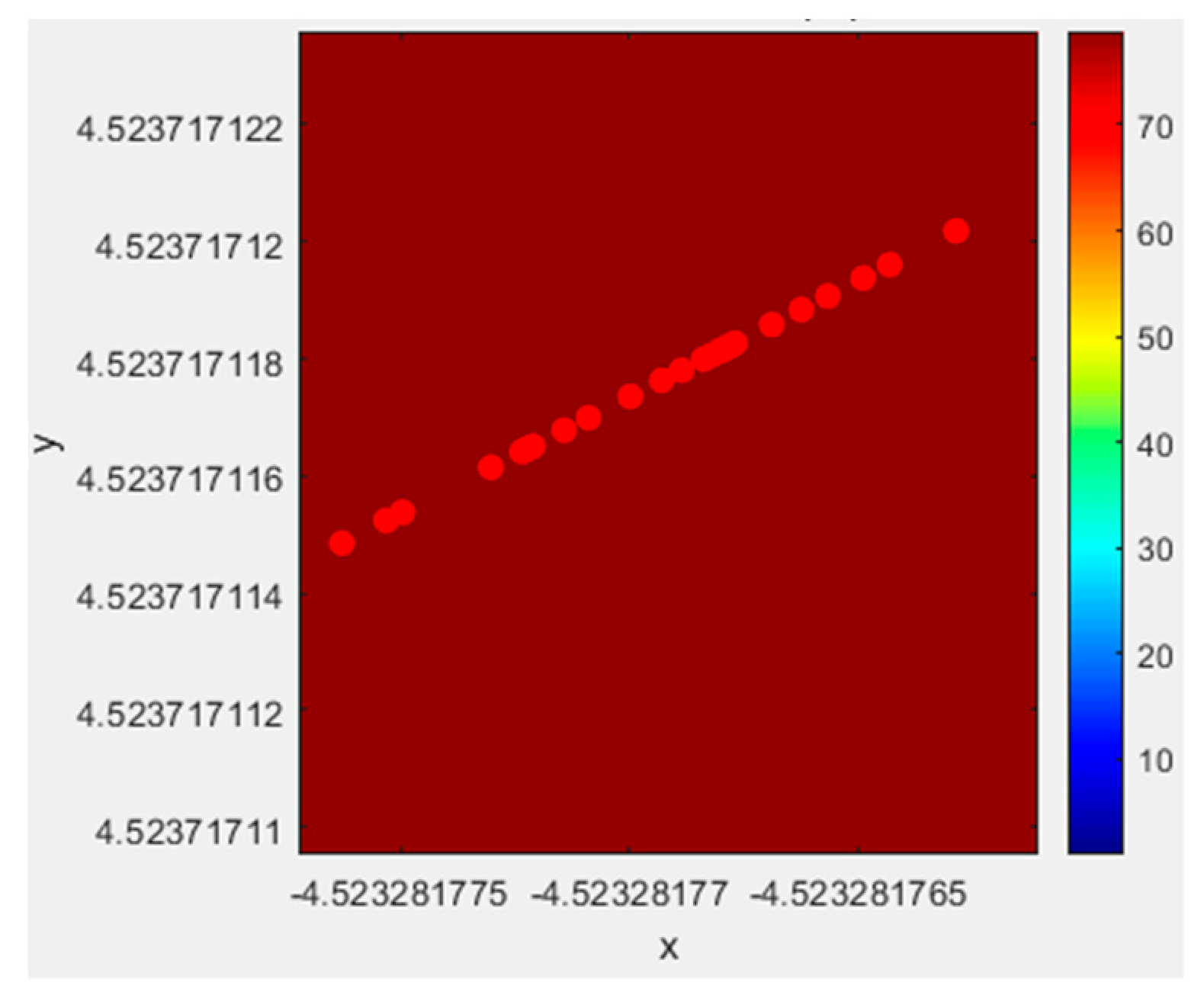
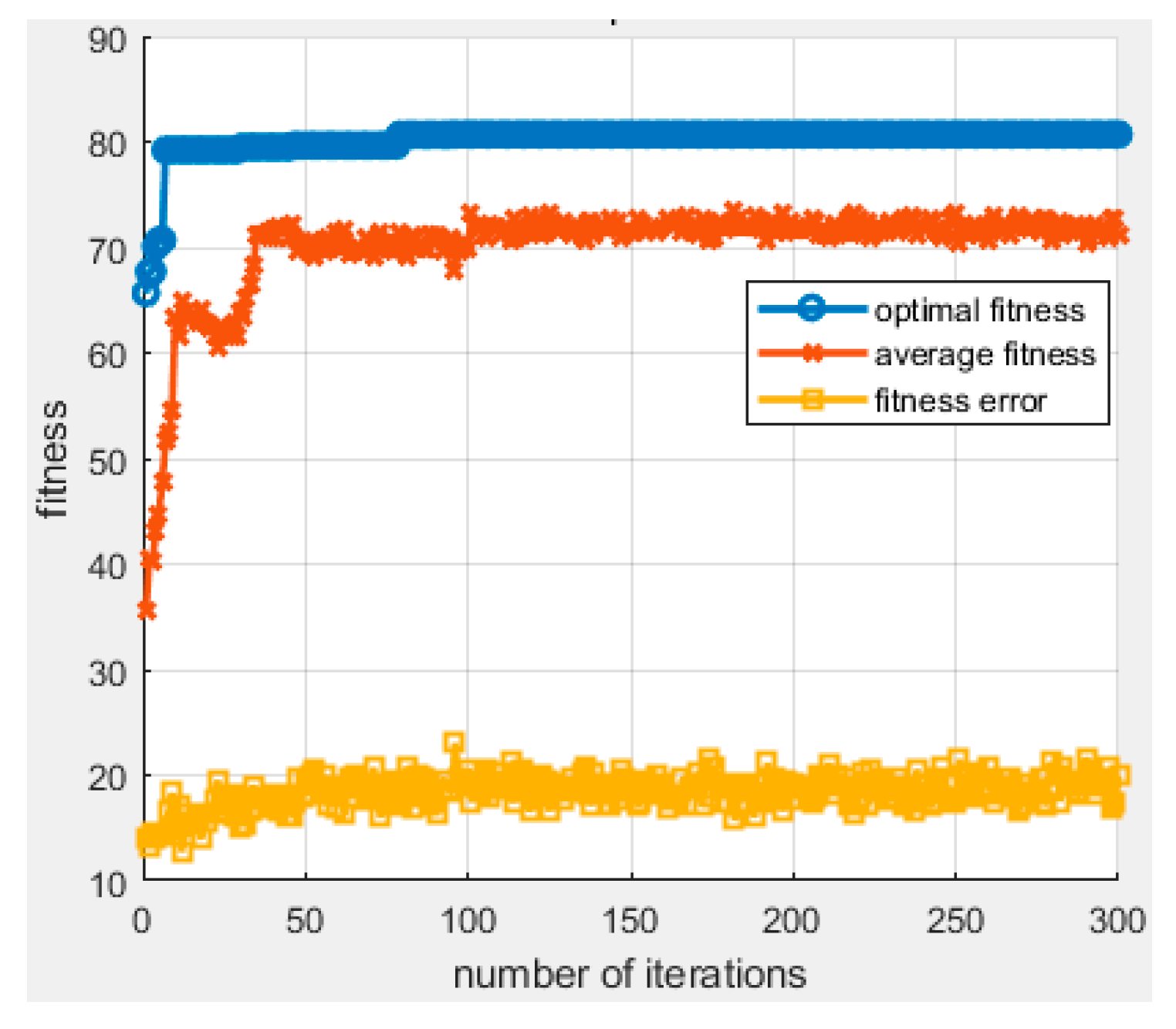
In our benchmark test, all optical flows were separated into four groups with periods of 2.0, 1.0, 0.6, 0.3, 0.2, and 0.1 ms, and packet sizes ranged from 32 to 256 bytes each. In the experiment, we measured the forwarding delay for each packet in these 100 optical flows, and the solution distributions for each optical flow are shown in the figure. For the convenience of drawing, multiple targets in Equation (14) were normalized to the interval [0, 25], and the higher the indicators, the higher the fitness.
To effectively evaluate the proposed optical flow scheduling algorithms, this benchmark test was focused on the forwarding delay within a single LED node and the optical flow scheduling on a single directed edge. It was assumed that there are optical flows to be forwarded in LED node and optical flows that need to be scheduled on the directed edge . Jitter is defined as the difference between the highest and minimum delays, and hence larger jitter indicates less consistent performance.
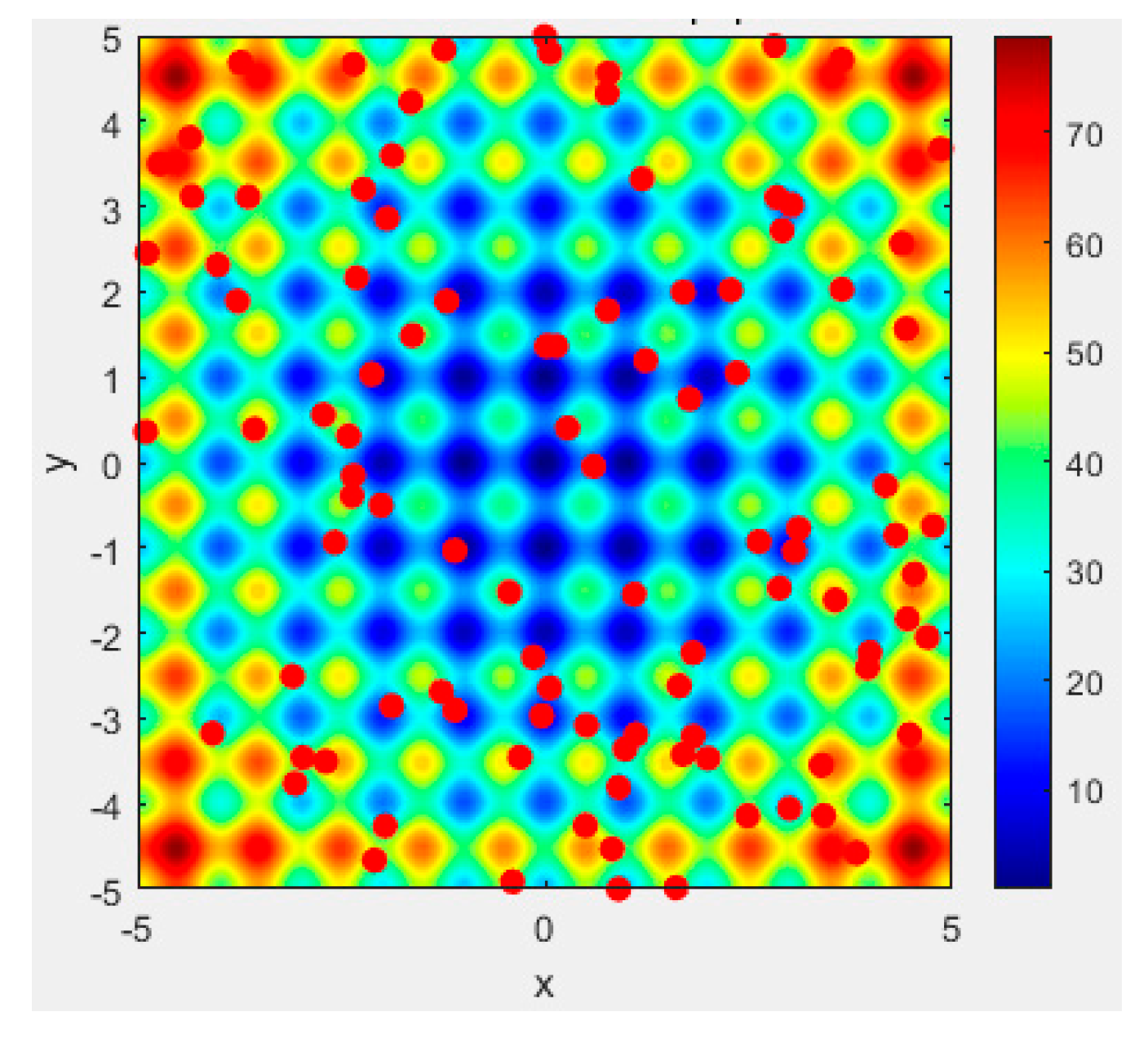
Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show our APC algorithm’s solution performance. The color bar represents the fitness level in the corresponding figure, with red indicating the maximum value and blue indicating the minimum value. Figure 3 shows a 3D subplot of the initial solution distribution, and Figure 4 presents a 2D subplot of the initial solution distribution. Figure 5 presents a 3D subplot of the final solution distribution, and Figure 6 provides a 2D subplot of the final solution distribution. Figure 7 shows a partial zoom at the optimal solution, and Figure 8 presents convergence curves.
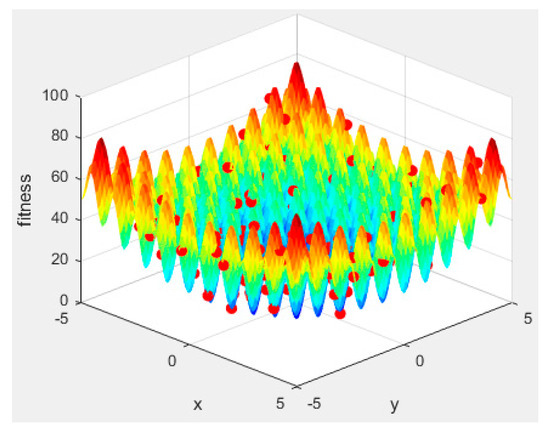
Figure 3.
A 3D subplot of initial distribution. The color represents the fitness level, with red indicating the maximum value and blue indicating the minimum value.
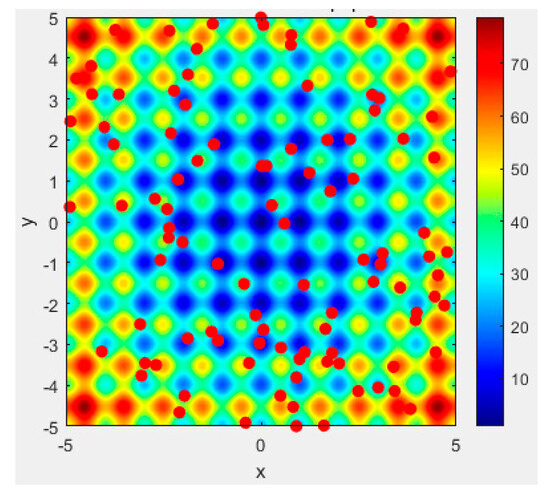
Figure 4.
A 2D subplot of initial distribution.
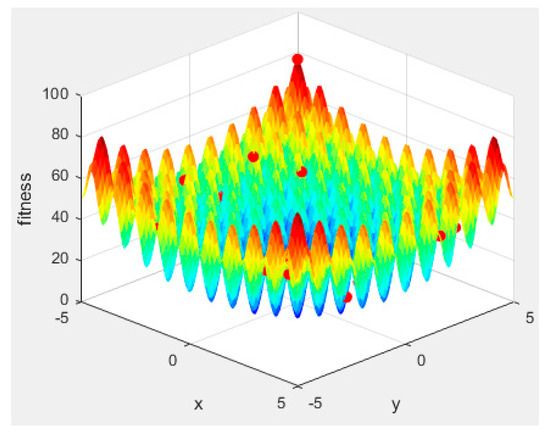
Figure 5.
A 3D subplot of final distribution. The color represents the fitness level, with red indicating the maximum value and blue indicating the minimum value.
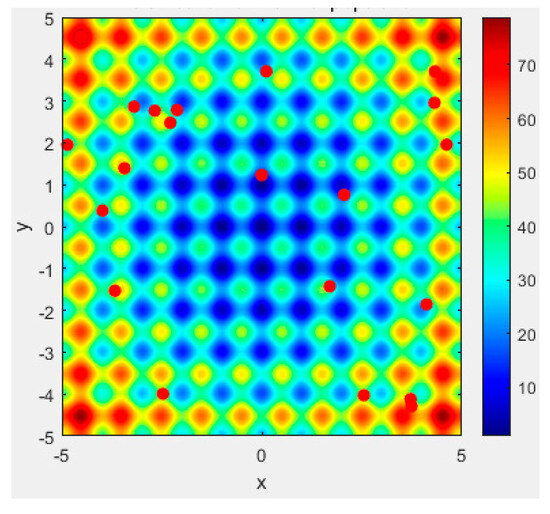
Figure 6.
A 2D subplot of final distribution.
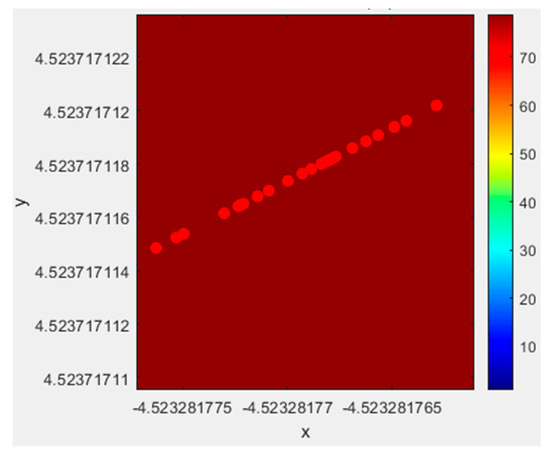
Figure 7.
Partial zoom at the optimal solution.
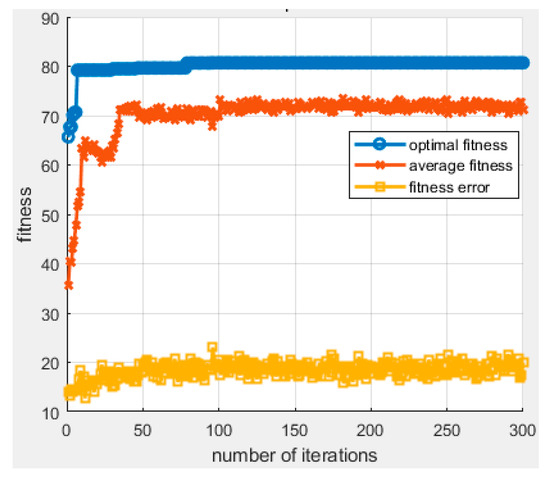
Figure 8.
Convergence curves.
From Figure 3 and Figure 4, it can be seen that our algorithm initially generates random seeds in the entire solution space; i.e., it globally searches for feasible solutions. In the first iteration, all plant individuals are seeds, and the solution of the artificial plant community algorithm does not depend on the initial solution.
From Figure 5 and Figure 6, it can be seen that after 300 iterations, most of the plant individuals and fruits in our algorithm are concentrated near the optimal solution, showing local convergence. There is also a portion of seeds that undergo random search, i.e., retaining the global search for feasible solutions.
Figure 7 magnifies the distribution of artificial plant individuals near the optimal solution in Figure 6, with only one local zoom. From Figure 7, it can be seen that a large number of artificial plant individuals are concentrated near the optimal solution and continuously searching, demonstrating enhanced local search capabilities.
Figure 8 shows the convergence process of this algorithm after 300 iterations, including the optimal fitness, average fitness, and fitness error of the population. This figure further demonstrates the performance of this algorithm. After 50 iterations, the APC algorithm becomes basically stable and has a very fast convergence speed. At the same time, after 50 iterations, it maintains strong global and local search capabilities, which can also be verified in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. In the end, the proposed APC algorithm obtained the optimal solution of 80.7065 after 300 iterations.
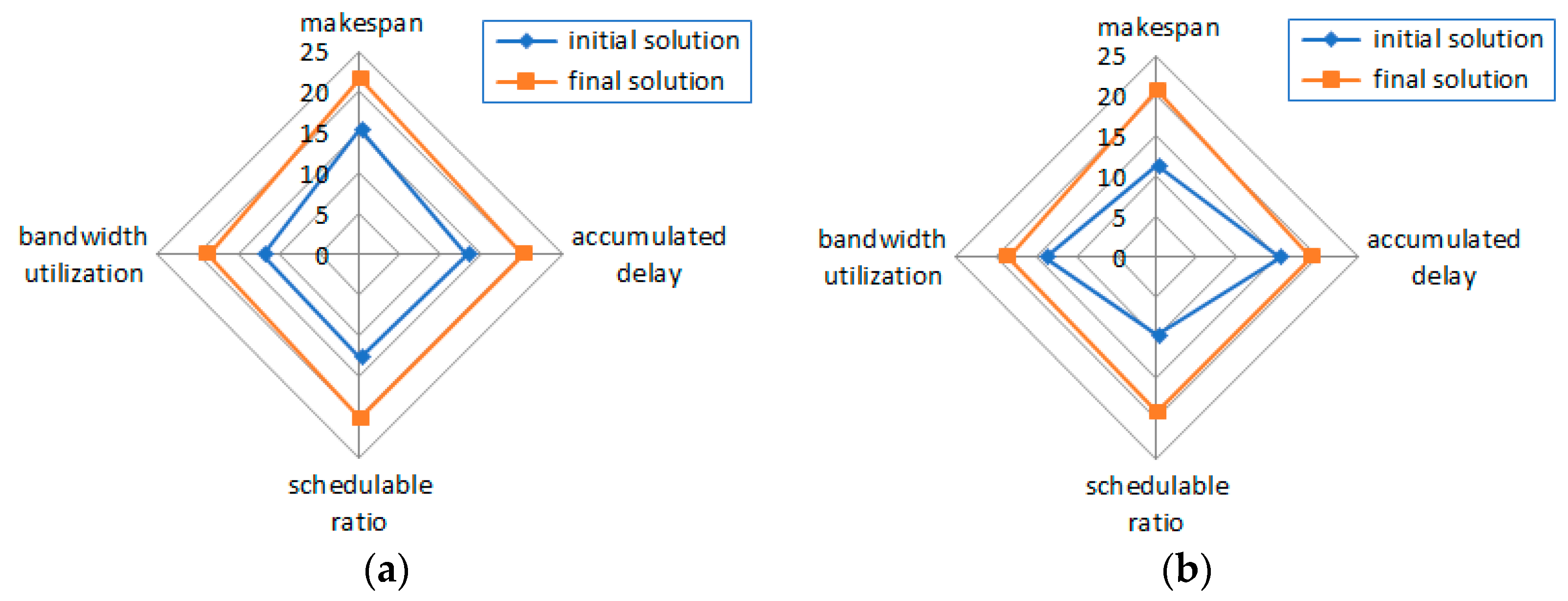
Figure 9a,b show the radar chart of our proposed APC algorithm for solving multi-objective functions, including objective 1 regarding the makespan in Equation (10), objective 2 regarding the accumulated delay in Equation (11), objective 3 regarding the schedulable ratio in Equation (12), and objective 4 regarding bandwidth utilization in Equation (13). There are two scenarios, i.e., the connect scene and disconnect scene. From Figure 9a, it can be seen that after 300 iterations, multiple objectives of the final solution are superior to the initial solution in the connect scene, and the optimal solution of 80.7065 is obtained.
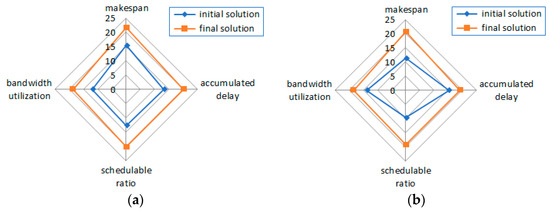
Figure 9.
Radar chart of our proposed APC algorithm. (a) Connect scene; (b) disconnect scene.
The impact of network disconnections on multi-objective functions is shown in Figure 9b, which is critical for reliability in IoV applications. It simulates the impact of unpredictable environmental factors such as weather, interference, or mobility dynamics on performance in real-world scenarios. It can be seen that after 300 iterations, multiple objectives of the final solution are superior to the initial solution in the disconnect scene, and the optimal solution of 77.4681 is obtained. Hence, our proposed APC algorithm can improve residual bandwidth utilization in network disconnections and can balance multiple conflicting targets by searching for maximum fitness.
Considering the highly dynamic nature of the Internet of Vehicles, optical flows usually should be sent to their destination within 0.5 ms while eliminating jitter. Figure 8 and Figure 9 show that the proposed APC algorithm can optimize optical flow scheduling with delays not exceeding 50 iterations for 20 optical flows concurrently within a node. This illustrates that the APC algorithm fits the highly dynamic requirements of time-sensitive applications in IoV, efficiently searching for optimal VVLC solutions on edge computing platforms.
5.3. Performance Comparison
This section implements a performance comparison for optical flow scheduling on using our proposed APC algorithm and some SOTA algorithms, i.e., DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. The optical flow number ranges from 100 to 500.
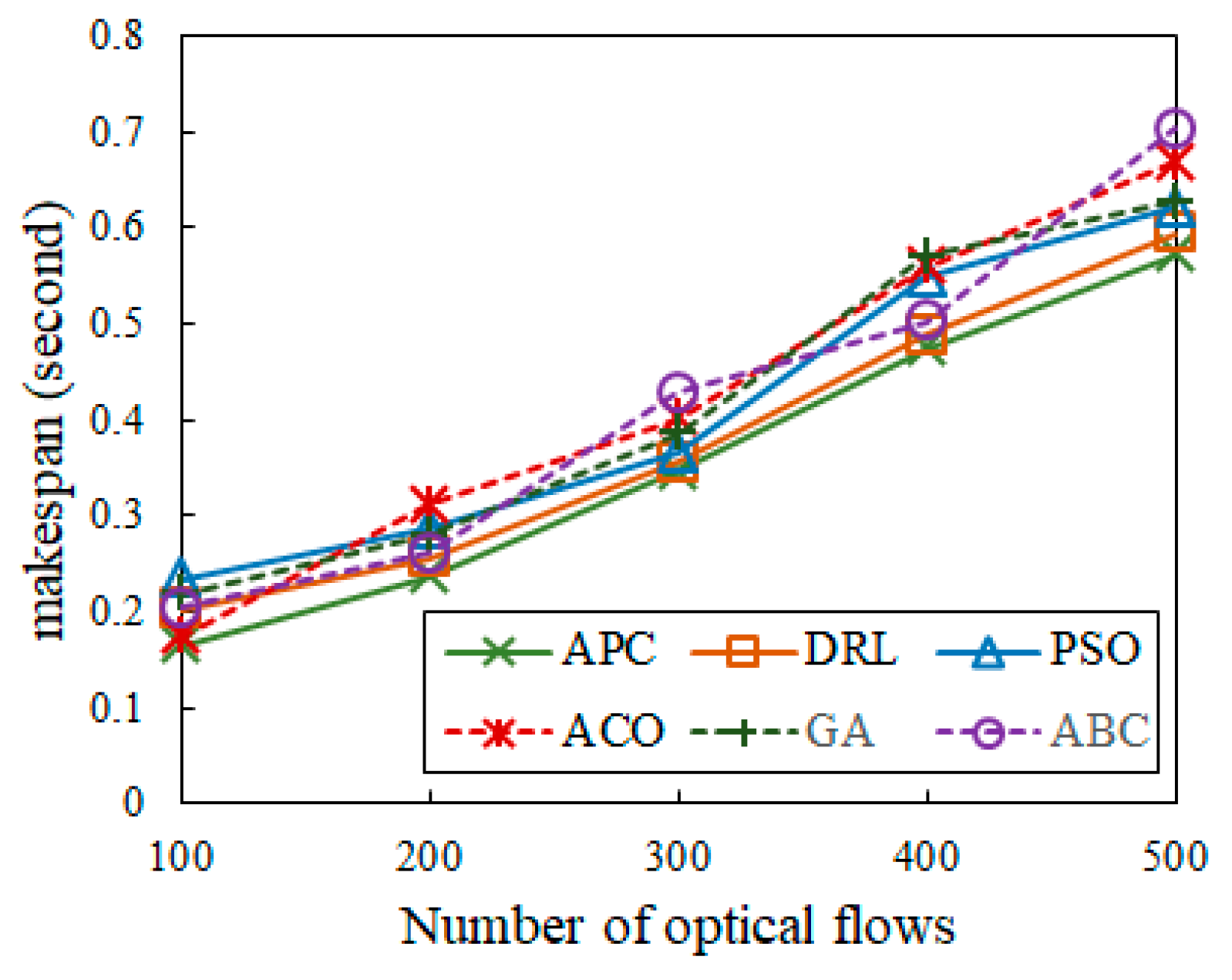
Figure 10 reveals the algorithm comparison of the makespan among APC, DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. As the number of optical flows grows from 100 to 500, makespans for DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27] increase faster than for APC. The results show that the average makespan for APC with 500 optical flows is 0.572 s, whereas those for DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27] are 0.594 s, 0.621 s, 0.668 s, 0.627 s, and 0.704 s, respectively. This fundamental distinction stems from the fact that optical flow scheduling must search for optimal solutions for all flow combinations in a short period with delay limits. Unlike traditional algorithms, APC simplifies the computing process and decreases the extra computation time for optical flows, considerably lowering the algorithm’s complexity and makespan.
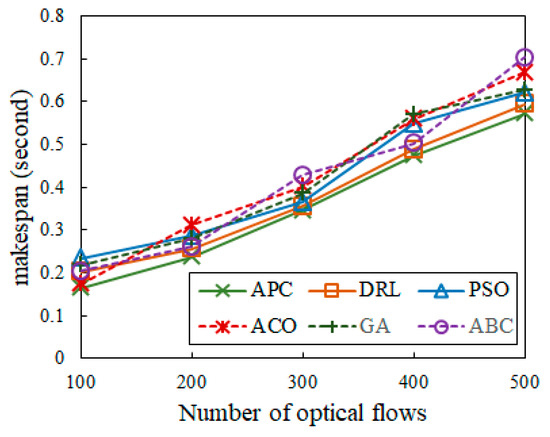
Figure 10.
Comparison of the makespan.
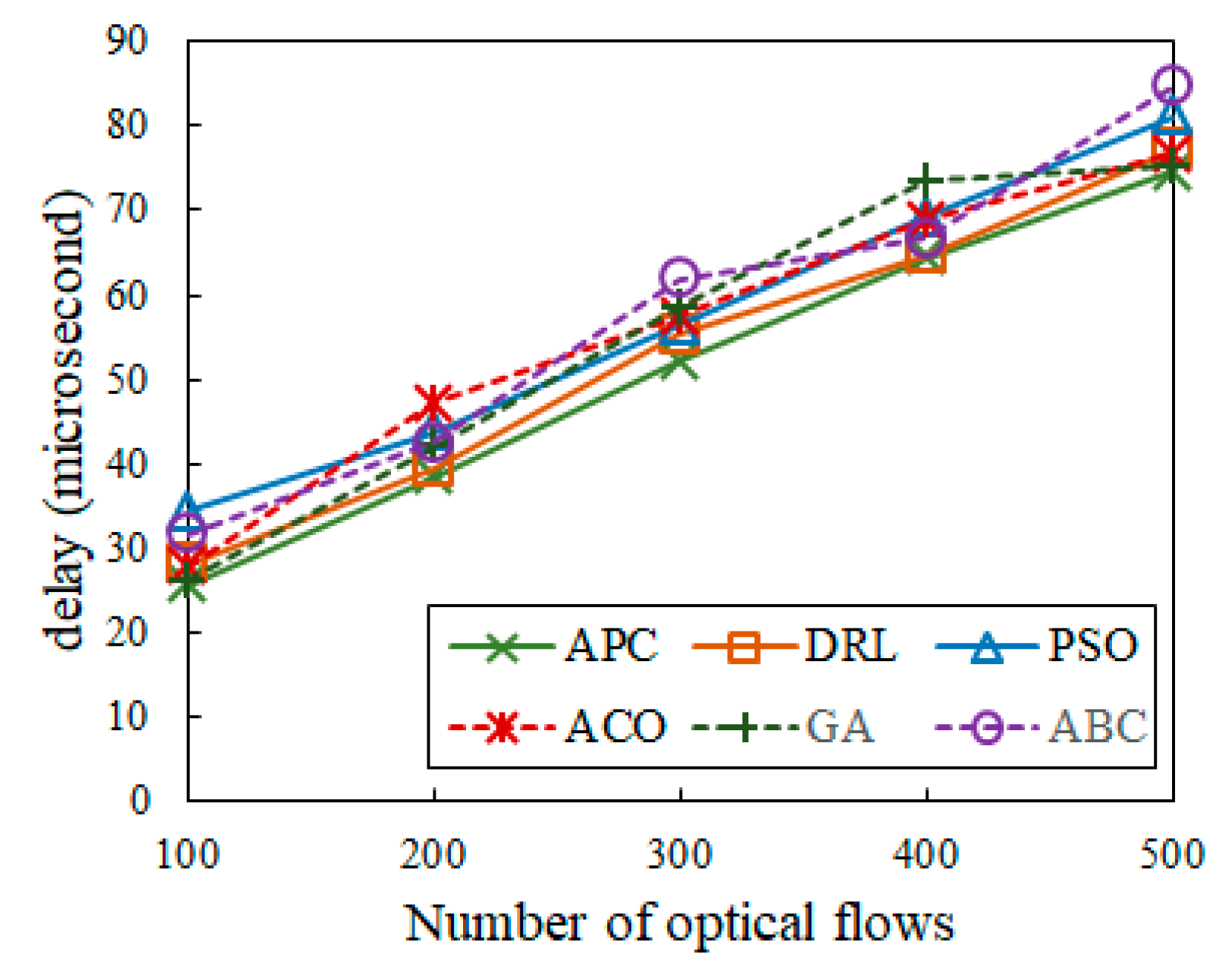
Figure 11 shows the algorithm comparison of accumulated delay among APC, DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. In comparison to the other four algorithms, APC achieves the optimal low-delay optical flow scheduling. Because the total transfer time for 100 to 500 optical flows is less than the average periods (2.0, 1.0, 0.6, 0.3, 02, and 0.1 ms), this guarantees the existence of a time-offset set that meets the low-delay requirement. Although the DRL [3,6,25] method achieves jitter-free scheduling, its delay is much longer than that of APC.
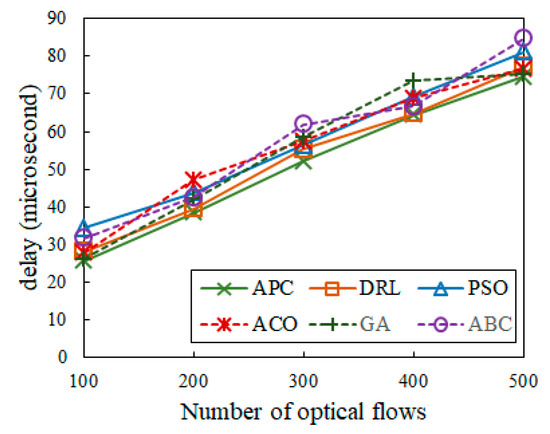
Figure 11.
Comparison of accumulated delay.
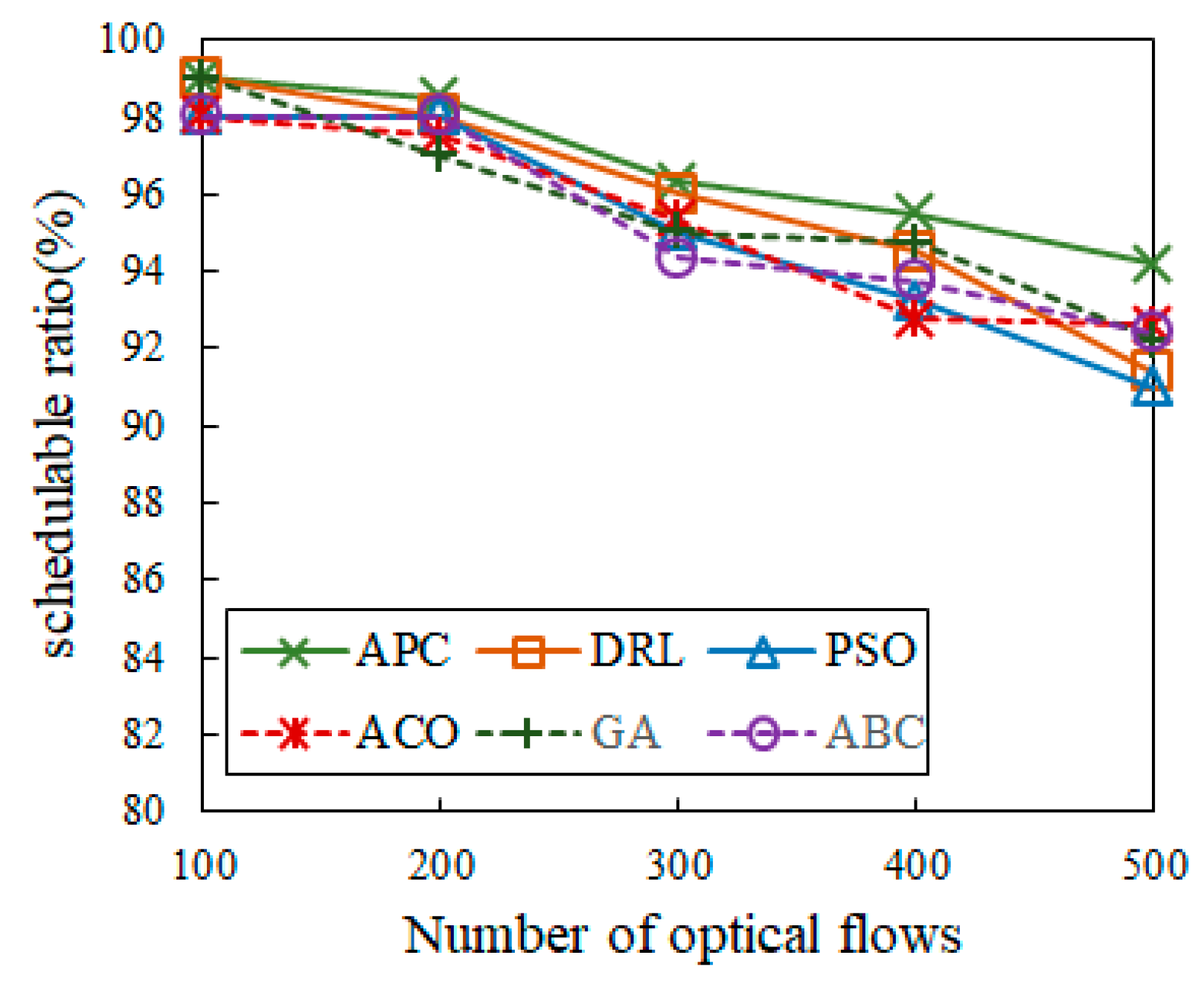
Figure 12 depicts the algorithm comparison of schedulable ratios among APC, DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. It shows that the schedulable ratio for APC is consistently high, whereas those for DRL [3,6,25], PSO [14], ACO [21], and ABC [27] decrease as the number of optical flows increases from 100 to 500. Our proposed APC algorithm comprehensively considers the multi-objective optimization of different optical flows. When all of the constraints are met, the optical flow scheduling can be determined via the efficient searching of the APC algorithm in a short time. This method employs simple parameters and operations, making it easier to determine the best scheduling solutions.
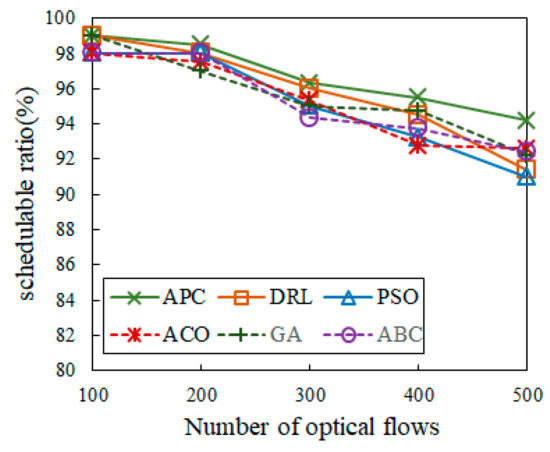
Figure 12.
Comparison of schedulable ratios.
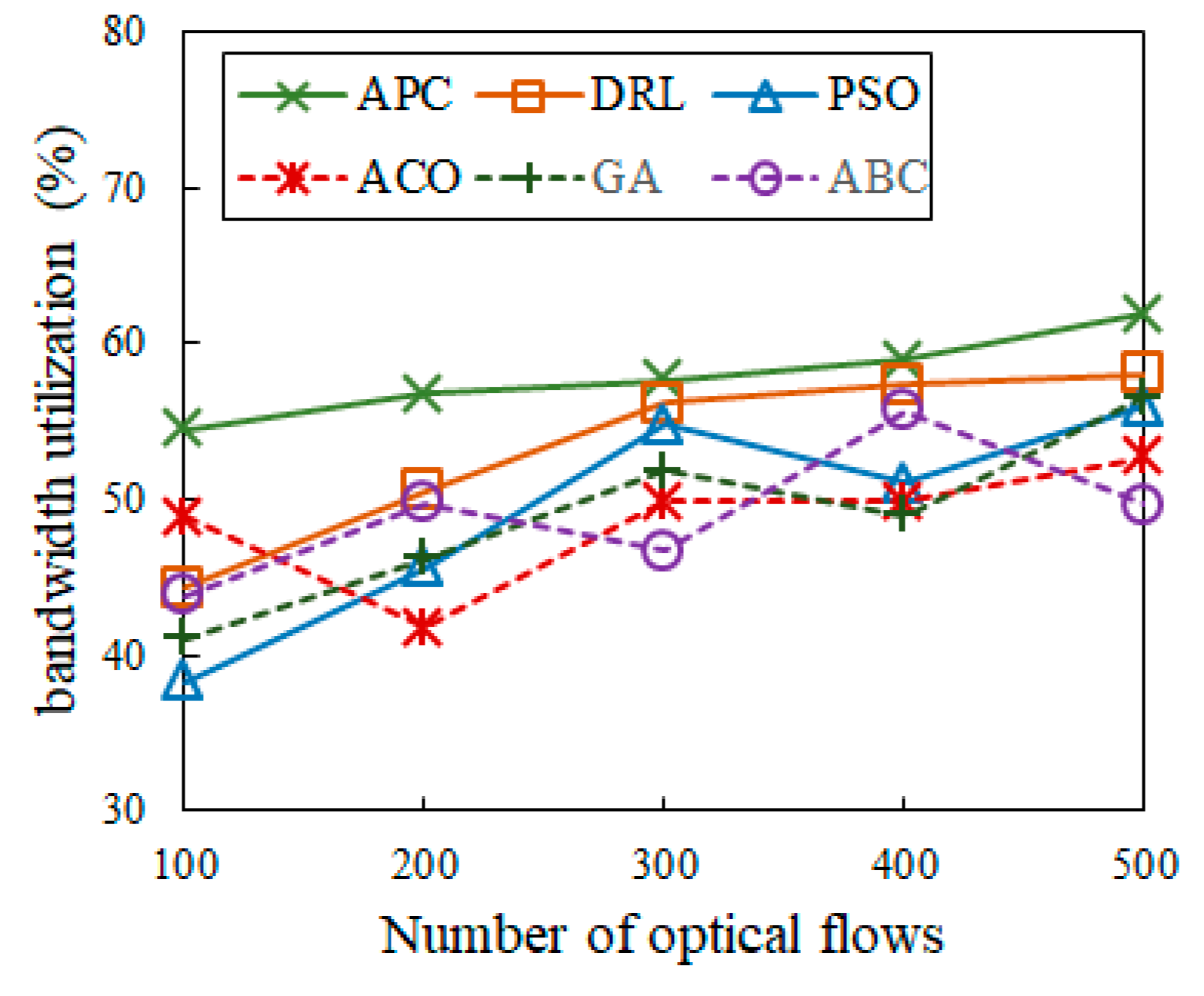
Figure 13 shows the algorithm comparison of bandwidth utilization among APC, DRL [3,6,25], PSO [14], ACO [21], GA [26], and ABC [27]. It demonstrates that the APC algorithm has the highest utilization. The difference in bandwidth consumption between APC and the other five algorithms widens as the number of time-sensitive optical flows grows from 100 to 500, and it also shows that APC has better bandwidth utilization than DRL [3,6,25], PSO [14], ACO [21], GA [26], or ABC [27]. This improvement is due to the enhanced global and local search capabilities in APC, which reduces the number of idle time slots. As a result, the optimal solution efficiently lowers packet loss due to queuing, which is especially beneficial to highly dynamic VVLC. Thus, APC makes an important contribution to attaining ultra-low-delay communication in IoV networks.
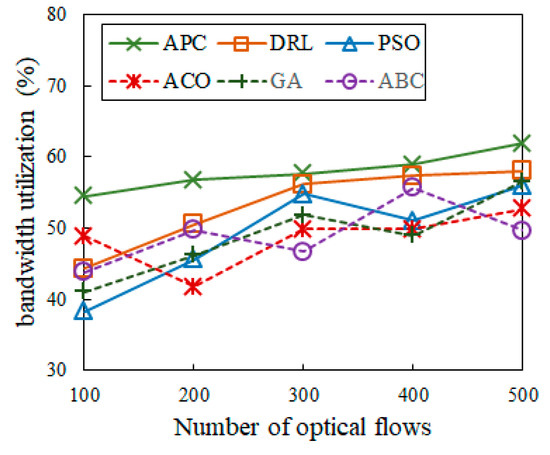
Figure 13.
Comparison of bandwidth utilization.
Table 3 unveils the statistical results of related work with time-sensitive optical flows ranging from 100 to 500. The main metrics include objective 1, the makespan in Equation (8); objective 2, accumulated delay in Equation (9); objective 3, the schedulable ratio in Equation (10); objective 4, bandwidth utilization in Equation (11); and the solution time (s). The mean makespan and accumulated delay detected in the APC algorithm are lower than the average delay, implying that the proposed algorithm is more effective at optical flow scheduling than other SOTA algorithms. The mean solution time attained with APC is less than that for other algorithms, while it also has a higher mean schedulable ratio and bandwidth utilization, suggesting that the proposed APC algorithm represents a more effective method for VVLC scheduling optimization.

Table 3.
Statistical results of related work.
5.4. Discussion
Based on the experimental results above, the following discussion can be presented.
Firstly, the optical flow scheduling in VVLC is a challenging problem. This is the first study to perform theoretical analyses on the multi-objective optimization of time-sensitive optical flow, including objective 1 regarding the makespan in Equation (10), objective 2 regarding the accumulated delay in Equation (11), objective 3 regarding the schedulable ratio in Equation (12), and objective 4 regarding bandwidth utilization in Equation (13). The proposed model effectively describes the characteristics of optical flow scheduling, which will guide the scheduling design and provide a theoretical basis for VVLC. To simplify the analysis, this manuscript did not consider additional indicators such as jitter-free scheduling and energy-efficient scheduling. Integrating jitter-free scheduling and energy efficiency as additional objectives in the multi-objective optimization model would be helpful to address the limited power constraints of edge vehicle devices.
Secondly, finding the optimal solution for optical flow scheduling is not an easy task, as it involves multiple conflicting objectives and nonlinear constraints. The conditions of multi-objective optimization for optical flows are so complex that traditional algorithms find it difficult to obtain exact solutions in a short period of time. For the APC algorithm, the global search ability is improved by randomly seeding, and the local search ability is enhanced by giving the optimal plant individuals more fruiting opportunities. The experimental results verify that the proposed algorithm is effective and has made progress compared to mainstream SOTA algorithms, including Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 and Table 3.
Thirdly, a benchmark experiment is designed to evaluate the scheduling performance of this algorithm and compare it with relevant SOTA algorithms. To assess performance, the number of time-sensitive optical flows ranges from 100 to 500, with five main metrics, including objective 1 regarding makespan, objective 2 regarding accumulated delay, objective 3 regarding the schedulable ratio, objective 4 regarding bandwidth utilization, and solution time (s). Table 3 shows a comparison of the main metrics for several algorithms. From the statistical results from related work based on 100 tests, our technique takes into account both the objective function and the solution time, allocating equal weight coefficients of 0.25 to the benefits of each objective. Our benchmark testing takes into account the IEEE standard for short-range optical wireless communications defined in IEEE Std 802.15.7a™-2024 [36], but it is still not entirely the same as the real situation. In an actual VVLC scenario, there may be thousands of vehicles or optical flows, which is far beyond the scope of our benchmark test set. In that scenario, computational costs may significantly increase with the expansion of problem scale.
Fourthly, in engineering applications, the proposed scheduling algorithm must consider the limited computing and storage capacity of the vehicle edge computing platform. Edge-enabled VVLC has seen a significant increase in the use of time-sensitive applications. For every time-sensitive application, the vehicle edge computing platform provides solutions for centralized scheduling and intelligent routing. Subsequently, the vehicle edge computing platform provides communication services, enabling packet delivery to meet the delay requirements of time-sensitive optical flows. In actual edge computing hardware, more practical factors need to be taken into account, such as the measurement of runtime, processor utilization, memory usage, or resource consumption on actual edge computing devices.
Fifthly, our method is not entirely perfect either. Advanced variants or hybrid methods with other algorithms may outperform the proposed APC algorithm in certain metrics. However, due to our limitations, we were unable to compare these in this manuscript. To improve makespan, accumulated delay, schedulable ratio, and bandwidth utilization, the APC scheduling method is introduced for schedule optical flows. Some other scheduling factors have been overlooked in this paper. For example, jitter-free scheduling may be available for the optical flows. All conflicting packets should be confirmed in advance, making it easy to eliminate future conflicts during the scheduling, but this is difficult to achieve in actual communication. In order to improve the operational efficiency of VVLC, it is assumed that the directed edge has enough bandwidth to handle all time-sensitive and best-effort optical flows. When the Internet of Vehicles is disconnected, this cannot be guaranteed. Users can adjust different goals and weights to guide the algorithm in modifying the fitness function to adapt to the impact of different scenarios, including unpredictable environmental factors, weather, interference, or mobility dynamics on performance in real-world scenarios. Due to the limitations of our abilities, larger networks with a large number of vehicles or optical flows are not considered here.
6. Conclusions
To address the challenges in time-sensitive optical flow scheduling of VVLC, a multi-objective optimization problem among multiple VVLC flows is built, and an improved artificial plant community algorithm with enhanced global search and local search capabilities is proposed to guarantee low-delay visible light communication. The global search ability has been improved by randomly seeding, and the local search ability has been enhanced by giving the optimal plant individuals more fruiting opportunities. The proposed method includes a static APC scheduling algorithm for an environment with a stable state at a certain moment and a dynamic APC scheduling algorithm for scenes of high-speed vehicle movement. The scheduling optimization of time-sensitive optical flows is accomplished by an APC algorithm through seeding, growing, and fruiting. A series of benchmark testing experiments were conducted and compared to verify the performances regarding multiple objectives, i.e., makespan, delay, schedulable ratio, bandwidth utilization, and solution time. The results show the effectiveness and superiority of the proposed APC algorithm, which is simple in calculation and suitable for deployment on the vehicle edge computing platform with limited computing and storage resources.
The shortcomings of this study include not considering more indicators and not conducting empirical research on real vehicle platforms. In the future, considering the actual situation of VVLC, introducing more indicators is an important direction. For example, jitter-free scheduling and energy efficient scheduling could further optimize VVLC performance. Validating the scalability and empirical research of the proposed algorithm on actual edge computing hardware or larger networks with a large number of vehicles or optical flows is also an important application direction. Additionally, it is very promising to integrate and compare various artificial intelligence algorithms and edge computing on VVLC, such as advanced or hybrid SOTA methods.
Author Contributions
Conceptualization, Z.C.; methodology, Z.C.; software, S.L. and J.L. (Jingyi Li); validation, S.L. and C.Y.; investigation, C.Y. and J.L. (Junyu Liu); data curation, S.L., C.Y. and J.L. (Junyu Liu); writing—original draft, S.L.; writing—review and editing, Z.C. and S.L.; project administration, Z.C. and G.G.; funding acquisition, Z.C. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (No. 71471102), Major Science and Technology Projects in Hubei Province of China (Grant No. 2020AEA012), and Yichang University Applied Basic Research Project in China (Grant No. A17-302-a13).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in this article.
Acknowledgments
Thank you to the anonymous reviewers for their valuable feedback on this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jing, X.; Wu, Y.; Yu, F.; Xu, Y.; Wang, X. Reconfigurable intelligent surface-aided security enhancement for vehicle-to-vehicle visible light communications. Photonics 2024, 11, 1151. [Google Scholar] [CrossRef]
- Sharda, P. Next generation based vehicular visible light communications: A novel transmission scheme. IEEE Trans. Veh. Technol. 2024, 73, 16735–16743. [Google Scholar] [CrossRef]
- Wang, J.; Luo, H.; Ruby, R.; Liu, J.; Wang, S.; Wu, K. Enabling reliable water–air direct optical wireless communication for uncrewed vehicular networks: a deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2024, 73, 11470–11486. [Google Scholar] [CrossRef]
- Li, Y.C.; Wu, L.; Zhang, Z.C.; Dang, J.; Zhu, B.C.; Zhang, X.C.; Wu, Y.P. Sensing assisted optical wireless communication for UAVs. IEEE Trans. Veh. Technol. 2024, 73, 18620–18634. [Google Scholar] [CrossRef]
- Zadobrischi, E. Traffic and vehicle management in roundabouts through systems based on dedicated short-range communications and visible light communications. Electronics 2025, 14, 317. [Google Scholar] [CrossRef]
- Bu, F.F.; Luo, H.J.; Ma, S.S.; Li, X.; Ruby, R.; Han, G.J. AUV-aided optical-acoustic hybrid data collection based on deep reinforcement learning. Sensors 2023, 23, 578. [Google Scholar] [CrossRef]
- Pointurier, Y.; Benzaoui, N.; Lautenschlaeger, W.; Dembeck, L. End-to-end time-sensitive optical networking: Challenges and solutions. J. Light. Technol. 2019, 37, 1732–1741. [Google Scholar] [CrossRef]
- Zeng, H.S.; Zhang, C.X.; Yi, X.S.; Xiong, R. Heuristic fragmentation-aware scheduling for a multicluster time-sensitive passive optical LAN. Opt. Fiber Technol. 2021, 66, 102662. [Google Scholar] [CrossRef]
- Peng, Y.F.; Shi, B.X.; Jiang, T.G.; Tu, X.D.; Xu, D.; Hua, K. A survey on in-vehicle time-sensitive networking. IEEE Internet Things J. 2023, 10, 14375–14396. [Google Scholar] [CrossRef]
- Xu, Y.L.; Shang, J.; Tang, H. Recent trends of in-vehicle time sensitive networking technologies, applications and challenges. China Commun. 2023, 20, 30–55. [Google Scholar] [CrossRef]
- Li, J.; Bose, S.K.; Shen, G.X. Cooperative resource scheduling for time-sensitive services in an integrated XGS-PON and Wi-Fi 6 network. IEEE Commun. Lett. 2022, 26, 1338–1342. [Google Scholar] [CrossRef]
- Su, C.; Zhang, J.W.; Ji, Y.F. Time-aware deterministic bandwidth allocation scheme in TDM-PON for time-sensitive industrial flows. J. Opt. Commun. Netw. 2023, 15, 255–267. [Google Scholar] [CrossRef]
- Waqar, M.; Mustafa, M.U.; Jabeen, F.; Shah, S.A. Performance improvement of time-sensitive fronthaul networks in 5G Cloud-RANs using reinforcement learning-based scheduling scheme. IEEE Access 2024, 12, 59756–59770. [Google Scholar] [CrossRef]
- Wang, N.; Liu, J.F.; Lu, J.; Zeng, X.Y.; Zhao, X.Y. Low-delay layout planning based on improved particle swarm optimization algorithm in 5G optical fronthaul network. Opt. Fiber Technol. 2021, 67, 102736. [Google Scholar] [CrossRef]
- Cai, Z.; Ma, Z.; Zuo, Z.; Xiang, Y.; Wang, M. An image edge detection algorithm based on an artificial plant community. Appl. Sci. 2023, 13, 4159. [Google Scholar] [CrossRef]
- Wei, T.; Lin, T.; Huang, N.; Fu, C.; Liu, X.; Su, L.; Tang, L.; Hu, Q.; Gong, C. Multi-user scheduling and channel characteristics for water-to-air unmanned vehicular visible light communication. IEEE Trans. Veh. Technol. 2024, 73, 18705–18718. [Google Scholar] [CrossRef]
- Di, Y.; Xu, A.; Chen, L.K. Performance enhancement via real-time image-based beam tracking for WA-OWC with dynamic waves and mobile receivers. J. Light. Technol. 2024, 42, 6671–6678. [Google Scholar] [CrossRef]
- Yang, W.; Liu, H.; Cheng, G. Modeling and performance study of vehicle-to-infrastructure visible light communication system for mountain roads. Sensors 2024, 24, 5541. [Google Scholar] [CrossRef]
- Singh, K.D.; Sood, S.K. QoS-aware optical fog-assisted cyber-physical system in the 5G ready heterogeneous network. Wirel. Pers. Commun. 2021, 116, 3331–3350. [Google Scholar] [CrossRef]
- Li, Y. Quality of service improvement in fiber-wireless networks using a fuzzy-based nature-inspired algorithm. Photon. Netw. Commun. 2022, 44, 82–89. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, X.; Wu, T.Y.; Qiu, Y. A routing algorithm for underwater acoustic-optical hybrid wireless sensor networks based on intelligent ant colony optimization and energy-flexible global optimal path selection. IEEE Sens. J. 2024, 24, 17116–17126. [Google Scholar] [CrossRef]
- Vyas, U. Deterministic lightpath scheduling and routing in elastic optical networks. Wirel. Pers. Commun. 2022, 124, 1593–1607. [Google Scholar] [CrossRef]
- Li, B.Q.; Zhu, Y.; Liu, Q.; Yao, X.X. Development of deterministic communication for in-vehicle networks based on software-defined time-sensitive networking. Machines 2024, 12, 816. [Google Scholar] [CrossRef]
- Mowla, M.M.; Ahmad, I.; Habibi, D.; Phung, Q.V.; Zahed, M.I.A. Green traffic backhauling in next generation wireless communication networks incorporating FSO/mmWave technologies. Comput. Commun. 2022, 182, 223–237. [Google Scholar] [CrossRef]
- Shin, H.; Baek, S.; Song, Y. Multidimensional beam optimization in underwater optical wireless communication based on deep reinforcement learning. IEEE Internet Things J. 2024, 11, 28623–28634. [Google Scholar] [CrossRef]
- Kamalakis, T.; Dogkas, L.; Simou, F. Optimization of a discrete multi-tone visible light communication system using a mixed-integer genetic algorithm. Opt. Commun. 2021, 485, 126741. [Google Scholar] [CrossRef]
- Arya, S.; Chung, Y.H. Artificial bee colony based iterative heuristic signal detection technique for optical wireless communications. IEEE J. Quantum Electron. 2023, 59, 8000311. [Google Scholar] [CrossRef]
- Singh, P.; Prakash, S. Implementation of marin predators algorithm for optimizing the position of multiple optical network units in fiber wireless access networks. Opt. Fiber Technol. 2022, 72, 102971. [Google Scholar] [CrossRef]
- Vieira, M.; Galvão, G.; Vieira, M.A.; Vestias, M.; Louro, P.; Vieira, P. Integrating visible light communication and AI for adaptive traffic management: a focus on reward functions and rerouting coordination. Appl. Sci. 2024, 15, 116. [Google Scholar] [CrossRef]
- Cai, Z.; Du, J.; Huang, T.; Lu, Z.; Liu, Z.; Gong, G. Energy-efficient collision-free machine/AGV scheduling using vehicle edge intelligence. Sensors 2024, 24, 8044. [Google Scholar] [CrossRef]
- Cai, Z.; Du, X.; Huang, T.; Lv, T.; Cai, Z.; Gong, G. Robotic edge intelligence for energy-efficient human–robot collaboration. Sustainability 2024, 16, 9788. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, Y.; Yang, S.X.; Hua, Q.; Sangaiah, A.K.; Yu, K. An intelligent deterministic scheduling method for ultralow latency communication in edge enabled industrial internet of things. IEEE Trans. Ind. Inf. 2023, 19, 1756–1767. [Google Scholar] [CrossRef]
- Li, P.; Wei, X.; Tang, X.; Deng, J.; Xu, J. UAV-assisted free space optical communication system with decode-and-forward relaying. IEEE Trans. Veh. Technol. 2024, 73, 14102–14112. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Q.; Fan, P.; Cheng, N.; Chen, W.; Letaief, K.B. DRL-based optimization for AoI and energy consumption in C-V2X enabled IoV. IEEE Trans. Green Commun. Netw. 2025. [Google Scholar] [CrossRef]
- P60802/D3.4, May 2025 - IEC/IEEE Draft International Standard Time-Sensitive Networking Profile for Industrial Automation. Date of Publication: 22 May 2025, Electronic ISBN: 979-8-8557-2246-8. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=11014762 (accessed on 7 July 2025).
- IEEE Std 802.15.7a 2024; IEEE Standard for Local and Metropolitan Area Networks—Part 15.7: Short Range Optical Wireless Communications Amendment 1: Higher Rate, Longer Range Optical Camera Communication (OCC). IEEE Computer Society: Washington, DC, USA, 2025.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).