A Mode-Selective Control in Two-Mode Superradiance from Lambda Three-Level Atoms
Abstract
1. Introduction
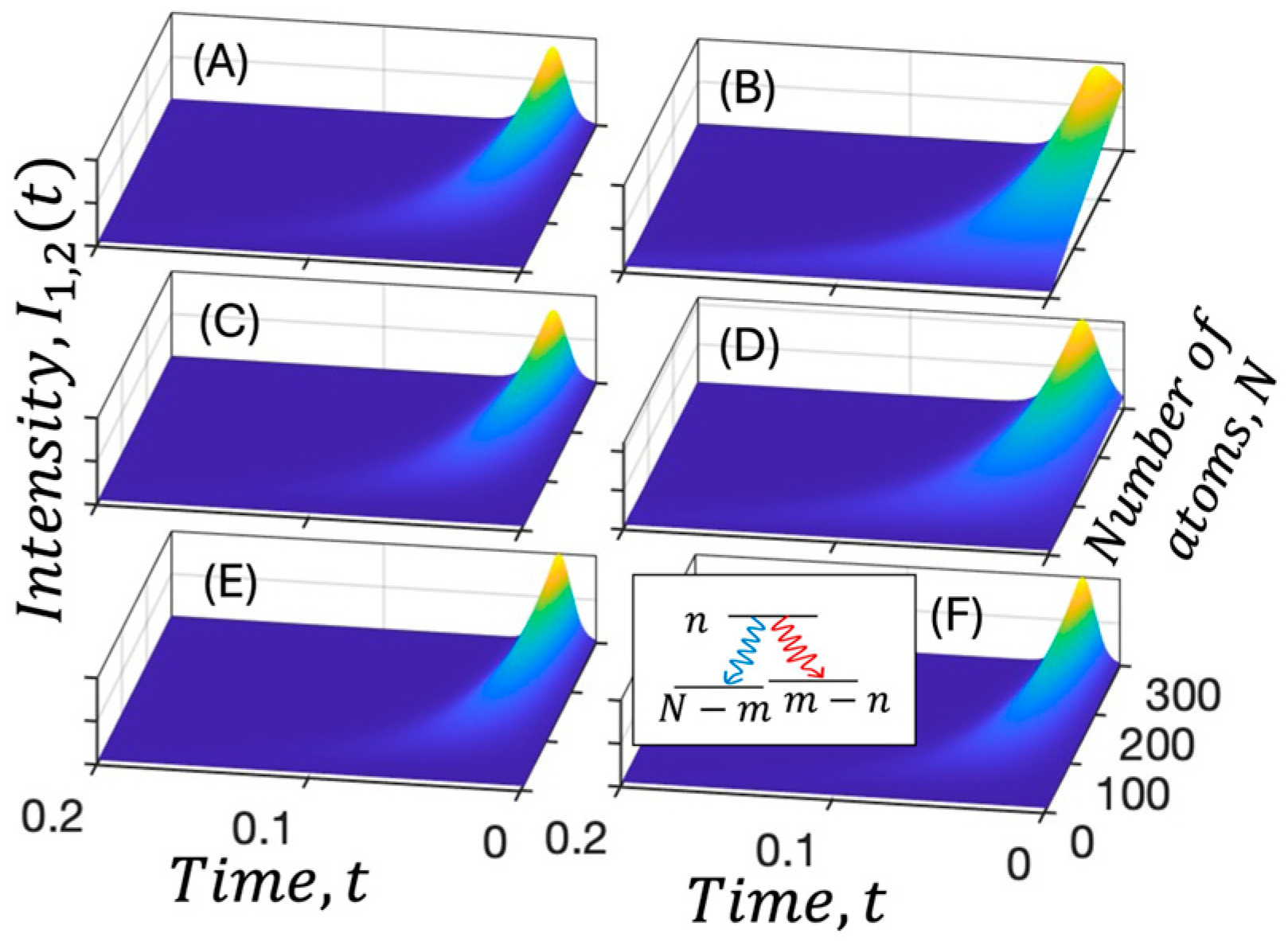
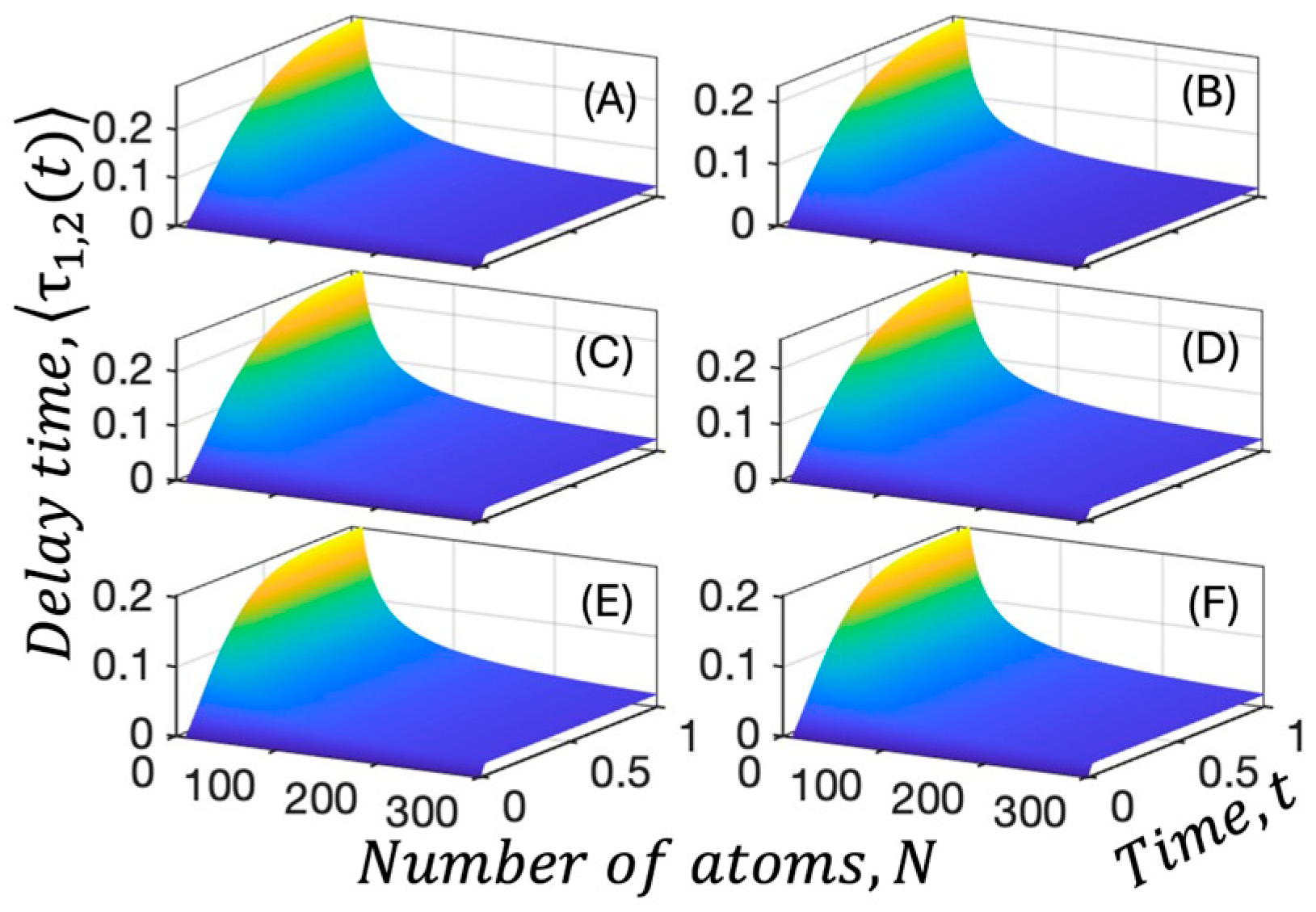
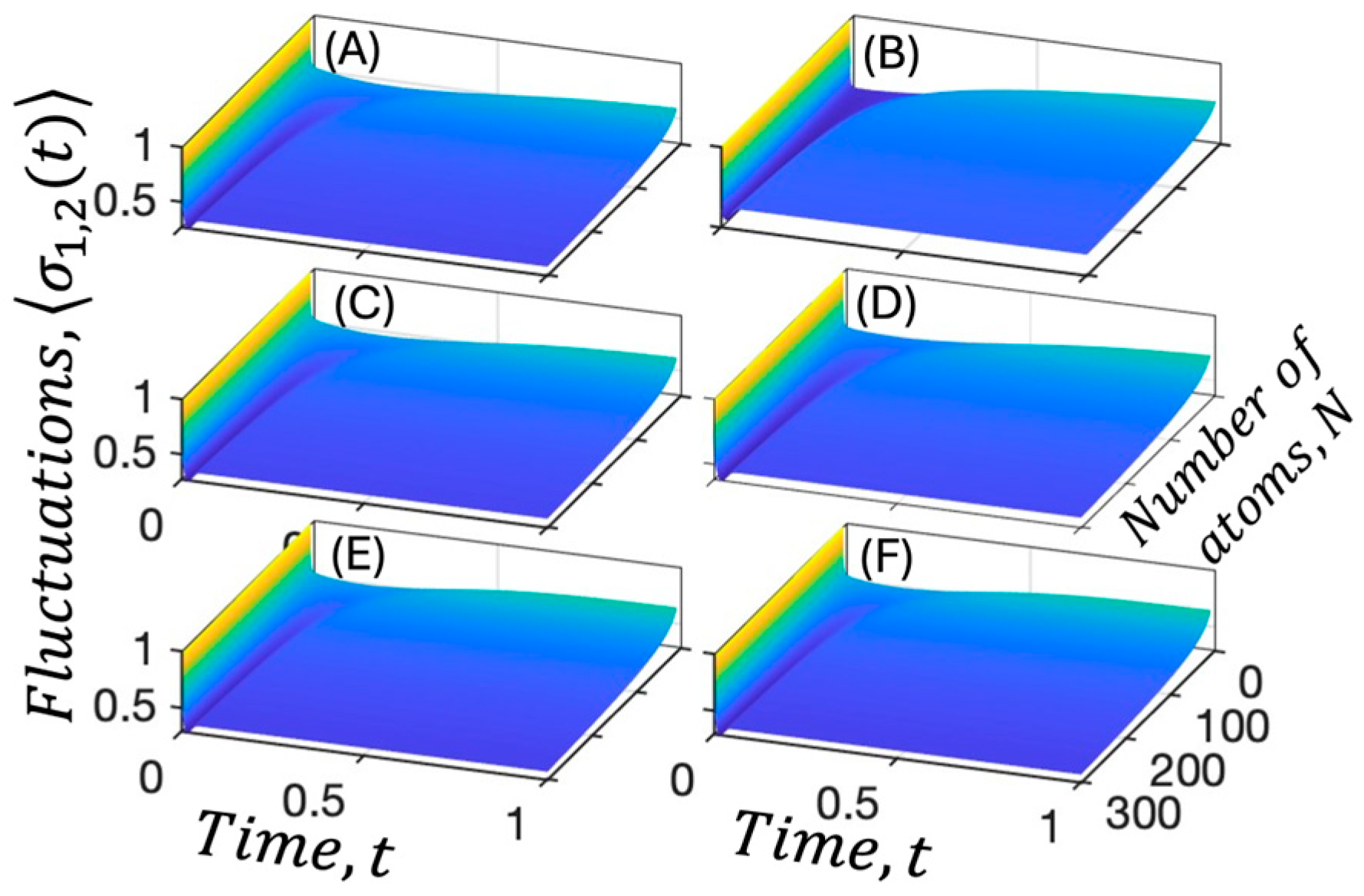
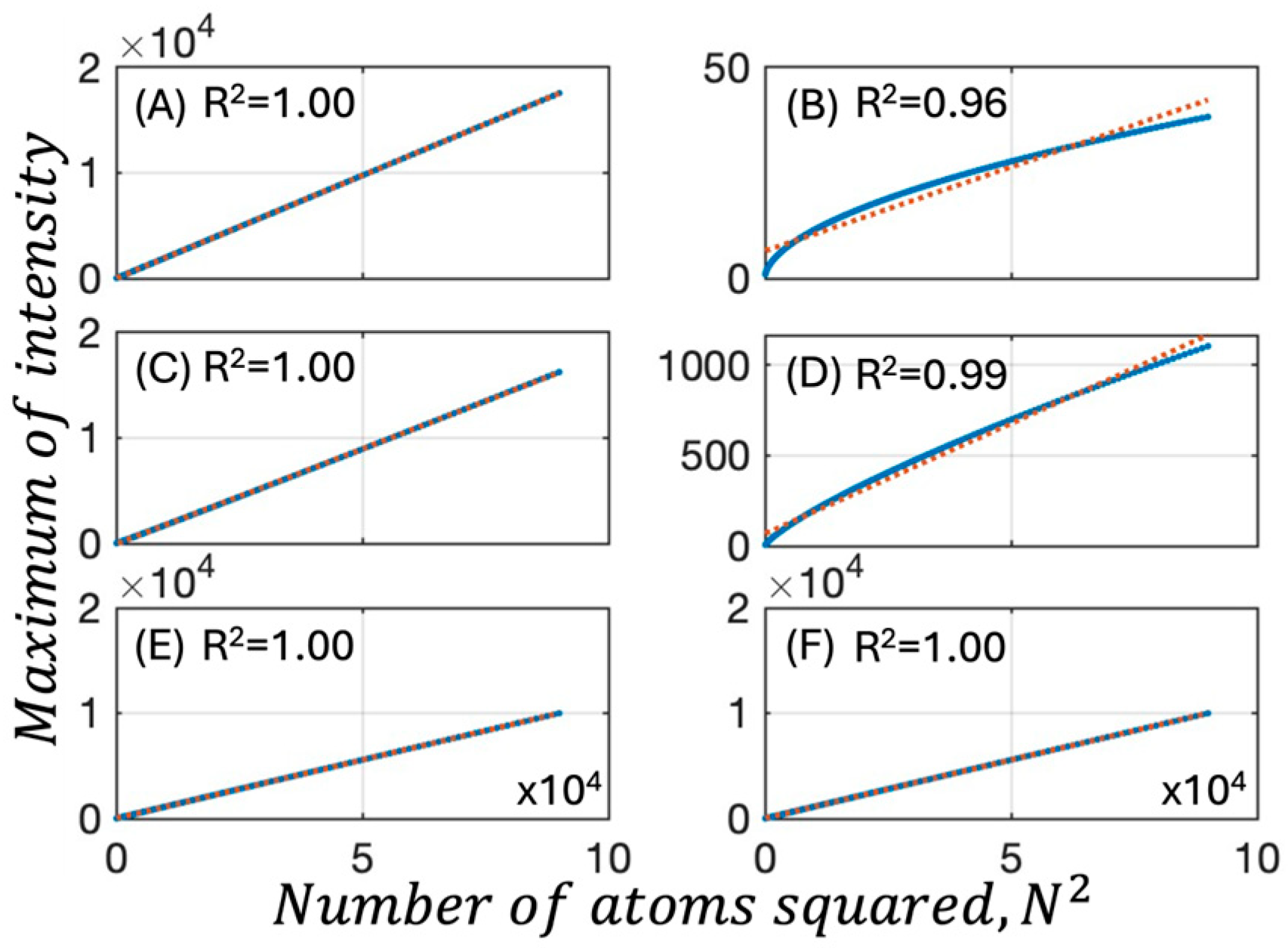
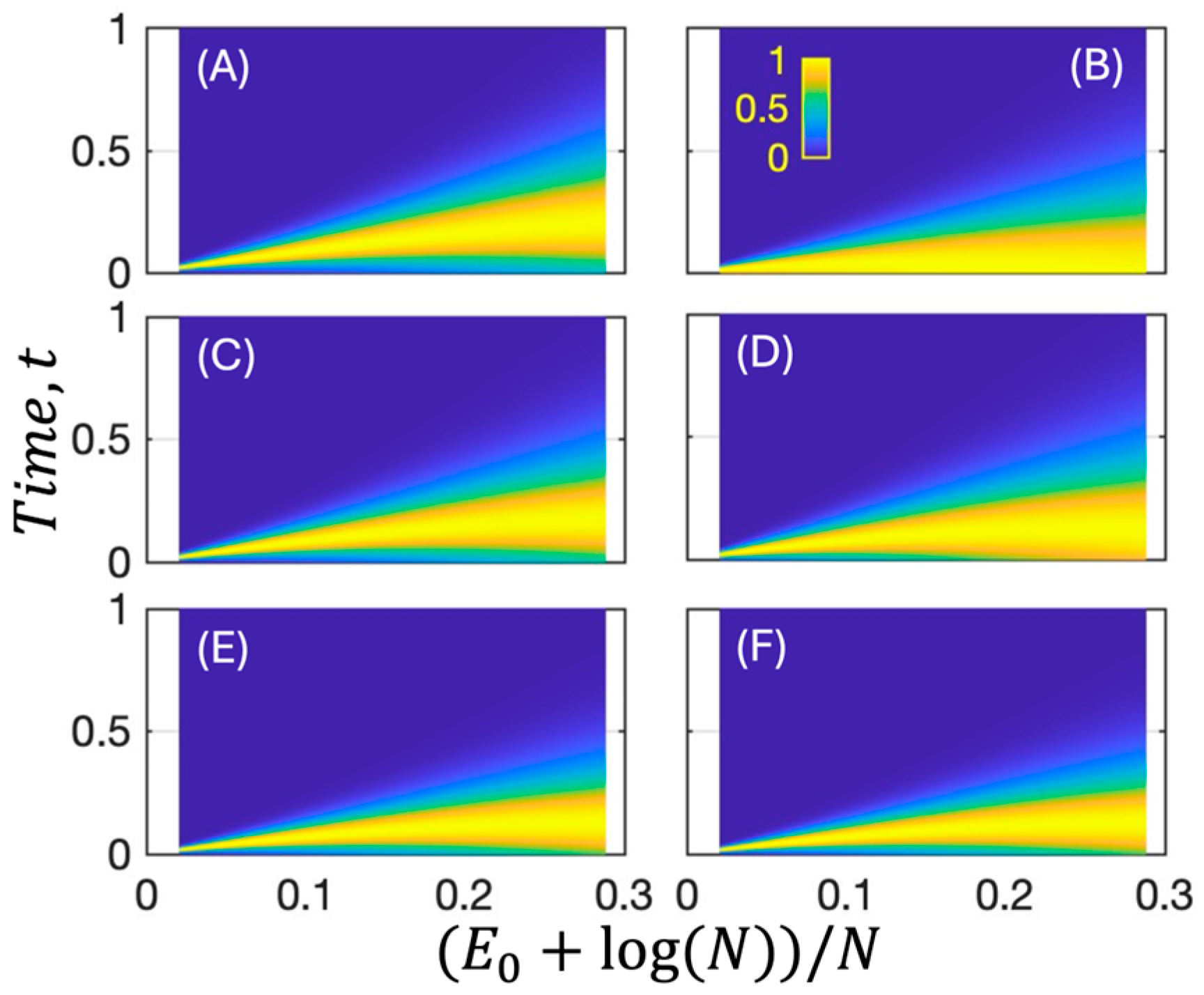
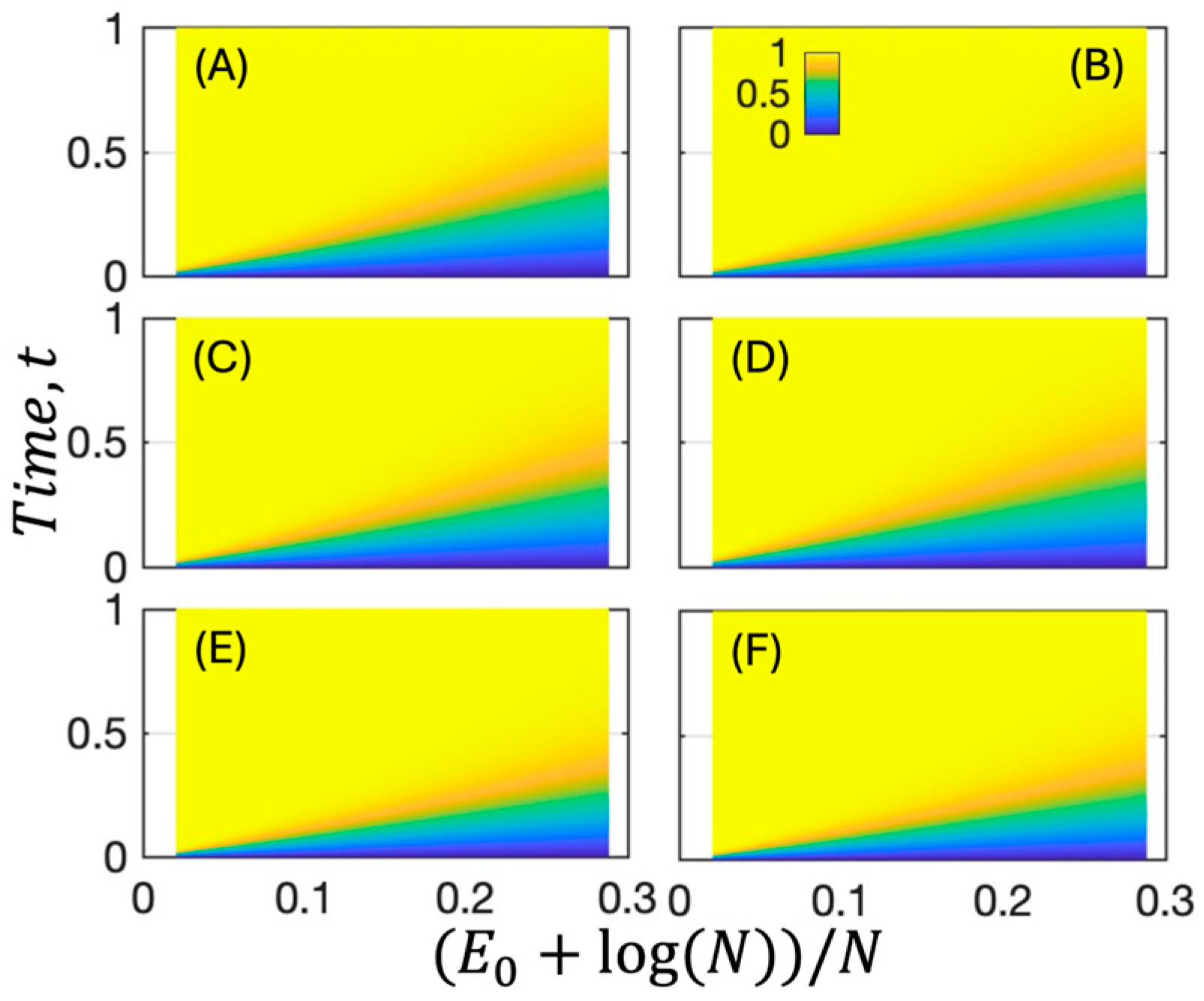
2. Results
3. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Averin, D.V.; Ruggiero, B.; Silvestrini, P. Macroscopic Quantum Coherence and Quantum Computing, 2001st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and Atoms; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1997. [Google Scholar]
- Kurizki, G.; Bertet, P.; Kubo, Y.; Mølmer, K.; Petrosyan, D.; Rabl, P.; Schmiedmayer, J. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. USA 2015, 112, 3866. [Google Scholar] [CrossRef] [PubMed]
- Bradac, C.; Johnsson, M.T.; van Breugel, M.; Baragiola, B.Q.; Martin, R.; Juan, M.L.; Brennen, G.K.; Volz, T. Room temperature spontaneous superradiance from single diamond nanocrystals. Nat. Commun. 2017, 8, 1205. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Green, K.K.; Huang, L.; Hallen, H.; Han, G.; Lim, S.F. Room-temperature upconverted superfluorescence a single lanthanide-doped up-conversion nanoparticle. Nat. Photonics 2022, 16, 737. [Google Scholar] [CrossRef]
- Findik, G.; Biliroglu, M.; Seyiitliiyev, D.; Mendes, J.; Barrette, A.; Ardekani, H.; Lei, L.; Dong, Q.; So, F.; Gundogdu, K. High-temperature superfluorescence in methyl ammonium lead iodide. Nat. Photonics 2021, 15, 676. [Google Scholar] [CrossRef]
- Biliroglu, M.; Findik, G.; Mendes, J.; Seyiitliiyev, D.; Lei, L.; Dong, Q.; Mehta, Y.; Temnov, V.V.; So, F.; Gundogdu, K. Room-temperature superfluorescence in hybrid perovskites and its origins. Nat. Photonics 2022, 16, 324. [Google Scholar] [CrossRef]
- Gundogdu, K.; So, F.; Brongersma, M.L.; Biliroglu, M.; Findik, G. Quantum analog of vibrational isolation: From Room-Temperature Superfluorescence to High-Temperature Superconductivity. arXiv 2022, arXiv:2204.09807. [Google Scholar]
- Dicke, R.H. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Rehler, N.E.; Eberly, J.H. Superradiance. Phys. Rev. A 1971, 3, 1735. [Google Scholar] [CrossRef]
- Bonifacio, R.; Lugiato, L.A. Cooperative radiation processes in two-level systems: Superfluorescence. Phys. Rev. A 1975, 11, 1507. [Google Scholar] [CrossRef]
- MacGillivray, J.C.; Feld, M.S. Theory of superradiance in an extended, optically thick medium. Phys. Rev. A 1976, 14, 1169–1189. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Kocharovsky, V.I.V.; Zheleznyakov, V.V.; Kocharovskaya, E.R.; Kocharovsky, V.V. Superradiance: The principles of generation and implementation in lasers. Usp. Fiz. Nauk 2017, 60, 345–384. [Google Scholar] [CrossRef]
- Cong, K.; Zhang, Q.; Wang, Y.; Noe II, G.T.; Belyanin, A.; Kono, J. Dicke superradiance in solids (invited review). J. Opt. Soc. Am. B 2016, 33, C80–C101. [Google Scholar] [CrossRef]
- Lin, G.-D.; Yelin, S.F. Superradiance: An Integrated Approach to Cooperative Effects in Various Systems. Adv. Atom. Mol. Opt. Phys. 2012, 61, 295. [Google Scholar]
- Skribanowitz, N.; Herman, I.P.; MacGillivray, J.C.; Feld, M.S. Observation of Dicke Superradiance in Optically Pumped HF Gas. Phys. Rev. Lett. 1973, 30, 309. [Google Scholar] [CrossRef]
- Marek, J. Observation of superradiance in Rb vapour. J. Phys. B 1979, 12, L229. [Google Scholar] [CrossRef]
- Vrehen, Q.H.; Schuurmans, M.F.; Polder, D. Superfluorescence: Macroscopic quantum fluctuations in the time domain. Nature 1980, 70, 285. [Google Scholar] [CrossRef]
- Vrehen, Q.H.F.; Der Weduwe, J.J. Quantum fluctuations in superfluorescence delay times. Phys. Rev. A 1981, 24, 2857. [Google Scholar] [CrossRef]
- Crubellier, A.; Liberman, S.; Pillet, P.; Schweighofer, M.G. Experimental study of quantum fluctuations of polarization in supperradiance. J. Phys. B Atom. Mol. Phys. 1981, 14, L177. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Quantum fluctuations of superfluorescence delay observed with ultrashort optical excitations. Phys. Lett. A 2012, 376, 335. [Google Scholar] [CrossRef]
- Bohnet, J.G.; Chen, Z.; Weiner, J.M.; Meiser, D.; Holland, M.J.; Thompson, J.K. A steady-state superradiant laser with less than one intracavity photon. Nature 2012, 484, 78. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Kash, M.M.; Sautenkov, V.A.; Li, H.; Rostovtsev, Y.V.; Welch, G.R.; Scully, M.O. Observation of Picosecond Superfluorescent Pulses in Rubidium Vapor Pumped by 100-Femtosecond Laser Pulses. Phys. Rev. A 2010, 82, 043421. [Google Scholar] [CrossRef]
- Rainò, G.; Becker, M.A.; Bodnarchuk, M.I.; Mahrt, R.F.; Kovalenko, M.V.; Stöferle, T. Superfluorescence from lead halide perovskite quantum dot superlattices. Nature 2018, 563, 671. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Temporal coherent control of superfluorescent pulses. Opt. Lett. 2012, 37, 2400. [Google Scholar] [CrossRef]
- Bohr, E.A.; Kristensen, S.L.; Hotter, C.; Schäffer, S.A.; Robinson-Tait, J.; Thomsen, J.W.; Zelevinsky, T.; Ritsch, H.; Müller, J.H. Collectively enhanced Ramsey readout by cavity sub- to superradiant transition. Nat. Commun. 2024, 15, 1084. [Google Scholar] [CrossRef]
- Gross, M.; Fabre, C.; Pillet, P.; Haroche, S. Observation of near-infrared Dicke superradiance on cascading transitions in atomic sodium. Phys. Rev. Lett. 1976, 36, 1035. [Google Scholar] [CrossRef]
- Okada, J.; Ikeda, K.; Matsuoka, M. Cooperative cascade emission. Opt. Commun. 1978, 26, 189–192. [Google Scholar] [CrossRef]
- Ikeda, K.; Okada, J.; Matsuoka, M. Theory of cooperative cascade emission. II. J. Phys. Soc. Jpn. 1980, 48, 1646–1654. [Google Scholar] [CrossRef]
- Brechignac, C.; Cahuzac, P. Population inversion on the resonance line of strontium by using cascading superfluorescences in a three-level system. J. Phys. B 1981, 14, 221. [Google Scholar] [CrossRef]
- Florian, R.; Schwan, L.O.; Schmid, D. Time-resolving experiments on Dicke super-fluorescence of O−2centers in KCl. Two-color superfluorescence. Phys. Rev. Lett. 1984, 29, 301–396. [Google Scholar]
- Brownell, J.H.; Lu, X.; Hartmann, S.R. Yoked superfluorescence. Phys. Rev. Lett. 1995, 75, 3265. [Google Scholar] [CrossRef]
- Kitano, K.; Maeda, H. Cascade and yoked superrfluorescence detected by sum frequency generation spectroscopy. Opt. Lett. 2023, 48, 69. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Scully, M.O. Ultrafast laser control of backward superfluorescence towards standoff sensing. Appl. Phys. Lett. 2014, 104, 021114. [Google Scholar] [CrossRef]
- Thompson, J.; Ballmann, C.; Cai, H.; Yi, Z.; Rostovtsev, Y.; Sokolov, A.; Hemmer, P.; Zheltikov, A.; Ariunbold, G.O.; Scully, M.O. Pulsed cooperative backward emissions from non-degenerate atomic transitions in sodium. New J. Phys. 2014, 16, 103017. [Google Scholar] [CrossRef]
- Ariunbold, G.O.; Sautenkov, V.A.; Li, H.; Murawski, R.K.; Wang, X.; Zhi, M.; Begzjav, T.; Sokolov, A.V.; Scully, M.O.; Rostovtsev, Y.V. Observations of Ultrafast Superfluorescent Beatings in a Cesium Vapor Excited by Femtosecond Laser Pulses. Phys. Lett. A 2022, 428, 127945. [Google Scholar] [CrossRef]
- Bonifacio, R.; Schwendimann, P.; Haake, F. Quantum statistical theory of super-radiance. I. Phys. Rev. A 1971, 4, 302–313. [Google Scholar] [CrossRef]
- Bonifacio, R.; Schwendimann, P.; Haake, F. Quantum statistical theory of super-radiance. II. Phys. Rev. A 1971, 4, 852–864. [Google Scholar]
- Degiorgio, V. Statistical properties of superradiant pulses. Opt. Commun. 1971, 2, 362–364. [Google Scholar] [CrossRef]
- Lee, C.T. Exact solutions of the superradiance master equation. I. Complete initial excitation. Phys. Rev. A 1977, 15, 2019. [Google Scholar] [CrossRef]
- Lee, C.T. Exact solution of the superradiance master equation. II. arbitrary initial excitation. Phys. Rev. A 1977, 16, 301–312. [Google Scholar] [CrossRef]
- Lee, C.T. Fluctuations in tipping angles and delay times of simple superfluorescence. Appl. Phys. Lett. 1982, 41, 821. [Google Scholar] [CrossRef]
- Agarwal, G.S. Quantum statistical theory of coherent emission from a system of multi-level atoms. Phys. Lett. 1973, 45A, 15. [Google Scholar] [CrossRef]
- Cho, Y.C.; Kurnit, N.A.; Gilmore, R. Coherence and Quantum Optics; Mandel, L., Wolf, E., Eds.; Plenum Publ. Co.: New York, NY, USA, 1973; p. 755. [Google Scholar]
- Gilmore, R. Coherent States in Modern Physics. In Coherence and Quantum Optics; Mandel, L., Wolf, E., Eds.; Plenum Publ. Co.: New York, NY, USA, 1973; p. 217. [Google Scholar]
- Agarwal, G.S.; Trivedi, S.S. Superradiance from three-level systems in atomic coherent state representation. Opt. Commun. 1976, 18, 417. [Google Scholar] [CrossRef]
- Ariunbold, G.O. A Cascade Superradiance Model. Phys. Lett. A 2022, 452, 128468. [Google Scholar] [CrossRef]
- Braggio, C.; Chiossi, F.; Carugno, G.; Ortolan, A.; Ruoso, G. Spontaneous formation of a macroscopically extended coherent state. Phys. Rev. Res. 2020, 2, 033059. [Google Scholar] [CrossRef]
- Chiossi, F.; Braggio, C.; Khanbekyan, A.; Carugno, G.; Ortolan, A.; Ruoso, G.; Calabrese, R.; Di Lieto, A.; Tomassetti, L.; Tonelli, M. Cascade superfluorescence in Er:YLF. Phys. Rev. Res. 2021, 3, 013138. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ariunbold, G.O.; Begzjav, T. A Mode-Selective Control in Two-Mode Superradiance from Lambda Three-Level Atoms. Photonics 2025, 12, 674. https://doi.org/10.3390/photonics12070674
Ariunbold GO, Begzjav T. A Mode-Selective Control in Two-Mode Superradiance from Lambda Three-Level Atoms. Photonics. 2025; 12(7):674. https://doi.org/10.3390/photonics12070674
Chicago/Turabian StyleAriunbold, Gombojav O., and Tuguldur Begzjav. 2025. "A Mode-Selective Control in Two-Mode Superradiance from Lambda Three-Level Atoms" Photonics 12, no. 7: 674. https://doi.org/10.3390/photonics12070674
APA StyleAriunbold, G. O., & Begzjav, T. (2025). A Mode-Selective Control in Two-Mode Superradiance from Lambda Three-Level Atoms. Photonics, 12(7), 674. https://doi.org/10.3390/photonics12070674






