Performance Analysis of Space-to-Ground Downlink for Polarization Shift Keying Optical Communications with a Gaussian-Schell Model Beam
Abstract
1. Introduction
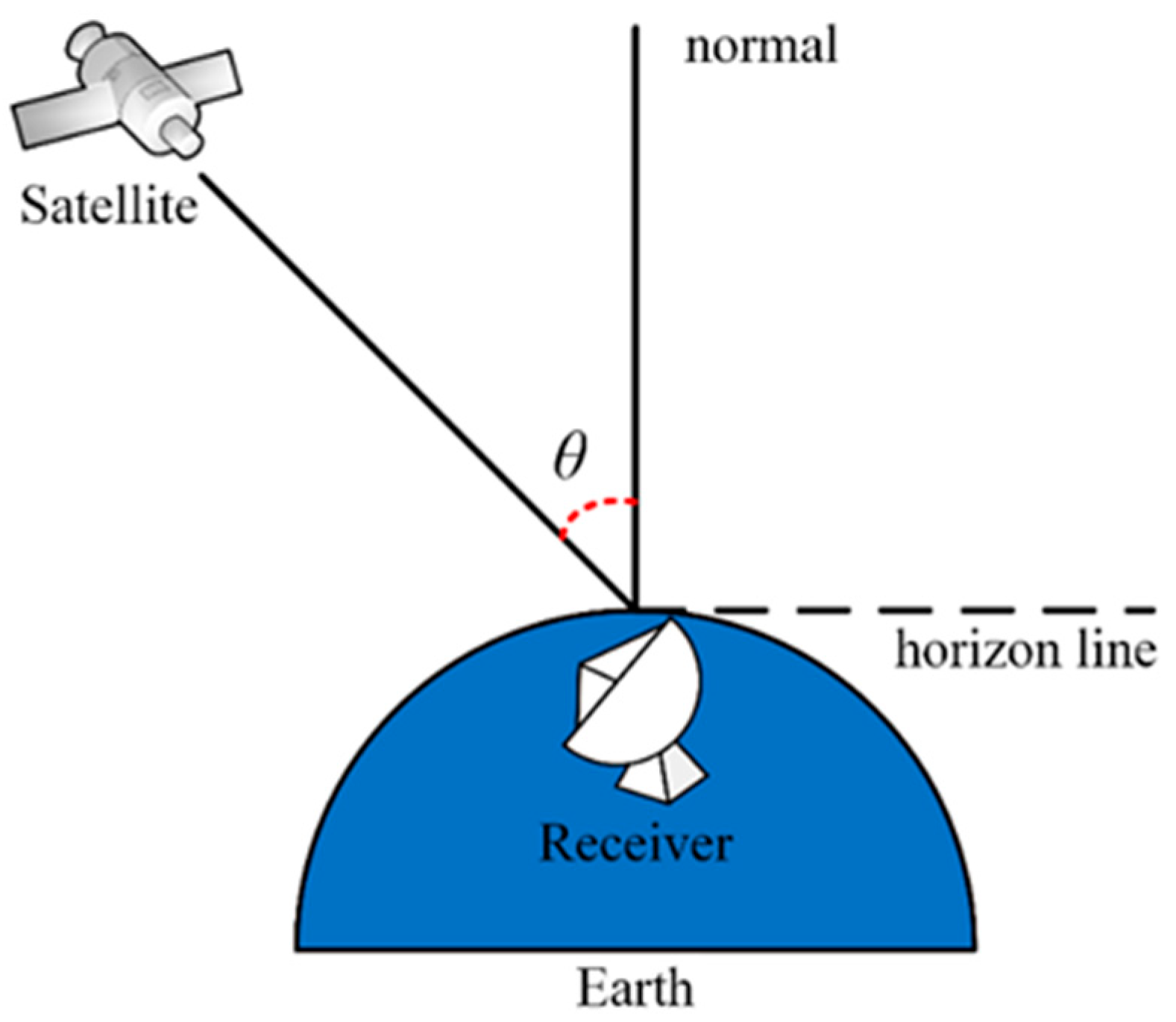
2. Theoretical Model of Polarization Characteristics
3. Performance Analysis of Direct Detection CPolSK System
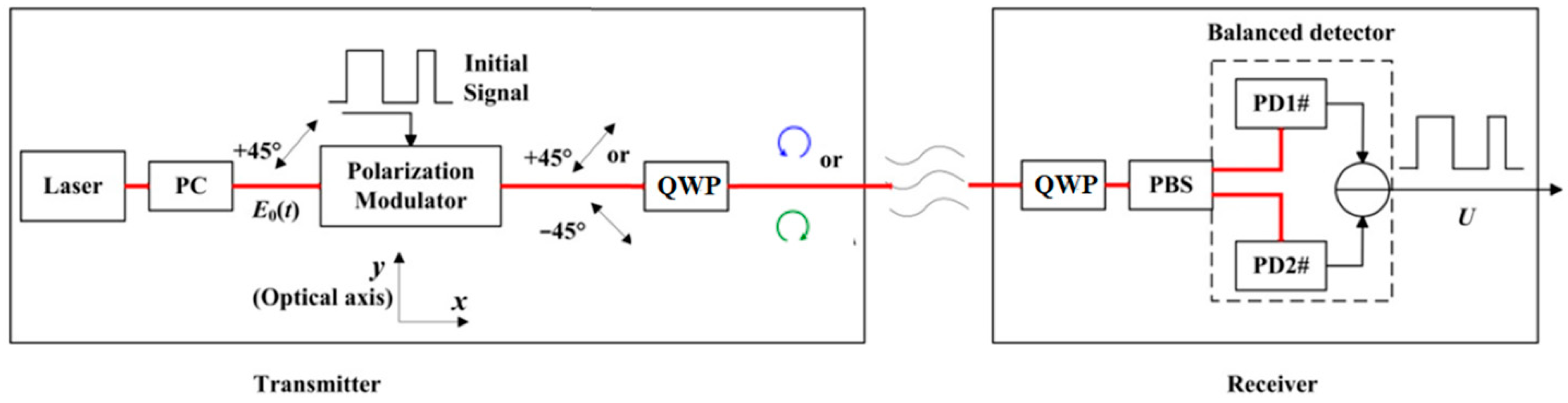
3.1. Direct Detection CPolSK System Model
3.2. Bit Error Rate
4. Numerical Results and Analysis
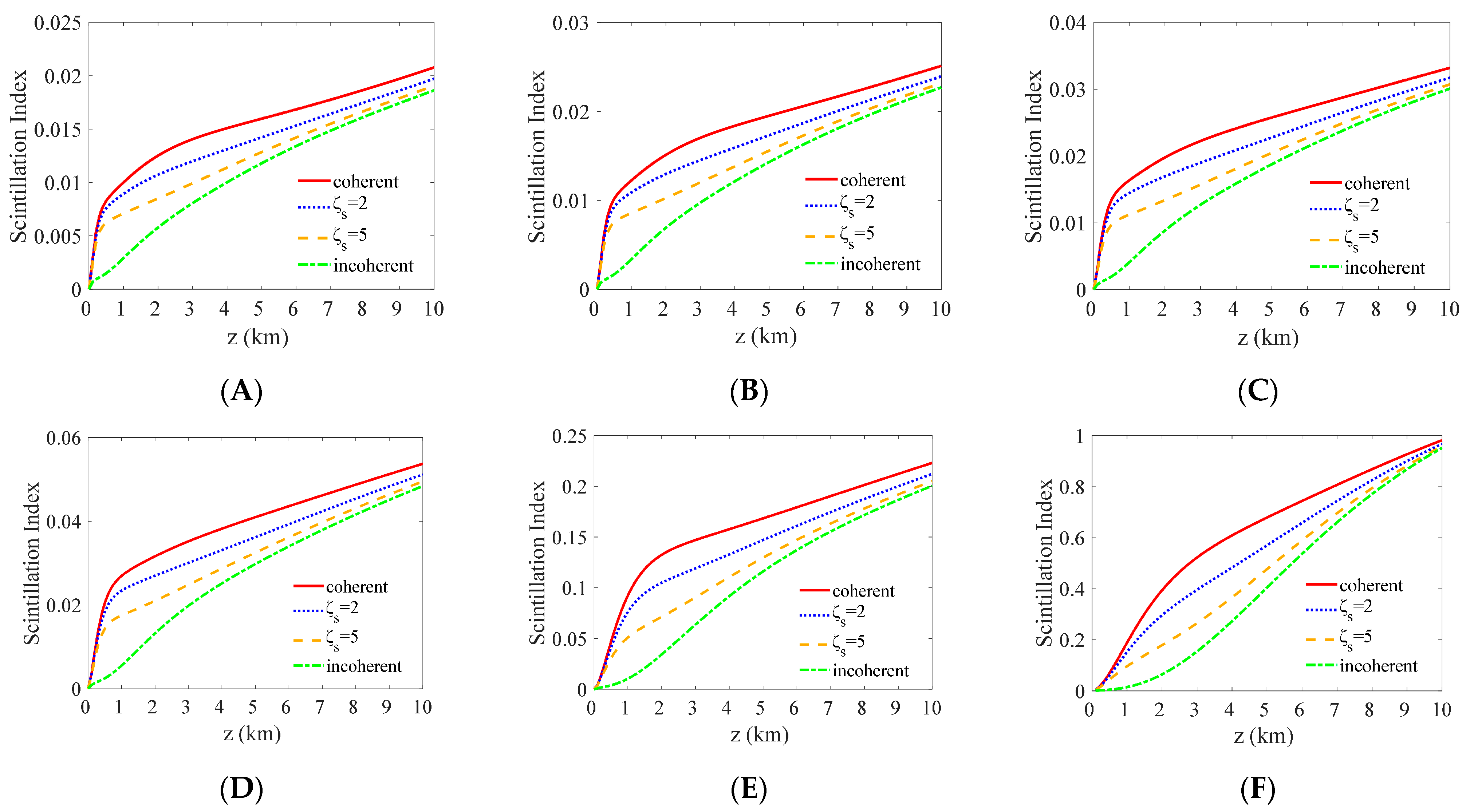
4.1. GSM Beam Scintillation Index in Space-to-Ground Link
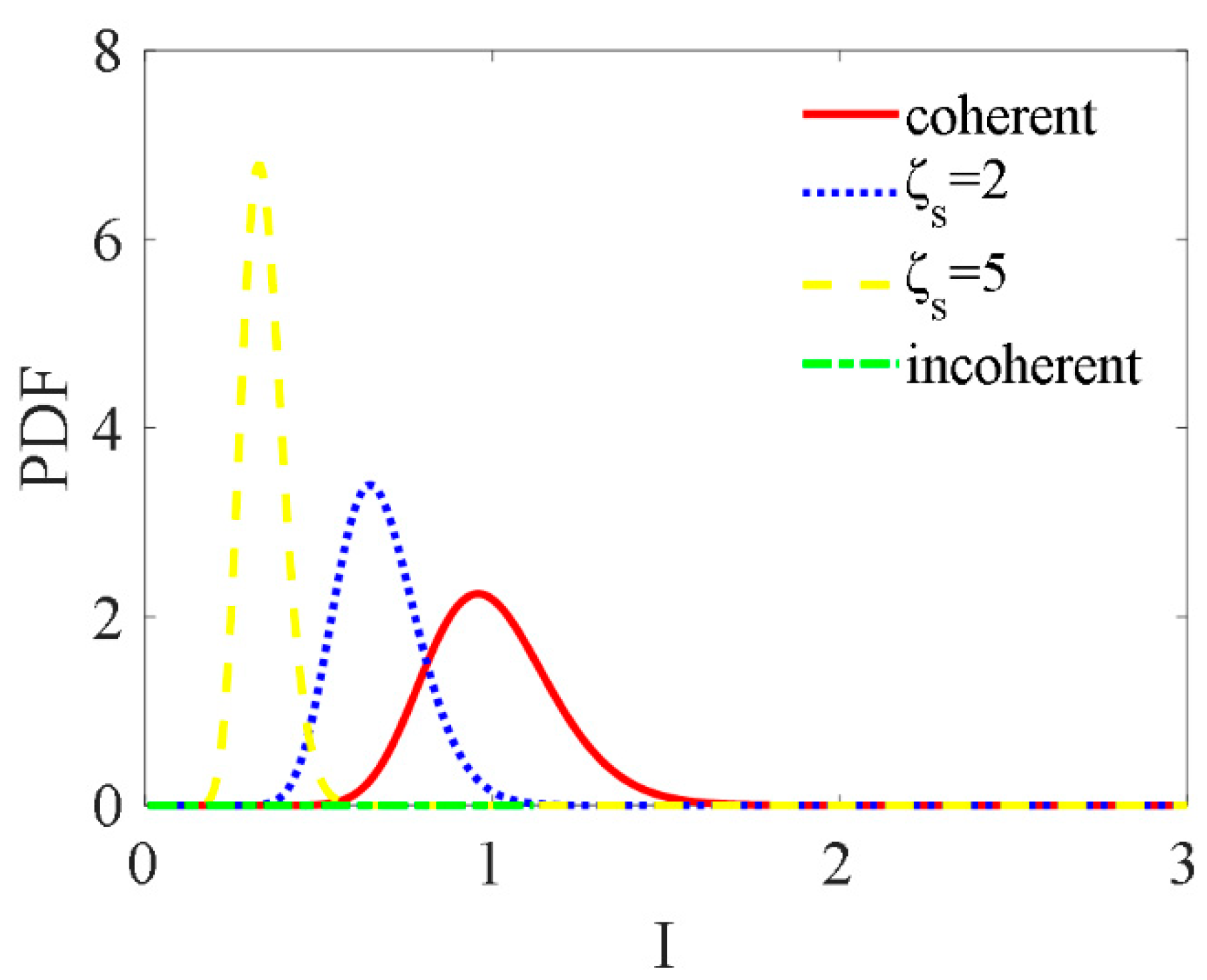
4.2. GSM Beam Probability Density Distribution of Receiving Optical Intensity
4.3. Performance of CPolSK-Modulated System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nykolak, G.; Szajowski, P.F.; Cashion, A.; Presby, H.M.; Tourgee, G.E.; Auborn, J.J. Low-cost active imaging of objects in water. Proc. SPIE 2000, 3932, 16–20. [Google Scholar]
- Nykolak, G.; Raybon, G.; Mikkelsen, B.; Brown, B.B.; Szajowski, P.F.; Auborn, J.J.; Presby, H.M. Optical imaging with time-domain resolution. Proc. SPIE 2001, 4214, 11–13. [Google Scholar]
- Berman, G.P.; Bishop, A.R.; Chernobrod, B.M.; Nguyen, D.C.; Gorshkov, V.N. Quantum interference in photonic crystal structures. Opt. Commun. 2007, 280, 264–270. [Google Scholar] [CrossRef][Green Version]
- Nykolak, G.; Szajowski, P.F.; Tourgee, G.; Presby, H. Observations of a new measurement technique. Electron. Lett. 1999, 35, 578–579. [Google Scholar] [CrossRef]
- Szajowski, P.F.; Nykolak, G.; Auborn, J.J.; Presby, H.M.; Tourgee, G.E. Analysis of a novel imaging system. Proc. SPIE 1998, 3532, 29–40. [Google Scholar]
- McFadden, M.J.; Iqbal, M.; Dillon, T.; Nair, R.; Gu, T.; Prather, D.W.; Haney, M.W. High-resolution imaging in optical systems. Appl. Opt. 2005, 45, 6358–6366. [Google Scholar] [CrossRef]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Spatial correlation and irradiance statistics in a multiple-beam terrestrial free-space optical communication link. Appl. Opt. 2007, 46, 6561–6571. [Google Scholar] [CrossRef]
- Gase, R.J. New perspectives on optical filtering. J. Mod. Opt. 1991, 38, 1107–1115. [Google Scholar] [CrossRef]
- Deschamps, J.; Courjon, D.; Bulabois, J. Gaussian Schell-model sources: An example and some perspectives. J. Opt. Soc. Am. 1983, 73, 256–261. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Friberg, T.; Sudol, R.L. Spatial coherence in laser beams. Opt. Commun. 1982, 41, 383–387. [Google Scholar] [CrossRef]
- Belenkii, M.S.; Mironov, V.L. Coherent and incoherent effects in laser light. Sov. J. Quantum Electron. 1980, 10, 595–597. [Google Scholar]
- Belenkii, M.S.; Kon, A.I.; Mironov, V.L. Studies in laser coherence. Sov. J. Quantum Electron. 1977, 7, 287–290. [Google Scholar]
- Wang, S.C.H.; Plonus, M.A. Optical beam propagation for a partially coherent source in the turbulent atmosphere. J. Opt. Soc. Am. 1979, 69, 1297–1304. [Google Scholar] [CrossRef]
- Fante, R.L. The effect of source temporal coherence on light scintillations in weak turbulence. J. Opt. Soc. Am. 1979, 69, 71–73. [Google Scholar] [CrossRef]
- Baykal, Y.; Plonus, M.A.; Wang, S. Application of radio wave propagation techniques. J. Radio. Sci. 1983, 18, 551–556. [Google Scholar] [CrossRef]
- Li, C.Q.; Zhang, H.Y.; Wang, T.F.; Liu, L.S.; Guo, J. Investigation on coherence characteristics of Gauss-Schell model beam propagating in atmospheric turbulence. Acta Phys. Sin. 2013, 62, 224203. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.Z.; Zeng, A.J.; Yang, K. Effect of atmospheric turbulence on the spatial coherence of quasi-monochromatic Gaussian Schell-model beams propagating in the slant path. Acta Phys. Sin. 2008, 57, 634–638. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M.; Weyrauch, T. Optical techniques in atmospheric propagation. In Optics in Atmospheric Propagation and Adaptive Systems IV; SPIE: Bellingham, WA, USA, 2001; Volume 4538, pp. 13–23. [Google Scholar]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Advances in adaptive optics systems. Proc. SPIE 2003, 4884, 95–103. [Google Scholar]
- Ricklin, J.C.; Davidson, F.M. Atmospheric optical communication with a Gaussian Schell beam. J. Opt. Soc. Am. A 2003, 20, 856–866. [Google Scholar] [CrossRef]
- Lü, B.D. Laser Optics: Beam Characterization, Propagation and Transformation. In Resonator Technology and Physics; Higher Education Press: Beijing, China, 2003. [Google Scholar]
- Andrews, L.C. Laser beam propagation through random media. In Laser Beam Propagation Through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Yu, P.T. Optical scintillations and fade statistics for a satellite-communication system. Appl. Opt. 1995, 34, 7742–7751. [Google Scholar] [CrossRef] [PubMed]
- Miller, W.B.; Ricklin, J.C.; Andrews, L.C. Log-amplitude variance and wave structure function: A new perspective for Gaussian beams. J. Opt. Soc. Am. A 1993, 10, 661–672. [Google Scholar] [CrossRef]
- Fried, D.L. Aperture Averaging of Scintillation. J. Opt. Soc. Am. 1967, 57, 169–175. [Google Scholar] [CrossRef]

| Title 1 | Title 2 | Title 3 |
|---|---|---|
| radius of curvature | F0 | ∞ |
| source coherence parameter | ζs | 1, 2, 5, ∞ |
| laser wavelength | λ | 1550 nm |
| receiving aperture | D | 1–10 cm |
| transmission distance | z | 10 km |
| beam waist width | W0 | 5 cm |
| zenith angle | θ | 0–88° |
| wind velocity | v | 21 m/s |
| refractive index parameter | C0 | 1.7 × 10−14 m−2/3 |
| transmission altitude | H0 | 20 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhang, Y.; Li, Q.; Yu, S.; Yu, J. Performance Analysis of Space-to-Ground Downlink for Polarization Shift Keying Optical Communications with a Gaussian-Schell Model Beam. Photonics 2025, 12, 643. https://doi.org/10.3390/photonics12070643
Wu J, Zhang Y, Li Q, Yu S, Yu J. Performance Analysis of Space-to-Ground Downlink for Polarization Shift Keying Optical Communications with a Gaussian-Schell Model Beam. Photonics. 2025; 12(7):643. https://doi.org/10.3390/photonics12070643
Chicago/Turabian StyleWu, Jiajie, Yuwei Zhang, Qingyan Li, Siyuan Yu, and Jianjie Yu. 2025. "Performance Analysis of Space-to-Ground Downlink for Polarization Shift Keying Optical Communications with a Gaussian-Schell Model Beam" Photonics 12, no. 7: 643. https://doi.org/10.3390/photonics12070643
APA StyleWu, J., Zhang, Y., Li, Q., Yu, S., & Yu, J. (2025). Performance Analysis of Space-to-Ground Downlink for Polarization Shift Keying Optical Communications with a Gaussian-Schell Model Beam. Photonics, 12(7), 643. https://doi.org/10.3390/photonics12070643





