Development and Verification of Sampling Timing Jitter Noise Suppression System for Phasemeter

Abstract

As the primary electronic payload of laser interferometry system for space gravitational wave detection, the core function of the phasemeter is ultra-high precision phase measurement. According to the principle of laser heterodyne interferometry and the requirement of 1 pm ranging accuracy of the phasemeter, the phase measurement noise should reach 2π μrad/Hz^1/2@(0.1 mHz–1 Hz). The heterodyne interference signal first passes through the quadrant photoelectric detector (QPD) to achieve photoelectric conversion, then passes through the analog-to-digital converter (ADC) to achieve analog and digital conversion, and finally passes through the digital phase-locked loop (DPLL) for phase locking. The sampling timing jitter of the heterodyne interference signal caused by the ADC is the main noise affecting the phase measurement performance and must be suppressed. This paper proposes a sampling timing jitter noise suppression system (STJNSS), which can set system parameters for high-frequency signals used for inter-satellite clock noise transmission, the system clock of the phasemeter, and the pilot frequency for suppressing ADC sampling timing jitter noise, meeting the needs of the current major space gravitational wave detection plans. The experimental results after the integration of SJNSS and the phase meter show that the phase measurement noise of the heterodyne interferometer signal reaches 2π μrad/Hz^1/2@(0.1 mHz–1 Hz), which meets the requirements of space gravitational wave missions.

1. Introduction

In 1916, Einstein formulated the theoretical framework of general relativity and first predicted the existence of gravitational waves. Nearly a century later, in 2015, the ground-based gravitational wave detector LIGO made the first direct detection of these waves [1,2], marking the beginning of gravitational wave astronomy. Due to the influence of Earth’s gravitational field variations, surface vibrations, and other environmental factors, ground-based detectors are primarily sensitive to frequencies above 10 Hz. To observe gravitational wave sources with greater mass, at larger distances, and in lower-frequency bands, it is essential to overcome the limitations inherent in ground-based detection [3]. Deploying space-based detectors with very long baselines presents the most promising solution. These detectors utilize the principle of laser heterodyne interferometry to measure the relative displacement between spacecraft by detecting the phase shift in the interference signal. The payload responsible for measuring this phase shift is referred to as a phasemeter. According to system-level performance requirements, the phasemeter must achieve a displacement sensitivity of 1 pm, corresponding to a phase measurement noise requirement of 2π μrad/Hz^1/2@(0.1 mHz–1 Hz) in the frequency range of 0.1 mHz to 1 Hz. Current major space-based gravitational wave detection initiatives include LISA [4,5], the Taiji program [6,7], and the Tianqin program [8,9].

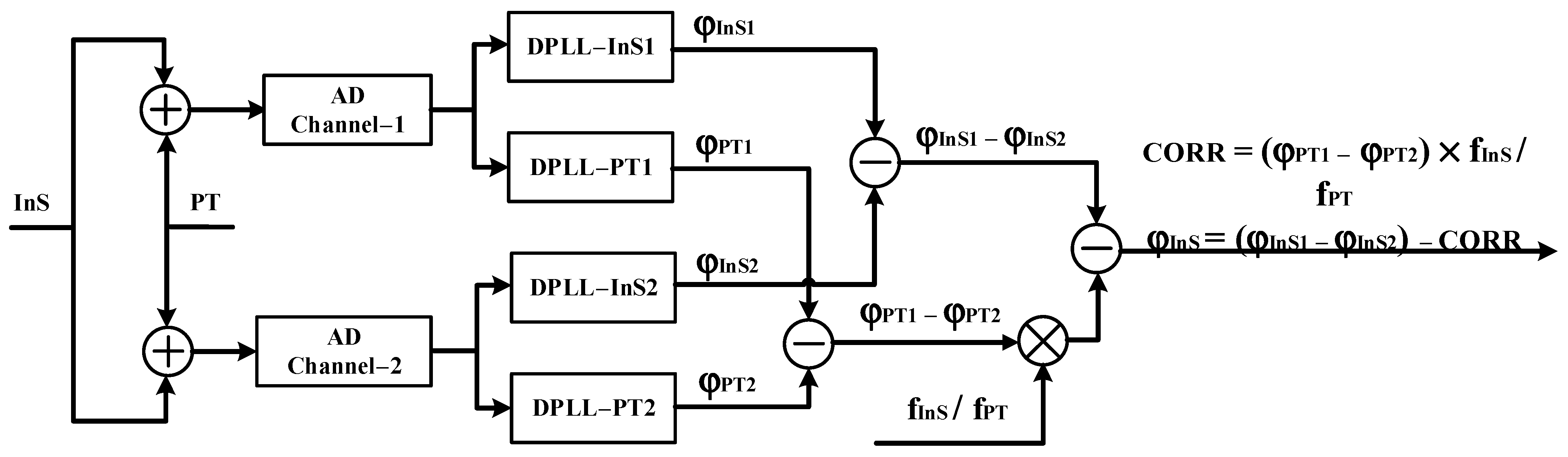
The interference signal is first rectified and filtered by a QPD and then digitized by an ADC, which converts the continuous-time, continuous-amplitude beat signal into a sequence of discrete digital values. Digitization is inherently a nonlinear process, as it involves rounding the analog signal to the nearest quantized level. The primary noise sources in the analog-to-digital conversion process are quantization noise and sampling timing jitter. Since the linear spectral density of phase noise induced by quantization is typically negligible, sampling clock jitter becomes the dominant source of phase noise in the digitization of beat frequency signals [10]. To mitigate this effect, noise suppression techniques are employed to compensate for ADC sampling delay mismatches across QPD detector channels, thereby improving the accuracy of phase measurement.

Currently, the major space-based gravitational wave detection programs employ a method based on pilot tone calibration for ADC sampling timing jitter correction [11,12,13]. This is achieved by injecting a stable reference pilot tone signal with a fixed frequency into the input of each ADC. The phase noise obtained from the phase measurement of the high-frequency pilot tone signal is primarily attributed to ADC sampling timing jitter. Adding a pilot tone signal to all ADC channels allows the phase jitter component of the beat signal’s phase measurement to be effectively eliminated through the phase measurement results from the pilot tone signal. Clock stability plays a critical role in the performance of phase measurement, making it essential to use an ultra-stable clock as the system clock for the phasemeter. To eliminate the phase noise from the oscillator generating the pilot tone and the phase jitter between interstellar pilot tones, the high-frequency signal, after frequency doubling of the pilot tone, is phase-modulated onto the laser link carrier [14]. This enables the transfer of interstellar clock noise, thereby facilitating subsequent data post-processing.

Barke [14] designed an interstellar frequency allocation system for the LISA mission according to its requirements. For the frequency range of 7 to 23 MHz of the heterodyne interference signals, the ADC sampling frequency was set to 80 MHz and the pilot tone frequency was set to 75 MHz. Kullmann [15] configured the ADC sampling frequency to 50 MHz and the pilot tone frequency to 72 MHz for the frequency range of 2 to 20 MHz of the heterodyne interference signals. Liang [13] proposed a method of adding a pilot tone to the measurement signal, with an ADC sampling frequency of 50 MHz and a pilot tone frequency of 24.3 MHz. Liu [16] conducted a phase noise test on a 14 MHz heterodyne interference signal, with an ADC sampling frequency of 80 MHz and a pilot tone frequency of 14 MHz. Huang [17] performed phase noise testing on a 15 MHz heterodyne interference signal, with a pilot tone frequency of 31 MHz. Zhang [18] tested phase noise for heterodyne interference signals at 5 MHz, 10 MHz, 15 MHz, 20 MHz, and 25 MHz, using an ADC sampling frequency of 80 MHz. The pilot tone frequencies used were 15.1 MHz, 25.1 MHz, 25.1 MHz, 25.1 MHz, and 29.1 MHz, respectively.

At present, many research teams conduct experiments on sampling timing jitter noise suppression by simulating pilot tones using signal generators. However, the high-frequency signal used for inter-satellite clock noise transfer, the system clock, and the pilot tone are indispensable components of the phasemeter. Therefore, it is essential to develop a dedicated sampling timing jitter noise suppression System (STJNSS). This system must also accommodate the diverse frequency requirements of future engineering applications. In this paper, we propose a comprehensive design of the STJNSS. It allows parameter adjustment of the high-frequency signal for inter-satellite clock noise transfer, the phasemeter’s system clock, and the pilot tone for suppressing ADC sampling timing jitter, in accordance with the requirements of current major space-based gravitational wave detection missions. Based on the authors’ previous research on phasemeters [19], for heterodyne signals with a dynamic frequency range of 5 to 25 MHz, we set the ADC sampling frequency to 80 MHz and the pilot tone frequency to 31 MHz. Phase measurement noise was better than 2 πμrad/Hz^1/2 in the 0.1 mHz–1 Hz band. We then integrated the STJNSS with the phasemeter and conducted phase noise evaluation experiments. With the pilot tone set to 75 MHz, the system clock at 80 MHz, and the heterodyne signal at 10 MHz, the results demonstrated phase measurement noise better than 2πμrad/Hz^1/2 in the 0.1 mHz–1 Hz band, satisfying space gravitational wave mission requirements. These results verify the feasibility and correctness of the STJNSS design and demonstrate its potential for future engineering deployment. This also marks a significant extension of existing phasemeter research and provides a valuable reference for future phasemeter design and optimization.

2. Design Scheme of STJNSS

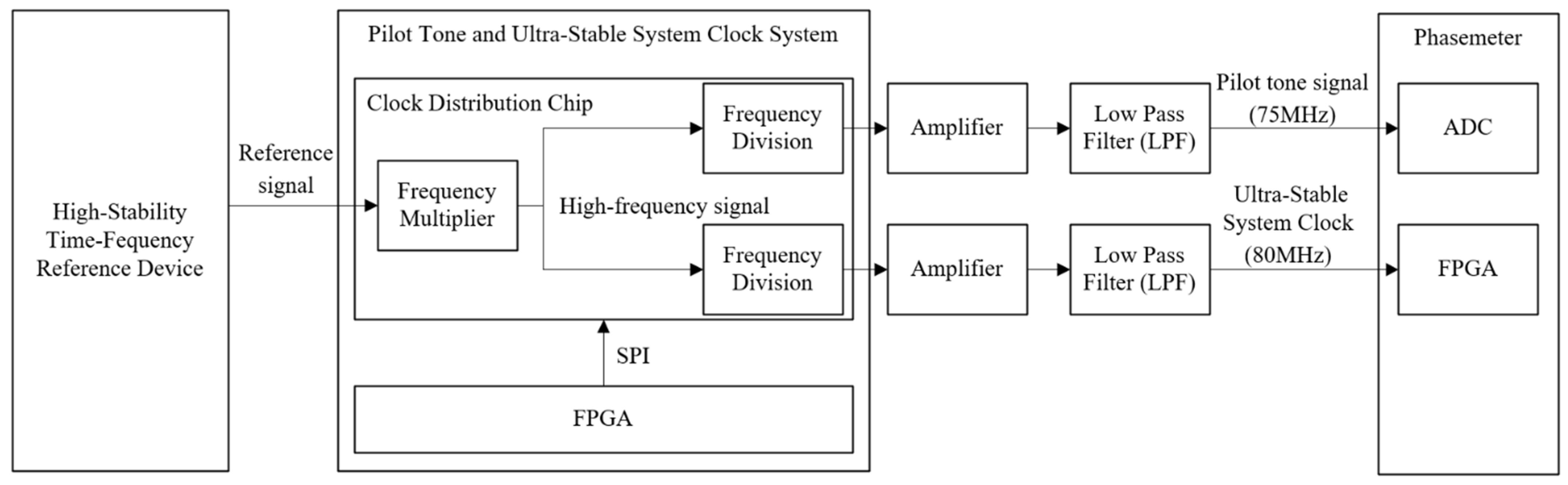
The design architecture of the STJNSS in this scheme is shown in Figure 1. The ultra-stable system clock and low phase noise pilot tone are important guarantees for the phasemeter to realize micro-radian scale phase measurement [20], at the same time taking into account the transfer characteristics of the pilot phase noise and clock noise in the interstellar link [21]. The system adopts the design scheme of frequency doubling followed by frequency division, in which the reference signal from the ultra-stable rubidium clock is doubled by the internal phase-locked loop of the clock distribution chip to generate a high-frequency clock signal, and then transmitted through the tunable frequency divider to obtain the target frequency signal. The field-programmable gate array (FPGA) dynamically configures the multiplication coefficient and division ratio of the chip through the serial peripheral interface (SPI) interface to realize the flexible adjustment of the output frequency. After further processing, the pilot tone and ultra-stable system clock are connected to the phasemeter‘s ADC module and FPGA module, respectively, via an amplifier and low-pass filter. By measuring the phase noise of the heterodyne interferometric signal at the phasemeter output, the design validity and engineering feasibility of the proposed sampling timing jitter noise suppression system are experimentally verified.

In terms of key component selection, the amplifier chosen is Mini-Circuits’ (Brooklyn, NY, USA) ZX60-33LNR-S+, which features a low noise figure across the 50 MHz to 3 GHz range, effectively suppressing link noise and improving the signal dynamic range. The low-pass filter selected is the VLFX-80+ from the same company, with a passband range of DC to 80 MHz, which filters out high-frequency interference and meets the bandwidth requirements of the pilot tone and ultra-stable system clock signals.

2.1. Clock Chip Selection and Peripheral Circuit Design

Texas Instruments (Dallas, TX, USA) LMK04828 is selected as the clock distribution chip for this design. The device integrates dual phase-locked loops (PLLs) and dual voltage-controlled oscillators (VCOs), with VCO operating frequency ranges of 2370–2630 MHz and 2920–3080 MHz, covering the GHz frequency range required for the design’s high-frequency clock. The chip supports 14 signal outputs, each with an independent frequency division ratio (1–32), allowing flexible adaptation to various pilot tone signals and ultra-stable system clock output requirements. Additionally, the chip’s built-in system reference clock module supports independent frequency division control, with a division range of 8–8191, enabling the high-frequency clock signals from the VCO to be divided as low as 3 kHz, extending the test signal frequency into the low-frequency range. In terms of signal integrity, the LMK04828 exhibits excellent phase noise performance. For example, at an output frequency of 245.76 MHz and within a measurement bandwidth of 12 kHz to 20 MHz, its phase jitter is only 88 fs RMS. Considering its wide frequency coverage, flexible output configuration, and low-noise characteristics, the LMK04828 is an ideal choice for the clock distribution module in this system.

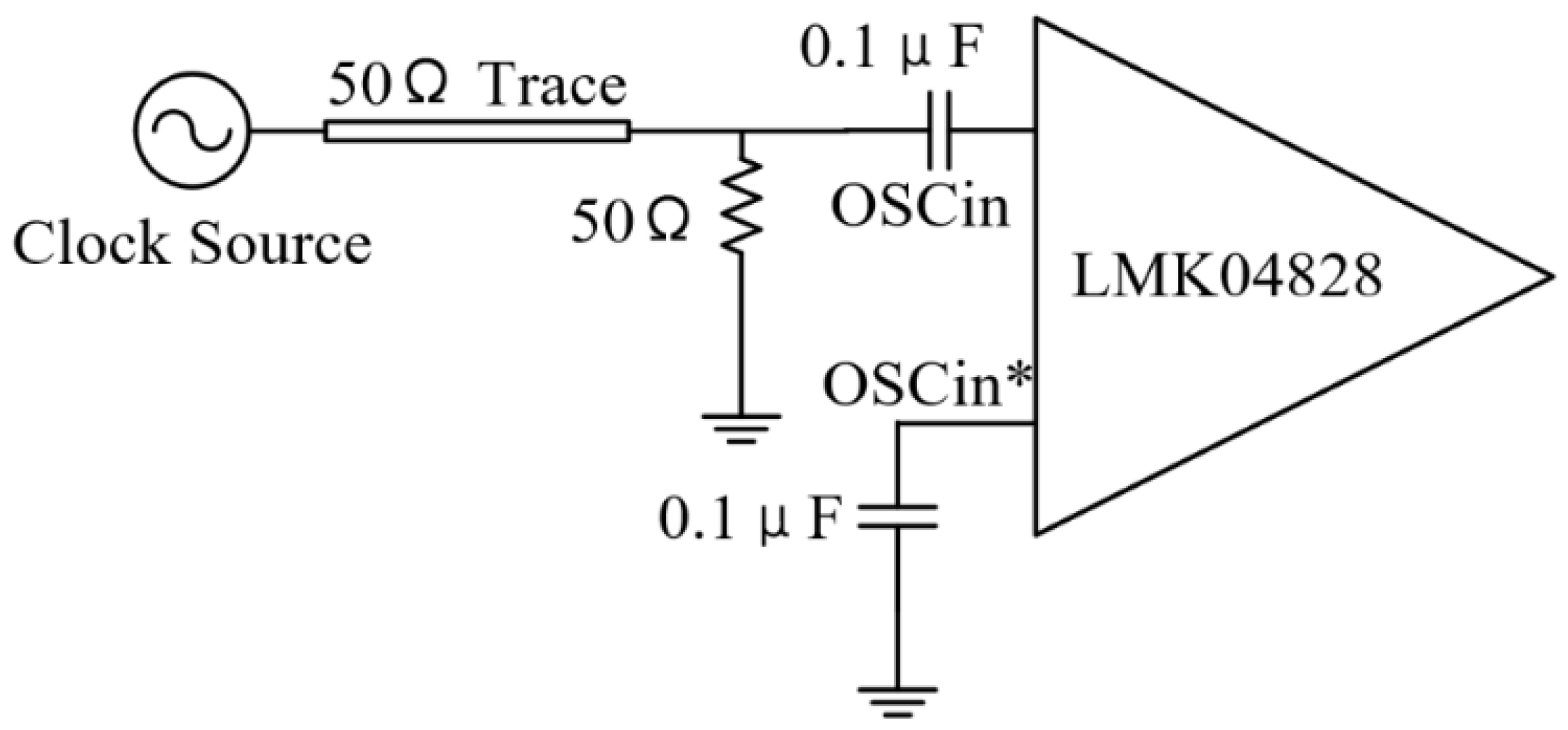
In the reference clock input design, the reference signal for the LMK04828 is provided by an ultra-stable rubidium clock, with the two connected via AC coupling (as shown in Figure 2), and a 0.1 μF isolation capacitor is connected in series in the signal link to achieve DC bias isolation.

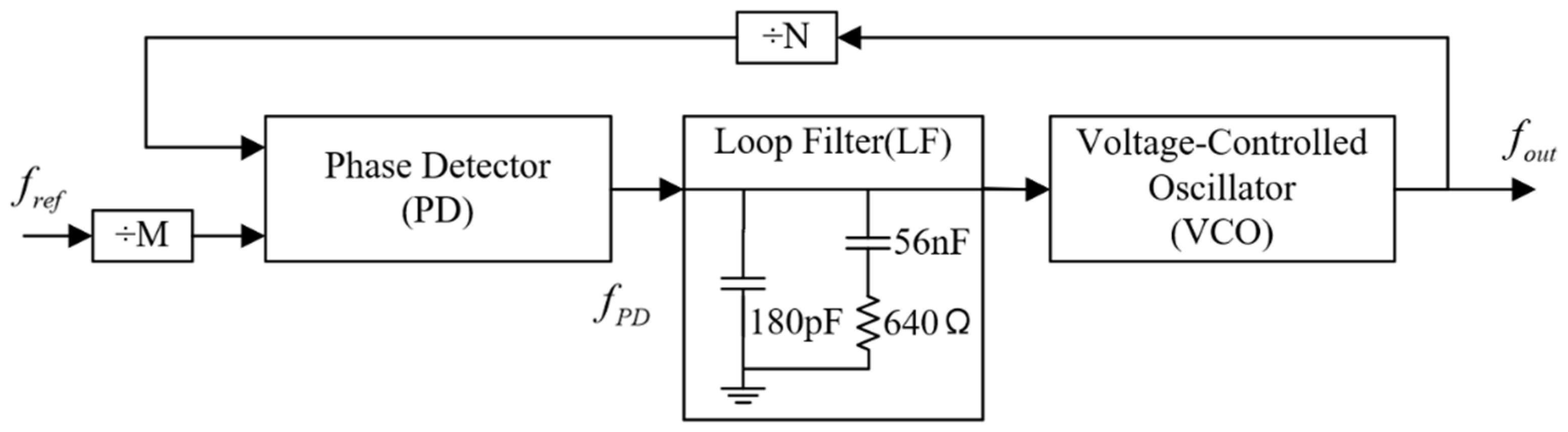
In this design, the core architecture of the phase-locked loop (PLL) consists of a phase discriminator (PD), a loop filter (LF), and a VCO (shown in Figure 3). To meet the application requirements of the LMK04828 chip, a dedicated LF needs to be designed for the peripheral circuitry. The core function of the filter is to filter out the high-frequency noise and error components in the PD’s output signal while retaining the low-frequency control voltage to accurately regulate the VCO. Its transfer function directly determines the key performance indicators of the PLL, such as phase margin, loop bandwidth, and locking time.

Theoretically, loop bandwidth is inversely related to lock time—a wider bandwidth results in faster system response and shorter lock time. However, its effect on noise suppression depends on the type of noise. For high-frequency noise from the reference clock (e.g., spurs beyond the loop bandwidth), a wider bandwidth may allow this noise to bypass the feedback path and reach the output, reducing suppression effectiveness. In contrast, for low-frequency noise from the VCO (e.g., flicker noise), a wider bandwidth enhances the loop’s ability to suppress such disturbances via negative feedback. Therefore, the PLL design must carefully balance loop bandwidth, system stability, and noise suppression performance based on the spectral characteristics of both the reference clock and the VCO to avoid performance degradation caused by an overemphasis on either bandwidth or phase margin [22]. In this design, the 10 MHz reference signal ($f_{ref}$) output from the ultra-stable rubidium clock is directly fed into the PD through the LMK04828 divider factor of 1, so the PD frequency ($f_{PD}$) equals $f_{ref}=10\mathrm{M}\mathrm{H}\mathrm{z}$. According to PLL engineering design guidelines, the LF bandwidth should generally be less than one-tenth of the PD frequency (i.e., less than 1 MHz), while ensuring that the phase margin is no less than 45° to maintain system stability. Based on these principles, this design adopts the LF scheme shown in Figure 3. According to verification by the simulation software, the final designed loop filter (LF) achieves a loop bandwidth of 25.15 kHz and a phase margin of 78.9°, effectively balancing locking speed, noise suppression, and system stability. The target signal $f_{out}$ in the GHz frequency range output by the VCO ultimately meets the requirements of a high-precision clock distribution system in terms of both frequency stability and phase noise.

2.2. Clock Signal Generation Principle

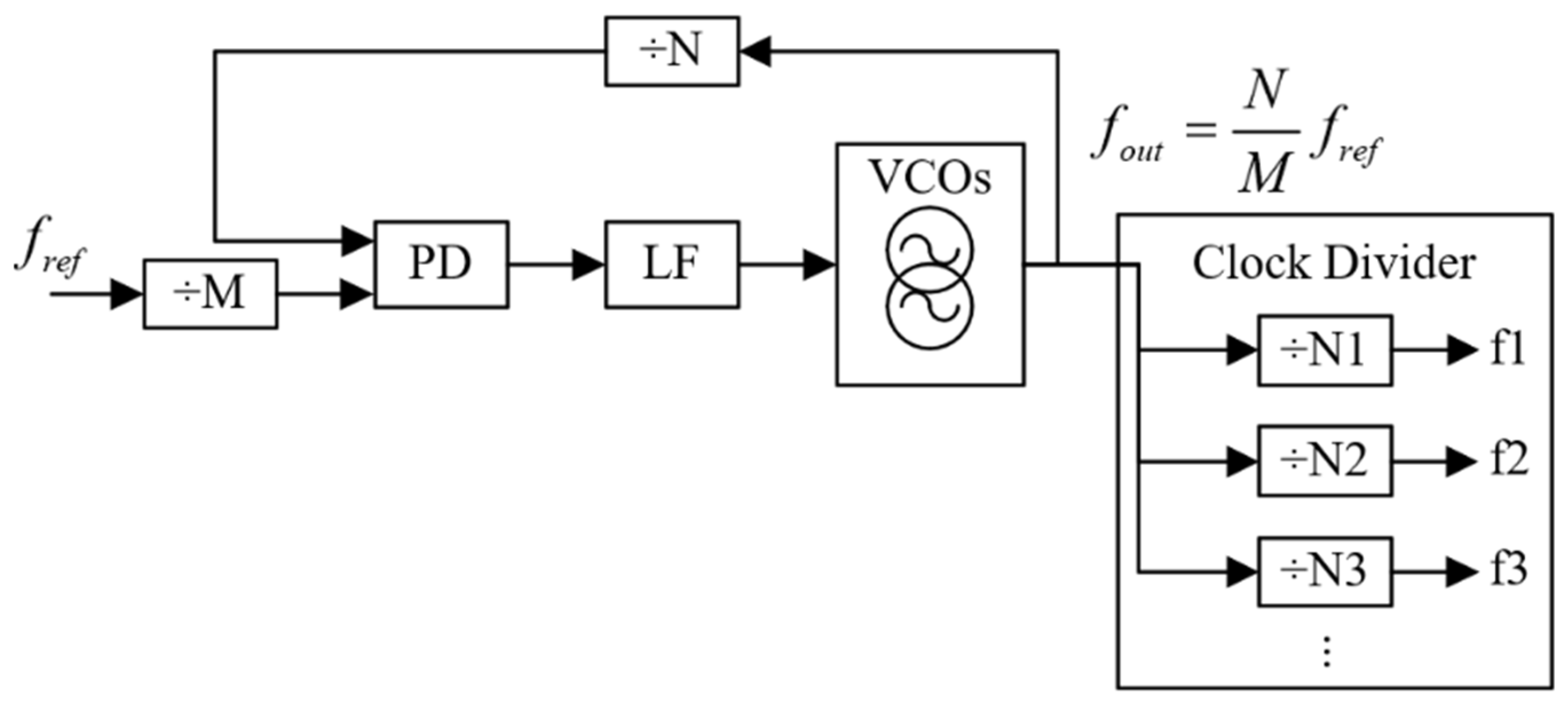
As shown in Figure 4, after the reference signal is input to the chip’s PLL module via the OSCin pin, a PD first compares the reference signal with the feedback signal and generates an error voltage corresponding to the phase difference. This voltage is then filtered by an LF to remove high-frequency noise and used to drive a VCO to adjust the output frequency, thereby achieving phase lock and frequency synthesis through a closed-loop feedback system. Benefiting from the chip’s built-in dual-PLL architecture, the module supports various reference frequency inputs (10 MHz–200 MHz), and by configuring different multiplication factors (integer or fractional mode), the VCO can generate stable GHz-range high-frequency clock signals in the 2370–2630 MHz and 2920–3080 MHz bands.

On the signal output side, the chip integrates 14 independent clock output channels, each equipped with a high-precision digital frequency divider. Each output channel supports the independent configuration of division ratios and drive levels. The division parameters can be flexibly set via the SPI interface to generate pilot tones and ultra-stable system clocks at various frequencies according to experimental requirements.

3. Performance Evaluation Method for STJNSS

3.1. Evaluation Method for Output Signal Quality of STJNSS

As the core module of this solution, the output signal quality of the STJNSS directly determines the effectiveness of jitter noise suppression and serves as a critical factor influencing the overall system performance. The output signal quality can be evaluated from four aspects: time-domain characteristics, eye diagram analysis, phase noise, and frequency-domain characteristics. These evaluation dimensions complement one another and collectively form a comprehensive signal quality assessment framework.

3.1.1. Time-Domain Characterization

For pilot tone signals and ultra-stable system clock circuits, the accurate analysis of output signal time-domain characteristics is a critical technical step for ensuring stable system operation and minimizing sampling timing jitter noise. Specifically, by using digital oscilloscopes with high bandwidth (≥4 GHz) and high sampling rates (≥20 GS/s), one can quantitatively evaluate key time-domain parameters such as mean value, peak-to-peak amplitude, root mean square (RMS) value, rise/fall time of signal edges, and overshoot and ringing.

1.

Mean Value

The mean value primarily reflects the DC component of the signal. For a discrete signal sequence$\left\{x\left(n\right)\right\}$, its mean value $\mu$ can be calculated using Equation (1), where N represents the number of signal samples.

$$\mu ={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{x}_i.$$

(1)

In ultra-stable clock circuits, if the mean value deviates from the ideal value, it indicates a bias issue within the circuit, which consequently affects the accuracy of the clock signal.

2.

Peak-to-Peak Amplitude

The peak-to-peak value is defined as the absolute difference between the maximum and minimum values of the signal and is calculated as shown in Equation (2).

$$V_{pp}=\left|V_{max}-V_{min}\right|.$$

(2)

In the pilot tone signal transmission link, the peak-to-peak value is a key indicator of signal amplitude fluctuations: if the peak-to-peak value is too large, it usually indicates that the system may experience interference or non-linear distortion; if the peak-to-peak value is too small, it may result in reduced signal recognition, which could affect the normal operation of the system.

3.

Root Mean Square (RMS)

The Root Mean Square (RMS) value is a key parameter used to characterize signal power and is computed as shown in Equation (3).

$$RMS=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{x}_i^2}.$$

(3)

From an energy perspective, the RMS value quantifies the average energy carried by a signal per unit time. In ultra-stable system clock circuits, significant fluctuations in the RMS value indicate unstable signal energy, which may induce sampling timing jitter and subsequently compromise the accuracy of data sampling and transmission.

4.

Rise/Fall Time of Signal Edges

The rise/fall time is an important parameter for measuring the response speed of a system and refers to the time it takes for a signal to jump from 10% to 90% of its amplitude. For sampling timing jitter noise suppression system circuits, shorter rise/fall times can reduce signal transmission delays, but too short a rise/fall time can introduce high-frequency noise and signal reflections, so it is necessary to find a balance between response speed and signal integrity.

5.

Overshoot and Ringing

Overshoot and ringing primarily occur in the step response of a signal. Overshoot indicates the extent of the system’s dynamic overreaction at the moment of a step change while ringing refers to the periodic oscillations that appear after the signal reaches its steady-state value. These two parameters are critical for assessing the damping characteristics of the system. Excessive overshoot and ringing can cause signal distortion and compromise system stability and must be mitigated by optimizing circuit parameters and refining filter design.

3.1.2. Eye Diagram

The eye diagram is a key tool for evaluating the STJNSS. By superimposing multiple signal periods, it visually reveals critical performance metrics such as signal integrity, noise margin, and system stability [23]. It is generated using the persistence mode of an oscilloscope, which captures and overlays signal waveforms over an extended time period, creating a visual pattern resembling an “eye” that provides a comprehensive view of complex signal characteristics. Quantitative analysis of the eye diagram relies on the following core parameters:

1.

Eye Height

Eye height measures the vertical opening of the eye diagram and directly reflects the signal’s noise tolerance, closely related to the SNR. During actual signal transmission, noise can cause amplitude fluctuations. A larger eye height indicates that the signal maintains a sufficient amplitude margin to distinguish logical levels despite noise interference. Eye height is calculated as the difference between the high-level $VH$ and the low-level $VL$ within the stable region of the eye diagram, as shown in Equation (4).

$$Ey{e}_{Height}=VH-VL.$$

(4)

A higher eye height indicates stronger noise immunity of the system and enhances the reliability of signal transmission.

2.

Eye Width

Eye width describes the horizontal opening of the eye diagram and visually represents the signal’s timing margin. In pilot tone and ultra-stable clock circuit systems, sampling timing jitter and timing skew may cause deviations in the signal sampling point. A larger eye width indicates greater timing tolerance, allowing the system to withstand higher levels of sampling timing jitter without causing bit errors, thereby reflecting better timing stability. Eye width is measured by determining the horizontal intercepts $tL$ and $tR$ on the left and right sides of the vertical center of the eye diagram and is computed as shown in Equation (5).

$$Eye\_Width=tR-tL.$$

(5)

This parameter provides a quantitative basis for optimizing system timing and ensuring precise timing control under complex operating conditions.

3.1.3. Signal Frequency-Domain Characterization

As a core method for evaluating the signal quality of sampling timing jitter noise suppression system circuits, frequency-domain analysis enables an in-depth examination of signal frequency components, energy distribution, and noise characteristics, providing critical insights for system optimization. The primary testing approach involves using a spectrum analyzer to perform the Fourier transform, converting the signal from the time domain to the frequency domain. For a continuous-time signal $x\left(t\right)$, its Fourier transform is defined as.

$$X\left(f\right)={\int }_{-\infty }^{\infty }x\left(t\right)e^{-j2\pi ft}dt.$$

(6)

where $X\left(f\right)$ is the frequency-domain representation of the signal $x\left(t\right)$, $f$ denotes the frequency, and j is the imaginary unit.

During frequency-domain analysis, Total Harmonic Distortion (THD) analysis can further reveal the extent of nonlinear distortion in the signal [24]. THD quantifies the total energy share of each harmonic component in the signal, providing an accurate reflection of the additional frequency components introduced by the nonlinear system during signal processing. When a signal passes through a circuit containing nonlinear devices such as transistors, operational amplifiers, etc., the original signal undergoes nonlinear distortion, generating harmonic components that are integer multiples of the fundamental frequency. The accumulation of these harmonic energies directly impacts both signal quality and system performance. The formula for calculating THD is shown in Equation (7).

$$THD=\sqrt{{\displaystyle \frac{\sum _{i=2}^{\infty }{P}_i}{P_1}}}\times 100\%.$$

(7)

where $P_1$ represents the power of the fundamental frequency signal, reflecting the energy level of the original signal; $P_i(i\ge 2)$ represents the distortion component generated by nonlinear effects. The lower the THD value, the smaller the proportion of harmonic components in the signal, the closer the waveform is to the ideal state, and the higher the system linearity and signal fidelity. Conversely, this indicates that the signal experiences severe distortion.

3.1.4. Phase Noise Analysis

Phase noise is essentially a random fluctuation of the signal’s phase or frequency [22]. Its generation mechanism is complex and can lead to signal spectrum broadening and a reduction in purity, severely affecting the synchronization performance and measurement accuracy of the system. Currently, single-sideband phase noise density is a commonly used quantitative evaluation metric, and its mathematical expression is shown in Equation (8).

$$L\left(f\right)=10log\left({\displaystyle \frac{P_{noise}\left(f\right)}{P_{carrier}\left(f\right)}}\right).$$

(8)

Among them, $P_{noise}\left(f\right)$represents the noise power in the unit bandwidth (1 Hz) at the offset carrier frequency $f$, reflecting the noise intensity distribution at a specific frequency point; $P_{carrier}$ is the power of the carrier signal, representing the carrier energy level. This index is measured in decibels (dBc/Hz), and the smaller the value, the lower the proportion of noise power at the same offset frequency, i.e., the smaller the random fluctuation of the signal phase, and the higher the phase stability and spectral purity of the signal source.

3.2. Phase Measurement Performance Evaluation Method

This paper utilizes the separation measurement method, applying a pilot tone to suppress the sampling timing jitter noise, and evaluates phase measurement noise through the amplitude-squared spectral density [25]. The underlying principle is illustrated in Figure 5 [19]. Specifically, the mixed signal consisting of the heterodyne interference signal (InS) and the pilot tone (PT) is separated into two signal groups: InSa and Pta, InSb and PTb. Four dedicated DPLLs are used to perform phase measurements on the separated signals, yielding the phases ${\phi }_{\mathrm{I}\mathrm{n}\mathrm{S}1}$, ${\phi }_{PT1}$, ${\phi }_{\mathrm{I}\mathrm{n}\mathrm{S}2}$, and ${\phi }_{PT2}$. By using the frequencies of the interference signal ($f_{\mathrm{I}\mathrm{n}\mathrm{S}}$) and the pilot tone ($f_{\mathrm{P}\mathrm{T}}$), the correction factor (CORR) that eliminates sampling timing jitter noise can be computed. The phase measurement noise of the corrected heterodyne interference signal is ${\phi }_{\mathrm{I}\mathrm{n}\mathrm{S}}$. Smoothing is performed using the LTPDA v3.0.13 (LISA Technology Package Data Analysis) toolbox, developed by the Albert Einstein Institute, Germany [26].

4. Verification of the STJNSS

4.1. Evaluation of the Output Signal Quality in the STJNSS

The system supports the output of various pilot tone signals and ultra-stable system clock signals, with output frequencies that can be flexibly configured as required. In the implementation, a 10 MHz ultra-stable reference clock generated by a rubidium clock is first frequency-multiplied to 2.4 GHz using the LMK04828 chip and then divided down to produce the desired output frequencies. This paper evaluates the signal quality of three representative outputs: 2.4 GHz, 80 MHz, and 75 MHz.

4.1.1. Time-Domain Testing of the STJNSS

In this study, a KEYSIGHT MSOS404A oscilloscope is used to perform time-domain and eye diagram measurements. The time-domain waveforms of the 2.4 GHz, 80 MHz, and 75 MHz output signals are shown in Figure 6, Figure 7, and Figure 8, respectively, while the corresponding eye diagrams are presented in Figure 9, Figure 10 and Figure 11. As summarized in

Table 1. Time-domain test results.

	2.4 GHz	80 MHz	75 MHz
Mean Value	614.38 μV	5.01 mV	2.37 mV
Peak-to-Peak Amplitude	242.44 mV	2.08 V	712.11 mV
RMS	84 mV	717 mV	246 mV
Rise/Fall Time of Signal Edges	125.71 ps/124.91 ps	3.66 ns/3.59 ns	3.63 ns/4.02 ns
Overshoot	0.114%	0.864%	0.51%
Eye Height	1.841 V	1.34 V	608 mV
Eye Width	6.12 ns	6.52 ns	6.47 ns

, the test results demonstrate that the output pilot tone and ultra-stable clock signals meet the design requirements in terms of time-domain stability and eye diagram performance, verifying the engineering feasibility of the STJNSS system.

4.1.2. Frequency-Domain Testing of the STJNSS

In this paper, a KEYSIGHT CXA Signal Analyzer is employed to perform frequency-domain characterization and phase noise measurements. For the frequency-domain tests, the video bandwidth is set to 240 Hz and the span to 25 kHz. The spectral profiles of the 2.4 GHz, 80 MHz, and 75 MHz output signals are shown in Figure 12, Figure 13, and Figure 14, respectively. During the phase noise measurements, a phase offset range of 100 Hz to 1 MHz is configured, with the results presented in Figure 15, Figure 16 and Figure 17. The corresponding test data are summarized in

Table 2. Results of frequency-domain characterization tests.

	2.4 GHz	80 MHz	75 MHz
Carrier Signal	−8.71 dBm	10.32 dBm	0.67 dBm
Second Harmonic	−32.78 dBm	−17.49 dBm	−21.64 dBm
THD	6.26%	4.07%	7.66%
Phase Noise @100Hz	−87.78 dBc/Hz	−97.04 dBc/Hz	−98.13 dBc/Hz
Phase Noise @1kHz	−93.4 dBc/Hz	−107.42 dBc/Hz	−108.33 dBc/Hz
Phase Noise @10kHz	−89.12 dBc/Hz	−109.68 dBc/Hz	−111.84 dBc/Hz
Phase Noise @100kHz	−126.84 dBc/Hz	−110.77 dBc/Hz	−110.84 dBc/Hz
Phase Noise @1MHz	−217.85 dBc/Hz	−130.46 dBc/Hz	−130.6 dBc/Hz

. All frequency-domain metrics of the system’s pilot tone and ultra-stable clock signals meet the design specifications. Notably, the phase noise remains below −85 dBc/Hz within the 100 Hz to 1 MHz offset range, fully satisfying the application requirements of high-precision clock signals in complex systems.

4.2. Phase Measurement Performance Evaluation

The environment for phase measurement performance evaluation is shown in Figure 18. The phasemeter can process 16-channel heterodyne interferometric signals in parallel. Based on previous phasemeter research by the research team [19], the phase measurement noise for heterodyne interferometric signals with a frequency dynamic range of 5 to 25 MHz is better than 2π μrad/Hz^1/2@(0.1 mHz–1 Hz). Therefore, by selecting a frequency of the heterodyne interferometric signal for phase measurement performance evaluation and the Mini-Circuits RLP-83+ low-pass filter of the phasemeter to meet the frequency characteristics of the pilot tone, the correctness and feasibility of integrating the STJNSS with the phasemeter can be verified. The KEYSIGHT signal generator (KEYSIGHT 33622A) provides the heterodyne interferometric signal, while the KEYSIGHT power supply (E36312A) provides the +12 V stabilized voltage source. The highly stable time–frequency reference device (HT 5825) developed by Xi’an Space Unlimited Electric Technology Research Institute provides highly stable synchronized clocks for the phasemeter, the sampling timing jitter noise suppression system, and the signal generator. The Mini-Circuits Power Splitter/Combiner (ZMSC-2-1+) is used for coupling the heterodyne interferometric signal with the pilot tone and for the separation of the coupled signals.

The frequency and Vpp amplitude of the phasemeter system clock output from the STJNSS are set to 80 MHz and 2 V, respectively, while the frequency and Vpp amplitude of the pilot tone are set to 75 MHz and 1.5 V. The signal generator (KEYSIGHT 33622A) outputs a sinusoidal signal with a frequency and amplitude of 10 MHz and 1.5 V, respectively, to simulate the heterodyne interference signal. Experiments were conducted to measure the phase noise of the phase meter in the 0.1 mHz to 1 Hz frequency range. The corresponding nominal system parameters are listed in

Table 3. Summary table of experimental parameters.

Parameter	Nominal Value
ADC Sampling Rate	80 MHz
Pilot Tone Frequency	75 MHz
Heterodyne Detection Frequency	10 MHz
System Clock Frequency	80 MHz
Pilot Tone Amplitude (Vpp)	1.5 V
System Clock Amplitude (Vpp)	2 V
Heterodyne Detection Amplitude (Vpp)	1.5 V
Phase Measurement Noise	<2π μrad/Hz1/2@(0.1 mHz–1 Hz)

.

The experimental results are shown in Figure 19. The PT1–PT2 and InS1–InS2 curves represent the phase measurement noise after suppressing the common-mode noise in the pilot tone and the heterodyne interference signal, respectively. The curve InS_PT_CORR shows the phase measurement noise after the sampling timing jitter noise of the heterodyne interference signal is eliminated using the pilot tone, which meets the task requirement of 2π μrad/Hz^1/2@(0.1 mHz–1 Hz). This demonstrates that the phasemeter, when operating with the proposed STJNSS, can effectively suppress phase noise induced by sampling timing jitter. The results validate both the correctness of the STJNSS design and its feasibility for future engineering implementation.

5. Summary and Outlook

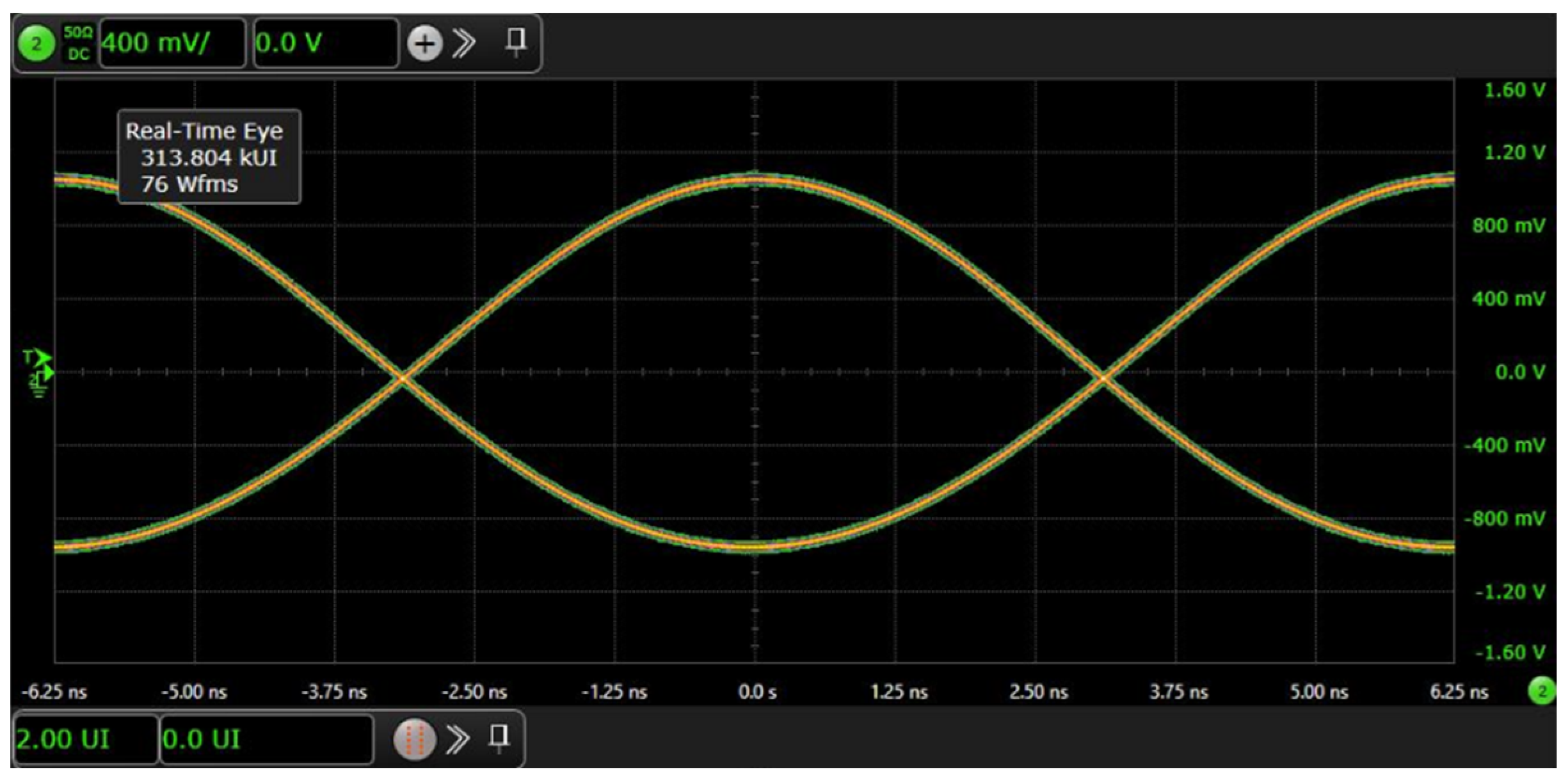
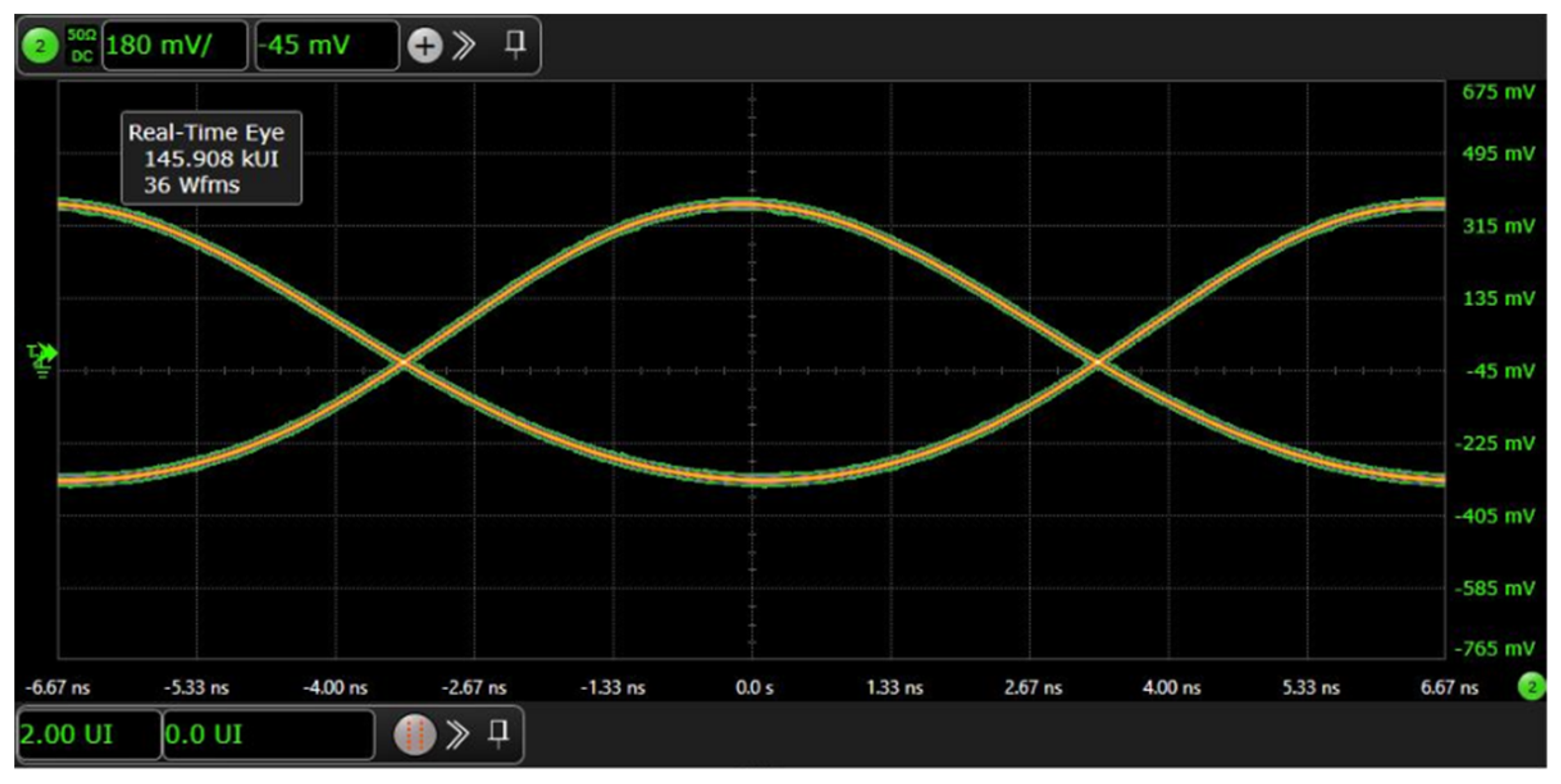
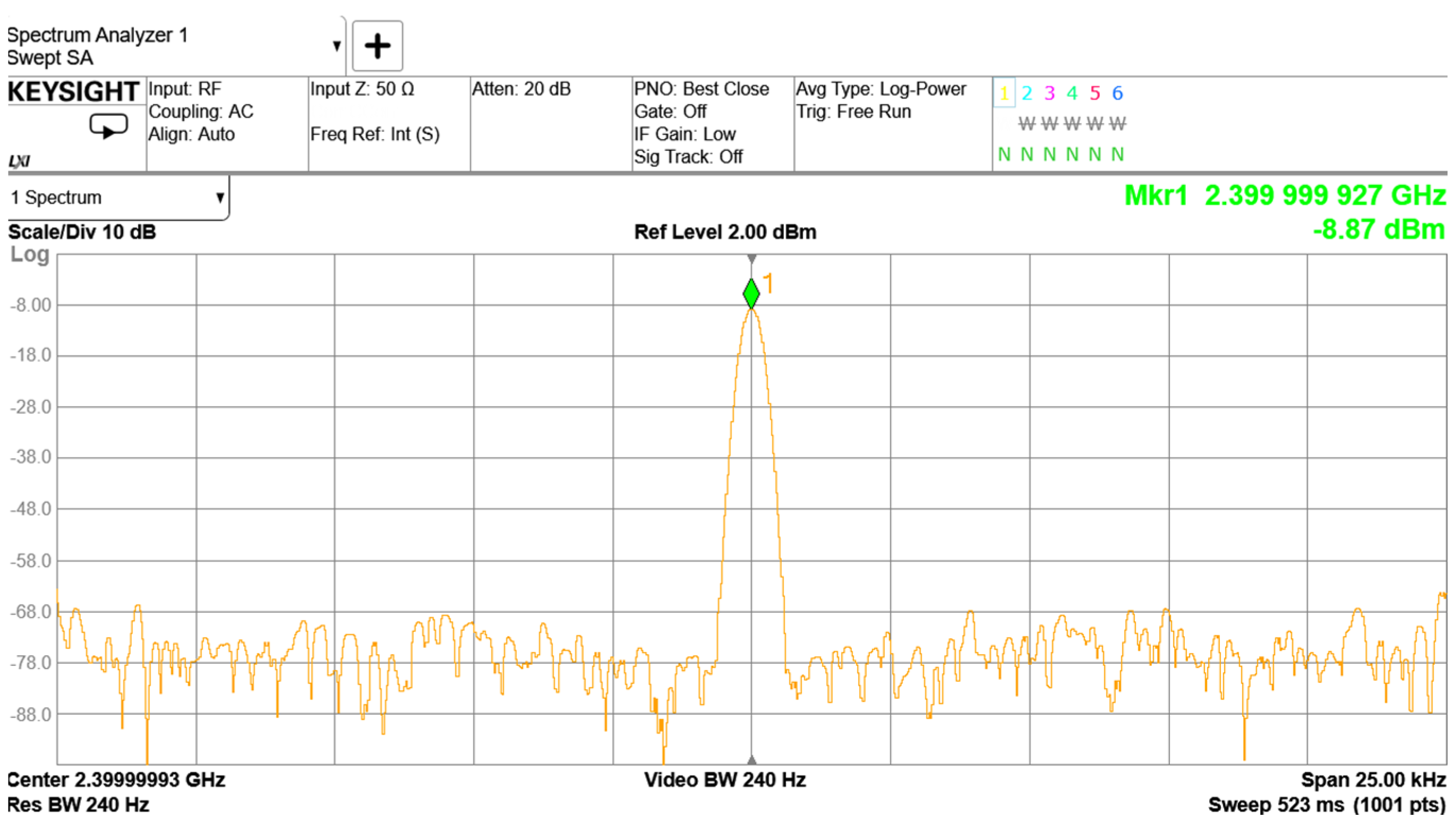
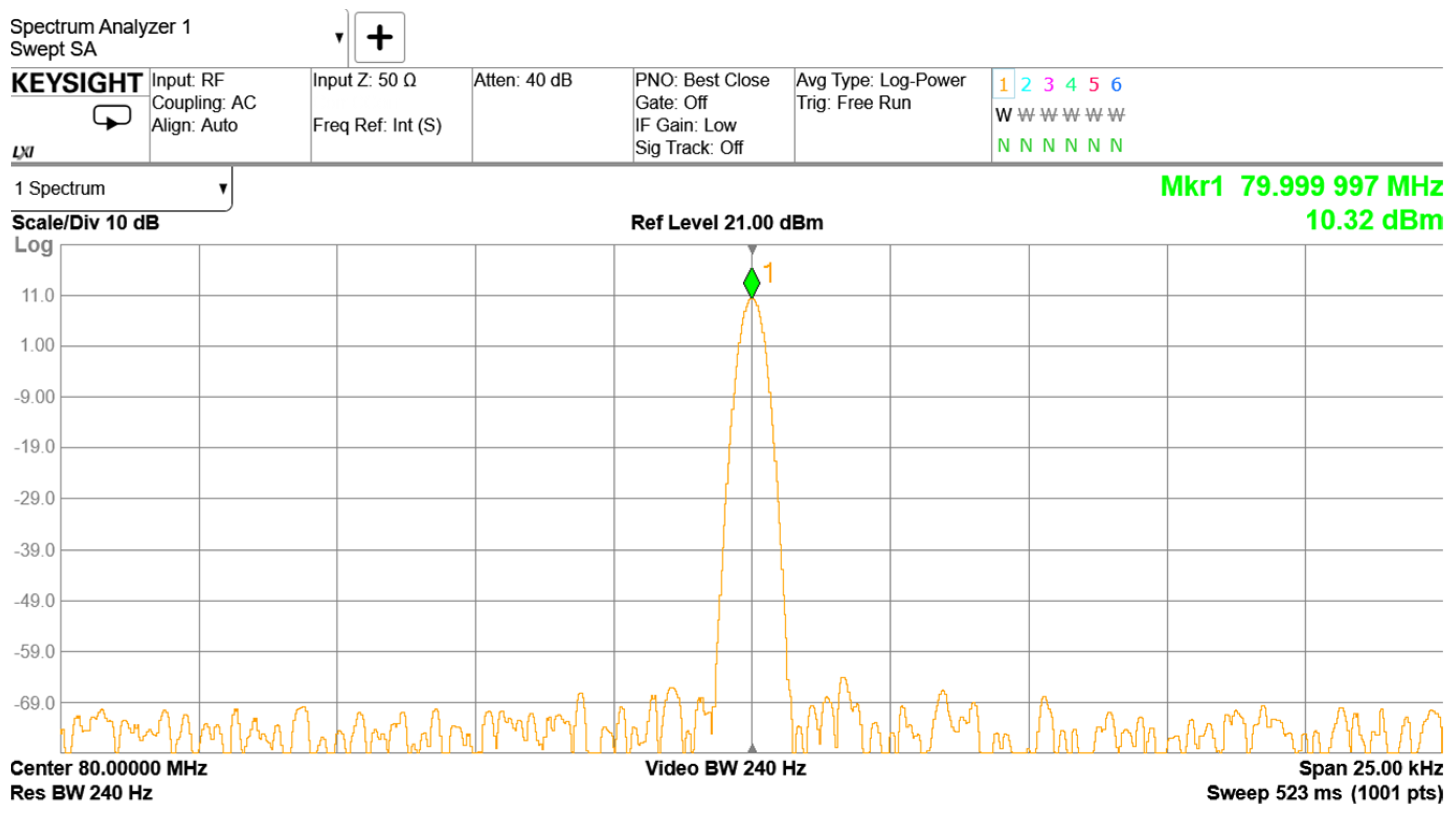
This paper proposes the design and implementation of an STJNSS, developed to meet the demanding requirements of current space-based gravitational wave detection missions. Specifically, the system allows flexible parameter adjustment of high-frequency signals for inter-satellite clock noise transfer, system clock signals for phasemeters, and pilot tones used to suppress ADC sampling timing jitter. The STJNSS is built upon the TI LMK04828 clock chip, which can flexibly generate GHz-level clock signals within two frequency bands: 2370–2630 MHz and 2920–3080 MHz. By configuring the chip’s internal programmable dividers (supporting division ratios from 1 to 32), it can provide various output frequencies, including pilot tones (e.g., 75 MHz) and ultra-stable system clocks (e.g., 80 MHz). In addition, the integrated SYSREF divider supports division ratios ranging from 8 to 8191, enabling an output of pilot tone signals as low as 3 kHz, fully covering the frequency range required by the phasemeter. The output amplitude of the system can also be flexibly configured using external RF amplifiers (such as ZX60-33LNR-S+), with actual output amplitudes ranging from 1 V to 5 V, thereby satisfying the phasemeter’s interface drive requirements.

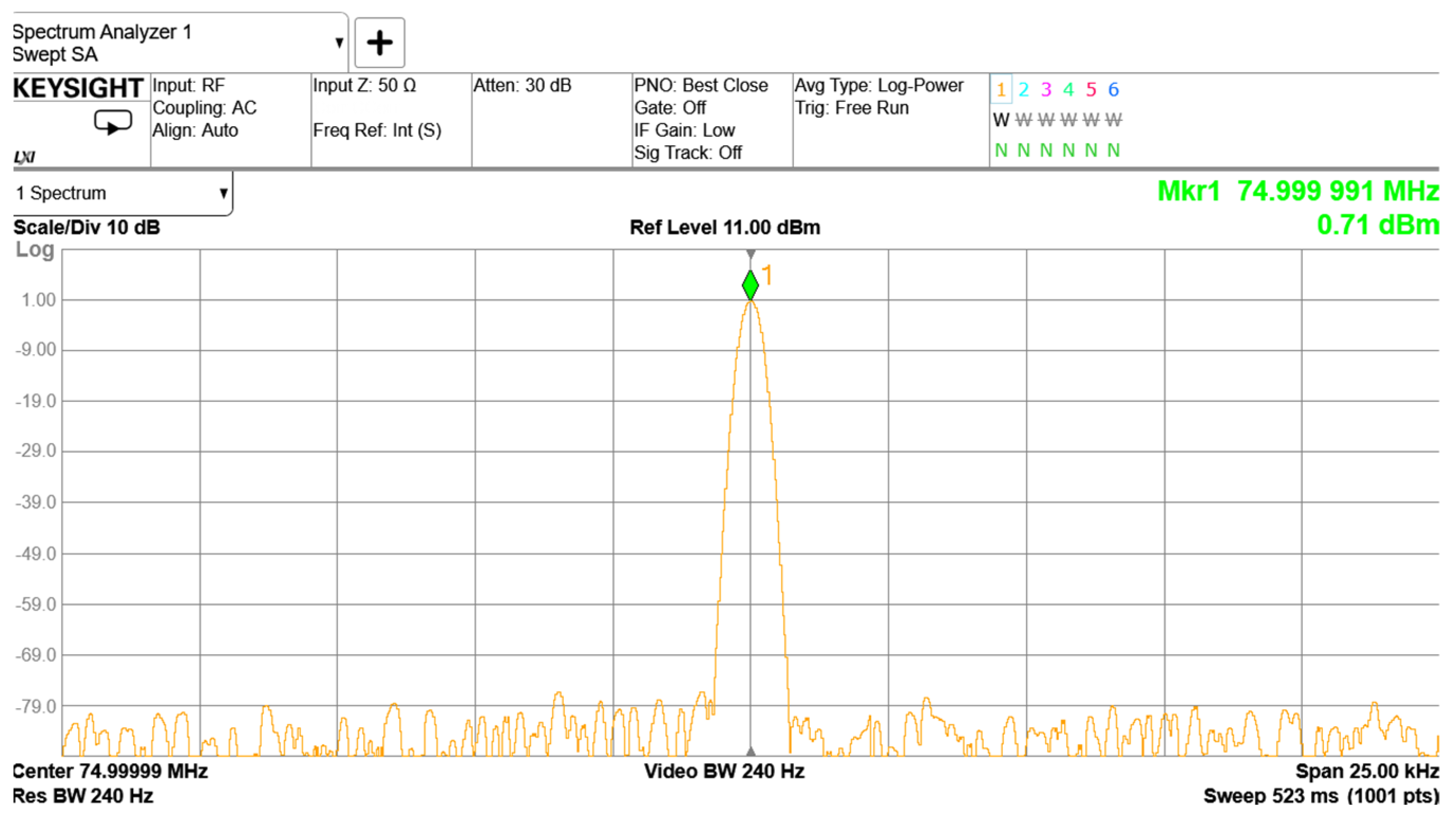
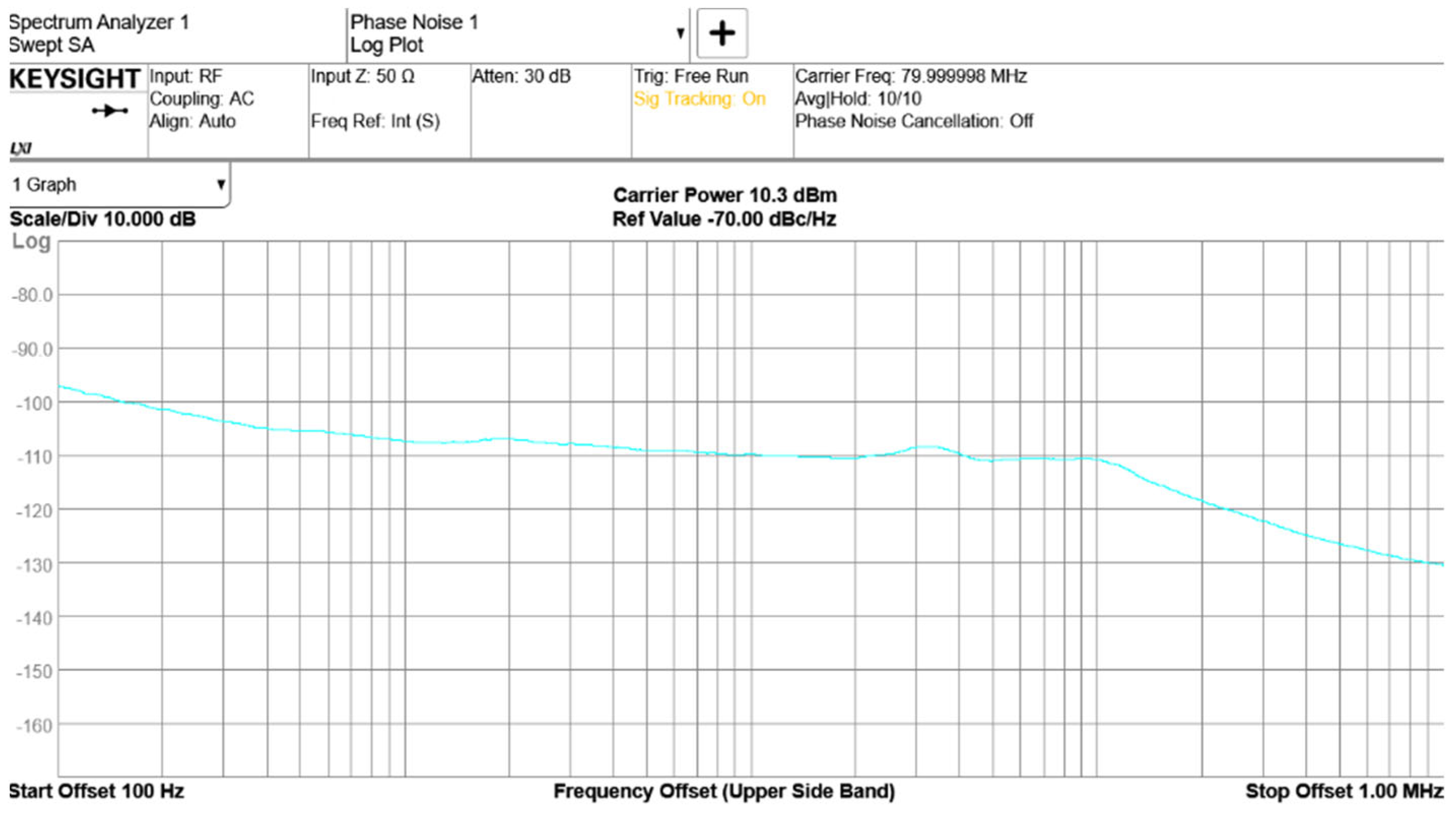
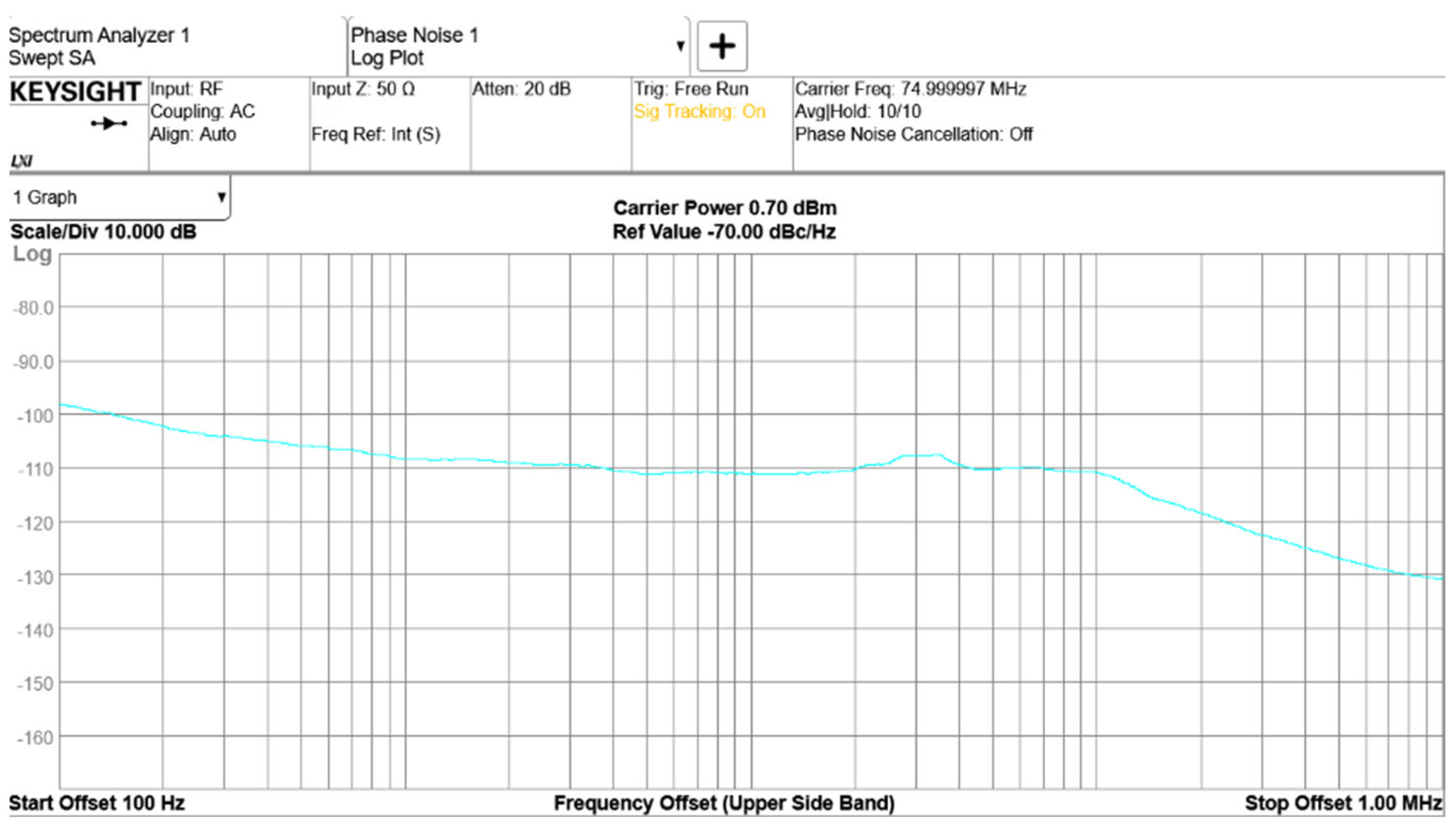
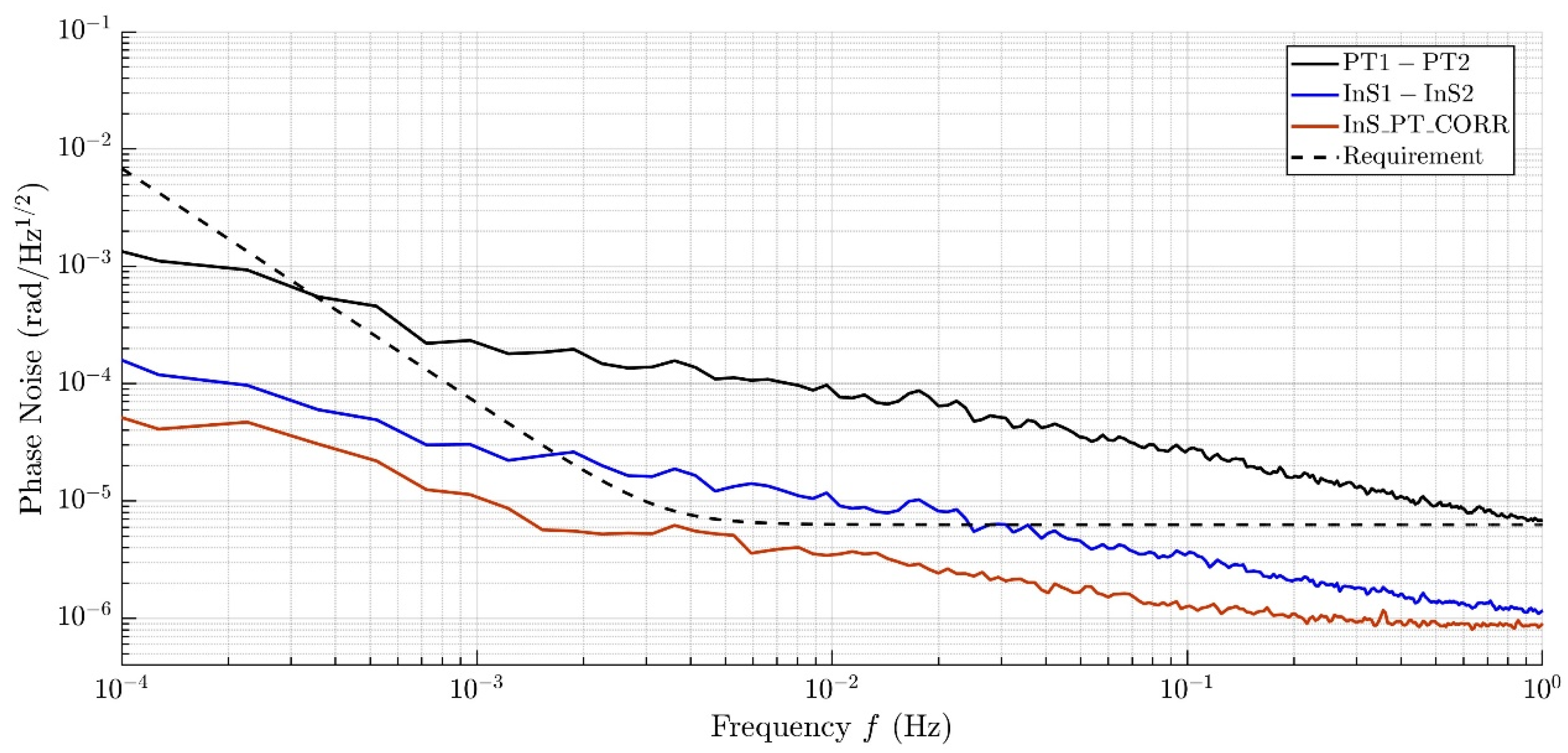
To validate the practical performance of the STJNSS, it was integrated with a phasemeter, and phase noise evaluation experiments were conducted. In the experiment, the pilot tone frequency was set to 75 MHz, the system clock to 80 MHz, and the heterodyne signal to 10 MHz. The results show that the phase meter achieves phase noise better than 2π μrad/Hz¹ᐟ² in the 0.1 mHz–1 Hz frequency range, meeting and even exceeding the performance requirements of space-based gravitational wave detection missions in the low-frequency regime. This confirms that the STJNSS can effectively suppress sampling timing jitter noise and demonstrates the feasibility of its engineering implementation.

Given that inter-satellite scientific interferometers must simultaneously support functions such as coupled relative ranging, absolute ranging, laser communication, and clock noise transfer, the phasemeter is required to simultaneously measure the phases of the main beat note and two sidebands, while also demodulating the laser communication signal. The STJNSS developed in this work significantly enhances the timing performance of the phasemeter system, laying a solid technical foundation and providing a reliable development and validation platform for future functional extensions. This demonstrates the system’s strong potential for engineering application in space missions.

6. Discussion

The space-based gravitational wave detection mission employs a three-satellite formation, with inter-satellite distances reaching hundreds of thousands to millions of kilometers. According to the principle of laser heterodyne interferometry, minute changes in the distances between inertial reference points of the satellites induced by gravitational wave events are converted into phase changes in the heterodyne interference signals, which are measured by the phasemeter. The mission requires a ranging accuracy of 1 picometer and a corresponding phase noise performance of 2π μrad/√Hz within the frequency range of 0.1 mHz to 1 Hz. Due to the inter-satellite Doppler effect, the dynamic frequency range of the heterodyne signals spans from 5 MHz to 25 MHz. To suppress sampling clock jitter noise introduced during digitization, our previous work proposed and verified a single pilot tone-based jitter noise suppression architecture, which demonstrated effective phase noise performance meeting the mission requirements within this dynamic frequency range.

Building on this foundation, this paper further develops and integrates the STJNSS as a key submodule within the phasemeter system. The STJNSS not only achieves the effective suppression of sampling timing jitter across a wide frequency dynamic range but also provides high-precision, configurable system clock and pilot tone outputs, thereby ensuring long-term timing and frequency stability of the system. The experimental results show stable phase noise performance at 10 MHz, further validating the feasibility and robustness of the single pilot tone jitter suppression architecture. This achievement significantly enhances the phasemeter system’s integration capability and engineering adaptability, laying a solid technical foundation for its application in future space-based gravitational wave detection missions.