Inverse Design of Plasmonic Nanostructures Using Machine Learning for Optimized Prediction of Physical Parameters
Abstract
1. Introduction
2. Theoretical Framework
3. Materials and Methods
3.1. Theoretical Dataset
3.2. Dataset Experimental
3.3. Regression
- Height = 300.0 nm;
- Wavelength () = 1184.0 nm;
- Material = copper (Cu).
- It loads the data and separates a fixed set for the final test phase.
- For each training proportion, from 40% to 80%, the remaining data are equally divided between test and validation sets.
- PyCaret is configured for regression, and candidate models are trained.
- Performance metrics MAE, MSE, and R2 are calculated for the training, validation, and test sets, thus enabling the analysis of possible overfitting.
- Graphs illustrating model performance are generated and saved.
- The best model is selected based on the lowest MAE from the internal validation set, and a final evaluation is performed using the reserved set.
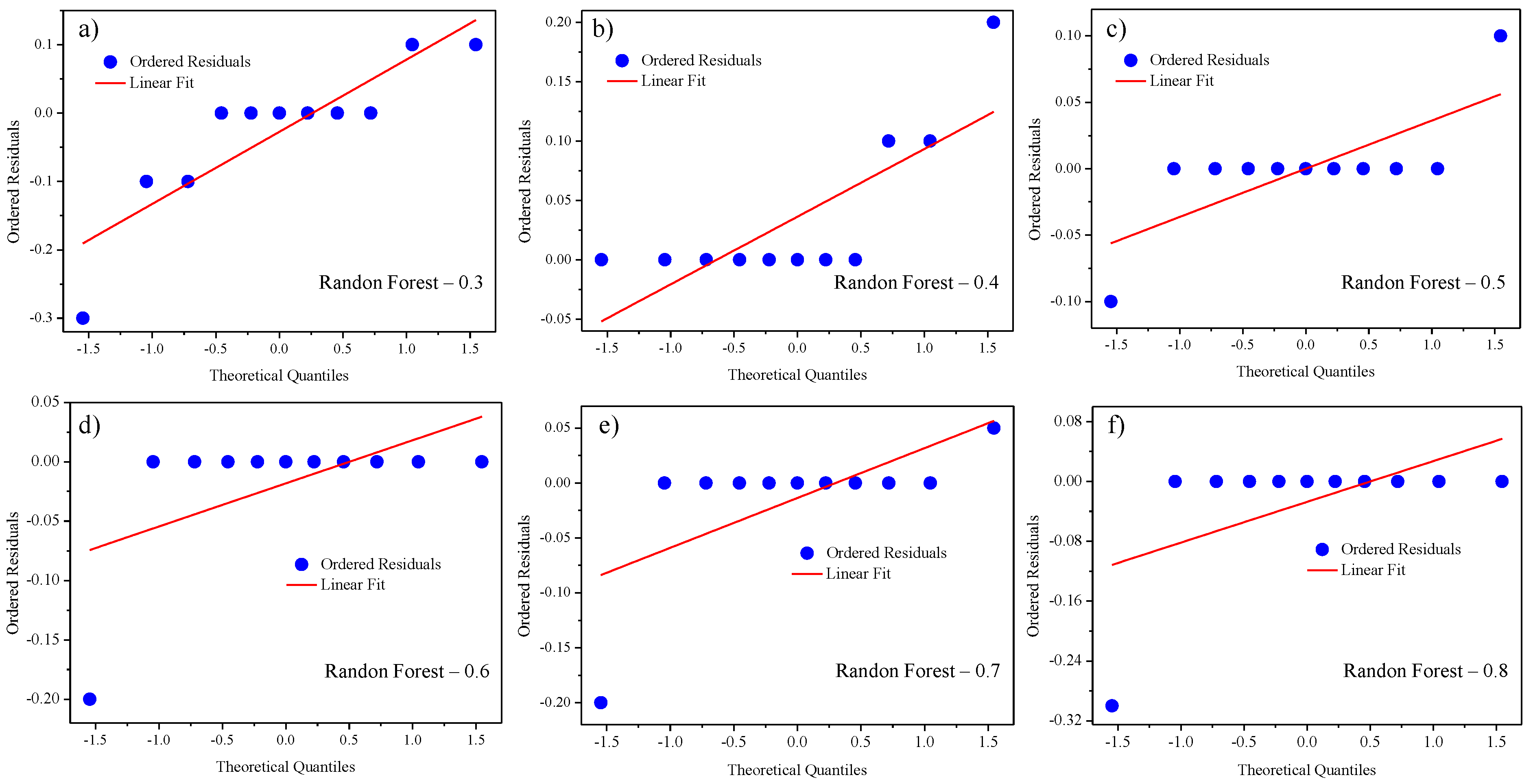
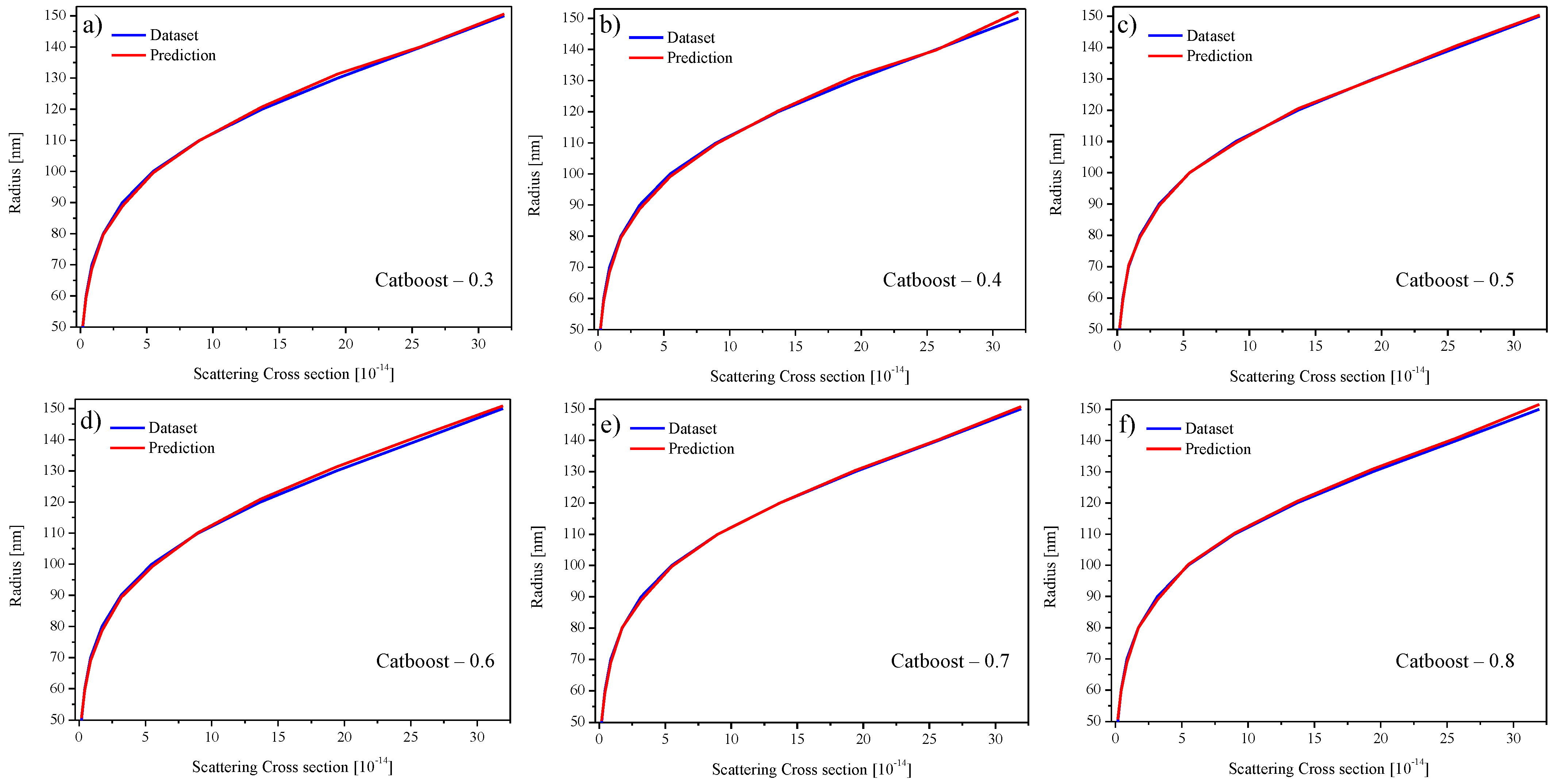
4. Results
4.1. Inverse Design Using Theoretical Data
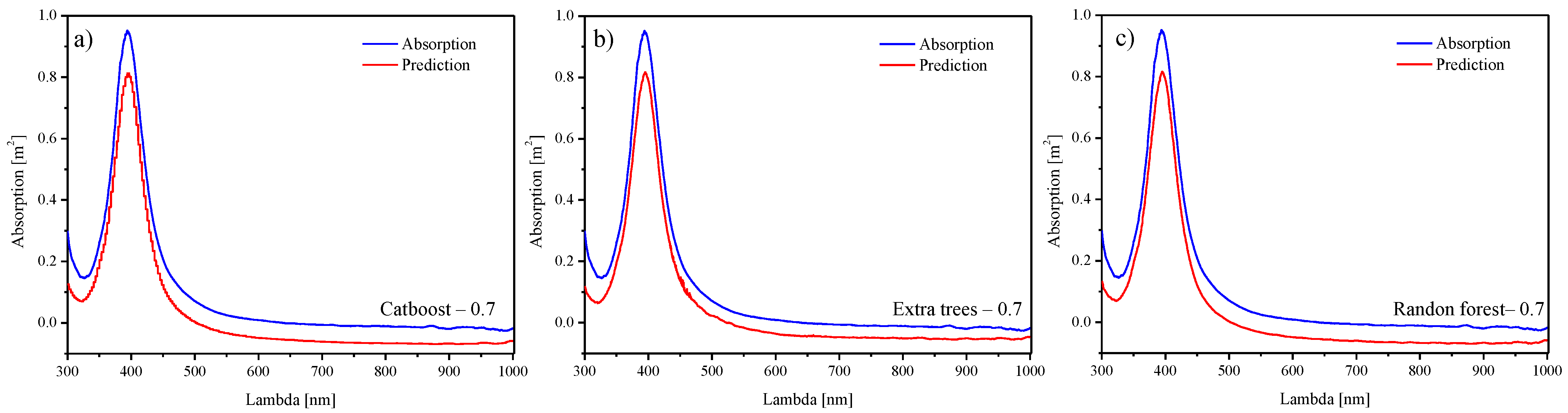
4.2. Direct Design Using Experimental Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| FDTM | Finite Domain Time Method |
| ML | Machine Learning |
| SEM | Scanning Electron Microscopy |
| TEM | Transmission Electron Microscopy |
| LSPR | Ressonance Plasmonic Surface Localized |
| SPR | Ressonance Plasmonic Surface |
| UV–Vis | UV–Visible |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| FEM | Finite Element Method |
References
- Shi, H.; Zhu, X.; Zhang, S.; Wen, G.; Zheng, M.; Duan, H. Plasmonic metal nanostructures with extremely small features: New effects, fabrication and applications. Nanoscale Adv. 2021, 3, 4349–4369. [Google Scholar] [CrossRef] [PubMed]
- Shabaninezhad Navrood, M.; Guda, R.; Team, M.S. Theoretical Investigation of Plasmonic Properties of Quantum-Sized Silver Nanoparticles. APS March Meet. Abstr. 2019, V21, 8. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Y.; Zhao, X.; Xu, Z. Plasmonic colorimetric biosensor for visual detection of telomerase activity based on horseradish peroxidase-encapsulated liposomes and etching of Au nanobipyramids. Sens. Actuators B Chem. 2019, 296, 126646. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Li, D.; Sun, Y.; Jiang, L. Engineering surface plasmons in metal/nonmetal structures for highly desirable plasmonic photodetectors. ACS Mater. Lett. 2022, 4, 343–355. [Google Scholar] [CrossRef]
- Carvalho, F.W.O.; Mejía-Salazar, J.R. Plasmonics for telecommunications applications. Sensors 2020, 20, 2488. [Google Scholar] [CrossRef]
- Zhang, H.C.; Zhang, L.P.; He, P.H.; Xu, J.; Qian, C.; Garcia-Vidal, F.J.; Cui, T.J. A plasmonic route for the integrated wireless communication of subdiffraction-limited signals. Light. Sci. Appl. 2020, 9, 113. [Google Scholar] [CrossRef]
- Mori, O.; Sawada, H.; Funase, R.; Morimoto, M.; Endo, T.; Yamamoto, T.; Tsuda, Y.; Kawakatsu, Y.; Kawaguchi, J.; Miyazaki, Y.; et al. First solar power sail demonstration by IKAROS. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2010, 8, To_4_25–To_4_31. [Google Scholar] [CrossRef]
- Ullery, D.C.; Soleymani, S.; Heaton, A.; Orphee, J.; Johnson, L.; Sood, R.; Kung, P.; Kim, S.M. Strong solar radiation forces from anomalously reflecting metasurfaces for solar sail attitude control. Sci. Rep. 2018, 8, 10026. [Google Scholar] [CrossRef]
- Jin, W.; Li, W.; Orenstein, M.; Fan, S. Inverse design of lightweight broadband reflector for relativistic lightsail propulsion. ACS Photonics 2020, 7, 2350–2355. [Google Scholar] [CrossRef]
- Sun, K.; Riedel, C.A.; Wang, Y.; Urbani, A.; Simeoni, M.; Mengali, S.; Zalkovskij, M.; Bilenberg, B.; de Groot, C.H.; Muskens, O.L. Metasurface optical solar reflectors using AZO transparent conducting oxides for radiative cooling of spacecraft. ACS Photonics 2018, 5, 495–501. [Google Scholar] [CrossRef]
- Hossain, M.M.; Jia, B.; Gu, M. A metamaterial emitter for highly efficient radiative cooling. Adv. Opt. Mater. 2015, 3, 1047–1051. [Google Scholar] [CrossRef]
- Scalia, T.; Bonventre, L. Nanomaterials in Space: Technology Innovation and Economic Trends. Adv. Astronaut. Sci. Technol. 2020, 3, 145–155. [Google Scholar] [CrossRef]
- Selvakumar, P.; Seenivasan, S.; Vijayakumar, G.; Panneerselvam, A.; Revathi, A. Application of Nanotechnology on Medicine and Biomedical Engineering. In Nanomaterials and the Nervous System; IGI Global: Hershey, PA, USA, 2025; pp. 195–210. [Google Scholar]
- Gade, R.; Dwarampudi, L.P.; Yamuna, K.; Maraba, N.; Fufa, G. Advanced Nanomaterials in Imaging and Diagnostics. In Exploring Nanomaterial Synthesis, Characterization, and Applications; IGI Global: Hershey, PA, USA, 2025; pp. 79–100. [Google Scholar]
- Puri, N. Novel Approaches for the Synthesis of Nanomaterials for Nanodevices in Medical Diagnostics. In Applications of Nanoparticles in Drug Delivery and Therapeutics; Bentham Science Publishers: Sharjah, United Arab Emirates, 2024; pp. 31–45. [Google Scholar]
- Tanabe, K. Nanostructured Materials for Solar Cell Applications. Nanomaterials 2021, 12, 26. [Google Scholar] [CrossRef]
- Sainz-Calvo, Á.J.; Sierra-Padilla, A.; Bellido-Milla, D.; Cubillana-Aguilera, L.; García-Guzmán, J.J.; Palacios-Santander, J.M. Fast, Economic, and Improved Nanostructured Polymeric pH Sensor for Agrifood Analysis. Chemosensors 2025, 13, 63. [Google Scholar] [CrossRef]
- Saha, S.; Sachdev, M.; Mitra, S.K. Design and Optimization of a Gold and Silver Nanoparticle-Based SERS Biosensing Platform. Sensors 2025, 25, 1165. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Abu-Dief, A.M.; El-Dabea, T. Functionalization of Nanomaterials for Energy Storage and Hydrogen Production Applications. Materials 2025, 18, 768. [Google Scholar] [CrossRef]
- Dahan, K.A.; Li, Y.; Xu, J.; Kan, C. Recent progress of gold nanostructures and their applications. Phys. Chem. Chem. Phys. 2023, 25, 18545–18576. [Google Scholar] [CrossRef]
- Majumder, D.; Ghosh, A. Optical tunability of mid-IR based AZO nano geometries through the characterisation of plasmon induced resonance modes. In Proceedings of the 2022 IEEE International Conference on Emerging Electronics (ICEE), Bangalore, India, 11–14 December 2022; pp. 1–7. [Google Scholar]
- Huang, X.; Zhang, B.; Yu, B.; Zhang, H.; Shao, G. Figures of merit of plasmon lattice resonance sensors: Shape and material matters. Nanotechnology 2022, 33, 225206. [Google Scholar] [CrossRef]
- Mourdikoudis, S.; Pallares, R.M.; Thanh, N.T.K. Characterization techniques for nanoparticles: Comparison and complementarity upon studying nanoparticle properties. Nanoscale 2018, 10, 12871–12934. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, D.; Yu, N.; Liang, B.; Yang, Z.; Asif, M.S.; Yan, R.; Liu, M. Machine learning enhanced optical microscopy for the rapid morphology characterization of silver nanoparticles. ACS Appl. Mater. Interfaces 2023, 15, 18244–18251. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.; Xu, K.; Deng, H.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Verma, S.; Chugh, S.; Ghosh, S.; Rahman, B.A. A comprehensive deep learning method for empirical spectral prediction and its quantitative validation of nano-structured dimers. Sci. Rep. 2023, 13, 1129. [Google Scholar] [CrossRef] [PubMed]
- Understanding Mesh Refinement and Conformal Mesh in FDTD. Available online: https://support.lumerical.com/hc/en-us/articles/360034382594-Understanding-Mesh-Refinement-and-Conformal-Mesh-in-FDTD (accessed on 11 March 2025).
- Acharige, D.; Johlin, E. Machine learning in interpolation and extrapolation for nanophotonic inverse design. ACS Omega 2022, 7, 33537–33547. [Google Scholar] [CrossRef] [PubMed]
- Vahidzadeh, E.; Shankar, K. Artificial neural network-based prediction of the optical properties of spherical core–shell plasmonic metastructures. Nanomaterials 2021, 11, 633. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Xu, Y.; Zhao, J.; Liu, Y.; Liu, Z. Localized Plasmonic Structured Illumination Microscopy Using Hybrid Inverse Design. Nano Lett. 2024, 24, 11581–11589. [Google Scholar] [CrossRef]
- Nugroho, F.A.A.; Bai, P.; Darmadi, I.; Castellanos, G.W.; Fritzsche, J.; Langhammer, C.; Baldi, A. Inverse Designed Plasmonic Metasurface with Parts per Billion Optical Hydrogen Detection. Nat. Commun. 2022, 13, 5737. [Google Scholar] [CrossRef]
- Liang, B.; Xu, D.; Yu, N.; Xu, Y.; Ma, X.; Liu, Q.; Asif, M.S.; Yan, R.; Liu, M. Physics-Guided Neural-Network-Based Inverse Design of a Photonic–Plasmonic Nanodevice for Superfocusing. ACS Appl. Mater. Interfaces 2022, 14, 26950–26959. [Google Scholar] [CrossRef]
- Nelson, D.; Kim, S.; Crozier, K.B. Inverse Design of Plasmonic Nanotweezers by Topology Optimization. ACS Photonics 2023, 10, 3552–3560. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. arXiv 2019, arXiv:1706.09516. [Google Scholar] [CrossRef]
- Harwood, J. Residual Plot Guide: Improve Your Model’s Accuracy. 2008. Available online: https://chartexpo.com/blog/residual-plot#introduction-to-residual-plot-analysis (accessed on 27 February 2025).
- Cribari-Neto, F.; Soares, A.C.N. Inferência em modelos heterocedásticos. Rev. Bras. De Econ. 2003, 57, 319–335. [Google Scholar] [CrossRef]







| Model | n_Estimators | Max_Depth | Learning_Rate | L2 Reg. | Strategy |
|---|---|---|---|---|---|
| catboost | 1000 | 6 | 0.03 | 3.0 | Ordered Boosting, Symmetric Trees |
| rf | 100 | None | – | – | Bootstrap + Gini/MSE |
| et | 100 | None | – | – | Totally Random Splits |
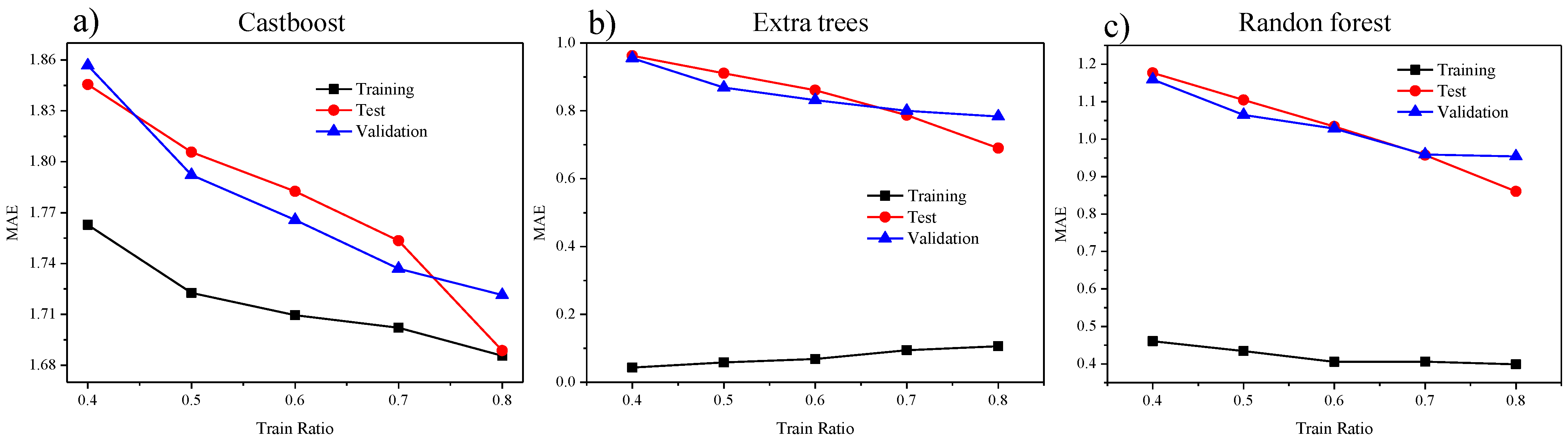
| Training Ratio | Model | r2 Training | Mae Training | r2 Test | Mae Test | r2 Valid | Mae Valid | Mae Ratio |
|---|---|---|---|---|---|---|---|---|
| 0.4 | catboost | 0.984 | 1.763 | 0.980 | 1.845 | 0.981 | 1.857 | 1.053 |
| 0.4 | rf | 0.996 | 0.460 | 0.978 | 1.177 | 0.980 | 1.159 | 2.518 |
| 0.4 | et | 0.998 | 0.043 | 0.978 | 0.962 | 0.979 | 0.955 | 22.212 |
| 0.5 | catboost | 0.984 | 1.723 | 0.979 | 1.806 | 0.982 | 1.792 | 1.040 |
| 0.5 | rf | 0.996 | 0.434 | 0.977 | 1.104 | 0.981 | 1.065 | 2.451 |
| 0.5 | et | 0.998 | 0.058 | 0.976 | 0.911 | 0.979 | 0.868 | 14.929 |
| 0.6 | catboost | 0.983 | 1.710 | 0.981 | 1.783 | 0.981 | 1.766 | 1.033 |
| 0.6 | rf | 0.996 | 0.406 | 0.978 | 1.034 | 0.978 | 1.028 | 2.534 |
| 0.6 | et | 0.998 | 0.069 | 0.975 | 0.861 | 0.977 | 0.832 | 12.114 |
| 0.7 | catboost | 0.983 | 1.702 | 0.982 | 1.753 | 0.983 | 1.737 | 1.020 |
| 0.7 | rf | 0.995 | 0.406 | 0.980 | 0.957 | 0.981 | 0.959 | 2.361 |
| 0.7 | et | 0.997 | 0.094 | 0.977 | 0.787 | 0.977 | 0.800 | 8.493 |
| 0.8 | catboost | 0.983 | 1.686 | 0.985 | 1.689 | 0.983 | 1.721 | 1.021 |
| 0.8 | rf | 0.994 | 0.399 | 0.984 | 0.861 | 0.980 | 0.954 | 2.389 |
| 0.8 | et | 0.996 | 0.106 | 0.981 | 0.690 | 0.975 | 0.783 | 7.374 |
| Material | Model | Mae Ratio |
|---|---|---|
| Gold | catBoost | 1.005 |
| Gold | rf | 2.293 |
| Gold | et | 8.199 |
| Silver | catBoost | 1.009 |
| Silver | rf | 2.292 |
| Silver | et | 8.069 |
| Copper | catBoost | 1.020 |
| Copper | rf | 2.361 |
| Copper | et | 8.493 |
| Modelo | Training Ratio | Predição Para 75 nm | Erro Absoluto (nm) |
|---|---|---|---|
| CatBoost | 0.3 | 74.63 | 0.37 |
| CatBoost | 0.7 | 74.75 | 0.25 |
| Extra Trees | 0.3 | 76.80 | 1.80 |
| Extra Trees | 0.7 | 78.00 | 3.00 |
| Random Forest | 0.3 | 77.40 | 2.40 |
| Random Forest | 0.7 | 78.00 | 3.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maia, L.S.P.; Barroso, D.A.; Silveira, A.B.; Oliveira, W.F.; Galembeck, A.; Fernandes, C.A.R.; Bandeira, D.G.C.; Cluzel, B.; Alexandria, A.R.; Guimarães, G.F. Inverse Design of Plasmonic Nanostructures Using Machine Learning for Optimized Prediction of Physical Parameters. Photonics 2025, 12, 572. https://doi.org/10.3390/photonics12060572
Maia LSP, Barroso DA, Silveira AB, Oliveira WF, Galembeck A, Fernandes CAR, Bandeira DGC, Cluzel B, Alexandria AR, Guimarães GF. Inverse Design of Plasmonic Nanostructures Using Machine Learning for Optimized Prediction of Physical Parameters. Photonics. 2025; 12(6):572. https://doi.org/10.3390/photonics12060572
Chicago/Turabian StyleMaia, Luana S. P., Darlan A. Barroso, Aêdo B. Silveira, Waleska F. Oliveira, André Galembeck, Carlos Alexandre R. Fernandes, Dayse G. C. Bandeira, Benoit Cluzel, Auzuir R. Alexandria, and Glendo F. Guimarães. 2025. "Inverse Design of Plasmonic Nanostructures Using Machine Learning for Optimized Prediction of Physical Parameters" Photonics 12, no. 6: 572. https://doi.org/10.3390/photonics12060572
APA StyleMaia, L. S. P., Barroso, D. A., Silveira, A. B., Oliveira, W. F., Galembeck, A., Fernandes, C. A. R., Bandeira, D. G. C., Cluzel, B., Alexandria, A. R., & Guimarães, G. F. (2025). Inverse Design of Plasmonic Nanostructures Using Machine Learning for Optimized Prediction of Physical Parameters. Photonics, 12(6), 572. https://doi.org/10.3390/photonics12060572





