Hybrid Self-Attention Transformer U-Net for Fourier Single-Pixel Imaging Reconstruction at Low Sampling Rates

Abstract

Fourier Single-Pixel Imaging exhibits significant advantages over conventional imaging techniques, including high interference resistance, broad spectral adaptability, nonlocal imaging capability, and long-range detection. However, in practical applications, FSPI relies on undersampling reconstruction, which inevitably leads to ringing artifacts that degrade image quality. To enhance reconstruction performance, a Transformer-based FSPI reconstruction network is proposed. The network adopts a U-shaped architecture, composed of multiple Hybrid Self-Attention Transformer Modules and Feature Fusion Modules. The experimental results demonstrate that the proposed network achieves high-quality reconstruction at low sampling rates and outperforms traditional reconstruction methods and convolutional network-based approaches in terms of both visual appearance and image quality metrics. This method holds significant potential for high-speed single-pixel imaging applications, enabling the reconstruction of high-quality images at extremely low sampling rates.

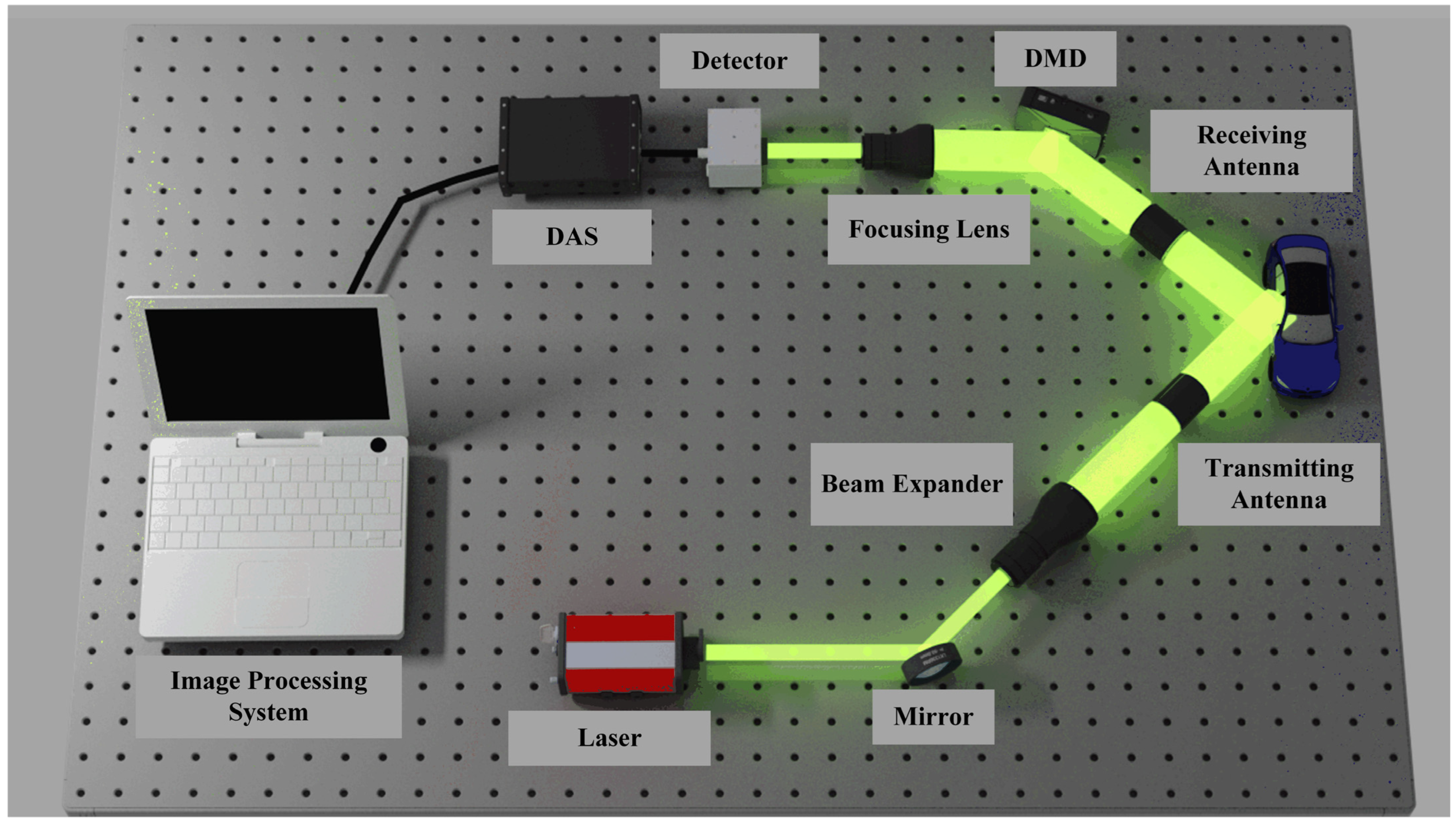
1. Introduction

Fourier Single-Pixel Imaging (FSPI), as an active optical imaging technique, has attracted extensive attention in the field of optical imaging in recent years [1,2]. Compared with conventional array detector-based techniques, FSPI exhibits superior flexibility and noise resistance, as well as broad spectral coverage [3,4], making it highly advantageous for a wide range of applications, including terahertz imaging [5], 3D imaging [6,7], multispectral imaging [8], target tracking [9,10,11], remote sensing [12,13,14], and other fields.

By illuminating the target with Fourier basis patterns, FSPI can acquire the Fourier spectrum of the target image. Since most of the information in natural images is concentrated in the low-frequency components, FSPI can adopt various undersampling strategies to effectively reduce the required number of measurements and lower imaging costs [15,16,17]. In the future, the multimodal characteristics of Perfect Vortex (PV) beams may also be exploited to design sparse sampling strategies that better adapt to the spectral distribution of natural images [18]. However, the undersampling process also introduces a significant problem: the reduction in the number of measurements markedly degrades the quality of the reconstructed images and leads to the appearance of ringing artifacts.

With the rapid advancement of deep learning, its advantages in the field of image reconstruction have become increasingly prominent. By learning representative features from large-scale datasets, deep learning has demonstrated strong reconstruction capabilities in Fourier Single-Pixel Imaging, enabling the rapid and high-quality reconstruction of images at extremely low sampling rates. In 2019, Rizvi et al. [19] proposed a deep convolutional autoencoder network (DCAN) with symmetric skip connections, which significantly improved the reconstruction quality of low-sampling images. In the following year, they further optimized this approach by designing a dual-branch network (FDCAN) [20]; the main branch focused on suppressing artifacts and noise, while the auxiliary branch aimed to preserve fine image details. The fusion of features from both branches enabled high-quality image reconstruction under extremely low sampling conditions. However, both DCAN and FDCAN adopted relatively shallow architectures, which limited their overall performance due to the simplicity of their structural design. In 2021, Yang et al. [21] introduced a generative adversarial network (GAN) architecture and proposed a generator composed of three cascaded U-Net modules. This design effectively overcame the performance bottlenecks of traditional DCAN and further enhanced the reconstruction quality of FSPI. Nevertheless, GAN-based models are inherently difficult to train due to instability issues, and the deep stacking of U-Net modules may result in feature degradation and performance deterioration. Subsequently, some researchers moved beyond merely refining network architectures and instead focused on enhancing reconstruction performance through deep learning mechanisms, such as sampling strategy optimization and self-supervised constraints. In 2023, Jiang et al. [22] proposed the S2O-FSPI method, which jointly trains sampling strategy optimization and the reconstruction network. A sampling optimization module was introduced and trained in an end-to-end fashion, thereby improving both sampling efficiency and reconstruction quality while addressing the resource inefficiencies of traditional empirically designed sampling schemes. In 2024, Chang et al. [23] explored a self-supervised learning framework by innovatively incorporating dual-domain constraints from the measurement and transformation domains into the network design. This approach eliminated the need for paired training data and pretrained models, effectively improving reconstruction performance in complex FSPI scenarios. In 2025, Wang et al. [24] further combined GANs with attention mechanisms and proposed the MaGanNet, which dynamically generates optimized sampling masks. This method significantly improved image reconstruction quality and system robustness under low-sampling conditions. Although these methods have achieved remarkable progress in FSPI reconstruction, they are still based on convolutional neural networks (CNNs), which are inherently incapable of modeling long-range dependencies. In FSPI reconstruction tasks, capturing such dependencies is crucial for recovering fine details and structural information.

To address this limitation, a Transformer-based image reconstruction network, termed Hybrid Self-Attention Transformer U-Net (HATU), is proposed. The network adopts a U-shaped architecture, with its core components being the Hybrid Self-Attention Transformer Module and the Feature Fusion Module. The U-shaped design facilitates a balanced trade-off between spatial information preservation and detail recovery through a series of downsampling and upsampling operations, ensuring effective multi-scale feature fusion. The Hybrid Self-Attention Transformer Module is designed to capture long-range dependencies within images, extract global contextual information, and enhance the network’s ability to comprehend complex semantic structures. Compared with conventional convolutional networks, the Transformer architecture overcomes the limitations of local receptive fields and enables more effective integration of global context information, which is particularly critical for image reconstruction at low sampling rates. The Feature Fusion Module further optimizes the integration of deep semantic features and shallow spatial features. Unlike simple concatenation or addition methods, the Feature Fusion Module dynamically adjusts the contributions of deep and shallow features, enabling a more precise and cohesive fusion. The mechanism not only effectively suppresses noise from shallow features but also preserves the rich semantic information from deeper layers, thereby enhancing both the detail representation and overall quality of the reconstructed images. The main contributions of the work are summarized as follows:

(1)

It introduces the Transformer architecture to enhance global modeling capabilities in FSPI reconstruction tasks, effectively improving image detail restoration and overall reconstruction quality.

(2)

It designs a Hybrid Self-Attention Transformer Module that integrates spatial window self-attention and channel self-attention mechanisms, achieving stronger global context modeling and significantly enhancing feature perception and representation capabilities.

(3)

It proposes a Feature Fusion Module that dynamically adjusts the weight allocation between shallow spatial features and deep semantic features, enabling more precise and efficient multi-level feature fusion.

2. Methods

2.1. Fourier Single-Pixel Imaging

The principle of Fourier Single-Pixel Imaging is illustrated in Figure 1. Firstly, the laser beam emitted from the laser source is directed onto a beam expander, where it is expanded before being projected onto the target scene through a transmitting antenna. The laser light reflected from the target scene is then collected by a receiving antenna and directed onto a digital micromirror device (DMD). The DMD spatially modulates the reflected light according to the modulation patterns transmitted from the computer. Finally, a detector captures the modulated signals. The computer processes the received light intensity signals to reconstruct the spatial spectral distribution of the target scene.

Assuming that the laser source emits a uniform light intensity, as denoted by E₀, the reflected light, E(x,y), from the target scene can be expressed as follows:

$$E\left(x,y\right)=E_{0}R\left(x,y\right)$$

(1)

where R(x,y) denotes the reflectivity distribution of the target scene.

In the FSPI system, Fourier basis patterns are loaded onto the digital micromirror device (DMD), and a four-step phase-shifting method is employed to extract the Fourier coefficients of the target. The Fourier basis patterns are pre-generated by the computer, and their spatial distribution can be expressed as follows:

$$P_{\phi }\left(x,y; f_x,f_y\right)=a+b·cos\left(2\pi f_{x}x+2\pi f_{y}y+\phi \right)$$

(2)

where a represents the average light intensity, b denotes the amplitude, x and y are the Cartesian coordinates on the target plane, f_x and f_y correspond to the spatial frequencies along the x direction and the y direction, respectively, and φ denotes the phase.

The reflected light from the target scene is projected onto the DMD, where it is spatially modulated according to the loaded Fourier basis patterns. The modulated light is then collected by a single-pixel detector, and the detected light intensity can be expressed as follows:

$$Z_{\phi }\left(f_x,f_y\right)=Z_n+\beta {\displaystyle \iint E\left(x,y\right)P_{\phi }\left(x,y; f_x,f_y\right)}dxdy$$

(3)

where β represents the amplification factor associated with the single-pixel detector, and Z_n denotes the environmental noise.

To obtain the Fourier spectrum that corresponds to the spatial frequency (f_x,f_y), four Fourier basis patterns with initial phases of 0, π/2, π, and 3π/2 are sequentially projected onto the target based on the four-step phase-shifting method. These four Fourier basis patterns are denoted as P₀, P_π/2, P_π, and P_3π/2, respectively, as follows:

$$\left\{\begin{array}{l}{P}_0\left(x,y; f_x,f_y\right)=a+b·cos\left(2\pi f_{x}y+0\right)\\ P_{\pi /2}\left(x,y; f_x,f_y\right)=a+b·cos\left(2\pi f_{x}y+\pi /2\right)\\ P_{\pi }\left(x,y; f_x,f_y\right)=a+b·cos\left(2\pi f_{x}y+\pi \right)\\ P_{3\pi /2}\left(x,y; f_x,f_y\right)=a+b·cos\left(2\pi f_{x}y+3\pi /2\right)\end{array}\right.$$

(4)

Accordingly, the respective detected light intensities can be represented as Z₀, Z_π/2, Z_π, and Z_3π/2, as follows:

$$\left\{\begin{array}{l}{Z}_0\left(f_x,f_y\right)=Z_n+\beta {\displaystyle \iint R\left(x,y\right)}{P}_0\left(x,y; f_x,f_y\right)E_{0}dxdy\\ Z_{\pi /2}\left(f_x,f_y\right)=Z_n+\beta {\displaystyle \iint R\left(x,y\right)}{P}_{\pi /2}\left(x,y; f_x,f_y\right)E_{0}dxdy\\ Z_{\pi }\left(f_x,f_y\right)=Z_n+\beta {\displaystyle \iint R\left(x,y\right)}{P}_{\pi }\left(x,y; f_x,f_y\right)E_{0}dxdy\\ Z_{3\pi /2}\left(f_x,f_y\right)=Z_n+\beta {\displaystyle \iint R\left(x,y\right)}{P}_{3\pi /2}\left(x,y; f_x,f_y\right)E_{0}dxdy\end{array}\right.$$

(5)

Based on the four detected light intensities, the Fourier spectrum value of the target object in the spatial frequency domain can be expressed as follows:

$$F\left(f_x,f_y\right)=\left[Z_0\left(f_x,f_y\right)-Z_{\pi }\left(f_x,f_y\right)\right]+j\left[Z_{3\pi /2}\left(f_x,f_y\right)-Z_{\pi /2}\left(f_x,f_y\right)\right]$$

(6)

where F(f_x,f_y) denotes the spatial spectrum value of the target scene at (f_x,f_y), and j represents the imaginary unit.

Since most of the spectral energy of the target scene is concentrated in the low-frequency components, selecting only the low-frequency portion of the sampled spectrum allows for the reconstruction of satisfactory image information with a reduced number of measurements. Subsequently, the sampled spatial spectrum is subjected to an inverse Fourier transform to obtain a preliminary reconstructed intensity image of the target scene. Accordingly, the preliminary reconstructed image can be expressed as follows:

$$I_{us}=IFFT\left\{D\left[F\left(f_x,f_y\right)\right]\right\}$$

(7)

where I_us denotes the preliminary reconstructed image, IFFT(·) represents the inverse Fourier transform, and D(·) indicates the undersampling process.

When the sampling rate is low, the quality of the reconstructed image deteriorates. Therefore, to enhance the reconstruction quality at low sampling rates, it is necessary to supplement the high-frequency information of the low-resolution intensity image. The process can be achieved using deep learning-based reconstruction methods. The process can be expressed as follows:

$$I_{rc}=IR(I_{us})$$

(8)

where I_rc denotes the image reconstructed by the reconstruction network, and IR represents the reconstruction network used to reconstruct low-sampling images. Through further processing of the low-sampling image by the reconstruction network, a high-resolution image can be obtained.

2.2. Network Architecture

The overall structure of the network is illustrated in Figure 2. A seven-layer encoder–decoder architecture is adopted, where each encoder and decoder layer are composed of Hybrid Self-Attention Transformer Modules. For a given undersampled image, I∈R^H×W×1, HATU first extracts shallow features, F₀∈R^H×W×C, through a 3 × 3 convolutional layer, where H × W denotes the spatial dimensions, and C represents the number of channels.

During the feature encoding stage, the shallow feature, F₀, sequentially passes through four encoder layers (L1, L2, L3, and L4). After each of the L1, L2, and L3 layers, a 3 × 3 convolutional layer with a stride of 2 is used for downsampling, progressively reducing the spatial dimensions of the feature maps. After each downsampling operation, both the height and width of the feature map are halved, while the number of channels is doubled.

In the decoding stage, the feature, F_L∈R^H/8×W/8×8C, output from the encoder is used as the input for hierarchical feature reconstruction. The feature maps are successively processed by three decoder layers (L5, L6, and L7). Before entering each of the L5, L6, and L7 layers, upsampling is performed through pixel shuffle operations, followed by a 1 × 1 convolutional layer, gradually increasing the spatial size of the feature maps to restore the initial input resolution while progressively reducing the number of channels. Finally, the output feature map from the decoder is denoted as F_r∈R^H×W×C.

To better recover image information, a skip connection mechanism is introduced into the network, where feature maps from the encoding stage are fused with the corresponding feature maps from the decoding stage. At each skip connection, a Feature Fusion Module is employed to adjust the weights between different feature maps, effectively integrating the low-level structural information from the encoder and the high-level semantic information from the decoder, thereby enhancing the completeness and robustness of feature representations. Subsequently, an additional 3 × 3 convolutional layer is applied to process the decoder output, F_r, thereby generating a residual image, R∈R^H×W. The residual image is designed to compensate for the detail information lost during the undersampling process, further improving the reconstruction quality. The final reconstructed image, I_rec, is obtained via the element-wise addition of the residual image, R, and the original undersampled input image, I, and can be expressed as follows:

$$I_{rec}=I+R$$

(9)

2.2.1. Hybrid Self-Attention Transformer Module

The self-attention mechanism was initially widely adopted in the field of natural language processing and has subsequently demonstrated substantial advantages in modeling global dependencies for computer vision tasks. It effectively captures long-range interactions by establishing fully connected relationships between all positions within the input, enabling each position to directly attend to every other position. The input features are first projected into three sets of vectors: query, Q, key, K, and value, V. The similarity between positions is computed by taking the dot product between each query and all keys, followed by Softmax normalization to produce a global attention matrix. Each row of this matrix represents the attention weights of one position with respect to all others. The final output is then obtained by computing a weighted sum over all value vectors according to these weights. Compared to traditional convolutional neural networks, which are constrained by local receptive fields and depend on deep hierarchical structures to propagate information over long distances, self-attention enables global context modeling within a single forward pass. Furthermore, the information transmission path length is independent of spatial distance, allowing even distant spatial positions to communicate directly. This greatly enhances the model’s capacity to capture global structures and long-range dependencies.

As shown in Figure 3, the Hybrid Self-Attention Transformer Module is composed of a Depthwise Separable Spatial Windows Self-Attention (DSConv Spatial Windows Self-Attention, DSWA) model, a Depthwise Separable Channel-wise Self-Attention (DSConv Channel-wise Self-Attention, DCWA) model, and a Gated Depthwise Separable Convolution Feed-Forward Network (Gated DSConv Feed-Forward Network, GDFN). By alternately applying the DSWA and DCWA mechanisms, HATU efficiently extracts global features along both spatial and channel dimensions. Specifically, DSWA focuses on capturing spatial contextual relationships, thereby enhancing the model’s capability for spatial global modeling, while DCWA emphasizes modeling the global dependencies among different channels, thereby improving the understanding of semantic information. The GDFN further enhances the model’s representational and feature learning capabilities through nonlinear transformations applied to the feature vectors at each spatial position. Through the Hybrid Self-Attention Transformer Module, HATU is able to handle complex image details and achieve higher expressiveness in feature representations.

DSConv Spatial Windows Self-Attention (DSWA): DSWA is designed to capture spatial information through attention computation within local windows. When processing an input feature map, X∈R^H×W×C, Depthwise Separable Convolution (DSconv) [25] is employed instead of linear projection to enhance the extraction of local contextual features. Specifically, Pointwise Convolution (PWC) is first applied to aggregate contextual information across channels, followed by 3 × 3 Depthwise Convolution (DWC) to encode spatial contextual information. The projection matrices for the query, Q, key, K, and value, V, can be expressed as follows:

$$Q=W_d^Q{W}_p^{Q}Y$$

(10)

$$K=W_d^K{W}_p^{K}Y$$

(11)

$$V=W_d^V{W}_p^{V}Y$$

(12)

where Y∈R^H×W×C denotes the output of the LayerNorm layer, W_p(·) represents the 1 × 1 Pointwise Convolution, and W_d(·) represents the 3 × 3 Depthwise Convolution. Bias-free convolutional layers are employed in these structures to ensure stability. Subsequently, Q, K, and V are partitioned into non-overlapping windows, and each window is flattened, with each window containing N_w pixels and a total of HW/N_w windows. After flattening, each window yields Q_S∈R^Nw×C, K_S∈R^Nw×C, and V_S∈R^Nw×C. Then, these matrices are divided into h attention heads, with each head having a dimensionality of d = C/h. The output for each head is defined as follows:

$$Y_s^i=Softmax\left({\displaystyle \frac{Q_s^i{\left(K_s^i\right)}^T}{\sqrt{d}}}+\Delta d\right)·V_s^i$$

(13)

where Y_sⁱ∈R^HW×d denotes the output of the i-th attention head. Δd represents the relative position encoding, which is used to capture the relative positional information within each window. Finally, by concatenating and reshaping the outputs of all heads, Y_sⁱ, the feature Ys∈R^H×W×C is obtained. This process can be expressed as follows:

$$Y_s=Concat(Y_s^1,Y_s^2,\dots ,Y_s^h)W_p$$

(14)

where W_p∈R^C×C denotes the linear projection matrix used to fuse all features. DSWA adopts the shifted window strategy inspired by the Swin Transformer [26,27], performing attention computation only within small local regions and enabling global information exchange through window shifting, which effectively reduces the complexity from the conventional self-attention’s O(N²) to O(N). By introducing Depthwise Separable Convolution, DSWA not only enhances the representation of local features but also provides richer contextual information for the subsequent computation of the spatial attention map (A = Q_sⁱ(K_sⁱ)^T), thereby further improving the overall performance of the model. In addition, Depthwise Separable Convolution significantly reduces the number of parameters and computational cost compared to standard convolutions or linear projections, making the module more efficient without sacrificing performance.

DSConv Channel Wise Self-Attention (DCWA): DCWA follows a process similar to that of DSWA, with the key difference being that its self-attention mechanism operates along the channel dimension and does not require position encoding. Its computational burden remains relatively low due to the significantly smaller number of channels compared to spatial dimensions; thus, it has a minimal impact on overall inference efficiency. Given an input feature, X∈R^H×W×C, Depthwise Separable Convolution is similarly used to generate the query, Q, key, K, and value, V, matrices, denoted as Q_C∈R^HW×C, K_C∈R^HW×C, and V_C∈R^HW×C, respectively. The matrices are also divided into h attention heads, with each head having a dimensionality of d = C/h. The output for each head in the channel self-attention is defined as follows:

$$Y_c^i=V_c^i·Softmax\left({\displaystyle \frac{{\left(Q_c^i\right)}^T{K}_c^i}{\alpha }}\right)$$

(15)

where Y_cⁱ∈R^HW×d denotes the output of the i-th attention head, and α is a learnable parameter used to scale the inner product results before applying the Softmax function. Finally, all outputs, Y_cⁱ, are concatenated and reshaped to obtain the attention feature, Y_c∈R^H×W×C, following the same process as described in Equation (14).

Gated DSConv Feed-Forward Network (GDFN): In the traditional Transformer architecture, the Feed-Forward Network (FFN) consists of a nonlinear activation layer and two linear projection layers. However, this design lacks effective modeling of spatial information. To address this limitation, a gating mechanism and Depthwise Separable Convolution are introduced into the FFN, resulting in the GDFN. The gating mechanism is implemented by performing element-wise multiplication between two parallel paths, where one path passes through the GELU activation function. Assuming that the input feature is X∈R^H×W×C, the process can be expressed as follows:

$$\left\{\begin{array}{l}Y=W_p^{0}Gating(X)+X\\ Gating(X)=\varphi (W_d^1{W}_p^1(LN(X))\odot W_d^2{W}_p^2(LN(X)))\end{array}\right.$$

(16)

where ⊙ denotes element-wise multiplication, ϕ represents the GELU activation function, LN refers to the LayerNorm layer, and Y∈R^H×W×C denotes the output feature. Compared with the traditional FFN, GDFN enhances feature learning capability and strengthens the modeling of local image structures by introducing a gating mechanism and Depthwise Convolution, thereby exhibiting superior performance and greater flexibility.

2.2.2. Feature Fusion Module

In the U-shaped architecture, features are first gradually extracted through downsampling and then recovered through upsampling. During the downsampling process, shallow features retain rich spatial structural information but are often accompanied by high levels of noise. As the network deepens, although deep features contain abundant semantic information, the spatial structural information is progressively lost. Traditional feature fusion methods typically concatenate or add deep and shallow features directly; however, due to the significant disparity between the two types of information, the fusion results are often suboptimal. To address this issue, a Feature Fusion Module is designed at the junction of deep and shallow features, as illustrated in Figure 2.

The Feature Fusion Module is designed to dynamically adjust the fusion weights between deep and shallow information, thereby more effectively integrating their complementary advantages and enhancing the expressiveness of feature fusion, as well as the quality of reconstruction. In the implementation, the two input feature maps are first added element-wise and then subjected to global average pooling to extract global channel-wise semantic information. A shared fully connected layer followed by a Softmax function is used to generate a fusion weight vector, whose length equals the sum of the channel numbers of the two input features. The weight vector is then split into two parts and applied to the corresponding feature maps via channel-wise multiplication. Finally, the weighted feature maps are added element-wise to achieve fine-grained and adaptive fusion between shallow and deep features. Assuming that the input features are X₁∈R^H×W×C and X₂∈R^H×W×C, the process can be expressed as follows:

$$\left\{\begin{array}{l}s=Softmax(FC(PWConv(GAP(X_1\oplus X_2))))\\ Y=s_1{X}_1\oplus s_2{X}_2\end{array}\right.$$

(17)

where s denotes the channel selection weights, FC represents the fully connected layer, PWConv refers to the Pointwise Convolution, GAP stands for global average pooling, and Y∈R^H×W×C denotes the output feature.

2.3. Loss Function of HATU

The loss function of the reconstruction network is mainly composed of pixel loss and perceptual loss. The pixel loss is primarily used to measure the difference between the reconstructed image and the ground truth image. The pixel loss can be expressed as follows:

$$L_{pixel}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N|y_{rc}-y|}$$

(18)

where y_rc denotes the reconstructed image, y denotes the ground truth image, and N represents the total number of pixels. The perceptual loss measures the reconstruction quality by computing the difference between images in the feature space, typically using features extracted by a pre-trained convolutional neural network such as VGG [28,29]. The perceptual loss can be expressed as follows:

$$L_{perceptual}={\displaystyle \frac{1}{M}}{\displaystyle \sum _{j=1}^M|f_j\left(y_{rc}-y\right){|}^2}$$

(19)

where ϕ_j denotes the feature map extracted from the j-th layer of the pre-trained network, and M represents the number of selected feature layers.

The total loss is expressed as follows:

$$L={\lambda }_1{L}_{pixel}+{\lambda }_2{L}_{perceptual}$$

(20)

where λ₁ and λ₂ are the weighting factors used to balance the relative importance of each loss component. In the training process, λ₁ and λ₂ are set to 1 and 2 × 10⁻⁸, respectively.

3. Experimental Results and Analysis

3.1. Dataset Preparation and Training Process

The car image dataset [30] used during training contains 16,185 images, covering 197 car models from various periods and categories, including sedans, SUVs, coupes, convertibles, pickups, hatchbacks, and station wagons, demonstrating substantial appearance diversity. All images are collected from real-world image repositories, such as Flickr, Google, and Bing, and span a wide range of natural capture conditions, with varying lighting environments (e.g., indoor/outdoor and sunny/cloudy) and background complexity (e.g., urban roads, parking lots, and street scenes). All images are converted to grayscale and uniformly resized to a resolution of 256 × 256 pixels. Subsequently, circular region sampling is performed on the images. Finally, the dataset is randomly divided into training, validation, and testing sets in a ratio of 7:2:1.

Model training and implementation are conducted on a unified hardware platform. The system is configured with an NVIDIA GEFORCE RTX-3090 GPU (24 GB VRAM), manufactured by NVIDIA Corporation, Santa Clara, CA, USA. The operating system used is Ubuntu 20.04, with the CUDA 11.3 toolkit and the PyTorch 1.12 deep learning framework installed. During training, the batch size is set to 16, and the optimizer used is AdamW, with a weight decay coefficient of 10⁻⁴. The total number of training epochs is 100. The initial learning rate is set to 10⁻⁴, with a linear warm-up strategy applied over the first five epochs, followed by cosine annealing to adjust the learning rate, with the minimum learning rate set to 10⁻⁶ in order to enhance training stability and improve model convergence performance.

3.2. Comparison of Image Reconstruction Performance

(1) Quantitative Analysis: To validate the performance advantages of the proposed HATU network in reconstruction tasks, a quantitative comparison is conducted against the traditional reconstruction method, FSPI, as well as the deep learning-based reconstruction networks, DCAN [19] and FSPI-GAN [21].

Table 1. Quantitative comparison of reconstruction methods at different sampling rates.

Sample Rate	Method	SSIM	PSNR	RMSE	LPIPS
1%	FSPI	0.525	19.751	0.1041	0.5803
	DCAN	0.559	20.145	0.0996	0.5471
	FSPI-Gan	0.585	20.323	0.0944	0.4798
	HATU (Ours)	0.614	20.760	0.0882	0.3631
%	FSPI	0.631	22.056	0.0803	0.4672
	DCAN	0.672	22.647	0.0751	0.4207
	FSPI-Gan	0.713	23.303	0.0699	0.3631
	HATU (Ours)	0.732	23.556	0.0638	0.3197
5%	FSPI	0.698	23.399	0.0692	0.4041
	DCAN	0.736	24.026	0.0645	0.3517
	FSPI-Gan	0.772	24.652	0.0595	0.2953
	HATU (Ours)	0.793	25.041	0.0537	0.2632
10%	FSPI	0.791	25.483	0.0551	0.3091
	DCAN	0.814	25.808	0.0529	0.2577
	FSPI-Gan	0.855	26.943	0.0468	0.2099
	HATU (Ours)	0.867	27.432	0.0399	0.1878

presents the average PSNR [31,32], SSIM [33,34], RMSE, and LPIPS [35] values achieved by different reconstruction methods at sampling rates of 1%, 3%, 5%, and 10%. Higher PSNR and SSIM values indicate better reconstruction quality, whereas lower RMSE and LPIPS values are preferred. In the table, the best results are highlighted in bold. The proposed HATU network achieves the best performance across all sampling rates. At the highly challenging 1% sampling rate, HATU attains an SSIM of 0.614 and a PSNR of 20.760 dB, outperforming the FSPI-GAN network by 0.029 and 0.377 dB, respectively. It also achieves an RMSE of 0.0882 and an LPIPS of 0.3631, which are 0.0062 and 0.1167 lower than those of FSPI-GAN, respectively, demonstrating its strong reconstruction capability under extremely low sampling conditions. At sampling rates of 3%, 5%, and 10%, HATU consistently outperforms FSPI-GAN, with SSIM improvements of 0.019, 0.021, and 0.012, PSNR gains of 0.253 dB, 0.389 dB, and 0.489 dB, RMSE reductions of 0.006, 0.058, and 0.0069, and LPIPS decreases of 0.0434, 0.0321, and 0.0221, respectively. These results confirm the superior reconstruction performance of HATU across various sampling rates.

As shown in

Table 2. Computational complexity and inference efficiency of reconstruction methods.

Method	Parameters (M)	FLOPs (G)	Inference Time (ms)
FSPI	/	/	/
DCAN	0.19	3.07	1.39
FSPI-Gan	79.85	14.66	21.28
HATU (Ours)	8.79	24.81	19.54

, although the HATU network has a higher FLOPs value compared to the FSPI-GAN network, it exhibits a lower parameter count and shorter inference time. Considering the significant improvement in reconstruction performance at low sampling rates, this computational cost is entirely acceptable, indicating a favorable balance between performance and computational complexity for the HATU network.

(2) Qualitative Analysis: To further demonstrate the reconstruction performance of the HATU network, a qualitative analysis is conducted across different sampling rates. As shown in Figure 4, the leftmost image is the original image. On the left side of the dashed line, the spatial frequency domain sampling distributions corresponding to each sampling rate are displayed sequentially, while on the right side of the dashed line, the reconstruction results at the four sampling rates are presented.

The reconstruction quality of all methods improves with increasing sampling rates. Overall, at high sampling rates, each method is able to recover the target structures relatively clearly, whereas at low sampling rates, the performance differences become particularly pronounced. The HATU network consistently demonstrates superior reconstruction performance across all sampling rates, with its advantages being especially prominent at low sampling rates. Specifically, at low sampling rates, the traditional FSPI reconstruction results exhibit severe blurring, making it difficult to distinguish target contours and causing almost complete loss of vehicle details. The DCAN network alleviates the ringing effect to some extent but remains blurry overall, particularly in high-frequency regions such as rooftops and wheels, due to its relatively simple network architecture, which struggles to effectively extract and represent critical features. Although the FSPI-GAN network enhances image sharpness to a certain degree through the generative adversarial mechanism, it still exhibits significant limitations at extremely low sampling rates. This is mainly because its generator structure employs multiple cascaded U-Nets, which, while increasing depth and parameter count, introduce cumulative errors during repeated encoding and decoding processes, leading to the progressive degradation of high-frequency details. In contrast, the HATU network is able to effectively reconstruct images, even at extremely low sampling rates, successfully recovering details such as rooftop contours and wheel structures. The reconstructed results are not only clearer and more natural but also show a significant reduction in ringing artifacts. The advantage is attributed to the Hybrid Self-Attention Transformer modules designed in HATU, which achieve long-range dependency modeling across both spatial and channel dimensions, significantly enhancing the network’s ability to represent image structures and fine details.

3.3. Experiments on Generalization Ability

To comprehensively evaluate the generalization ability of the proposed reconstruction network, a generalization test experiment is designed to verify the model’s performance on out-of-distribution data. The model trained exclusively on the car dataset is directly applied to an image that did not appear during the training or validation stages. The image is not included in the car dataset and belongs to a completely new category and sample distribution. The purpose of this experiment is to assess whether the model has learned generalized feature representations rather than relying on category-specific structural information for reconstruction, thereby further verifying the network’s robustness and adaptability to unseen data and providing a strong reference for real-world deployment scenarios.

As shown in Figure 5, an image with a dog as the main subject is selected for testing. In addition to displaying the reconstruction results, the PSNR, SSIM, RMSE and LPIPS metrics are provided below each result for quantitative comparison. From a visual perspective, at the extremely low sampling rate of 1%, the HATU network demonstrates a superior ability to recover the overall outline and local key details of the dog image compared to other methods, especially achieving higher clarity in critical regions such as the head, eyes, and nose. Furthermore, the carpet texture details in the background are better preserved. At higher sampling rates, the HATU network continues to outperform the other methods, more accurately restoring fine texture information and overall scene structure. In addition, based on the quantitative PSNR, SSIM, RMSE and LPIPS results, the HATU network consistently achieves the best scores across all sampling rates, further confirming its strong generalization capability.

To further evaluate the generalization capability of the HATU network, additional image samples spanning a wider range of categories, including animals, insects, toys, furniture, and plants, are selected from the ImageNet-1k dataset [36]. The analysis is conducted under the most challenging 1% sampling rate condition to thoroughly assess the network’s ability to generalize across diverse data distributions. Figure 6 presents a comparison of reconstruction methods in this setting. The results demonstrate that the HATU network consistently preserves structural contours and critical details and achieves superior performance in terms of PSNR, SSIM, RMSE, and LPIPS compared to other methods, exhibiting strong robustness and generalization.

3.4. Ablation Experiments

To validate the effectiveness of each module, several configurations are defined: Scheme (1) replaces the Hybrid Self-Attention Transformer Module with convolution and removes the Feature Fusion Module from the HATU network; Scheme (2) replaces only the Hybrid Self-Attention Transformer Module with convolution; and Scheme (3) removes only the Feature Fusion Module. Ablation experiments are conducted at a 1% sampling rate. The qualitative and quantitative results of the experiments are presented in Table 2 and Figure 7, respectively.

Table 3. Quantitative ablation results for HATU at the 1% sampling rate.

Method	SSIM	PSNR	RMSE	LPIPS
HATU	0.614	20.760	0.0882	0.3631
(1)	0.565	20.201	0.0973	0.4967
(2)	0.571	20.284	0.0957	0.4755
(3)	0.606	20.660	0.0904	0.4028

presents the quantitative results of ablation experiments for different modules of the HATU network at the 1% sampling rate. By comparing (1) with (2) and (3) with the complete HATU network, it can be seen that the inclusion of the Feature Fusion Module leads to improvements in both SSIM and PSNR, as well as reductions in RMSE and LPIPS, indicating its positive effect on multi-level feature integration and detail restoration. A further comparison of the performance metrics between (1) and (3), as well as between (2) and the complete HATU network, clearly shows that the Hybrid Self-Attention Transformer module contributes more significant performance gains. This demonstrates that the module plays a key role in modeling global dependencies and effectively enhances the reconstruction capability of the network. Finally, the complete HATU network achieves the best performance across all metrics, validating the importance of the synergy between the two modules.

Additionally, Figure 7 presents the qualitative results of ablation experiments for different modules of the HATU network at the 1% sampling rate. By comparing (1) with (2) and (3) with the complete HATU network, it can be seen that the Feature Fusion Module effectively enhances the expressiveness of feature fusion and improves reconstruction quality by dynamically adjusting the fusion weights between deep and shallow features. For example, in the first row, (1) still exhibits slight ringing artifacts around the car contour, which are mostly eliminated in (2). The front wheel of the car in (3) is also less clear compared to that in the complete HATU network. Further comparisons between (1) and (3), as well as between (2) and HATU, clearly show that the Hybrid Self-Attention Transformer module significantly improves network performance. The schemes incorporating this module—(3) and HATU—produce more detailed and sharper reconstructions. This can be attributed to the Transformer’s ability to model global dependencies across both spatial and channel dimensions, thereby enabling more comprehensive feature representation and superior reconstruction performance. Overall, the HATU network, which integrates both the Feature Fusion Module and the Hybrid Self-Attention Transformer module, achieves the best visual results.

4. Discussion

This study aims to enhance the reconstruction quality of FSPI at low sampling rates. The experimental results demonstrate that the proposed HATU network exhibits superior image reconstruction performance for FSPI tasks, particularly at extremely low sampling rates. Compared with traditional FSPI reconstruction methods, the DCAN network, and the FSPI-GAN approach, HATU consistently achieves better metrics across all sampling rates. These results validate the initial hypothesis proposed in this work: by introducing Transformer-based global modeling capabilities, combined with a Feature Fusion Module, the image quality of FSPI reconstructions can be significantly improved.

From the perspective of previous research, early CNN-based FSPI reconstruction methods (such as DCAN and FDCAN) achieved preliminary success in artifact suppression and detail restoration. Subsequently, methods incorporating generative adversarial mechanisms, such as FSPI-GAN, further improved image clarity and visual quality. However, due to the inherent limitations of convolutional networks with local receptive fields, these methods struggle to capture long-range dependencies, which are critical for image reconstruction at low sampling rates. In contrast, the HATU network addresses this limitation by leveraging a hybrid self-attention mechanism to model long-range dependencies across both spatial and channel dimensions, thereby effectively enhancing feature representation and reconstruction quality.

In summary, the HATU network, constructed with the Hybrid Self-Attention Transformer module and the Feature Fusion Module, significantly enhances the reconstruction quality of FSPI at low sampling rates and holds great potential for advancing the development of Fourier Single-Pixel Imaging technology. In addition, recent advances in diffractive neural networks implemented in the electromagnetic or optical domain [37,38] offer a promising direction for future FSPI hardware realization, especially in scenarios that require low-latency and energy-efficient computation.

5. Conclusions

This paper proposes an image reconstruction network based on the Transformer architecture named the Hybrid Self-Attention Transformer U-Net (HATU), aiming to enhance reconstruction quality for Fourier Single-Pixel Imaging tasks. The network adopts a U-shaped architecture, with its core composed of a Hybrid Transformer Module and a Feature Fusion Module. By performing downsampling and upsampling operations, it effectively integrates multi-scale features and achieves a balanced trade-off between spatial structure preservation and detail recovery. The Hybrid Self-Attention Transformer Module captures long-range dependencies across spatial and channel dimensions, improving the network’s ability to acquire global information and overcoming the limitations imposed by the local receptive fields of conventional convolutional networks, which makes it particularly suitable for image reconstruction at low sampling rates. The Feature Fusion Module dynamically adjusts the weighting between deep semantic features and shallow spatial features, enabling finer multi-level feature integration, suppressing noise from shallow features, and preserving critical semantic information. The experimental results demonstrate that the HATU network significantly improves the detail representation and overall visual quality of reconstructed images at low sampling rates and consistently outperforms traditional methods and convolution-based approaches in terms of both image quality metrics and visual performance. Through the synergistic optimization of global modeling across spatial and channel dimensions, combined with dynamic feature fusion, HATU effectively improves imaging performance at low sampling rates, providing a more efficient deep learning solution for Fourier Single-Pixel Imaging systems.

Nevertheless, several limitations remain in the current study. Although the HATU network demonstrates strong performance across various sampling rates and generalization scenarios, its reconstruction capability may still be constrained in certain complex environments, such as underwater imaging, where factors like light scattering, absorption, and turbulence introduce additional challenges that are not fully accounted for by the current model. Moreover, although several measures have been adopted to reduce computational complexity, the overall network remains relatively heavy due to the inclusion of multiple self-attention modules, which may hinder real-time deployment on edge devices. Future work will focus on enhancing the adaptability of the model to challenging real-world environments, like underwater or low-light conditions, possibly through domain-specific training or physical modeling integration. In parallel, exploring lightweight network architectures, model compression, or knowledge distillation may help reduce computational overhead.