Study on the Evolutionary Characteristics of Airyprime Beams in Gaussian-Type PT Symmetric Optical Lattices
Abstract
1. Introduction
2. Theoretical Model
3. Numerical Calculations and Analysis
3.1. Profile of an Optical Lattice Potential
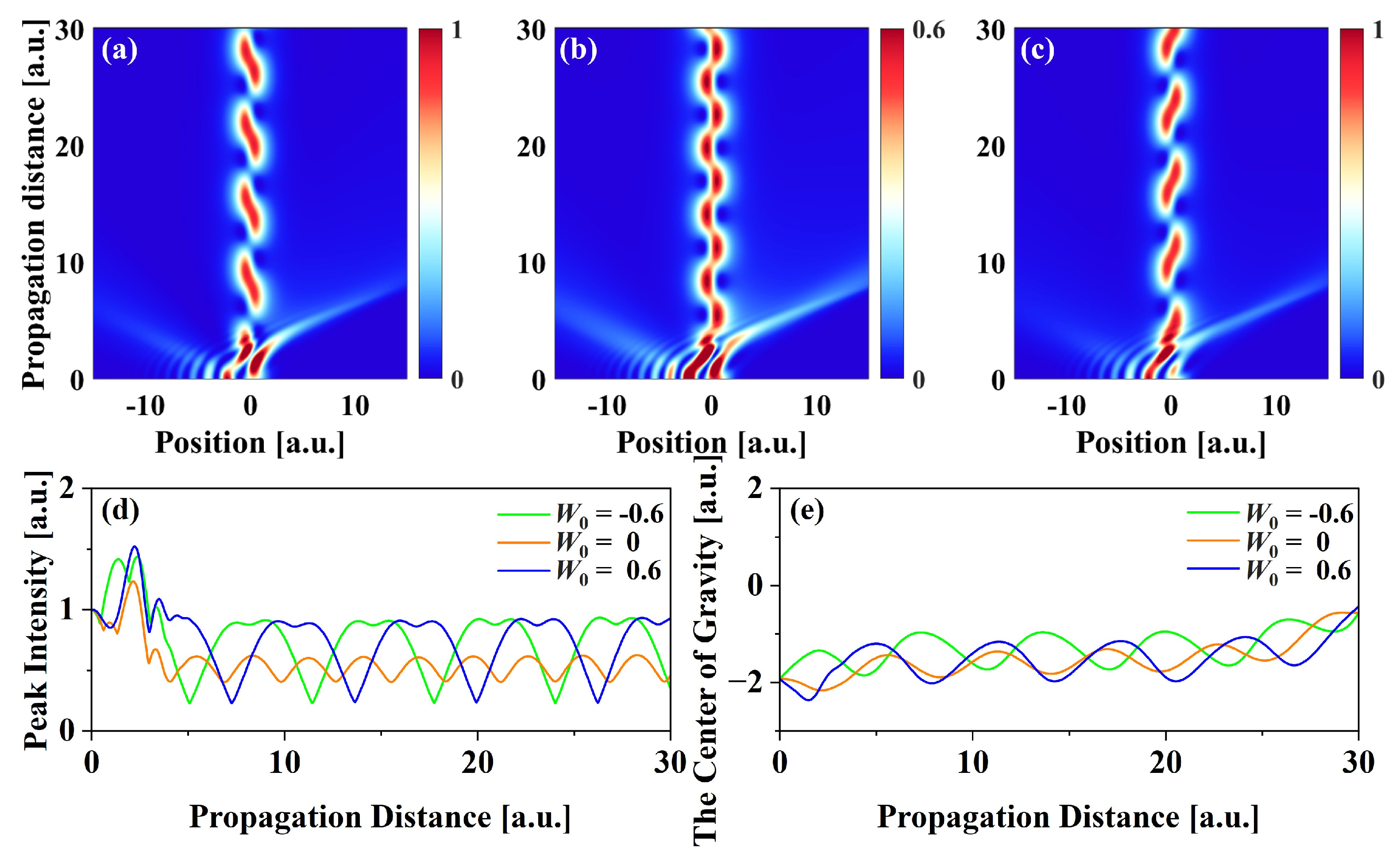
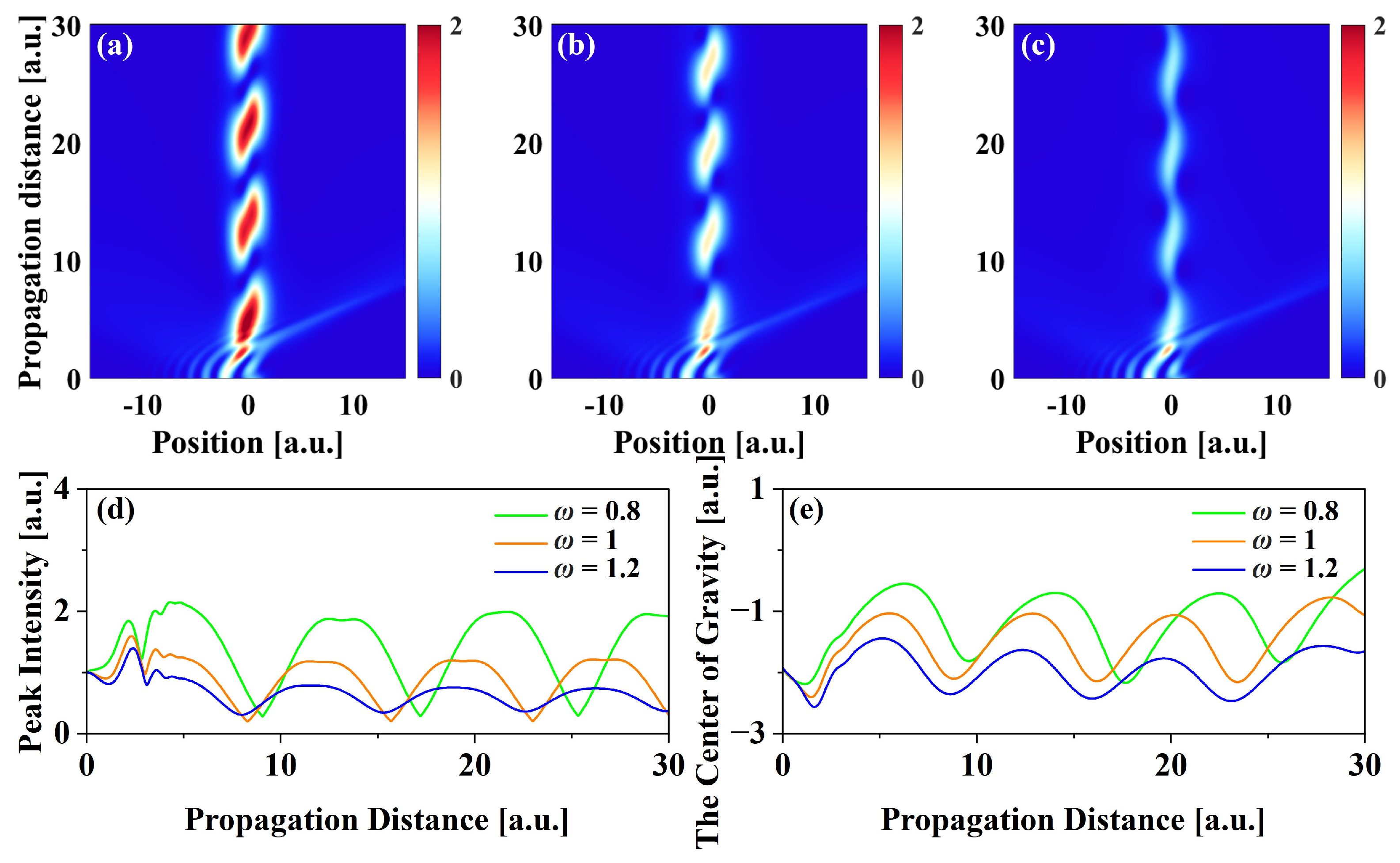
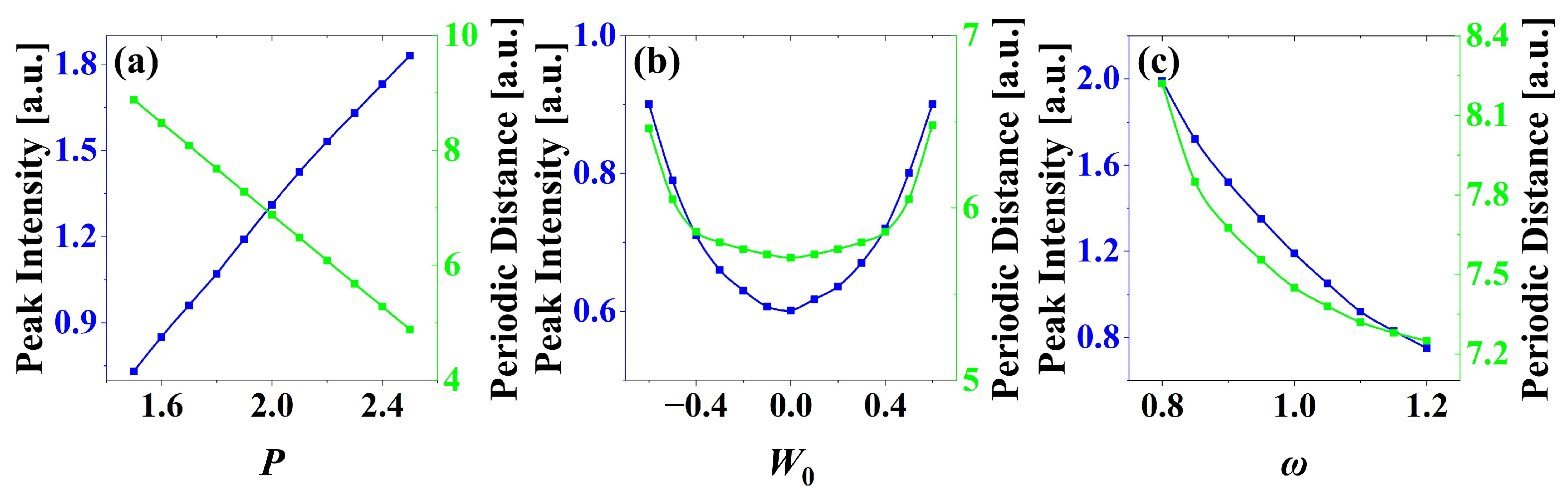
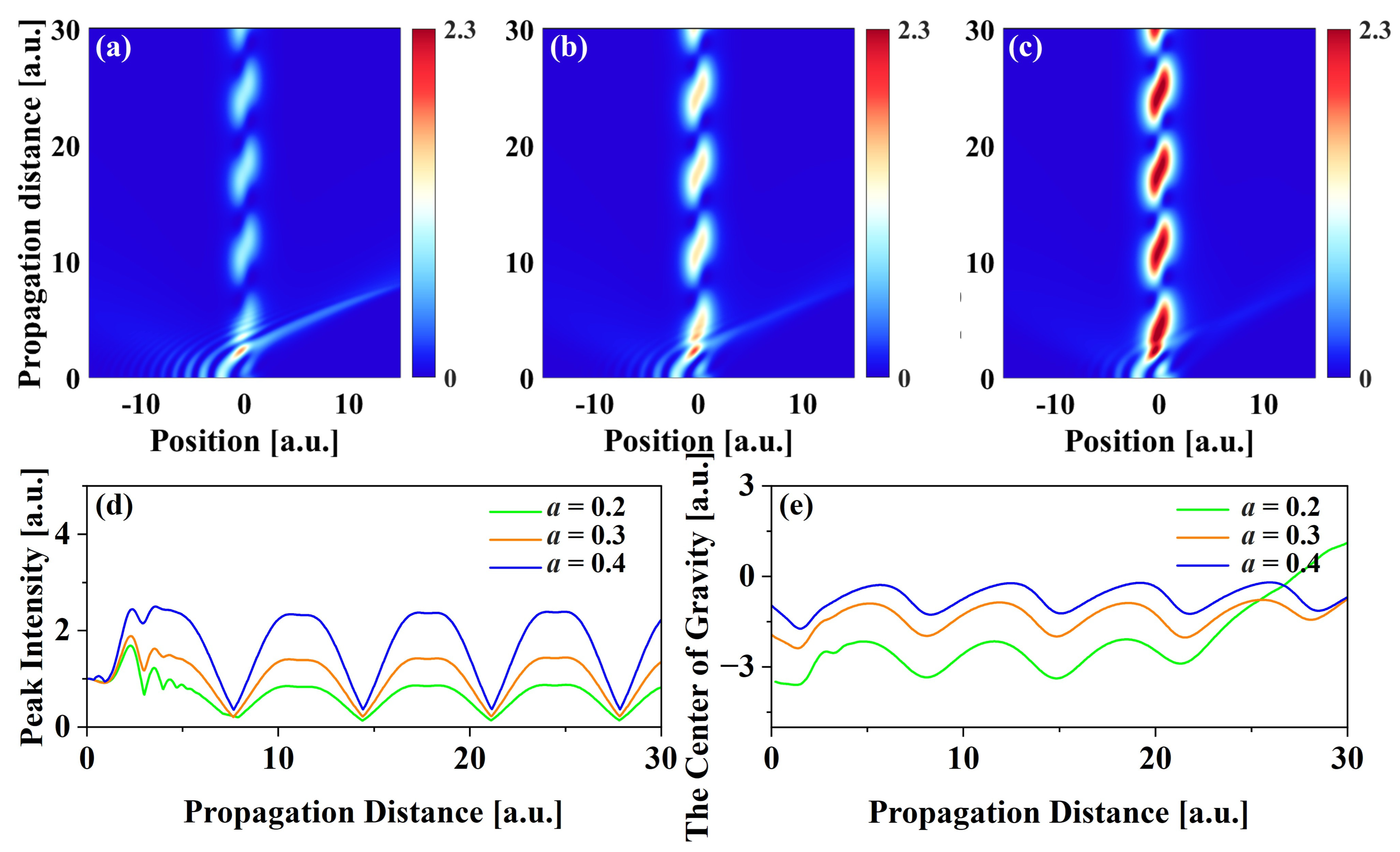
3.2. The Influence of Optical Lattice Parameters
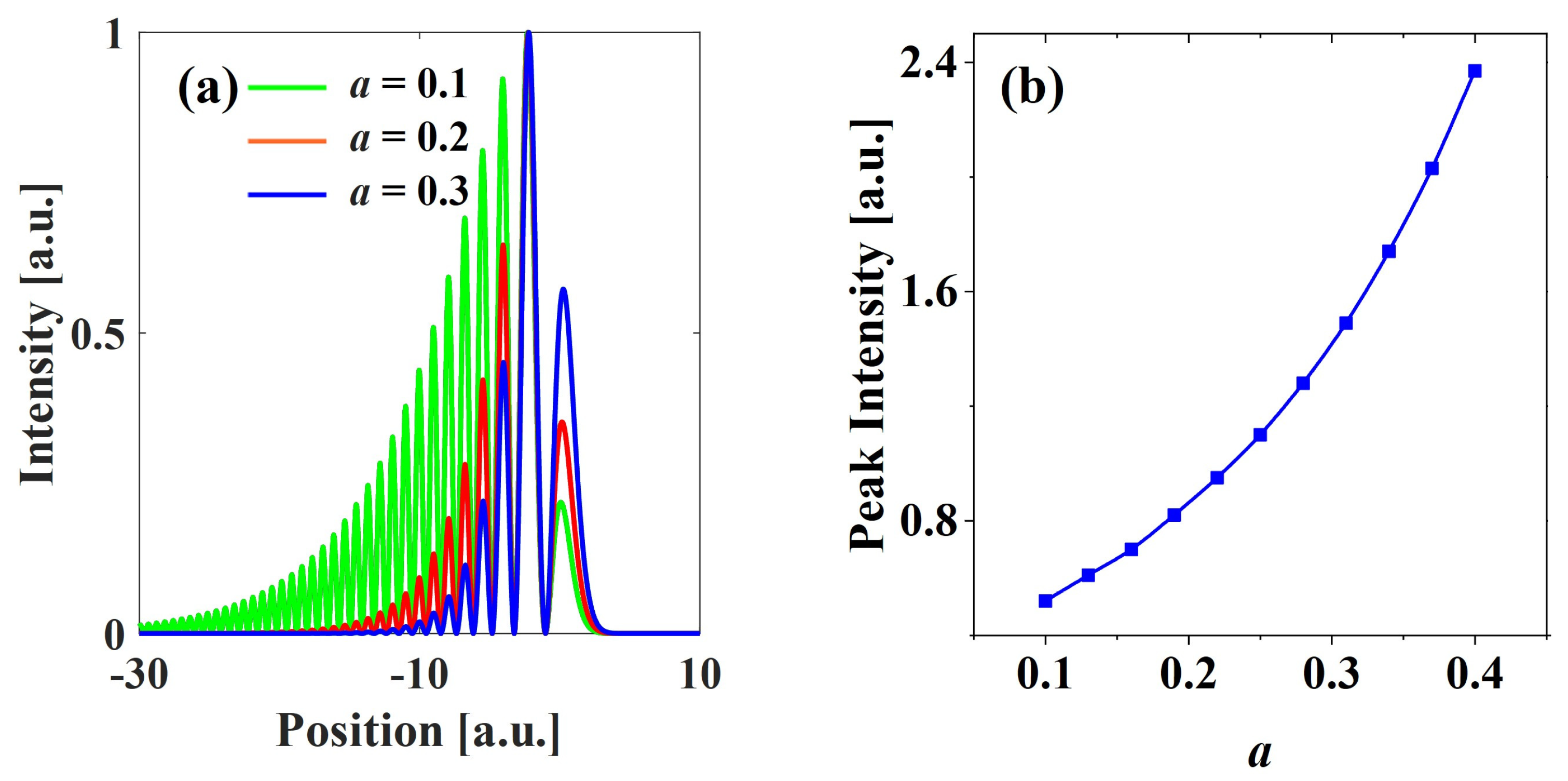
3.3. The Influence of Airyprime Beam Parameters
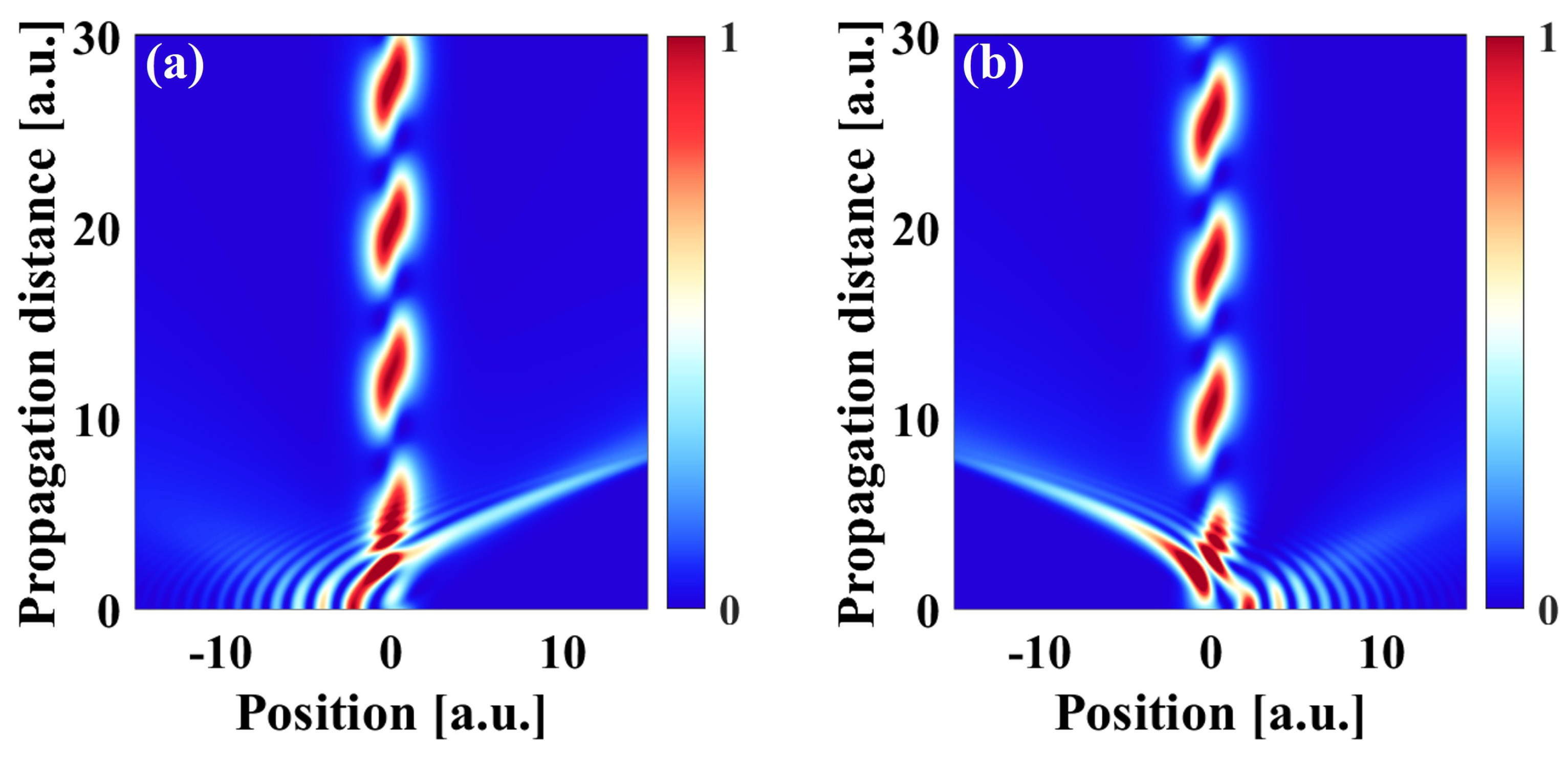
3.4. Comparison of Trailing Leading and Trailing Lagging Airyprime Beams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bayraktar, M. Propagation of Airyprime Beam in Uniaxial Crystal Orthogonal to Propagation Axis. Optik 2021, 228, 166183. [Google Scholar] [CrossRef]
- Bayraktar, M. Performance of Airyprime Beam in Turbulent Atmosphere. Photonic Netw. Commun. 2021, 41, 274–279. [Google Scholar] [CrossRef]
- Zang, X.; Dan, W.S.; Zhou, Y.M.; Lv, H.; Wang, F.; Cai, Y.J.; Zhou, G.Q. Abruptly Autofocusing of Generalized Circular Airy Derivative Beams. Opt. Express 2022, 30, 3804. [Google Scholar] [CrossRef]
- Zang, X.; Dan, W.S.; Zhou, Y.M.; Wang, F.; Cai, Y.J.; Zhou, G.Q. Simultaneously Enhancing Autofocusing Ability and Extending Focal Length for a Ring Airyprime Beam Array by a Linear Chirp. Opt. Lett. 2023, 48, 912–915. [Google Scholar] [CrossRef]
- Zhou, Y.M.; Zang, X.; Dan, W.S.; Wang, F.; Chen, R.P.; Zhou, G.Q. Design and Realization of an Autofocusing Airyprime Beams Array. Opt. Laser Technol. 2023, 162, 109303. [Google Scholar] [CrossRef]
- Dan, W.S.; He, J.; Zang, X.; Wang, F.; Zhou, Y.M.; Chu, X.X.; Zhou, G.Q. Abrupt Autofocusing Performance of a Circular Airyprime Beam with Vortex Pairs. Results Phys. 2023, 47, 106377. [Google Scholar] [CrossRef]
- He, J.; Zang, X.; Dan, W.S.; Zhou, Y.M.; Wang, F.; Cai, Y.J.; Zhou, G.Q. Key to an Extension or Shortening of Focal Length in The Enhancement of Autofocusing Ability of a Circular Airyprime Beam Caused by a Linear Chirp Factor. Opt. Lett. 2023, 48, 2365. [Google Scholar] [CrossRef]
- Wang, W.X.; Mi, Z.W.; Zhang, L.P.; Wang, B.Y.; Han, K.Z.; Lei, C.X.; Man, Z.S.; Ge, X.L. The Abruptly Autofocusing Characteristics of The Circular Airyprime Beam in a Chiral Medium. Opt. Commun. 2023, 549, 129879. [Google Scholar] [CrossRef]
- Zhang, L.P.; Yang, S.; Li, S.Y.; Man, Z.S.; Ge, X.L.; Lei, C.X.; He, S.L.; Zhang, W.F.; Deng, D.M.; Chen, C.D. Controllable Circular Airyprime Beam with the Astigmatic Phase in a Parabolic Potential. Chaos Solitons Fractals 2024, 181, 114506. [Google Scholar] [CrossRef]
- Zheng, X.Q.; Yang, Y.Z.; Liu, Y.J.; Lin, X.J.; Liang, Z.H.; Liu, J.; Deng, D.M. Adjustable Focusing Property of Circular Airyprime Beam Through Fourier Space Modulation. Opt. Lett. 2024, 49, 4393. [Google Scholar] [CrossRef]
- Sheng, J.T.; Miri, M.A.; Christodoulides, D.N.; Xiao, M. PT-symmetric Optical Potentials in a Coherent Atomic Medium. Phys. Rev. A 2013, 88, 041803. [Google Scholar] [CrossRef]
- Demirkaya, A.; Kapitula, T.; Kevrekidis, P.G.; Stanislavovat, M.; Stefanov, A. On the Spectral Stability of Kinks in Some PT-Symmetric Variants of the Classical Klein–Gordon Field Theories. Stud. Appl. Math. 2014, 133, 298–317. [Google Scholar] [CrossRef]
- Dai, C.Q.; Zhang, X.F.; Fan, Y.; Chen, L. Localized Modes of the (n+1)-dimensional Schrödinger Equation with Power-law Nonlinearities in PT-symmetric Potentials. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 239–250. [Google Scholar] [CrossRef]
- Konotop, V.V.; Zezyulin, D.A. Odd-Time Reversal PT Symmetry Induced by an Anti-PT-Symmetric Medium. Phys. Rev. Lett. 2018, 120, 123902. [Google Scholar] [CrossRef]
- Novitsky, D.V.; Shalin, A.S.; Novitsky, A. Nonlocal Homogenization of PT-symmetric Multilayered Structures. Phys. Rev. A 2019, 99, 043812. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, X.; Liu, Y.C.; Yao, Y.W.; Wu, F.G.; Zhao, D.G. Novel Acoustic Flat Focusing Based on the Asymmetric Response in Parity-time-symmetric Phononic Crystals. Sci. Rep. 2019, 9, 10048. [Google Scholar] [CrossRef]
- Shestakov, P.Y.; Komissarova, M.V.; Marchenko, V.F. Peculiarities of Light Pulse Propagation in Quasi-PT Symmetric Periodic Structures. J. Opt. Soc. Am. B 2021, 38, 990–996. [Google Scholar] [CrossRef]
- Tsvetkov, D.M.; Bushuev, V.A.; Mantsyzov, B.I. Chirped Pulse Propagation in a Quasi-PT-symmetric Medium with a Broadband Exceptional-point Condition. Opt. Express 2021, 29, 14548. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.H.; Chen, R.P. Collapse Dynamics of Vortex Beams in a Kerr Medium with Refractive Index Modulation and PT-Symmetric Lattices. Photonics 2022, 9, 249. [Google Scholar] [CrossRef]
- Dang, T.T.; Wang, J.F.; An, Y.D.; Liu, X.L.; Zhang, Z.X.; Yang, L.Z. Transmission and control of bright solitons in parity-time symmetric waveguide. Acta Phys. Sin. 2015, 64, 064211, (Chinese Version). [Google Scholar] [CrossRef]
- Zhou, K.Y.; Wei, T.T.; Sun, H.P.; He, Y.J.; Liu, S.T. Soliton Dynamics in a PT-Symmetric Optical Lattice with a Longitudinal Potential Barrier. Opt. Express 2015, 23, 16903. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.N.; Fu, X.Q.; Huang, X.W.; Yang, Y.J.; Bai, Y.F. The robustness of truncated Airy beam in PT Gaussian potentials media. Opt. Commun. 2018, 410, 717–722. [Google Scholar] [CrossRef]
- Deng, Y.B.; Wen, B.; Chen, L.Z.; Zhang, S.W.; Zhang, G.F.; Xiong, C.X.; Leng, X.L. Propagation properties of cosh-Airy beams in an inhomogeneous medium with Gaussian PT-symmetric potentials. Open Phys. 2022, 20, 1031–1040. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Jiang, D.; Xiao, Z. Study on the Evolutionary Characteristics of Airyprime Beams in Gaussian-Type PT Symmetric Optical Lattices. Photonics 2025, 12, 566. https://doi.org/10.3390/photonics12060566
Chen D, Jiang D, Xiao Z. Study on the Evolutionary Characteristics of Airyprime Beams in Gaussian-Type PT Symmetric Optical Lattices. Photonics. 2025; 12(6):566. https://doi.org/10.3390/photonics12060566
Chicago/Turabian StyleChen, Depeng, Dongchu Jiang, and Zhewen Xiao. 2025. "Study on the Evolutionary Characteristics of Airyprime Beams in Gaussian-Type PT Symmetric Optical Lattices" Photonics 12, no. 6: 566. https://doi.org/10.3390/photonics12060566
APA StyleChen, D., Jiang, D., & Xiao, Z. (2025). Study on the Evolutionary Characteristics of Airyprime Beams in Gaussian-Type PT Symmetric Optical Lattices. Photonics, 12(6), 566. https://doi.org/10.3390/photonics12060566



