Numerical Study of Electric Field Enhancement in Inverted-Pyramid Gold Arrays with Tunable Spacing
Abstract
1. Introduction
2. Materials and Methods
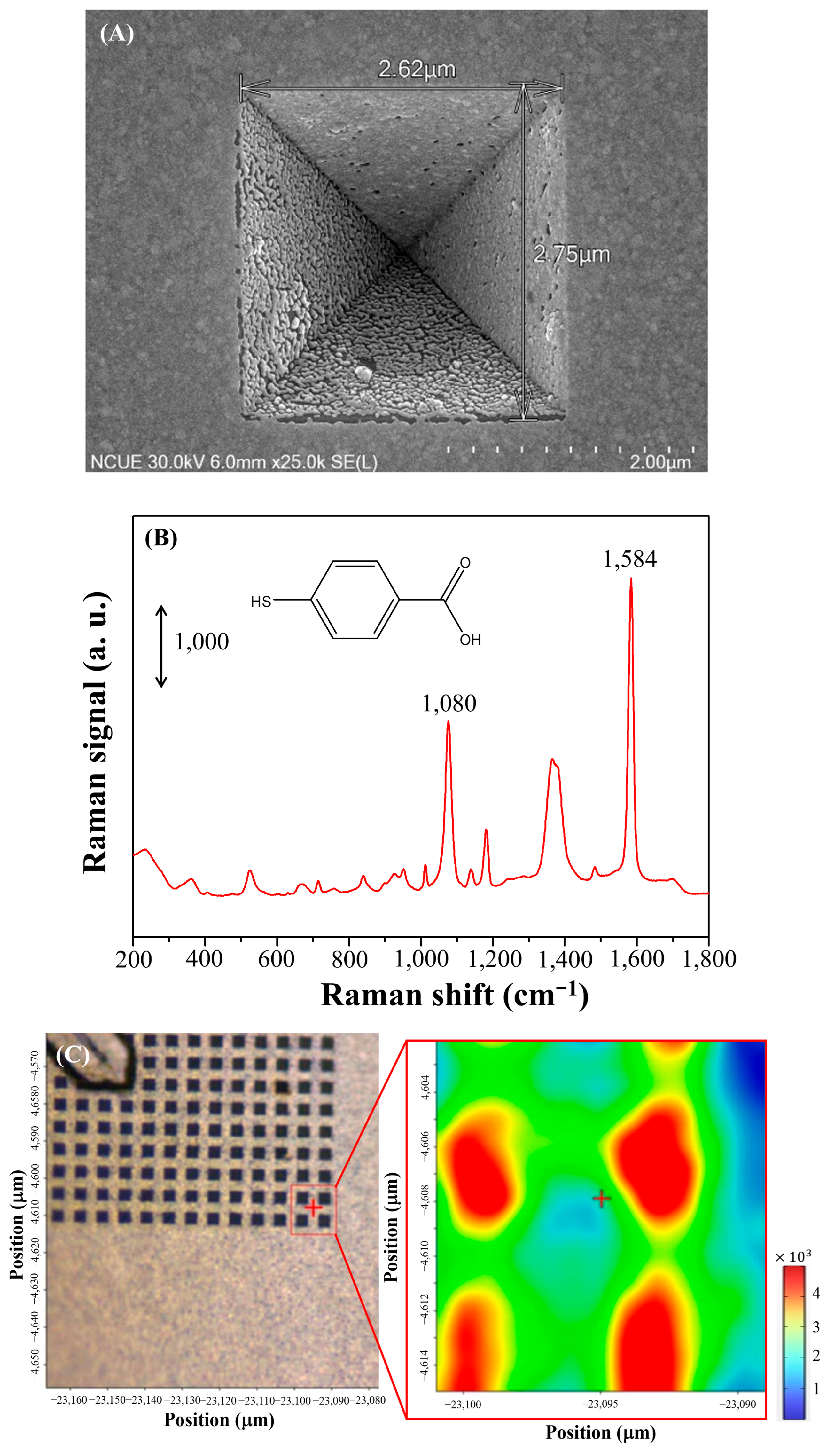
2.1. Fabrication and Characterization of the Prepared Inverted-Pyramidal Au Array
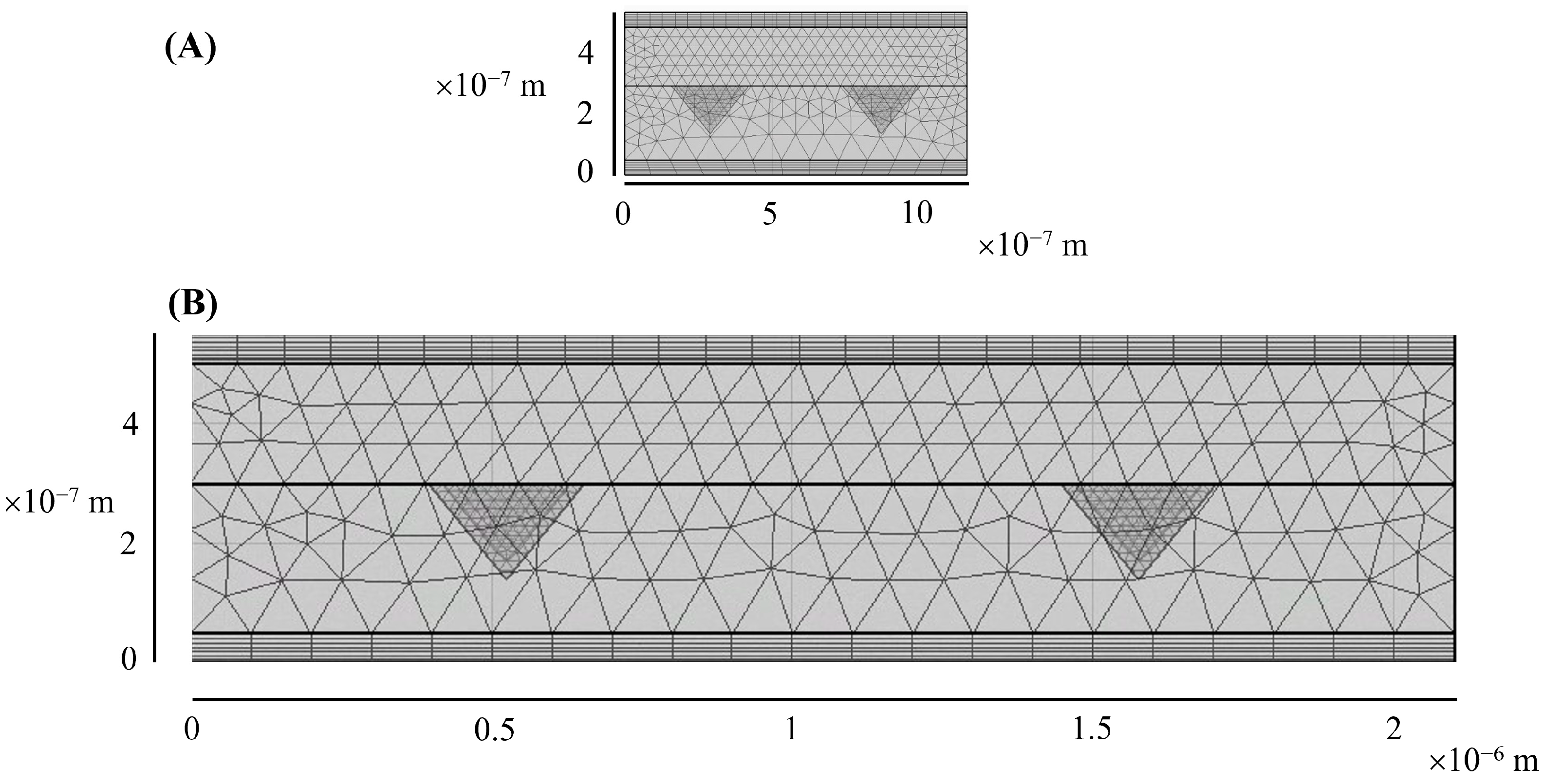
2.2. Numerical Simulation
2.3. Raman Measurement
3. Results and Discussion
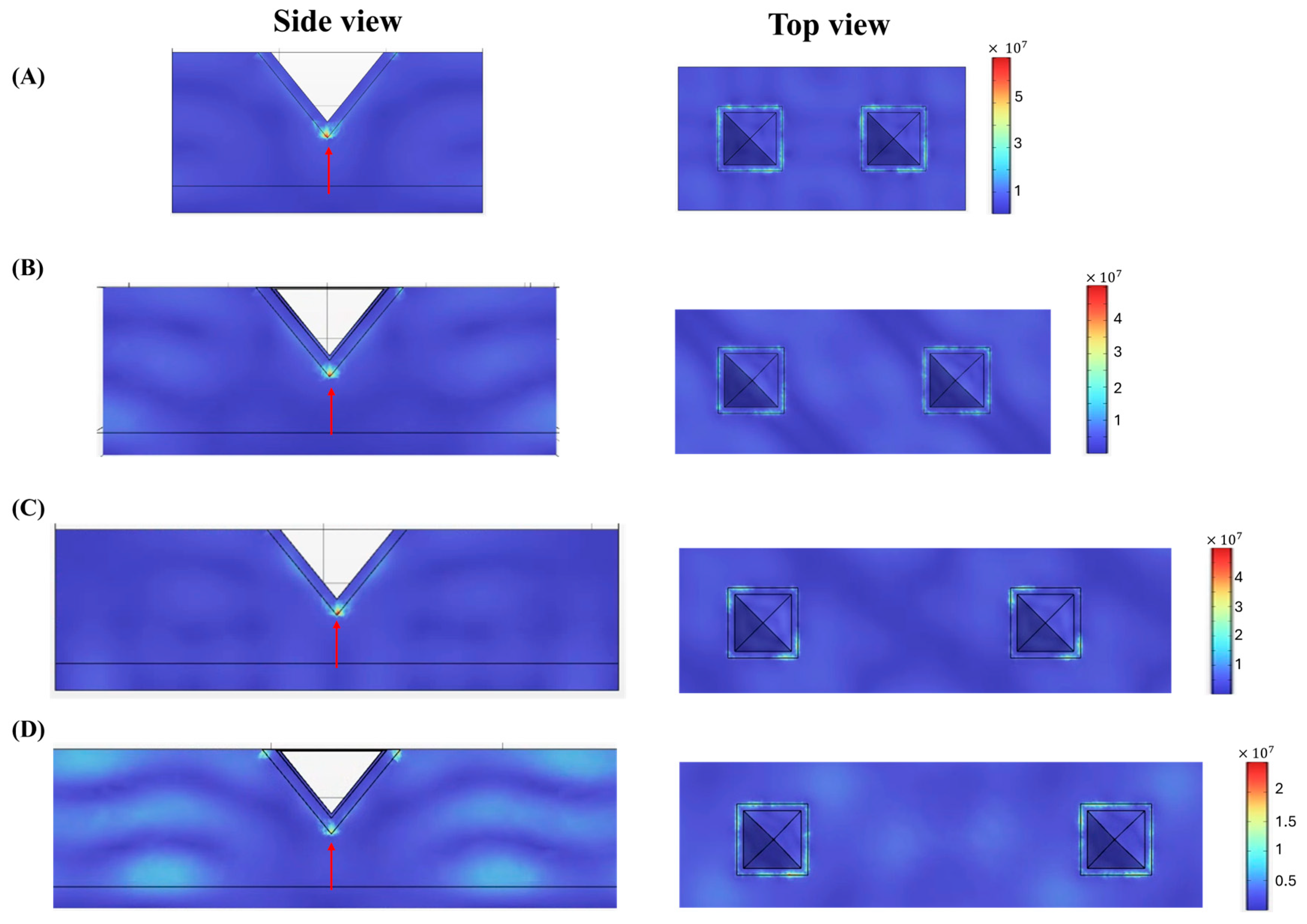
3.1. Electric Field of the Inverted-Pyramidal Au Array
3.2. Numerical Simulation of Electric Field Distribution of the Inverted-Pyramidal Au Array
3.3. Raman Images of the Inverted-Pyramidal Au Array Substrate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patel, B.; Darji, P.; Fnu, P.I.J.; Nalla, S.; Khatri, V.; Parikh, S. A comprehensive review and insight into the latest advancements in nanotechnology. Biosci. Biotech. Res. Asia 2024, 21, 985–1000. [Google Scholar] [CrossRef]
- Kalashgrani, M.Y.; Mousavi, S.M.; Akmal, M.H.; Gholami, A.; Omidifar, N.; Chiang, W.H.; Althomali, R.H.; Lai, C.W.; Rahman, M.M. Gold fluorescence nanoparticles for enhanced SERS detection in biomedical sensor applications: Current trends and future directions. Chem. Record 2024, Early View, e202300303. [Google Scholar] [CrossRef]
- Veg, E.; Hashmi, K.; Raza, S.; Joshi, S.; Rahman Khan, A.; Khan, T. The role of nanomaterials in diagnosis and targeted drug delivery. Chem. Biodivers. 2025, 22, e202401581. [Google Scholar] [CrossRef] [PubMed]
- Ganesh, K.M.; Bhaskar, S.; Cheerala, V.S.K.; Battampara, P.; Reddy, R.; Neelakantan, S.C.; Reddy, N.; Ramamurthy, S.S. Review of gold nanoparticles in surface plasmon-coupled emission technology: Effect of shape, hollow nanostructures, nano-assembly, metal–dielectric and heterometallic nanohybrids. Nanomaterials 2024, 14, 111. [Google Scholar] [CrossRef]
- Ashrafi, T.M.S.; Mohanty, G. Surface plasmon resonance sensors: A critical review of recent advances, market analysis, and future directions. Plasmonics 2025, 1–21. [Google Scholar] [CrossRef]
- Mcoyi, M.P.; Mpofu, K.T.; Sekhwama, M.; Mthunzi-Kufa, P. Developments in localized surface plasmon resonance. Plasmonics 2024, 1–40. [Google Scholar] [CrossRef]
- Verma, S.; Pathak, A.K.; Rahman, B.A. Review of biosensors based on plasmonic-enhanced processes in the metallic and meta-material-supported nanostructures. Micromachines 2024, 15, 502. [Google Scholar] [CrossRef] [PubMed]
- Goel, R.; Chakraborty, S.; Awasthi, V.; Bhardwaj, V.; Dubey, S.K. Exploring the various aspects of surface enhanced Raman spectroscopy (SERS) with focus on the recent progress: SERS-active substrate, SERS-instrumentation, SERS-application. Sens. Actuator A-Phys. 2024, 376, 115555. [Google Scholar] [CrossRef]
- Philip, A.; Kumar, A.R. The performance enhancement of surface plasmon resonance optical sensors using nanomaterials: A review. Coord. Chem. Rev. 2022, 458, 214424. [Google Scholar] [CrossRef]
- Gedney, S. Introduction to the Finite-Difference Time-Domain (FDTD) Method for Electromagnetics; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Amirjani, A.; Sadrnezhaad, S.K. Computational electromagnetics in plasmonic nanostructures. J. Mater. Chem. C 2021, 9, 9791–9819. [Google Scholar] [CrossRef]
- Dieperink, M.; Skorikov, A.; Claes, N.; Bals, S.; Albrecht, W. Considerations for electromagnetic simulations for a quantitative correlation of optical spectroscopy and electron tomography of plasmonic nanoparticles. Nanophotonics 2024, 13, 4647–4665. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, Y.; Lin, C.; Xu, M.; Zhao, S.; Masaki, T.; Yang, Y. Research progress and application of two-dimensional materials for surface-enhanced Raman scattering. Surf. Sci. Technol. 2024, 2, 14. [Google Scholar] [CrossRef]
- Gomez-Cruz, J.; Bdour, Y.; Stamplecoskie, K.; Escobedo, C. FDTD analysis of hotspot-enabling hybrid nanohole-nanoparticle structures for SERS detection. Biosensors 2022, 12, 128. [Google Scholar] [CrossRef]
- Tang, J.; Hao, J.; Li, Z.; Bai, J. Towards understanding hybrid influencing mechanisms of substrate microstructure on SERS effect. Appl. Surf. Sci. 2024, 660, 159974. [Google Scholar] [CrossRef]
- Xie, Y.; Xu, J.; Shao, D.; Liu, Y.; Qu, X.; Hu, S.; Dong, B. SERS-based local field enhancement in biosensing applications. Molecules 2024, 30, 105. [Google Scholar] [CrossRef]
- Dai, Y.; Yue, L.; Li, W.; Pang, L. Plasmon-enhanced Raman spectroscopy to estimate near-electric-field enhancement. Phys. Rev. A 2024, 109, 053516. [Google Scholar] [CrossRef]
- Liu, J.; Meng, Z.; Zhou, J. High electric field enhancement induced by modal coupling for a plasmonic dimer array on a metallic Film. Photonics 2024, 11, 183. [Google Scholar] [CrossRef]
- Lee, Y.-M.; Kim, S.-E.; Park, J.-E. Strong coupling in plasmonic metal nanoparticles. Nano Converg. 2023, 10, 34. [Google Scholar] [CrossRef]
- Wu, T.; Lin, Y.-W. Surface-enhanced Raman scattering active gold nanoparticle/nanohole arrays fabricated through electron beam lithography. Appl. Surf. Sci. 2018, 435, 1143–1149. [Google Scholar] [CrossRef]
- Mao, F.; Ngo, G.L.; Nguyen, C.T.; Ledoux-Rak, I.; Lai, N.D. Direct fabrication and characterization of gold nanohole arrays. Opt. Express 2021, 29, 29841–29856. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Puebla, R.A. Effects of the Excitation Wavelength on the SERS Spectrum. J. Phys. Chem. Lett. 2012, 3, 857–866. [Google Scholar] [CrossRef] [PubMed]
- McFarland, A.D.; Young, M.A.; Dieringer, J.A.; Van Duyne, R.P. Wavelength-scanned surface-enhanced Raman excitation spectroscopy. J. Phys. Chem. B 2005, 109, 11279–11285. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.-J.; Yoo, J.; Park, E.; Song, E.H.; Nam, J.-M. Plasmonic nanogap probes for surface-enhanced Raman scattering-based bioimaging and analysis. J. Phys. Chem. C 2024, 128, 17815–17824. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Rao, G.; Wang, Y.; Du, X.; Hu, A.; Hu, Y.; Gong, C.; Wang, X.; Xiong, J. Coupling enhancement mechanisms, materials, and strategies for surface-enhanced Raman scattering devices. Analyst 2021, 146, 5008–5032. [Google Scholar] [CrossRef]
- Itoh, T.; Yamamoto, Y.S. Between plasmonics and surface-enhanced resonant Raman spectroscopy: Toward single-molecule strong coupling at a hotspot. Nanoscale 2021, 13, 1566–1580. [Google Scholar] [CrossRef]
- Ko, T.-S.; Hsieh, H.-Y.; Lee, C.; Chen, S.-H.; Chen, W.-C.; Wang, W.-L.; Lin, Y.-W.; Wu, S. Electric field-enhanced SERS detection using MoS2-coated patterned Si substrate with micro-pyramid pits. Nanomaterials 2024, 14, 1852. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Yang, L.; He, Y.; Liu, R.; Ran, W.; Wang, Z.; Shao, B. An improved multiple competitive immuno-SERS sensing platform and its application in rapid field chemical toxin screening. Toxics 2022, 10, 605. [Google Scholar] [CrossRef]
- Lee, H.; Kim, W.; Song, M.Y.; Kim, D.H.; Jung, H.S.; Kim, W.; Choi, S. One-stop plasmonic nanocube-excited SERS immunoassay platform of multiple cardiac biomarkers for rapid screening and progressive tracing of acute myocardial infarction. Small 2024, 20, 2304999. [Google Scholar] [CrossRef]
- Yang, S.J.; Lee, J.U.; Jeon, M.J.; Sim, S.J. Highly sensitive surface-enhanced Raman scattering-based immunosensor incorporating half antibody-fragment for quantitative detection of Alzheimer’s disease biomarker in blood. Anal. Chim. Acta 2022, 1195, 339445. [Google Scholar] [CrossRef]
- Augustyniak, M.; Usarek, Z. Finite element method applied in electromagnetic NDTE: A review. J. Nondestruct. Eval. 2016, 35, 39. [Google Scholar] [CrossRef]
- Mohaghegh, F.; Tehrani, A.M.; Materny, A. Investigation of the importance of the electronic enhancement mechanism for surface-enhanced Raman scattering (SERS). J. Phys. Chem. C 2021, 125, 5158–5166. [Google Scholar] [CrossRef]
- Khurana, K.; Jaggi, N. Localized surface plasmonic properties of Au and Ag nanoparticles for sensors: A review. Plasmonics 2021, 16, 981–999. [Google Scholar] [CrossRef]
- Mhlanga, N.; Ntho, T.A. A theoretical study of 4-mercaptobenzoic acid assembled on Ag for surface-enhanced Raman scattering applications. Mater. Today Commun. 2021, 26, 101698. [Google Scholar] [CrossRef]
- Suganami, Y.; Oshikiri, T.; Mitomo, H.; Sasaki, K.; Liu, Y.E.; Shi, X.; Matsuo, Y.; Ijiro, K.; Misawa, H. Spatially uniform and quantitative surface-enhanced raman scattering under modal ultrastrong coupling beyond nanostructure homogeneity limits. ACS Nano 2024, 18, 4993–5002. [Google Scholar] [CrossRef] [PubMed]
- Grzeskiewicz, B.; Ptaszynski, K.; Kotkowiak, M. Near and far-field properties of nanoprisms with rounded edges. Plasmonics 2014, 9, 607–614. [Google Scholar] [CrossRef]
- Magdy, M. A conceptual overview of surface-enhanced Raman scattering (SERS). Plasmonics 2023, 18, 803–809. [Google Scholar] [CrossRef]
- Zhu, L.; Meng, Z.; Hu, S.; Zhao, T.; Zhao, B. Understanding metal–semiconductor plasmonic resonance coupling through surface-enhanced Raman scattering. ACS Appl. Mater. Interfaces 2023, 15, 22730–22736. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, P.; Qiao, K.; Bai, Y.; Xie, Y.-H. Coupling SPP with LSPR for enhanced field confinement: A simulation study. J. Phys. Chem. C 2015, 120, 527–533. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Maximum element size | 1.00 × 10−7 | m |
| Minimum element size | 4.00 × 10−8 | m |
| Maximum element growth rate | 1.3 | - |
| Curvature factor | 0.2 | - |
| Resolution of narrow regions | 1 | - |
| Spacing (μm) | Au Thickness (nm) | Electric Field Strength (V/m) |
|---|---|---|
| 3.2 | 20 | 5.88 × 107 |
| 30 | 6.75 × 107 | |
| 40 | 3.04 × 107 | |
| 5.5 | 20 | 3.59 × 107 |
| 30 | 4.82 × 107 | |
| 40 | 1.94 × 107 | |
| 7.9 | 20 | 3.37 × 107 |
| 30 | 4.65 × 107 | |
| 40 | 1.38 × 107 | |
| 10 | 20 | 4.39 × 106 |
| 30 | 1.92 × 107 | |
| 40 | 4.21 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arta, Y.; Santoso, I.; Chang, H.; Tsai, Y.-P.; Hsiao, F.-L.; Ko, T.-S.; Lin, Y.-W. Numerical Study of Electric Field Enhancement in Inverted-Pyramid Gold Arrays with Tunable Spacing. Photonics 2025, 12, 522. https://doi.org/10.3390/photonics12050522
Arta Y, Santoso I, Chang H, Tsai Y-P, Hsiao F-L, Ko T-S, Lin Y-W. Numerical Study of Electric Field Enhancement in Inverted-Pyramid Gold Arrays with Tunable Spacing. Photonics. 2025; 12(5):522. https://doi.org/10.3390/photonics12050522
Chicago/Turabian StyleArta, Yaumalika, Iman Santoso, Hao Chang, Ying-Pin Tsai, Fu-Li Hsiao, Tsung-Shine Ko, and Yang-Wei Lin. 2025. "Numerical Study of Electric Field Enhancement in Inverted-Pyramid Gold Arrays with Tunable Spacing" Photonics 12, no. 5: 522. https://doi.org/10.3390/photonics12050522
APA StyleArta, Y., Santoso, I., Chang, H., Tsai, Y.-P., Hsiao, F.-L., Ko, T.-S., & Lin, Y.-W. (2025). Numerical Study of Electric Field Enhancement in Inverted-Pyramid Gold Arrays with Tunable Spacing. Photonics, 12(5), 522. https://doi.org/10.3390/photonics12050522








