Advanced DFE, MLD, and RDE Equalization Techniques for Enhanced 5G mm-Wave A-RoF Performance at 60 GHz
Abstract
1. Introduction
2. Proposed Equalization Algorithms
2.1. Decision Feedback Equalizer
- []: the equalizer input sequence.
- : the coefficients for the feedforward filter.
- : the coefficients for the feedback filter.
- : the order length of the feedforward filter.
- : the order length of the feedback filter.
- ]: the previously detected symbols.
- t(n): the equalizer decision sequence.
- f{n}: the decision function.
- e(n): the error signal.
2.2. Maximum Likelihood Sequence Detection Algorithm
2.3. Radius-Directed Equalization
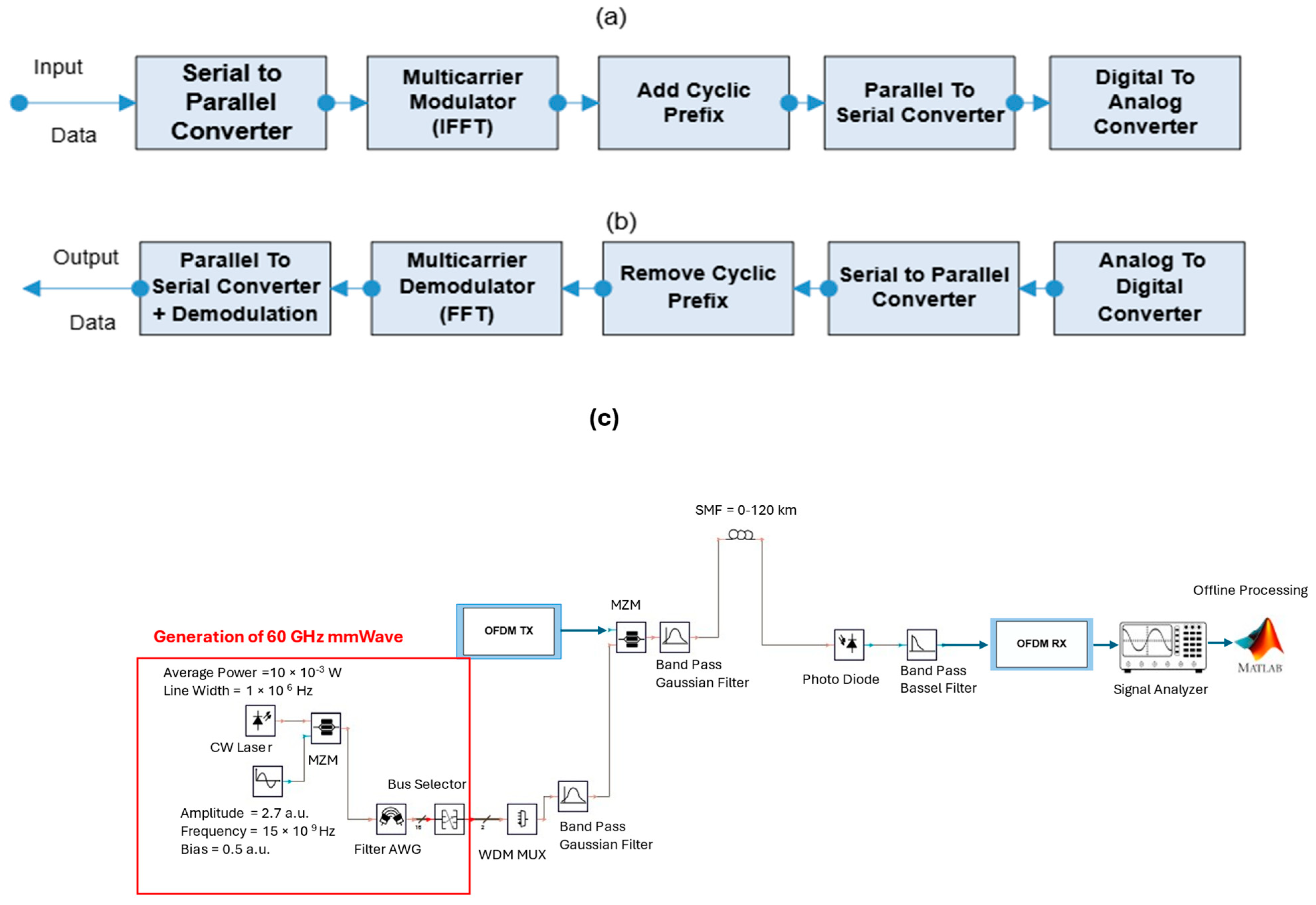
3. Simulation Setup
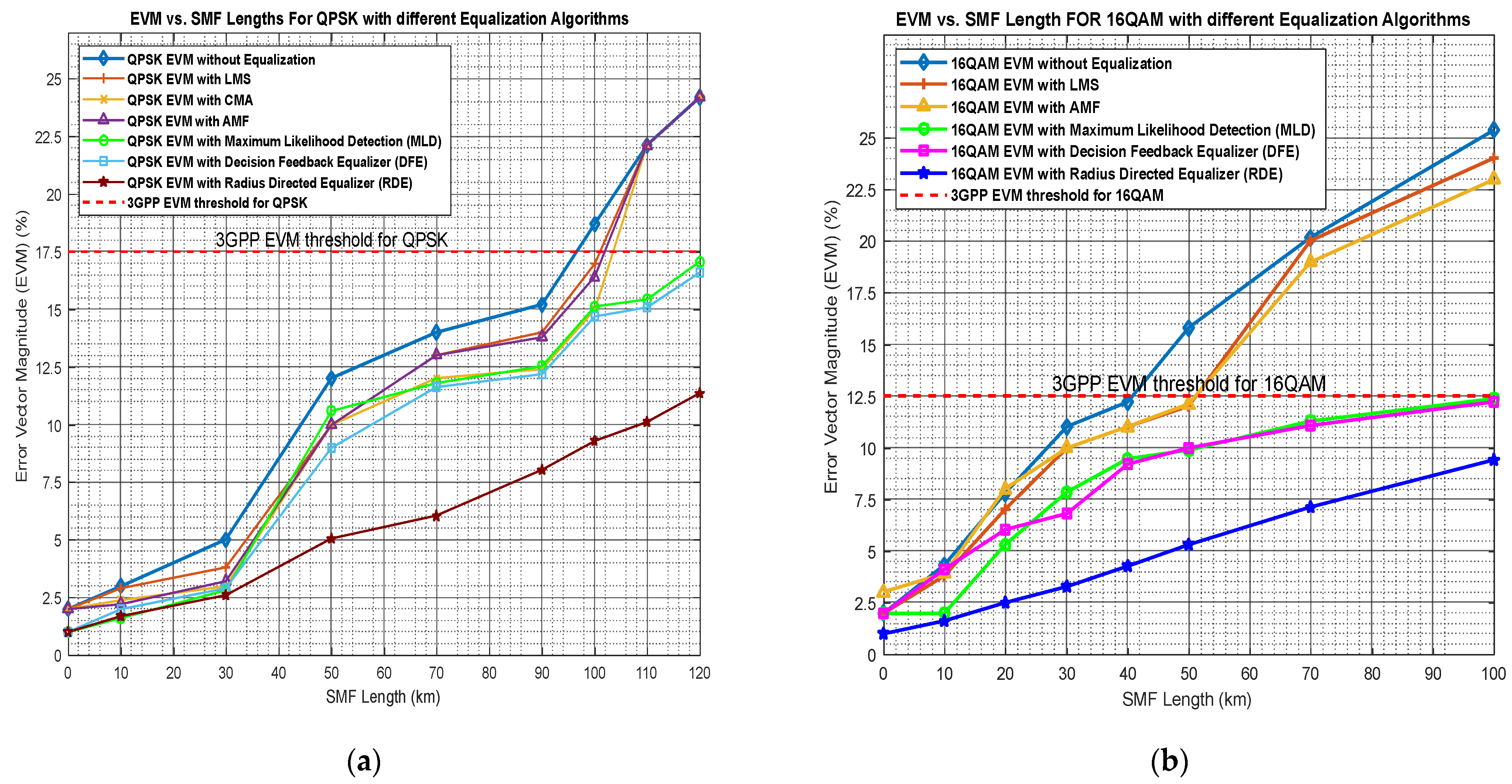
4. Comparisons of Results for DFE, MLD Algorithms
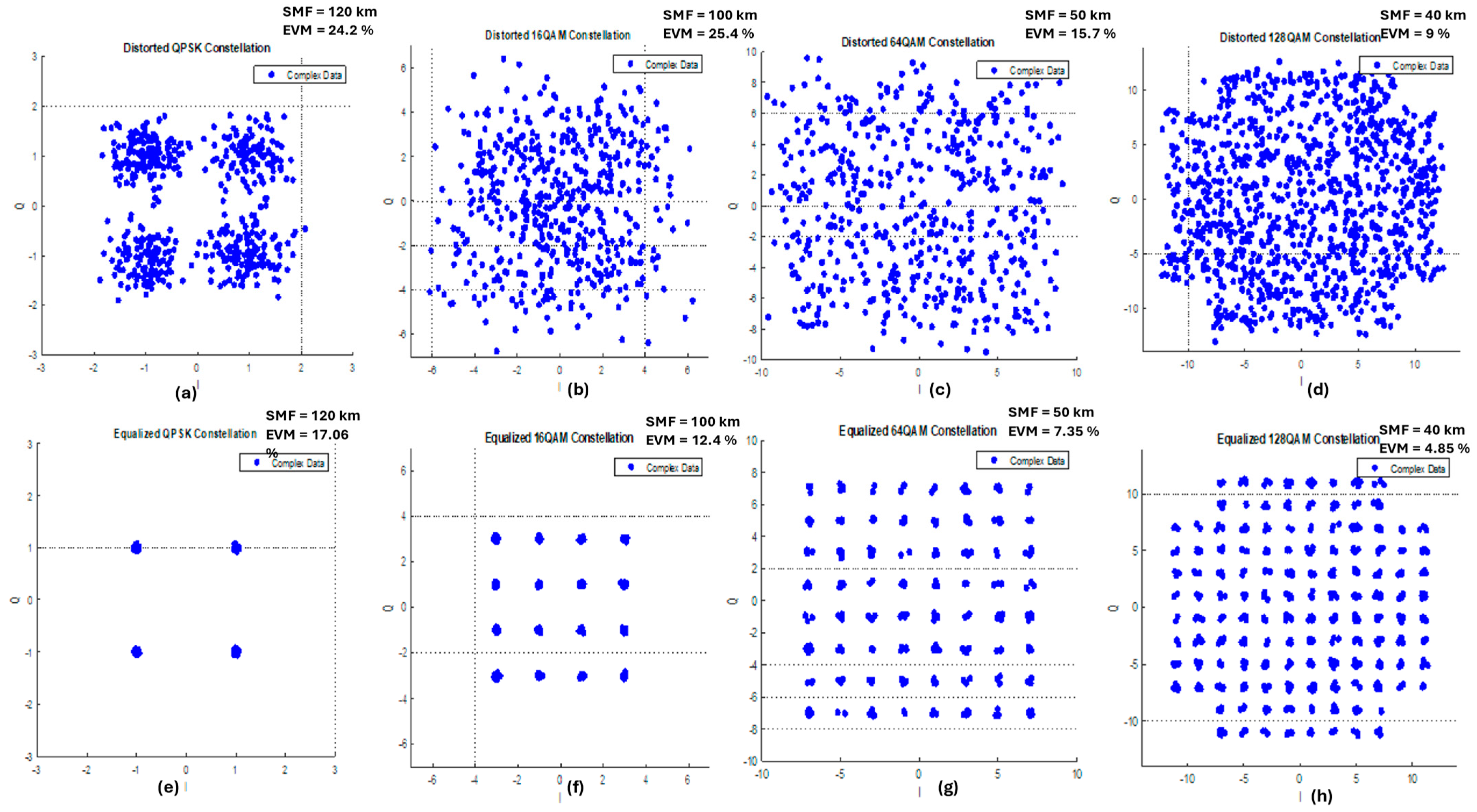
4.1. Equalization by Maximum Likelihood Detection (MLD) Algorithm
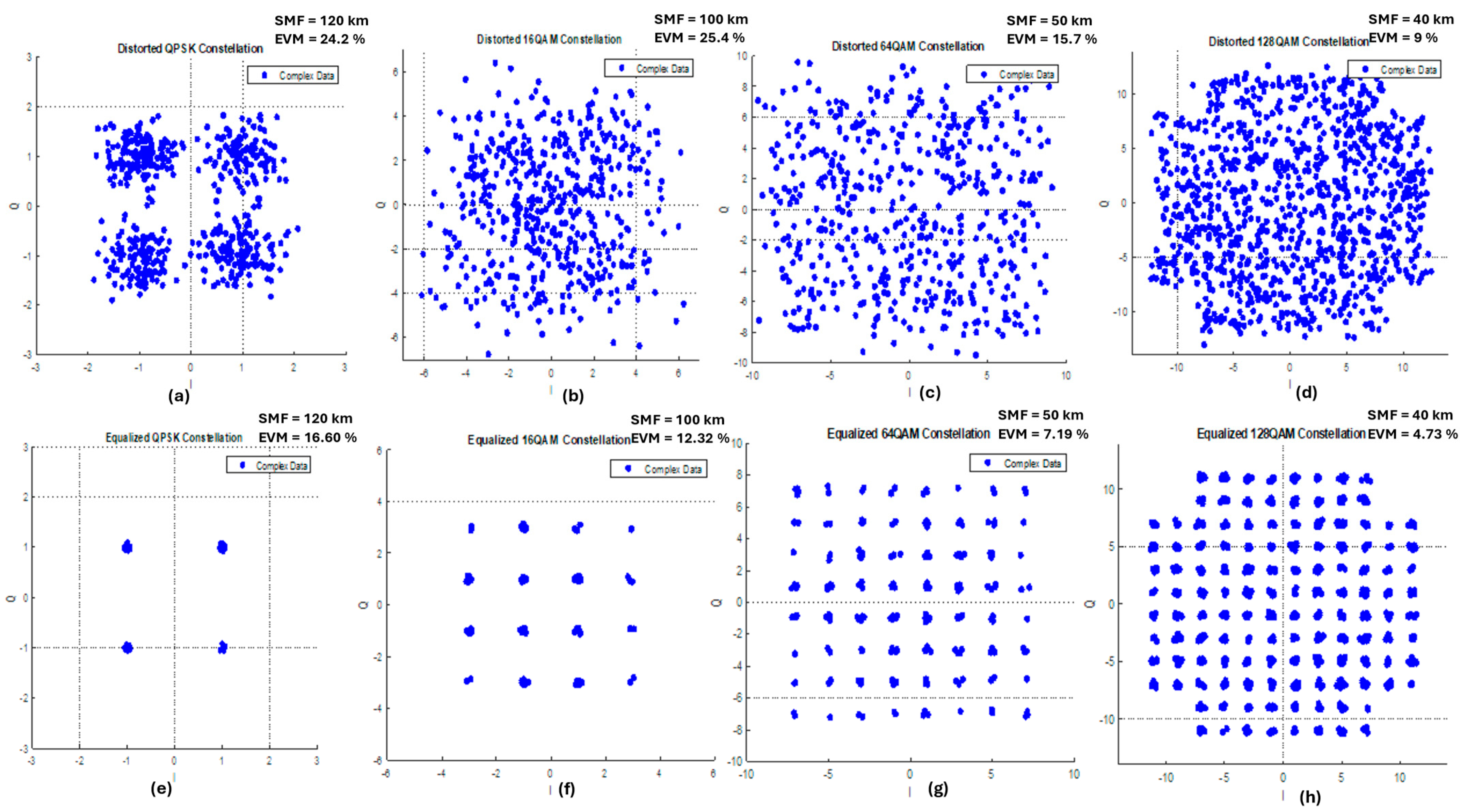
4.2. Equalization by Decision Feedback Equalizer
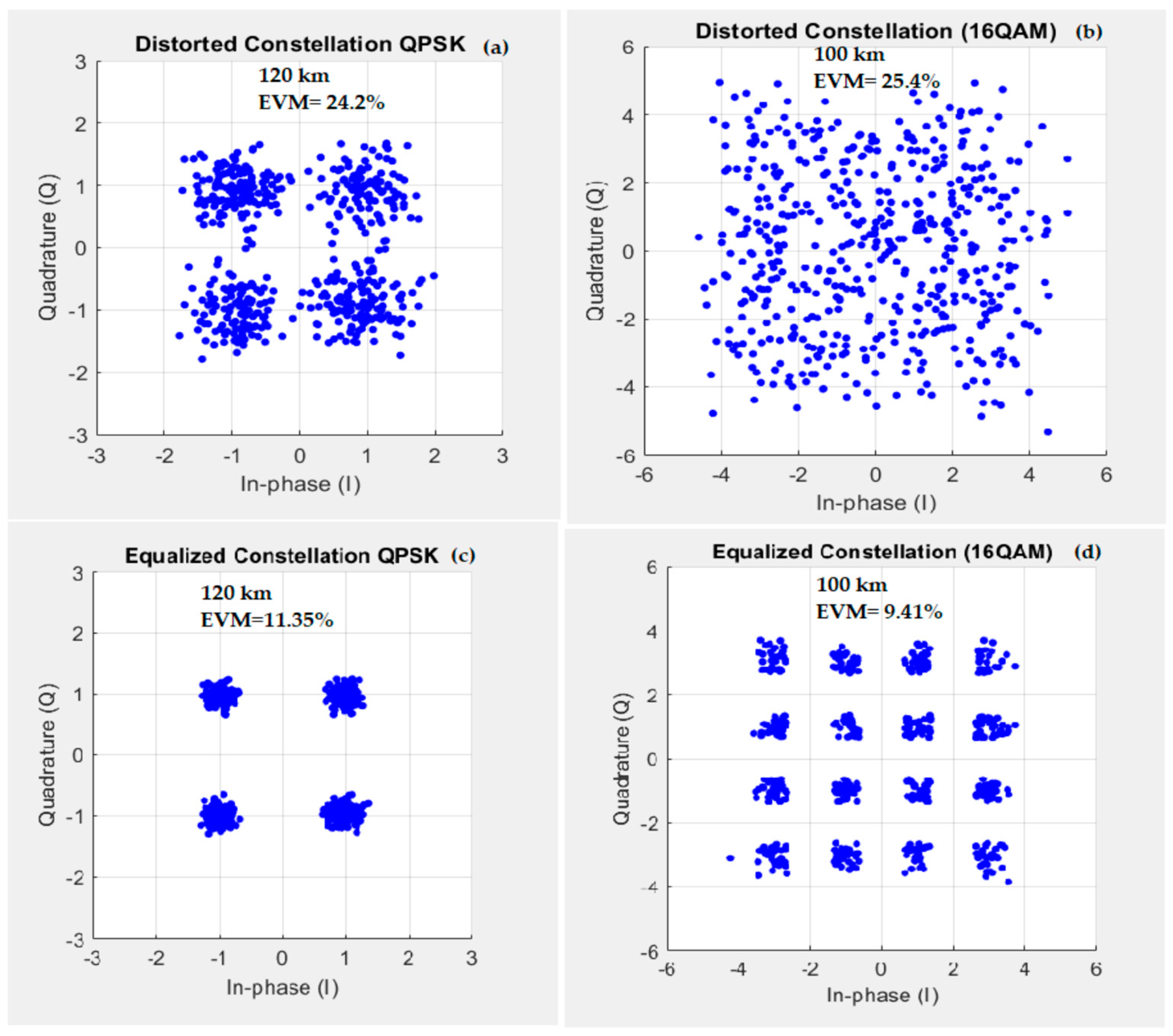
4.3. Equalization by Radius-Directed Equalizer
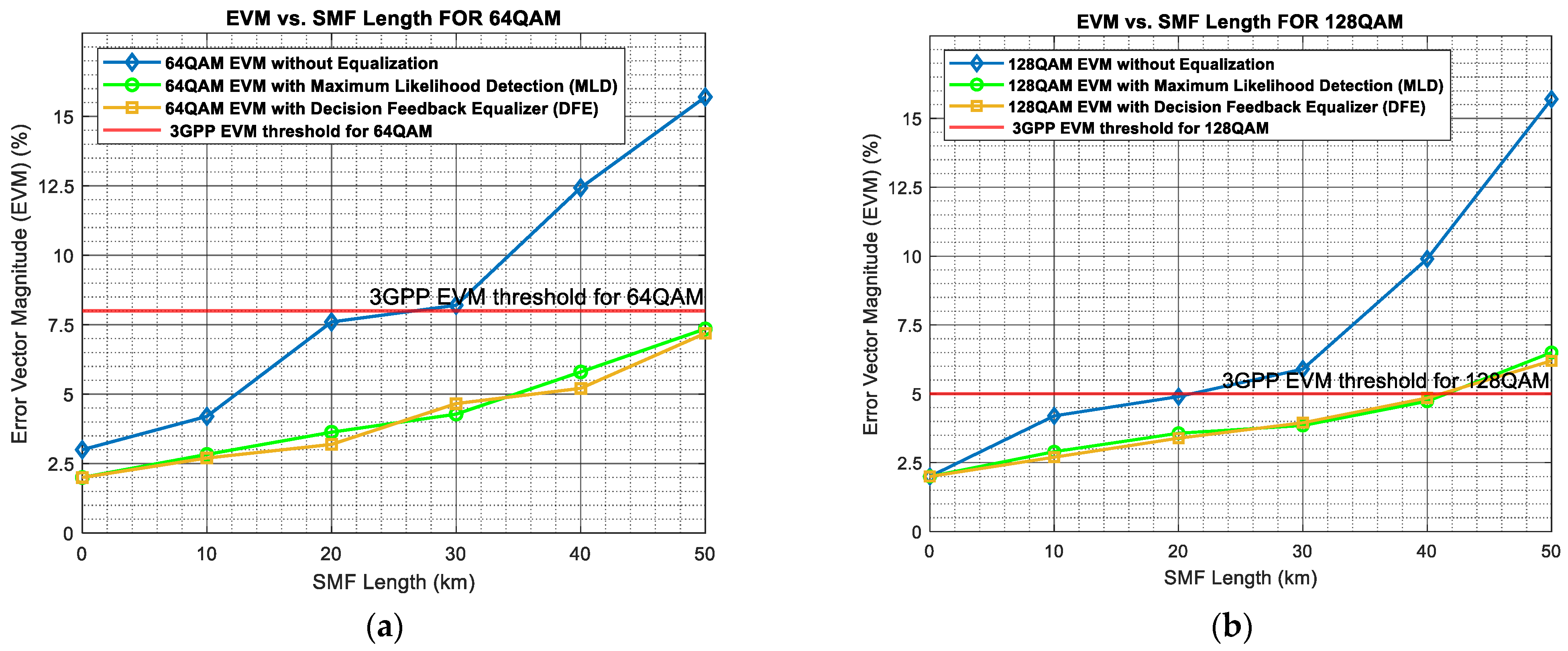
4.4. EVM Performance as a Function of Fiber Length
5. Assessment of Algorithms Against Prior Research Results
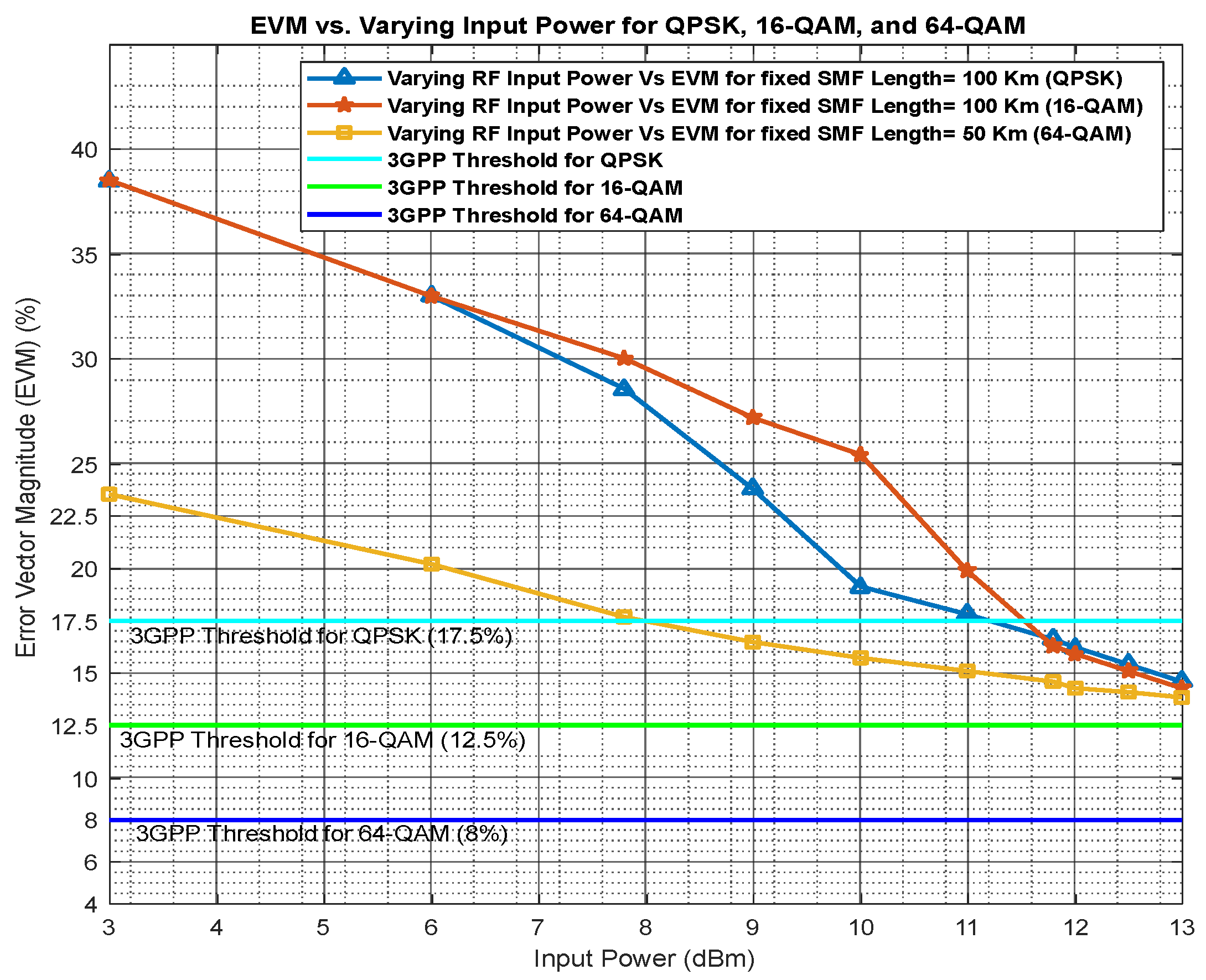
6. Relationship Between RF Input Power and EVM for Different Modulation Formats
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- G.989.1: 40-Gigabit-Capable Passive Optical Networks (NG-PON2): General Requirements. Available online: https://www.itu.int/rec/T-REC-G.989.1/e (accessed on 10 October 2024).
- Singya, P.K.; Shaik, P.; Kumar, N.; Bhatia, V.; Alouini, M.S. A survey on higher-order QAM constellations: Technical challenges, recent advances, and future trends. IEEE Open J. Commun. Soc. 2021, 2, 617–655. [Google Scholar] [CrossRef]
- Mohamed, A.E.N.A.; Rashed, A.N.Z.; Tabbour, M.S.F. Transmission characteristics of radio over fiber (ROF) millimeter wave systems in local area optical communication networks. Int. J. Adv. Netw. Appl. 2011, 2, 876–886. [Google Scholar]
- Kumar, P.; Sharma, S.K.; Singla, S.; Gupta, V.; Sharma, A. A review on mmWave-based energy-efficient RoF system for next-generation mobile communication and broadband systems. J. Opt. Commun. 2024, 45, 303–318. [Google Scholar] [CrossRef]
- Ali, S.H.; Al-Maqdici, R.Z.Y. Improving the performance of cost-effective millimeter wave-based front-haul RoF system for up to 140 km link length using pre-distortion device and FBG technique. Soft Comput. 2024, 28, 787. [Google Scholar] [CrossRef]
- Vagionas, C.; Ruggeri, E.; Kalfas, G.; Sirbu, B.; Leiba, Y.; Kanta, K.; Giannoulis, G.; Caillaud, C.; Cerulo, G.; Mallecot, F.; et al. An end-to-end 5G fiber wireless A-RoF/IFoF link based on a 60 GHz beam-steering antenna and an InP EML. In Proceedings of the Broadband Access Communication Technologies XIV, San Francisco, CA, USA, 4–5 February 2020; SPIE: Bellingham, WA, USA, 2020; pp. 63–68. [Google Scholar]
- Dat, P.T.; Kanno, A.; Inagaki, K.; Rottenberg, F.; Louveaux, J.; Yamamoto, N.; Kawanishi, T. High-speed radio-on-free-space optical mobile fronthaul system for ultra-dense radio access network. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020; Optica Publishing Group: Washington, DC, USA, 2020; p. W2A-37. [Google Scholar]
- Fatah, S.Y.A.; Hamad, E.K.I.K.I.; Swelam, W.; Allam, A.M.M.A.; Sree, M.F.A.; Mohamed, H.A. Design and implementation of UWB slot-loaded printed antenna for microwave and millimeter wave applications. IEEE Access 2021, 9, 29555–29564. [Google Scholar] [CrossRef]
- Ishimura, S.; Bekkali, A.; Tanaka, K.; Nishimura, K.; Suzuki, M. 1.032-Tb/s CPRI-equivalent rate IF-over-fiber transmission using a parallel IM/PM transmitter for high-capacity mobile fronthaul links. J. Light. Technol. 2018, 36, 1478–1484. [Google Scholar] [CrossRef]
- Yu, H.; Doylend, J.; Lin, W.; Nguyen, K.; Liu, W.; Gold, D.; Dahal, A.; Jan, C.; Herrick, R.; Ghiurcan, G.A.; et al. 100Gbps CWDM4 Silicon Photonics Transmitter for 5G applications. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Lim, C.; Tian, Y.; Ranaweera, C.; Nirmalathas, T.A.; Wong, E.; Lee, K.-L. Evolution of radio-over-fiber technology. J. Light. Technol. 2019, 37, 1647–1656. [Google Scholar] [CrossRef]
- Dat, P.T.; Kanno, A.; Inagaki, K.; Kawanishi, T. High-capacity wireless backhaul network using seamless convergence of radio-over-fiber and 90-GHz millimeter-wave. J. Light. Technol. 2014, 32, 3910–3923. [Google Scholar] [CrossRef]
- Song, T.; Lim, C.; Nirmalathas, A. Performance Analysis of a 28 GHz Wideband Analog Radio-over-Fiber Fronthaul with Channel Nonlinearity Compensation. J. Light. Technol. 2024, 1, 7588–7595. [Google Scholar] [CrossRef]
- Liu, S.; Xu, M.; Wang, J.; Lu, F.; Zhang, W.; Tian, H.; Chang, G.K. A multilevel artificial neural network nonlinear equalizer for millimeter-wave mobile fronthaul systems. J. Light. Technol. 2017, 35, 4406–4417. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Zhang, W.; Shen, G.; Tian, H. An adaptive activated ANN equalizer applied in millimeter-wave RoF transmission system. IEEE Photonics Technol. Lett. 2017, 29, 1935–1938. [Google Scholar] [CrossRef]
- Gadze, J.D.; Akwafo, R.; Agyekum, K.A.-P.; Opare, K.A.-B. A 100 Gbps OFDM-Based 28 GHz Millimeter-Wave Radio over Fiber Fronthaul System for 5G. Optics 2021, 2, 70–86. [Google Scholar] [CrossRef]
- Ouyang, X.; Talli, G.; Power, M.; Townsend, P.D. Iterative block decision feedback equalization for IM/DD-based OCDM to compensate chromatic-dispersion-induced power fading. J. Light. Technol. 2019, 37, 4349–4358. [Google Scholar] [CrossRef]
- Dodane, D.; Santacruz, J.P.; Bourderionnet, J.; Rommel, S.; Feugnet, G.; Jurado-Navas, A.; Vivien, L.; Monroy, I.T. Optical phase-locked loop phase noise in 5G mm-wave OFDM ARoF systems. Opt. Commun. 2023, 526, 128872. [Google Scholar] [CrossRef]
- Lee, J.; He, J.; Wang, Y.; Fang, C.; Wang, K. Experimental demonstration of millimeter-wave radio-over-fiber system with convolutional neural network (CNN) and binary convolutional neural network (BCNN). arXiv 2020, arXiv:2001.02018. [Google Scholar]
- Liu, T.; Wang, Y.; Zhou, J. Using Volterra Nonlinear Equalizer and Probabilistic Shaping in an IM/DD System. In Proceedings of the Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 1209–1214. [Google Scholar]
- Zhang, J.L.; Xu, C.; Gao, G.J.; Liu, H.D.; Yang, Z. Direct detection of a single-channel 112 Gb/s PAM-4 signal using an 18 GHz directly modulated laser and Maximum-Likelihood Sequence Estimation (MLSE) equalization. In Frontier Research and Innovation in Optoelectronics Technology and Industry; CRC Press: Boca Raton, FL, USA, 2018; pp. 385–391. [Google Scholar]
- Cartledge, J.C.; Karar, A.S. 100 Gb/s intensity modulation and direct detection. J. Light. Technol. 2014, 32, 2809–2814. [Google Scholar] [CrossRef]
- Kamran, R.; Naaz, S.; Goyal, S.; Gupta, S. High-capacity coherent DCIs using pol-muxed carrier and LO-less receiver. J. Light. Technol. 2020, 38, 3461–3468. [Google Scholar] [CrossRef]
- Patil, Y.; Sharma, A.; Nambath, N.; Gupta, S. Analog processing-based coherent optical receiver for 16-QAM signals with 12.5 GBd baud rate. In Proceedings of the Twenty Second National Conference on Communication (NCC), Guwahati, India, 4–6 March 2016; IEEE: New York, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Qi, W.; Xu, Z.; Zhu, Y.; Ji, T.; Ji, H.; Yang, Y.; Qiao, G.; Cheng, C.; Tang, J.; Zhao, T.; et al. High-Speed Dispersion-Unmanaged DML-Based IM-DD Optics at C-band With Advanced Nonlinear Equalization and Noise Whitening. J. Light. Technol. 2024, 42, 5591–5598. [Google Scholar]
- Tang, J.; Li, Y.; Cheng, C.; Wang, X.; Yang, B.; Zhao, T.; Hao, Y.; Fan, L.; Wu, Q.; Sun, Z.; et al. A Record 131 Gb/s IM/DD Optical Data Link at 2-Micron Waveband Using Only Commercial Components. In Proceedings of the ECOC 2024—50th European Conference on Optical Communication, Frankfurt, Germany, 22–26 September 2024; VDE: Frankfurt am Main, Germany, 2024; pp. 914–917. [Google Scholar]
- Hossain, M.S.B.; Böcherer, G.; Lin, Y.; Li, S.; Calabrò, S.; Nedelcu, A.; Rahman, T.; Wettlin, T.; Wei, J.; Stojanović, N.; et al. Experimental comparison of PAM-8 probabilistic shaping with different Gaussian orders at 200 Gb/s net rate in IM/DD system with O-band TOSA. In Proceedings of the ECOC 2022, Basel, Switzerland, 18–22 September 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. We2D-3. [Google Scholar]
- Wei, J.; Lam, C.F.; Zhou, J.; Aldaya, I.; Giacoumidis, E.; Richter, A.; Cheng, Q.; Penty, R.; White, I. Low complexity DSP for high speed optical access networking. Appl. Sci. 2021, 11, 3406. [Google Scholar] [CrossRef]
- Wettlin, T.; Calabrò, S.; Rahman, T.; Wei, J.; Stojanovic, N.; Pachnicke, S. DSP for high-speed short-reach IM/DD systems using PAM. J. Light. Technol. 2020, 38, 6771–6778. [Google Scholar] [CrossRef]
- Wei, J.L.; Sánchez, C.; Giacoumidis, E. Fair comparison of complexity between a multi-band CAP and DMT for data center interconnects. Opt. Lett. 2017, 42, 3860–3863. [Google Scholar] [CrossRef]
- Farooq, U.; Miliou, A. Channel Equalization for converged OFDM-Based 5G mm-wave A-RoF System at 60 GHz. In Proceedings of the IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 27–30 January 2021; pp. 1263–1267. [Google Scholar]
- Farooq, U.; Miliou, A. Assessment of Different Channel Equalization Algorithms for a Converged OFDM-Based 5G mm-wave A-RoF System at 60 GHz. Appl. Sci. 2022, 12, 1511. [Google Scholar] [CrossRef]
- MATLAB & Simulink–MathWorks. Available online: https://www.mathworks.com/products/matlab.html (accessed on 1 June 2024).
- Tuzlukov, V. Generalized Receiver with Decision-Feedback Equalizer for Multicode Wideband DS-CDMA. WSEAS Trans. Circuits Syst. 2022, 21, 202–222. [Google Scholar] [CrossRef]
- Barry, J. Equalization. In Academic Press Library in Mobile and Wireless Communications; Academic Press: New York, NY, USA, 2016; pp. 283–331. [Google Scholar]
- Pulford, G.W. Developments in Non-Linear Equalization; Australian National University: Canberra, Australia, 1992. [Google Scholar]
- Xiuqin, C.; Wang, W.; Wang, J.; Wu, F.; Luo, Y.; Guo, W.; Li, N.; Li, Y. A novel decision feedback equalization structure for nonlinear high-speed links. IEEE Access 2020, 8, 59135–59144. [Google Scholar]
- Rontogiannis, A.A.; Berberidis, K. Efficient decision feedback equalization for sparse wireless channels. IEEE Trans. Wirel. Commun. 2003, 2, 570–581. [Google Scholar] [CrossRef]
- Benvenuto, N.; Giovanni, C.; Stefano, T. Algorithms for Communications Systems and Their Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Xu, H. Simplified maximum likelihood-based detection schemes for M-ary quadrature amplitude modulation spatial modulation. IET Commun. 2012, 6, 1356–1363. [Google Scholar] [CrossRef]
- El-Mashed, M.G.; El-Rabaie, S. Near optimum OSIC-based ML algorithm in a quantized space for LTE-A downlink physical layer. Digit. Signal Process. 2015, 40, 250–257. [Google Scholar] [CrossRef]
- Li, J.; Letaief, K.B.; Cheng, R.S.; Cao, Z. Multi-stage low complexity maximum likelihood detection for OFDM/SDMA wireless LANs. In Proceedings of the IEEE International Conference on Communications. Conference Record (Cat. No. 01CH37240), Helsinki, Finland, 11–14 June 2001; IEEE: New York, NY, USA, 2001; pp. 1152–1156. [Google Scholar]
- Li, J.; Letaief, K.B.; Cao, Z. A reduced-complexity maximum-likelihood method for multiuser detection. IEEE Trans. Commun. 2004, 52, 289–295. [Google Scholar] [CrossRef]
- Fazel, K.; Kaiser, S. MULTI-Carrier and Spread Spectrum Systems: From OFDM and MC-CDMA to LTE and WiMAX; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Fatadin, I.; Ives, D.; Savory, S.J. Blind equalization and carrier phase recovery in a 16-QAM optical coherent system. J. Light. Technol. 2009, 27, 3042–3049. [Google Scholar] [CrossRef]
- Ready, M.J.; Gooch, R.P. Blind equalization based on radius directed adaptation. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; IEEE: New York, NY, USA, 1990; pp. 1699–1702. [Google Scholar]
- VPIphotonics: Simulation Software and Design Services. Available online: https://www.vpiphotonics.com/ (accessed on 1 June 2024).
- Sulong, S.M.; Idris, A.; Salih, N.M.; Ali, D.M. Reduction of Time Complexity for CLS-DFE MIMO-OFDMA System. J. Phys. Conf. Ser. 2020, 1529, 052099. [Google Scholar] [CrossRef]
- Shao, M.; Chen, W.K.; Yu, C.Y.; Liu, Y.F.; Ma, W.K. One-Bit MIMO Detection: From Global Maximum-Likelihood Detector to Amplitude Retrieval Approach. arXiv 2024, arXiv:2407.11079. [Google Scholar]
- Gatherer, A.; Auslander, E. The Application of Programmable DSPs in Mobile Communications; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Fevrier, I.J.; Gelfand, S.B.; Fitz, M.P. Reduced complexity decision feedback equalization for multipath channels with large delay spreads. IEEE Trans. Commun. 1999, 47, 927–937. [Google Scholar] [CrossRef]
- Browning, C.; Farhang, A.; Saljoghei, A.; Marchetti, N.; Vujicic, V.; Doyle, L.E.; Barry, L.P. 5G wireless and wired convergence in a passive optical network using UF-OFDM and GFDM. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; IEEE: New York, NY, USA, 2017; pp. 386–392. [Google Scholar]
- Moshirian, S.; Ghadami, S.; Havaei, M. Blind Channel Equalization. arXiv 2012, arXiv:1208.2205. [Google Scholar]
- Amir, A.; Wax, M. Constant modulus algorithms via low-rank approximation. Signal Process. 2019, 160, 263–270. [Google Scholar]
- Romano, J.M.T.; Attux, R.; Cavalcante, C.C.; Suyama, R. Unsupervised Signal Processing: Channel Equalization and Source Separation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Yazdi, H.S.; Homayouni, F. Impulsive Noise Suppression of Images Using Adaptive Median Filter. Int. J. Signal Process. Image Process. Pattern Recognit. 2010, 3, 1–12. [Google Scholar]
- Moussa, A.; Pouliquen, M.; Frikel, M.; Bedoui, S.; Abderrahim, K.; M’Saad, M. An overview of blind equalization algorithms for digital communications. In Proceedings of the 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; IEEE: New York, NY, USA, 2019; pp. 491–496. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Yang, G.R.; Wang, X.J. Artificial Neural Networks for Neuroscientists: A Primer. Neuron 2020, 107, 1048–1070. [Google Scholar] [CrossRef]



| Literature Review | Approach/Methods Used | Comments |
|---|---|---|
| [13] | Nonlinear post-equalizers, such as a Volterra series-based equalizer and a neural network-based (NN) equalizer to combat signal degradation in a 28 GHz mm-wave A-RoF 10 km fiber link for OFDM 16-QAM, and 64-QAM. |
|
| [14] | Artificial neural network nonlinear equalizer (ANN-NLE) for single-carrier 16-QAM and 64QAM signal transmissions in the 60 GHz RoF transmission system of length 15 km. |
|
| [16] | DSP unit in simulated software for 5 to 35 km direct and coherent detection 16-PSK, 16-QAM, and 64-QAM 100 Gbit/s data rate link at 28 GHz. |
|
| [17] | Use of the iterative block (IB) decision feedback equalization (DFE) method for an intensity modulation and direct-detection (IM/DD) based optical code division multiplexing (OCDM) system. |
|
| [18] | Adaptive activated artificial neural network nonlinear equalizer (ANN-NLE) to enhance BER performance. |
|
| [19] | Convolutional neural network (CNN) and binary convolutional neural network (BCNN)-based decision schemes. |
|
| [21] | Transmission of a single channel 112 Gb/s PAM-4 direct detection signal using the maximum likelihood sequence estimation (MLSE) algorithm. |
|
| [22] | Experimental generation, detection and transmission of a 112 Gb/s dual-polarization, single- and dual-carrier 16-QAM half-cycle Nyquist subcarrier modulation, over 4 km of SMF length for short-reach IM/DD systems using CMA and RDE algorithms for equalization |
|
| [23] | Experimental demonstration of 200 Gbps 32 Gbaud polarization-multiplexed carrier-based self-homodyne (PMC-SH) system using 16-QAM 10 km SSMF link. Offline equalization is executed by cascading RDE with a DFE. |
|
| [24] | 12.5 GBd 16-QAM analog processing-based coherent receiver built and simulated in 130 nm BiCMOS. RDE-based equalization and Costas loop-based carrier phase compensation are used in the receiver for a transmission over 10 km-long fiber. |
|
| [28,29] | LMS, CMA, and AMF-based equalization in converged mm-wave A-RoF system at 60 GHz. |
|
| [This Work] | Converged OFDM-based mm-wave A-RoF system at 60 GHz with signal processing using DFE, MLD, and RDE algorithms. |
|
| Literature Review | Frequency (GHz) | Maximum Fiber Length (km) | Modulation Format | Algorithm | Computational Complexity |
|---|---|---|---|---|---|
| [13] | 28 | 10 | OFDM 16-QAM | Voltera and neural network-based equalizers | High |
| [14] | 60 | 20 | OFDM 16-QAM and 64-QAM | Complex valued (ANN-NLE) | High |
| [16] | 28 | 5–35 | 16-PSK, 16-QAM and 64-QAM | Built-in DSP unit in simulation software | Low |
| [18] | 60 | 10 | BPSK | ANN-NLE | High |
| [19] | 60 | 20 | 2-PAM | Convolutional neural network (CNN) and binary convolutional neural network (BCNN)-based decision schemes | High |
| [28] | 60 | 25 | QPSK and 16-QAM | LMS Algorithm | Low |
| [29] | 60 | 100 | QPSK and 16-QAM | LMS, CMA, and AMF Algorithms | Low |
| [This work] | 60 | 0–120 | QPSK, 16-QAM, 64-QAM and 128-QAM | DFE, MLD, and RDE Algorithms | Moderate |
| Link Design Components | Values |
|---|---|
| Carrier Frequency | 7.5 GHz |
| Laser CW | 10 dBm |
| Wavelength | 1553 nm |
| RIN | −130 dB/Hz |
| Radio Frequency | 60 GHz mm-wave |
| Bit Rate Default | 40 Gbit/s |
| Bits per Symbol | 2, 4, 6, 7 |
| SSMF Length | Up to 120 km |
| Dispersion | 16 ps/nm/km |
| Dispersion Slope | 0.08 × 103 s/m3 |
| SSMF Attenuation Coefficient | 0.2 dB/km |
| Photo Diode Model | PIN |
| Responsivity | 0.8 A/W |
| Thermal Noise | 10−12 A/Hz1/2 |
| Shot Noise | ON |
| Cyclic Prefix | 0.125 |
| Modulation Scheme | EVM for MLD After Equalization (%) | EVM for DFE After Equalization (%) | EVM Improvement (%) | Max Fiber Length (km) |
|---|---|---|---|---|
| QPSK | 17.06 | 16.60 | 0.46 | 120 |
| 16-QAM | 12.40 | 12.32 | 0.08 | 100 |
| 64-QAM | 7.35 | 7.19 | 0.16 | 50 |
| 128-QAM | 4.85 | 4.73 | 0.12 | 40 |
| Algorithm | QPSK | 16-QAM | ||
|---|---|---|---|---|
| EVM (%) | Fiber Length (km) | EVM (%) | Fiber Length (km) | |
| MLD | 17.06 | 120 | 12.4 | 100 |
| DFE | 16.6 | 120 | 12.32 | 100 |
| LMS | - | 120 | 23.75 | 100 |
| CMA | - | 120 | - | 100 |
| AMF | - | 120 | 23.00 | 100 |
| RDE | 11.35 | 120 | 9.41 | 100 |
| Performance Indicator | LMS | CMA | DFE | MLD | RDE | AMF |
|---|---|---|---|---|---|---|
| Error Vector Magnitude (EVM) | Moderate | Moderate | Low | Low | Very low (with restrictions in our system) | Moderate |
| Convergence Rate | Slow | Moderate | Moderate | Slow | Fast | Fast |
| Time Complexity | Low | Moderate | Moderate | High | Moderate | Low |
| Space Complexity | Low | Low | Moderate | High | Moderate | Low |
| Adaptability | Moderate | Moderate | Moderate | Moderate | High | Moderate |
| Memory Usage | Low | Low | Moderate | High | Moderate | Low |
| Convergence Time | Moderate | Moderate | Fast | Slow | Moderate | Fast |
| Number of Taps | Low | Moderate | High | High | Moderate | Low |
| Computational Complexity | Low | Low | Moderate | Moderate | Low | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, U.; Miliou, A. Advanced DFE, MLD, and RDE Equalization Techniques for Enhanced 5G mm-Wave A-RoF Performance at 60 GHz. Photonics 2025, 12, 496. https://doi.org/10.3390/photonics12050496
Farooq U, Miliou A. Advanced DFE, MLD, and RDE Equalization Techniques for Enhanced 5G mm-Wave A-RoF Performance at 60 GHz. Photonics. 2025; 12(5):496. https://doi.org/10.3390/photonics12050496
Chicago/Turabian StyleFarooq, Umar, and Amalia Miliou. 2025. "Advanced DFE, MLD, and RDE Equalization Techniques for Enhanced 5G mm-Wave A-RoF Performance at 60 GHz" Photonics 12, no. 5: 496. https://doi.org/10.3390/photonics12050496
APA StyleFarooq, U., & Miliou, A. (2025). Advanced DFE, MLD, and RDE Equalization Techniques for Enhanced 5G mm-Wave A-RoF Performance at 60 GHz. Photonics, 12(5), 496. https://doi.org/10.3390/photonics12050496






