Fuzzy Logic-Based Performance Enhancement of FSO Systems Under Adverse Weather Conditions
Abstract
1. Introduction
1.1. Existing Works
1.2. Main Contributions
- (i)
- FLC Development and Computational Efficiency:
- We have developed a fuzzy control system that dynamically adjusts the BER threshold at the receiver in response to FSO link impairments (rain, fog, and distance).
- We have conducted a complexity analysis of the FLC to demonstrate that its computational complexity is O(1). Therefore, it ensures constant-time execution.
- We have implemented and tested the FLC using MATLAB (R2017b)’s fuzzy logic toolbox on an Intel Core i7-1165G7 (2.80 GHz) processor (UX435E Notebook PC, ASUSTeK Computer Inc., Taipei, Taiwan)
- Experimental results confirm that the FLC executes under 4 ms per decision cycle, making it suitable for real-time applications.
- (ii)
- FSO-OCDMA System Integration and Optimization:
- We have integrated the FLC within an end-to-end FSO-OCDMA setup to enhance adaptability to varying atmospheric conditions.
- We have analyzed the FSO system and optimized BER threshold levels to maintain reliable communication under rain and fog conditions.
- (iii)
- Theoretical and Performance Analysis:
- We have conducted theoretical performance and analysis of the FSO-FLC-OCDMA system using the Single Sigma Matrix (SSM) code.
- The system behavior is evaluated under different attenuation levels (dB/km) across varying distances from very-short-range (200 m) to long-range (3 km).
- (iv)
- Performance Gains and System Efficiency:
- In this work, we have demonstrated that the proposed system supports a higher number of users while extending transmission distances compared to conventional methods.
- In this work, it is ensured that optical transmission requirements were met with minimal effective transmitted source power.
1.3. Organization
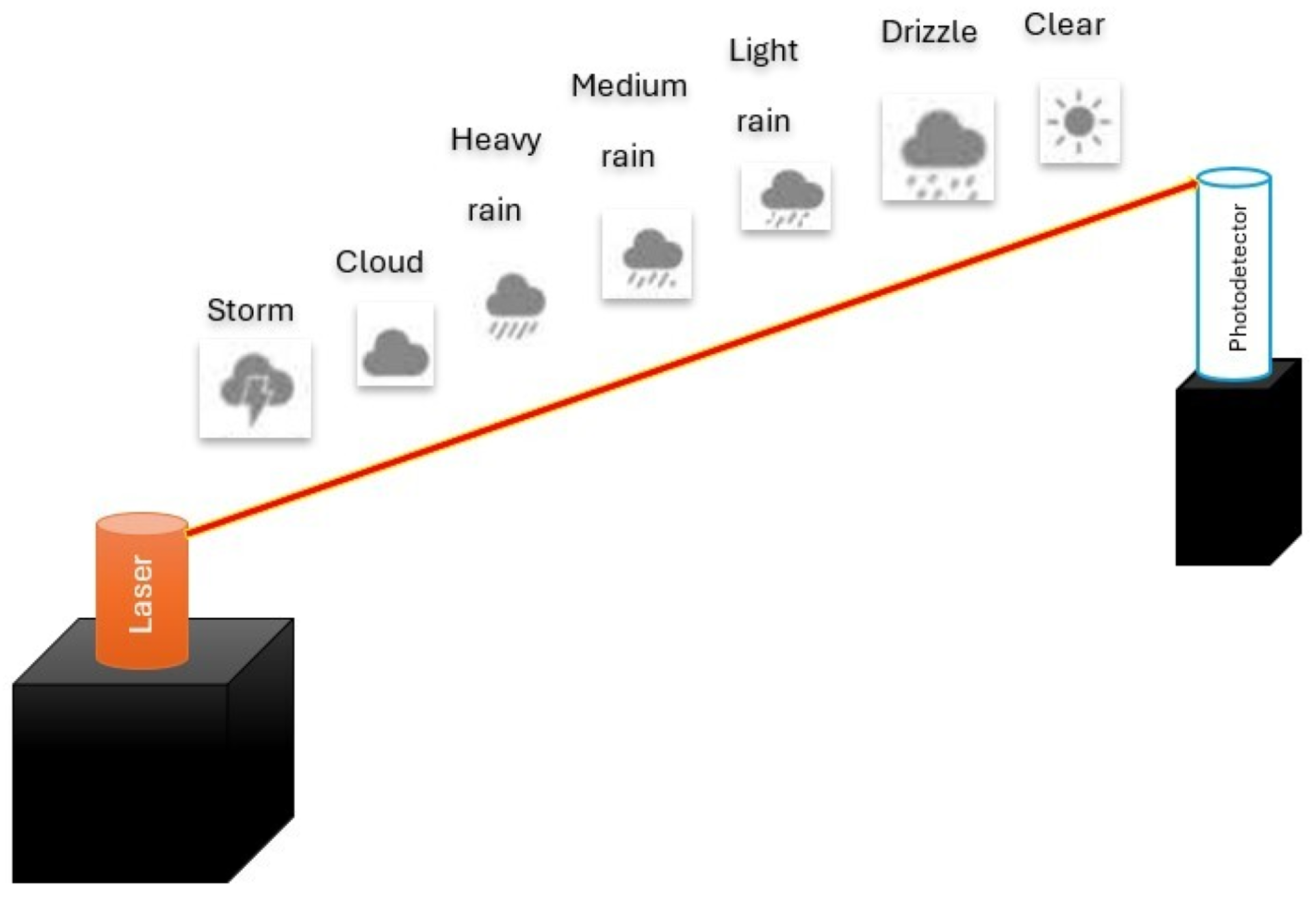
2. Modeling of Rain and Fog Impairments in FSO System
2.1. Rain
2.2. Fog
3. Fuzzy Modeling for Enhancing Receiver Performance in FSO System
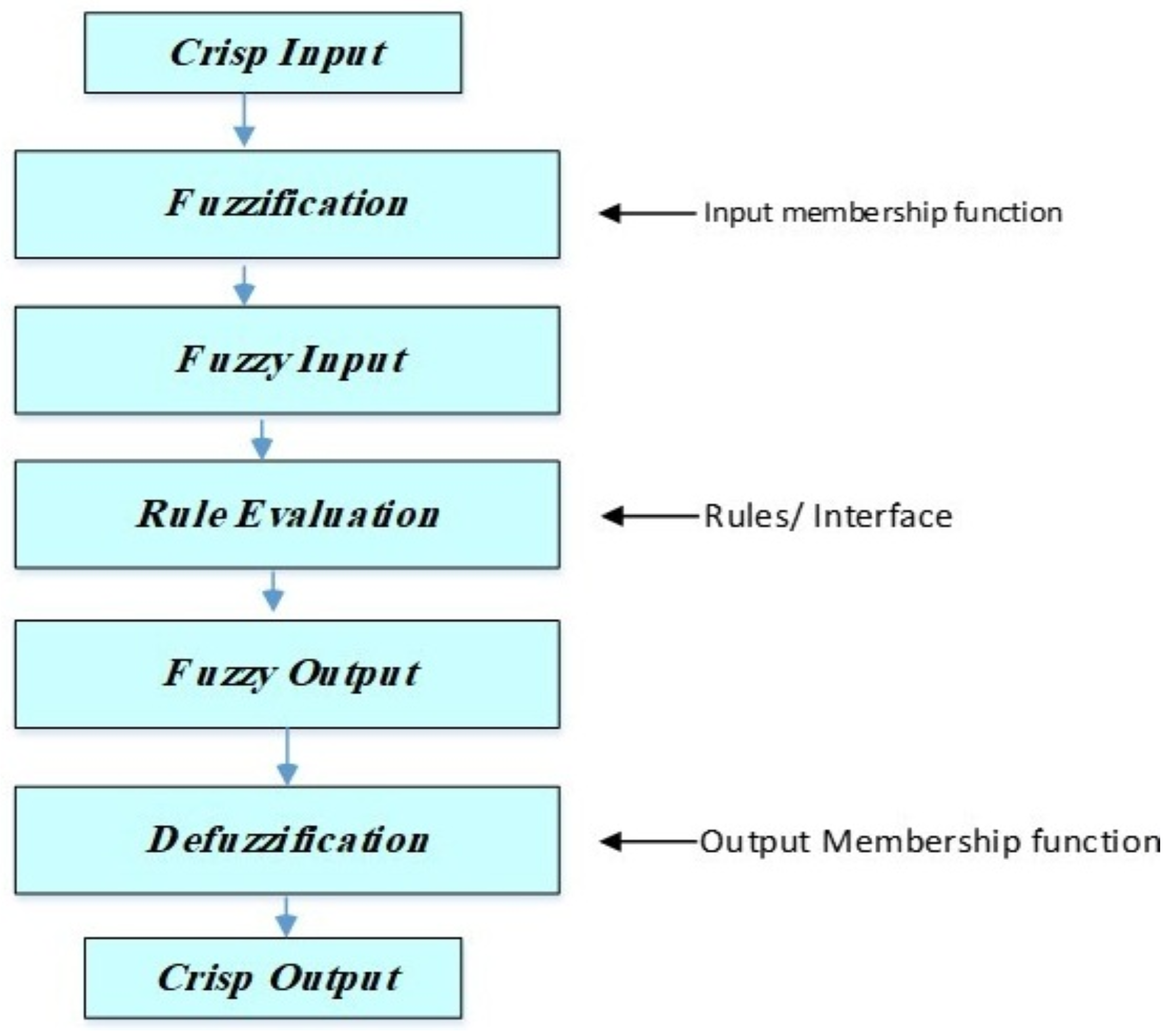
3.1. Fuzzy Logic
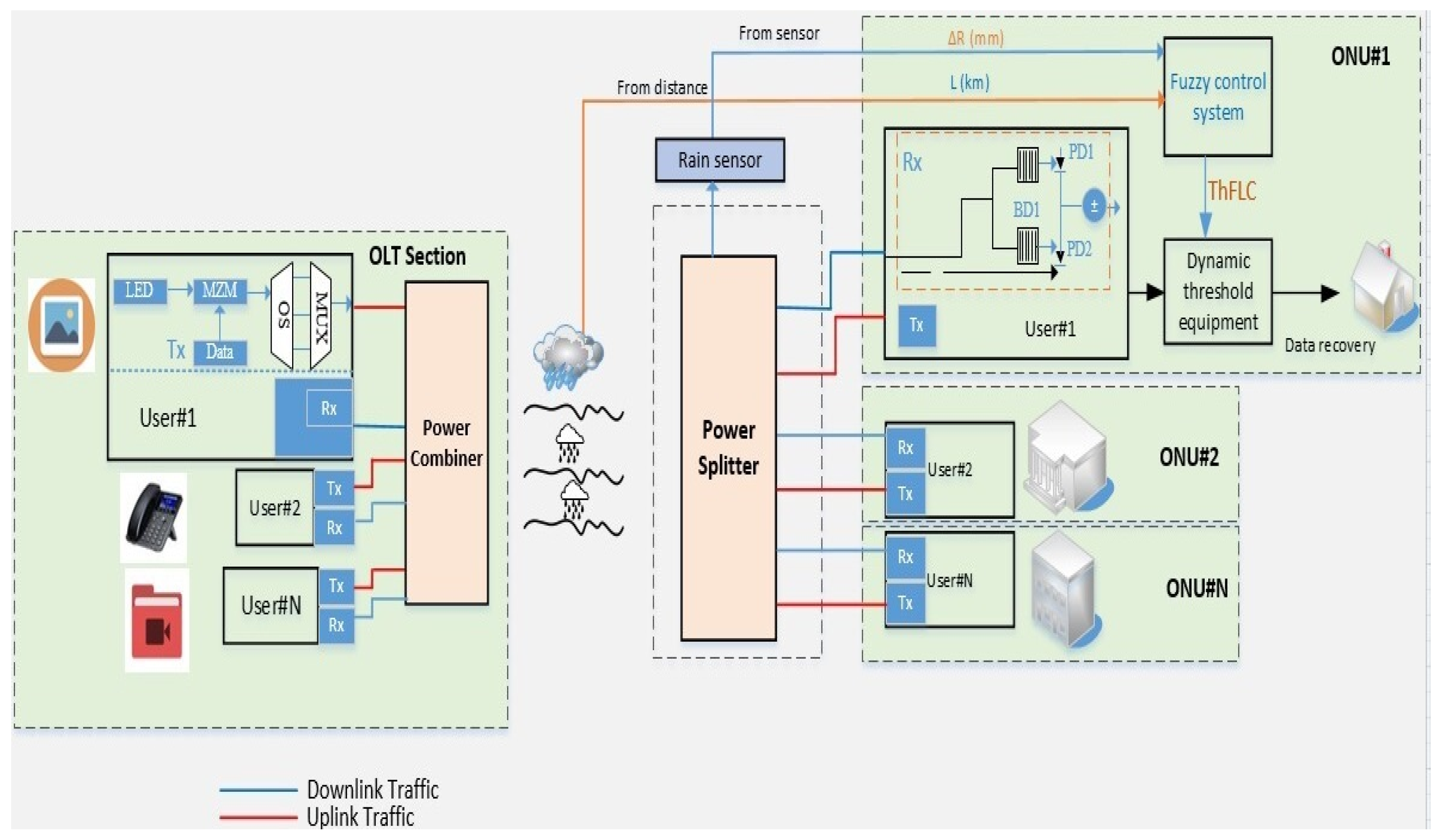
3.2. Motivation and Architecture of the FLC-Based Adaptive Receiver for FSO-OCDMA Systems
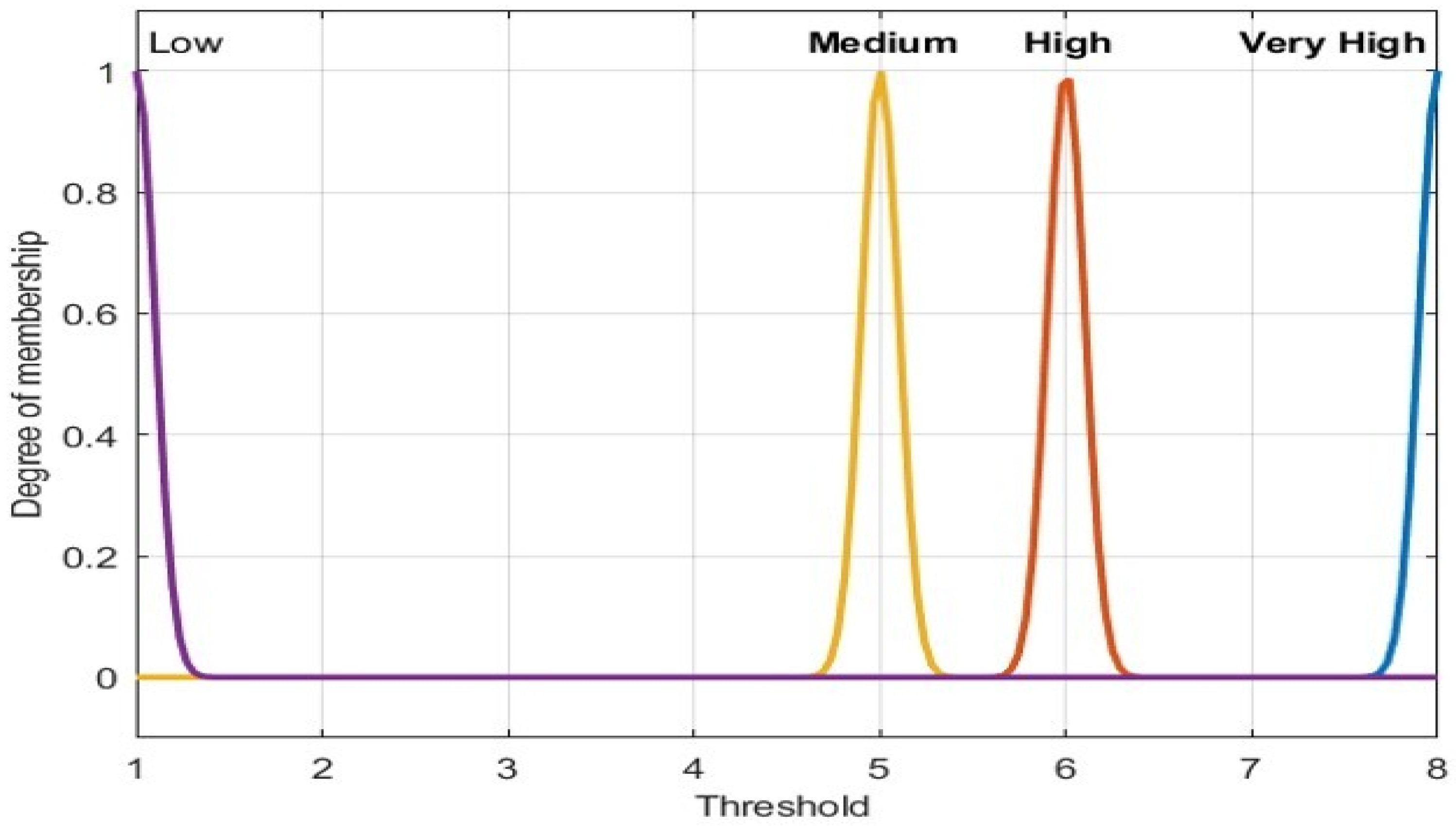
3.3. Selection of Input and Output Membership Functions
- Rain (R): Intensity of rainfall (0 to precipitation rate > 50 mm).
- Fog (F): Density of fog (0 to 1.5 ).
- Distance (D): Distance between the FSO transceivers (0 to 3 km).
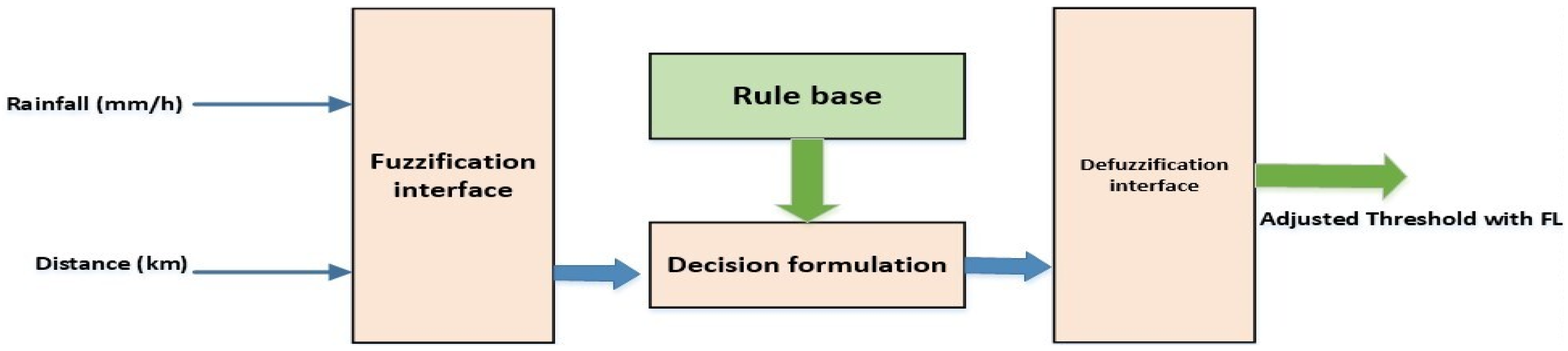
3.4. Fuzzy Rule Base and Inference Mechanism
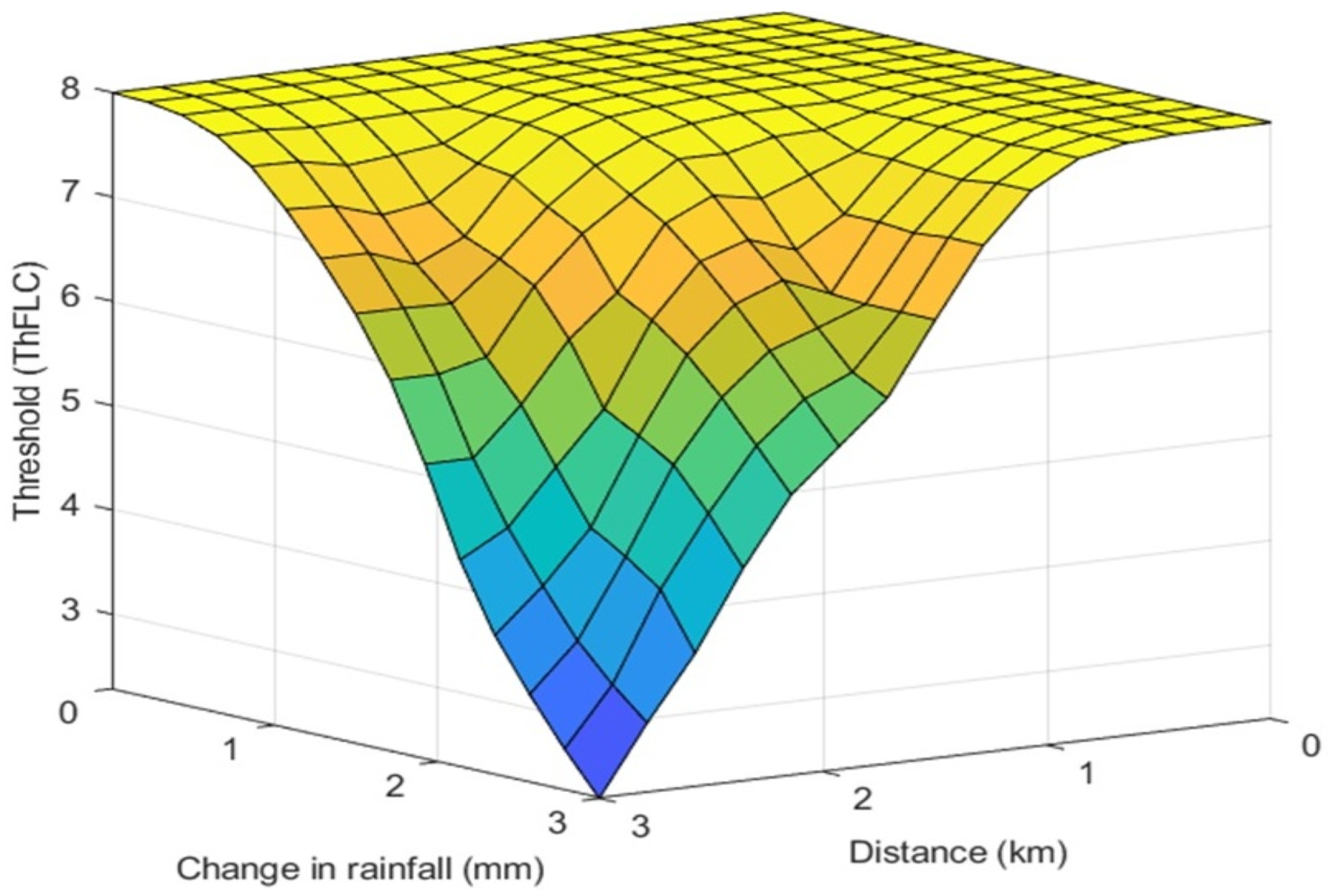
3.5. Adaptive BER Threshold Adjustment Mechanism for FSO-FLC-OCDMA Receivers
| Algorithm 1 Dynamic BER threshold adjustment. |
Input: rainfall rate, fog density, distance Input: SSM priorities (w, L, K, ⋯) Output: = Fuzzy BER threshold Output: adjustments = {Dynamic Threshold Adjustment; Receiver Gain Control; Noise Filtering} Output: Request Define , , and Define Low = [, ], Medium = [, ], High = [, ] Define , , , and 1 Step 1: Define Fuzzy Membership Functions rain = FuzzyVariable(“Rain”, Light = [0; 10], Moderate = [10; 20], Heavy = [20; 30]) fog = FuzzyVariable(“Fog”, Light = [0, 5], medium = [5; 15], Heavy = [15; 30]) distance = FuzzyVariable(“Distance”, VL = [0; 0.5], LD = [0.5; 1], MD = [1; 1.5], HD = [1.5; 2]) 2 Step 2: Define fuzzy output variable for dynamic BER threshold (T-BER) 3 Step 3: Define fuzzy rules for rules = 3.1 FuzzyRule(if Rain.high & Fog.high & Distance.long then T-BER.high), 3.2 FuzzyRule(if Rain.medium & Fog.medium & Distance.medium then T-BER.medium), 3.3 FuzzyRule(if Rain.low & Fog.low & Distance.short then T-BER.low), 3.4 … 3.5 … 3.6 FuzzyRule(if Rain.low & Fog.low & Distance.short then T-BER.low) 4 Step 4: Create fuzzy system = FuzzySystem(rules) 5 Step 5: Monitor environmental conditions 5.1 = GetCurrentRain() 5.2 = GetCurrentFog() 5.3 = GetCurrentDistance() 6 Step 6: Calculate dynamic BER threshold (T-BER) = .compute(rain = , fog = , distance = ) 7 Step 7: Monitor actual BER = MeasureActualBER() 8 Step 8: Decision based on BER if adjustments = AdjustReceiverSettings(rain = , fog = , distance = ) else: Request = MaintainSettings() 9 Step 9: return adjustments return Request |
| Algorithm 2 Receiver adjustment settings. |
Input: currentR = rainfall rate Input: currentF = fog density Input: currentD = distance Output: adjustments = {dynamic_threshold; gain_control; N_filtering} Step 1: Dynamic Threshold Adjustment if ( or ) adjustments[‘dynamic_threshold’] = adjust_threshold(level=‘high’) elsif ( or ) adjustments[‘dynamic_threshold’] = adjust_threshold(level=‘medium’) else: adjustments[‘dynamic_threshold’] = adjust_threshold(level=‘low’) Step 2: Receiver Gain Control if ( or ) adjustments[‘gain_control’] = enhance_gain(method=‘AGC’, linearity=‘high’) elsif ( and ) adjustments[‘gain_control’] = maintain_gain() else adjustments[‘gain_control’] = enhance_gain(method=‘AGC’, linearity=‘medium’) Step 3: Advanced Filtering if ( or or ) adjustments[‘N_filtering’] = apply_advanced_filter(method=‘adaptive_LMS’, intensity=‘high’) elsif ( or ) adjustments[‘N_filtering’] = apply_advanced_filter(method=‘adaptive_LMS’, intensity=‘medium’) else adjustments[‘N_filtering’] = apply_basic_filter(method=‘low_pass’) Step 4: return adjustments |
3.5.1. Fuzzy T-BER Computation Using FLC (Algorithm 1)
- Step 1—Define Fuzzy Membership Functions: Establish fuzzy membership functions that represent linguistic variables related to environmental factors, signal quality, and BER. Therefore, fuzzy sets (very low, low, medium, and high) for rain, fog, distance, and BER will be defined.
- Step 2—Define the fuzzy output variable T-BER, which categorizes the dynamic BER threshold into three linguistic levels: Low, Medium, and High based on the severity of environmental conditions.
- Step 3—Define Fuzzy Rules for T-BER: Develop a set of fuzzy logic rules to determine the target BER (T-BER) based on input conditions, using the defined membership functions.
- Step 4—Create Fuzzy System: Build a fuzzy inference system (FIS) that processes the defined rules and membership functions to calculate outputs dynamically.
- Step 5—Monitor Environmental Conditions: Continuously track environmental parameters such as rain (), fog (), and distance () that could affect the signal in the FSO communication system.
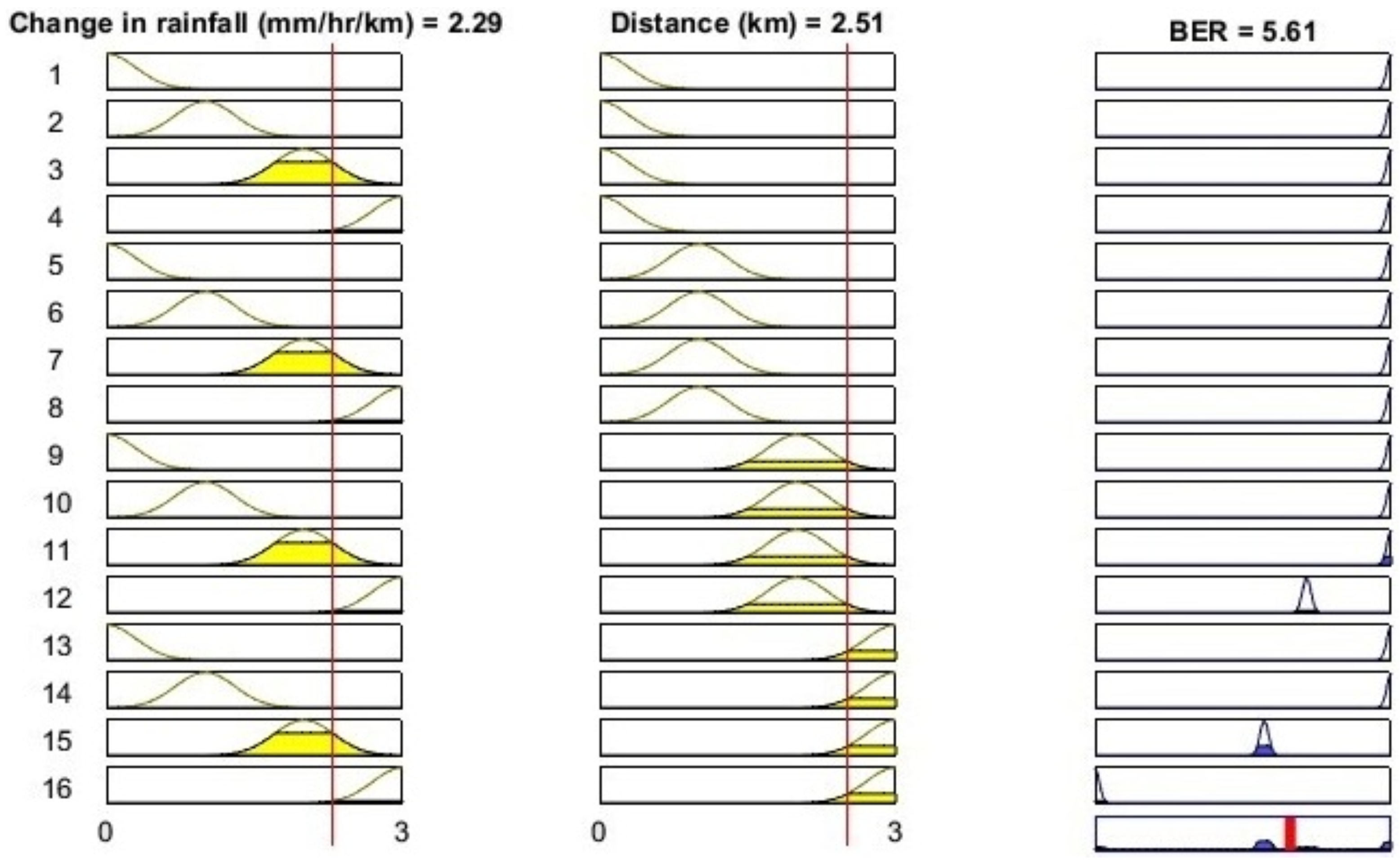
- Step 6—Calculate Dynamic BER Threshold: Using the fuzzy system, compute a dynamic threshold for BER based on the monitored environmental conditions and the defined rules. In the FSO system in this work, the fuzzy logic controller utilizes the max–min inference method. In this approach, the fuzzy operator AND selects the minimum value from the antecedents, while for aggregation, the maximum value is used. The defuzzification process then converts the fuzzy output from the inference mechanism into a precise value for the dynamic threshold device (). The Center of Gravity (COG) method is employed for defuzzification, as it delivers an accurate result by calculating the Weighted Average of multiple output membership functions [26].
- Step 7—Monitor Actual BER: Regularly measure the actual BER of the FSO transceiver to detect fluctuations or changes in signal quality. The is measured in real-time based on the current values of rain, fog, and distance (, , and ).
- Step 8—Decision Based on BER: If the measured BER () exceeds the dynamic threshold () set by the fuzzy logic system, the system will trigger adjustments to improve communication quality (adjustments= AdjustReceiverSettings()). These actions can include three mechanisms: Dynamic Threshold Adjustment, Receiver Gain Control, or Noise Filtering. When the BER is below the dynamic threshold, the system maintains the current settings or optimizes resources (Request = MaintainSettings()).
3.5.2. Adaptive Receiver Control (Algorithm 2)
- AdjustReceiverSettings() function:
- MaintainSettings() function:
3.6. Computational Efficiency and Real-Time Feasibility of the FLC
3.6.1. Computational Complexity Analysis
- Fuzzification:
- Inference Mechanism:
- Defuzzification:
3.6.2. Execution Time Estimation
- Fuzzification: 0.2–1 ms
- Inference (36-rule evaluation): 0.5–2 ms
- Defuzzification (Centroid Method, 3 MFs): 0.3–1 ms
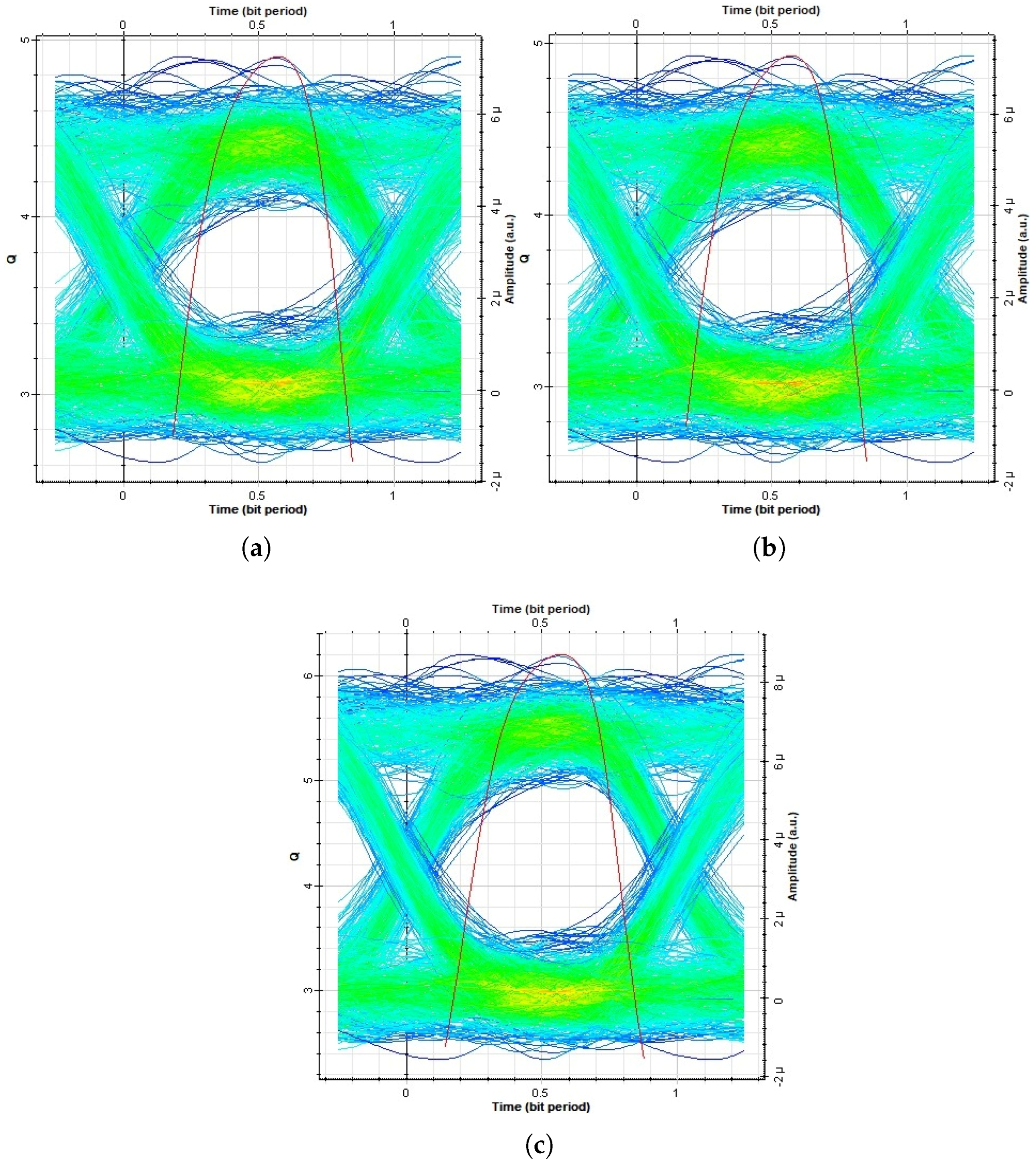
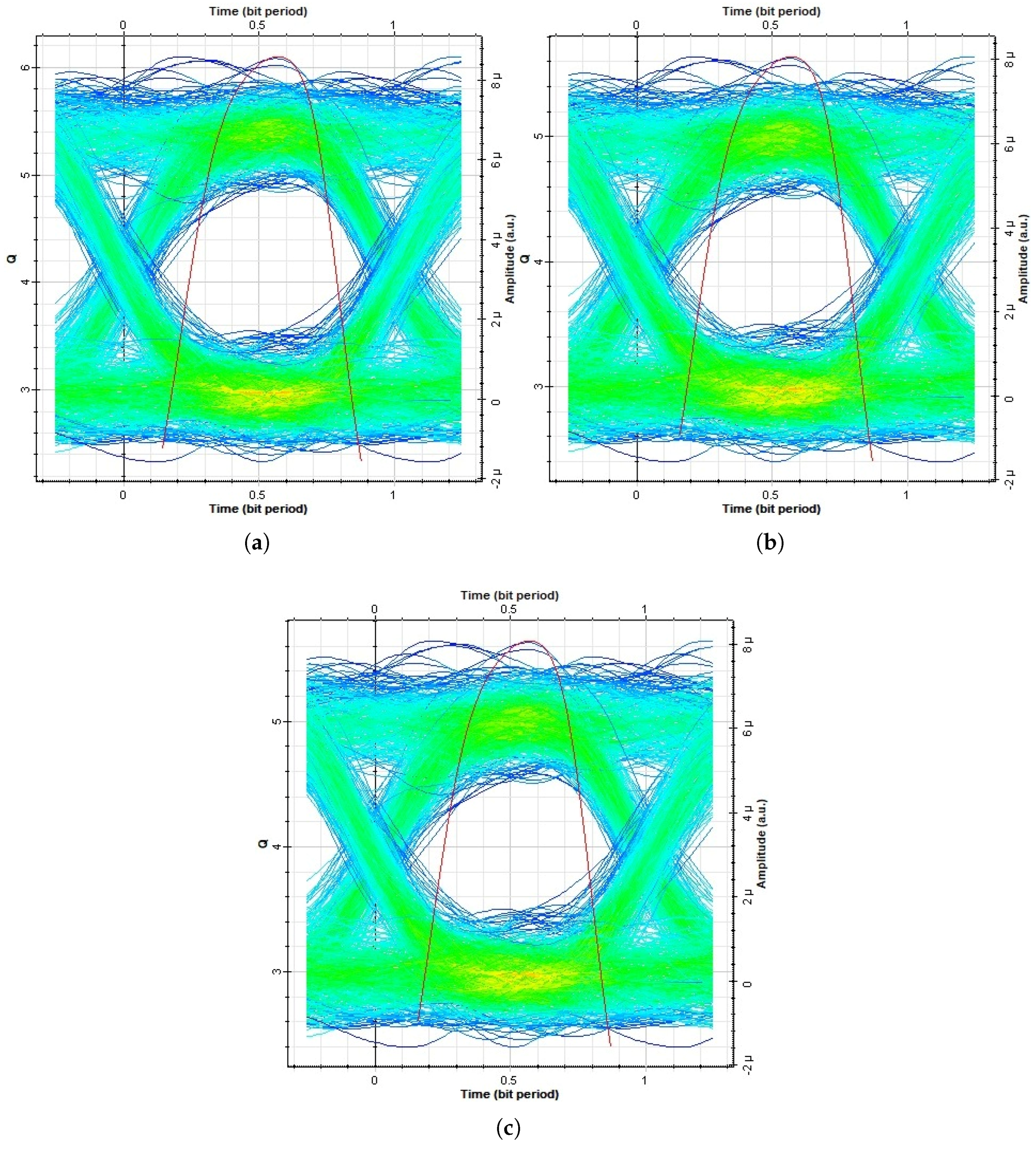
4. Results and Discussion
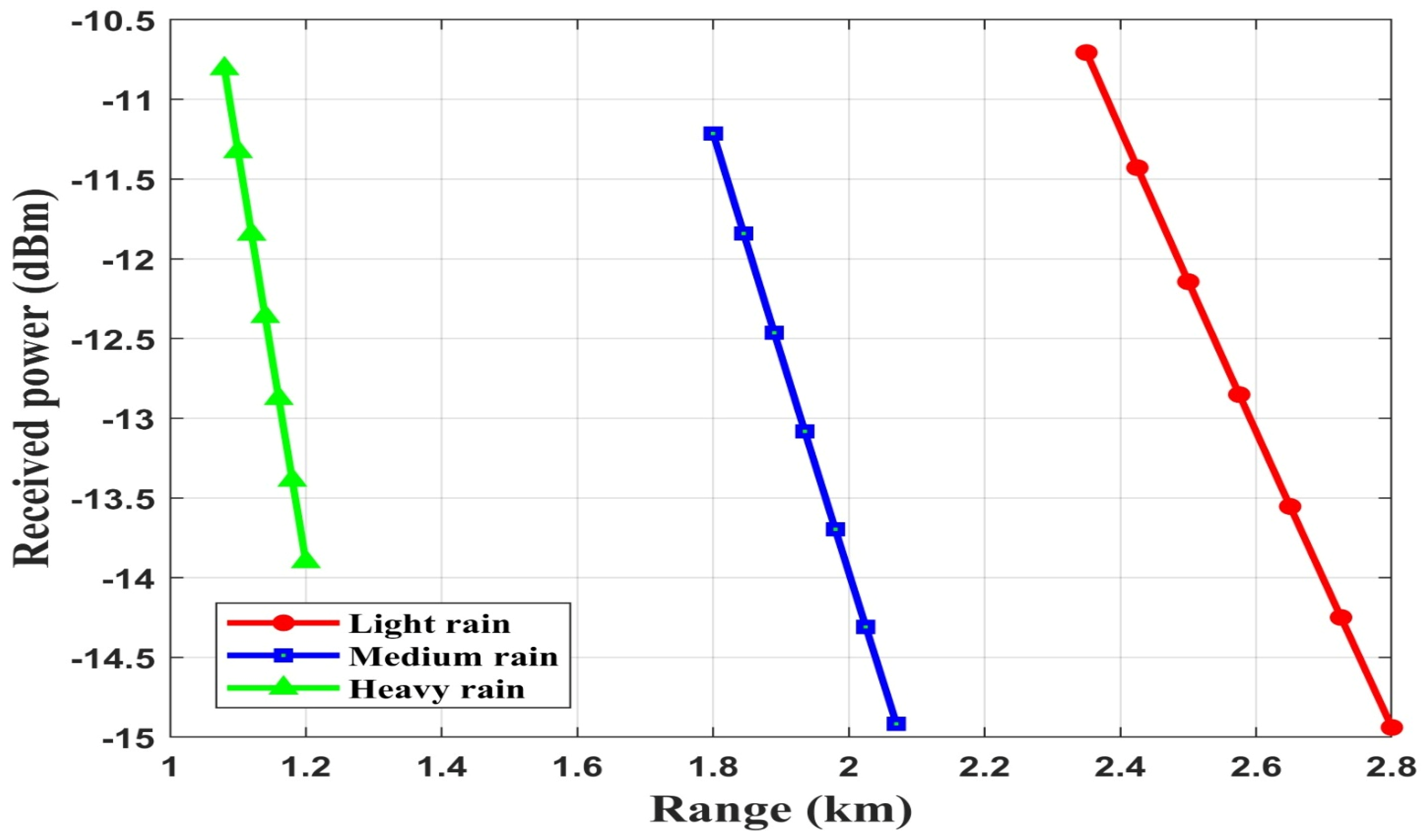
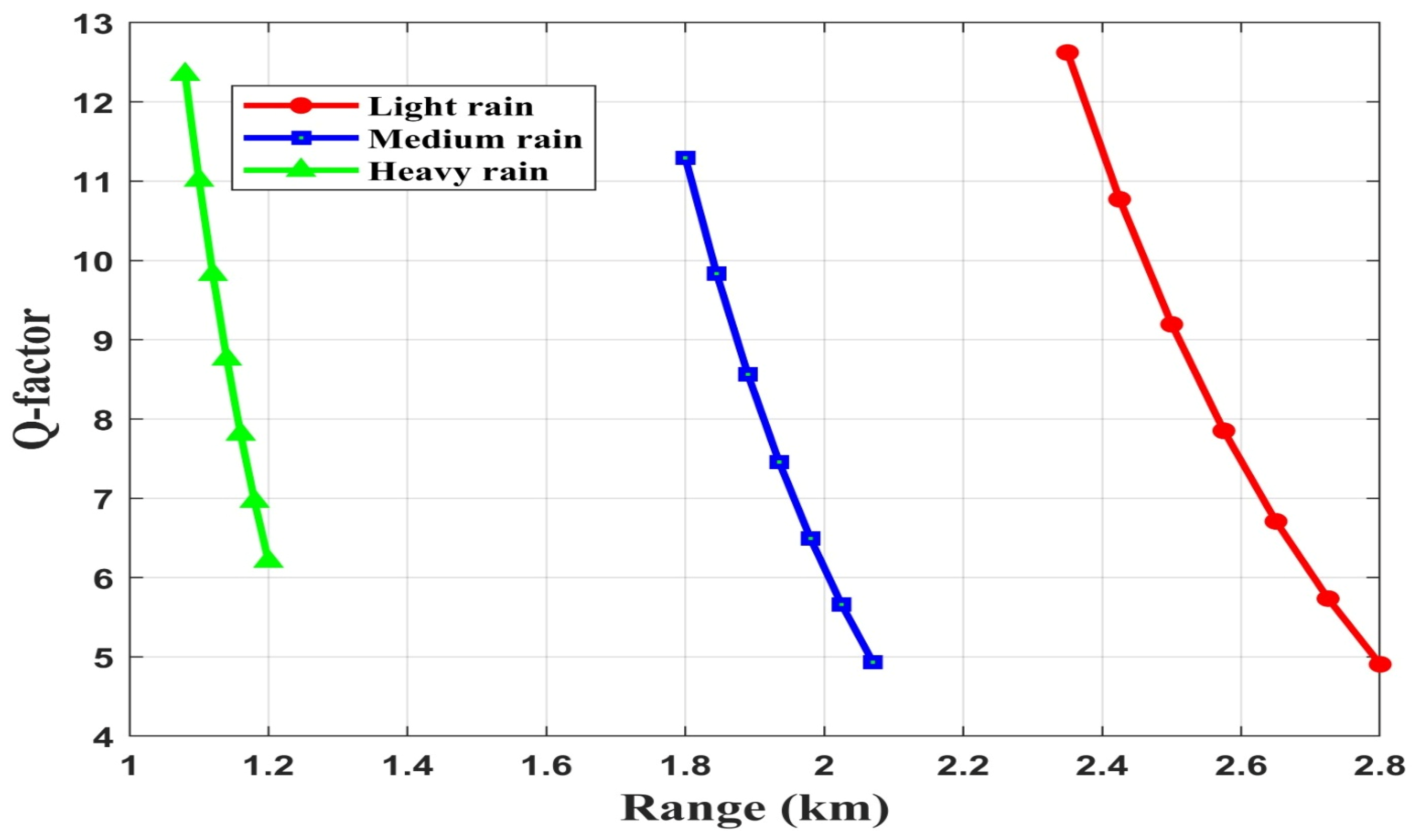
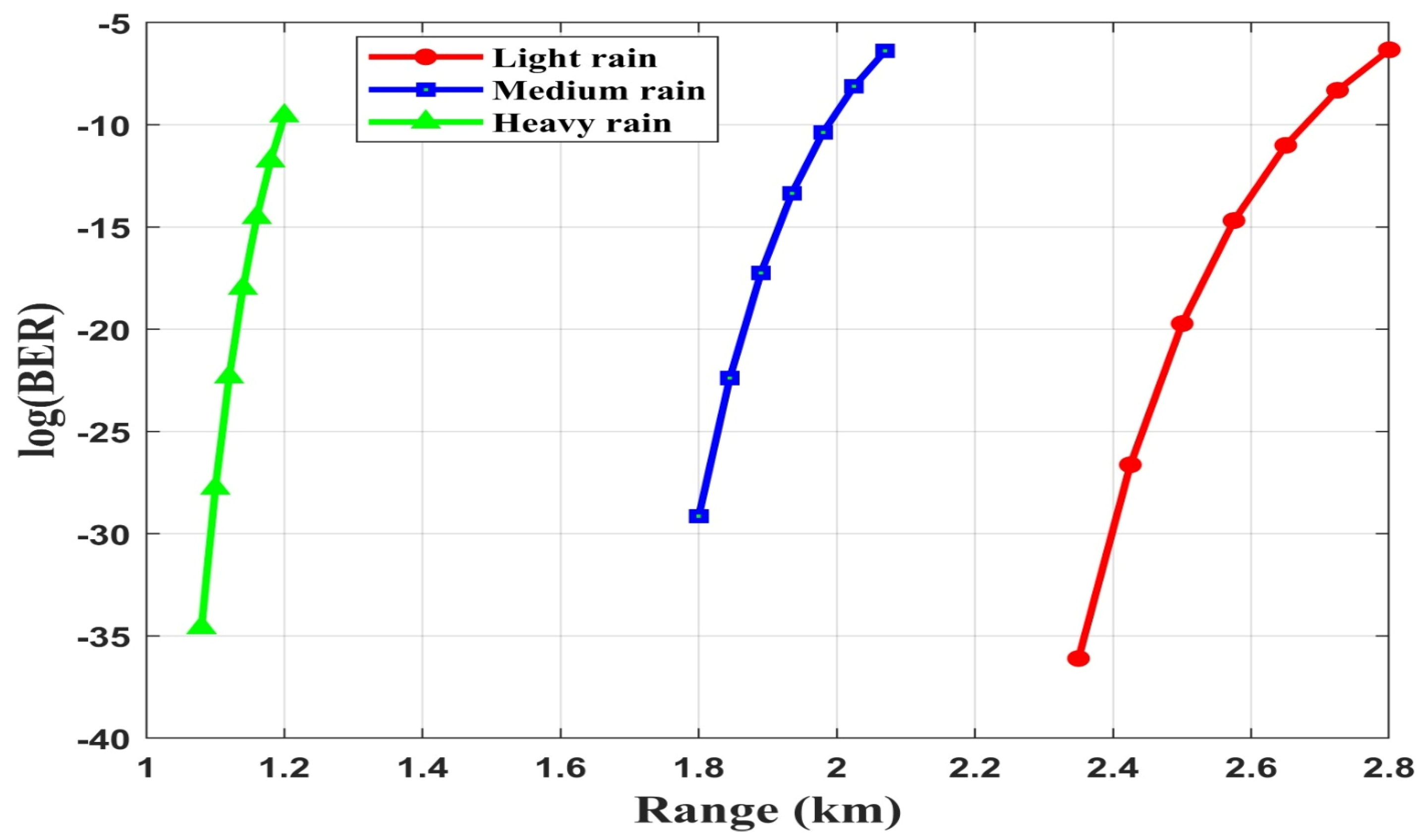
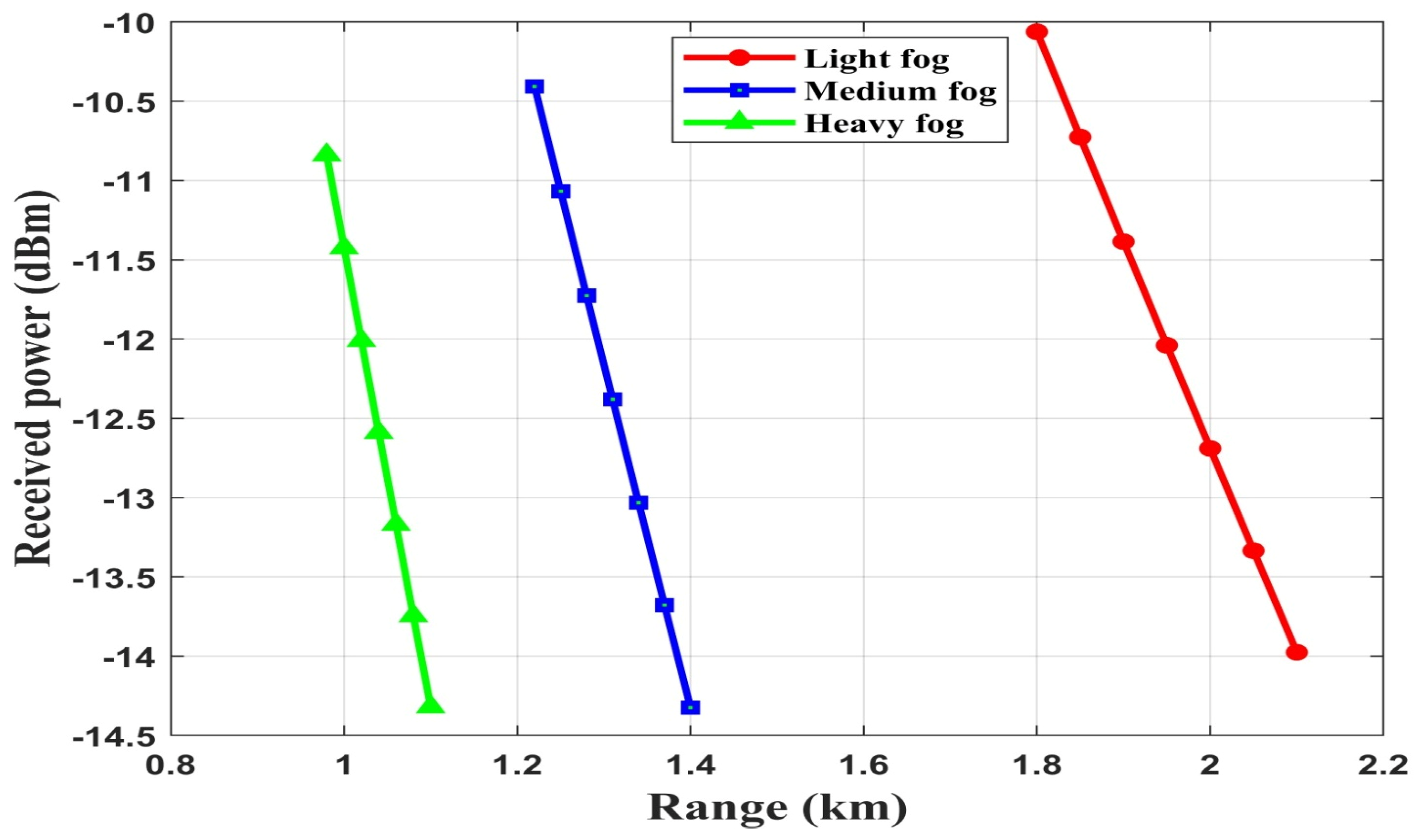
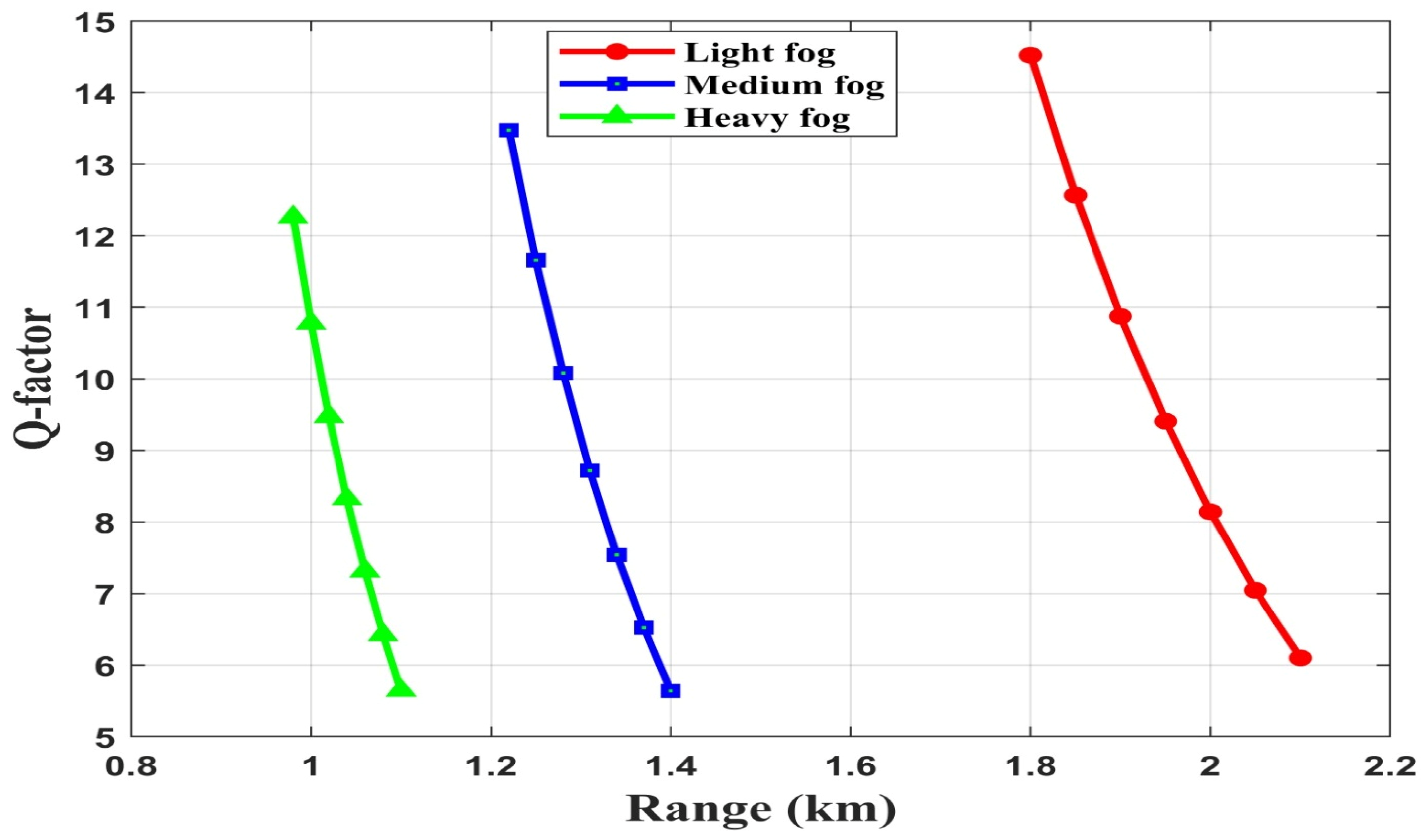
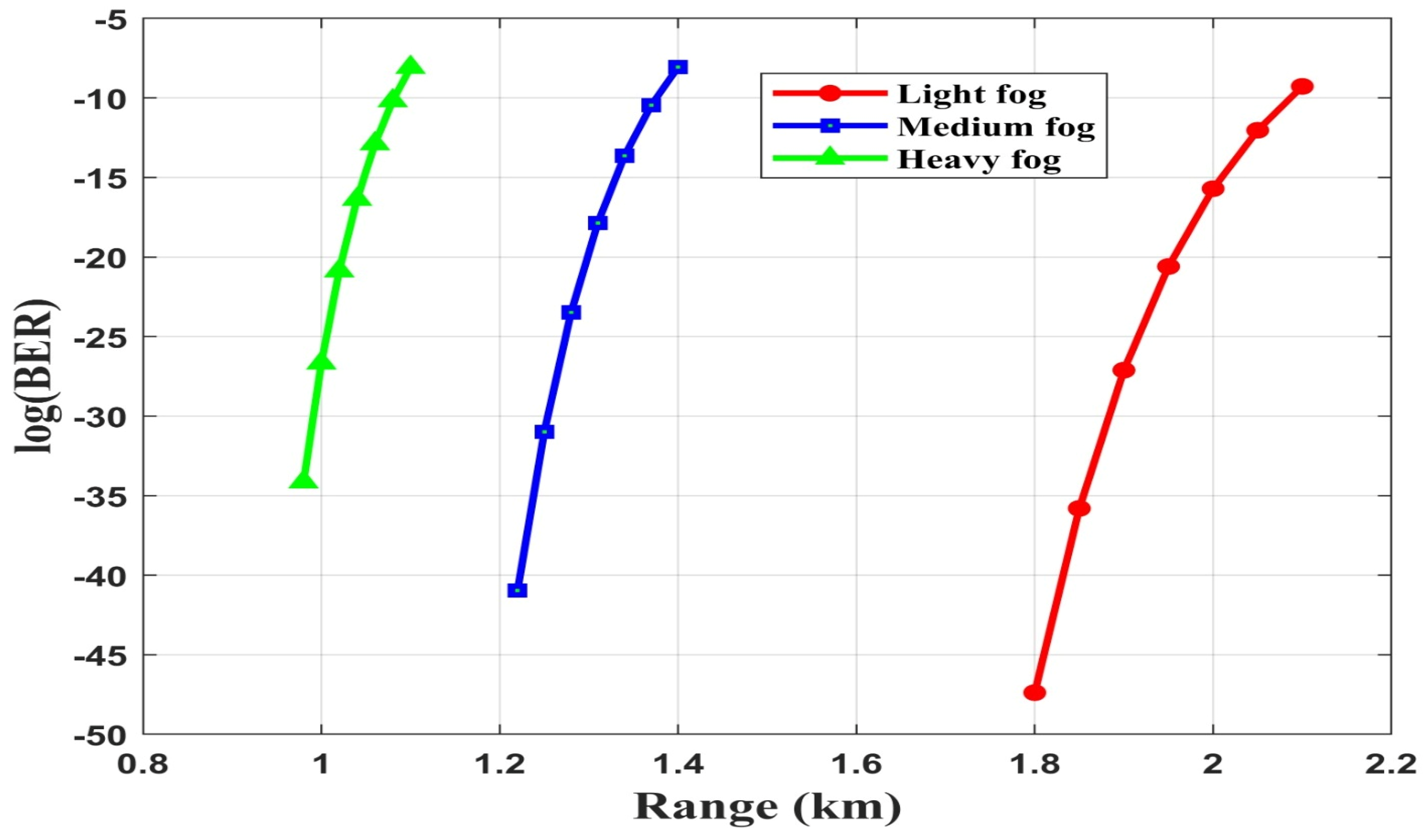
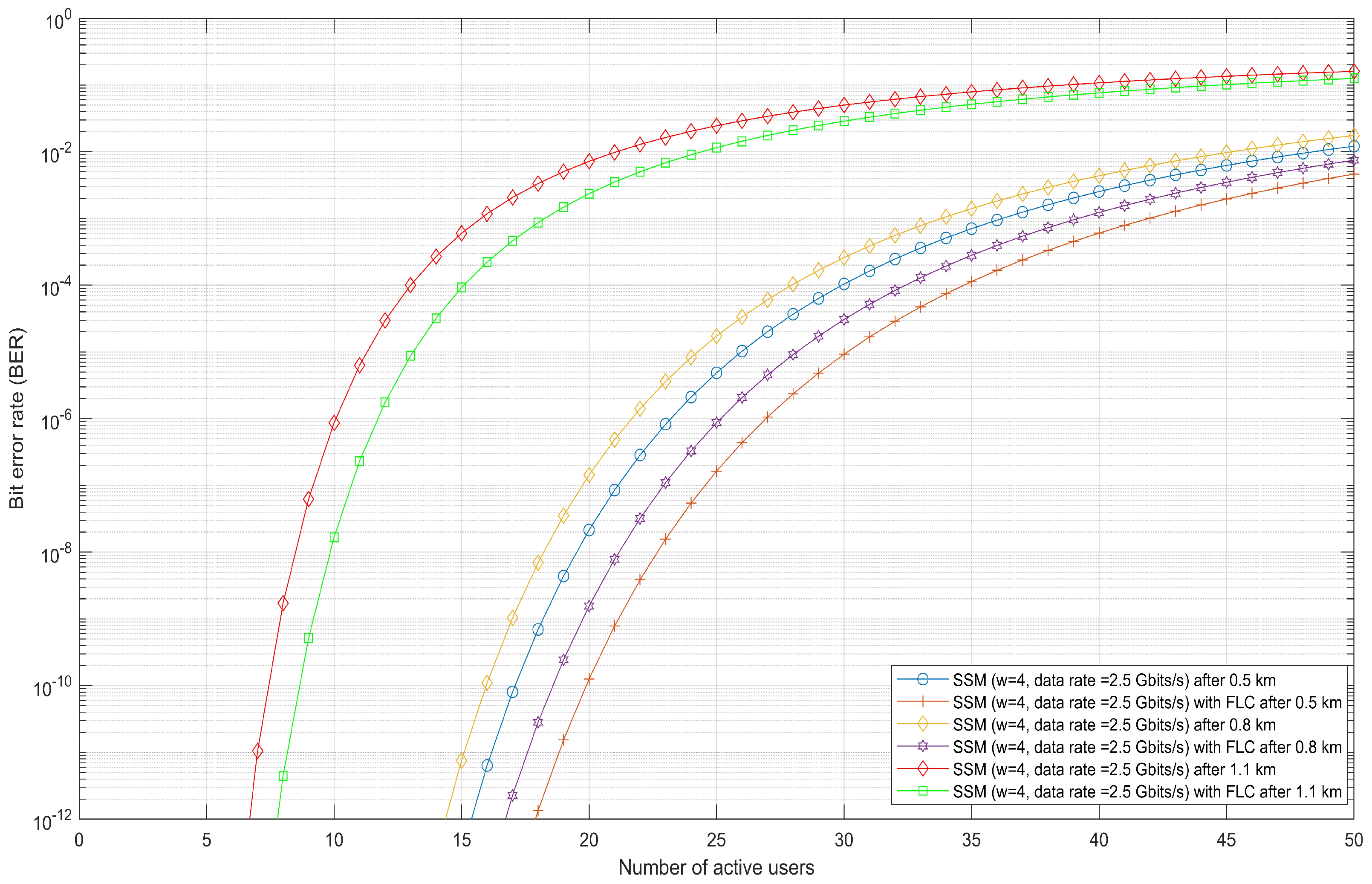
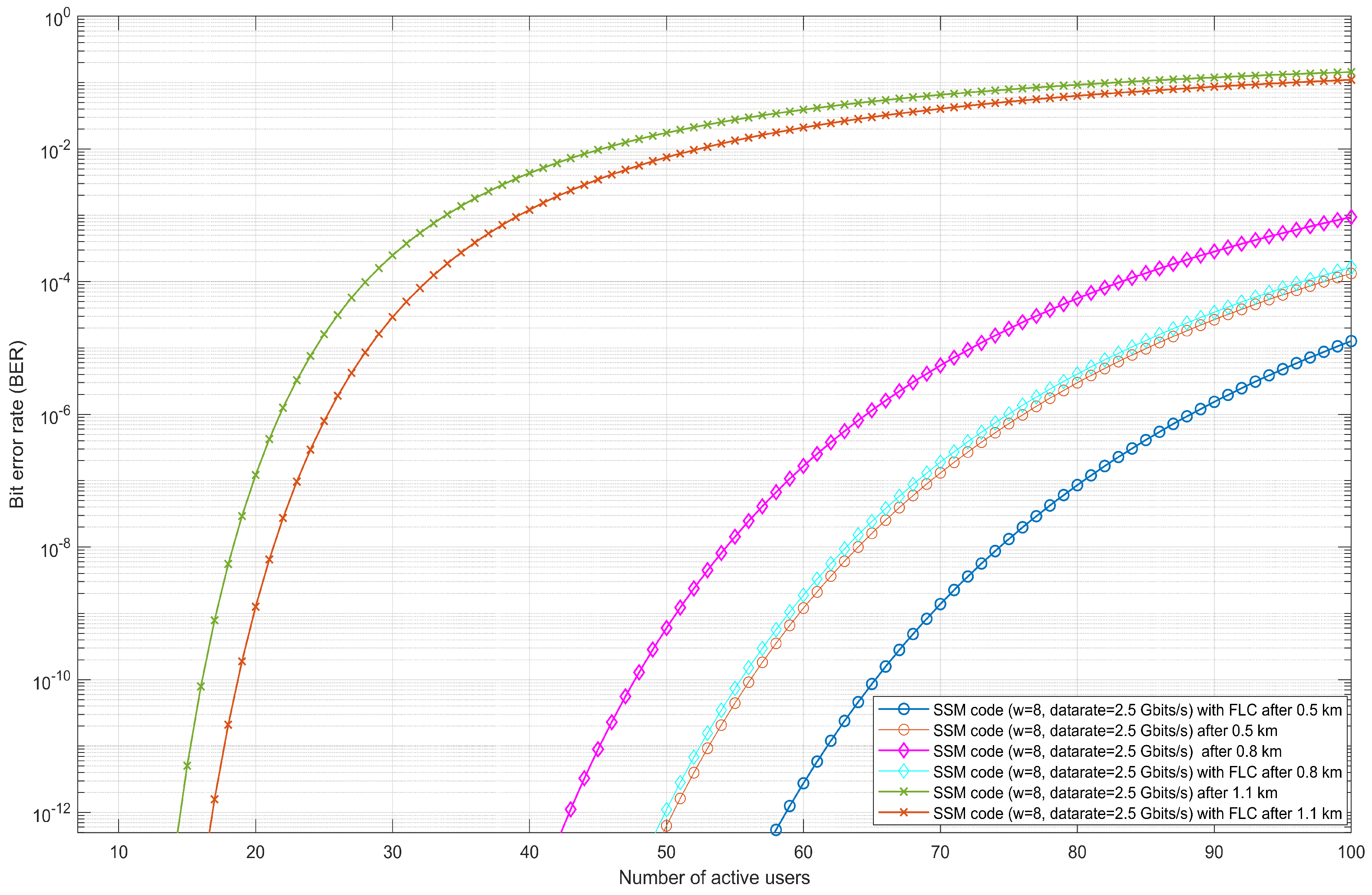
4.1. Performance Evaluation of FSO-SSM System Without FLC Under Rain and Fog
4.1.1. Rainy Weather
4.1.2. Foggy Weather
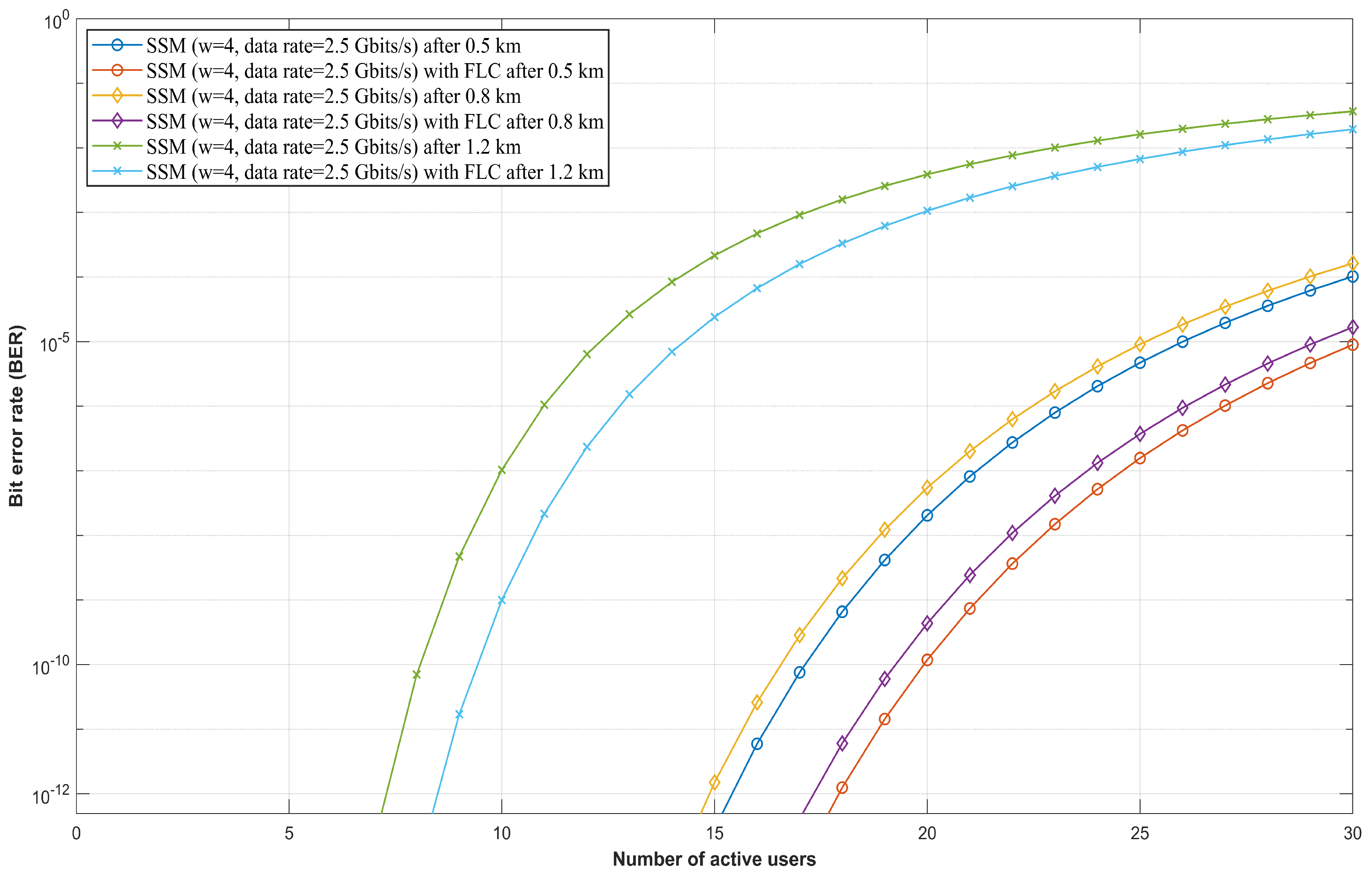
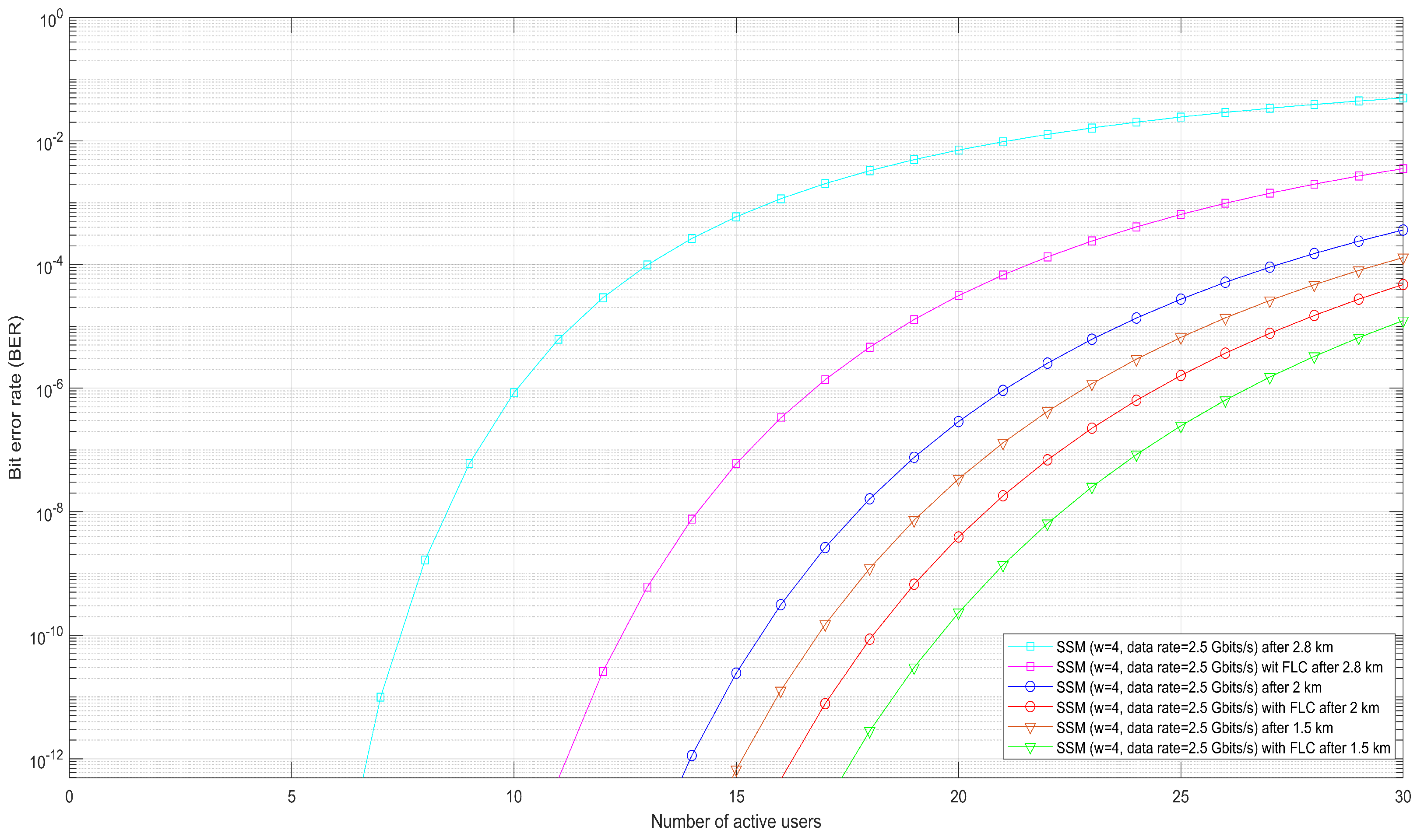
4.2. Performance Evaluation of FSO-SSM System with FLC Under Rain and Fog
4.2.1. Rainy Weather
4.2.2. Foggy Weather
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OCDMA | Optical Code-Division Multiple-Access |
| FSO | Free-Space Optics |
| FLC | Fuzzy Logic Control |
| BER | Bit Error Rate |
| OWC | Optical wireless communication |
| RF | Radio Frequency |
| OFDM | Orthogonal Frequency Multiplexing |
| WDM | wavelength division multiplexing |
| SAC | Spectral Amplitude Coding |
| ONoC | Optical Network-on-chip |
| SSM | Single Sigma Matrix |
References
- Arnon, S.; Barry, J. Advanced Optical Wireless Communication Systems; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Esmail, M.A.; Fathallah, H.; Alouini, M.-S. Analysis of fog effects on terrestrial Free Space Optical communication links. In Proceedings of the 2016 IEEE International Conference on Communications Workshops (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 151–156. [Google Scholar]
- Stathis, A.; Ntanos, A.; Lyras, N.K.; Giannoulis, G.; Panagopoulos, A.D.; Avramopoulos, H. Toward converged satellite/fiber 1550 nm DS-BB84 QKD networks: Feasibility analysis and system requirements. Photonics 2024, 11, 609. [Google Scholar] [CrossRef]
- Nadeem, F.; Kvicera, V.; Awan, M.S. Weather effects on hybrid FSO/RF communication link. IEEE J. Sel. Areas Commun. 2009, 27, 1687–1697. [Google Scholar] [CrossRef]
- Wani, M.Y.; Pathak, H.; Kaur, K.; Kumar, A. Free space optical communication system under different weather conditions. J. Opt. Commun. 2023, 44, 103–110. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef]
- Khan, A.N.; Younis, U.; Mehmood, M.Q.; Zubair, M. Atmospheric propagation of space-fractional Gaussian-beam waves in a FSO communication system. Opt. Express 2022, 30, 1570. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, S.; Amphawan, A.; Nisar, K. Realization of free space optics with OFDM under atmospheric turbulence. Optik 2014, 125, 5196–5198. [Google Scholar] [CrossRef]
- Zabidi, S.A.; Al Khateeb, W.; Islam, M.R.; Naji, A.W. The effect of weather on free space optics communication (FSO) under tropical weather conditions. In Proceedings of the International Conference on Computer and Communication Engineering (ICCCE’10), Kuala Lumpur, Malaysia, 11–12 May 2010. [Google Scholar]
- Fadhil, H.A.; Amphawan, A.; Shamsuddin, H.A.; Abd, T.H.; Al-Khafaji, H.M.; Aljunid, S.A.; Ahmed, N. Optimization of free space optics parameters: An optimum solution for bad weather conditions. Optik 2013, 124, 3969–3973. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on free space optical communication: A communication theory perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Moghaddasi, M.; Mamdoohi, G.; Noor, A.S.M.; Mahdi, M.A.; Anas, S.B.A. Development of SAC OCDMA in FSO with multi-wavelength laser source. Opt. Commun. 2015, 356, 282–289. [Google Scholar] [CrossRef]
- Abd El-Mottaleb, S.A.; Singh, M.; Chehri, A.; Ahmed, H.Y.; Zeghid, M.; Khan, A.N. Capacity enhancement for free space optics transmission system using orbital angular momentum optical code division multiple access in 5G and beyond networks. Energies 2022, 15, 7100. [Google Scholar] [CrossRef]
- Ijaz, M.; Ghassemlooy, Z.; Pesek, J.; Fiser, O.; Le Minh, H.; Bentley, E. Modeling of fog and smoke attenuation in free space optical communications link under controlled laboratory conditions. J. Lightw. Technol. 2013, 31, 1720–1726. [Google Scholar] [CrossRef]
- Israr, A.; Israr, A.; Khan, F.; Khan, F. Optimal modulation technique for MIMO FSO link. Wirel. Pers. Commun. 2019, 109, 695–714. [Google Scholar] [CrossRef]
- Olyaee, S.; Akbari, M. Performance analysis of total attenuation effects and different values of transmitter power on bit error rate and signal-to-noise ratio for free space optical communication. Recent Adv. Electr. Electron. Eng. 2022, 15, 234–242. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- dos Reis, J.V.; Raddo, T.R.; Sanches, A.L.; Borges, B.H.V. Mitigation of environmental temperature variation effects using fuzzy systems and source-matched spreading codes for OCDMA networks. In Proceedings of the 2014 16th International Conference on Transparent Optical Networks (ICTON), Graz, Austria, 6–10 July 2014. [Google Scholar]
- ITU-R Recommendation P.1814, Prediction Methods Required for the Design of Terrestrial Free-Space Optical Links, ITU-R. 2007. Avalaible online: https://www.itu.int/rec/R-REC-P.1814-0-200708-I (accessed on 9 April 2025).
- ITU-R Recommendation P.1817, Propagation Data Required for the Design of Terrestrial Free-Space Optical Links, ITU-R. 2012. Available online: https://www.itu.int/rec/R-REC-P.1817-1-201202-I (accessed on 9 April 2025).
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Cloud attenuation statistics prediction from Ka-band to optical frequencies: Integrated liquid water content field synthesizer. IEEE Trans. Antennas Propag. 2017, 65, 319–328. [Google Scholar] [CrossRef]
- Iancu, I. A Mamdani type fuzzy logic controller. In Fuzzy Logic: Controls, Concepts, Theories and Applications; InTech: London, UK, 2012; pp. 325–350. [Google Scholar]
- Farghal, A.E.A. On the performance of OCDMA/SDM PON based on FSO under atmospheric turbulence and pointing errors. Opt. Laser Technol. 2019, 114, 196–203. [Google Scholar] [CrossRef]
- Singh, M.; Abd El-Mottaleb, S.A.; Aljunid, S.A.; Ahmed, H.Y.; Zeghid, M.; Nisar, K.S. Performance investigations on integrated MMF/FSO transmission enabled by OAM beams. Results Phys. 2023, 51, 106656. [Google Scholar] [CrossRef]
- Ahmed, H.Y.; Zeghid, M.; Mohyeldien, M.; Abd El-Mottaleb, S.A. Multi-dimensional Sigma Shift Matrix (nD-SSM) code with adaptable transmitter-receiver architecture to support multiclass users for SAC-OCDMA system. IEEE Access 2024, 12, 76919–76935. [Google Scholar] [CrossRef]
- dos Reis, J.V., Jr.; Raddo, T.R.; Sanches, A.L.; Borges, B.H.V. Fuzzy logic control for the mitigation of environmental temperature variations in OCDMA networks. J. Opt. Commun. Netw. 2015, 7, 480–488. [Google Scholar] [CrossRef]


| Rain Intensity | Attenuation (dB/km) |
|---|---|
| Storm | 59.7 |
| Cloud burst | 20.99 |
| Heavy rain (HR) | 19.28 |
| Medium rain (MR) | 9.64 |
| Light rain (LR) | 6.27 |
| Drizzle | 0.44 |
| Very clear | 0.22 |
| Clear | 0.06 |
| Weather Condition | Attenuation (dB/km) |
|---|---|
| Thin fog | 9 |
| Light fog (LF) | 13 |
| Medium fog (MF) | 16 |
| Heavy fog (HF) | 22 |
| Light haze (LH) | 1.537 |
| Medium haze (MH) | 4.285 |
| Weather Condition | VL | LD ≤ 1 km | MD [1 km, 2 km] | HD [2 km, 3 km] |
|---|---|---|---|---|
| CA | Th8 | Th8 | Th8 | Th8 |
| Light rain | Th8 | Th8 | Th8 | Th8 |
| Moderate rain | Th8 | Th8 | Th8 | Th5 |
| Heavy rain | Th8 | Th8 | Th5 | Th1 |
| Weather Condition | VL | LD ≤ 0.5 km | MD [0.5 km, 1 km] | HD [1 km, 1.5 km] |
|---|---|---|---|---|
| CA | Th8 | Th8 | Th8 | Th8 |
| Light fog | Th8 | Th8 | Th8 | Th8 |
| Medium fog | Th8 | Th8 | Th8 | Th5 |
| Heavy fog | Th8 | Th8 | Th5 | Th1 |
| Weather Condition | No. of Users | BER with FLC | BER Without FLC | Improvement (%) |
|---|---|---|---|---|
| Low Rain | 22 | 98.47% | ||
| Medium Rain | 20 | 98.69% | ||
| Heavy Rain | 10 | 90.32% | ||
| Low Fog | 21 | 98.39% | ||
| Medium Fog | 19 | 98.82% | ||
| Heavy Fog | 9 | 99.17% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.Y.; Zeghid, M.; Khan, A.N.; Abd El-Mottaleb, S.A. Fuzzy Logic-Based Performance Enhancement of FSO Systems Under Adverse Weather Conditions. Photonics 2025, 12, 495. https://doi.org/10.3390/photonics12050495
Ahmed HY, Zeghid M, Khan AN, Abd El-Mottaleb SA. Fuzzy Logic-Based Performance Enhancement of FSO Systems Under Adverse Weather Conditions. Photonics. 2025; 12(5):495. https://doi.org/10.3390/photonics12050495
Chicago/Turabian StyleAhmed, Hassan Yousif, Medien Zeghid, Akhtar Nawaz Khan, and Somia A. Abd El-Mottaleb. 2025. "Fuzzy Logic-Based Performance Enhancement of FSO Systems Under Adverse Weather Conditions" Photonics 12, no. 5: 495. https://doi.org/10.3390/photonics12050495
APA StyleAhmed, H. Y., Zeghid, M., Khan, A. N., & Abd El-Mottaleb, S. A. (2025). Fuzzy Logic-Based Performance Enhancement of FSO Systems Under Adverse Weather Conditions. Photonics, 12(5), 495. https://doi.org/10.3390/photonics12050495





